网络连接数据即为包含数据点之间关联信息的网状结构数据. 1991年, CERFNet、PSINet及AlterNet商业化, 世界步入互联网时代. 随着计算机技术的发展和物联网的广泛应用, 数据的增长速度和应用范围已达到前所未有的高度. 根据思科(Cisco)的2023年全球网络趋势报告, 全球数据流量在过去5年中增长了近4倍. IDC预测到2025年将达到每年163 ZB[1]. 伴随数据量的爆炸式扩张, 数据的种类和结构也日益多元化. 不止单个人或物的属性信息被详细记录, 人与人、人与物的关联信息也被以网络结构记录下来. 常见的数据网络包括社交网络、电力网络、生物网络、病毒传播网络、道路交通网络等. 网络数据的记录为其统计分析提供有效的增量信息[2]. 例如, 在社交网络中, 对用户之间互动模式的分析, 可以深入理解社会趋势和信息传播机制[3]. 在生物信息学领域, 对网络数据的分析有助于揭示生物分子间的相互作用, 从而推动对疾病机理的理解和新药的开发[4]. 在金融领域, 对资产之间网络关系的分析, 可以更好地理解市场风险和指导投资决策[5]. 在物联网技术中, 网络分析对于提高系统效率和设备安全也至关重要.
面对如此快速增长和多样化的数据环境, 各领域的模型和方法也在迅速演变. 传统的统计模型, 如基于独立同分布假设的模型, 面临着新的挑战. 这些模型往往假设数据点之间是独立的, 但在网络连接数据中数据点之间的相互关联和依赖是核心特征. 因此需要新的分析方法来解读这些复杂的关系, 尤其是在面对网络数据的多维特征和动态关联时. 这种转变要求各领域不断创新, 开发出能够有效处理网络连接数据的新方法和技术. 网络连接数据的建模和有效利用已成为当前计算机科学、社会科学和统计学等多个领域的重点研究方向之一.
现有的网络连接模型的研究, 根据研究方向的不同, 可分为两类. 一类聚焦于识别关系数据中隐含的网络结构, 例如机器学习领域的社区检测[6], 研究了如何在复杂网络中识别出具有紧密联系的节点群组. 另一类旨在发展一般的数据分析框架以利用网络数据进行回归和预测. 网络连接数据的回归问题被关注初期, 一些学者针对某些特定情况下的网络结构加以利用, 例如自回归模型[7]及它的变体组间交互效应和组间固定效应模型[8]. 这些模型先假定网络对数据分析的影响的具体形式, 比如内生效应、外生效应或是相关效应等, 之后将研究的重点放在效应的识别上. 融合惩罚的提出为网络连接数据的统计处理提供了新的视角. 这一思想最初由Stephanie等[9]和Tibshirani等[10]引入, 旨在缩减网络分析中相互关联节点之间回归系数的差异, 被视为点估计的回归版本, 或是在贝叶斯框架中被视作马尔可夫随机场的先验回归. 基于这一理论基础, Li等[11]提出网络一致性模型, 为网络连接数据回归分析提供了一个创新而实用的框架.
针对网络连接数据的复杂性, 一个关键的任务是如何从庞大的网络数据中提取出最有意义的特征. 这不仅涉及识别数据点间的关联关系, 还要理解这些关系如何影响整体网络的行为和性质. 在这个过程中, 变量选择[12]成为一个重要的环节, 它有助于简化模型, 增强其解释性和预测能力. 例如, 在计算机科学领域许多实际应用如自然语言处理[13]、图像识别[14,15]和推荐系统[16]等都涉及大量特征, 并非所有特征都对最终任务有实质性贡献. 有效的变量选择方法能显著提高模型效率和性能, 有助于更深入地理解和利用网络结构数据. 近些年涌现了许多创新的变量选择方法, 包括了经典的前向选择、后向选择、逐步回归[17]以及基于正则化的方法, 如Lasso、岭回归和弹性网[18–20]等. 机器学习技术[21,22]也为变量选择提供了广泛思路.
在现有的网络连接数据变量选择研究中, 通常采用基于p值的方法, 但面临着明显的局限性. 这主要是因为网络连接数据通常具有高度的结构依赖性和复杂性, 传统的基于p值的变量选择方法大多建立在数据点相互独立的假设之上. 在这种情况下, p值方法无法准确反映变量之间的真实关系, 尤其是在面对高维网络数据时, 这种方法很容易导致错误的发现, 从而影响模型的准确性和可靠性.
Benjamini等[23]最早引入错误发现率(false discovery rate, FDR)的概念, 用于描述在所有选出特征中错选比例的期望. 2015年Barber等[24]提出Knockoff仿变量方法以有效地控制多重假设检验中的错误发现率(FDR), 对于避免过度发现与伪发现相关问题具有重要意义. Knockoff仿变量方法通过构建用作控制变量的独立于原始变量的仿冒变量, 模仿原始协变量的依赖结构. 通过比较原始变量与仿冒变量的表现情况, 挑选出真正与响应变量相关的特征. 为了适应因变量对协变量的任意依赖结构, Candes等[25]在一般高维非线性模型中引入Knockoff框架, 提出Model-X Knockoff方法. Fan等[26]在Model-X Knockoff模型的基础上做了改进, 将Knockoff方法拓展到协变量的联合分布未知的情况, 提出Knockoff变量选择框架下的RANK方法.
为了克服相互依赖数据无法精确计算p值这一局限性, 本文提出一种基于错误发现率控制的网络连接数据变量选择方法(NLKF). NLKF方法通过模拟原始数据的结构创建原始特征的“Knockoff特征”, 并利用网络内聚性惩罚机制, 使相互连接的节点在独立效应上趋于一致, 进而挑选出与目标变量相关的重要特征. 文章从理论和实验两方面说明本文提出的NLKF方法能够将网络连接数据变量选择的错误发现率控制在预设水平. 该方法不依赖于网络结构的先验信息, 广泛适用于网络数据分析的实际应用场景. NLKF方法在处理复杂和高维数据方面表现出色, 能够更有效地满足现代数据分析的需求.
1 具有FDR控制的网络连接数据变量选择方法在实际回归及预测问题中, 通常只有少数几个样本属性与目标变量相关. 在线性模型问题中, 意味着回归系数向量
考虑下面一个网络内聚性回归模型:
| Y=α+Xβ+ε | (1) |
其中, 截距项
无向连接图
上述模型中, 网络数据节点
| Loss(α,β)=‖ | (2) |
其中,
网络内聚性惩罚项
| {{\boldsymbol{\alpha }}^{\mathrm{T}}}{\boldsymbol{L\alpha }} = \sum\limits_{(u, v) \in E} {{{({\alpha _u} - {\alpha _v})}^2}} |
由上式可知, 网络内聚性惩罚思想, 是通过惩罚相互连接的节点之间的差异, 使得相互连接节点的独立效应
为协变量
定义1. Network-Knockoff特征. 对于网络连接数据
| \tilde {\boldsymbol{X}} = ( {{\tilde x_1}}, \cdots , {\text{ }}{\tilde x_n}) \in {R^{n \times p}} | (3) |
其中,
| {\tilde x_i}|{x_i}\sim N({\boldsymbol{C}}{x_i}, {{\boldsymbol{B}}^2}) |
| {\boldsymbol{C}} = {{\boldsymbol{I}}_p} - {\mathrm{diag}}\{ s\} {\boldsymbol{\Omega }} |
| {\boldsymbol{B}} = {(2{\mathrm{diag}}\{ s\} - {\mathrm{diag}}\{ s\} {\boldsymbol{\Omega }}{\mathrm{diag}}\{ s\} )^{1/2}} |
其中,
由上述定义可知2p维随机向量
| \left\{\begin{array}{l} cov({x_i}) = {{\mathbf{\Sigma }}_0}\;\\ cov({x_i}, {\tilde x_i}) = {{\mathbf{\Sigma }}_0}{\mathbf{C}}\; \\ cov({\tilde x_i}) = {{\boldsymbol{B}}^2} + {\boldsymbol{C}}{{\boldsymbol{\Sigma }}_0}{{\mathbf{C}}^{\mathrm{T}}} \end{array}\right. |
则
实际应用中, 一种更符合实际的情况是网络连接数据的协方差未知, 需要提前估计数据的协方差
求解式(1)中
| \hat{{\boldsymbol{\beta}} }(\lambda )=\mathrm{arg}\mathrm{min}\{\Vert ({\boldsymbol{Y}}-{\boldsymbol{\alpha}} )-{[{\boldsymbol{X}}\tilde{{\boldsymbol{X}}}]}^{{\mathrm{T}}}\hat{{\boldsymbol{b}}}{\Vert }_{2}^{2}+\mu {{\boldsymbol{\alpha}} }^{{\mathrm{T}}}{\boldsymbol{L\alpha}} +\lambda \Vert \hat{{\boldsymbol{b}}}{\Vert }_{1}\} | (4) |
其中,
| \begin{split} {{\hat {\boldsymbol{\beta}} }}(\lambda ) =& {\mathrm{argmin}}\{ ||({\boldsymbol{Y}} - {\boldsymbol{\alpha }}) - {[{\boldsymbol{X}}\;{{\tilde {\boldsymbol{X}}}}]^{\mathrm{T}}}\hat {\boldsymbol{b}}||_2^2 \\ &+\mu \sum\limits_{(u,v) \in E} {{{({\alpha _u} - {\alpha _v})}^2}} + \lambda ||\hat {\boldsymbol{b}}||{_1}\} \end{split} | (5) |
变量选择的可靠性由错误发现率和统计功效(Power)二者度量, 计算方法如下:
| {\textit{FDR}}:=E\left[\frac{\#\left\{j: \beta_j=0 \text { and } {j} \in \hat{S}\right\}}{\#\{j: j \in \hat{S}\} \vee 1}\right] | (6) |
| { Power }:=E\left[\frac{\#\left\{j: \beta_j \neq 0 \text { and } {j} \in \hat{S}\right\}}{\#\left\{j: \beta_j \neq 0\right\}}\right] | (7) |
其中, “#{j:条件}”表示满足条件的j的数量,
构造一个服从充分性和反对称性质的一般统计量
| {W_j}({[{\boldsymbol{X}}\;{{\tilde {\boldsymbol{X}}}}]_{swap\left( S \right)}}, {\boldsymbol{y}}) = {W_j}([{\boldsymbol{X}}\;{{\tilde {\boldsymbol{X}}}}], {\boldsymbol{y}}) \cdot \left\{ {\begin{array}{*{20}{l}} { + 1},&{j \notin S } \\ { - 1},&{j \in S} \end{array}} \right.{\text{ }} | (8) |
其中,
式(1)的回归系数
| {W_j} = |{{{\hat {\boldsymbol{b}}}}_j}| - |{{{\hat {\boldsymbol{b}}}}_{j + p}}|, {\text{ }}j \in \{ 1, \cdots , p\} | (9) |
将上述统计量
| T = \min\left\{ t \in \mathcal{W}:\frac{{\# \{ j:{W_j} \leqslant - t\} }}{{\# \{ j:{W_j} \geqslant t\} \vee 1}} \leqslant q\right\} | (10) |
其中,
为使FDR被更好地控制, 定义一个修正的阈值
| T_ + = \min\left\{ t \in \mathcal{W}:\frac{{1 + \# \{ j:{W_j} \leqslant - t\} }}{{\# \{ j:{W_j} \geqslant t\} \vee 1}} \leqslant q\right\} | (11) |
当上述集合是空集时, 取
由式(10)和式(11)知,
| \hat S = \{ j:{W_j} \geqslant T\} |
| {\hat S_ + } = \{ j:{W_j} \geqslant {T_ + }\} |
设置目标FDR水平为
本节从理论上证明NLKF方法对变量选择FDR的控制. 这一证明过程说明了本文方法的统计可行性, 为网络数据特征筛选的可信度提供保障.
2.1 错误发现率控制在目标水平首先, 介绍两个关键引理.
引理1. 对于任意集合
| [{\boldsymbol{X}}\;\tilde {\boldsymbol{X}}]_{swap(S)}^{\mathrm{T}}{\boldsymbol{A}}{[{\boldsymbol{X}}\;\tilde {\boldsymbol{X}}]_{swap(S)}} = {[{\boldsymbol{X}}\;\tilde {\boldsymbol{X}}]^{\mathrm{T}}}{\boldsymbol{A}}[{\boldsymbol{X}}\;\tilde {\boldsymbol{X}}] |
即为, 对于任意
引理2. 记
引理2的证明见附录A.
基于上述引理, 可给出本文关键的错误发现率控制定理及其证明如下.
定理1. FDR控制定理. 对于统计量
| E\left[\frac{{\# \{ j:{\beta _j} = 0\;{\text{and}}\;{{j}} \in \hat S\} }}{{\# \{ j:j \in \hat S\} + 1/q}}\right] < q |
其中,
| E\left[\frac{{\# \{ j:{\beta _j} = 0\;{\text{and}}\;{{j}} \in \hat S\} }}{{\# \{ j:j \in \hat S\} \vee 1}}\right] < q |
其中,
证明: 由引理2可知, 统计量
| \begin{gathered} E\left[\frac{{\# \{ j:{\beta _j} = 0\;{\mathrm{and}}\;{W_j} \leqslant - T\} }}{{1 + \# \{ j:{\beta _j} = 0\;and\;{W_j} \geqslant T\} }}\right] \\ \leqslant E\left[\frac{{\# \{ j:{\beta _j} = 0\;{\mathrm{and}}\;{W_j} \leqslant 0\} }}{{1 + \# \{ j:{\beta _j} = 0\;{\mathrm{and}}\;{W_j} \geqslant 0\} }}\right] \\ = E\left[\frac{Y}{{1 + {p_0} - Y}}\right] \leqslant 1 \\ \end{gathered} |
由于
| \begin{gathered} {\textit{FDR}} = \mathbb{E}\left[\frac{{\# \{ j:{\beta _j} = 0\;{\mathrm{and}}\;{W_j} \geqslant T\} }}{{\# \{ j:{W_j} \geqslant T\} \vee 1}}\right] \\ = E\left[\frac{{\# \{ j:{\beta _j} = 0\;{\mathrm{and}}\;{W_j} \geqslant T\} }}{{1 + \# j:{\beta _j} = 0\;{\mathrm{and}}\;{W_j} \leqslant - T}} \cdot \frac{{1 + \# \{ j:{W_j} \leqslant T\} }}{{\# \{ j:{W_j} \geqslant T\} \vee 1}}\right] \\ \leqslant E\left[\frac{{\# \{ j:{\beta _j} = 0\;{\mathrm{and}}\;{W_j} \geqslant T\} }}{{1 + \# j:{\beta _j} = 0\;{\mathrm{and}}\;{W_j} \leqslant - T}} \cdot q\right] \leqslant q \\ \end{gathered} |
定理1说明了本文方法能确保所选特征集合的FDR维持在预定的目标之内, 为变量选择的可靠性和网络数据分析的可重复性提供了保证. 由第1节可知,
定理2. 解的存在性. 对于网络内聚性回归模型, 见式(1), 网络一致性惩罚的回归系数可求解为:
| \hat {\boldsymbol{b}} = {({\hat {\boldsymbol{\beta}} ^{\mathrm{T}}}, {\hat {\tilde {\boldsymbol{\beta}} }^{\mathrm{T}}})^{\mathrm{T}}} = {[{\boldsymbol{X}}, \tilde {\boldsymbol{X}}]^{\mathrm{T}}}{\boldsymbol{A}}{[{\boldsymbol{X}}, \tilde {\boldsymbol{X}}]^{ - 1}}{[{\boldsymbol{X}}, \tilde {\boldsymbol{X}}]^{\mathrm{T}}}{\boldsymbol{AY}} |
其中,
证明: 求解模型式(1), 最小化下方损失函数:
为保证解一定存在, 使用
在实际应用中, 我们经常遇到具有内部依赖性的网络数据, 这类数据的复杂性使得传统的变量选择方法难以有效处理. 为应对这一挑战, 本文第1节提出了一种新的方法, 即网络连接数据变量选择方法(NLKF), 下文将详细阐述这一方法的具体实现流程.
为网络连接数据变量选择的
算法1. NLKF算法
输入:
输出:
1) 给定协方差矩阵
2) 根据定义1, 构造Network-Knockoff特征
3) 引入网络内聚性惩罚函数, 即式(2):
求解模型
其中,
4) for j=1 to p do:
end
5) 求阈值
6) return
当原始变量协方差结构已知时, 使用定义1构造原始特征的Network-Knockoff特征
本节主要考察使用网络连接数据仿变量方法(
模拟数据的网络结构由随机图模型生成, 共有
各个节点
设置目标错误发现率(FDR)水平为0.2. 两类方法NLKF和NCL分别借助R程序包“knockoff”和 “glmnet”实现. 用10折交叉验证的方法调优参数.
4.1 数值模拟1: 信号强度比较实验为观察信号强度的大小对实验结果的影响, 设置
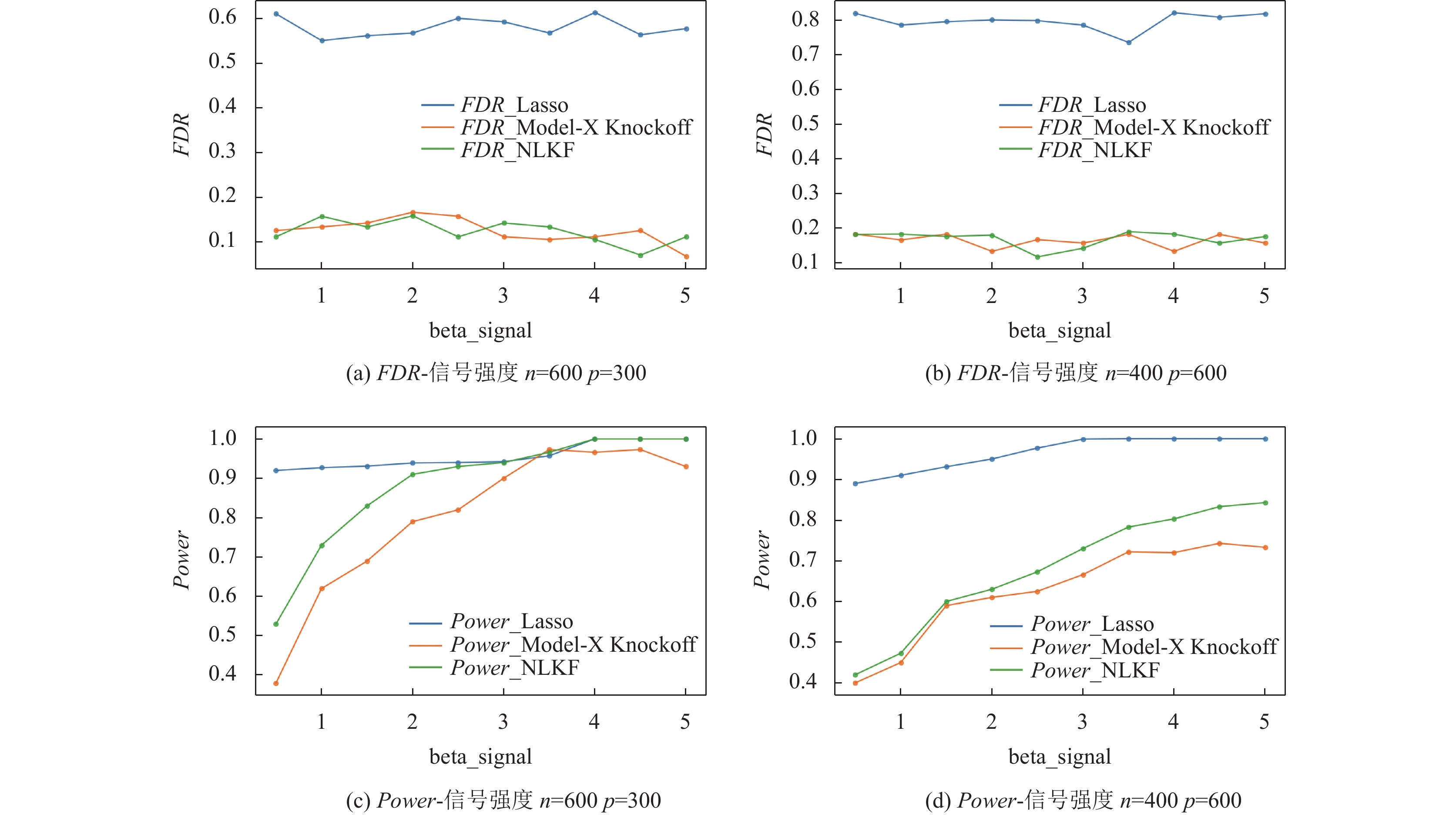
|
图 1 不同信号强度下, NLKF、Model-X Knockoff与Lasso变量选择效果图 |
实验结果可知, NLKF方法明显优于经典的Model-X Knockoff和Lasso变量选择方法. 低维弱信号强度情况下, NLKF方法的Power比Model-X Knockoff提高0.1, 且随着信号强度的增强, 二者的Power有明显提升, 且相比于Lasso方法, NLKF方法能够将FDR控制在目标水平. 高维弱信号强度情况下, NLKF方法表现与经典的Model-X Knockoff方法差别不大, 随着信号强度的增强, NLKF方法的Power明显优于Model-X Knockoff和Lasso变量选择方法.
4.2 数值模拟2:设置信号强度均值为3.5,
|
表 1 数值模拟结果1 ( |
4.3 数值模拟3: 泛化能力测试
设置信号强度均值3.5,
|
表 2 数值模拟结果2 ( |
3个数值模拟分别从不同角度验证本文方法在数据计算上的可行性、实用性和可靠性. 从模拟结果来看, 本文提出的
使用沪深两市股票的因子数据及股票所属申万一级行业构建的网络关系做实证分析. 因子是指在股票市场中, 能够解释股票收益率的一些特定因素. 常见的因子包括市场风险溢酬因子、市值因子、账面市值比因子等. 使用因子来构建投资组合的方法有很多种, 其中最常见的方法是基于因子收益率的方法. 具体来说, 首先根据投资需求制定投资目标. 然后从因子池中选择合适因子、计算单因子对个股收益率贡献、进而基于各个股票的因子表现来构建股票投资组合. 最后根据自己的需求和风险偏好, 适时调整每个因子在投资组合中的权重以适应市场变化. 其中, 能否从因子库中选出对股票收益率具有更好解释性的因子直接决定了后续投资的表现.
本文使用2022年1–12月沪深两市的4 000只A股(
对相同数据集使用Lasso变量选择方法可选出54个对当前收益率具有较强解释性的因子, 详情见附录B.
对比Lasso变量选择方法选出的54个特征,
2022年12月, 食品饮料、酒店航空等消费行业呈现了较为明显的复苏态势. 从分析结果中可以看到, 短期反转、季节反转因子、波动性因子等都是影响A股股票收益率的关键因素. 并且, 公司本身的经营状况和资产质地也是影响公司价值的重要指标, 因此流动资产比总资产、资产周转率等指标也被视为重要变量被挑选出来.
| 表 3 实证结果记录表 |
6 结论与展望
2023年2月, 《数字中国建设整体布局规划》明确提出, 到2025年基本形成横向打通、纵向贯通、协调有力的一体化格局, 数字中国建设取得重要进展. 到2035年, 数字化发展水平进入世界前列, 数字中国建设取得重大成就, 同时要把中国数字化建设方面的技术和资源大量输出到国外, 为推动全球数字化经济发展做出重要贡献. “数据”作为新时代的“关键能源”, 将成为新时代的重要生产力和发展引擎.
本文将网络连接数据的融合惩罚和Knockoff思想结合, 提出了针对网络结构数据变量选择的
| [1] |
IDC. Data age 2025: The evolution of data to life-critical don’t focus on big data; focus on the data that’s big. https://www.seagate.com/www-content/our-story/trends/files/Seagate-WP-DataAge2025-March-2017.pdf. [2023-04-20].
|
| [2] |
Sengupta S. Statistical network analysis: Past, present, and future. arXiv:2311.00122, 2023.
|
| [3] |
Saqr M, Alamro A. The role of social network analysis as a learning analytics tool in online problem based learning. BMC Medical Education, 2019, 19(1): 160. DOI:10.1186/s12909-019-1599-6 |
| [4] |
Barabási AL, Oltvai ZN. Network biology: Understanding the cell’s functional organization. Nature Reviews Genetics, 2004, 5(2): 101-113. DOI:10.1038/nrg1272 |
| [5] |
Allen F, Babus A. Networks in finance. SSRN Electronic Journal, 2008, 6(1): 383–419. [doi: 10.2139/ssrn.1094883]
|
| [6] |
Girvan M, Newman MEJ. Community structure in social and biological networks. Proceedings of the National Academy of Sciences of the United States of America, 2002, 99(12): 7821-7826. DOI:10.1073/pnas.122653799 |
| [7] |
Bramoullé Y, Djebbari H, Fortin B. Identification of peer effects through social networks. Journal of Econometrics, 2009, 150(1): 41-55. DOI:10.1016/j.jeconom.2008.12.021 |
| [8] |
Lee LF. Identification and estimation of econometric models with group interactions, contextual factors and fixed effects. Journal of Econometrics, 2007, 140(2): 333-374. DOI:10.1016/j.jeconom.2006.07.001 |
| [9] |
Stephanie RL, Friedman JH. Variable fusion: A new adaptive signal regression method. Technical Report, Pittsburgh: Department of Statistics, Carnegie Mellon University Pittsburgh, 1997.
|
| [10] |
Tibshirani R, Saunders M, Rosset S, et al. Sparsity and smoothness via the fused Lasso. Journal of the Royal Statistical Society Series B: Statistical Methodology, 2005, 67(1): 91-108. DOI:10.1111/j.1467-9868.2005.00490.x |
| [11] |
Li TX, Levina E, Zhu J. Prediction models for network-linked data. The Annals of Applied Statistics, 2019, 13(1): 132-164. DOI:10.1214/18-AOAS1205 |
| [12] |
Guyon I, Elisseeff A. An introduction to variable and feature selection. The Journal of Machine Learning Research, 2003, 3: 1157-1182. |
| [13] |
Brown PF, Cocke J, Della Pietra SA, et al. A statistical approach to machine translation. Computational Linguistics, 1990, 16(2): 79-85. |
| [14] |
LeCun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 1998, 86(11): 2278-2324. DOI:10.1109/5.726791 |
| [15] |
He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 770–778.
|
| [16] |
Cheng HT, Koc L, Harmsen J, et al. Wide & deep learning for recommender systems. Proceedings of the 1st Workshop on Deep Learning for Recommender Systems. Boston: ACM, 2016. 7–10. [doi: 10.1145/2988450.2988454]
|
| [17] |
Wang MC, Wright J, Brownlee A, et al. A comparison of approaches to stepwise regression on variables sensitivities in building simulation and analysis. Energy and Buildings, 2016, 127: 313-326. DOI:10.1016/j.enbuild.2016.05.065 |
| [18] |
Tibshirani R. Regression shrinkage and selection via the Lasso. Journal of the Royal Statistical Society: Series B (Methodological), 1996, 58(1): 267-288. DOI:10.1111/j.2517-6161.1996.tb02080.x |
| [19] |
Hoerl AE, Kennard RW. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics, 1970, 12(1): 55-67. DOI:10.1080/00401706.1970.10488634 |
| [20] |
Zou H, Hastie T. Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society Series B: Statistical Methodology, 2005, 67(2): 301-320. DOI:10.1111/j.1467-9868.2005.00503.x |
| [21] |
Ziegel ER. The elements of statistical learning. Technometrics, 2003, 45(3): 267-268. DOI:10.1198/tech.2003.s770 |
| [22] |
Deng L, Yu D. Deep learning: Methods and applications. Foundations and Trends® in Signal Processing, 2014, 7(3–4): 197-387. DOI:10.1561/2000000039 |
| [23] |
Benjamini Y, Hochberg Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. Journal of the Royal Statistical Society: Series B (Methodological), 1995, 57(1): 289-300. DOI:10.1111/j.2517-6161.1995.tb02031.x |
| [24] |
Barber RF, Candès EJ. Controlling the false discovery rate via Knockoffs. The Annals of Statistics, 2015, 43(5): 2055-2085. DOI:10.1214/15-AOS1337 |
| [25] |
Candès E, Fan YY, Janson L, et al. Panning for gold: ‘Model-X’ Knockoffs for high dimensional controlled variable selection. Journal of the Royal Statistical Society Series B: Statistical Methodology, 2018, 80(3): 551-577. DOI:10.1111/rssb.12265 |
| [26] |
Fan YY, Demirkaya E, Li GR, et al. RANK: Large-scale inference with graphical nonlinear Knockoffs. Journal of the American Statistical Association, 2020, 115(529): 362-379. DOI:10.1080/01621459.2018.1546589 |
 2024, Vol. 33
2024, Vol. 33



