化石能源如煤炭、石油等是中国的主要能源来源, 但过度使用会导致能源枯竭和环境问题^[1]. 为解决能源危机和环境问题, 实现2030年二氧化碳排放达峰和2060年碳中和的目标, 中国积极推动可再生能源的大规模发展^[2]. 风力发电是目前全球应用最广泛和最成熟的可再生能源技术之一^[3], 有广阔的发展前景和应用价值. 然而, 风力发电受多种因素影响, 给电网安全运行和实时调度带来巨大挑战^[4–6]. 因此, 准确地预测风电功率对于保障电网稳定运行, 推动智能电网建设具有重要意义^[7]. 本文旨在改进Informer预测模型, 提高对风电功率的准确预测, 为电网系统安全稳定运行提供数据支持.

风电功率预测方法主要分为物理方法、统计方法和人工智能方法3类, 其中人工智能方法由于强大的非线性拟合能力和自适应学习能力, 成为当前技术热点. 包括支持向量机 (SVM)、循环神经网络 (RNN)、长短期记忆网络 (LSTM) 和门控循环单元网络 (GRU) 等. 文献[8,9]提出遗传算法和灰狼算法对SVM中的学习参数进行优化, 提高对风电功率的预测精度. 然而, SVM及其改进模型在时序预测任务中存在计算效率低和易陷入局部最优解等问题. 文献[10]提出K-means长短期记忆神经网络对风电功率特征进行分类并建立预测模型; 文献[11]提出一种基于Copula函数和LSTM的模型, 这些方法虽然在风电预测任务中取得了一定的效果, 但也存在局限性, 如易陷入局部最优解, 无法捕获远程依赖关系. Transformer模型^[12]是基于自注意力机制的神经网络结构, 可以对输入序列中的每个元素进行均匀处理, 具有捕获远程依赖关系的潜力, 被广泛应用于时间序列预测领域^[13–15]. 文献[16]提出一种改进Transformer的多步预测模型Informer, 该模型从3个方面对Transformer模型在时序预测方面进行了针对性优化: 提出概率稀疏自注意力机制有效降低注意力计算过程中的时间复杂度; 提出蒸馏机制有效减少特征图的时间维度; 提出并行生成式解码器机制大幅提高长序列预测的效率. 风电数据存在较强时序依赖关系, 所以对于风电预测模型来讲, 捕获长距离特征可以提供更多趋势信息, 提升预测精度. Informer在捕获长序列输入信息方面拥有较强的能力, 预测性能也优于现有主流预测模型, 被逐渐应用于风电功率预测领域^[17–19], 并通过与其他模型的组合或改进, 提高了风电功率预测精度. 然而, Informer模型本身仍存在一些局限性: 首先, 概率稀疏自注意力机制虽然降低了原始注意力机制的复杂性, 但其逐点计算过程仍需要较高的计算量, 并且忽略了时间序列步长之间的语义关联; 其次, 概率稀疏自注意力过于关注全局信息而忽略了数据中的局部信息特征, 导致注意力机制在匹配查询对局部上下文不敏感的键时可能产生异常情况.

针对以上问题, 本文提出一种改进Informer的风电预测模型PCI-Informer. 该模型包含以下3点改进: 首先, 将序列数据分割为子序列级补丁作为模型输入, 补丁内部序列通过注意力计算提取特征信息, 与补丁特征进行整合, 提高了模型对序列数据的处理能力和效果; 其次, 使用多尺度因果卷积生成自注意力计算中的查询向量、键向量和值向量, 在自注意力计算中实现多尺度局部信息的融合, 解决了模型忽略序列局部特征问题; 最后, 引入反向残差前馈网络 (IRFFN), 在保持计算和参数效率的同时增强模型对局部结构信息的提取和保留能力.

为了评估PCI-Informer模型的有效性, 本文采用风电场近一年的运行数据进行实验. 试验结果表明, 与主流预测模型相比, PCI-Informer模型在不同预测步长下均取得了更好的预测效果.

1 理论基础 1.1 Informer模型

Informer模型是一种新型的基于注意力机制的Transformer模型, 旨在解决传统Transformer模型在时间序列预测中遇到的问题, 包括自注意力机制的二次时间复杂度、堆叠层导致的内存瓶颈以及缓慢的预测速度. Informer模型提出概率稀疏自注意力机制, 该机制使得时间复杂度和内存使用方面的开销达到${\rm{O}}(L\log L)$, 有效降低计算成本, 使模型在处理长序列输入时表现更加出色; 为了减少输出维度和网络参数量, 并突出主导注意力, 提出自注意力蒸馏机制, 这一机制通过对每个注意力层的输出应用正则卷积和池化操作, 将每层的输出减半, 使模型能够更加专注于关键信息, 同时减轻网络的计算负担; 提出并行生成式解码器机制, 通过一次前向计算即可输出所有预测结果, 避免误差累积, 提高时间序列预测的推理速度.

Informer的整体架构如图1所示, 架构图左侧表示编码过程, 右侧表示解码过程, 编码器通过多层概率稀疏自注意力模块处理输入序列提取特征, 解码器接收序列输入 (预测目标部分设置为0), 通过多头注意力与编码特征进行交互, 直接输出预测结果. 具体原理如下.

(1) 概率稀疏自注意力机制: Transformer的自注意力特征图是长尾分布, 突出点积会导致对映的注意力分布远离均匀分布, 根据上述原理, Informer采用KL散度 (Kullback-Leibler divergence) 度量分布距离, 相对熵越大, 则其是重要性部分的概率越大, 第i个查询向量query的稀疏性度量公式如下:

$ M\left({q}_{i}, K\right)=\mathrm{ln}\sum _{j=1}^{{L}_{K}}{\rm e}^{\frac{{q}_{i}{k}_{j}^{\rm T}}{\sqrt{d}}}-\frac{1}{{L}_{K}}\sum _{j=1}^{{L}_{K}}\frac{{q}_{i}{k}_{j}^{\rm T}}{\sqrt{d}} $

(1)

其中, 第1项是查询向量的Log-Sum-Exp (LSE); 第2项是算术平均值. 基于上述方法则得到概率稀疏自注意力计算公式如下:

$ {{attention}}(Q, K, V) = {\mathit{Softmax}}\left( {\frac{{\bar Q{K^{\rm{T}}}}}{{\sqrt d }}} \right)V $

(2)

其中, Q、K、V分别是查询向量、键向量和值向量组成的矩阵, d是防止梯度消失而增加的比例因子, Softmax是激活函数, $ \bar Q $是经过上述概率稀疏衡量方法得到的查询向量.

(2) 自注意力蒸馏机制: 在每一层使用蒸馏操作来提取主导特征, 并在下一层生成紧凑的自注意力特征图. 蒸馏过程从第j层到第j+1层的公式如下:

$ X_{j + 1}^t = {\mathit{MaxPooling}}\left( {{\mathit{ELU}}\left( {{\mathit{Conv}}1{\mathit{d}}\left( {{{\left[ {X_j^t} \right]}_{{\text{att}}}}} \right)} \right)} \right) $

(3)

其中, ${[X_j^t]_{\rm att}}$表示注意力块, Conv1d表示卷积操作, ELU为激活函数, MaxPooling为最大池化操作.

(3) 生成式解码器结构: 采用了标准的解码结构, 由两个相同的多头注意力层组成, 并通过一个前馈网络来产生预测输出. 解码器的输入向量如下:

$ {X}_{\rm feed.de }^{t}=\mathit{Concat}\left({X}_{\rm token }^{t}, {X}_{0}^{t}\right)\in {R}^{\left({L}_{\rm token }+{L}_{y}\right){d}_{\rm model }} $

(4)

其中, $ X_{\rm feed.de}^t $是解码器的第t个输入序列, $ X_{\rm token}^t $是第t个输入序列的起始令牌, $ X_0^t $是目标序列的0值占位符. 与编码器中的自注意力机制不同, 两者处理不同类型的输入数据. 编码器处理一组长期数据序列, 而解码器则处理与预测序列长度相同的序列和零值的组合, 具体如图2所示.

1.2 反向残差前馈网络 (IRFFN)

为了增强模型提取和保留局部结构信息的能力. 本文引入反向残差前馈网络处理Informer模型自注意力层的输出. 反向残差前馈网络由扩展层、深度卷积层和投影层组成: 扩展层用于增加输入通道的数量, 使用1×1的卷积核进行线性变换; 深度卷积层用于在空间维度上对输入进行局部感知, 使用3×3的深度卷积核进行非线性变换; 投影层用于减少输出通道的数量, 使用1×1的卷积核进行线性变换. 其网络结构示意图如图3所示.

首先将输入的低维特征图扩增到高维, 然后用深度卷积方式做卷积运算, 残差连接增强梯度跨层传播, 最后使用一个线性的卷积将其映射到低维空间中. 这样做可以减少参数量和计算量, 同时增强模型提取和保留局部结构信息的能力, 其公式如下:

$ {\text{IRFFN}}(X) = {{Conv}}({\mathbf{F}}({{Conv}}(X))) $

(5)

$ {\mathbf{F}}(X) = {\mathit{DWConv}}(X) + X $

(6)

其中, X为输入特征向量, F代表激活函数, Conv代表卷积层, DWConv代表深度可分离卷积层.

2 改进模型PCI-Informer 2.1 补丁机制

Informer模型的概率稀疏自注意力虽然降低了原始注意力机制的复杂性, 但其逐点计算方式仍然需要较高的计算量, 并且忽略了相邻时间步长之间的语义关联, 导致模型无法有效提取局部语义信息. 所以, 提取局部语义信息是改进Informer时序预测性能的关键.

Autoformer^[20]通过自相关建立补丁级别的联系, 但不能充分利用补丁内部的信息. Triformer^[21]提出了补丁注意力, 但其目的是降低计算复杂度而使用伪时间戳作为补丁查询, 没有将补丁作为输入单元来处理, 也没有揭示其背后的语义重要性. 本文提出一种补丁机制: 将输入序列划分为可重复的子序列级补丁, 并在补丁内部嵌入Transformer-block (由一个多头自注意力层和一个全连接层组成), 通过注意力计算挖掘补丁内部序列特征. 通过线性变换将补丁内部序列特征聚合到补丁嵌入空间, 并将其作为模型的输入, 具体如图4所示. 补丁机制带来了以下3点优势: 补丁对比单个数据具有局部语义信息, 提高模型对序列数据的处理能力和效果; 降低噪声或异常数据的影响, 提高模型鲁棒性; 减轻模型的计算负担和内存需求, 更好地处理大规模的序列数据, 提高模型的运行效率.

具体操作: 将输入序列均匀分割为若干个补丁, 每个补丁包含m个数据点.

$ {{{X}}^{{i}}} = [{x^{i, 1}}, {x^{i, 2}}, \cdots, {x^{i, m}}] $

(7)

其中, $ {{x}}^{i, j} $代表第i个补丁中的第j个数据点. 通过线性投影, 将补丁内部序列进行Embedding操作.

$ {Y^i} = [{y^{i, 1}}, {y^{i, 1}}, \cdots, {y^{i, m}}], {y^{i, j}} = FC\left( {Vec\left( {{x^{i, j}}} \right)} \right) $

(8)

其中, y表示补丁内每个数据的Embedding输出结果, FC代表全连接层 (fully connected layer), Vec表示对输入数据x进行Embedding操作. 整个计算有两个数据流, 其中一个处理补丁序列, 另一个处理每个补丁内部的序列. 对于补丁内部的序列, 使用Transformer-block通过多头自注意力和MLP来探索补丁内部的局部信息.

$ Y'^{i}_l = Y_{l - 1}^i + {\mathit{MSA}}\left( {LN\left( {Y_{l - 1}^i} \right)} \right) $

(9)

$ Y_l^i = Y_l^{\prime i} + {\mathit{MLP}}\left( {LN\left( {Y_L^i} \right)} \right) $

(10)

对于补丁级, 创建补丁Embedding来存储补丁级表示序列:

$ {Z_0} = [{\textit{z}}_0^1, {\textit{z}}_0^2, \cdots, {\textit{z}}_0^n] \in {R^{(n + 1) \times d}} $

(11)

它们都被初始化为0, 并在每一层中, 通过线性投影将补丁内部Embedding向量转换为补丁Embedding域, 并添加到补丁Embedding向量中:

$ {Z^i} = Z_0^i + FC\left( {Vec\left( {Y_l^i} \right)} \right) $

(12)

全连通层FC使维度匹配, 通过上述加法运算, 补丁的Embedding向量得到了序列级特征的增强. 最后通过Informer对补丁Embedding向量之间的关系建模:

$ Z'_l = {Z_{l - 1}} + {\mathit{MSA}}\left( {LN\left( {{Z_{l - 1}}} \right)} \right) $

(13)

$ {Z_l} = Z'_l + {\mathit{MLP}}\left( {LN\left( {Z_l^\prime } \right)} \right) $

(14)

综上所述, 整个流程可以表示为:

$ {Y_l}, {Z_l} = {\mathit{PATCH}}\left( {{Y_{l - 1}}, {Z_{l - 1}}} \right) $

(15)

2.2 多尺度因果卷积自注意力机制

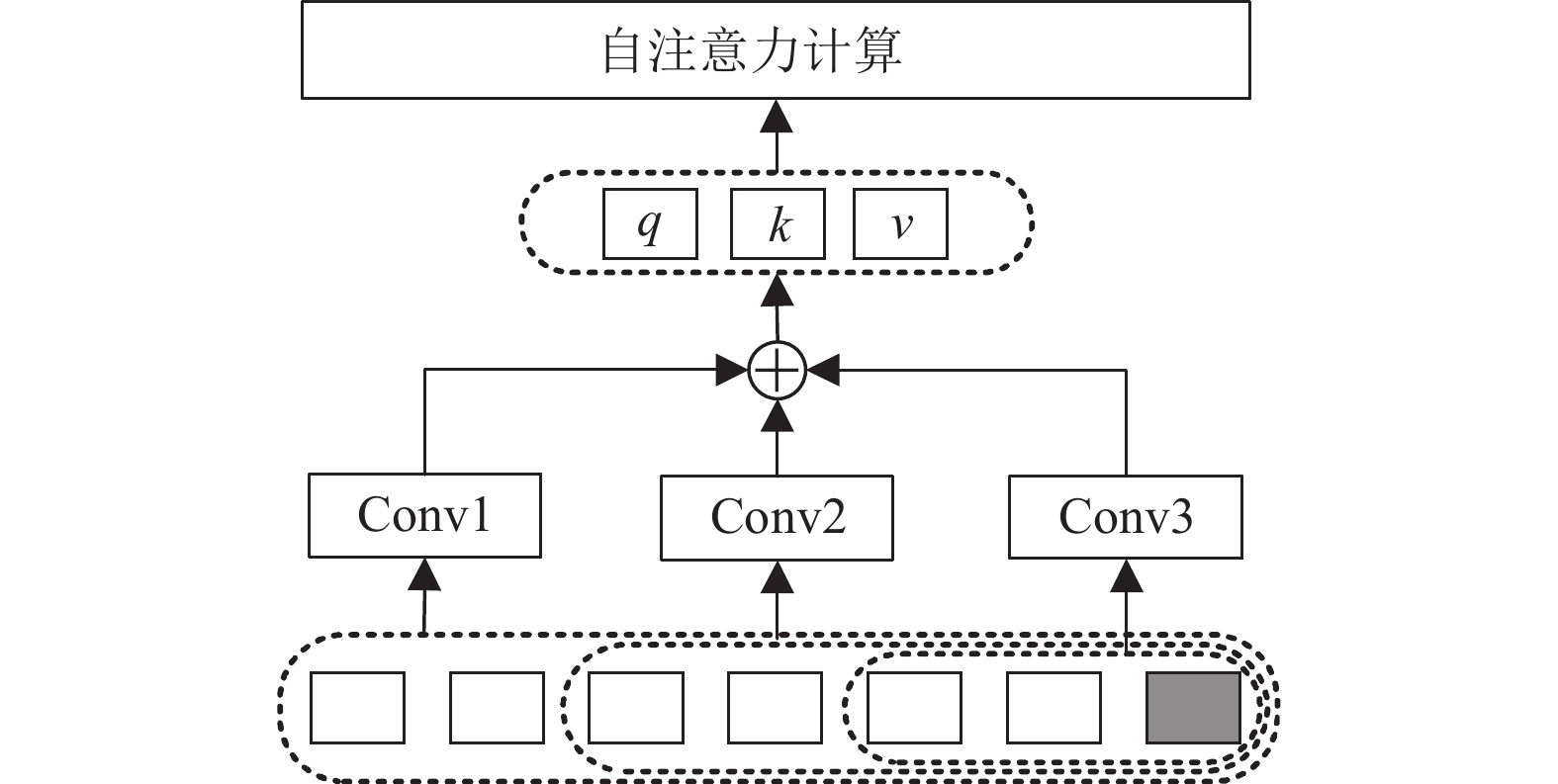
Informer模型中自注意力的计算方式导致模型过于关注全局特征信息, 忽略了数据中的局部信息特征, 导致模型对局部上下文不敏感. 为此, 本文提出多尺度因果卷积自注意力机制, 通过使用3个大小不同的因果卷积处理输入序列, 经过向量拼接融合生成自注意力计算所需的查询向量、键向量和值向量, 实现多尺度局部特征信息融合. 所提出的多尺度卷积自注意力的架构视图如图5所示.

2.3 PCI-Informer模型

风电数据存在较强的时序依赖关系, 所以对于风电预测模型来讲, 捕获长距离特征可以提供更多趋势信息, 提升预测精度. Informer在捕获长序列输入信息方面拥有较强的能力, 预测性能也优于现有主流预测模型, 然而该模型在应用于风电功率预测任务时仍存在一些问题: 首先, 概率稀疏自注意力虽然降低了原始注意力机制的复杂性, 但其逐点计算方式仍然需要较高的计算量, 并且忽略了相邻时间步长之间的语义关联, 导致模型无法有效提取局部语义信息. 其次, 模型自注意力计算机制过于关注全局特征信息, 忽略了数据中的局部特征信息, 导致模型无法准确地捕捉到局部上下文中的重要信息. 为此, 本文提出一种改进Informer的风电功率预测模型PCI-Informer. 提出补丁机制, 解决逐点计算方式忽略了时间步长之间的语义关联, 提高模型对序列数据的处理能力和效果; 采用多尺度因果卷积自注意力机制, 实现多尺度局部信息的融合, 解决了Informer模型提取局部特征信息较弱的问题; 引入反向残差前馈网络处理Informer自注意力层的输出, 在保持计算和参数效率的同时增强模型对局部结构信息的提取和保留能力. PCI-Informer模型的整体架构如图6所示. 首先对输入数据进行预处理操作, 包括缺失值处理和异常值处理等操作, 然后通过补丁机制将输入序列分成多个子序列补丁, 并通过多尺度因果卷积处理补丁序列, 生成具有多尺度局部特征信息的查询向量、键向量和值向量, 经过Informer模型的编码器和解码器处理, 最终输出预测结果.

3 实验内容 3.1 实验环境

本文的实验环境基于Windows 10操作系统, 使用Python的PyTorch库搭建模型, 计算机处理器为Intel Xeon E5-2678 v3, GPU为NVIDIA GeForce RTX 2080 Ti, 内存为32 GB DDR4.

3.2 数据预处理 3.2.1 实验数据集

本文数据集来源于“中国软件杯”大学生软件设计大赛所提供的标准数据集 (https://aistudio.baidu.com/competition/detail/887/0/introduction), 包含10个风电场一年的运行数据, 共计30万余条. 随机选取了一个风电场的数据作为实验对象, 数据时间粒度为15 min, 共34097条. 数据按照7:2:1的比例划分为训练集、测试集和验证集. 数据集特征见表1所示.

3.2.2 数据处理

(1) 缺失值处理: 风电数据存在较强的波动性和随机性. 面对数据较大范围的连续缺失情况, 选择直接丢弃; 小范围的缺失值使用线性插值补充.

(2) 异常值处理: 由于风电数据在采集和传输过程中可能受到信号干扰、设备故障或电网限制等因素影响, 导致部分数据出现异常. 这些异常数据会降低模型的预测精度, 需要在数据预处理阶段进行检测与修复. 根据风力机的数学模型, 发电量与风速的3次方成正比, 如式(16)所示.

$ P = \frac{1}{2}{C_p}\rho A{v^3} $

(16)

其中, P为发电量, ${{{C_p}}}$为风力机风能利用系数, A为叶轮扫掠面积, ρ为空气密度, v为实际风速.

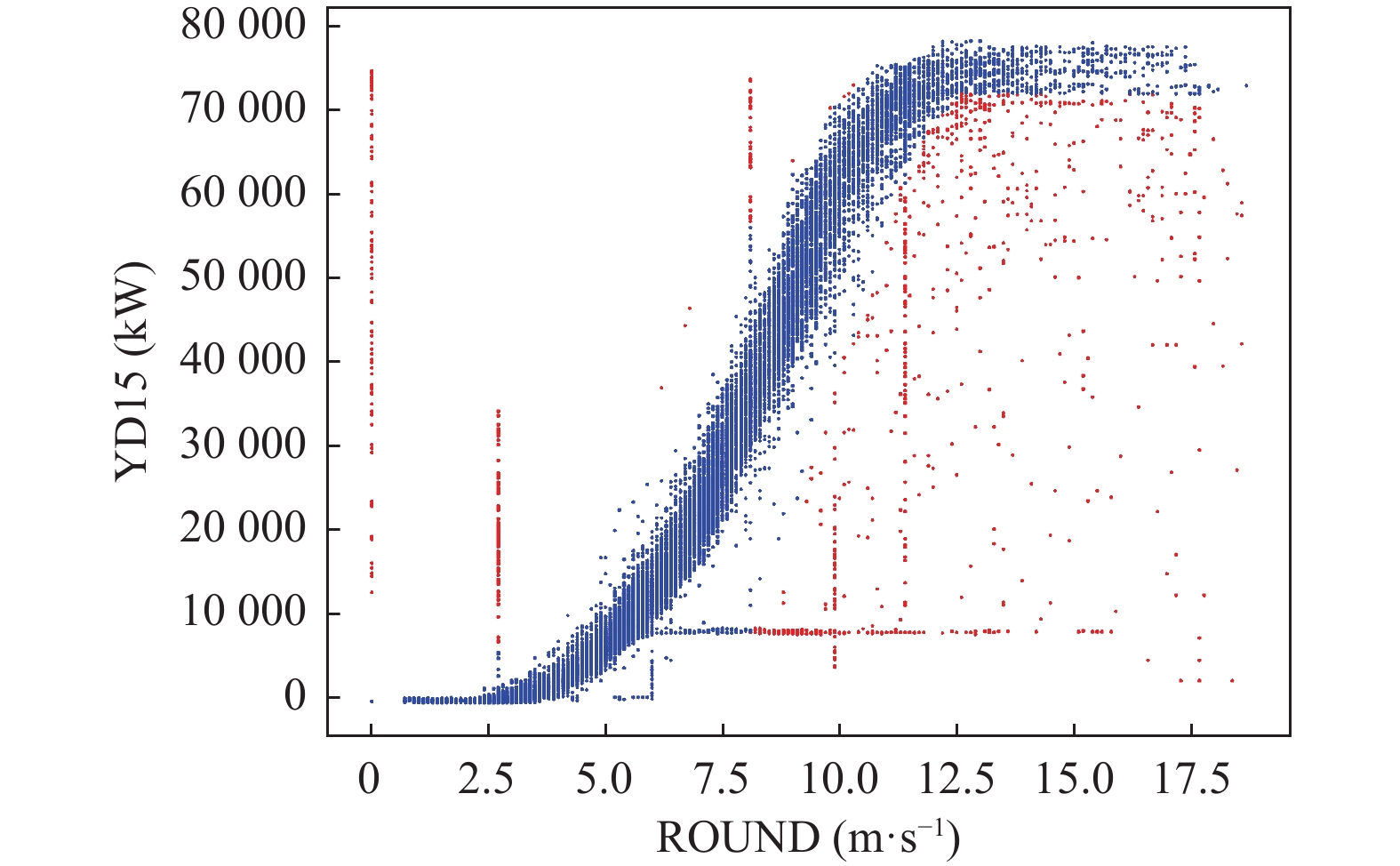
在风速-发电量的散点图上, 正常数据应呈现S形分布. 本文使用隔离森林算法^[22]识别偏离S形分布较远的异常数据点, 图7展示了异常检测结果, 其中红色点和蓝色点分别表示异常数据和正常数据. 使用风速和发电量的风力机正常数据来训练LightGBM模型^[23], 并使用该模型对异常部分进行预测修复校正. 图8展示了异常值修复结果.

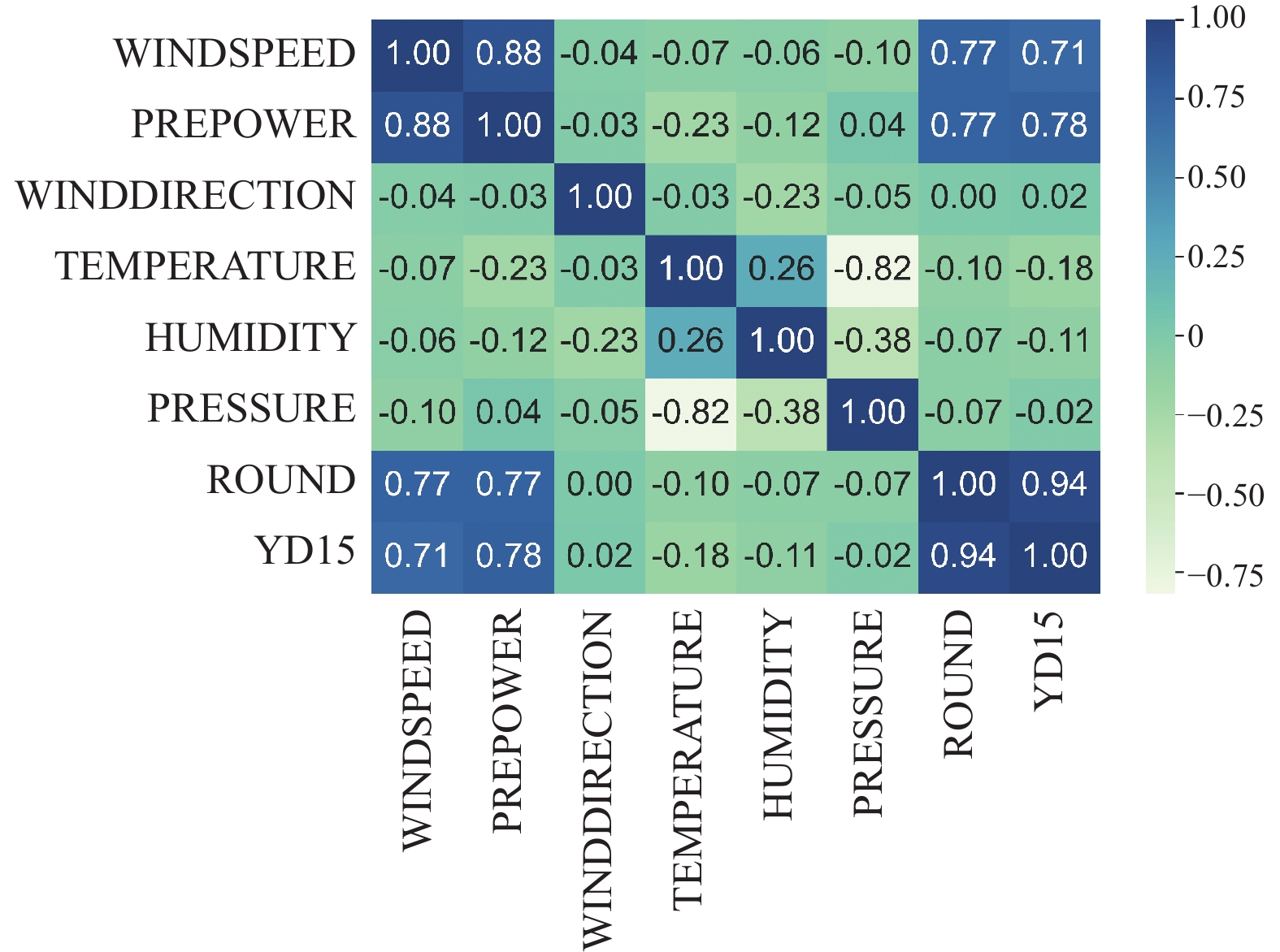
(3) 特征选择: 为了提高模型的计算效率和泛化能力, 本文从原始数据集中删除了一些不相关或多余的特征. 图9描述了所有特征的相关性矩阵, 根据特征相关性, 删除了风向和湿度两个特征, 因为它们对发电功率的影响较小, 不适合用于预测.

(4) 数据归一化: 为消除不同特征之间的量纲差异, 提高模型的收敛速度和稳定性, 对数据进行Min-Max归一化处理, 将数据的数值范围统一到[0, 1]区间, 转换公式如式(17)所示. 本文最后对预测值以及误差进行反归一化操作, 还原到实际数据值范围, 更直观地反映预测误差的实际意义和大小.

$ {x_{\rm new}} = \frac{{x - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}} $

(17)

其中, x是原始数据值, $ {x_{\min }} $是原始数据中的最小值, $ {x_{\max }} $是原始数据中的最大值.

3.3 数据分析

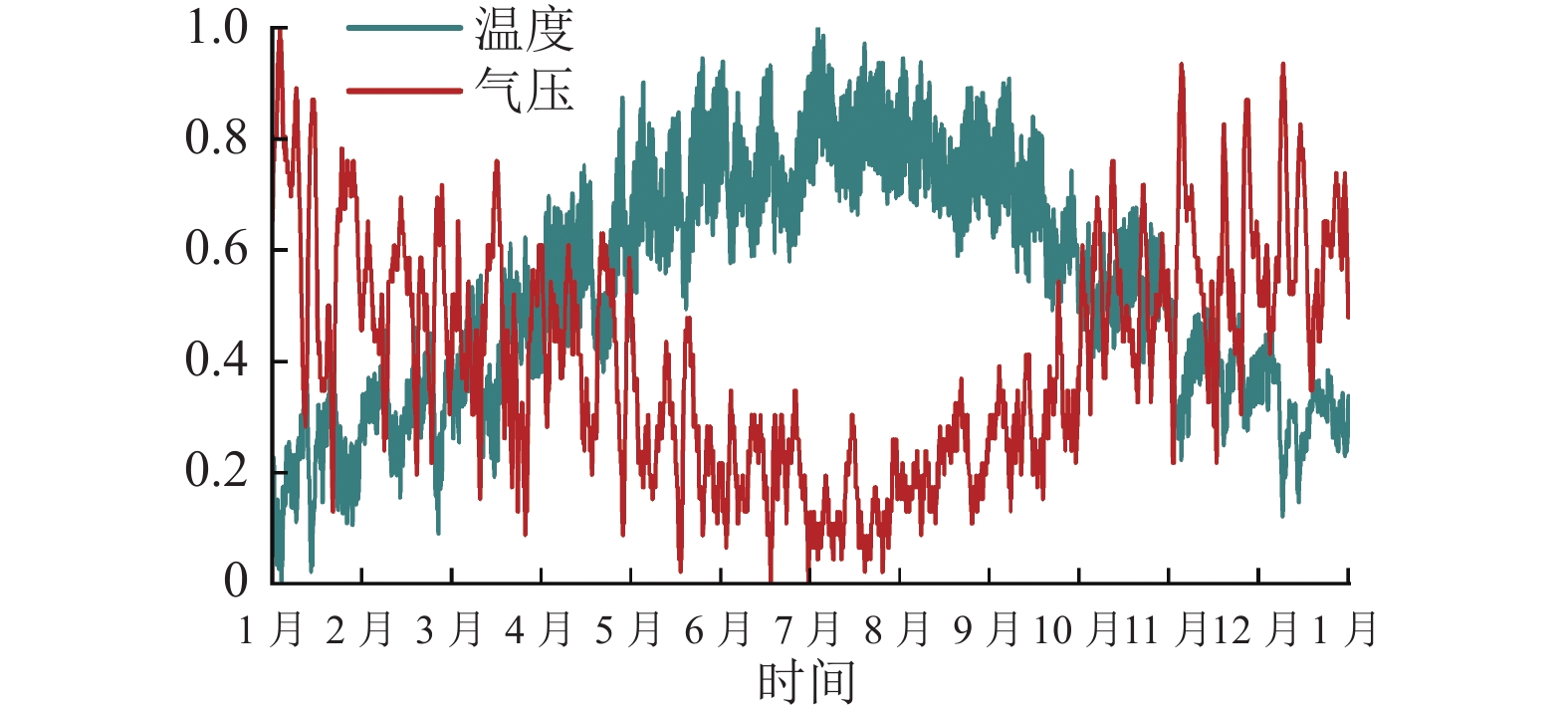
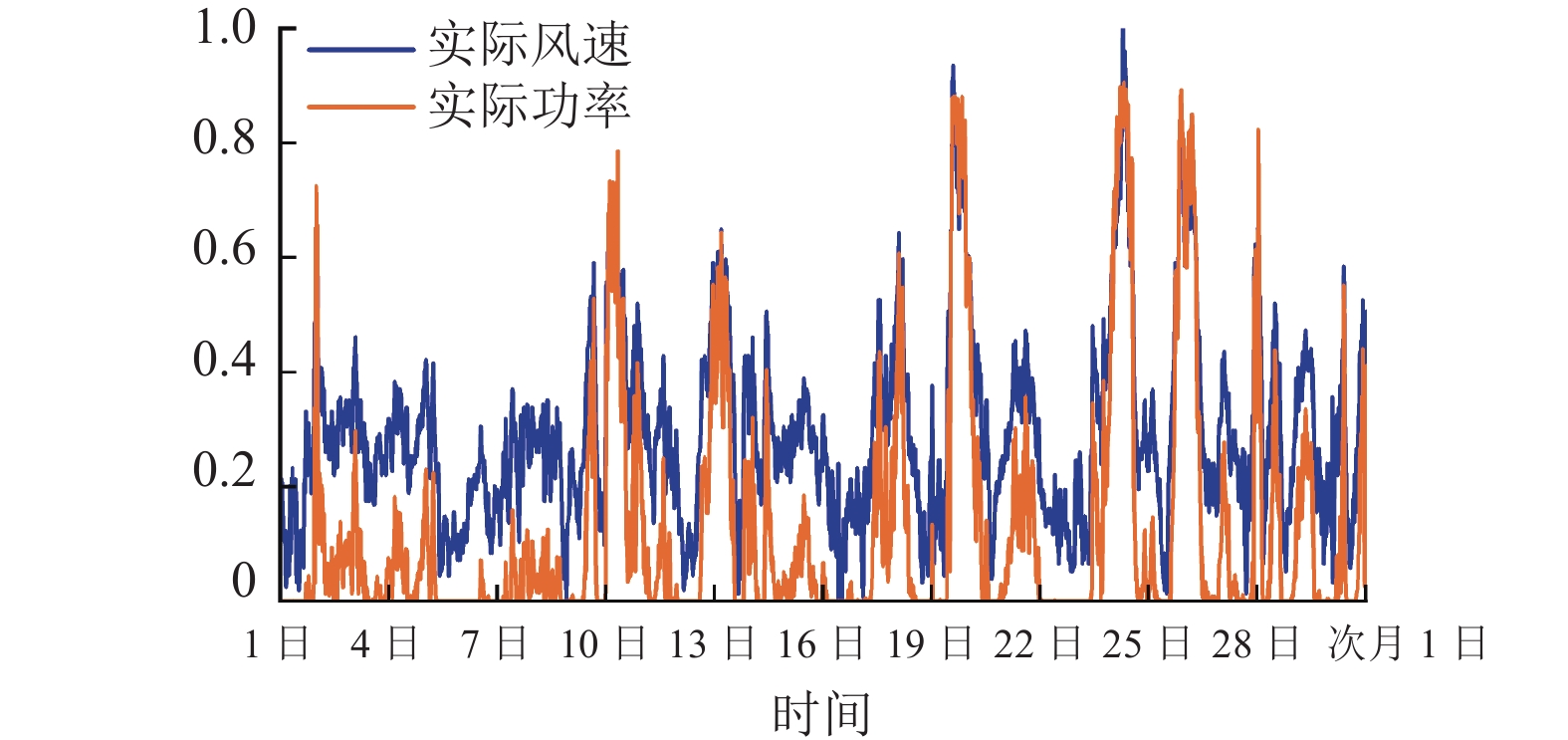
本文选取气压、温度、实际风速和实际功率4个变量, 分析风电场的数据特征. 如图10所示, 气压和温度呈现明显的季节性和长期趋势, 因此采用Informer模型进行长期特征提取, 并利用补丁机制扩大模型感受野, 以适应气压和温度特征的周期性和趋势性. 如图11所示, 实际风速和实际功率则表现出较强的随机性和间歇性, 为了学习和预测它们的瞬时变化, 利用多尺度因果卷积自注意力机制和反向残差前馈网络提高Informer模型对局部信息的提取和保留能力. 本文提出的PCI-Informer模型综合利用了数据的长期和短期特征, 以提高风电功率预测效果.

3.4 评价指标

本文各算法预测性能采用均方根误差 (root mean square error, RMSE) 和平均绝对误差 (mean absolute error, MAE) 进行评估. 公式如下:

$ {\epsilon }_{\rm RMSE}=\sqrt{\frac{1}{n}\sum _{i=1}^{n}{\left({p}_{i}-{p}'_{i}\right)}^{2}} $

(18)

$ {\epsilon }_{\rm MAE}=\frac{1}{n}\sum _{i=1}^{n}|{p}_{i}-{p}'_{i}| $

(19)

其中, $ {p_i} $代表风电功率预测值; $ p'_i $代表风电功率实际值.

3.5 对比试验

PCI-Informer模型的超参数设置见表2.

3.5.1 预测性能结果分析

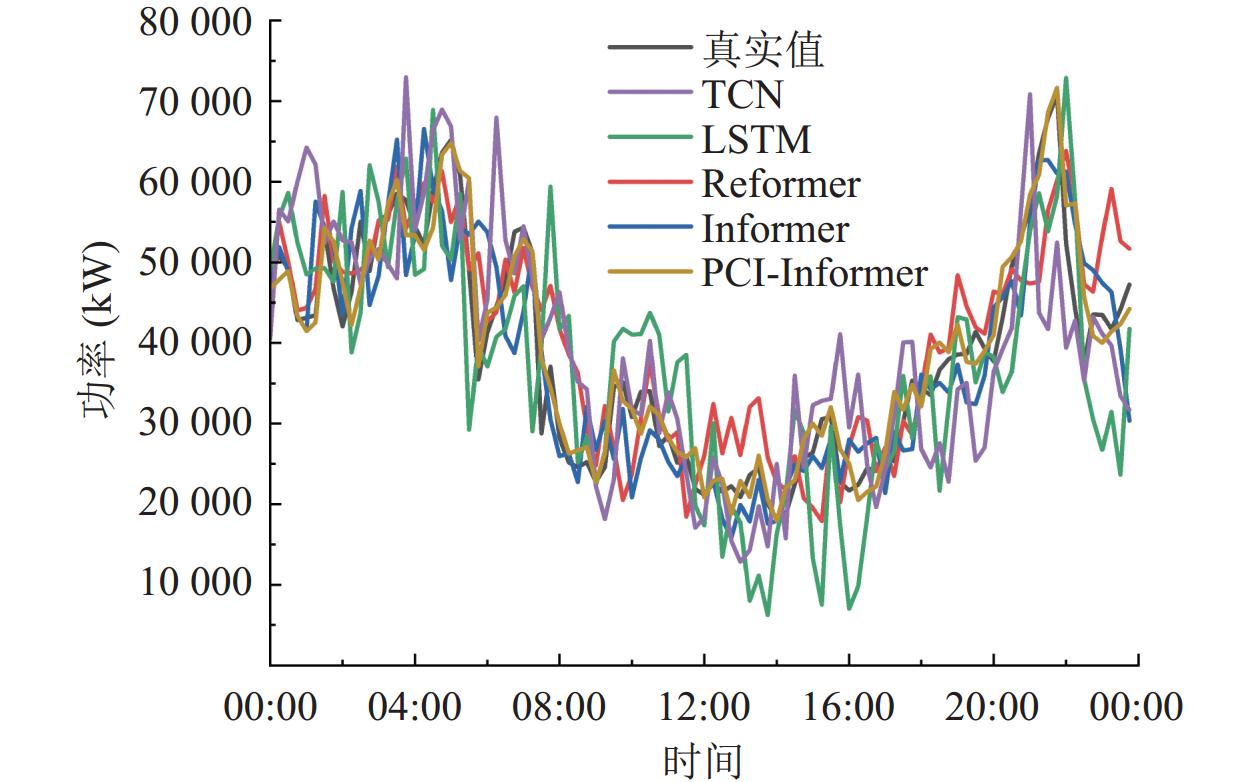
表3展示了PCI-Informer与其他4种预测模型 (Informer、Reformer、TCN和LSTM)在不同预测步长下的预测性能比较. 从表4可以看出, 在预测长度分别为48、96和192时, PCI-Informer模型在各项指标上都明显优于其他模型, 证明该模型具有更高的预测精度. 与Informer相比, PCI-Informer模型利用补丁机制、卷积操作和反向残差前馈网络, 增加了模型的鲁棒性、感受野和特征多样性, 更好的结构信息提取和保留能力, 在多步预测过程中取得了更好的效果. PCI-Informer模型相比于Informer模型, 在MAE上分别降低了9.16% (48)、10.99% (96)、13.09% (192). 图12展示了各模型在某日00:00–23:45时段内对实际功率的预测结果.

3.5.2 消融实验分析

本节内容主要围绕PCI-Informer模型的消融研究展开对不同结构模型进行了比较和分析. 消融实验中, 在PCI-Informer模型结构的基础上, 将去除反向残差前馈网络的模型命名为PC-Informer, 去除反向残差前馈网络和多尺度因果卷积自注意力机制的模型命名为P-Informer. 表4给出了PCI-Informer、PC-Informer、P-Informer和Informer模型在不同预测步长下的性能对比结果. 从表4中可以看出, 相较于Informer模型, 加入补丁机制、多尺度因果卷积自注意力机制和反向残差前馈网络的模型性能都有明显提升. 这说明: 补丁机制提高模型对序列数据的处理能力和效果, 从而提高预测准确性; 多尺度因果卷积使自注意力计算实现多尺度局部信息的融合, 改善了模型局部特征提取能力较弱的问题; 反向残差前馈网络可以增强模型提取和保留局部结构信息的能力. 将这些网络结构融合到Informer模型中, 形成PCI-Informer模型, 结果表明, 在不同预测步长下都取得了最好的效果. 这说明了各个网络结构之间的协同作用, 可以相互补充优势, 提高模型的性能. 相较于其他模型, 在风电功率预测任务中具有更好的性能.

4 结论

本文针对风电功率预测这一具有挑战性的任务, 提出了一种改进Informer的风电预测模型PCI-Informer. 使用某风电场风电数据进行实验验证, 并与其他4种主流预测模型 (Informer、Reformer、TCN和LSTM) 进行比较. 结果表明: 补丁机制将数据分割为子序列级补丁并进行特征提取和整合, 能够提高模型对序列数据的处理能力和效果, 同时减轻计算负担, 提升模型鲁棒性; 采用多尺度因果卷积自注意力机制, 能够更好地捕捉风电数据的局部特征信息, 减小模型预测误差; 反向残差前馈网络使模型在保持计算量和参数效率的同时增强了局部特征信息的提取和保留能力. 本文所提出的模型为风电预测提供了一种有效的方法, 为电力系统的稳定运行提供了技术支持. 未来工作将进一步优化模型结构和参数, 研究风力涡轮机的空间分布, 以及涡轮机内部状态等因素对风电功率的影响, 使模型更好地提取时序数据的底层特征, 提升预测精度.