永磁同步电机(permanent magnet synchronous motor, PMSM)因其高功率密度和稳定性, 在机器人、船舶、新能源汽车以及航空航天等领域得到了广泛应用[1–4]. 尽管如此, 由于其内部模型的复杂性, 精确地控制PMSM的运转速度仍然是一个技术难题[5].
PID控制器因其简洁和易操作的特性, 在实际应用中得到广泛使用, 但参数调整仍是个挑战, 不恰当的参数配置可能会引起系统的不稳定或震荡. 众多的研究已经探索如何通过集成智能控制技术来增强PID的性能. Ab Ghani等人[6]研究通过融合模糊控制优化PID, 提高了控制效果和抗干扰性. Quang等人[7]进行的研究将多层感知器神经网络用于PID自整定, 展现出良好的鲁棒性和适应性. 在Sanatel等人的研究中[8], 针对非线性系统的轨迹跟踪控制问题, 将长短期记忆网络(LSTM)应用于PID控制器的参数更新中, 利用LSTM对PID控制器的
近年来随着人工智能领域的飞速进展, 深度强化学习作为其核心子领域受到了广大关注. 这种技术主要通过让代理与环境互动, 从数据中学习并优化决策策略. PID控制参数的调整被视为黑盒优化问题, 深度强化学习为PID参数整定提供了新方向[9]. Shi等人[10]使用Q-learning的自适应PID控制器调整控制增益, 但其不适用于连续状态-动作空间. Liao等人[11]则结合Actor-Critic算法和增量式PID, 用BP神经网络近似策略与价值函数, 取得良好性能, 但由于计算延迟问题, 无法做到实时调整. Lu等人[12]利用DDPG的PID策略实时补偿PID参数, 但DDPG对超参数敏感, 并易过估计值函数. Fujimoto等人[13]提出了TD3算法, 引入了双Q网络(twin Q-networks)的概念, 对两个Q网络的预测取最小值来抑制过估计. 由于TD3算法的优越性, Shi等人[14]将TD3算法与PID控制结合, 实现PID参数的动态整定. 为了改进DDPG算法的稳定性, TD3在策略网络的输出上添加噪声以鼓励探索. 然而, 由于噪声的加入, 算法有时会对状态或动作的边界进行过度探索, 尤其是在动作空间有限制的情境下, 导致出现局部最优解.
本文以永磁同步电机作为研究对象, 使用改进的TD3算法对电机的PID控制器的参数进行自整定, 本文针对电机速度控制的时序特征, 在Actor网络和Critic网络中引入BiLSTM以实现对状态序列的双向分析, 从而使网络能够综合考虑历史和未来信息, 显著提高控制策略的精确性和鲁棒性. 此外, 研究还提出一种结合熵正则化和好奇心驱动的探索策略来加强探索能力. 通过引入熵正则化保持一定的探索性, 从而避免过早地收敛到一个确定性的策略, 并利用好奇心驱动的内在奖励机制来激励代理探索环境中未知的状态空间. 为了验证所提方法的有效性, 研究构建了永磁同步电机的仿真模型, 并将改进后的TD3算法、传统的TD3算法以及Z-N方法自整定PID参数进行了比较, 实验结果证明, 本研究提出的方法不仅提升了探索能力, 还能够以更稳定、更高效的工作方式寻找到最佳控制策略, 确保永磁同步电机的最优运行.
1 永磁同步电机模型分析永磁同步电机的速度控制系统采用双闭环设计, 其中内环为电流环主要用于对电流的控制, 外环为速度环专注于对速度的控制[15]. 永磁同步电机系统框架如下图所示. 在此系统中, 速度环通过PID控制器来调节电机速度, 输入参考速度
(1)电机定子绕组的三相在空间上对称分布.
(2)空间磁场呈正弦分布.
(3)不计磁滞和涡流损耗.
(4)忽略铁心饱和.
(5)忽略齿槽转矩及其他扰动影响.
根据上述的假设, 通常选择同步旋转坐标系D-Q下,
| {ud=Rid+Ldddtid−ωeLeiquq=Riq+Lqddtiq+ωe(Ldid+ψf) | (1) |
其中,
电磁转矩方程可以写为:
| Te=32pniq[id(Ld−Lq)+ψf] | (2) |
电机机械运动方程表示为:
| Jdωmdt=Te−TL−Bωm | (3) |
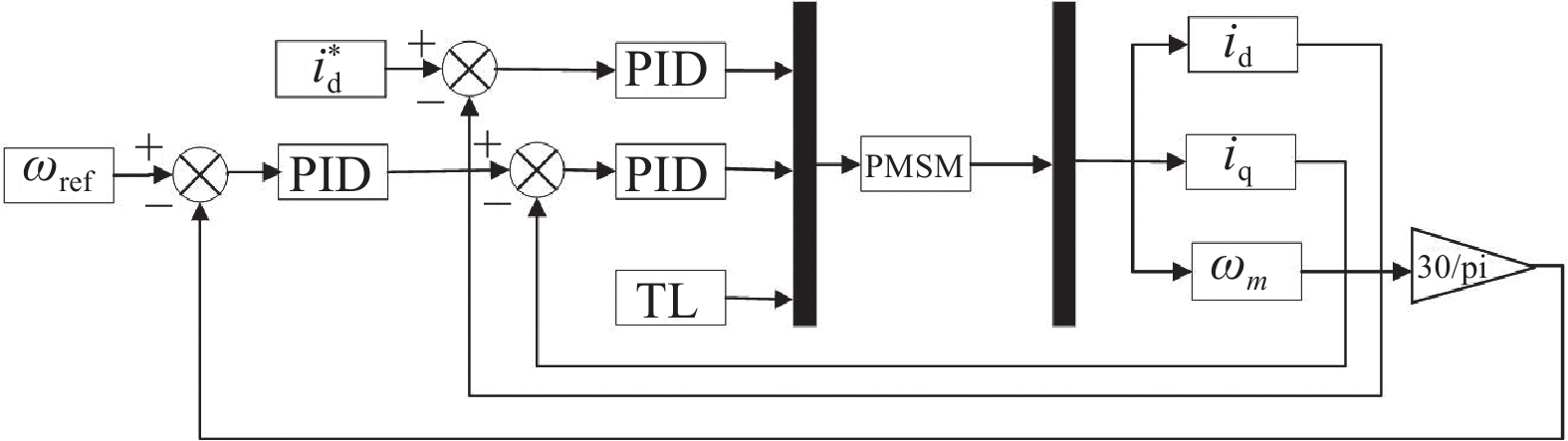
电机参数如表1所示. 永磁同步电机控制原理图如图1所示, 其中30/pi为角速度至转速的转换操作.
| 表 1 永磁同步电机参数 |
|
图 1 基于PID控制的永磁同步电机结构图 |
2 PID控制与深度强化学习 2.1 PID控制
PID控制器之所以被称为PID控制器, 是因为它的输出是3个变量的总和: 比例项
| u(t)=KP×e(t)+KI×∫t0e(t)dt+KD×de(t)dt | (4) |
强化学习(reinforcement learning, RL)是机器学习的一个分支, 核心思想在于学习如何采取最佳的行动策略, 使得智能体在与环境的交互中能够获得最大的累积奖励
| R(t)=T∑t=0γtrt+1,γ∈(0,1] | (5) |
其中,
为了更好地描述和解决强化学习问题, 通常将强化学习问题表示为马尔可夫决策过程(Markov decision process, MDP), 其中
策略(policy)定义了在给定状态下智能体应该采取的动作的概率. 具体来说, 策略通常表示为:
| π(a∣s)=P(At=a∣St=s) | (6) |
为了评估策略的好坏, 引入状态价值函数
| {Vπ(s)=Eπ(Rt+1+γVπ(St+1)∣St=s)Qπ(s,a)=Eπ(Rt+1+γQπ(St+1,At+1)∣St=s,At=a) | (7) |
TD3算法也是Actor-Critic (AC)框架下的一种确定性深度强化学习算法, 它结合了深度确定性策略梯度算法和双重Q学习, 主要是在DDPG算法的基础上提出了3个关键技术[18].
(1)双重网络 (double network): 采用两个Critic网络, 计算目标值时取二者中的较小值, 从而抑制网络过估计问题.
(2)目标策略平滑正则化 (target policy smoothing regularization): 计算目标值时, 在下一个状态的动作上加入扰动, 从而使得价值评估更准确.
(3)延迟更新 (delayed update): Critic网络更新多次后, 再更新Actor网络, 从而保证Actor网络的训练更加稳定.
为了计算期望的未来奖励, 首先使用Actor目标网络估算下一个状态
| a′=μ′(s′∣θμ′) | (8) |
为了增加算法的探索性, 在动作上加上噪声:
| a′=a′+ε(ε∼clip(N(0,σ),−c,c)) | (9) |
TD3算法使用两个Critic目标网络来估算动作的Q值. 为了避免过度估计, 选择两者中的最小值作为目标Q值.
| y=r+γmini=1,2Q′i(s′,a′∣θQ′i) | (10) |
然后利用梯度下降算法最小化评估值和目标值之间的误差
| Lci=(Qi(s,a∣θQ′i)−y)2(i=1,2) | (11) |
在Critic1和Critic2网络更新d步之后, Actor网络更新. 首先利用Actor网络计算出状态
| anew=μ(s∣θμ) | (12) |
然后利用Critic1或者Critic2网络来计算状态动作对
| qnew=Q1(s,anew∣θQ1) | (13) |
最后, 为了确保学习的稳定性, TD3采用了“软更新”的策略, 使用一个小的权重因子
| θQ′i=τθQ′i+(1−τ)θQ′i(i=1,2) | (14) |
| θμ′=τθμ+(1−τ)θμ′ | (15) |
PMSM的控制涉及对时间序列数据的处理, 其中电机的当前状态不仅取决于当前的输入, 还受到过去状态的影响. 本文在传统的TD3算法中将BiLSTM引入Actor网络和Critic网络, 能有效处理这种时间序列数据, 同时还引入了好奇心和熵正则化的联合探索策略, 本文提出的BiLSTM-TD3-ICE算法自整定PID参数的整体框架图如图2所示.

|
图 2 改进的TD3-PID整体框架图 |
3.2 状态、动作、奖励函数定义
本文将永磁同步电机的速度环控制问题表述为MDP模型, 对环境的状态空间、动作空间和奖励函数进行设置, 旨在提高电机的抗干扰能力和跟踪精度.
状态空间包括电机的实际运行速度
| st={ωt,et,KP,KI} | (16) |
动作空间定义为PID参数, 即比例增益
| a={KP,KI} | (17) |
奖励函数综合考虑了速度误差、电机的健康状态和温度. 这样的设计不仅可以最小化速度误差, 而且可以保持电机在一个良好的健康状态. 具体来说, 奖励计算包含以下部分.
(1)速度误差(
| et=ωref−ωt | (18) |
(2)电机健康状态(health): 该参数反映了电机的健康状态, 考虑电机健康状况超出特定阈值时的影响, 其惩罚值(
| HP=(1.0−h)×0.1 | (19) |
其中, h表示电机的健康状况, 是一个介于0–1之间的值, 其中0代表最差的健康状态, 而1代表最佳的健康状态. 若温度超过特定阈值, h值会相应减少, 模拟电机因高温而逐渐损坏. 这一机制确保了强化学习算法在优化控制策略时, 同时考虑电机的长期健康.
(3)电机温度(temperature): 表示电机在每个时间步的实时温度. 电机温度惩罚(
| TP=|Tactual−Tideal| | (20) |
综合这些误差项, 得到综合误差:
| μ=0.9×|e(t)| + 0.1×|u(t)|−HP + TP | (21) |
最终奖励使用以下方程计算:
| reward = exp(−12(μσ)2) + 0.01×r | (22) |
其中,
双向长短时记忆网络 (bidirectional long short-term memory), 简称BiLSTM, 是一种特殊类型的循环神经网络(RNN), 它集成了长短时记忆网络(LSTM)的能力和双向网络结构的优势[19]. 因此BiLSTM结合了正向和反向两个方向的数据流, 使得模型不仅能学习到从过去到未来的时序信息, 也能从未来到过去的信息中学习, 这使其在处理需要双向上下文的复杂序列任务时表现出色. 在使用PID控制器对永磁同步电机(PMSM)的速度进行控制时, 需要综合考虑电机的过去和未来运行状态及性能指标, LSTM可能无法充分利用未来的信息来调整参数, 而BiLSTM通过其双向学习机制, 在预测控制器的响应和优化参数时更为有效. 本研究将BiLSTM融合TD3的Actor网络和Critic网络中, 构建了如图3所示的BiLSTM-Actor和如图4所示BiLSTM-Critic网络架构. 在BiLSTM-Actor网络中设置多个批量标准化层, 每个层都对应一个时间步的输入

|
图 3 BiLSTM-Actor |
3.4 基于好奇心和熵正则化的联合探索策略
为了促进更强大和多元化的探索, 本文引入了一个基于好奇心和熵正则化的联合探索策略. 这种方法结合了两种策略来鼓励代理更多地探索环境.
(1)基于好奇心的探索
本文设计了一个额外的神经网络来预测下一个状态, 并根据其预测误差来产生一个“好奇心奖励”[20]. 这种奖励机制可以鼓励代理更多地探索环境. 内在奖励信号
| rc = β⋅||st+1−ˆst+1||2 | (23) |
其中,
(2)熵正则化
本文还引入了熵正则化来鼓励策略保持一个高熵, 这可以避免策略过早地收敛到一个确定性策略. 熵正则化定义如下:
| E=−α⋅∑p(a∣s)⋅logp(a∣s) | (24) |
其中,
在本文策略的实现中, 好奇心奖励和熵正则化项是联合使用的, 它们一起工作来指导代理的探索策略. 具体来说, 将好奇心奖励添加到奖励环境中, 以鼓励代理去探索之前未探索的状态空间. 同时, 还在策略优化过程中加入了熵正则化项, 来鼓励策略保持一定的探索性. 因此, 本文总奖励函数可以表示为:
| rtotal=reward+rc−α⋅E | (25) |
通过这种方式, 本文提出的策略不仅可以更好地探索环境, 而且还可以避免过早地收敛到一个确定性策略, 从而在学习过程中保持一定的多样性.
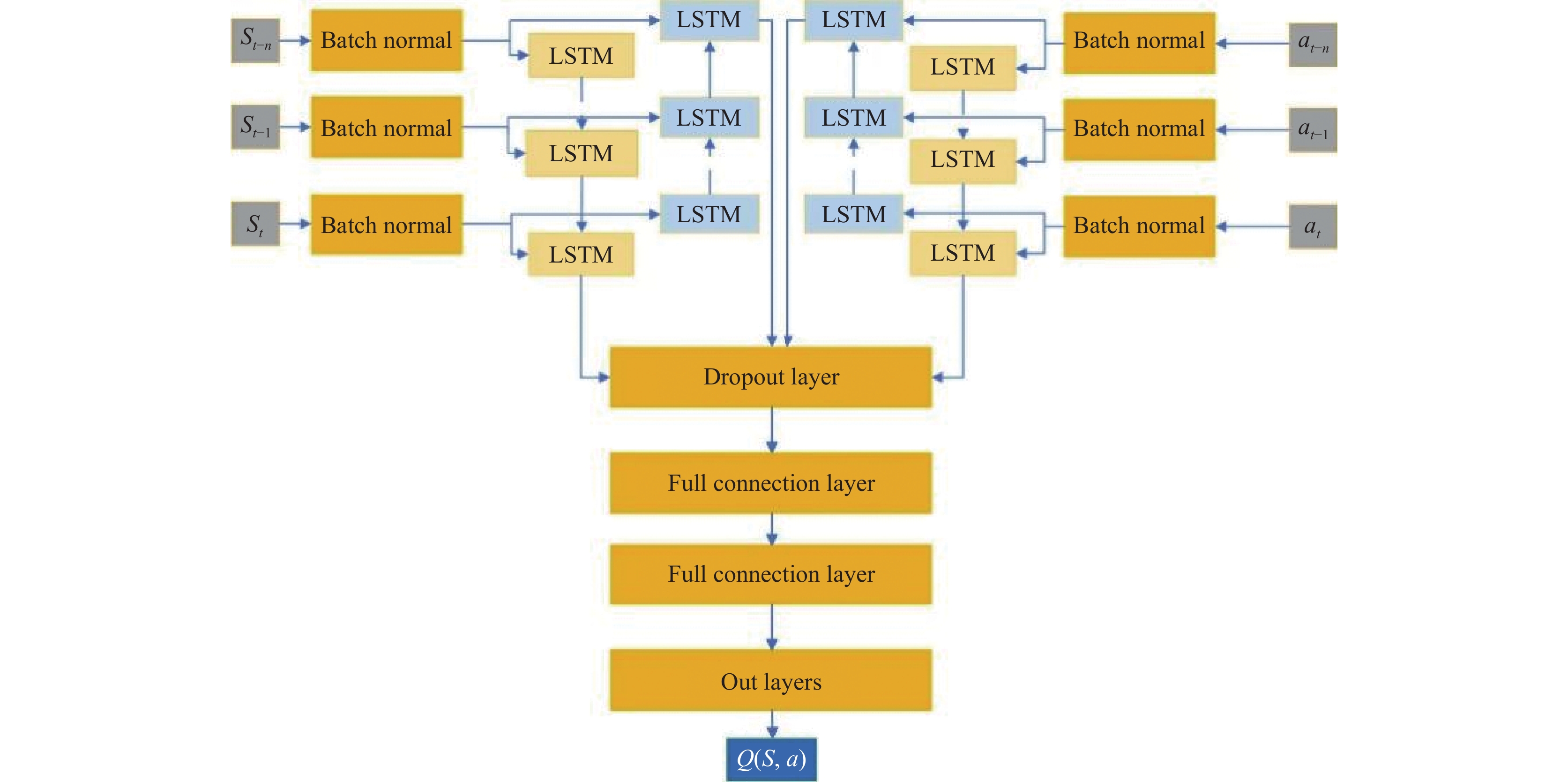
|
图 4 BiLSTM-Critic |
4 实验及结果分析 4.1 实验配置
本文基于PyTorch平台构建了一个永磁同步电机PID控制的仿真环境, 实验中使用了经典的Ziegler-Nichols (Z-N)方法、标准的TD3算法, 以及本研究新提出的BiLSTM-TD3-ICE算法进行比较分析. 本文在不同的参考速度情形下进行了测试, 包括固定速度的空载启动、加入扰动后的空载启动, 以及正弦波和方波参考速度跟踪. 动作空间范围为
本文的分析基于不同时间步的奖励分析来比较两种算法的性能和效率. 对比TD3算法与BiLSTM-TD3-ICE算法训练的奖励图如图5所示.
| 表 2 BiLSTM-TD3-ICE算法训练参数 |
在实验的早期阶段, TD3算法出现了显著的奖励波动, 这反映了其在进行广泛状态探索时的不稳定性. 该现象是由于TD3算法在探索过程中尝试了多种策略以理解环境动态, 导致在某些策略下经历了奖励的下降. 相比之下, BiLSTM-TD3-ICE算法表现出更加优秀的探索行为和较快的学习速度, 这得益于BiLSTM网络的能力在处理时间序列数据方面的优势, 以及结合好奇心激励和熵正则化的探索策略. 随着训练进入中期和后期阶段, TD3算法虽然开始展现出一定的学习进步和稳定性, 但相比之下, BiLSTM-TD3-ICE算法在保持较高奖励水平方面显示了更为显著的稳定性和快速的收敛速度. 总的来说, BiLSTM-TD3-ICE算法在学习效率、稳定性以及收敛速度方面相较于标准TD3算法具有显著的优势, 这些特点使其在处理需要理解和适应长期依赖性信息的复杂环境中有更大优势.

|
图 5 奖励对比图 |
4.2.2 跟踪速度实验对比分析
在永磁同步电机的速度跟踪实验中, 设定了4组实验分别为无干扰下的固定速度1500 rad/s, 在0.2 s处产生扰动的固定速度、转速设置为正弦函数
对于无干扰下的固定速度的实验如图6所示, 与Z-N法和传统的TD3算法相比, 本文提出的方法能够迅速并准确地跟踪命令信号, 显示出较高的响应速度以及更小的超调量.

|
图 6 无干扰速度跟踪实验对比图 |
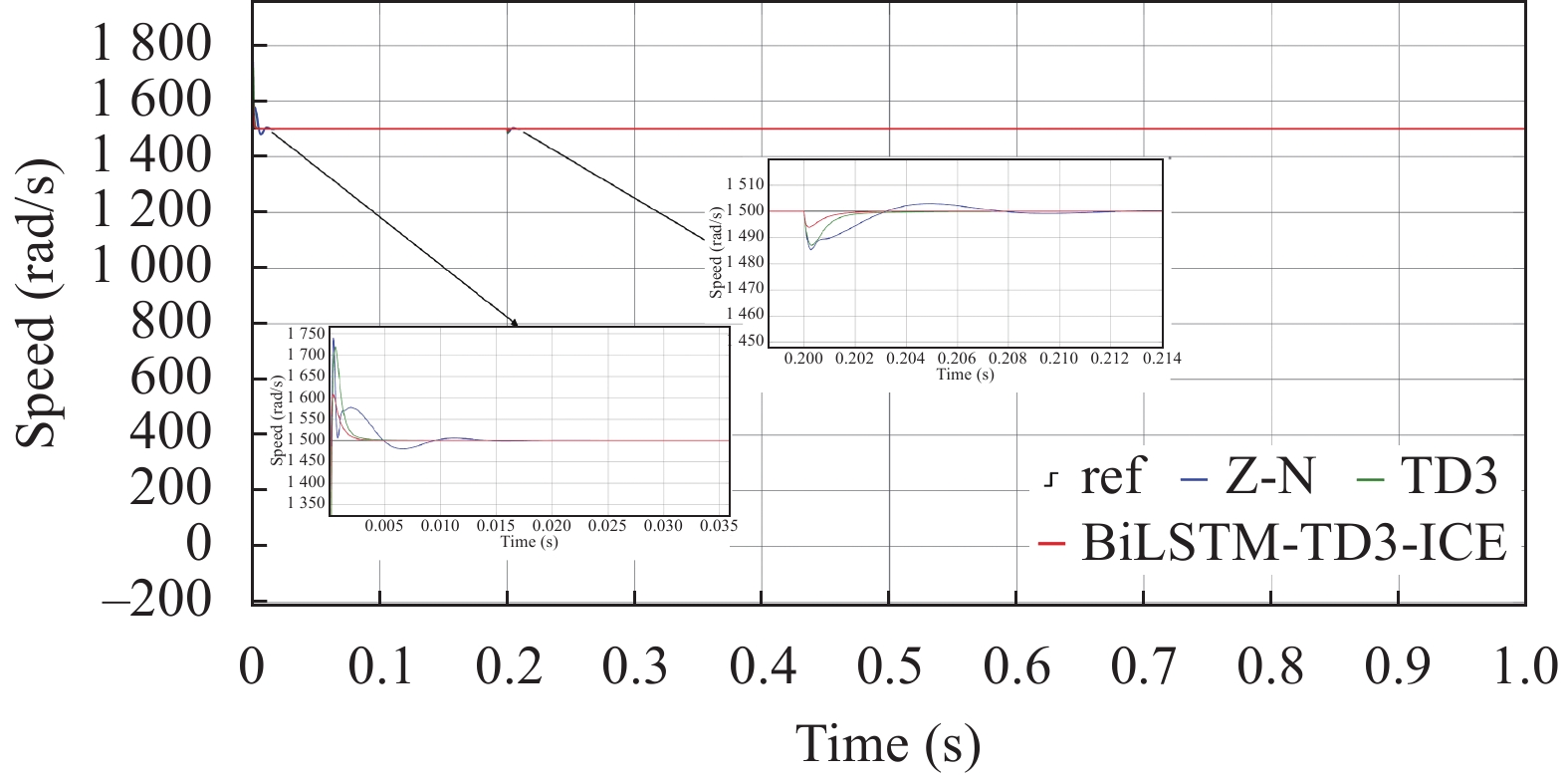
当在
|
图 7 有干扰速度跟踪实验对比图 |
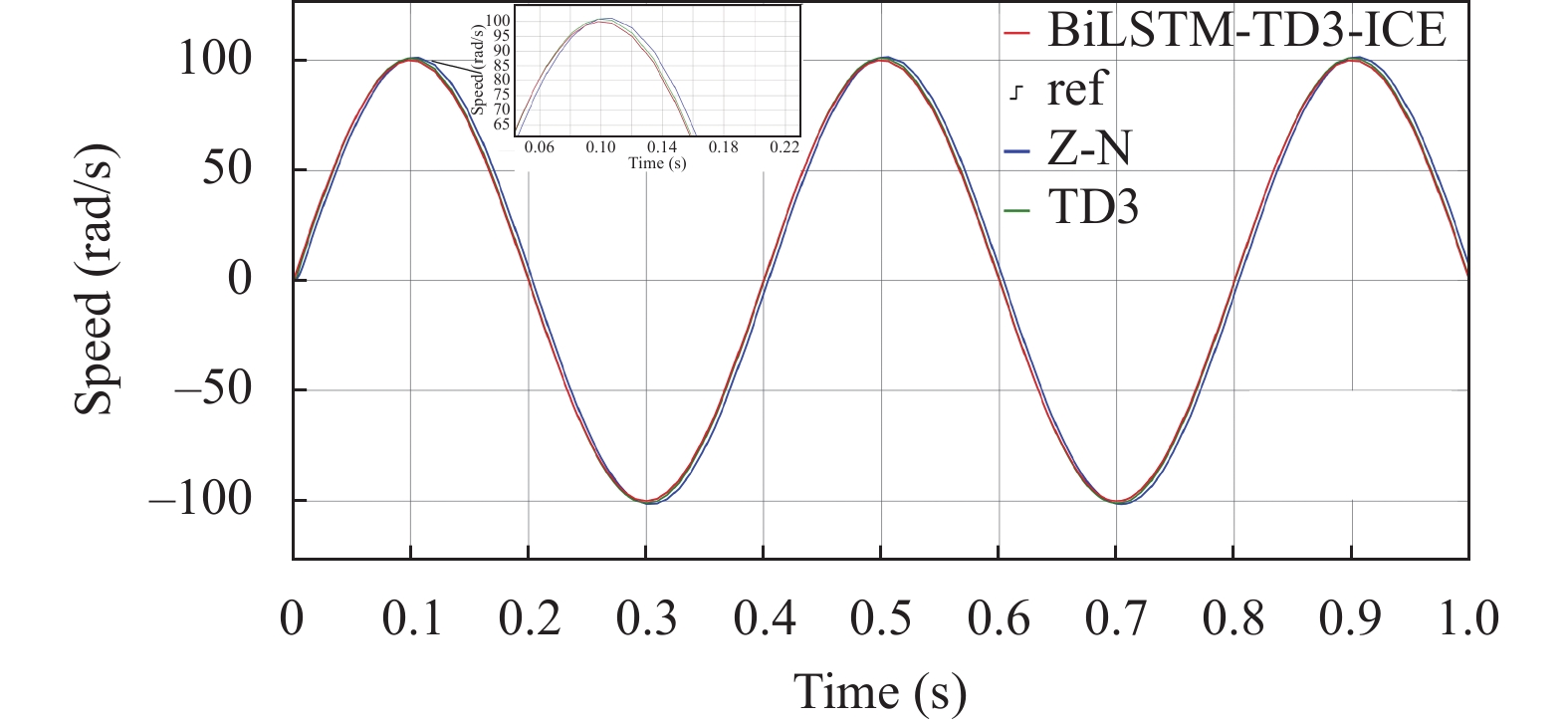
对于正弦函数参考速度的实验结果如图8所示, 我们进一步验证了Z-N方法、TD3和BiLSTM-TD3-ICE算法的性能差异. 在正弦函数实验中, 期望的速度呈现出周期性的波动, 这意味着电机需要不断地进行调整以跟随这一变化趋势. 3种算法都展示了迅速的速度响应. 由于正弦波的周期性特点, 要求电机在高点和低点之间进行精确的切换. BiLSTM-TD3-ICE算法对于正弦参考速度的追踪效果显然更为出色. Z-N方法和TD3算法在高峰和低谷的转换过程中存在一些振荡. 相比之下, BiLSTM-TD3-ICE算法不仅保持了速度的平稳性, 而且在各个转折点上都表现出了较高的精确度, 准确地跟随了期望的速度曲线.
|
图 8 正弦速度跟踪实验对比图 |
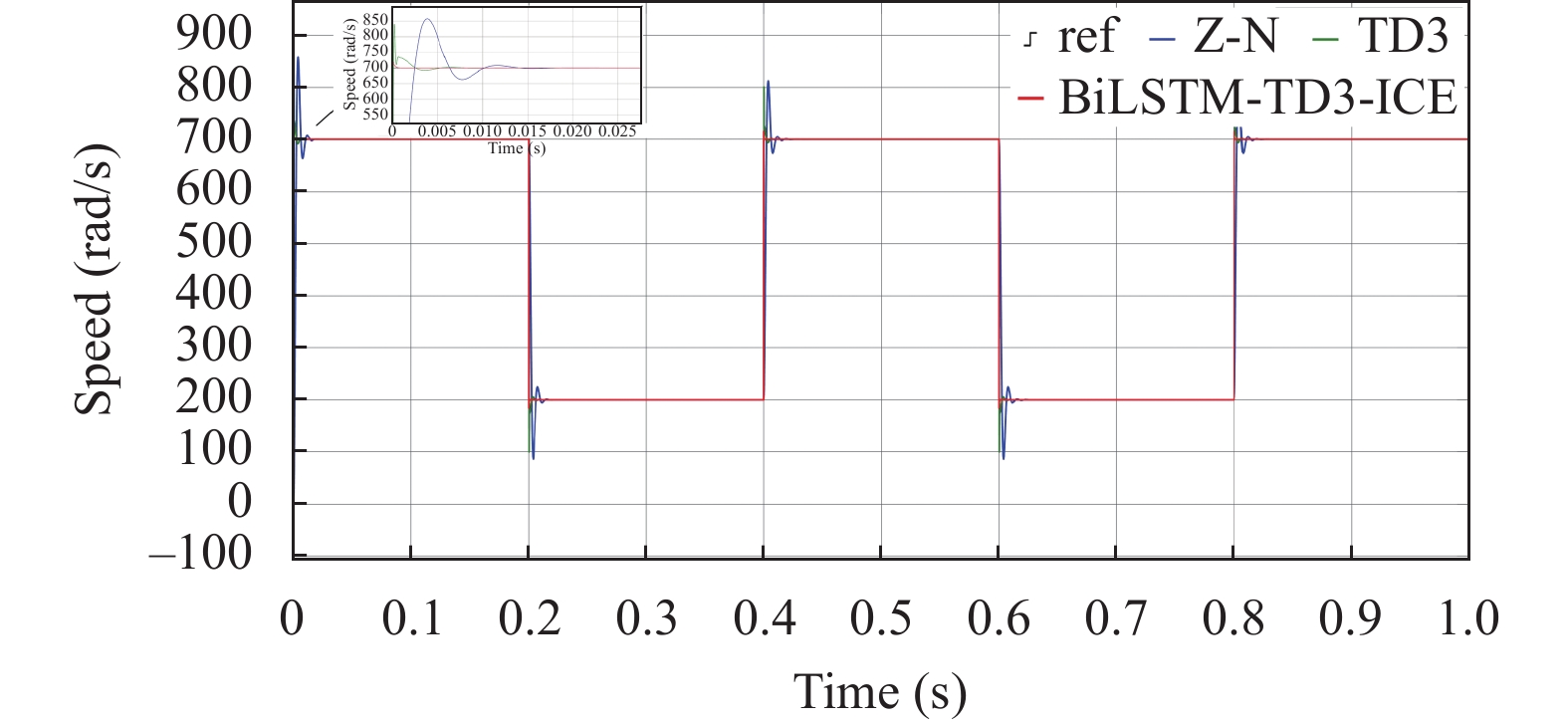
在针对方波信号的实验中, 控制算法需对具有急剧跳变的参考信号进行精确跟踪. 方波信号的特性要求控制系统具备迅速的响应能力以及高度的稳定性, 以便在每次跳变后快速达到新的稳态值, 同时最小化超调和振荡. 实验结果如图9显示, BiLSTM-TD3-ICE算法在处理方波信号时表现出较传统方法更加卓越的性能. 具体来说, 该算法在方波信号的每个上升沿和下降沿处能够实现快速且准确的跟踪, 这得益于BiLSTM网络的能力在处理时间序列数据时提供了额外的上下文信息, 有助于算法预测和适应速度的急剧变化. 与Z-N方法和传统TD3算法相比, BiLSTM-TD3-ICE在速度的高峰和低谷处的振荡显著减少, 表明其在速度跳变时具有更好的控制稳定性.
|
图 9 方波速度跟踪实验对比图 |
本研究通过比较TD3算法和BiLSTM-TD3-ICE算法在不同速度跟踪场景中的表现, 展示了BiLSTM-TD3-ICE算法在处理复杂动态系统时的显著优势. 在无干扰固定速度跟踪实验中, BiLSTM-TD3-ICE算法比传统的Z-N方法和TD3算法显示出更快的响应速度和更低的超调量. 当面临突发扰动时, BiLSTM-TD3-ICE算法能够迅速调整PID参数, 确保电机速度迅速恢复到稳定状态, 而其他算法则在恢复过程中遇到了挑战. 特别是在正弦函数和方波信号的跟踪任务中, BiLSTM-TD3-ICE算法利用BiLSTM网络捕捉时间序列的全局特性, 实现了高精度的周期性速度跟踪和对急剧跳变信号的准确响应, 表现出较少的振荡和更高的控制稳定性.
5 结论在本文的研究中, 针对PID控制器优化问题深入探讨, 对TD3算法进行了多方面的深度优化, 本研究通过结合BiLSTM网络到TD3算法的Actor和Critic网络中, 并引入了内在好奇心和熵正则化策略, 从而全面提升了算法的鲁棒性和控制性能. 仿真实验结果表明, 这些改进使BiLSTM-TD3-ICE算法在获得奖励、加速收敛过程以及提升控制精度方面超越了传统TD3算法. 特别是在复杂的速度跟踪任务中, BiLSTM-TD3-ICE算法利用BiLSTM网络的长短期记忆能力和内在好奇心激励的探索策略, 显著提高了对PMSM动态的理解和适应能力, 进而产生了更为平滑和准确的速度跟踪性能. 本文研究成果显著, 但仍有优化空间. 未来可研究更高级的策略和复杂网络结构来提升系统性能. 为增加策略的实用价值, 可在更多实际场景中应用并与其他优化技术结合.
| [1] |
Yuan TQ, Wang DZ, Wang XH, et al. High-precision servo control of industrial robot driven by PMSM-DTC utilizing composite active vectors. IEEE Access, 2019, 7: 7577-7587. DOI:10.1109/ACCESS.2018.2890539 |
| [2] |
Chen H, Wang X, Benbouzid M, et al. Improved fractional-order PID controller of a PMSM-based wave compensation system for offshore ship cranes. Journal of Marine Science and Engineering, 2022, 10(9): 1238. DOI:10.3390/jmse10091238 |
| [3] |
Chen SC, Hao XH, Gao CZ, et al. An effective nontransient active short-circuit method for PMSM in electric vehicles. IEEE Transactions on Industrial Electronics, 2023, 70(4): 3571-3580. DOI:10.1109/TIE.2022.3176315 |
| [4] |
Wang YC, Fang SH, Hu JX. Active disturbance rejection control based on deep reinforcement learning of PMSM for more electric aircraft. IEEE Transactions on Power Electronics, 2023, 38(1): 406-416. DOI:10.1109/TPEL.2022.3206089 |
| [5] |
Wang YQ, Feng YT, Zhang XG, et al. A new reaching law for antidisturbance sliding-mode control of PMSM speed regulation system. IEEE Transactions on Power Electronics, 2020, 35(4): 4117-4126. DOI:10.1109/TPEL.2019.2933613 |
| [6] |
Ab Ghani MS, Zin NM, Zakaria F, et al. Speed control design for permanent magnet synchronous motor drive based on PID-fuzzy controller. Proceedings of the 3rd International Conference on Artificial Intelligence and Data Sciences (AiDAS). IPOH: IEEE, 2022. 170–175.
|
| [7] |
Quang NK, Anh NK, Than H, et al. Neural network PID controller for PMSM drives. Proceedings of the 7th National Scientific Conference on Applying New Technology in Green Buildings (ATiGB). Da Nang: IEEE, 2022. 146–149.
|
| [8] |
Sanatel Ç, Günel GÖ. Long short term memory based self tuning regulator design for nonlinear systems. Neural Processing Letters, 2023, 55(3): 3045-3079. DOI:10.1007/s11063-022-10997-1 |
| [9] |
Xue Z, Wang YY, Li L, et al. An adaptive speed control method based on deep reinforcement learning for permanent magnet synchronous motor. In: Jia YM, Zhang WC, Fu YL, et al., eds. Proceedings of the 2021 Chinese Intelligent Systems Conference: Vol. I. Singapore: Springer, 2022. 275–286.
|
| [10] |
Shi Q, Lam HK, Xiao B, et al. Adaptive PID controller based on Q-learning algorithm. CAAI Transactions on Intelligence Technology, 2018, 3(4): 235-244. DOI:10.1049/trit.2018.1007 |
| [11] |
Liao JR, Liu SY, Wu QH, et al. PID control of permanent magnet synchronous motor based on improved Actor-Critic framework. Journal of Physics: Conference Series, 2022, 2213: 012005. DOI:10.1088/1742-6596/2213/1/012005 |
| [12] |
Lu PW, Huang WK, Xiao JL. Speed tracking of brushless DC motor based on deep reinforcement learning and PID. Proceedings of the 7th International Conference on Condition Monitoring of Machinery in Non-stationary Operations (CMMNO). Guangzhou: IEEE, 2021. 130–134.
|
| [13] |
Fujimoto S, Van Hoof H, Meger D. Addressing function approximation error in Actor-Critic methods. Proceedings of the 35th International Conference on Machine Learning. Stockholm: PMLR, 2018. 1587–1596.
|
| [14] |
Shi Q, Lam HK, Xuan CB, et al. Adaptive neuro-fuzzy PID controller based on twin delayed deep deterministic policy gradient algorithm. Neurocomputing, 2020, 402: 183-194. DOI:10.1016/j.neucom.2020.03.063 |
| [15] |
Ullah K, Guzinski J, Mirza AF. Critical review on robust speed control techniques for permanent magnet synchronous motor (PMSM) speed regulation. Energies, 2022, 15(3): 1235. DOI:10.3390/en15031235 |
| [16] |
Dubey V, Goud H, Sharma PC. Role of PID control techniques in process control system: A review. In: Nanda P, Verma VK, Srivastava S, et al., eds. Proceedings of the 2021 SSIC Data Engineering for Smart Systems. Singapore: Springer, 2022. 659–670.
|
| [17] |
李茹杨, 彭慧民, 李仁刚, 等. 强化学习算法与应用综述. 计算机系统应用, 2020, 29(12): 13-25. DOI:10.15888/j.cnki.csa.007701 |
| [18] |
Yuan XM, Wang Y, Zhang RC, et al. Reinforcement learning control of hydraulic servo system based on TD3 algorithm. Machines, 2022, 10(12): 1244. DOI:10.3390/machines10121244 |
| [19] |
Siami-Namini S, Tavakoli N, Namin AS. The performance of LSTM and BiLSTM in forecasting time series. Proceedings of the 2019 IEEE International Conference on Big Data (Big Data). Los Angeles: IEEE, 2019. 3285–3292.
|
| [20] |
Li J, Shi XX, Li JH, et al. Random curiosity-driven exploration in deep reinforcement learning. Neurocomputing, 2020, 418: 139-147. DOI:10.1016/j.neucom.2020.08.024 |
 2024, Vol. 33
2024, Vol. 33



