子群发现是一种广泛适用的数据挖掘技术, 旨在发现集合的不同属性或变量(描述变量)之间关于用户感兴趣的特定属性(目标变量)的有趣关系[1], 提取的模式通常以规则的形式表示. 这项任务的一个重要特点是从数据集中提取的模式在目标变量上的统计分布显著不同于目标变量上的总体统计分布, 这样的模式可以认为是有趣的[2]. 例如, 模式: (年龄≥65∧吸烟=true)→患有肺癌=true代表了年龄大于等于65岁且作为吸烟者的一个子群, 相对于其他人群成为肺癌患者的可能异常的高. 通过子群发现算法可以使用户更好地了解数据特征之间的关系, 并且已经应用于许多特定领域中[1], 例如, 在医疗和生物信息学领域中, 子群发现可以帮助研究人员识别患有特定疾病的人群, 并进一步深入探索疾病的原因和治疗方法; 在人口统计领域, 子群发现可以帮助专家找到高收入或者低收入人群的内部和外部影响因素, 从而为接下来的研究以及决策提供方向.
数据通常分为许多类型, 包含二值变量、名义变量、数值变量, 其中数值变量由于取值是非离散的, 大大增加了搜索空间的大小, 从中提取有趣的子群也变得更加困难. 此外, 数据集分为两个部分: 描述变量以及目标变量. 最近的子群发现主要是针对数值型描述变量和二值或名义型目标变量进行研究[1,2]. 但是随着数值型目标变量数据集以及应用需求的增加, 数值型目标变量的子群发现受到越来越多的关注, 传统的方法只是将数值目标变量进行离散化, 而忽略了数值目标的原有信息. 为解决这个问题, Lemmerich等人[3]提出SD-MAP*算法, 基于SD-MAP算法[4]所使用的基于最小支持阈值的FP树增长的策略, 并增加了严格乐观估计[5]来对树进行剪枝, 但是该算法对数值描述变量进行离散化, 从而导致信息的损失, 只能发现次优的子群. Nguyen等人[6]提出了FLEXI算法, 通过对每个属性的不同取值区间进行装箱, 可以适用于任何目标变量, 并且通过最大化所有箱的平均质量来找到较优的子群, 在数据量大的时候可以通过较少的采样来保证算法运行效率, 但是需要微调超参数以取得更好的结果. Millot等人[7]提出了OSMIND算法, 不用事先进行离散化, 并且利用在正例上闭合(close on the positive, COTP)的间隔模式[8]、最小边界改变(MinIntChange)[9]、严格乐观估计[5]等策略来修剪搜索空间, 保证可以搜索到最优子群, 但结果缺少多样性, 并且对大的模式搜索空间进行穷举搜索需要大量的时间甚至难以进行.
为了在不进行离散化的情况下高效挖掘大数据集中的多样性模式集, Bosc等人[10]和Mathonat等人[11]提出了基于蒙特卡洛树搜索(MCTS)的子群发现方法MCTS4DM和MonteCloPi算法. MCTS是一种基于模拟采样的最佳优先搜索算法, 每次迭代根据先前的采样结果来构建非对称的搜索树, 将搜索集中在最有希望的区域. 在子群发现中利用MCTS处理大的模式搜索空间时可以取得比其他传统算法更好的结果[11], 并且可以随时输出多样性模式集, 随着可用时间的增加最终会收敛到穷举搜索. 但是目前基于MCTS的子群发现算法限制了目标为二值属性, 因此研究如何将MCTS应用至数值目标子群发现任务中具有重要意义.
将MCTS应用于特定领域中需要根据问题背景对原始MCTS策略进行相应的调整. 例如文献[12,13]中汇总了MCTS在棋盘游戏和电子游戏等领域中的应用以及改进方法, 主要包括: 针对原始MCTS算法中分支因子过多、不同场景下UCB公式中C值的选取等问题的解决方法. 在其他领域中, 文献[14]使用MCTS来求解问题规模较大的混合整数线性规划模型, 根据问题的约束条件修剪没有希望的分支, 在更短的时间内可以取得更好的效果.
因此, 受到上述文献中将MCTS应用于特定领域所做工作的启发, 再结合数值目标子群发现任务的特点, 本文分别从UCB公式中C值的调整、动态调整待拓展结点权重和对搜索树应用剪枝、采用自适应top-k均值更新策略等方面来改进MonteCloPi算法的选择、拓展和更新策略, 将其拓展到了数值目标数据集上, 可以在不进行离散化的情况下随时获得高质量的多样性模式集. 本文第1节介绍MonteCloPi算法. 第2节介绍改进后适用于数值目标的MonteCloPi算法. 第3节对改进的MonteCloPi算法进行实验并分析实验结果. 第4节总结本文的工作和未来的研究方向.
1 MonteCloPi算法在MonteCloPi算法中, D=(O, A, C)表示数据集, O表示一组样本, A表示一组描述属性, C表示一个目标属性, O+表示C取值为+的样本, 即正例样本. 间隔模式p提供了在各个描述属性上的限制, p的覆盖为满足p中每个限制的样本集合, 记作ext(p), 支持度supp(p)=|ext(p)|, 即覆盖样本的个数. int将样本集合映射到最严格的间隔模式上, 例如int(ext(p))表示p的闭合间隔模式, 任何比它更小的间隔模式将会至少失去一个样本. ext+(p)表示满足p中每个限制的正例样本集合, p的在正例上闭合(COTP)间隔模式为COTP(p)=int(ext+(p)). 对于间隔模式p和q, MEET运算
MonteCloPi算法中使用的子群质量度量φ(p)为:
| $ WRAcc(p, D, {D_c}) = \frac{{supp(p, D)}}{{\left| D \right|}} \times \left( {\frac{{supp(p, {D_c})}}{{supp(p, D)}} - \frac{{\left| {{D_c}} \right|}}{{\left| D \right|}}} \right) $ | (1) |
其中, Dc为目标值为c的数据集, |D|和|Dc|分别为数据集D和Dc中样本个数.
MonteCloPi算法的模式集挖掘目标为找到高质量的非θ-冗余模式集R, 即对于给定的相似度阈值θ
| $ sim(p, q) = \frac{{\left| {{{e}}xt(p) \cap ext(q)} \right|}}{{\left| {{{e}}xt(p) \cup ext(q)} \right|}} $ | (2) |
MonteCloPi算法先从数据集D中挖掘最佳模式集S, 再对S进行后处理移除冗余模式, 获得非冗余结果模式集R. 后处理流程[10]如下: 将模式集S中所有模式按质量递减排序, 先将最优的模式存入R, 之后遍历模式集S, 对遍历到的模式与结果模式集R中每个模式按式(2)计算相似程度, 若小于阈值θ则将其加入R, 否则丢弃该模式, 重复上述过程直至R包含k个模式, 此时R是一个非θ-冗余模式集并且其中包含top-k个非冗余子群. R的形式化定义如下:
| $ R={\mathrm{argmax}}_{R\subseteq S}\frac{1}{k}{\displaystyle \sum _{r\in R}\varphi (r), \;\forall p, q\in R且p\ne q, sim(p, q)\leqslant \theta } $ | (3) |
MonteCloPi算法通过不断迭代构建搜索树来挖掘最佳模式集S, 直至达到给定的时间预算或者探索了整个搜索空间, 每次迭代分为4个步骤: 选择、拓展、模拟、更新.
MonteCloPi算法的步骤如算法1所示.
算法1. MonteCloPi算法
输入: 数据集D, 时间预算timeBudget, 质量度量φ.
输出: 含top-k个非冗余子群的模式集R.
1)初始化: S=优先级队列, 根结点⊥为空
2) while 没有达到timeBudget do
3) psel←从根结点⊥递归选择具有最大UCB值且还未完全拓展的子结点//选择
4) o+←从psel的候选正例随机选择一个 //拓展
5) p+←o+转化为对应的间隔模式
6) pexp←MEET(psel, p+)
7) S.add(pexp, φexp) //将模式及其质量加入队列中
8) proll←pexp的随机一个属性设为该属性的随机值, 其他属性设为[−∞, +∞] //模拟
9) S.add(proll, φroll) //将模式及其质量加入队列中
10) for each p
11)
12) end for
13) end while
14) R←S.topK() //使用后处理获得非冗余模式集R
在算法1中, 第1行的S用于保存当前最优模式集合, 根结点⊥不含任何样本; 第3–12行对应于一次迭代过程, 不断重复直至达到给定的时间预算; 其中第3行对应于选择步骤, UCB公式由式(4)给出, 通过UCB可以选择出具有较优质量的结点或者很少被访问的结点, 未完全拓展的结点为没有覆盖所有正例的结点; 第4–6行对应于拓展步骤, 这一步将拓展结点加入搜索树中来构建搜索树, 候选正例为还未被当前结点的COTP间隔模式所覆盖的正样本, 正例对应的间隔模式为将正例的各个描述属性值作为对应间隔上下限的间隔模式, 例如o=(2, 4)对应的间隔模式为〈[2, 2], [4, 4]〉; 第8行对应于模拟步骤, 通过快速将拓展结点模拟至终点状态(覆盖所有样本)附近来估计该结点下分支的好坏; 第10–12行对应于更新步骤, 根据模拟的质量
| $ {\textit{UCB}}(i) = {\overline \varphi _i} + C\sqrt {\frac{{{\mathrm{ln}}(N)}}{{{N_i}}}} $ | (4) |
其中,
将MonteCloPi 算法应用于数值目标, 还存在一些问题: 1)使用针对数值目标的质量度量时, 计算的质量可能会很大, 式(4)的第1项会过大而弱化第2项的效果, 从而导致更少去探索很少被探索的空间; 2)拓展时以相同概率随机选取样本, 算法缺乏稳定性, 并且拓展了过多无意义分支; 3)在局部最优值点较少且比较分散的情况下, 结点的平均质量可能会因为访问到大量低质量模式而接近0, 从而忽略了该结点下有趣的模式. 为此, 本文提出了MCTSIND (Monte Carlo tree search in numerical data)算法, 根据数值目标子群发现任务的特点分别改进MCTS 的选择、拓展和更新策略来解决以上问题.
2.1 MCTS策略的改进在本文中使用适用于数值目标的基于平均值的质量度量:
| $ \varphi (p) = {\left| {ext(p)} \right|^a} \times \left( {{\mu _{ext(p)}} - {\mu _{ext(p_D )}}} \right), a \in \left[ {0, 1} \right] $ | (5) |
其中,
对于选择策略, 为了平衡搜索树的探索和利用, 需要对UCB中的C值进行调整. 考虑到传统MCTS算法中通常限制UCB的第1项在[0, 1]之间[13], 因此本文中调整C值为归一化式(5)所需的分母部分:
| $ C = {\left| D \right|^a} \times \left( {{T_{\max}} - {\mu _{ext(p_D )}}} \right) $ | (6) |
其中, Tmax为目标变量最大值. 本文采用调整后的C值来计算UCB值.
对于拓展策略, 考虑拓展大于等于
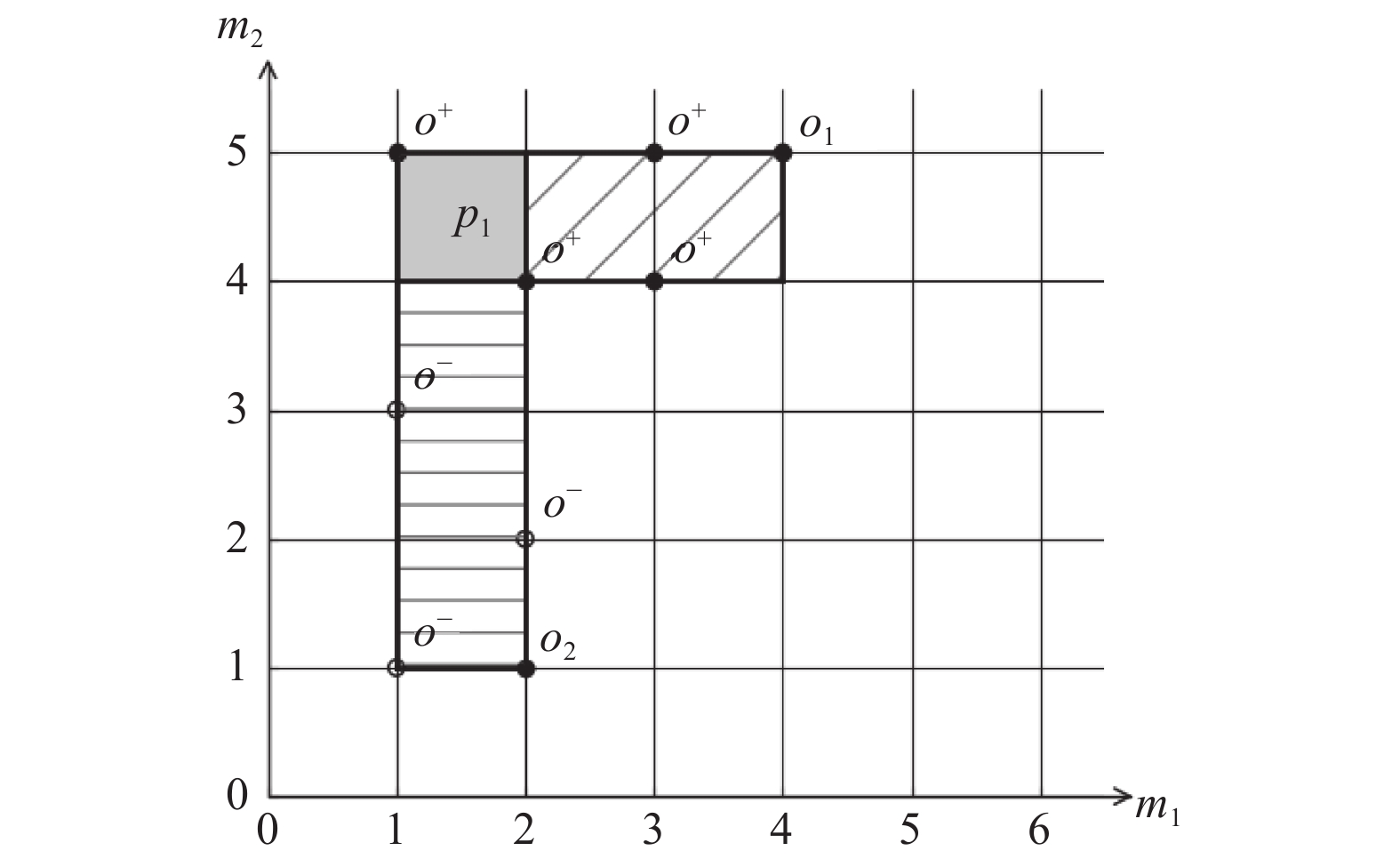
|
图 1 可能的拓展情况 |
图1中m1和m2为样本的两个属性, 实心点o+为目标值大于等于
因此, 本文定义了质量增益比
| $ w({o_i}) = \frac{{{\varphi _{{\mathrm{exp}}}}}}{{{\varphi _{{\mathrm{sel}}}}}}w({o_i}) $ | (7) |
其中, φexp表示拓展后结点的质量, φsel表示拓展前结点的质量. 对于图1的情况, 可以使拓展后能获得更高质量模式的样本具有更高的权重, 从而有更高概率在后续被拓展, 因为这些样本周围可能有较密集的高目标值样本.
拓展或模拟结点后需要将该模式及其质量加入当前最优模式集合S中, S有一个模式个数上限, 此时可以根据S中的最低质量φmin对没有希望的分支进行剪枝. 步骤如下: 首先设置模式的支持度上限maxsupp=0.2|D|, 即总样本数的20%, 再根据φmin来计算阈值
| $ {\mu _{{\mathrm{thresh}}}} = \frac{{{\varphi _{{\mathrm{min}}}}}}{{{\textit{maxsupp}}{^a}}} + {\mu _{ext(p_D )}} $ | (8) |
只有拓展目标值大于该阈值的样本才有可能提高S中的模式质量.
记某个结点p已覆盖的样本集合为S1, 可拓展样本集合
| $ \left(\frac{1}{{\left| {{S_1} \cup {S_2}} \right|}}\sum\limits_{o \in {S_1} \cup {S_2}} {T_o} \right) < {\mu _{{\mathrm{thresh}}}} $ | (9) |
则将结点p下的所有分支修剪, 此时p完全拓展, 因为将其子结点拓展到搜索树中并进行探索对提升当前最优模式集合S的质量没有帮助.
对于更新策略, 文献[10]中提出了top-k均值更新策略来解决局部最优值点较少且比较分散的问题: 使用更新到该结点的前k个最优质量的平均值来更新该结点质量, 使搜索树“记住”从该结点出发可以发现高质量的模式, 从而可以更多地“利用”该结点. 但是原策略需要指定额外的超参数k, 因此本文提出自适应top-k均值更新策略: 结点p的top-k队列Qp的初始上限k为2, 之后更新到p的质量若大于Qp的均值才加入Qp, 此时k也随之增加. 在本文中使用自适应top-k均值更新策略来对MonteCloPi算法进行改进.
2.2 算法描述基于第2.1节中对MonteCloPi算法中UCB公式C值的选取、样本拓展权重的调整、对搜索树进行剪枝和使用自适应top-k均值更新策略的改进, 本文提出的MCTSIND算法如算法2所示.
算法2. MCTSIND算法
输入: 数据集D, 时间预算timeBudget, 质量度量φ.
输出: 含top-k个非冗余子群的模式集R.
1)初始化: S=优先级队列, 根结点⊥为空
2) while 没有达到timeBudget do
3) psel←从根结点⊥递归选择具有最大UCB值且还未完全拓展的子结点(使用式(6)中新的C值) //选择
4) o+←按权重概率
5) p+←o+转化为对应的间隔模式
6) pexp←MEET(psel, p+)
7) 按式(7)更新o+的权重
8) S.add(pexp, φexp) //将模式及其质量加入队列中
9) 若S已满, 按式(8)和式(9)对搜索树中的结点进行剪枝
10) proll←pexp的随机一个属性设为该属性的随机值, 其他属性设为[−∞, +∞]//模拟
11) S.add(proll, φroll) //将模式及其质量加入队列中
12) 若S已满, 按式(8)和式(9)对搜索树中的结点进行剪枝
13) for each p
14) if p的top-k质量队列Qp未满 then
15) 将φroll加入Qp
16) else 当φroll>Qp中质量的均值时才将φroll加入Qp
17) end if
18)
19) end for
20) end while
21) R←S.topK() //使用后处理获得非冗余模式集R
算法2与算法1不同之处在于: 第3行选择步骤使用式(6)中新的C值; 第4行按权重概率从待拓展样本中进行选取, 待拓展样本为目标值大于等于
本文使用的数值目标数据集是UCI 提供的 auto MPG (AMPG)、concrete compressive strength (CCS)、airfoil self-noise (ASN)、wine quality-red (WQR)、wine quality-white (WQW)、air quality (AQ)这6个数据集. 此外还使用national health and nutrition examination survey (NHANES) 提供的听力测试数据集 Audiometry 2011–2012, 2015–2016 (AUD11–16)和 Audiometry 2017–2018 (AUD17–18), 如表1所示.
| 表 1 数据集信息 |
NHANES是一项基于人群的横断面调查, 旨在收集美国成人和儿童的健康和营养状况的信息. 其听力测试的对象是20–69岁的人群, 数据集的描述变量对应多种可能导致听力损失的因素, 并含有多个数值类型的目标变量, 分别对应左右耳在不同频率(0.5、1、2、3、4、6、8 kHz)下的听力阈值(最小听清的分贝数), 阈值越大说明听力越差, 本文中将0.5–2 kHz归为低频, 3–8 kHz归为高频, 低频中听力阈值>25 dB和高频中听力阈值>35 dB定义为听力损失, 以此作为感兴趣的阈值, 将表1和式(5)中的
在实验中, 使用式(5)作为质量度量φ, 其中a=0.5, 并且设置时间预算为60 s, 模式集相似度阈值θ=0.5, 最小支持度minsupp为样本总数的10%, FLEXI算法的初始分箱数设为20.
3.2 UCI数据集实验结果分析首先, 使用表1的UCI数据集部分, 将MCTSIND与MonteCloPi (直接使用式(5)的质量度量φ)、SD-MAP*、FLEXI和OSMIND这些子群发现算法挖掘的非冗余模式集基于以下两个方面进行比较.
(1)基于给定的时间预算, 比较各个算法在数据集上使用后处理步骤所提取出的top-5非冗余子群关于质量度量φ的平均性能的相对值, 如图2所示.
从图2中可以看出, 在UCI数据集中, MCTSIND发现的top-5非冗余子群的平均质量在大多数情况下都要优于其他4个算法, 仅在WQR数据集中比FLEXI要略低一些. 这得益于MCTS的探索与利用的折中, 可以尽可能多地发现不同的局部最优值点以提高最终结果的平均质量, 如果能给出更多的时间预算, MCTSIND在WQR数据集上的表现可能会超过FLEXI. 同时还可以看出将MonteCloPi直接应用于数值目标数据集难以发现高质量的多样性模式集.
(2)使用不同的时间预算来研究各个算法随着时间的增加对算法性能的影响, 时间预算分别设置为1 s、5 s、10 s、20 s、40 s、60 s、80 s、100 s、120 s, 图3描述了各个算法随着时间预算的变化所给出top-5非冗余子群的平均质量.

|
图 2 top-5非冗余子群的平均质量相对值对比 |

|
图 3 top-5非冗余子群平均质量随时间变化对比 |
从图3中可以看出, SD-MAP*和FLEXI很快就因为探索完其修剪后的搜索空间而收敛, 由于使用了离散化导致较差的结果. 此外, MCTSIND的总体表现比MonteCloPi更好, 虽然刚开始模式集质量增长较慢, 但是随着时间的增加不断给出更好的结果, 并且在不同样本个数的数据集上面表现稳定. OSMIND的可伸缩性较差, 在WQR、WQW、AQ等大样本数据集上需要更多时间才能达到与其他算法相同的水平, 在AMPG、CCS这些样本个数略少的数据集才会获得较好的表现.
3.3 NHANES数据集应用研究最后, 使用表1中的NHANES听力测试数据集来研究20–69岁人群中低频和高频听力损失的可能因素. 分别将左右耳在各个频率下的听力阈值作为目标变量, 运行MCTSIND和OSMIND算法, 后者在文献[7]的实验中可以获得比SD-MAP*更有解释性的子群. 下文将时间预算延长至300 s, 并且使用所得到的top-1子群质量的平均值和各个间隔模式区间的并集来进行对比, 如表2所示.
| 表 2 MCTSIND与OSMIND提取的间隔模式对比 |
表2的每列对应数据集的一个描述属性, 值表示间隔模式中对该描述属性的限制, ×代表不存在该属性, —代表该属性没有提供限制. 可以看出在4个听力测试数据集中, MCTSIND比OSMIND发现的top-1子群质量都更优. 此外, OSMIND在描述高频和低频听力损失的可能因素时使用了相同的描述属性, 不能很好地区分出两者之间的差异. 而MCTSIND对于高频和低频听力损失所用的描述属性不同, 可以很容易地看出两者的不同: 例如AUQ020 (过去24 h是否感冒、鼻窦炎或者耳痛)和AUXROC (耳朵耵聍程度)不是高频听力损失的影响因素, AUQ040 (距上次听到噪音过去多少小时)和AUQ610 (距上次使用耳机过去多少小时)不是低频听力损失的影响因素. 并且MCTSIND使用了更少的描述属性, 相比于OSMIND提取出的结果可以被我们更好地理解和利用.
接下来分析MCTSIND所提取出的间隔模式含义. 对于非声阻抗测定因素(表2的前5列描述属性), MCTSIND认为高频听力损失与在过去的24 h内暴露于噪声之中或者使用耳机听音乐有关; 低频听力损失与在过去的24 h内有感冒、鼻窦炎或者耳痛症状、耳道中有过多的耵聍有关. 文献[15]中验证了过多暴露于噪声之中会影响高频听力, 感冒、耳痛会影响低频听力, 这可以说明MCTSIND所提取模式的有效性.
对于声阻抗测定因素(表2的后4列描述属性), 结合文献[16]给出的成年人的正常值范围: AUXTMEP (中耳压力) [−150, 50] daPa, AUXTPV (外耳道容积) [0.6, 1.5] cc, AUXTWID (鼓室图宽度) [50, 100] daPa, AUXTCOM (声顺值) [0.3, 1.4] cc, 可以分析出MCTSIND认为高频听力损失与外耳道容积过大和声顺值过高有关; 低频听力损失与中耳压力过低、鼓室图宽度过大和较低的声顺值有关. 对于声阻抗测定因素对高低频听力损失的影响方面, 目前还找不到相关的文献, 基于MCTSIND提取出的结果可以辅助相关人员对听力损失原因进行分析.
4 结论与展望针对MonteCloPi算法只适用于二值目标变量的问题, 本文提出了MCTSIND算法. 该算法结合了数值目标子群发现任务的特点, 改进了MonteCloPi算法的MCTS策略: 为UCB公式选取合适的C值、在拓展阶段动态调整各个样本的权重并且定义目标值阈值对搜索树进行剪枝、使用自适应top-k均值更新策略, 将MonteCloPi算法拓展到了数值目标. 最后, 在UCI和NHANES数据集上的实验结果表明MCTSIND算法可以有效处理数值目标数据集, 其发现的top-5非冗余子群的平均质量比其他算法更优; 对高低频听力损失因素进行研究时可以发现比OSMIND算法更高质量和更具有可解释性的子群. 未来的工作中将研究如何将MCTSIND算法拓展到多个目标变量的情况.
| [1] |
Herrera F, Carmona CJ, González P, et al. An overview on subgroup discovery: Foundations and applications. Knowledge and Information Systems, 2011, 29(3): 495-525. DOI:10.1007/s10115-010-0356-2 |
| [2] |
Meeng M, Knobbe A. For real: A thorough look at numeric attributes in subgroup discovery. Data Mining and Knowledge Discovery, 2021, 35(1): 158-212. DOI:10.1007/s10618-020-00703-x |
| [3] |
Lemmerich F, Atzmueller M, Puppe F. Fast exhaustive subgroup discovery with numerical target concepts. Data Mining and Knowledge Discovery, 2016, 30(3): 711-762. DOI:10.1007/s10618-015-0436-8 |
| [4] |
Atzmueller M, Puppe F. SD-Map—A fast algorithm for exhaustive subgroup discovery. Proceedings of the 10th European Conference on Principles of Data Mining and Knowledge Discovery. Berlin: Springer, 2006. 6–17.
|
| [5] |
Grosskreutz H, Rüping S, Wrobel S. Tight optimistic estimates for fast subgroup discovery. Proceedings of the 2008 Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Antwerp: Springer, 2008. 440–456.
|
| [6] |
Nguyen HV, Vreeken J. Flexibly mining better subgroups. Proceedings of the 2016 SIAM International Conference on Data Mining (SDM). Miami: The Society for Industrial and Applied Mathematics, 2016. 585–593. [doi: 10.1137/1.9781611974348.66]
|
| [7] |
Millot A, Cazabet R, Boulicaut JF. Optimal subgroup discovery in purely numerical data. Proceedings of the 24th Pacific-Asia Conference on Knowledge Discovery and Data Mining. Singapore: Springer, 2020. 112–124.
|
| [8] |
Belfodil A, Belfodil A, Kaytoue M. Anytime subgroup discovery in numerical domains with guarantees. Proceedings of the 2019 Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Dublin: Springer, 2019. 500–516. [doi: 10.1007/978-3-030-10928-8_30]
|
| [9] |
Kaytoue M, Kuznetsov SO, Napoli A. Revisiting numerical pattern mining with formal concept analysis. Proceedings of the 22nd International Joint Conference on Artificial Intelligence. Barcelona: AAAI Press, 2011. 1342–1347. [doi: 10.5591/978-1-57735-516-8/IJCAI11-227]
|
| [10] |
Bosc G, Boulicaut JF, Raïssi C, et al. Anytime discovery of a diverse set of patterns with Monte Carlo tree search. Data Mining and Knowledge Discovery, 2018, 32(3): 604-650. DOI:10.1007/s10618-017-0547-5 |
| [11] |
Mathonat R, Nurbakova D, Boulicaut JF, et al. Anytime subgroup discovery in high dimensional numerical data. Proceedings of the 8th IEEE International Conference on Data Science and Advanced Analytics (DSAA). Porto: IEEE, 2021. 1–10. [doi: 10.1109/DSAA53316.2021.9564223]
|
| [12] |
Browne CB, Powley E, Whitehouse D, et al. A survey of Monte Carlo tree search methods. IEEE Transactions on Computational Intelligence and AI in Games, 2012, 4(1): 1-43. DOI:10.1109/TCIAIG.2012.2186810 |
| [13] |
Świechowski M, Godlewski K, Sawicki B, et al. Monte Carlo tree search: A review of recent modifications and applications. Artificial Intelligence Review, 2023, 56(3): 2497-2562. DOI:10.1007/s10462-022-10228-y |
| [14] |
邱云飞, 于智龙, 郭羽含, 等. 蒙特卡洛树搜索下的整合多目标可持续闭环供应链网络优化. 计算机集成制造系统, 2022, 28(1): 269-293. DOI:10.13196/j.cims.2022.01.025 |
| [15] |
Shargorodsky J, Curhan GS, Curhan CG, et al. Change in prevalence of hearing loss in US adolescents. JAMA, 2010, 304(7): 772-778. DOI:10.1001/jama.2010.1124 |
| [16] |
Roup CM, Wiley TL, Safady SH, et al. Tympanometric screening norms for adults. American Journal of Audiology, 1998, 7(2): 55-60. DOI:10.1044/1059-0889(1998/014) |
 2024, Vol. 33
2024, Vol. 33


