面向平层多房间的内墙作业移动机器人路径规划

引用本文

靳徐明, 林云汉, 张磊, 闵华松. 面向平层多房间的内墙作业移动机器人路径规划. 计算机系统应用, 2024, 33(5): 254-261.http://www.c-s-a.org.cn/1003-3254/9495.html

Jin XM, Lin YH, Zhang L, Min HS. Mobile Robot Path Planning for Interior Wall Operation in Flat Multi-room. Computer Systems and Applications, 2024, 33(5): 254-261(in Chinese).http://www.c-s-a.org.cn/1003-3254/9495.html

面向平层多房间的内墙作业移动机器人路径规划

靳徐明^1,2, 林云汉^1,2,3, 张磊⁴, 闵华松³

1. 武汉科技大学计算机科学与技术学院, 武汉 430065;
2. 武汉科技大学智能信息处理与实时工业系统湖北省重点实验室, 武汉 430065;
3. 武汉科技大学机器人与智能系统研究院, 武汉 430065;
4. 北京电子科技职业学院汽车工程学院, 北京 100081

收稿日期：2023-11-13; 修改日期：2023-12-22; 采用时间：2024-01-05; csa 在线出版时间：2024-03-15

基金项目：国家重点研发计划(2022YFB4700400); 国家自然科学基金(62073249); 湖北省重点研发计划(2023BBB011)

通讯作者：林云汉, E-mail: yhlin@wust.edu.cn.

摘要：本文针对多房间的移动机器人内墙作业的路径规划任务, 提出一种两阶段路径规划方法. 第1阶段针对沿墙作业过程中环境存在灰尘或雾气造成的传感器失效问题, 以及房间多出口时路径规划不完整问题, 我们提出起点自动选择沿墙路径规划方法, 基于栅格地图离线生成沿墙规划路径. 第2阶段, 针对点到点路径规划过程中的动态避障问题, 我们提出一种基于PSAC (prioritized experience replay soft actor critic)算法的点到点路径规划方法, 在软行动者-评论家(soft actor critic, SAC)的中引入优先级经验回放策略, 实现机器人的动态避障. 实验部分设计了沿墙路径规划对比实验和动态避障的对比实验, 验证本文所提出的方法在室内沿墙路径规划和点到点路径规划的有效性.

关键词: 两阶段路径规划方法沿墙路径规划强化学习 PSAC

Mobile Robot Path Planning for Interior Wall Operation in Flat Multi-room

JIN Xu-Ming^1,2, LIN Yun-Han^1,2,3, ZHANG Lei⁴, MIN Hua-Song³

1. School of Computer Science and Technology, Wuhan University of Science and Technology, Wuhan 430065, China;
2. Hubei Province Key Laboratory of Intelligent Information Processing and Real-time Industrial System, Wuhan University of Science and Technology, Wuhan 430065, China;
3. Institute of Robotics and Intelligent Systems, Wuhan University of Science and Technology, Wuhan 430065, China;
4. School of Automotive Engineering, Beijing Polytechnic, Beijing 100081, China

Abstract: This study proposes a two-stage path planning method for the path planning task of the inner wall operation of a mobile robot in multi-room. In the first stage, for the sensor failure caused by dust or fog in the environment during wall operation and incomplete path planning when there are many exits in a room, the study proposes a start-point automatically selected wall following path planning method, which is based on grid maps to generate the wall following paths offline. In the second stage, for the dynamic obstacle avoidance problem during point-to-point path planning, it proposes a point-to-point path planning method based on the prioritized experience replay soft actor critic (PSAC) algorithm, which introduces the prioritized experience playback strategy in the soft actor critic (SAC) to achieve dynamic obstacle avoidance. The comparison experiments of wall following path planning and dynamic obstacle avoidance are designed to verify the effectiveness of the proposed method in the indoor wall following path planning and point-to-point path planning.

Key words: two-stage path planning method wall following path planning reinforcement learning prioritized experience replay soft actor critic (PSAC)

1 介绍

随着AI技术的飞速发展, 为避免沿墙作业的产物对人体健康造成严重危害, 墙面作业任务正在逐渐被墙面操作机器人所取代^[1]. 机器人室内墙面作业任务主要是对房间内的墙面进行抛光、打磨或者喷漆等, 而要完成这项任务, 规划出能够覆盖所有墙面的沿墙路径对于机器人完成墙面作业任务起着关键性的作用^[2]. 室内墙面作业任务的作业范围主要包括房间出口和窗户上边缘的所有墙面, 要实现自动化的完整墙面作业, 机器人的沿墙作业路径不仅需要保证机器人能够在单个房间内实现墙体跟随^[3], 更需要考虑机器人在完成一个房间的墙面作业任务后需要移动到另一个房间的问题. 平层多房间室内沿墙路径规划任务主要分为房间内的沿墙路径规划任务和移动机器人在房间之间移动的路径规划任务, 房间内的沿墙路径规划负责生成机器人单房间内的沿墙路径, 房间之间的路径规划负责生成移动机器人在多房间之间移动时点到点的路径规划, 并在环境中存在工作人员或者其他障碍物的条件下, 实现机器人的动态避障.

房间内的传统沿墙路径规划方法主要依赖于传感器获取机器人和墙体之间的位置和方向等信息, 墙体跟随算法根据传感器实时数据调整机器人的姿态, 实现墙体跟随. Van Turennout等人^[4]首次提出了墙体跟随的概念, 在运动学模型的基础上使用了超声波传感器测量机器人和墙体之间的距离, 实现了简单的机器人墙体跟随, 但难以适应墙体存在裂缝的情况. Holder等人^[5]将超声波传感器换成了旋转声呐传感器来对机器人进行沿墙导航, 使用声呐传感器来进行机器人和墙体之间距离的测量, 但是串扰镜面反射问题使得机器人对距离有错误的判断, 墙体跟随效果并不理想. Wu等人^[6]是使用红外传感器来解决声呐传感器带来的串扰镜面反射问题, 但红外传感器收集到的信息有限, 且精度较低. 另一部分学者使用模糊神经网络融合视觉传感器和激光雷达传感器收集到的信息, 通过判断机器人位姿的方式来控制机器人进行墙体跟随. 传统的沿墙规划算法属于在线沿墙路径规划, 当机器人进行墙面作业任务导致环境产生大量灰尘或者雾气时, 传感器会失效, 墙面作业机器人无法继续进行工作. 另外, 当室内房间出现多出口时, 传统沿墙路径规划算法也难以生成完整的沿墙规划路径.

房间之间的点到点路径规划方法主要分为传统路径规划方法和基于强化学习的路径规划方法. 传统的路径规划方法实现动态避障依赖于高精度的实时地图, 根据已知的地图信息生成路径点. A*算法^[7]使用启发式的搜索引导搜索的方向在地图中搜索最优路径. Jiang等人^[8]为了提高JPS (jump point search)算法的工作效率, 在JPS算法的基础上加入了预处理, 提出了JPS+算法. Karaman等人^[9]的RRT*算法引入代价函数来不断迭代优化初始路径, 使得初始路径收敛为一条最佳路径.

基于强化学习的路径规划方法通过不断在环境中学习最优的学习策略, 并将奖励信号映射到动作上来学习最优策略. Xin等人^[10]首次在机器人领域引入了深度Q网络(deep Q-network, DQN), 实现了从传统路径规划算法到基于强化学习的路径规划算法的过渡. DeepMind团队进一步对DQN算法进行了迭代, 提出了双Q学习算法(double DQN)^[11]对Q值进行估计, 取较小的Q值进行网络更新, 一定程度上解决了DQN算法中Q值高估的问题. 竞争深度Q学习算法(dueling deep Q learning algorithm, Dueling DQN)^[12]算法在DQN算法的基础上加入了价值函数网络和优势函数网络优化神经网络, 线性组合两个网络的输出估计Q值, 加快网络的收敛速度. 优先级经验回放(prioritized experience replay, PER)^[13]算法则是通过改变经验池中经验的权重, 提高权重大的经验的采样率加快算法的收敛速度. 为了解决DQN算法在高维空间中容易因为动作空间维度过多出现维度灾难问题, Silver等人^[14]引入确定性策略(deterministic policy gradient, DPG)对机器人进行连续控制, 使用Actor网络预测出动作, 缓解了DQN算法中动作维度过多的问题. Fujimoto等人^[15]提出了双延迟深度确定性策略(twin delayed deep deterministic policy gradient, TD3), 使用双延迟和高斯噪声的方法来增加算法的稳定性并加快算法的收敛速度. Tan等人^[16]在TD3算法的基础上引入PER策略, 进一步提高了TD3算法在动态环境中算法的收敛速度. 然而, 相比于软行动者-评论家算法(soft actor critic, SAC)^[17], TD3算法在相同效率的条件下具备更多的参数, 增加了网络的训练的难度和网络复杂度. 基于强化学习的路径规划方法虽然可以处理点到点的路径规划问题, 但在动态环境中还是存在收敛速度慢的问题.

对于多房间的墙面操作任务, 由于墙面操作带来重灰尘或者雾气等可能导致传感器失效, 此外在跨房间移动的过程中还可能会和障碍物发生碰撞. 为解决上述问题, 本文提出两阶段路径规划方法, 该方法可以离线生成沿墙路径, 并完成动态环境中跨房间移动的点到点的路径规划.

本文的主要贡献如下.

1) 为解决灰尘或雾气导致的传感器失效问题, 以及房间存在多出口路径规划不完整问题. 本文提出一种新的起点自动选择沿墙路径规划方法, 基于栅格地图离线规划沿墙路径.

2) 为解决动态环境中点对点路径规划收敛速度慢的问题. 本文提出PSAC (prioritized experience replay soft actor critic)算法, 利用PER策略改变经验池中经验的优先级, 加快SAC算法的收敛速度.

3) 为了验证本文方法的优越性, 本文针对不同的房间类型设计了点云地图, 并在动态环境对本文方法进行了比较分析.

本文的总体结构如下: 第2节给出两阶段路径规划方法框架. 第3节通过实验验证了两阶段路径规划方法的有效性. 第4节是本文的总结.

2 两阶段路径规划方法

两阶段路径规划方法包括起点自动选择沿墙路径规划和基于强化学习的路径规划方法. 对三维点云地图进行处理得到栅格地图. 起点自动选择沿墙路径规划方法以栅格地图为输入, 基于栅格地图生成各房间的起点, 并生成房间的沿墙路径. 基于PSAC的路径规划方法使得机器人在动态的环境中能够进行动态避障, 并完成点到点的路径规划. 我们提出的两阶段路径规划方法结构如图1所示.

图 1 两阶段路径规划方法框架

2.1 起点自动选择沿墙路径规划方法

机器人沿墙路径规划的实质是根据机器人所处的环境, 通过有限的实时传感器数据完成对机器人的实时控制. 传统的基于移动机器人运动学模型的控制器方法, 在多房间的工作环境中, 移动机器人的工作过程中过于复杂, 且容易出现多出口规划路径不完整、墙面操作产生的灰尘或大雾使得传感器失效等问题.

我们提出的起点自动选择沿墙路径规划方法以多房间墙面作业为出发点, 解决多房间沿墙路径规划问题. 经过调研发现常规房间的门和窗户的上边缘均和天花板存在一定的距离, 从地面到天花板的方向为z轴正方向, 取不同高度的横截面进行处理, 获得标准多房间的顶部栅格图和底部栅格图如图2(b)和图2(c)所示. 顶部栅格图中每个房间没有出口, 而底部栅格图则保存各房间的出口位置.

图 2 三维点云地图和栅格地图

栅格地图由多个像素点组成. 基于顶部栅格图, 使用起点自动选择沿墙路径规划方法获得每个房间的起点. 其中起点选择框如图3所示, 起点选择框是一个正方形, 边长是单个像素点边长的整数倍. 起点选择框在顶部栅格图上遍历, 对顶部栅格图中的像素点进行评估. 评估公式如下:

$\rho = \frac{{\displaystyle\sum\limits_n^i {{A_{i0}} + \displaystyle\sum\limits_n^j {{A_{oj}}} } }}{{2{{n}}}}$

(1)

$\beta = \frac{{\displaystyle\sum\limits_n^{i + 1} {\displaystyle\sum\limits_n^{j + 1} {{A_{{{ij}}}}} } }}{{{{{n}}^2} - 2{{n}}}}$

(2)

其中, $\;\rho$ 和 $\;\beta$ 是我们的评估值, 当 $\;\rho$ 趋近于1, $\;\beta$ 趋近于0时, 该点被标记为预选起点, 便于后续筛选. n表示起点选择框的边长, ${{{A}}_{ij}}$ 表示起点选择框内元素的像素值, ${{{A}}_{i0}}$ 为起点选择框第1列像素点的像素值, ${{{A}}_{0j}}$ 为起点选择框第1行像素点的值. 该起点框在顶部栅格图上进行连续过滤, 评估出顶部栅格图中所有满足条件的预选起点在顶部栅格图中的位置. 对顶部栅格图中检测两个预选起点之间的连通性进行评估, 保存存在连通性且 ${{i}}$ 和 ${{j}}$ 之和较小的预选起点作为各房间沿墙路径规划的起点.

图 3 起点自动选择框

起点自动选择沿墙墙体跟随路径规划方法基于起点和顶部栅格图生成室内沿墙规划路径. 算法的伪代码如算法1.

算法1. Start-point automatic select wall following path planning

输入: Grid map.

输出: The list of path points.

$\scriptstyle {\textit{TR}}$ , $\scriptstyle {\textit{TR}}'$ , $\scriptstyle {\textit{TL}}$ , $\scriptstyle {\textit{TL}'}$ , $\scriptstyle {T}$ , distance, $\scriptstyle {\text{list}}$ // Initialization parameters

While distance <= 0.1 do

　Get the value of $\scriptstyle {\textit{TR}}'$ and $\scriptstyle {\textit{TL}'}$

　if $\scriptstyle {\textit{TR}}'$ or $\scriptstyle {\textit{TL}'}$ then

　　 $\scriptstyle {\textit{TR}}$ ← $\scriptstyle {\textit{TR}}$ + 1, $\scriptstyle {\textit{TL}}$ ← $\scriptstyle {\textit{TL}}$ + 1

　　 $\scriptstyle {\text{list}}$ ← $\scriptstyle (x, y)\triangleright$ Save path points in list

　else

　　 $\scriptstyle {\text{list}}$ ← $\scriptstyle (x, y)$

　end if

　 $\scriptstyle {{T}}$ ← $\scriptstyle {\textit{TL}}$ – $\scriptstyle {\textit{TR}}$

　Get Direction by $\scriptstyle {T}$

　Get next point $\scriptstyle (x, y)$

end while

面向平层多房间的墙面作业问题, 移动机器人很难直接生成平层多房间的整体沿墙规划路径. 顶部栅格图的目的是将平层多房间墙面作业问题分解为单个封闭房间内的墙面作业问题. 在封闭环境中进行单房间的沿墙路径规划时, 起点和目标点重合. 当机器人回到起点, 标志着单个房间内的沿墙路径规划完成. 参数 ${\text{Direction}}$ 用来记录机器人的方向, ${\text{Direction}}$ 的获取公式如下:

${\text{Direction}} = (T {\text{%}} 4 + 4) {\text{%}} 4$

(3)

${\textit{TR}}'$ 和 $\textit{TL}{'}$ 分别记录机器人沿着行进方向右转和左转的坐标. ${T}$ 是 ${\textit{TR}}$ 和 ${\textit{TL}}$ 的差值. 在栅格地图中, 设定 ${\text{X}}$ 的正方向为垂直向下, ${\text{Y}}$ 的正方向为水平向右. ${\text{Direction}}$ 的取值方式如下:

$\text{Direction}=\left\{\begin{array}{l}0, \; \text{X}正方向\\ 1, \; \text{Y}正方向\\ 2, \; \text{X}负方向\\ 3, \; \text{Y}负方向\end{array} \right.$

(4)

移动机器人在栅格地图上的整体路径规划方向沿逆时针方向, 如图4所示. distance是当前位置和目标位置之间的距离, 当distance小于阈值时, 表示房间内的沿墙路径规划完成. 当起点自动选择沿墙路径规划方法依据起点选择框生成的预选起点生成顶部栅格图中所有单个房间的起点时, 机器人平层多房间的沿墙路径规划任务完成.

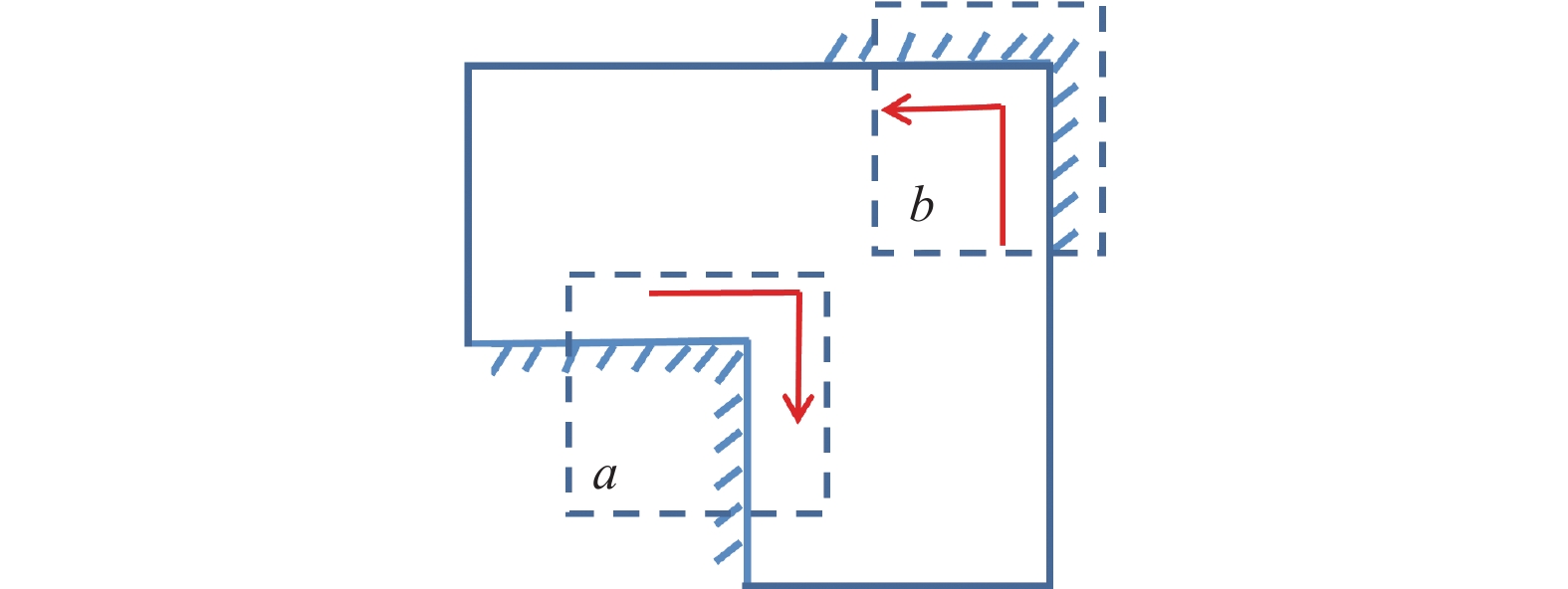
图 4 阴阳角示意图

2.2 PSAC算法

在机器人平层多房间沿墙作业任务的路径规划过程中, 点对点路径规划是机器人在进行跨房间移动需要解决的问题. 当机器人处于动态环境中时, 传统路径规划算法依赖于传感器获得的实时高精度地图实现机器人的路径规划, 但高精度的传感器的要求很难得到满足. 基于强化学习的路径规划方法在动态环境中虽然表现出了更好的动态避障能力, 但复杂的环境极大地影响了算法的收敛速度.

我们提出一种基于PSAC的路径规划方法, 该方法能够根据机器人当前的状态生成动作驱动机器人在动态环境中实现动态避障. 基于PSAC的路径规划方法是在基于SAC的路径规划方法中加入了优先级经验更新策略, 使得PSAC算法在训练的过程中, PSAC算法中的优先级经验更新策略能够根据TD-error(temporal difference error)的绝对值更新经验池中不同样本的权重, 提高PSAC算法在训练阶段从经验池中采样到有益于网络收敛的样本的概率, 进而加快PSAC算法在动态环境中的收敛速度.

PSAC算法结构如图5所示.

图5中S是机器人当前所处的状态, A是策略网络基于机器人当前的状态预测的动作A_t. 基于S控制机器人角速度的频率为20 Hz, S'是机器人执行动作A_t后的新状态, R是机器人执行动作A_t后获得的奖励.

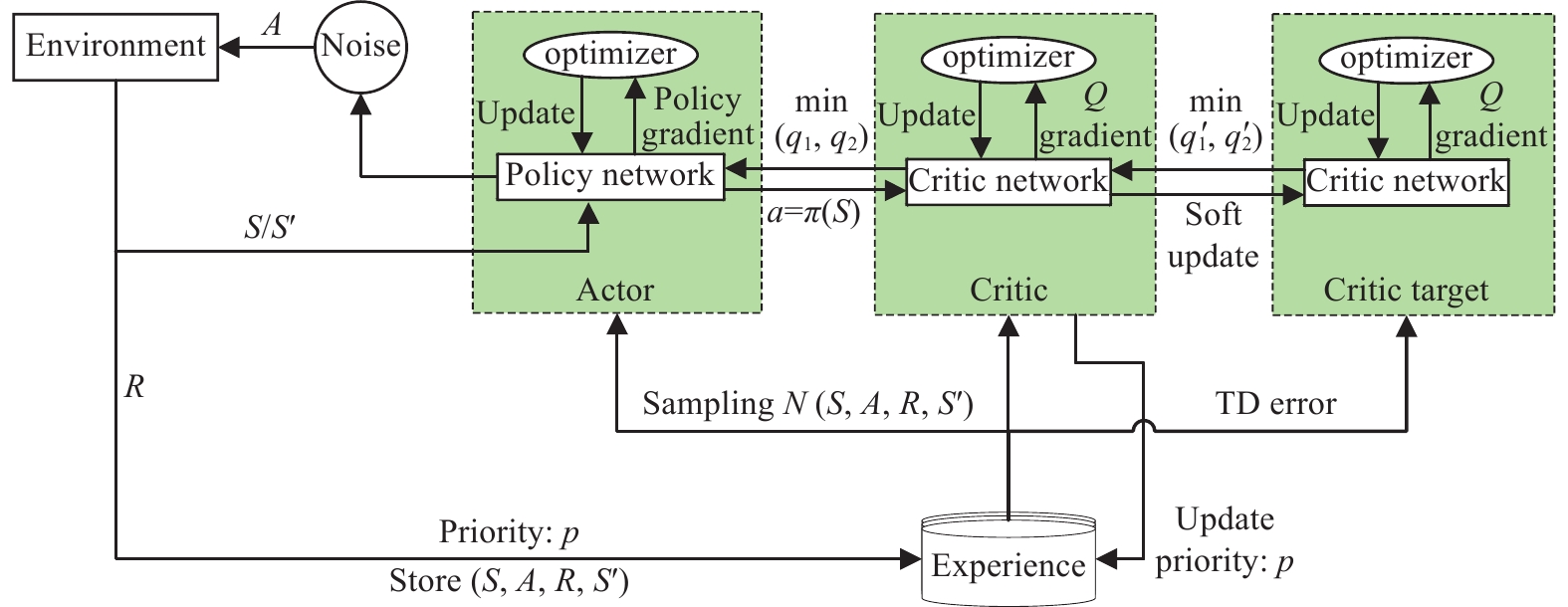
图 5 PSAC算法结构

在迭代的过程中, p表示样本中经验的优先级, p越大表示样本被抽样的概率越大. 加入PER策略后, 考虑样本优先级后PSAC算法中Q网络的损失函数为:

${\textit{Loss}} = \frac{1}{{{m}}}{\sum\limits_{j = 1}^m {{w_j}({y_j} - Q({S_j}, {A_j}, w))} ^2}$

(5)

其中, ${{{w}}_{{j}}}$ 是第 ${{j}}$ 个样本的优先级权重, 通过对TD-error进行归一化获得. TD-error的计算方法如下:

${\delta _{{j}}} = {y_j} - Q({S_j}, {A_j}, w)$

(6)

通过神经网络的梯度反向传播来更新Q网络的所有参数 $w$ , 在Q网络进行梯度更新之后, 重新计算TD误差并更新到经验池的SumTree中所有节点.

3 实验分析

为了验证本文方法的有效性, 针对两阶段路径规划方法设置了两种实验. 针对平层多房间沿墙路径规划中存在的传感器失效和路径规划不完整的问题, 我们设计了存在多出口的平层房间, 通过对比生成的沿墙作业路径的条数和生成路径的完整程度两个指标, 验证两阶段路径规划方法的可行性. 针对基于强化学习的路径规划方法收敛速度慢的问题, 我们搭建了相应的仿真环境, 通过对比算法的收敛速度、生成路径的长度和执行时间3个指标, 验证两阶段路径规划方法的有效性.

3.1 起点自动选择沿墙路径规划方法实验

根据房间的形状将房间分为矩形、凹矩形、凸矩形和多边形, 不同类型的房间的形状如图6所示. 在我们的实验中, 我们使用CloudCompare软件将不同种类的房间, 按照正常房间的高度和宽度等比例进行组合设计了三维点云图, 如图2(a)所示.

针对上述4种不同类型的房间, 使用起点自动选择框对各个房间进行单独实验, 基于顶部栅格图获取各房间的起点. 实验结果如图7所示.

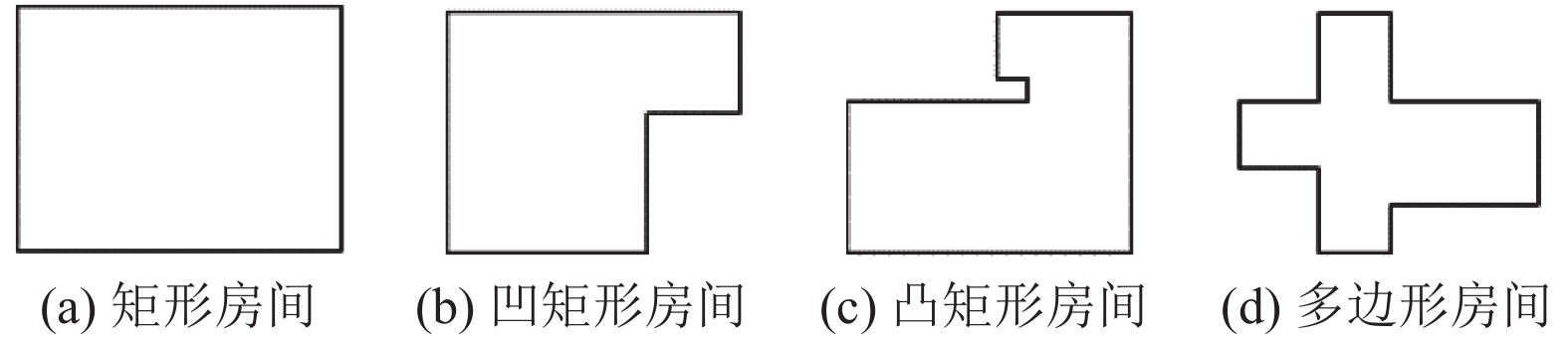
图 6 不同房间形状

图 7 生成的各房间起点 (黑色的点是起点位置)

图7中的实验结果表明, 起点自动选择框能够针对不同类型的房间自动生成各房间的起点. 利用图7中各房间的起点, 使用传统沿墙路径规划算法和起点自动选择沿墙路径规划方法分别在地图中进行实验, 生成各房间的沿墙规划路径, 实验结果如图8(a)和图8(c)所示. 在不考虑起点位置的条件下, 使用传统沿墙路径规划方法对各房间进行沿墙路径规划, 生成的沿墙规划路径图8(b)所示.

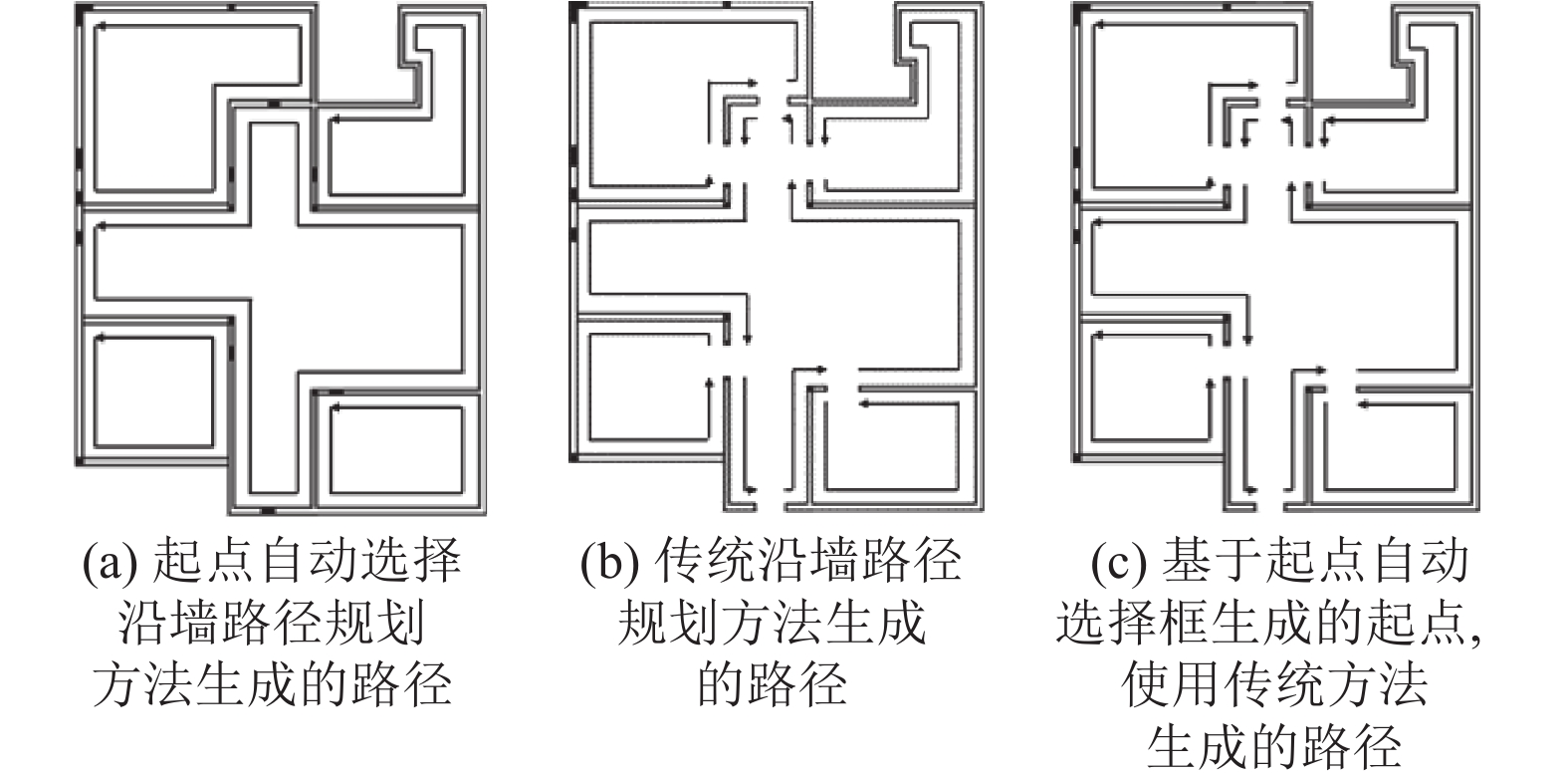
图 8 不同方法生成的多房间的沿墙路径规划

图8的实验结果对比表明, 我们的起点自动选择沿墙路径规划算法能够适应不同类型的房间, 准确识别房间中阳角和阴角的位置, 生成的路径包含出口的上边缘的墙面, 路径的完整程度比传统沿墙路径规划方法生成的沿墙路径更高.

针对房间多出口以及环境中存在灰尘或者烟雾等问题, 我们对两种沿墙路径规划方法生成的路径段数(即需要作业的墙体数量)和规划路径是否完整进行了对比, 对比结果如表1所示.

表1的实验结果表明, 当房间只有一个出口时, 两种沿墙路径规划方法的沿墙规划路径相当; 当房间存在多出口时, 传统沿墙路径规划方法生成的沿墙路径和出口数量有关, 需要根据出口的位置对每段墙壁分别设置起点. 而本文所提方法能够仅基于起点自动选择框生成的起点完成沿墙路径规划, 且每段路径能够使得机器人进行单房间内的全部墙面作业.

表 1 不同条件下的沿墙路径对比

当传感器失效时, 基于传感器的传统沿墙路径规划方法无法完成沿墙路径规划. 起点自动选择沿墙路径规划方法属于离线路径规划方法, 在离线的条件下能够完成室内沿墙路径规划, 不受环境因素的影响, 保证机器人能够有效地完成墙面作业任务.

3.2 动态避障实验.

多房间室内动态仿真环境是基于图2(c)的底部栅格图搭建的, 如图9所示, 白色柱子代表动态障碍物, 带箭头的线是动态障碍物的运动轨迹. 黑色的机器人在地图的左上角, 仿真地图的墙由24面墙组成. 我们在仿真地图中比较了PSAC算法和SAC算法的训练的收敛速度以及进行路径规划的能力.

图 9 仿真环境

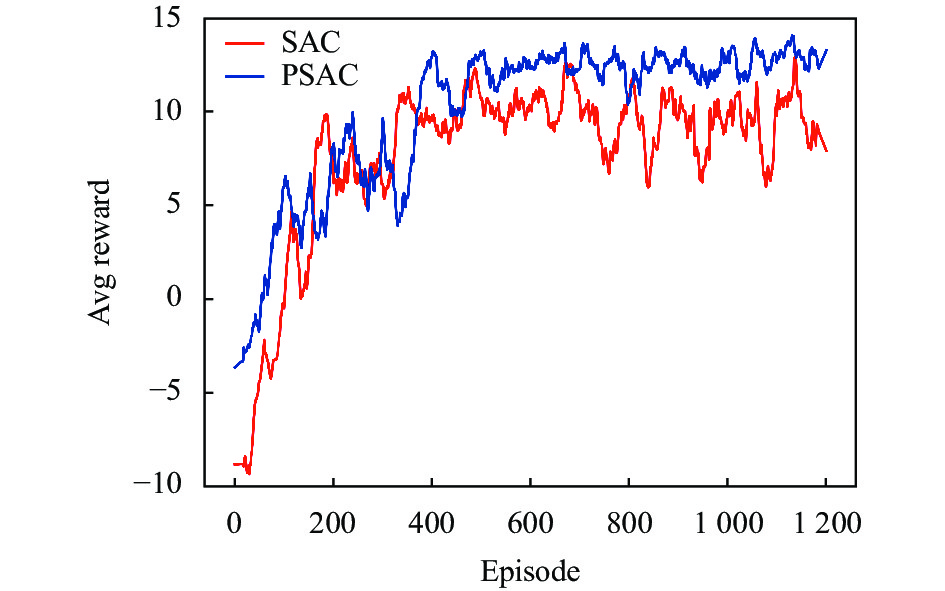
图10的实验结果表明, 在动态环境中, 加入PER策略后的PSAC算法要比SAC算法收敛速度更快, 且获得的奖励更高. 这证明PER策略能够通过改变SAC算法经验池中样本的权重, 提高智能体在训练的过程中从经验池中获取有价值经验的效率, 加快算法的收敛速度.

我们在动态仿真环境中分别设置了两种动态避障实验, 一种是大范围避障, 另一种是狭窄范围避障. 机器人的起始位置和目标位置如图11所示, 分别使用PSAC算法和SAC算法在动态环境中生成机器人的动态避障路径如图12所示, 其中SAC算法生成的路径用红色表示, PSAC算法生成的路径用紫色表示. 表2给出了PSAC算法和SAC算法生成的路径长度与执行时间的比较.

图 10 动态环境下PSAC算法和SAC算法的奖励比较

图 11 动态环境 (方块区域为目标位置)

图 12 动态环境下SAC和PSAC的路径

表 2 路径长度和执行时间对比

图12和表2的实验结果表明, PSAC算法对环境变化比SAC算法更加敏感, 可以在与障碍物保持安全距离的同时完成点到点的路径规划, 且规划的路径和执行时间更短. 相比之下, SAC算法在动态环境中对环境的变化较为迟钝, 在遇到障碍物之前选择先移动到较远的位置, 然后再继续向目标位置移动. 在实验过程中, PSAC算法生成的路径相比于SAC算法, 在路径长度上要缩短了近22%, 执行时间减少了约28%.

3.3 基于真实地图的实验

真实场景的实验分成两个部分进行验证. 第1部分是基于真实场景的点云地图生成平层所有房间的栅格地图, 在栅格地图上使用两阶段路径规划方法进行沿墙路径规划. 第2部分是在基于真实场景搭建的仿真地图中进行点到点的动态避障实验, 验证PSAC算法在点到点的路径规划的动态避障能力. 两个平层毛坯房间的三维点云地图如图13所示, 实验中使用两阶段路径规划方法对两个平层毛坯房分别进行路径规划.

图 13 平层毛坯房间点云地图

3.3.1 起点自动选择沿墙路径规划方法实验

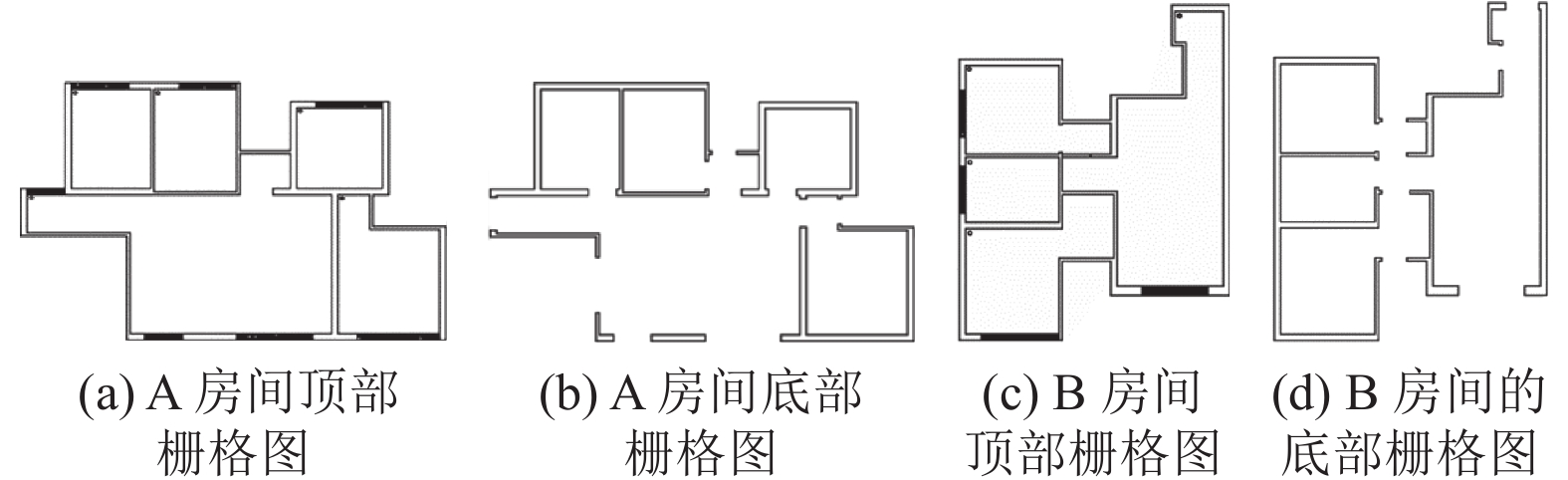
毛坯房间A和房间B的三维点云地图生成的顶部栅格图和底部栅格图如图14所示, 基于房间A的顶部栅格图14(a)和房间B的顶部栅格图14(c), 使用起点自动选择框生成各房间的起点如图14(a)和图14(c)所示. 使用起点自动选择沿墙路径规划方法生成的沿墙规划路径如图15(a)和图15(c)所示. 基于起点自动选择框给出的各房间的起点位置, 传统沿墙路径规划方法生成沿墙路径如图15(b)和图15(d)所示.

图 14 毛坯房间的栅格地图

图 15 两种算法生成的毛坯房间沿墙路径

实验结果采用两个评价指标来评价沿墙规划算法的有效性. 一是机器人完成沿墙作业的路径的条数. 起点自动选择沿墙路径规划算法可以营造封闭的作业环境, 生成的路径段数更少. 另一个是生成路径的完整程度. 传统沿墙路径规划方法生成的沿墙路径会忽略出口位置的上边缘到天花板部分的墙壁作业. 图14 和图15的实验结果证明, 我们的起点自动选择沿墙路径规划算法可以在离线的条件下对毛坯房的沿墙作业进行沿墙路径规划, 可以极大程度地避免机器人在进行沿墙作业过程中传感器失效的问题.

表3的实验对比结果显示, 在缺乏人工干预和不考虑传感器失效的条件下, 两种沿墙路径规划方法都能生成沿墙路径, 但传统沿墙路径规划方法生成的沿墙路径的条数和房间的出口数量有关, 显著多于起点自动选择沿墙路径规划方法. 另一方面, 传统沿墙路径规划方法在进行沿墙路径规划时会主动忽略出口位置, 机器人无法进行出口上边缘位置的墙面作业, 造成机器人作业路径的不完整. 相比之下, 起点自动选择沿墙路径规划方法表现出了卓越的沿墙路径规划能力, 完成了机器人的沿墙路径规划.

表 3 不同条件下两个房间的沿墙路径对比

3.3.2 动态避障实验

在多房间的沿墙路径规划过程中, 动态避障发生在机器人跨房间移动的过程中, 因此要验证真实环境中PSAC算法的动态避障能力, 只需要针对跨房间移动中的动态避障问题进行单独验证. 为了验证PSAC算法在跨房间移动过程中动态避障的有效性, 我们搭建了如图16(a)和图16(b)所示的场景, 基于该场景生成仿真地图, 模拟机器人在动态环境中点到点的路径规划. 图16(c)中①为起始位置, ②为终点, ③为移动的障碍物, ④为碰撞区域. 图16(d)中①表示SAC算法规划的路径, ②表示PSAC算法规划的路径.

图 16 真实场景地图

该场景下的底部栅格图如图16(c)所示, 我们在该场景中进行多次重复实验以验证算法在真实场景中的动态避障能力. 采用两个指标来评价PSAC算法的动态避障的有效性. 一个是PSAC算法进行动态避障后的规划路径总距离, PSAC算法生成的算法受障碍物的影响较小, 生成的路径的总长度更短. 另一个是到达目标点的执行时间, 评价机器人的速度. 其中PSAC算法和SAC算法生成的规划路径如图16(d)所示.

我们同时对PSAC算法和SAC算法生成的路径的长度和执行时间进行了对比, 对比结果如表4所示.

表 4 实验中路径长度和执行时间对比表

表4的实验对比结果表明, 在真实场景中, PSAC算法和SAC算法都能够在动态环境中进行动态避障, 但相较于SAC算法, 我们的二阶段路径规划方法中的PSAC算法对收集到的动态环境中的信息更加敏感, 为机器人的动态避障发出正确的指令同时, 生成更短的路径, PSAC算法在实验中表现出了更好的稳定性, 规划的路径平均长度更短且执行时间更少.

4 结论与展望

针对平层多房间墙面作业机器人路径规划问题, 本文提出了两阶段路径规划方法, 解决了房间内墙面作业过程中传感器失效和机器人跨房间移动时动态避障与训练收敛速度慢的问题. 实验结果证明, 两阶段路径规划能够离线生成机器人室内墙面作业的沿墙路径, 规避机器人进行室内沿墙作业过程中多尘或多雾造成的传感器失效问题, 同时解决了出口上边缘墙面被忽略的问题. 两阶段路径规划方法中的基于PSAC的路径规划算法在训练的过程中具有更快的收敛速度, 且在实验的过程中能够感知环境中的动态障碍物, 并根据机器人所处的状态规划出更短的路径, 实现机器人的点到点的动态避障.

在未来的工作中, 我们将进一步构建出更加复杂的实验场景, 并在实验场景中验证该方法的可行性, 同时考虑多机器人在动态环境中的协同作业.

参考文献

[1]	Bormann R, Jordan F, Hampp J, et al. Indoor coverage path planning: Survey, implementation, analysis. Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA). Brisbane: IEEE, 2018. 1718–1725.
[2]	Xiao XS, Liu B, Warnell G, et al. Motion planning and control for mobile robot navigation using machine learning: A survey. Autonomous Robots, 2022, 46(5): 569-597. DOI:10.1007/s10514-022-10039-8
[3]	Zuo SX, Ou YS, Zhu XR. A path planning framework for indoor low-cost mobile robots. Proceedings of the 2017 IEEE International Conference on Information and Automation (ICIA). Macao: IEEE, 2017. 18–23.
[4]	Van Turennout P, Honderd G, Van Schelven LJ. Wall-following control of a mobile robot. Proceedings of the 1992 IEEE International Conference on Robotics and Automation. Nice: IEEE, 1992. 280–285.
[5]	Holder MB, Trivedi MM, Marapane SB. Mobile robot navigation by wall following using a rotating ultrasonic scanner. Proceedings of the 13th International Conference on Pattern Recognition. Vienna: IEEE, 1996. 298–302.
[6]	Wu GD, Zhu ZW, Chien CW. Sparse-sensing-based wall-following control design for a mobile-robot. Proceedings of the 2016 IEEE International Conference on Control and Robotics Engineering (ICCRE). Singapore: IEEE, 2016. 1–5.
[7]	Song R, Liu YC, Bucknall R. Smoothed A* algorithm for practical unmanned surface vehicle path planning. Applied Ocean Research, 2019, 83: 9-20. DOI:10.1016/j.apor.2018.12.001
[8]	Jiang CJ, Sun SF, Liu JL, et al. Global path planning of mobile robot based on improved JPS+ algorithm. Proceedings of the 2020 Chinese Automation Congress (CAC). Shanghai: IEEE. 2020. 2387–2392.
[9]	Karaman S, Frazzoli E. Sampling-based algorithms for optimal motion planning. The International Journal of Robotics Research, 2011, 30(7): 846-894. DOI:10.1177/0278364911406761
[10]	Xin J, Zhao H, Liu D, et al. Application of deep reinforcement learning in mobile robot path planning. Proceedings of the 2017 Chinese Automation Congress (CAC). Jinan: IEEE, 2017. 7112–7116.
[11]	Van Hasselt H, Guez A, Silver D. Deep reinforcement learning with double Q-learning. Proceedings of the 30th AAAI Conference on Artificial Intelligence. Phoenix: AAAI, 2016. 2094–2100.
[12]	Wang ZY, Schaul T, Hessel M, et al. Dueling network architectures for deep reinforcement learning. Proceedings of the 33rd International Conference on International Conference on Machine Learning. New York: JMLR, 2016. 1995–2003.
[13]	Schaul T, Quan J, Antonoglou I, et al. Prioritized experience replay. Proceedings of the 4th International Conference on Learning Representations. San Juan: ICLR, 2015.
[14]	Silver D, Lever G, Heess N, et al. Deterministic policy gradient algorithms. Proceedings of the 31st International Conference on International conference on machine learning. Beijing: JMLR, 2014. 387–395.
[15]	Fujimoto S, Hoof H, Meger D. Addressing function approximation error in actor-critic methods. Proceedings of the 35th International Conference on Machine Learning. Stockholm: PMLR, 2018. 1587–1596.
[16]	Tan YJ, Lin YH, Liu T, et al. PL-TD3: A dynamic path planning algorithm of mobile robot. Proceedings of the 2022 IEEE International Conference on Systems, Man, and Cybernetics (SMC). Prague: IEEE, 2022. 3040–3045.
[17]	Haarnoja T, Tang HR, Abbeel P, et al. Reinforcement learning with deep energy-based policies. Proceedings of the 34th International Conference on Machine Learning. Sydney: JMLR, 2017. 1352–1361.