在线教育课堂正逐渐兴起, 源于西方的MOOC(massive open online courses)也迅速遍布全球, MOOC学习作为一种新型学习模式, 吸引了成千上万的学习者. 随着学习者人数的增多, 带来一个矛盾, 即庞大的学习者群体与紧缺的教师资源之间的矛盾^[1]. 以MOOCs edX为例, 它曾经开设的“Circuits and Electronics” (6.002x)课程有155 000名学习者注册, 教学团队仅有12名^[2]. 由于学习者人数众多, 教师或助教无法为所有的解决方案进行打分, 因此迫切需要提出一种可扩展的替代传统学生评估的方法. 而同伴互评成为解决这一问题的实用解决方法, 即将解决方案分发给学习者的同伴, 由学习者的同伴进行解决方案的评估, 评估完成后将结果反馈给学习者. 同伴互评不仅减轻了教师批改解决方案的压力, 而且有助于加深学习者的理解^[3].

同伴互评中的评估者通常根据课程教师提供的准则或基准对其他学习者提交的解决方案进行评估, 其中解决方案的最终得分是分数的某种聚合, 这种聚合通常是评估者给出的同伴互评分数的中值或平均值. 但由于评估者自身的知识储备不足以及缺乏准确评估他人的动机, 或是出于保护自身利益而做出的战略性评估(如评估者为了获取更高的分数而恶意降低被评估者的评分或评估者受人际关系的影响给予被评估者不应有的高分等评估行为), 导致同伴互评的准确性和可靠性降低, 得出不公平或不准确的分数. 因此, 关于同伴互评的一个直接问题是同伴互评分数的准确性. 为了得到更准确的同伴互评分数, 许多学者对在线学习环境下同伴互评的真实分数估计展开了研究, 其中基于加权聚合的估计方法常用于评估者给予解决方案的反馈内容为分数的情况. 具体来说, 基于加权聚合的估计方法会因为评估者的评估准确性和可靠性去补偿在同伴互评过程中引入的故意或无意的偏见, 从而估计得出同伴互评的真实分数.

现有的基于加权聚合的估计方法大多基于这样的假设, 评估者的评估准确性通过评估者评估或提交的解决方案的质量来衡量. 而衡量评估者的评估准确性的方法主要分为两类, 一类是仅通过学生评估者自身提交或评估的解决方案来进行衡量, 没有使用教师或助教评估者评估的解决方案作为对比^[4–6]; 另一类则是使用了教师或助教评估者评估的解决方案作为对比^[7,8]来进行衡量.

然而, 在上述关于评估者评估准确性的考虑中仍然存在一些限制, 现有的考虑评估者评估准确性的因素大多与评估者的评估行为有关, 缺少对同伴互评过程中由于社交利益而存在的战略性评估的研究. 例如, 评估者对自身解决方案的评估与对同伴解决方案的评估之间的差异会在同伴互评过程中引入偏见, 而这种偏见并没有被考虑到影响评估者评估准确性的因素中去.

文献[9]提出了一种由社会所有权评估网络SOAN(social-ownership-assessment network)和图卷积网络GCN (graph convolution network)构成的半监督聚合方法GCN-SOAN. 在该机制中没有任何特定的或限制性的归纳偏见, 并且适应于各种模式的同伴互评. SOAN中存在评估关系、社会关系以及所有权关系. 评估关系与所有权关系可以表示为节点类型为评估者与解决方案的加权图, 在评估关系中评估者与解决方案之间的边为同伴互评的分数, 在所有权关系中评估者与解决方案之间的边为评估者评估和解决的解决方案的数量. 社会关系则表现为节点类型为评估者的单类型图, 评估者之间的边展现了评估者之间的社交利益关系, 但并没有给出衡量社交利益关系的方法. 文中将在图卷积的过程中聚合邻居节点信息的操作视为同伴互评分数的加权聚合, 使用教师评估作为基本事实, 通过最小化其均方根误差来学习网络的参数, 以此来预测同伴互评的分数. 但GCN在聚合邻居节点时使用固定的邻居权重进行信息聚合, 无法有效地区分不同邻居节点的重要性.

本文在文献[9]的工作上提出了ITSA (is there a strategic assessment)方法用于获取社交利益关系, 在ITSA方法中定义了评估者具有两个特征: 自我评分能力以及同伴评分能力, 通过比较两者的差异获得社交利益关系和社交利益因子, 创建了社交利益关系所有权评估网络SIROAN (social interest relationship ownership assessment network), 同伴评分能力的计算方法则参考了文献[8]中评估者的评分能力的计算方法. 并引入了图注意力网络(graph attention network, GAT)^[10], 在邻域聚合过程中使用自适应的注意力机制来计算节点的注意力系数, 允许每个节点对其邻居节点分配不同的权重, 考虑每个节点的重要性, 以此来聚合同伴互评的分数. 使用教师评分成绩作为基本事实, 通过最小化其均方根误差学习网络的参数, 来预测同伴互评分数. 我们的方法考虑了评估者之间的社交利益关系, 考虑了评估者如何相互影响和相互作用, 在一定程度上阻止了评估者之间的战略性评估. 并且在聚合过程中考虑了注意力系数, 每个节点可以根据与其他节点的关系进行不同程度的注意, 使得在聚合过程中更加关注相关节点的特征, 降低对无关节点的依赖, 从而提高了预测能力, 能够得到更准确的同伴互评预测分数.

1 相关工作 1.1 同伴互评的真实分数估计

在同伴互评的真实分数估计方面已有许多研究工作, 根据评估者对解决方案评估内容的是质量的排名还是分数的高低, 同伴互评的真实分数估计方法可以分为序数(ordinal)估计方法和基数(cardinal)估计方法. 在序数估计方法中, 评估者对解决方案的评估内容是质量高低的排名, 主要利用矩阵分解^[11]、模糊决策^[12]、贝叶斯^[13]等方法来估计同伴互评解决方案的质量. 在基数估计方法中, 评估者对解决方案的评估内容则是分数. 当前流行的基数估计方法有基于概率图模型的估计方法以及基于加权聚合的估计方法. 基于概率图模型的估计方法的核心思想是把与解决方案存在一定联系的真实分数、评估者的可靠性及偏见、互评分数视作显性或隐性的随机变量, 并建模为服从一定概率分布的模型, 然后基于显性的互评分数来推断隐性随机变量的值. 现有的概率图模型有PG1–PG7^[14–16]. 基于加权聚合的估计方法定义了评估者的准确性和信任度, 并根据它们的差异赋予不同的权重, 然后聚合评估者对同一解决方案的真实分数^[17]. 基于加权聚合的估计方法将在第1.2节进行详细阐述.

1.2 基于加权聚合的估计方法

在基于加权聚合的估计方法中评估者的准确性和信任度与其提交或评估的解决方案质量有关. 例如, 文献[4]提出的Voncouver算法, 该算法将不同评估者对同一份解决方案的评估差异视作评估者的评分准确性, 然后赋予准确性高的评估者更高的权重, 最后加权聚合得到该解决方案的一致分数. 文献[6]则假设评估者提交的解决方案与其评估能力有关, 受到Google的网页排序PageRank算法^[18]的启发提出了另一种迭代加权算法PeerRank^[6], 对每一份提交解决方案的多个同伴互评分数进行加权求和. 文献[5]则将评估者的学习参与度视作影响评估解决方案真实分数准确性的因素, 赋予学习参与度高的评估者更高的权重. 而这种参与度只能通过线上课堂来获取, 对于传统课堂可以采用电子签到的形式来获取评估者的学习参与度^[19]. 文献[7]则在PeerRank基础上提出了RankwithTA, RankwithTA使每个学习者获得的分数取决于他们提交的解决方案的质量, 以及他们的审查和评估工作的质量, 以激励评估者正确评分, 并且通过由教师或助教对一些解决方案的评估来进行外部校准, 以提供准确性的基础. 在SSPA方法中, 文献[8]使用了教师评估的分数作为基本事实, 提出了通过对比学生与教师的直接相似性(如果学生与教师存在至少两份共同的评估)与间接相似性(如果学生与教师没有共同的评估)来衡量学生的评分能力, 最后加权聚合同伴互评分数来推断出每个学生的最后得分. 文献[20]提出了一种基于图的信任传播方法, 该方法把评估者、解决方案视作节点, 评估关系视作边, 将其建模为节点权重为评估者可靠性以及解决方案质量的加权图. 然后提出了基于图结构的解决方案分数更新策略以及评估者可靠性的传播策略, 以此推断解决方案真实分数以及评估者的评分可靠性. 此外, 文献[21]把学生的学习行为以及评语视作评估者的可靠性, 然后量化学生的评分可靠性作为权值, 对他们给出的评估分数进行加权聚合, 最后得到解决方案的真实分数. 文献[22]则使用了教师或助教对历史解决方案的评估纠正学生的偏见, 再从评语内容中提取学生的仔细度, 学生的评估仔细度越高, 其给出的评估越值得信赖, 则给该学生所打的分数赋予更高的权重以提升对解决方案真实分数估计的准确性. 文献[9]将评估者与解决方案建模为图表示模型SOAN, 并引入了图卷积神经网络来预测同伴互评分数. SOAN模型为更广泛的同伴互评图神经网络方法的研究提供了根基, 本文在SOAN的基础上考虑了评估者之间的社交利益与其解决方案的相关性, 提出了衡量同伴互评之间社交利益关系的方法ITSA, 构建了SIROAN, 使用GAT来预测同伴互评分数, 并将该方法称为GAT-SIROAN.

2 GAT-SIROAN方法

本文提出的GAT-SIROAN方法用于预测同伴互评分数, GAT-SIROAN由多关系加权网络SIROAN以及图注意力网络GAT两个模块组成. GAT-SIROAN的目标是从嘈杂的同伴互评中预测基本事实评估.

GAT-SIROAN方法如图1所示, 分为多关系网络SIROAN的构建和同伴互评分数预测两个阶段.

多关系网络SIROAN的构建: 给定同伴互评数据提取出评估者与解决方案之间的评估关系、所有权关系以及评估者与评估者之间的社交利益关系. 将提取出来关系转换为评估矩阵A、所有权矩阵O、社交利益关系矩阵SIR, 由这3个关系矩阵初始化矩阵${ X} = \left[ {\begin{array}{*{20}{c}} {\textit{SIR}}&{O + A} \\ {{{\left( {O + A} \right)}^{\text{T}}}}&{{0_m}} \end{array}} \right] + I$, 作为第2阶段同伴互评分数预测的输入, 其中T为转置运算符, ${0_m}$为$m \times m$值为0的矩阵.

同伴互评分数预测: 将节点特征初始化为十维全为1的向量, 同时将X输入到GAT中进行同伴互评分数的预测. 预测过程中在节点执行自我注意力机制去考虑每个节点的重要性, 最终获得同伴互评的预测分数.

SIROAN由评估关系、所有权关系以及社交利益关系构成. 评估关系由采用评估分数构成评估矩阵A表示. 所有权关系使用所有权矩阵O表示, 该矩阵反映了解决方案所有权的分配情况, 其中解决方案的数量通过提交或评估来确定. 社交利益关系由社交利益关系矩阵SIR来表示, 采用社交利益因子构成, 其中社交利益因子由ITSA方法计算得出.

2.1 本文的主要符号及含义

本文的主要符号及其含义如表1所示.

评估矩阵A: 一组有n个学生, 不同类型的解决方案被随机分配给任意的学生, 学生对解决方案的评估分数则收集在评估矩阵A中. 其中$A_{_{{{{I}}_{{{g {\textit{-}} t}}}} \leftarrow \alpha }}^{}$表示学生$\alpha $对来自g组类型为t的解决方案的评估分数. ${I_{g {\textit{-}} t}}$表示解决方案来自g组且类型为t. 教师或助教对学生提交的解决方案的子集进行评估, $A_{_{{{{I}}_{{{g {\textit{-}} t}}}} \leftarrow ta}}^{}$表示教师或助教ta对来自g组类型为t的解决方案的评估分数. 评估矩阵可以建模为有向加权图, 节点表示评估者以及解决方案, 有向边具有权值$A_{{I_{g {\textit{-}} t}} \leftarrow \alpha }^{}$表示评估者$\alpha $对来自g组类型为t的解决方案${I_{g {\textit{-}} t}} \leftarrow \alpha $的评估分数, $I$表示解决方案的集合, $P$表示评估者的集合包括教师助教以及学生, $T$表示评估者为教师或助教的集合, $\xi $表示评估者为学生的集合, 其中$T \subset P,\; \xi \subset P_{}^{}, \;T \not\subset \xi , \; \xi \not\subset T$.

所有权矩阵O: 在所有权矩阵O中, 使用1表示某一解决方案是由评估者$\alpha $提交或评估的, 若是评估者$\alpha $没有提交或评估某一解决方案则用0表示. 例如评估者$\alpha $提交了解决方案${I_{g1 {\textit{-}} t1}}$则用1表示, 评估者$\alpha $评估了解决方案${I_{g2 {\textit{-}} t2}}$用1表示, 若是评估者$\alpha $没有评估解决方案${I_{g2 {\textit{-}} t2}}$则用0表示.

社交利益关系矩阵SIR: SIR社交利益关系矩阵收集了同伴互评之间的社交利益因子, 而社交利益因子则使用本文提出的ITSA方法计算得出.

评估矩阵, 所有权矩阵以及社交利益关系矩阵都从SIROAN提取出.

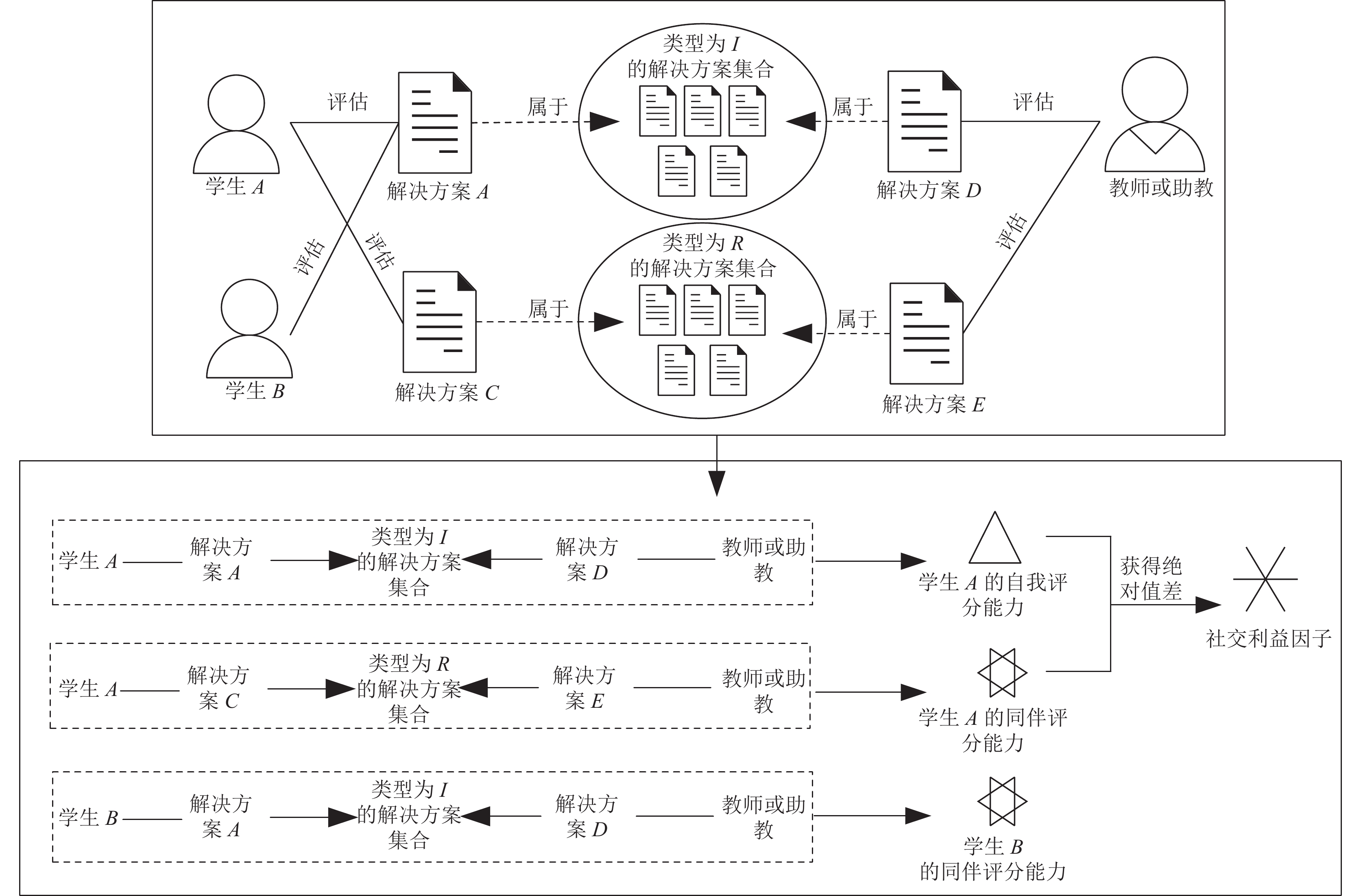
2.2 ITSA方法

ITSA的基本思想如下: 每个评估者拥有自我评分能力(即评估自己解决方案的能力); 以及同伴评分能力(即评估他人解决方案的能力). 自我评分能力被表征为每个评估者对解决方案评估的认知度, 同伴评分能力则被表征为每个评估者对被评估者解决方案的认可度. 通过比较自我评分能力和同伴评分能力得到社交利益因子和社交利益关系, ITSA方法如图2所示.

每个学生的自我评分能力通过自我评估分数与教师或助教对该解决方案的评估分数进行相似度比较得出, 这种相似性通过皮尔逊系数计算(如果评估者自我评估的解决方案与教师评估的解决方案大于2份)或余弦相似性计算(如果评估者自我评估的解决方案与教师评估的解决方案小于等于2份), 如式(1)所示:

$ {\textit{SA}} = \left\{ \begin{array}{l} \dfrac{\displaystyle\sum_I\left(A_{I_{g{\textit{-}}t} \leftarrow \alpha}^\alpha-\bar{A}_I\right)\left(A_{I_{g{\textit{-}}t} \leftarrow T} - \bar{A}_I\right)}{\displaystyle\sum_I \sqrt{\left(A_{I_{g{\textit{-}}t} \leftarrow \alpha}^\alpha - \bar{A}_I\right)^2} \sqrt{\left(A_{{I g{\textit{-}}t} \leftarrow T} - \bar{A}_I\right)^2}},\; I \in(2,+\infty) \\ \dfrac{\displaystyle\sum_I\left(A_{I g{\textit{-}}t \leftarrow \alpha}^\alpha A_{I g{\textit{-}}t \leftarrow T}\right)}{\sqrt{\displaystyle\sum_I\left(A_{I_{g{\textit{-}}t} \leftarrow \alpha}^\alpha - \bar{A}_I\right)^2} \sqrt{\displaystyle\sum_I\left(A_{I_{g{\textit{-}}t} \leftarrow T} - \bar{A}_I\right)^2}}, \;I \in(0,2] \end{array}\right. $

(1)

而同伴评分能力则参考了文献[8]所提出的SSPA方案中衡量评估者评分能力的方法, 通过学生和教师或助教之间的相似性来衡量, 这种相似性是直接的(学生与教师或助教评估了同一解决方案)或间接的(学生与教师或助教没有评估同一解决方案), 如式(2)所示:

$ PA = \left\{ \begin{array}{l} {{S_D}(\alpha , \beta )}\\ {{{S_I}(\alpha , T)}} \end{array} \right. $

(2)

直接相似性是指学生与教师或助教至少评估了两份共同的解决方案, 相似值是他们评估在共同作业中的相似性的平均值. 如式(3)所示:

$ {S_D} = \sum\nolimits_N {sim(A_{{I_{g {\textit{-}} t}} \leftarrow \alpha }^p, } A_{{I_{g {\textit{-}} t}} \leftarrow \beta }^p)/{N_{\alpha , \beta }} $

(3)

其中, ${N_{\alpha , \beta }}$表示学生$\alpha $与学生$\beta $评估的解决方案的集合.

$ sim(A_{{I_{g {\textit{-}} t}} \leftarrow \alpha }^p, A_{{I_{g {\textit{-}} t}} \leftarrow \beta }^p) = 1 - |A_{{I_{g {\textit{-}} t}} \leftarrow \alpha }^p - A_{{I_{g {\textit{-}} t}} \leftarrow \beta }^p|/\lambda $

(4)

间接相似性指学生与教师或助教之间没有共同评估的解决方案, 考虑一系列的评估者来计算这种相似性, 将其作为一种传递性度量, 每个相似性链Q都有直接相似性. 间接相似性定义为:

$ {S_I} = \mathop {\max }\limits_{q \in Q(\alpha , t)} \prod {{S_D}} (\alpha , \beta ) $

(5)

通过对自我评分能力与同伴评分能力的比较得到该评估者对被评估者的社交利益关系, 社交利益因子则定义为自我评分能力绝对值与同伴评分能力绝对值的差值, 如式(6)所示:

$ sir = |{\textit{SA}}| - |PA| $

(6)

将计算得出的sir收集在SIR中.

2.3 图注意力网络

通过ITSA方法完成3个关系矩阵的构建, 然后初始化矩阵X, 将X矩阵和节点特征$\vec h $输入到GAT中, $\vec h $被初始化为10维全为1的向量.

为了获得足够的表达能力, 将输入特征转化为更高层次的特征, 将节点特征应用一次权重化矩阵$W$, 作一次可学习的线性变化得到$W\vec h $. 考虑到在领域聚合时每个节点重要性的不同, 在节点上执行自我注意力机制, 将更高层次的特征$W\vec h $与一个可学习的参数矩阵$\alpha $相乘, 来计算注意力系数${e_{{I_{g {\textit{-}} t}}C}}$ (${e_{{I_{g {\textit{-}} t}}C}}$表示作业节点${I_{g {\textit{-}} t}}$与评估者节点之间的注意力系数). 将计算得出的注意力系数经过一个Softmax函数进行归一化操作得到最后的结果${\alpha _{{I_{g {\textit{-}} t}}C}}$, 最后通过激活函数得到评估者节点的最终特征表示$W\vec {{h^{'}}} $.

图3给出了计算获得评估者C节点新特征的过程, 评估者节点C与作业节点${I_{{g1} {\textit{-}} {t1}}}$相连接, 节点${I_{{g1} {\textit{-}} {t1}}}$与节点C经过一次可学习的线性变化后的特征为: $W{\vec h _{{I_{{g1} {\textit{-}} {t1}}}}}$、$W{\vec h _C}$. 将变化后的特征与一个可学习的参数矩阵$\alpha $相乘后得到注意力系数: ${e_{{I_{{g1} {\textit{-}} {t1}}}C}}$, 通过Softmax函数进行归一化操作后得到: ${\alpha _{{I_{{g1} {\textit{-}} {t1}}}C}}$. 最后通过一个激活函数后得到节点C的最终特征$W{\vec h' _C}$.

本文将通过最小化其预测的均方根误差来学习GAT-SIROAN的参数:

$ L(\theta |\varsigma , D) = \frac{1}{{|D|}}\sum\limits_{{I_{g {\textit{-}} t}} \leftarrow \xi = 1}^{|D|} {({A_\xi } - f(} {I_{g {\textit{-}} t}} \leftarrow \xi = 1|\theta , \varsigma ){)^2} $

(7)

其中, $|D|$是训练数据集中的项数, $f({I_{g {\textit{-}} t}} \leftarrow \xi |\theta , \varsigma )$是解决方案${I_{g {\textit{-}} t}} \leftarrow \xi $的GAT-SIROAN的估值. 可以通过梯度下降的优化技术来最小化损失函数.

本文采用了自注意力机制来计算节点注意力系数, 考虑每个节点的重要性, 以此来聚合同伴互评的成绩, 同样使用教师评分成绩作为基本事实, 通过最小化其均方根误差来学习网络的参数, 最终预测解决方案的同伴互评分数, GAT-SIROAN阻止了评估者之间的战略性评估, 并且在聚合过程中考虑的注意力系数, 提高了预测能力, 能够得到更准确的评分.

3 实验分析 3.1 数据集

本文采用了文献[23]提供的同伴互评数据集, 其中包含了219名学生在6种类型解决方案上的同伴互评分数、自我评估分数以及教师或助教评估的分数. 其中每种类型解决方案包括2–5个练习题, 本文选择了练习题数量大于2的解决方案类型, 一共有4个类型的解决方案, 即类型1、类型2、类型3、类型4. 所有学生被分成79组, 每组学生人数不同, 组内学生数量最多3人. 此外, 所有解决方案都由6名助教中的一名评估. 学生和助教都被提供了详细评估标准, 包括需要注意的错误以及如何分配分数. 将所有解决方案视为集合$I$, 并将解决方案的集合细分为来自哪个组的哪种类型的解决方案即${I_{g {\textit{-}} t}}$, 其中${I_{g {\textit{-}} t}} \in I$. 学生评估者视为集合$\xi $, 助教评估者视为集合$T$, 所有评估者视为集合$P$, 其中$\xi \not\subset T, \;_{}^{}T \not\subset \xi , \;_{}^{}\xi \subset P, \;_{}^{}T \subset P$. 与文献[9]一样, 将同伴互评分数、自我评估分数以及教师或助教评估的分数定在了[0, 1]的范围内, 分别在4个类型的解决方案上进行了实验, 在实验过程中使用了评估关系以及社交利益关系, 并且区分了是否添加自我评估分数. 这些数据的结果汇总统计如表2所示.

3.2 实验设置与评价指标

本文基于PyTorch^[24]和PyTorch geometry^[25]实现了GAT-SIROAN. 在所有的实验中, 使用了两个嵌入层, 嵌入维数为64, 并没有使用多头注意力机制, 使用了单头注意力机制. 将指数线性单元(ELU)作为所有隐层的激活函数. 使用Adam优化器^[26]和0.02的学习速率训练了1500个周期. 将值为1的向量初始化节点嵌入. 蒙特卡罗交叉验证^[27]用于验证, 训练-测试分割比为1:4, 即有20%的数据用于训练, 其余用于测试. 为了使结果更加可靠, 分别在4次随机分割上运行GAT-SIROAN, 并报告这些分割的平均误差.

为了评估预测性能, 本文使用的同伴互评真实分数估计中常用的评价指标均方根误差RMSE (root mean square error). RMSE是一种常见的用于衡量预测值与真实值之间差异的指标, 它是将预测误差的平方和取平均后开方得到的. RMSE可以用来评估模型的性能, 其中较小的RMSE值表示模型的预测较准确, 而较大的RMSE值则表示预测误差较大.

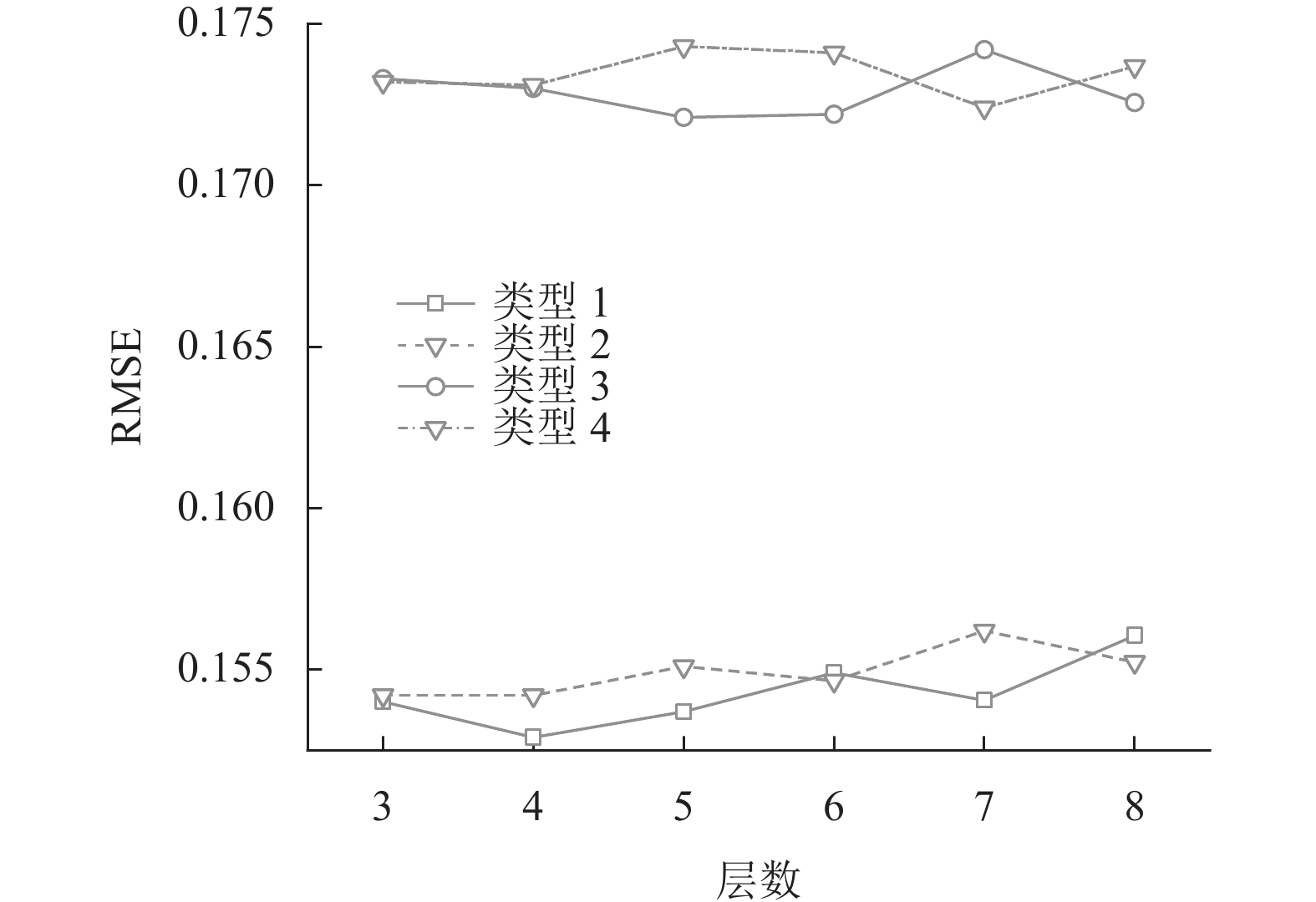
3.3 参数分析

网络层数与预测性能之间的关系是一个复杂且依赖于特定任务和数据集的问题, 一般来说, 增加网络的层数可以提供更多的非线性表示能力, 从而有可能提高模型的预测性能. 因此, 本文对在不同网络层数下模型所获得的性能进行了对比实验. 如图4所示, 本文选择了RMSE指标来显示GAT-SIROAN的性能是如何随网络层数的数量变化而变化的. 可以看到随着层数的增加均方根误差并没有太大的变化. 而产生这个现象的原因与GAT模型的中的“过渡平滑”问题有关^[28].

在X矩阵的初始化中, 除了本文提出的使用ITSA得出的社交利益关系矩阵SIR外, 所有权矩阵O也是一个重要的参数. 因此本文还探讨了所有权矩阵O的加入是否能进一步提高GAT-SIROAN的性能, 如图5所示, 所有权矩阵O的加入, 模型在各个类型的解决方案上的RMSE提高, 性能降低. 当X矩阵中只存在评估矩阵A与社交利益关系矩阵SIR时, 模型性能最佳, 进一步说明了ITSA方法的有效性.

3.4 消融实验

为了验证本文提出GAT-SIROAN方法中各模块的有效性, 采用以下两种消融方案进行实验: (1)使用SIROAN与两层GCN结合; (2)使用SOAN与两层GAT结合. 评价指标采用均方根误差RMSE.

如图6所示, 对于不同类型解决方案的数据集, 使用SIROAN在经过两层GCN运行后, 很明显GCN-SIROAN在8个数据集上的RMSE都低于5个基线方法. GCN-SIROAN在4类解决方案中, 仅有同伴互评的情况下, 性能上比表现最好的GCN-SOAN提高了0.97%、0.47%、0.33%、0.6%. 在添加了自我评分后, 在性能上提高了1.15%、0.5%、0.11%、0.25%. 说明加入ITSA方法后SIROAN能在一定程度上提升同伴互评分数预测的准确性. 图7展示了使用SOAN在经过两层GAT后在数据集上运行的结果. 仅存在同伴互评的情况下, GAT-SOAN在类型1、类型3、类型4这3个数据集上的RMSE均比其他基线方法低, 在性能上提高了1.06%、0.48%、0.21%. 在添加了自我评估后, GAT-SOAN在类型1、类型3两个数据集上的RMSE都低于其他基线方法, 在性能上提高了0.21%、0.4%. GAT也在一定程度上提高了预测能力.

3.5 基线实验

为了证明GAT-SIROAN优势, 将GAT-SIROAN与5种基线方法进行了比较, 使用了两个无监督的同伴互评方法: 平均值(所有同伴互评分数的平均值)以及中位数(所有同伴互评分数的中位数), 使用了两个机器学习的同伴互评方法: 没有使用教师或助教评估的分数作为校准的PeerRank^[6]以及使用了教师或助教评估的分数作为校准的RankwithTA^[7], 还使用了深度学习的同伴互评方法GCN-SOAN^[9].

表3展示了GAT-SIROAN以及其他5个基线方法平均值、中位数、PeerRank^[6]、RankWithTA^[7]、GCN-SOAN^[9]的性能. 如表3所示, 在无监督方法中平均值表现得最好, 相较于中位数, 在4类解决方案中平均值的RMSE都低于中位数, 性能高于中位数. 而GAT-SIROAN在4类解决方案中, 不论是否添加自我评估的分数, RMSE都低于平均值, 性能上分别提升了3.24%、1.31%、1.6%、2.71%、4.08%、1.22%、3.03%、3.92%. 在机器学习方法中, GAT-SIROAN在仅有同伴互评分数的情况下, 在类型1、类型2两个数据集上的RMSE都低于表现最好的PeerRank^[6], 在性能上分别提升了3.2%、1.81%, 在类型3、类型4两个数据集上的RMSE低于RankwithTA^[7], 性能上分别提升了4.41%、0.22%. 添加了自我评估分数后, 在类型1、类型3、类型4这3个数据集上的RMSE低于Rankwith-TA^[7], 性能上提高了3.48%、4.17%、0.67%, 在类型2上的RMSE低于PeerRank^[6], 性能提高了1.62%. 在深度学习方法中, 不论是否添加自我评估分数, 在4类解决方案上GAT-SIROAN的RMSE都比GCN-SOAN^[9]低, 性能上分别提升了2.02%、0.92%、1.27%、1.04%、2.42%、0.62%、1.2%、0.92%. 在所有基线中, GAT-SIROAN在仅有同伴互评分数的情况下, 在类型1、类型2、类型3这3个数据集上的RMSE比基线方法中表现最优的GCN-SOAN^[9]低, 性能上提高了2.02% 、0.92%、1.27%, 在类型4数据集上的RMSE比基线方法中表现最优的RankwithTA^[7]低, 性能上提高了0.22%. 添加了自我评估分数后, 在类型1、类型2、类型3这3个数据集上的RMSE比基线方法中表现最优的GCN-SOAN^[9]低, 性能上提升了2.42%、0.62%、1.2%, 在类型4数据集上的RMSE比基线方法中表现最优的RankwithTA^[7]低, 性能上提升了0.67%. 这些结果表明, 与这些基线方法相比, 本文提出的GAT-SIROAN方法在同伴互评真实分数估计的评估指标方面取得了最好的性能. 使用ITSA方法改进后的SIROAN在一定程度上阻止了评估者的战略性评估, 而在聚合过程中使用自适应的注意力机制能更好地捕捉节点之间的关系, 能使预测分数更接近基本事实.

4 结论与展望

在本文中, 提出了一种融合社交利益与图注意力网络的同伴互评分数预测方法GAT-SIROAN, 该方法考虑了同伴互评过程中的战略性评估行为, 提出了获取同伴互评过程中社交利益关系的方法ITSA, ITSA通过对比自我评分能力以及同伴评分能力计算得出了社交利益因子从而得出互评过程中的社交利益关系, 以此创建了社交利益关系矩阵SIR. 并将评估关系、所有权关系以及社交利益关系建模为加权网络SIROAN. 利用SIROAN引入了GAT来预测同伴互评分数. GAT-SIROAN阻止了评估者之间的战略性评估, 并且在聚合过程中考虑的注意力系数, 提高了预测能力, 能够得到更准确的评分. 在真实数据集上的实验结果表明, GAT-SIROAN方法比现有的同伴互评方法表现得更好.

在未来会在社交利益关系矩阵初始化方面^[9]以及针对关于浅层网络的过渡平滑现象进行研究^[28], 以提高网络的性能.