2. 湖州师范学院 信息工程学院, 湖州 313000
2. School of Information Engineering, Huzhou University, Huzhou 313000, China
工业管道是工业企业内所有管状设施的总称, 已广泛应用于石油、化工等行业. 随着工业管道数量的快速扩大和服役时间增长, 管道内的腐蚀问题逐渐突出, 导致其容易发生穿孔、泄漏和开裂等失效现象, 给人民群众的生命安全和社会生态环境安全带来了巨大的隐患[1,2]. 管道内腐蚀率的预测, 能够了解管道内腐蚀的状况, 为检测和维保措施提供依据, 具有重要的研究意义. 然而, 由于腐蚀速率与腐蚀因素之间存在复杂的非线性关系, 这给预测模型的构建带来了很大的挑战.
随着人工智能的快速发展, 大量研究人员将机器学习方法应用到管道腐蚀率预测中. 文献[3]采用原子搜索优化算法(atom search optimization, ASO)对BP神经网络的权值和偏置进行优化, 建立了基于ASO-BP的管道腐蚀率预测模型. 文献[4]采用核主成分分析(kernel principal component analysis, KPCA)对影响管道腐蚀的因素进行降维, 并将提取的腐蚀变量主成分输入到反向传播神经网络(back-propagation neural network, BRANN)中, 建立了一种基于KPCA- BRANN的管道腐蚀率预测模型. 文献[5]采用了萤火虫算法(firefly algorithm, FFA)对支持向量回归(support vector regression, SVR)中的参数进行了优化, 建立了基于FFA-SVR的管道的腐蚀率预测模型. 文献[6]采用主成分分析(principal component analysis, PCA)提取影响管道腐蚀率因素的主要特征, 利用混沌粒子群优化算法(chaos particle swarm optimization, CPSO)优化SVR中的参数对其进行腐蚀率预测, 提出一种基于PCA-CPSO-SVR的管道腐蚀率预测模型. 文献[7]采用KPCA对外腐蚀速率的影响因素进行降维处理, 利用CS对支持向量机(support vector machine, SVM)中的参数进行优选, 建立了一种基于KPCA-CS-SVM的管道腐蚀率预测模型. 文献[8]采用灰色关联度算法(grey relational analysis, GRA)对外腐蚀速率的影响因素进行降维处理, 利用改进鱼群算法(improved fish swarm algorithm, IFA)对最小二乘支持向量机(least squares support vector machine, LSSVM)中的参数进行优选, 建立了一种基于GRA-IFA-LSSVM的管道腐蚀率预测模型. 文献[9]采用KPCA提取影响混输管道内壁均匀腐蚀因素的主要特征, 利用改进布谷鸟搜索(improved cuckoo search, ICS)对极限学习机(extreme learning machine, ELM)中的参数进行优选, 建立了一种基于KPCA-ICS-ELM的管道腐蚀率预测模型. 虽然上述方法取得了较好的预测结果, 但由于特征提取和预测模型是人工设计的, 需要依赖专家经验, 预测结果仍有很大的提升空间.
近年来, 随着计算机计算能力的提升, 深度学习方法在图像识别[10]、自然语言处理[11]、语音识别[12]等许多领域有着广泛的应用. 其中, 作为深度学习模型代表之一的CNN能够对数据进行卷积、池化等操作, 逐步学习到数据的深层次抽象特征. 循环神经网络(recurrent neural network, RNN)[13]可以学习历史信息, 研究表明RNN在处理时间序列数据方面优于卷积神经网络. 作为RNN的变体, LSTM[14,15]能够通过记忆单元和门控机制捕获数据的长期依赖关系, 弥补了RNN带来的梯度爆炸、梯度消失导致的网络模型难以训练的问题. 文献[16]提出基于LSTM的管道腐蚀率预测模型, 预测精度优于BP神经网络和RNN. 文献[17]针对传统LSTM模型特征提取不足和超参数选择的问题, 提出一种基于改进的LSTM管道腐蚀率预测模型, 通过在LSTM网络前添加全连接层提取数据特征, 并利用网格搜索方法对模型的超参数进行优化. 实验结果优于传统的LSTM模型和BP神经网络, 但模型的泛化能力仍有提升空间.
基于上述分析本文结合CNN和LSTM各自的优势, 通过CS算法实现超参数优化, 提出了一种基于CNN-LSTM-CS的工业管道腐蚀速率预测方法. 本文的主要研究工作如下: (1)构建CNN-LSTM预测模型, 有效解决特征提取能力不足和时间序列长期依赖的问题; (2)利用CS算法对整个模型的超参数进行寻优, 有效避免人工设计参数依赖经验和稳定性差等问题, 提高了模型最优学习能力; (3)在采集的工业管道腐蚀数据集上验证了提出方法的有效性.
1 相关原理 1.1 卷积神经网络CNN的主要结构包括输入层、卷积层、池化层、全连接层和输出层[18,19]. 第l层的卷积运算可表示为:
| xlj=f(∑xi∈Ml−1xl−1i∗klij+blj) | (1) |
其中,
LSTM与RNN相比, 具有不同的传输加权模式, 除了权重矩阵节点输入之外, 还引入了用于状态保存的隐藏层, 有助于模型的长期记忆和梯度消失[20]. LSTM结构如图1所示.
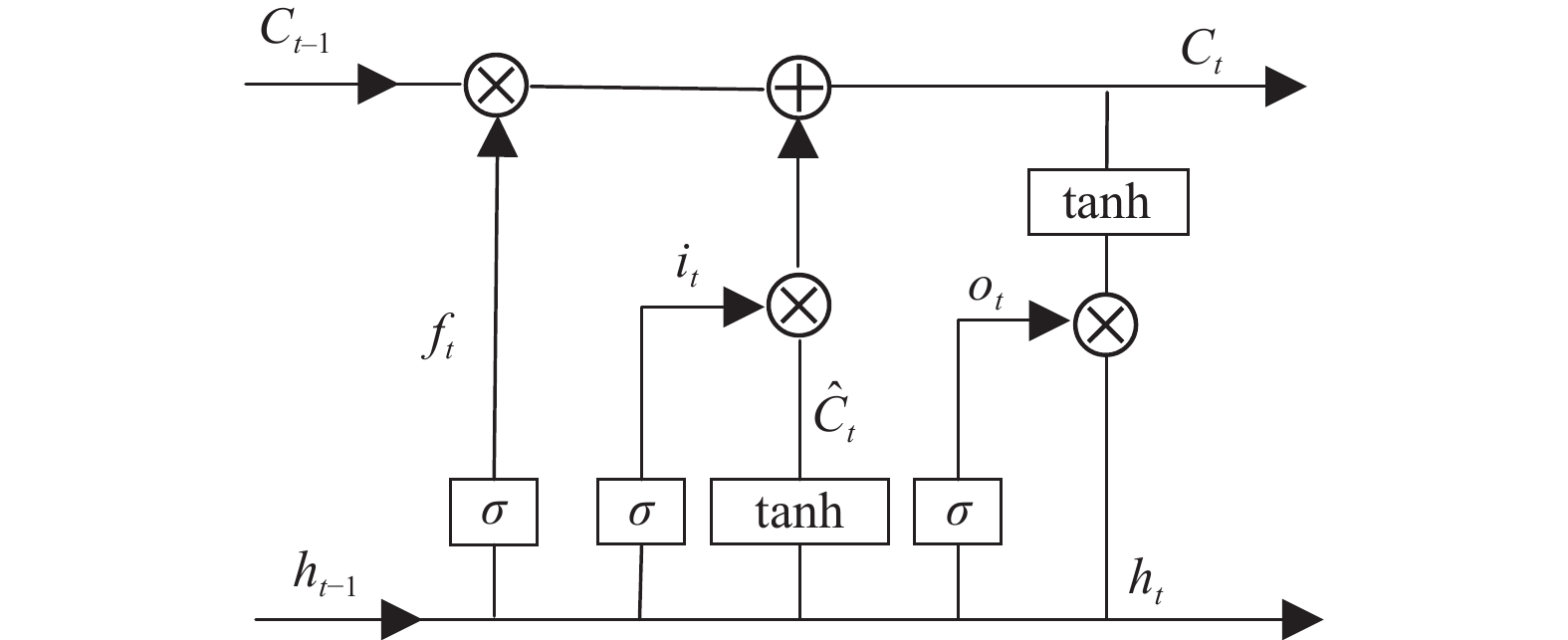
|
图 1 LSTM结构示意图 |
由图1可知, LSTM包括遗忘门、输入门、输出门3个门控部分组成. 计算流程可表示为:
| ft=σ(Wf⋅[ht−1,xt]+bf) | (2) |
| it=σ(Wi⋅[ht−1,xt]+bi) | (3) |
| ot=σ(Wo⋅[ht−1,xt]+bo) | (4) |
| ˆCt=tanh(WC⋅[ht−1,xt]+bC) | (5) |
| Ct=ftCt−1+it⋅ˆCt | (6) |
| ht=ot⋅tanh(Ct) | (7) |
其中,
CS是一种元启发式算法, 其灵感来自杜鹃物种向其他鸟巢产卵的自然行为[21,22]. 全局随机游走表示为:
| xt+1i=xti+α⊗Levy(s, λ) | (8) |
其中,
| Levy(s, λ)≈λΓ(λ)⋅sin(πλ/2)π1s1+λ,s≫s0>0 | (9) |
| α=α0(xti−xtbest) | (10) |
其中,
| s=μ|v|1/λ | (11) |
其中,
| {μ∼N(0,σ2μ) , v∼N(0,σ2v),σμ={Γ(1+λ)⋅sin(πλ/2)Γ[(1+λ)/2]⋅λ⋅2(λ−1)/2} , σv=1 | (12) |
式(9)中的s0表示Levy分布的初始步长, 局部随机游走可表示为:
| xt+1i={xti+r⋅(xtr1−xtr2),rand>Paxti,其他 | (13) |
其中,
针对传统管道腐蚀率预测模型特征提取能力不足的问题, 本文提出一种基于CNN和LSTM结合的管道腐蚀率预测模型. 该模型网络结构如图2所示, 主要包括3个一维卷积层、1个全连接层和2个LSTM层. 卷积层之后通过添加BN层和激活函数ReLU实现数据的归一化和非线性操作, 从而加快模型收敛速度和解决梯度消失的问题, 提取出影响管道腐蚀率因素的深层次特征; 将提取的深层特征输入到LSTM更好地预测出特征信息.
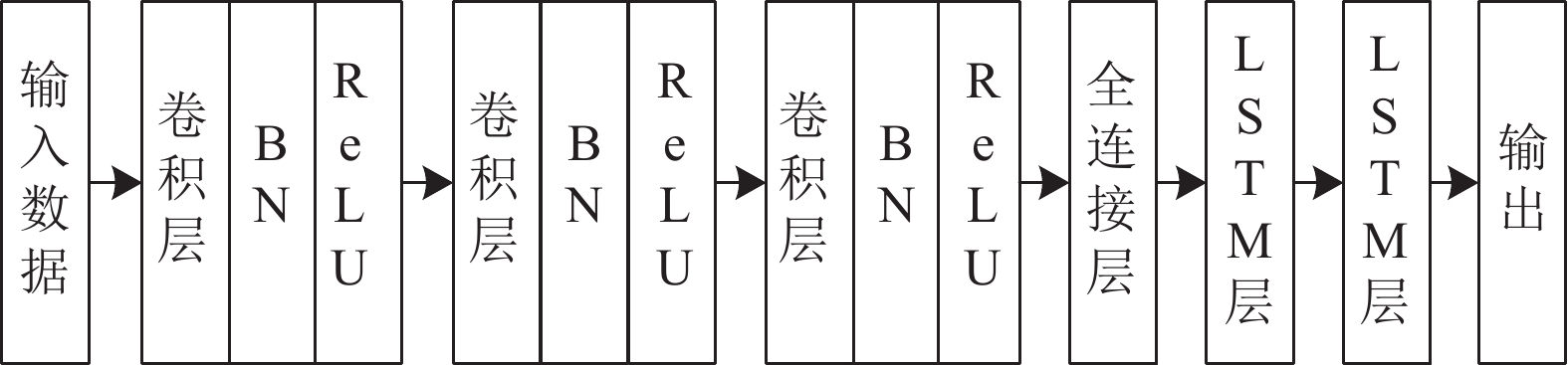
|
图 2 CNN-LSTM网络结构 |
2.2 CNN-LSTM-CS模型构建
在使用CNN-LSTM进行腐蚀率预测时, 其精度与卷积核数量、全连接层神经元个数、LSTM隐藏神经元个数具有很强的关联. 因此, 本文采用CS算法对这些参数进行优化, 提高模型的泛化能力, 最终建立用于工业管道腐蚀率预测的组合模型(CNN-LSTM-CS). 该模型的流程如图3所示, 包括CNN-LSTM预测主流程和CS优化两个部分. CNN-LSTM预测主流程用于对影响管道腐蚀因素数据进行预测, CS优化部分用于对CNN-LSTM网络模型进行优化.
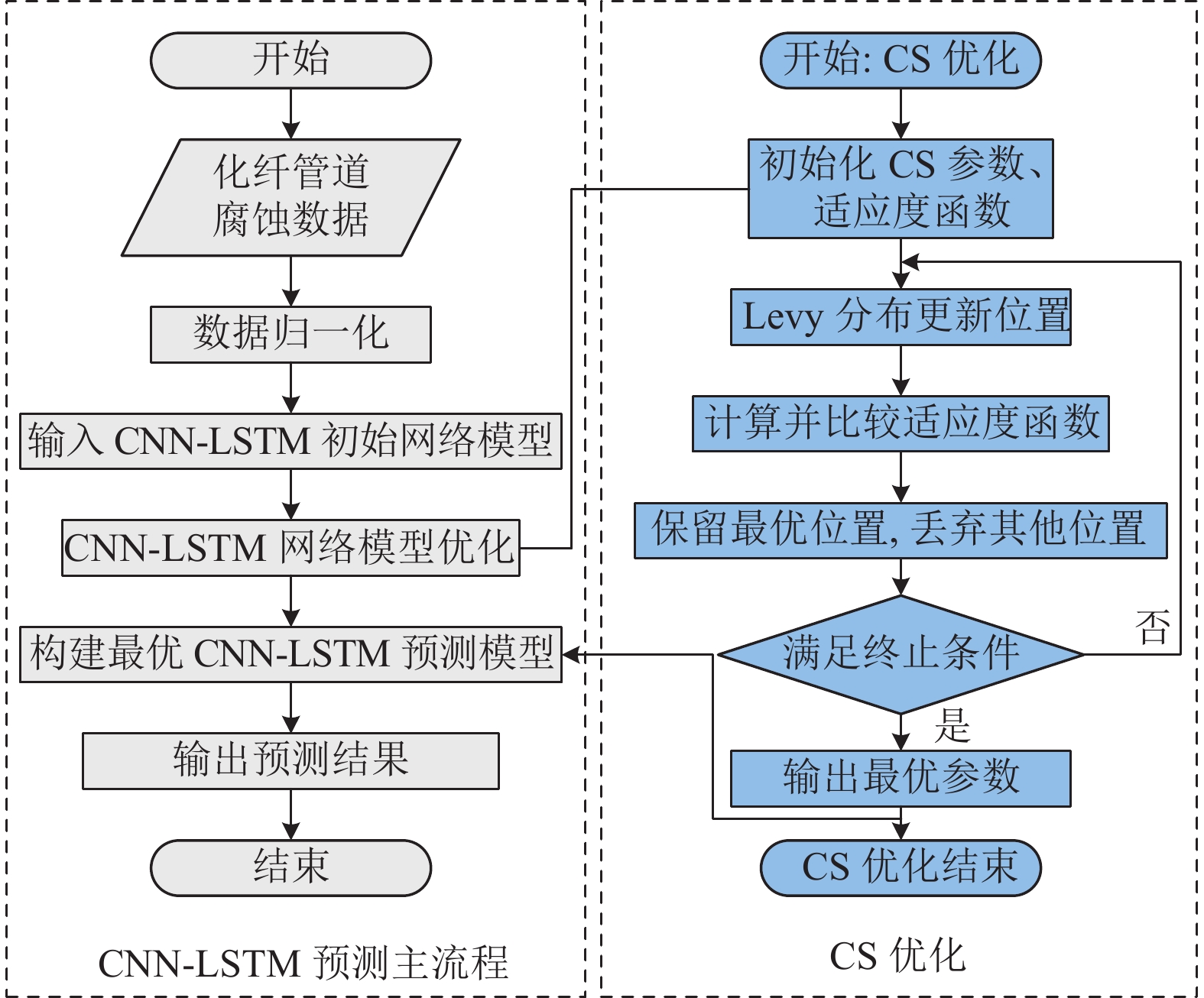
|
图 3 CNN-LSTM-CS模型流程图 |
提出方法的具体步骤如下.
(1) 采集并整理影响管道腐蚀因素数据集, 然后利用最大-最小化方法对数据进行归一化处理, 计算方法可表示为:
| x′=x−xminxmax−xmin | (14) |
其中,
(2) 构建CNN-LSTM网络模型结构, 将整个数据集按条件随机划分训练集和测试集两部分. 其中训练集用于训练CNN-LSTM模型, 测试集用来对CNN-LSTM模型进行评价.
(3) 设定CS参数, 以及CNN-LSTM模型中所优化参数的取值范围.
(4) 利用CS算法对CNN-LSTM模型进行优化, 设置CS算法的适应度函数作为网络的损失函数.
(5) 设置CS算法的搜索参数、迭代次数等进行布谷鸟的位置更新、选择和剔除等寻优操作.
(6) CS算法寻优结束得到最优参数组合输入到CNN-LSTM模型中, 将测试样本输入训练好的模型, 输出预测结果进行分析.
3 实验结果与分析 3.1 实验数据本文数据来源于浙江省湖州市新凤鸣集团湖州中石科技有限公司, 该厂内主要使用的工业管道主要包括动力管道和工艺管道, 按照输送介质不同可分为蒸汽管道、导热油管道、工艺介质管道. 以输送高温热媒的导热油管道为例, 材质为ASTM A53, 绝热层材料为石棉, 绝热层厚度为100–150 mm, 管道尺寸为DN60–DN812, 壁厚2.9–9.53 mm. 采集了温度、系统压力、CO2分压、pH值、介质流速、Cl–浓度、CO2浓度和H2S浓度8种管道腐蚀速率主要影响参数. 实验共采集854个样本, 部分数据见表1.
| 表 1 部分工业管道腐蚀影响因素数据 |
3.2 实验设置
所有实验均在处理器为Intel Core i9、64 GB内存和Nvidia RTX3060 (24 GB)显卡下完成. 采用Python语言, 深度学习模型基于Keras框架. 选取754个样本作为训练样本集, 剩余100个样本作为测试样本集. 本文通过CS算法对网络模型中的参数进行优化, 设置CS算法的搜索空间维度为4, 种群规模为50, 迭代次数为30,
为全面分析预测模型的有效性以及准确性, 选取以下4个指标来评估模型的性能.
平均绝对误差(mean absolute error, MAE), 适用于预测值与实际实测值之间存在显著差异的情况. 由于MAE可以避免误差抵消问题, 因此可以准确地反映实际预测误差的大小, 表示为:
| MAE=1nn∑i=1|yi−ˆyi| | (15) |
均方误差(mean square error, MSE)反应的是预测值和真实值偏差程度的一种度量. MSE误差越小表明预测值与真实值重合度越高, 可以表示为:
| MSE=1nn∑i=1(yi−ˆyi)2 | (16) |
均方根误差(root mean square error, RMSE)是均方误差的算术平方根, 是预测值与真实值偏差的平方和与观测次数
| RMSE=√1nn∑i=1(yi−ˆyi)2 | (17) |
平均绝对百分比误差(mean absolute percentage error, MAPE)表示将每个点的误差进行了归一化处理, 在一定程度上降低了个别点对平均绝对误差的影响. MAPE越小代表模型的预测精度越高, 计算公式为:
| MAPE=100%×1nn∑i=1|yi−ˆyiyi| | (18) |
其中,
为了验证不同特征参数对管道腐蚀率的影响, 本文利用Pearson相关系数法计算不同特征参数与管道腐蚀率的相关系数, 结果见表2. 由表2可知, 几种特征参数与管道腐蚀率的相关系数由大到小分别是H2S浓度、CO2浓度、温度、pH值、Cl–浓度、介质流速、系统压力. 每种特征参数与管道腐蚀率的相关系数都相对较高, 均超过了0.5. 因此, 本文选取采集的8种特征参数作为模型的输入, 管道的腐蚀率作为模型的输出.
| 表 2 不同特征参数与管道腐蚀率相关系数 |
3.5 实验结果与对比分析
为了验证本文方法的有效性, 选择BP神经网络、SVR、CNN、LSTM、CNN-LSTM和CNN-LSTM-CS这6种方法进行实验对比, 图4为6种方法对管道腐蚀率预测结果曲线. 由图4可以看出经CS优化的CNN-LSTM的方法更接近真实情况, 预测性能明显优于其他5种方法.
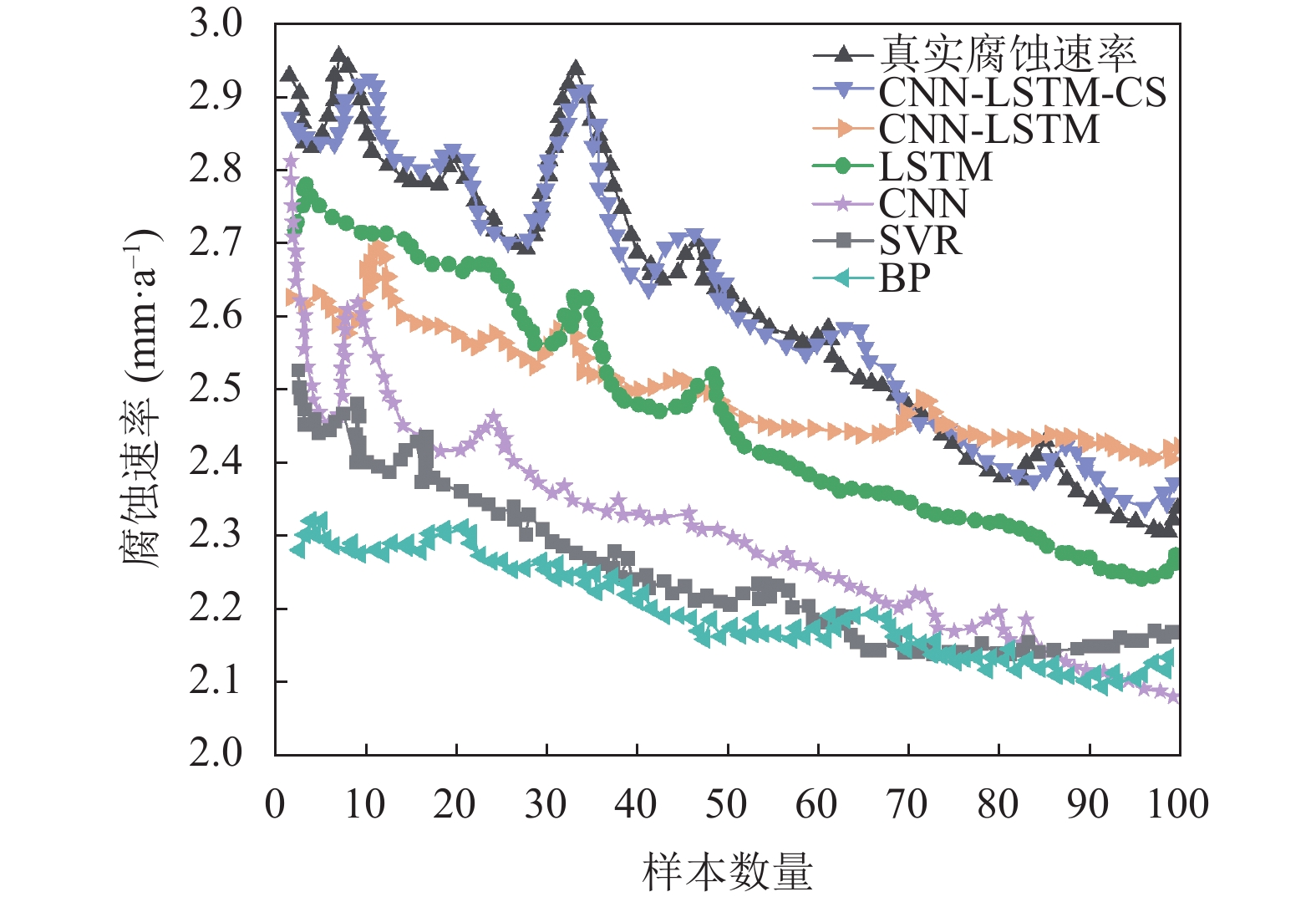
|
图 4 6种方法对管道腐蚀率预测结果曲线图 |
表3为各项指标的具体误差值. 由表3可知, 本文提出的CNN-LSTM-CS的MAE、MSE、RMSE以及MAPE这4个指标分别为0.19674、0.58529、0.59332以及0.039 55. 对比BP神经网络、SVR、CNN、LSTM、CNN-LSTM的MAE分别降低了0.30753、0.2817、0.20864、0.25298和0.11908; MSE降低了0.11614、0.10217、0.06505、0.04918和0.01908; RMSE降低了0.44248、0.40036、0.34493、0.28125和0.06161; MAPE降低了0.05062、0.04567、0.03476、0.0492和0.00524. CNN、LSTM、CNN-LSTM和CNN-LSTM-CS这4种基于深度学习方法的预测结果优于传统基于机器学习的BP神经网络和SVR方法;与CNN-LSTM和CNN-LSTM-CS方法相比, CNN仅使用单一的卷积神经网络模型对其腐蚀率进行预测, 而LSTM仅利用时间特征对其腐蚀率进行预测, 这两种方法预测的误差较大;与CNN-LSTM方法相比, 本文提出的CNN-LSTM-CS方法利用CS对网络参数进行自主寻优, 在各种误差指标下都呈现最优的预测性能.
| 表 3 模型预测误差指标 |
图5为6种方法的误差对比直方图. 由图5可以直观地看出6种方法的预测性能, 其中BP神经网络、SVR、CNN和LSTM方法的各项指标都较大, CNN-LSTM和CNN-LSTM-CS方法的误差较小, CNN-LSTM-CS方法的误差均小于其他5种方法.

|
图 5 6种方法的误差对比直方图 |
表4为6种方法的运行时间对比结果. 从几种方法的运行时间比较中可以看出, 本文方法CNN-LSTM-CS的运行时间比BP神经网络、SVR、CNN和LSTM的运行时间长, 但低于CNN-LSTM方法. CNN-LSTM-CS方法虽然在运行时间上没有取得最优的效率, 但是在可控范围之内, 综合预测精度等各项指标, 本文方法具有更好的应用性.
| 表 4 模型运行时间对比(s) |
4 结论
(1) 提出一种基于CNN-LSTM-CS工业管道腐蚀率预测模型, 实现了对采集的管道腐蚀数据腐蚀率的智能预测.
(2) 针对高度非线性的管道腐蚀数据, 利用CS算法对构建的CNN-LSTM模型中参数进行优化, 使模型避免陷入局部最优的情况, 提高了模型的泛化能力.
(3) CNN-LSTM-CS方法相对于CNN-LSTM、LSTM和CNN模型, 各项指标均取得了最优的结果, 能够满足工业管道腐蚀率智能预测的需求, 为工业管道检测智能化发展提供了技术支撑.
虽然本文方法具有较高的预测精度和较好的实用性, 但该方法存在训练时间较长的不足. 因此, 下一步研究工作是通过在预测模型中引入可分离卷积, 从而实现在提高管道腐蚀率预测准确度的同时提升模型的性能.
| [1] |
罗涛, 高观玲, 田晓江, 等. 中低压燃气管网的腐蚀泄漏规律及关键影响因素. 腐蚀与防护, 2023, 44(4): 104-106, 118. |
| [2] |
吴硕. N公司天然气长输管道安全管理问题研究 [硕士学位论文]. 太原: 太原理工大学, 2022.
|
| [3] |
肖荣鸽, 王栋, 王勤学. 基于ASO-BP神经网络的海底油气管道腐蚀速率预测. 化学工业与工程, 2022, 39(6): 109-116. |
| [4] |
Li XH, Jia RC, Zhang RR, et al. A KPCA-BRANN based data-driven approach to model corrosion degradation of subsea oil pipelines. Reliability Engineering & System Safety, 2022, 219: 108231. |
| [5] |
Seghier MEAB, Keshtegar B, Tee KF, et al. Prediction of maximum pitting corrosion depth in oil and gas pipelines. Engineering Failure Analysis, 2020, 112: 104505. DOI:10.1016/j.engfailanal.2020.104505 |
| [6] |
Peng SB, Zhang Z, Liu EB, et al. A new hybrid algorithm model for prediction of internal corrosion rate of multiphase pipeline. Journal of Natural Gas Science and Engineering, 2021, 85: 103716. DOI:10.1016/j.jngse.2020.103716 |
| [7] |
黄港港, 周阳, 闫骁瑾, 等. 基于KPCA-CS-SVM的埋地管道外腐蚀速率预测研究. 热加工工艺, 2022, 51(16): 38-43. |
| [8] |
周阳, 王寿喜. 基于GRA-IFA-LSSVM模型的气田集输管道内腐蚀速率预测. 腐蚀与防护, 2022, 43(8): 86-93. |
| [9] |
郭永强, 李希, 周忠强, 等. 基于KPCA-ICS-ELM模型的油气水混输管道腐蚀速率预测分析. 热加工工艺, 2022, 51(16): 54-59, 63. |
| [10] |
马瑶, 智敏, 殷雁君, 等. CNN和Transformer在细粒度图像识别中的应用综述. 计算机工程与应用, 2022, 58(19): 53-63. |
| [11] |
Magge A, Tutubalina E, Miftahutdinov Z, et al. DeepADEMiner: A deep learning pharmacovigilance pipeline for extraction and normalization of adverse drug event mentions on Twitter. Journal of the American Medical Informatics Association, 2021, 28(10): 2184-2192. DOI:10.1093/jamia/ocab114 |
| [12] |
Kumar LA, Renuka DK, Rose SL, et al. Deep learning based assistive technology on audio visual speech recognition for hearing impaired. International Journal of Cognitive Computing in Engineering, 2022, 3: 24-30. DOI:10.1016/j.ijcce.2022.01.003 |
| [13] |
胡中源, 薛羽, 查加杰. 演化循环神经网络研究综述. 计算机科学, 2023, 50(3): 254-265. |
| [14] |
许珠路, 王兴芬, 刘亚辉. 融合CNN-BiLSTM-Attention的集成学习价格预测. 计算机系统应用, 2023, 32(6): 32-41. DOI:10.15888/j.cnki.csa.009137 |
| [15] |
Karri M, Annavarapu CSR. A real-time embedded system to detect QRS-complex and arrhythmia classification using LSTM through hybridized features. Expert Systems with Applications, 2023, 214: 119221. DOI:10.1016/j.eswa.2022.119221 |
| [16] |
贾彤华, 范磊, 程光旭, 等. 长短期记忆神经网络模型改进及其在循环冷却水管道腐蚀预测的应用. 石油化工设备, 2022, 51(4): 1-6. |
| [17] |
张雯莹, 代英宸, 张云龙. 基于LSTM的钢铁厂清循环系统浓缩倍数与腐蚀速率预测. 冶金动力, 2021(4): 61-64. |
| [18] |
Wang Q, Ye M, Wei M, et al. Deep convolutional neural network based closed-loop SOC estimation for lithium-ion batteries in hierarchical scenarios. Energy, 2023, 263: 125718. DOI:10.1016/j.energy.2022.125718 |
| [19] |
吴则举, 焦翠娟, 陈亮. 基于改进Faster R-CNN的轮胎缺陷检测方法. 计算机应用, 2021, 41(7): 1939–1946. 吴则举, 焦翠娟, 陈亮. 基于改进Faster R-CNN的轮胎缺陷检测方法. 计算机应用, 2021, 41(7): 1939–1946. |
| [20] |
张达, 郭特, 丁瑞, 等. 具有多层次优化能力的EEG生成模型. 计算机系统应用, 2022, 31(8): 369-379. DOI:10.15888/j.cnki.csa.008658 |
| [21] |
Khadanga RK, Kumar A, Panda S. A modified grey wolf optimization with cuckoo search algorithm for load frequency controller design of hybrid power system. Applied Soft Computing, 2022, 124: 109011. DOI:10.1016/j.asoc.2022.109011 |
| [22] |
张露潆. 基于改进布谷鸟算法的配送车辆路径优化方法. 吉林大学学报(信息科学版), 2023, 41(1): 118-123. |
 2024, Vol. 33
2024, Vol. 33



