2. 国网辽宁省电力有限公司 营口供电公司, 营口 115002
2. Yingkou Power Supply Company, State Grid Liaoning Electric Power Supply Co. Ltd., Yingkou 115002, China
当前新能源大规模融入电力系统, 导致影响负荷的因素更加多样化, 电力需求的变化更具随机性, 短期负荷预测研究至关重要[1]. 考虑到负荷序列的波动性、周期性变化和非线性特征, 因此需要开发有效的模型和方法解决负荷的多样性和不确定性, 确保电力系统的稳定性和可靠性[2].
针对电力负荷预测方法大致包括两类: 基于数学统计方法和机器学习方法. 基于数学统计方法包括自回归模型[3]、自回归移动平均模型[4]、指数平滑法[5]和卡尔曼滤波[6]等. 数学统计方法模型更多地依赖于数据的周期性和离群值. 然而, 电力负荷数据与其他参数之间的关系通常是复杂和非线性的, 并且由于这些原因, 很难用统计方法获得准确的预测值. 而机器学习方法主要包括传统机器学习方法和深度学习方法. 传统机器学习方法例如: 支持向量机(SVM)[7]、决策树[8]、随机森林(RF)[9]等. 与数学统计方法相比, 传统机器学习方法能够解决相对复杂的数据特征关系等问题, 但无法在较大的数据集上准确预测电力负荷, 同时存在对数据间的相关性考虑不全等问题. 随着机器学习方法的发展, 深度学习方法逐渐被应用于电力负荷预测. 在文献[10]中, 提出了基于长短期记忆(LSTM)的电力负荷预测模型, 结果表明, LSTM可以产生更好的预测性、实现更高的精度, 但是其训练复杂并且涉及更多参数, 增加了训练和调整模型的复杂性. 作为LSTM的变体, 门控循环单元(GRU)具有更简单的网络结构. 在文献[11]中, GRU被引入用于短期电力负荷预测. 然而, 由于模型中缺乏卷积, 因此仍然有必要提高特征提取的性能. 为了解决这些问题, 卷积神经网络(CNN)已被采用其出色的功能提取. 在文献[12]中, 利用CNN进行特征提取与筛选, 减少了运算过程中的过拟合. 然而CNN对长期依赖关系的建模能力较弱, 无法满足电力负荷预测的需求. 因此, 在文献[13]中, 提出了长期和短期时间序列网络(LSTNet). 其通过卷积层、递归层和递归跳过层提取时间序列的短期局部依赖模式并发现长期趋势. 实验结果表明, LSTNet成功地捕捉了数据中的短期和长期重复模式, 并结合了线性和非线性模型进行稳健预测. 然而, 单一的深度学习方法面临着诸如计算复杂度和低计算效率等挑战, 为了应对这些问题, 在文献[14]中提出了基于CNN-BiLSTM的短期电力负荷预测方法. 研究结果表明, 两种单一模型组合, 不仅弥补各自存在的问题, 而且提高预测精确度.
然而对于电力负荷预测而言, 提高其预测精度, 挖掘电力负荷数据的规律性与预测模型的优化同样关键. 因此, 为降低非线性和波动性的影响, 文献[15–18]中提出了结合平稳小波变换的短期电力负荷预测方法, 有效提高了预测准确性. 同时, 文献[19]的经验模式分解(EMD)算法为数据分解提供了显著性能改进. 此外, 文献[20]采用变分模态分解(VMD)算法进行数据处理, 解决了EMD算法中的模态混叠问题, 并展现出更好的分解效果和较高的鲁棒性. 然而, VMD算法的二次惩罚因子可能导致内部跳跃过度惩罚, 从而引发预测误差.
综上所述, 现有的短期电力负荷预测方法存在以下不足: (1)上述文献大多直接利用VMD将输入模型数据分解为具有不同特征频率的子序列, 以简化负荷特性, 提高预测精度. 但VMD中的参数设置具有主观性, 可能人为影响预测结果, 导致模型的普适性和泛化能力略差. (2)大部分以改进优化模型来提高预测精度, 却忽略了电力负荷数据本身的特征和表达能力.
因此, 本文提出RIME-VMD-BLSTNet-CBAM的短期电力负荷模型方法. 首先, 采用RIME算法优化VMD方法的参数. 适应度函数选用包络熵, 这使得获得加载子序列具有较低的时间复杂度. 其次, 使用LSTNet预测模型, 该模型与其他神经网络相比, LSTNet可以从长期和短期历史序列中捕捉到不同的特征和趋势. 为了更准确地捕捉到时间序列数据中动态变化和趋势, 将其递归层的LSTM更替为BiLSTM. 之后在LSTNet中嵌入CBAM注意力机制, 可以减少过拟合和增强模型的泛化能力. 最后用巴拿马地区的实际电力负荷数据集, 通过仿真对比实验来验证本文提出的模型的有效性和准确性.
1 算法原理 1.1 变分模态分解(VMD)VMD是一种用于处理非平稳信号的自适应分解估计方法. VMD可以将历史电力负荷等序列非递归分解, 得到多个不同频率的特征趋势. 其不仅具有良好的噪声鲁棒性, 而且降低了原始序列的不稳定性. 该方法使用维纳滤波进行降噪, 对相关参数进行初始化, 得到K估计的中心频率
| {min{uk}{ωk}{∑k‖∂t[(δ(t)+jπt)∗uk(t)]e−jωkt‖22}s.t.∑kuk=f | (1) |
其中, {
| L({uk},{ωk},λ)=α∑k‖∂t[(δ(t)+jπt)∗uk(t)]e−jωkt‖22+‖f(t)−∑kuk(t)‖22+⟨λ(t),f(t)−∑kuk(t)⟩ | (2) |
采用交替方向乘子法进行优化, 迭代更新
| ⌢un+1k(ω)=⌢f(ω)−∑i≠k⌢u(ω)+⌢λ(ω)21+2α(ω−ωk)2 | (3) |
| ωn+1k=∫∞0ω|ˆuk(ω)|2dω∫∞0|ˆuk(ω)|2dω | (4) |
| ⌢λn+1(ω)=⌢λn(ω)+τ(⌢f(ω)−∑k⌢un+1k(ω)) | (5) |
其中,
定义最大迭代次数为N, 使n满足
| ∑k‖⌢un+1k−⌢unk‖‖⌢unk‖<ε | (6) |
RIME[21]是由Su等人在2023年2月提出的一种基于霜冰物理现象的高效优化算法. RIME算法通过模拟冰晶的软霜和硬霜生长过程, 构造软霜搜索策略和硬霜打孔机制, 不断对种群更新从而实现优化, 找到最优解. RIME优化算法过程如下.
(1)初始化种群: 随机生成一组冰晶(候选解), 每个冰晶代表一个潜在解.
(2)受软霜成长的启发, 利用霜冰的强随机性和覆盖性, 提出软霜搜索策略. 针对霜冰粒子的5种运动特征, 模拟了各个粒子的凝聚过程. 其计算公式为:
| Rnewij=Rbestj+r1⋅cosθ⋅β⋅(h⋅(Ubij−Lbij)+Lbij),r2<E | (7) |
其中,
| θ=π⋅t10⋅T | (8) |
其中, t是当前迭代次数, T是算法的最大迭代次数.
| β=1−[w⋅tT]/[w⋅tT]ww | (9) |
其中, w默认值为5, 用于控制阶跃函数的段数.
| E=√t/tTT | (10) |
(3)通过对硬霜生长过程的模拟, 提出硬霜打孔机制. 用于霜冰粒子间的置换, 其计算公式为:
| Rnewij=Rbestj,r3<Fnormr(Si) | (11) |
其中,
LSTNet是为了解决电力负荷序列中长期周期性和短期非线性混合的挑战而设计的. 其结合卷积层捕获短期模式和递归神经网络层捕获长期模式. 然而, 这导致了输出不敏感于输入比例的问题. 为解决这一问题, LSTNet引入了全连接层, 模拟自回归过程, 使输出可以更好地适应输入的尺度变化, 提高了模型的鲁棒性.
1.3.1 卷积层LSTNet卷积层是一个没有池化层的卷积神经网络. 该层用于捕获电力负荷数据的短期模式和局部依赖关系. 其包括多个宽度为
| hk=ReLU(ωk∗X+bk) | (12) |
其中, 卷积运算由*表示;
递归层的输出同时输入递归层和递归跳跃层. 递归层部分采用LSTM神经网络, 其核心部分是单元状态和门, 作为历史信息的过滤器, 同时可以提供更大的适应性. 其计算公式为:
| ft=σ(Wfht−1+Ufxt+bf) | (13) |
| it=σ(Wiht−1+Uixt+bi) | (14) |
| ˜ct=ReLU(Wcht−1+Ucxt+bc) | (15) |
| ot=σ(W0ht−1+U0xt+b0) | (16) |
| ct=ft⊗ct−1+it⊗˜ct | (17) |
| ht=ot⊗ReLU(ct) | (18) |
其中,
为解决LSTM在长时间序列上的梯度消失问题, 引入了递归跳跃层, 以增强长期模式的捕获. 递归跳跃层的计算公式为:
| rt=σ(xtWxr+ht−pWhr+br) | (19) |
| ut=σ(xtWxu+ht−pWhu+bu) | (20) |
| ot=σ(xtWxu+ht−pWho+bo) | (21) |
| ˜ct=ReLU(xtWxc+ht−pWhc+bc) | (22) |
| ct=ut⊗ct−p+rt⊗˜ct | (23) |
| ht=ot⊗ReLU(ct) | (24) |
递归跳跃层的输入等于卷积层的输出, 其中, p表示跳跃的隐藏层状态的数量;
利用全连接层融合递归层和递归跳跃层的输出作为非线性部分的预测结果, 其计算公式为:
| hDt=WRhRt+p−1∑i=0WSihSt−i+b | (25) |
其中,
虽然卷积模块和递归跳跃模块都具有非线性特性, 但其对输入数据的敏感性有限, 会降低预测精度. 因此, LSTNet模型通过添加自回归(AR)模型来解决这个问题. 其计算公式为:
| hLt,i=qar−1∑k=0Warkyt−k,i+bar | (26) |
其中, AR模型的预测结果由
为了获得LSTNet的最终预测结果, 神经网络部分的输出和AR模型的结果进行叠加:
| ˆYt=hDt+hLt | (27) |
其中,
CBAM[22]具有空间注意力模块和通道注意力模块, 可以捕捉关键特征, 忽略无用特征. 在卷积神经网络生成特征图之后, CBAM模块通过在通道和空间维度上计算特征图的权重图; 然后, 其将这个权重图与输入的特征图相乘, 从而实现了自适应学习. 这一轻量级通用模块可以无缝集成到多种卷积神经网络中, 同时支持端到端的训练. 给定特征图F, 通道注意力模块能推导出1D通道注意力向量
| F′=Mc(F)⊗F | (28) |
| F″=Ms(F′)⊗F′ | (29) |
其中,
| Mc(F)=σ(MLP(AvgPool(F))+MLP(MaxPool(F))) | (30) |
空间注意力模块主要关注的是信息中的哪个位置是有意义的, 也是对通道注意力模块的补充. 其计算公式为:
| Ms(F)=σ(Conv([AvgPool(F);MaxPool(F)])) | (31) |
其中,
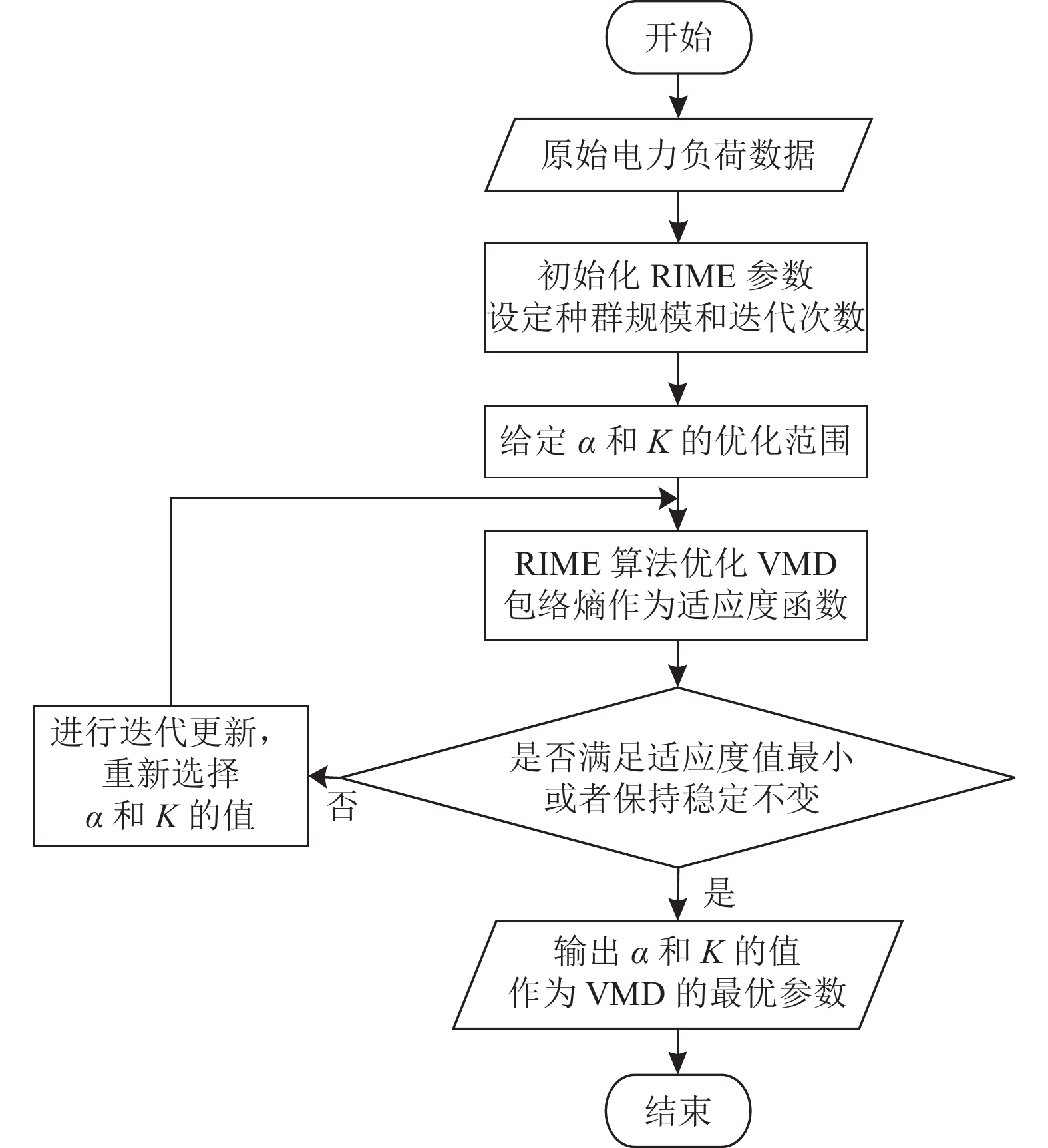
由于电力负荷数据具有非平稳性, 而且VMD分解需要预先定义模态数量
|
图 1 RIME算法优化VMD流程图 |
2.2 改进LSTNet模型
由于递归层部分采用单一的LSTM神经网络, 只考虑对过去的上下文信息进行数据挖掘, 而忽视了未来的上下文信息内容, 因此, 采用双向循环神经网络(BiLSTM)来作为递归层的基本单元. 选择BiLSTM可以提升模型的建模, 能够基于LSTM执行正向和反向双向传播, 从而更有效地捕捉电力负荷数据中的复杂关系. 其计算公式为:
| ht=LSTM(xt,ht−1) | (32) |
| hi=LSTM(xt,hi−1) | (33) |
| Ht=atht+bthi+ct | (34) |
其中, LSTM表示当方程中的
为了有效地处理更多电力负荷数据并捕捉长期依赖关系, 单一的LSTNet框架表现出训练速度较慢, 进而影响预测准确性. 因此, 引入卷积块注意力机制模块(CBAM), 将其置于递归层之后. CBAM采用三重注意力机制, 有助于更好地交互通道信息和空间信息, 从而更好地捕捉时间序列数据的复杂特征和关系. 这一改进有助于提高模型在短期电力负荷预测中的准确性和鲁棒性. 其改进的LSTNet模型框架图如图2所示.
2.3 RIME-VMD-BLSTNet-CBAM模型预测流程本文旨在提高短期负荷预测的准确性, 结合了经过优化的VMD和改进的LSTNet模型. 首先, 对原始数据进行预处理, 包括负荷数据和相关特征变量. 利用VMD将预处理后的负荷数据分解成多个子序列, 但由于VMD分解需要事先定义模态数量

|
图 2 改进的LSTNet模型框架图 |
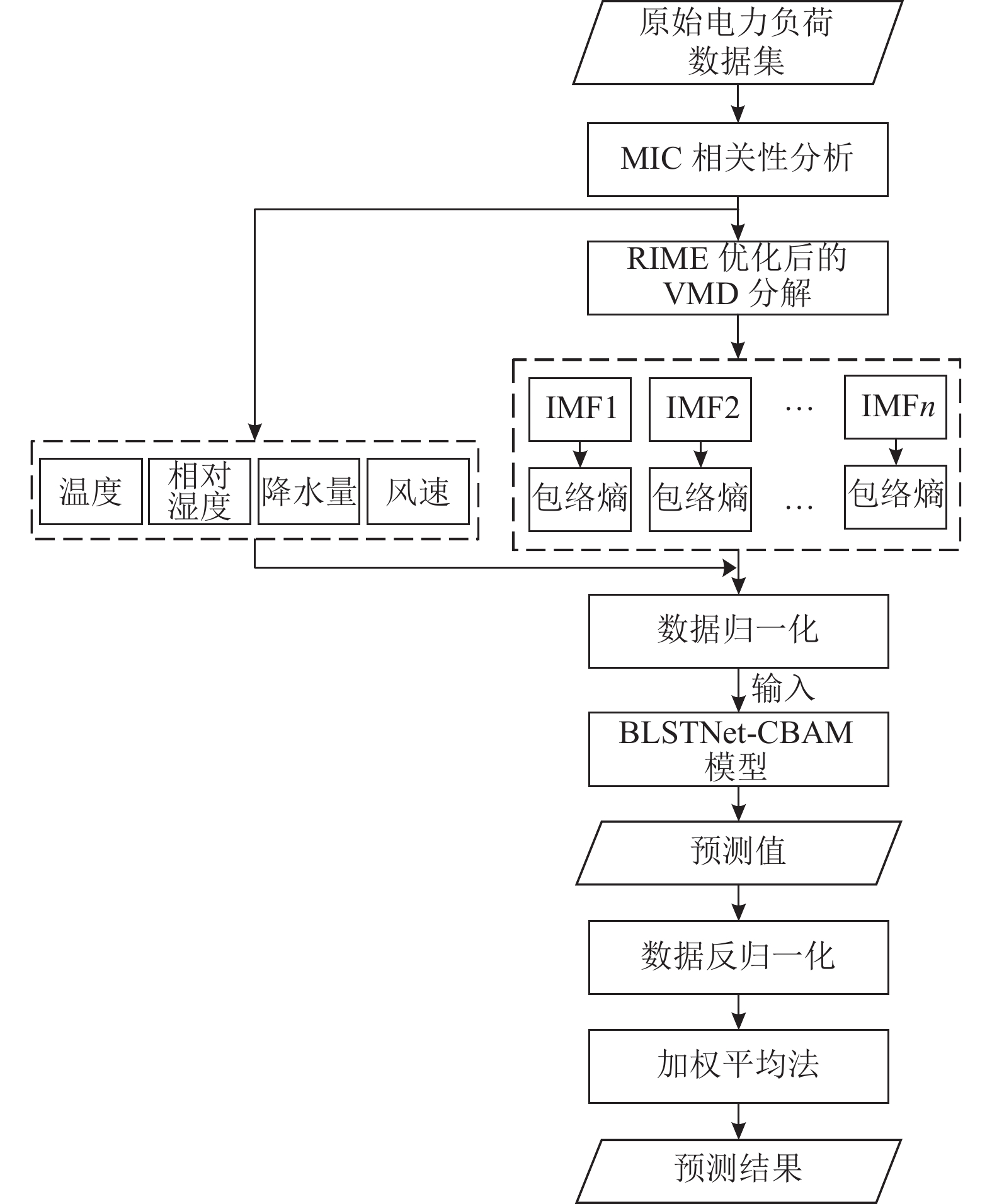
|
图 3 RIME-VMD-BLSTNet-CBAM组合模型流程 |
3 算例及结果分析 3.1 实验数据选取及数据预处理
本文选取了Kaggle平台上发布的巴拿马在2019年5月1日–2020年5月7日的电力负荷数据集作为实验对象. 该数据集涵盖5个特征向量, 这些特征的引入有助于更准确地预测电力负荷的变化趋势. 在实验过程中, 以每1小时为一个采样点, 并采用滑动窗口方法进行负荷预测. 具体而言, 将滑动窗口的大小设置为24, 滑动步长为1, 以此来利用过去24个时间点的历史数据进行下一时刻电力负荷的预测. 为了全面评估模型的性能, 将数据集前8784个样本划分为训练集, 其余为测试集, 以确保对模型的泛化能力进行有效验证. 由于数据集不包含任何缺失值或离群值, 同时为了消除不同数据类型之间的量纲差异, 采用归一化方法. 归一化是一种数学变换技术, 能够将数据压缩至[−1, 1]的范围内, 从而使得短期电力负荷预测模型能够更好地适应各种数据类型. 具体而言, 归一化方法遵循式(35):
| xnormi,s=xi,s−xminsxmaxs−xmins | (35) |
其中,
使用VMD对数据预处理后的电力负荷数据进行分解需要设置多个参数. 其中, 采用RIME优化算法来确定这些参数的最佳值; 采用包络熵作为RIME优化算法的适应度函数. RIME优化VMD参数设置最优值如表1所示.
| 表 1 RIME优化VMD参数设置 |
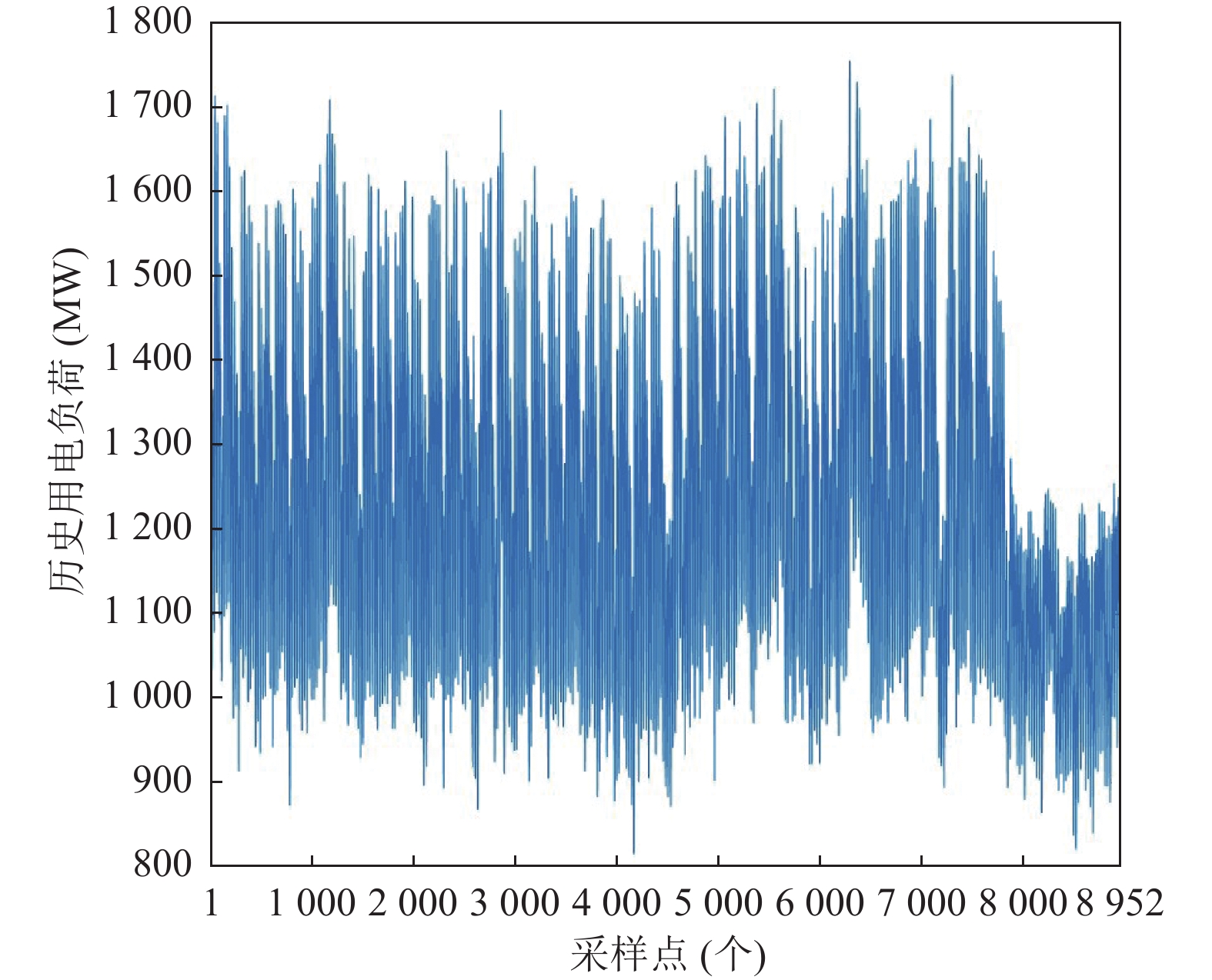
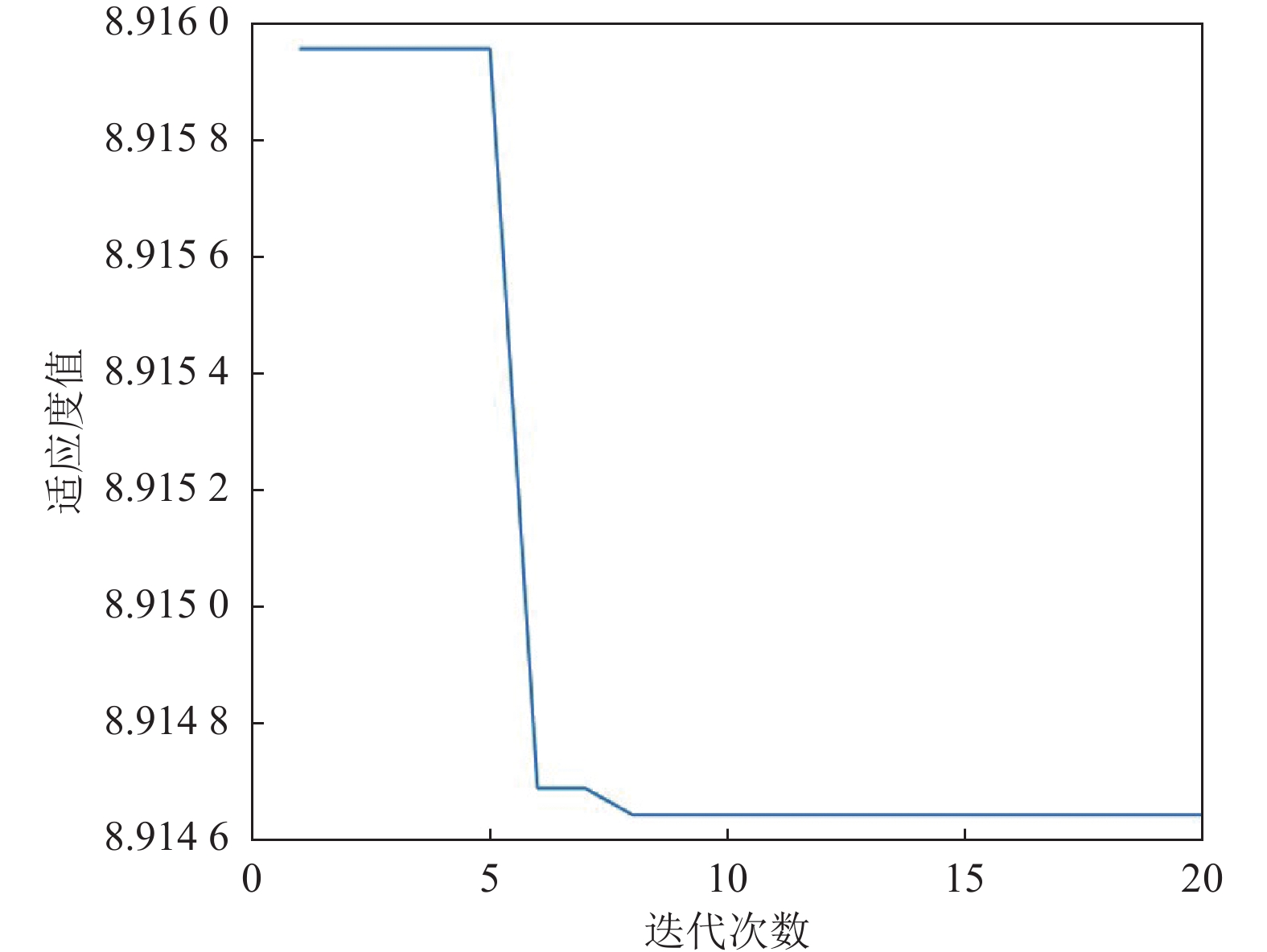
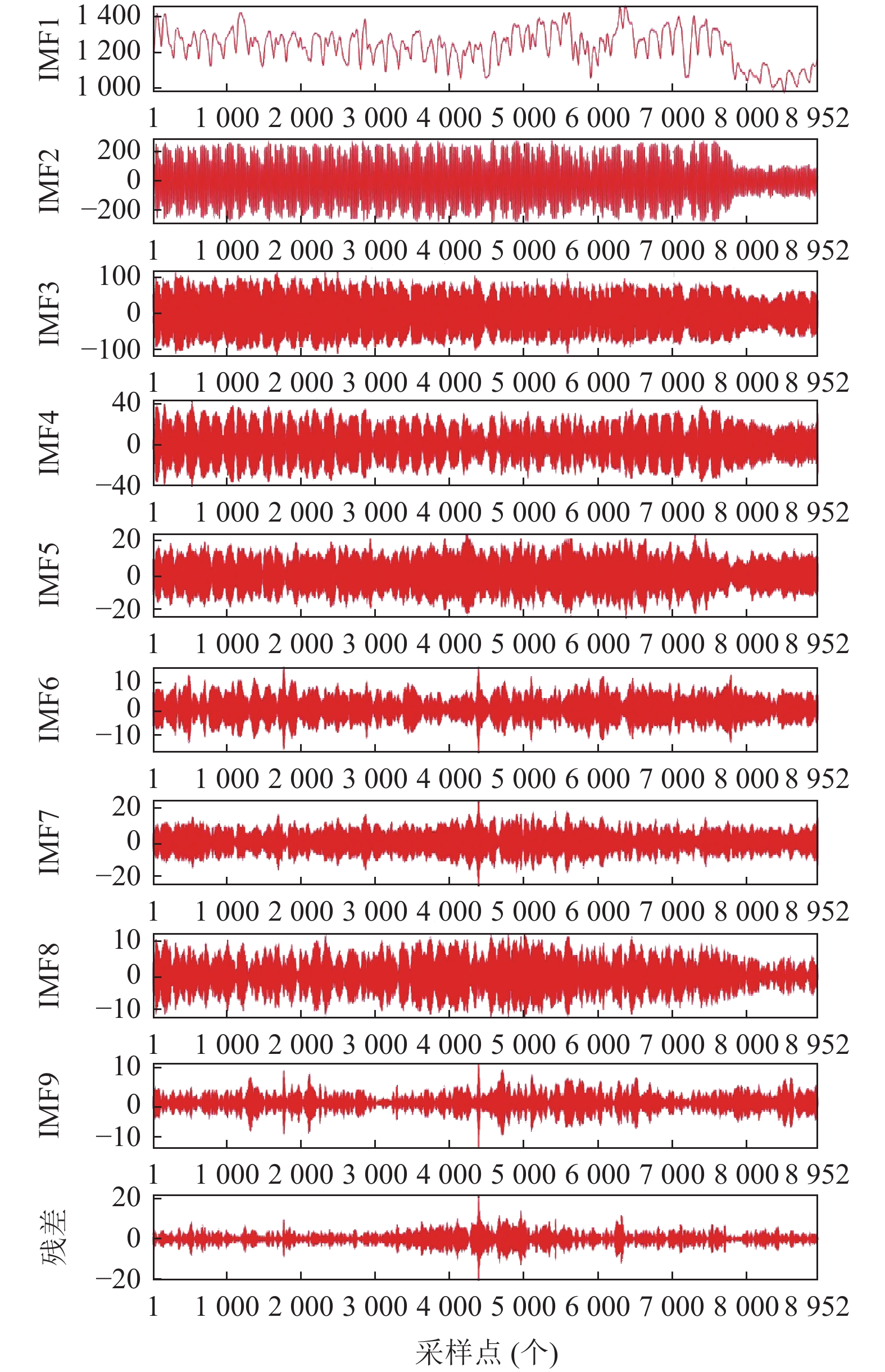
图4表示预处理后的负荷数据的原始信号, 从图4可以看出负荷数据具有很大的波动性, 图5表示RIME优化VMD得到的最优迭代次数和最佳适应度值, 图6表示RIME-VMD的分解结果, 一共分解出9个IMF分量和1个残差量. IMF1分量具有相对平坦的趋势, 表明其是低频分量, 而其他分量表示高频分量. 这些分量与天气数据、日期数据和其他相关要素相结合, 以创建模型的输入要素. 图7表示分解出10个分量的频谱图. 从图7可以看出每个分量在不同时间尺度上的波动.
|
图 4 负荷数据原始信号 |
|
图 5 RIME优化VMD参数的迭代曲线图 |
3.3 特征选择分析
鉴于各影响因素与电力负荷数据之间存在复杂的非线性关系, 采用MIC相关性分析[23]来检验各变量的显著性. MIC的值界定在[0, 1]之间. 当MIC值越大时, 表示两个变量之间的相关性越强; 反之, 当MIC值较小时, 则表明两个变量之间的相关性较弱. 其主要表达式为:
| MMIC(X,Y)=maxxy<B(N){M(D)x,y} | (36) |
| M(D)x,y=I∗(D,x,y)log2min{x,y} | (37) |
其中,
|
图 6 RIME-VMD分解结果 |
图8显示了各个影响因素和电力负荷数据之间的相关性. 从图8中可以看出, 与历史用电负荷量相关性最强的是温度, 其MIC值为0.38; 而相对湿度、降水量、风速的MIC值均为0.04, 表明温度、相对湿度、降水量、风速与历史用电负荷量之间存在一定的相关性. 其中nat_demand代表历史用电负荷量; T2M_roc代表温度; QV2M_toc代表相对湿度; TQL_toc代表降水量; W2M_toc代表风速.
3.4 实验评估指标将RIME-VMD优化的BLSTNet-CBAM的预测模型与其他模型作对比实验, 所有预测模型输入的数据保持一致, 确保对比实验的有效性. 实验采用多种评估指标对模型的预测性能进行全面评估, 这些指标包括平均绝对误差(MAE)、平均百分比误差(MAPE)和均方根误差(RMSE). 其中, 较低的误差值代表着预测值与实际值之间的更大接近度, 这也就意味着模型具有较高的准确度. 这些评估指标为模型的性能提供了全面的评估, 从而有助于更好地理解和改进模型的性能. 其计算公式为:
| eMAE=1nn∑t=1|ˉyt−ˆyt| | (38) |
| eMAPE=1nn∑t=1|ˉyt−ˆyt|ˉyt×100% | (39) |
| eRMSE=√1nn∑t=1(ˉyt−ˆyt)2 | (40) |
其中,
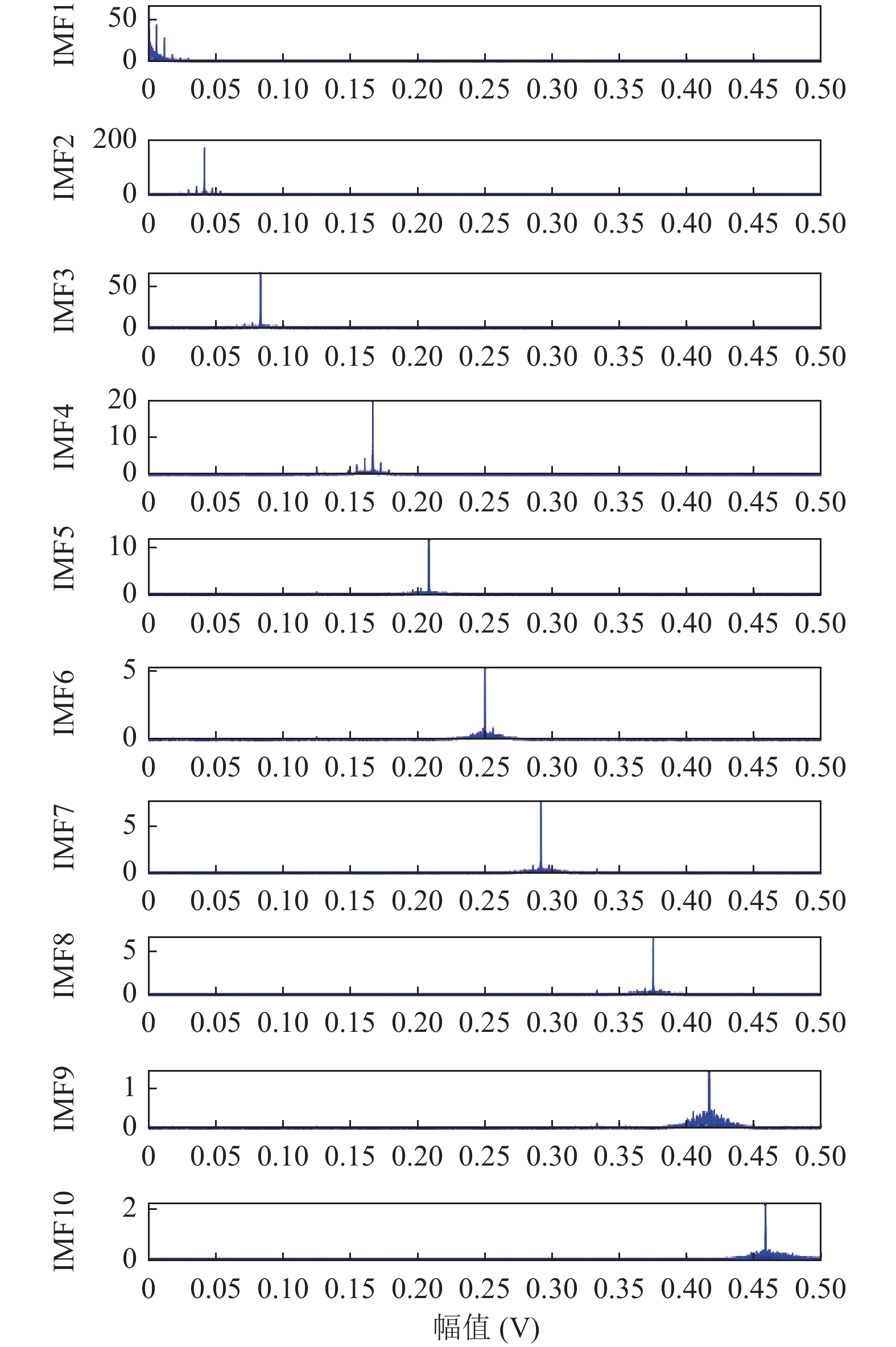
|
图 7 分解出IMF子序列的频谱图 |
3.5 实验设置
采用12th Gen Intel® Core™ i5-12500H 2.50 GHz处理器和GPU RTX 3080服务器作为硬件平台. 对于RIME-VMD模态分解部分, 该部分采用Matlab语言编写, 而其余部分则使用Python 3.8语言编写. 整体实验架构基于PyTorch框架进行设计与实现.
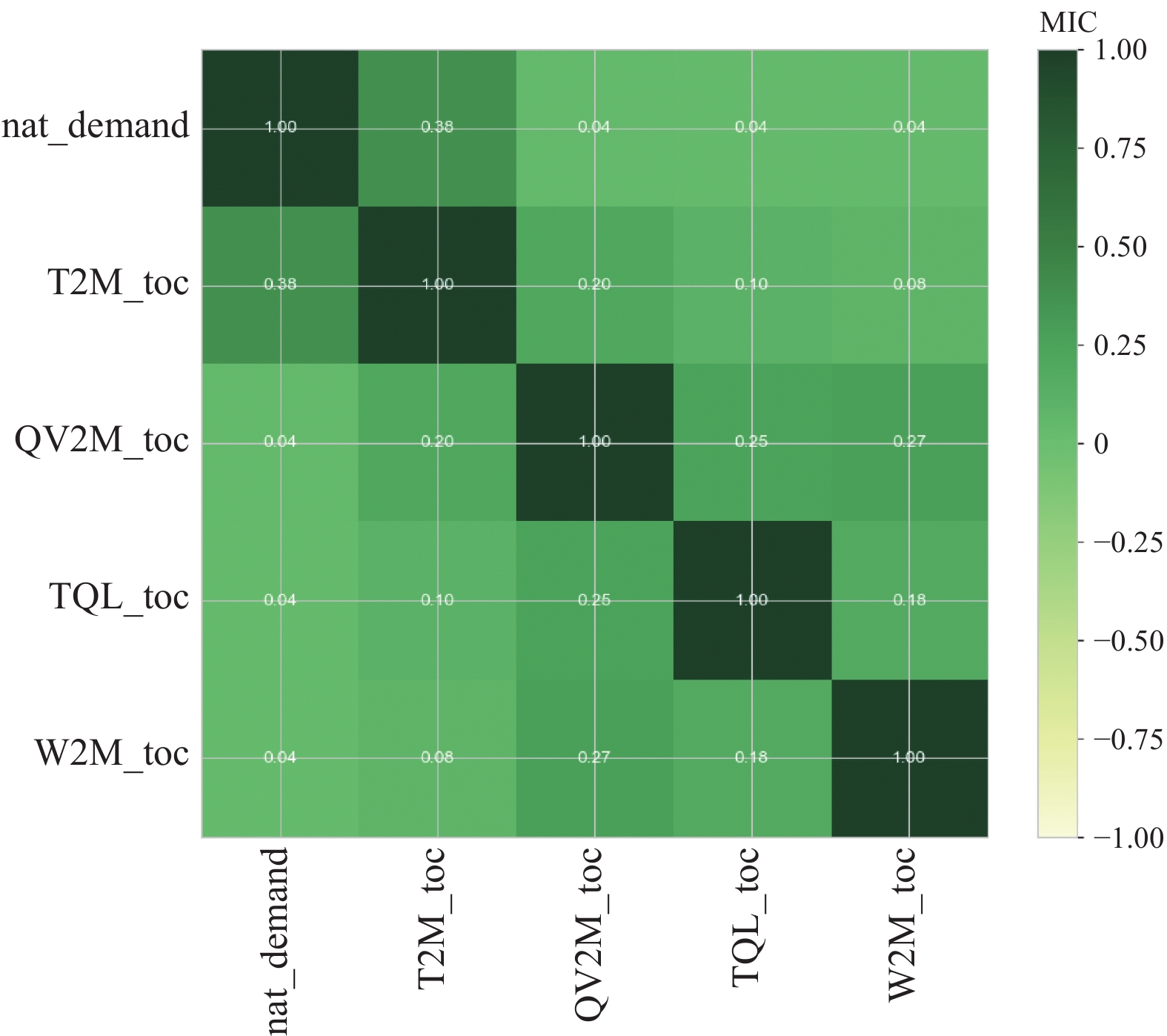
|
图 8 特征相关热图 |
BLSTNet-CBAM网络参数包括64个神经元的卷积层、64个神经元的递归层、20个神经元的递归跳跃层, 使用Adam算法[24]的优化以及64个训练批量和100次迭代.
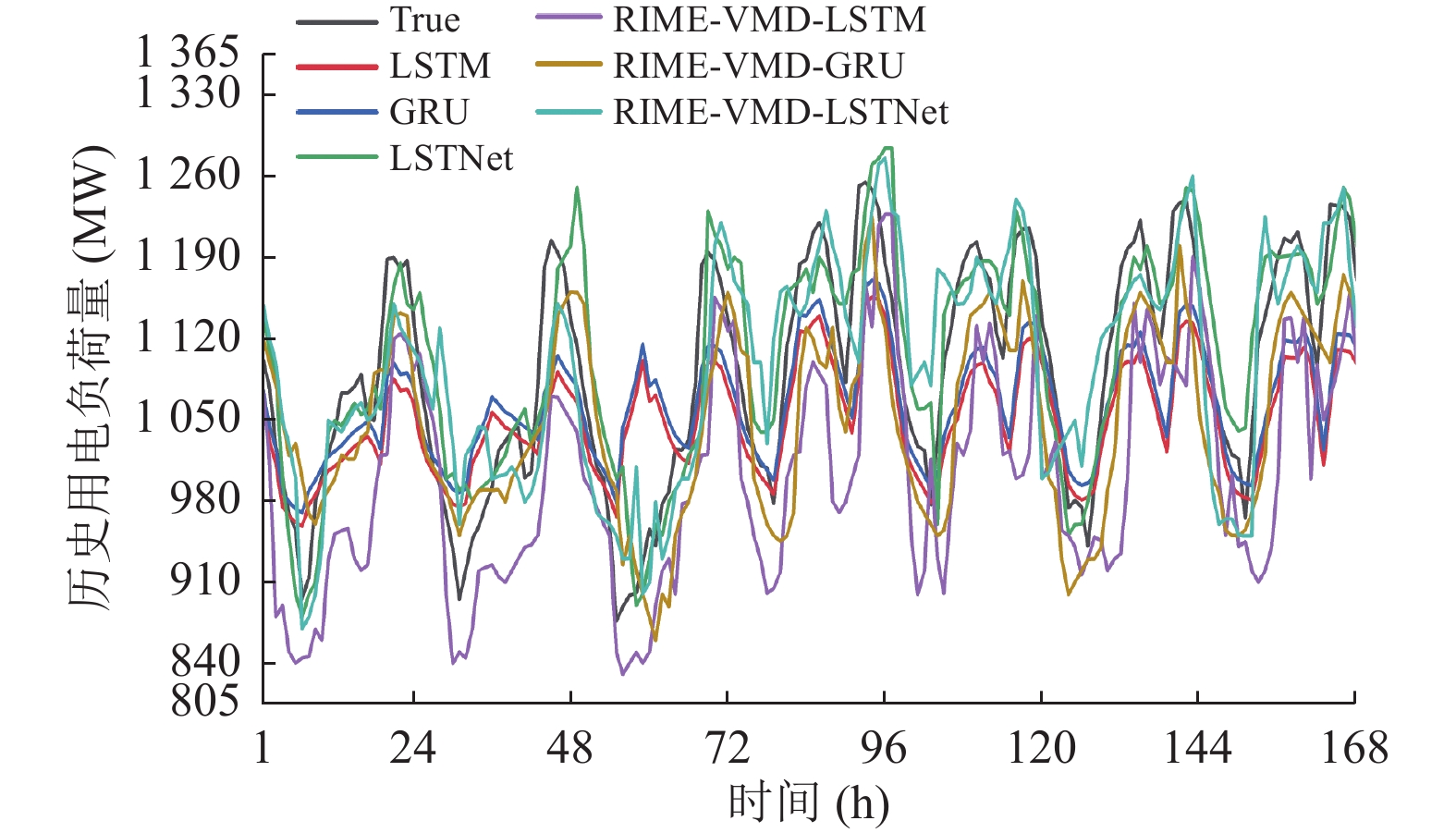
3.6 基于优化的VMD-LSTNet预测结果及对比分析 3.6.1 RIME-VMD分解对模型预测精度的影响分析为了评估本文提出的模型的有效性, 将RIME-VMD优化3个单一模型: LSTM、GRU和LSTNet中, 将预测模型优化前和优化后的预测性能进行比较. 如图9和表2所示.
|
图 9 RIME-VMD优化前后模型预测的比较 |
从图9中可以看出, LSTM、GRU、LSTNet在采用RIME-VMD优化后, 其预测产生了更好的结果, 表明RIME-VMD的分解方法有助于提高模型的预测精度. 同时表2显示出在已优化的模型中, RIME-VMD-LSTNet表现最好, MAE为28.877, MAPE为0.022, RMSE为35.558, 结果表明通过使用RIME优化的VMD分解负荷序列获得的输入特征提高了模型的预测精度, 同时适应于不同的预测模型.
| 表 2 RIME-VMD分解方法优化前后模型评价指标对比 |
3.6.2 BLSTNet-CBAM预测模型的比较分析
对于短期电力负荷预测, 本文提出的BLSTNet-CBAM模型与其他模型的评估指标如表3所示, 预测对比结果如图10所示.
| 表 3 所提出的模型和其他模型评估指标 |
|
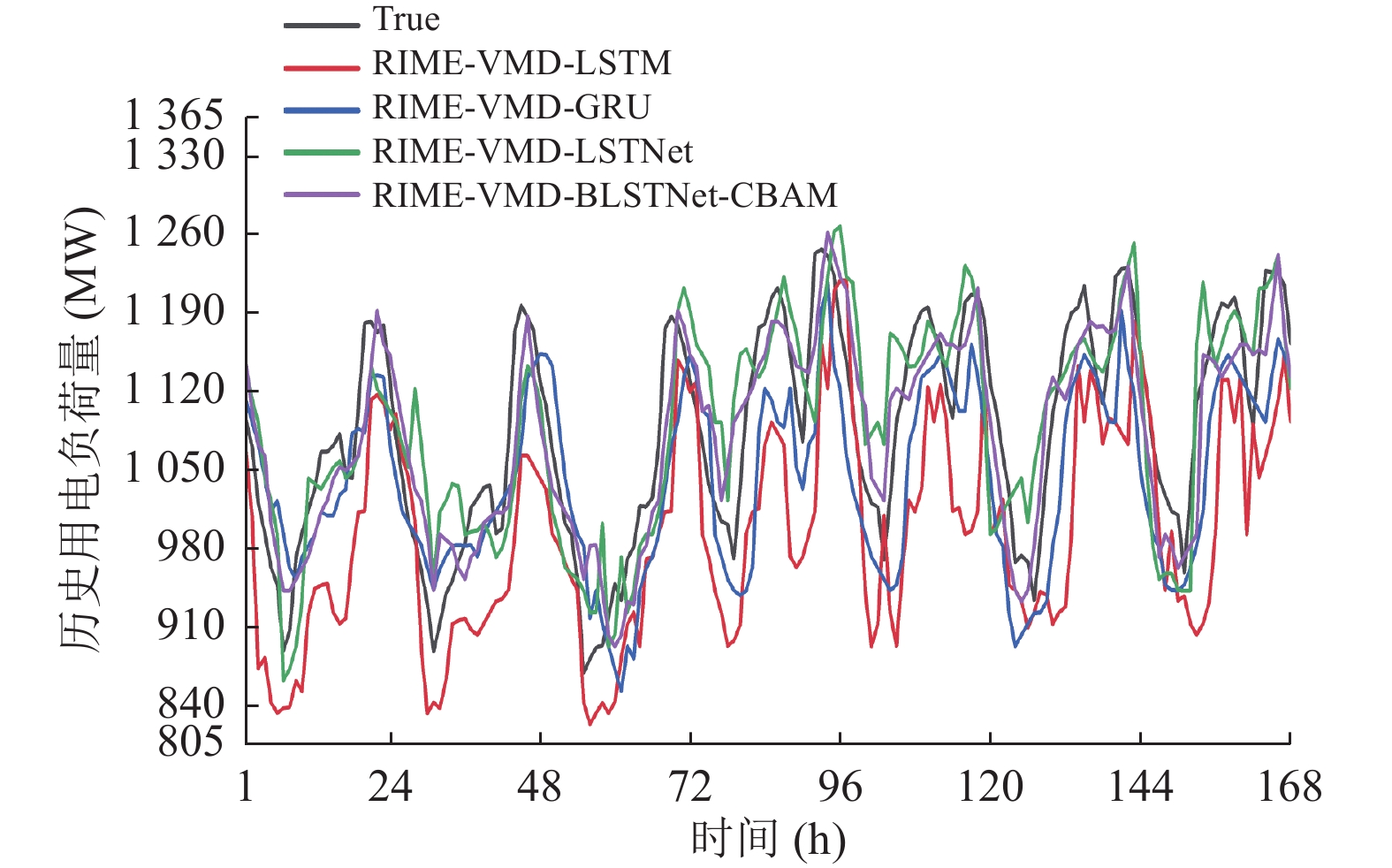
图 10 模型预测曲线对比图 |
图10显示了短期电力负荷预测中BLSTNet-CBAM和其他模型的预测结果曲线. 从图中可以明显看出, BLSTNet恰当地捕捉了电力负荷数据的非线性和非平稳性, 从而比LSTM、GRU和LSTNet具有更高的预测精度. 此外还表明了CBAM注意力机制可以提高模型的预测精度. 表3显示了BLSTNet-CBAM和其他模型的评估结果. 从表中可以清楚地看出, BLSTNet-CBAM模型均优于其他模型, 与LSTNet相比MAE、MAPE、RMSE分别降低了1.746、0.004、0.518. 从而证明本文提出的模型更有效地提取关键特征, 与现有模型相比具有更高的预测精度.
3.6.3 消融实验为验证所提出的预测模型RIME-VMD-BLSTNet-CBAM中各部分的有效性, 进行了一系列的消融实验, 其目的是分析模型中不同组件对预测性能的影响.
首先建立了一个基准模型, 即不包含任何消融组件的LSTNet模型. 接着, 逐步引入VMD模态分解、RIME优化算法优化VMD、将LSTNet的递归层LSTM替换为BiLSTM层以及CBAM注意力机制等组件. 通过逐步添加这些组件, 评估其对模型性能的贡献, 进而有助于揭示各个组件的作用和影响, 因此更全面地理解模型的性能改进. 消融实验结果如表4所示.
| 表 4 消融实验评估误差指标 |
通过消融实验的结果表明, 引入VMD模态分解和RIME优化算法显著提高了模型的预测性能. VMD模态分解将输入时间序列数据分解成不同频率的子序列, 使得每个子序列在相对较窄的频率范围内更易于建模, 其中与单一的LSTNet相比, MAE、MAPE、RMSE分别降低了1.955、0.001、4.341. 通过使用RIME优化算法对VMD分解进行优化, 与直接采用VMD分解相比, MAE、MAPE、RMSE分别降低了1.649、0.007、4.879. 结果说明RIME-VMD分解更好地提取了有用的子序列, 并减少误差噪声的影响, 从而改善了预测准确性.
将LSTNet的递归层LSTM替换为BiLSTM也在一定程度上改善了模型的性能. 相比融合RIME-VMD但未改进的LSTNet模型, MAE、MAPE、RMSE分别降低了1.219、0.002、0.311. 实验结果证明BiLSTM具有更好的建模能力, 能够更好地捕捉时间序列数据中的长期依赖关系. 此外, 引入CBAM注意力机制进一步提升了模型的性能, 其通过对时间序列数据的通道和空间特征进行有针对性的注意力操作, 能够有效捕捉关键特征信息. 与未引入CBAM注意力机制模型相比, MAE、MAPE、RMSE分别降低了0.527、0.002、0.207. 从而证明CBAM注意力机制有助于模型更好地聚焦于重要信息, 从而提高短期负荷预测性能.
综上所述, 消融实验的结果验证了RIME-VMD-BLSTNet-CBAM模型中各部分的有效性. VMD模态分解和RIME优化、使用BiLSTM替换LSTM的改进以及嵌入CBAM注意力机制, 都对模型的预测性能产生了积极影响, 为短期电力负荷预测任务提供了一种有效的建模方法.
4 结论为了解决现代电力负荷特征提取和提高预测精度的难题, 本文提出了一种基于RIME优化的VMD分解方法, 将负荷序列分解作为关键因素, 并结合BLSTNet预测模型和嵌入CBAM注意力机制, 构建了RIME-VMD-BLSTNet-CBAM短期电力负荷预测框架. 为了验证RIME-VMD和BLSTNet-CBAM算法的有效性, 给出了算法实例, 并得出以下结论.
(1)通过RIME优化后的VMD分解方法对电力负荷数据进行分解, 克服了VMD分解方法需要人工调整参数的需要. 采用包络熵作为适应度函数, 以最小的时间复杂度分解负荷分量, 从而促进预测模型的学习和特征提取. 所提出的方法使模型的精度得到了提高, 从而验证了计算分析的有效性.
(2)算例验证了BLSTNet-CBAM模型具有高预测精度, 这得益于RIME优化的VMD负荷序列构造, BLSTNet对负荷特征的高效学习和准确预测能力, 以及CBAM注意力机制对输入序列权重的分配. 通过将两者紧密结合, 解决了电力负荷特征提取的难题, 提高了模型的预测精度, 并最终获得了更高精度的预测结果.
| [1] |
Yildiz B, Bilbao JI, Sproul AB. A review and analysis of regression and machine learning models on commercial building electricity load forecasting. Renewable and Sustainable Energy Reviews, 2017, 73: 1104-1122. DOI:10.1016/j.rser.2017.02.023 |
| [2] |
张大海, 孙锴, 和敬涵. 基于相似日与多模型融合的短期负荷预测. 电网技术, 2023, 47(5): 1961-1969. DOI:10.13335/j.1000-3673.pst.2022.1110 |
| [3] |
万昆, 柳瑞禹. 区间时间序列向量自回归模型在短期电力负荷预测中的应用. 电网技术, 2012, 36(11): 77-81. DOI:10.13335/j.1000-3673.pst.2012.11.044 |
| [4] |
Alberg D, Last M. Short-term load forecasting in smart meters with sliding window-based ARIMA algorithms. Vietnam Journal of Computer Science, 2018, 5(3–4): 241-249. DOI:10.1007/s40595-018-0119-7 |
| [5] |
杨国华, 郑豪丰, 张鸿皓, 等. 基于Holt-Winters指数平滑和时间卷积网络的短期负荷预测. 电力系统自动化, 2022, 46(6): 73-82. DOI:10.7500/AEPS20210409003 |
| [6] |
陈培垠, 方彦军. 基于卡尔曼滤波预测节假日逐点增长率的电力系统短期负荷预测. 武汉大学学报(工学版), 2020, 53(2): 139-144. DOI:10.14188/j.1671-8844.2020-02-007 |
| [7] |
万强, 王清亮, 王睿豪, 等. 基于支持向量机的某地区电网短期电力负荷预测. 电网与清洁能源, 2016, 32(12): 14-20. DOI:10.3969/j.issn.1674-3814.2016.12.003 |
| [8] |
孙英云, 何光宇, 翟海青, 等. 一种基于决策树技术的短期负荷预测算法. 电工电能新技术, 2004, 23(3): 55-58, 75. DOI:10.3969/j.issn.1003-3076.2004.03.013 |
| [9] |
李焱, 贾雅君, 李磊, 等. 基于随机森林算法的短期电力负荷预测. 电力系统保护与控制, 2020, 48(21): 117-124. DOI:10.19783/j.cnki.pspc.191594 |
| [10] |
李鹏, 何帅, 韩鹏飞, 等. 基于长短期记忆的实时电价条件下智能电网短期负荷预测. 电网技术, 2018, 42(12): 4045-4052. DOI:10.13335/j.1000-3673.pst.2018.0433 |
| [11] |
王增平, 赵兵, 纪维佳, 等. 基于GRU-NN模型的短期负荷预测方法. 电力系统自动化, 2019, 43(5): 53-58. DOI:10.7500/AEPS20180620003 |
| [12] |
吕志星, 张虓, 王沈征, 等. 基于K-means和CNN的用户短期电力负荷预测. 计算机系统应用, 2020, 29(3): 161-166. DOI:10.15888/j.cnki.csa.007287 |
| [13] |
Lai GK, Chang WC, Yang YM, et al. Modeling long- and short-term temporal patterns with deep neural networks. Proceedings of the 41st International ACM SIGIR Conference on Research & Development in Information Retrieval. Ann Arbor: Association for Computing Machinery, 2018. 95–104. [doi: 10.1145/3209978.3210006]
|
| [14] |
朱凌建, 荀子涵, 王裕鑫, 等. 基于CNN-BiLSTM的短期电力负荷预测. 电网技术, 2021, 45(11): 4532-4539. DOI:10.13335/j.1000-3673.pst.2021.0470 |
| [15] |
叶淳铮, 常鲜戎, 顾为国. 基于小波变换和支持向量机的电力系统短期负荷预测. 电力系统保护与控制, 2009, 37(14): 41-45. DOI:10.7667/j.issn.1674-3415.2009.14.009 |
| [16] |
赵志强, 陆凤怡. 基于小波分解和ID3算法的短期日负荷最大值预测方法. 南方电网技术, 2010, 4(6): 98-102. DOI:10.13648/j.cnki.issn1674-0629.2010.06.018 |
| [17] |
张平, 潘学萍, 薛文超. 基于小波分解模糊灰色聚类和BP神经网络的短期负荷预测. 电力自动化设备, 2012, 32(11): 121-125, 141. |
| [18] |
王玉龙, 崔玉, 李鹏, 等. 基于小波分析改进的神经网络模型电力系统负荷预测. 电网与清洁能源, 2015, 31(2): 16-20, 27. DOI:10.3969/j.issn.1674-3814.2015.02.003 |
| [19] |
刘建华, 李锦程, 杨龙月, 等. 基于EMD-SLSTM的家庭短期负荷预测. 电力系统保护与控制, 2019, 47(6): 40-47. DOI:10.7667/PSPC180365 |
| [20] |
杨胡萍, 余阳, 汪超, 等. 基于VMD-CNN-BIGRU的电力系统短期负荷预测. 中国电力, 2022, 55(10): 71-76. |
| [21] |
Su H, Zhao D, Heidari AA, et al. RIME: A physics-based optimization. Neurocomputing, 2023, 532: 183-214. DOI:10.1016/J.NEUCOM.2023.02.010 |
| [22] |
Woo S, Park J, Lee JY, et al. CBAM: Convolutional block attention module. Proceedings of the 15th European Conference on Computer Vision. Munich: Springer, 2018. 3–19.
|
| [23] |
Reshef DN, Reshef YA, Finucane HK, et al. Detecting novel associations in large data sets. Science, 2011, 334(6062): 1518-1524. DOI:10.1126/science.1205438 |
| [24] |
Kingma DP, Ba J. Adam: A method for stochastic optimization. Proceedings of the 3rd International Conference on Learning Representations. San Diego: ICLR, 2015.
|
 2024, Vol. 33
2024, Vol. 33



