物联网的兴起使得大量的传感器设备和智能设备连接到网络, 产生了大量的数据. 据估计, 到2026年, 中国物联网连接规模将增加至102.5亿个^[1]. 然而, 由于数据的敏感性和隐私性, 将这些数据集中存储在一个中心化的服务器上进行训练存在一定的风险和难度.

为了解决数据隐私和集中式训练的问题, 联邦学习(federated learning, FL)^[2]应运而生. 联邦学习可以充分利用物联网中的分布式数据资源, 同时保护用户的数据隐私.

然而, 在边缘设备上执行FL面临着一系列的挑战. 首先, 边缘设备通常具有有限的计算能力和存储容量^[3], 而传统的深度神经网络(DNN)模型通常包含数万甚至数亿个参数, 导致模型训练的计算和内存需求巨大. 这使得在边缘设备上执行FL变得困难^[4], 可能导致训练时间过长或无法完成训练任务. 其次, 边缘设备的通信带宽和稳定性通常受限, 这会给模型参数的传输带来挑战. 高维和频繁的参数更新会产生较高的通信成本, 而边缘设备的有限带宽可能无法承受大量的参数传输, 甚至在不稳定的网络环境下导致传输失败.

为使联邦学习过程在资源受限的边缘端正常运行, 本文提出一种基于强化学习的新型联邦剪枝框架, 称为FRLP (federated reinforcement learning pruning). 其包含强化泛化剪枝方法RGP (reinforcement generalization pruning)和稀疏模型聚合方法FedSA (federated sparse averaging)两部分. 本文贡献包含以下几点.

(1)提出基于强化学习的联邦剪枝框架FRLP, 将强化学习与联邦剪枝相结合, 在减少模型规模同时保证模型效果.

(2)提出一种强化泛化剪枝方法RGP. 首先使用模型泛化性指导强化学习剪枝过程, 改善模型泛化能力. 随后抽象剪枝过程形成通用强化学习剪枝方法, 适应不同剪枝环境, 避免更换数据集及模型时需重新训练. 通过迭代剪枝和更新, RGP方法能够逐渐优化模型, 提高模型效果.

(3)提出一种稀疏模型聚合方法FedSA, 通过仅融合模型中的非零权重, 降低0权重对全局模型的干扰, 进一步提高模型的稀疏性.

(4)进行广泛的实验, 以使用流行的 DNN 模和公开可用的数据评估FRLP的性能, 证明了FRLP可以保证模型的泛化性, 同时在具有较快的收敛速度.

1 相关工作 1.1 联邦学习

联邦学习是谷歌于2016年提出的一种分布式机器学习框架, 用于移动互联网手机终端的隐私保护. 联邦学习将数据分散到各个节点(客户端)上进行本地训练, 然后通过交换模型参数来更新和改进模型. 这种技术可以实现在保护用户隐私的同时进行高效的模型训练. 联邦学习通常由一个中心服务器和若干客户端组成, 中心服务器负责协调和管理整个联邦学习过程, 客户端则拥有自己的本地数据并执行模型训练任务. 联邦学习训练过程通常包括以下几个步骤.

(1)中心服务器将全局模型参数发送给各个客户端.

(2)每个客户端使用本地数据和全局模型参数进行本地训练, 得到本地模型.

(3)客户端将本地模型参数上传至中心服务器.

(4)中心服务器聚合所有客户端的模型参数, 更新全局模型.

(5)中心服务器将更新后的全局模型发送给所有客户端.

(6)重复执行步骤(2)–(5), 直到达到预设的训练次数或满足其他停止条件.

1.2 模型剪枝

模型剪枝^[5]是一种模型优化技术, 通过去除模型中不必要的参数和连接来减少模型的大小和复杂度^[6]. 模型剪枝步骤包含预训练、剪枝和微调3个步骤: 首先模型使用训练集进行训练, 以学习数据的分布和规律; 随后对该模型执行剪枝操作, 以减少模型的复杂度; 最后对模型进行微调使模型更好地适应本地数据分布.

剪枝方法通常基于参数重要性的度量, 例如权重的绝对值^[6]或梯度^[7]等. 常见的模型剪枝方法包括结构化剪枝^[8]和非结构化剪枝^[9].

NISP^[10]通过计算神经元的重要性分数来移除不重要的神经元, 实现了细粒度的剪枝和更高的灵活性. Kim等人^[11]提出CPrune, 用于支持所需目标精度的目标感知的深度神经网络的高效执行. SlimGNN^[12]减少GNN模型和输入图中的冗余信息, 简化训练过程, 加速训练.

现有的剪枝技术访问全局数据分布以达到较好的效果, 模型训练时间长, 计算量大. 这并不适用于数据分散的FL系统, 并且难以在资源受限的移动和物联网设备上正常运行.

1.3 联邦剪枝

联邦剪枝(federated pruning)^[13]是一种针对联邦学习场景的模型剪枝技术, 将剪枝与联邦学习相结合, 实现模型的压缩和精简, 减少通信和计算开销. 现有的联邦剪枝方法从剪枝算法改进^[7]、与量化相结合^[14]等方向展开研究以提高算法准确性和减少开销. Prakash等人^[14]提出一种基于模型压缩的FL方法GWEP, 通过联合量化和模型修剪以提高通信效率, 加快训练过程. 但模型修剪置于客户端, 增加其计算压力. Yao等人^[15]提出FedHM, 将异构低秩模型分发给客户端, 然后将它们聚合到全局全秩模型. Jiang等人^[16]提出修剪机制CS, 通过在服务器和客户端完成互补和协作修剪完成低开销和高精度的要求. 二者都使用固定剪枝比例进行剪枝或模型分解, 缺少与环境交互的能力. FedDUAP^[17]利用服务器上的贡献数据进行动态更新并根据维度和重要性进行唯一一次自适应剪枝, 可能导致剪枝不充分或过度剪枝, 进而影响模型的性能和准确性.

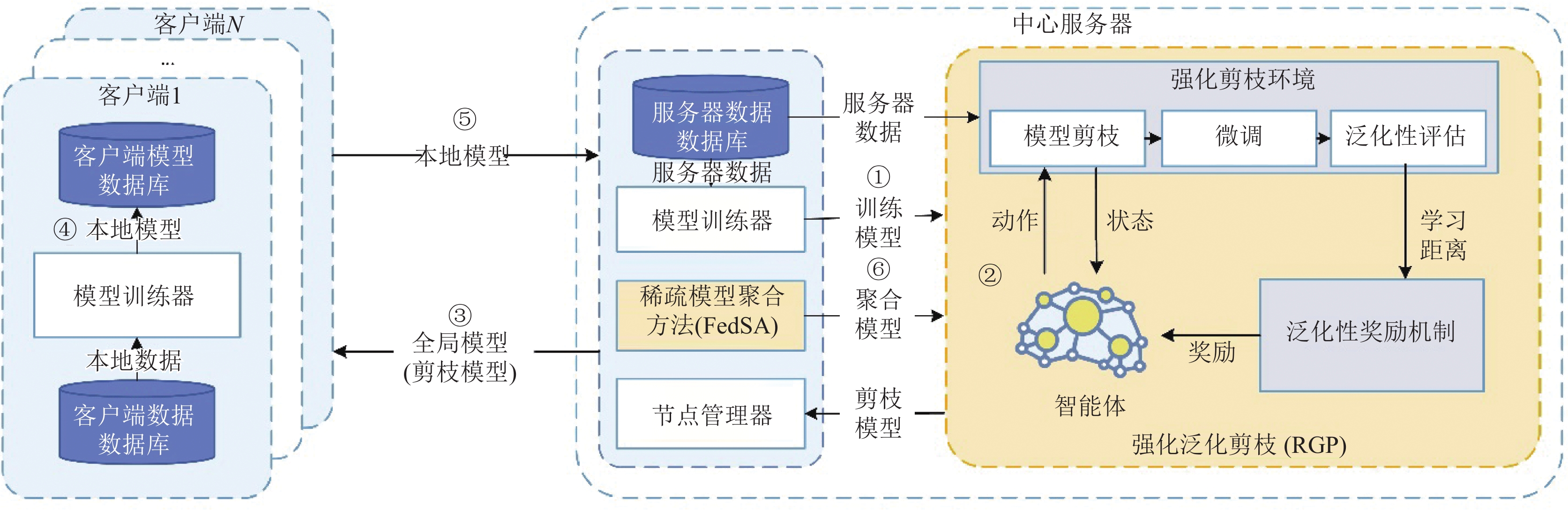
2 基于联邦强化学习的分布式模型剪枝 2.1 系统架构

所提出的FRLP框架依赖于联邦学习, 包含强化泛化剪枝策略RGP与稀疏模型聚合方法FedSA两部分. RGP以泛化性为指标, 动态地调整剪枝策略, 在减少参数数量的同时保持模型的性能. FedSA以非0平均的方式聚合各客户端剪枝率不同的模型. FRLP总体架构如图1所示.

假设本文所提出的FRLP框架处于具有一个服务器和N个客户端的联邦学习系统中. 服务器同客户端一样也具有训练数据以支撑强化学习. 设${D_n}$是客户端${{n}} \in \left\{ {1, 2, \cdots , {{N}}} \right\}$的本地数据集, 则联邦学习的目的是找到模型权重$w$使全局经验损失${{F}}\left( {{w}} \right)$最小:

$ \begin{array}{*{20}{c}} {\mathop {\min }\limits_w F\left( {{w}} \right) = \displaystyle\mathop \sum \limits_{n = 1}^N {p_n}{F_n}\left( w \right)} \end{array} $

(1)

$ \begin{array}{*{20}{c}} {{F_n}\left( w \right) = \dfrac{1}{{\left| {{D_n}} \right|}}\displaystyle\mathop \sum \limits_{i \in {D_n}} {f_i}\left( w \right)} \end{array} $

(2)

其中, ${p_n}$是客户端n的权重且$\displaystyle\mathop \sum \limits_{n = 1}^N {p_n} = 1$, ${f_i}\left( w \right)$是客户端n对于其数据集样本$i$的损失函数.

将强化泛化剪枝方法RGP与稀疏模型聚合方法FedSA集成到原始联邦学习训练过程中形成FRLP. 如图1所示, FRLP的训练过程由多轮组成, 每轮包含6个步骤, 第t轮训练步骤描述如下: 若t=0, 执行步骤①, 服务器${{S}}$初始化模型参数, 并使用服务器数据训练初始密集模型$M_G^{{t}}\left( {M_G^0} \right)$.

若t为指定剪枝轮次, 执行步骤②, 服务器${{S}}$使用强化泛化剪枝方法RGP对全局模型$M_G^t$执行剪枝操作, 得到剪枝后模型$M_{Gp}^t$. 随后通过步骤③使用节点管理器筛选参与此次参预训练的客户端并下发剪枝后模型$M_{Gp}^t$. 否则直接通过步骤③下发全局模型$M_G^t$至客户端.

在步骤④中, 客户端n接收全局模型$M_G^t$并使用本地数据${D_n}$进行本地微调, 生成$M_n^t$. 随后通过步骤⑤将本地模型$M_n^t$传输至服务器, 并使用FedSA进行模型聚合得到新的全局模型$M_G^{t + 1}$以完成步骤⑥.

在强化泛化剪枝RGP中, 智能体每次都会根据当前状态选择一个动作来执行, 其表示对全局模型$M_G^{{t}}$执行剪枝率为p的剪枝操作. 随后, 强化剪枝环境根据智能体选择的动作对$M_G^{{t}}$进行非结构化剪枝, 得到智能体状态转移, 并使用服务器数据进行模型微调和泛化性评估计算出模型的学习距离. 泛化性奖励机制依据学习距离计算此次动作的奖励, 并使用奖励值更新强化学习模型.

2.2 强化泛化剪枝RGP

本节提出强化泛化剪枝方法RGP, 将剪枝过程视为一个RL问题, 并使用模型泛化性指导剪枝决策. 随后泛化RL模型, 使其具备通用性, 可以应用于其他剪枝任务中, 避免了重复训练的时间和计算资源消耗, 提高了剪枝的效率和可扩展性.

He等人^[18]发现了模型剪枝过程中的稀疏双下降现象, 并且证明了学习距离和模型性能之间的关系. 本文受其研究成果启发, 并对其进行扩展. 泛化性是衡量模型性能的一个重要指标, 因为剪枝后的模型需要在未见过的数据上表现良好. 因此, 本文使用泛化性作为剪枝的评估指标.

本文将学习距离D定义为模型与其初始化的${l_2}$距离. 学习距离越小, 模型泛化性越强. 定义${W_{{\mathrm{init}}}} \in {R^d}$为密集模型初始化权重, ${W_{{\mathrm{finetune}}}} \in {R^d}$为剪枝后微调的模型权重, 则学习距离D的计算公式见式(3):

$ \begin{array}{*{20}{c}} {D\left( {{W_{{\mathrm{finetune}}}}} \right) = {{\left| {\left| {{W_{{\mathrm{init}}}} - {W_{{\mathrm{finetune}}}}} \right|} \right|}_2}} \end{array} $

(3)

为提高强化学习训练速度以及避免过度剪枝, 设置单次剪枝范围和模型稀疏上限. 若使用RL直接在设置范围内搜索泛化性最高点的剪枝率, 则存在搜索空间大、搜索时间长、搜索困难的问题. 另外环境变化后均需重新训练使之学习当前环境, 资源消耗巨大, 且此时选择的剪枝率可能极接近0, 无法体现剪枝效果.

为了解决以上问题, 本系统将剪枝问题抽象为经典的一维场景探索问题, 使训练好的强化学习模型适用于其他剪枝任务. 首先在设定范围进行采样, 并以泛化性最高点作为RL初始状态点. 设初始状态点的剪枝率为${p_0}$, 此时修剪后微调的模型为${W_{{p_0}}}$. 在t时刻, 设模型剪枝率为${p_t}$. 通过式(4)确定智能体终点:

$ \begin{array}{*{20}{c}} {\left| {\frac{{D\left( {{W_{{p_t}}}} \right)}}{{D\left( {{W_{{p_0}}}} \right)}} - y} \right| < \varepsilon } \end{array} $

(4)

其中, 参数$y$和$\varepsilon $是超参数, 在本文中, 分别设置为1.05和0.015. 式(4)的目的是在最小化泛化性变化量的同时提高剪枝率.

设计马尔可夫链所需要素如状态、动作、策略和奖励, 详细介绍如下.

状态: 状态反映了智能体的情况. 本文使用整数表示网络状态${{s}}$, 其具体意义是状态${{s}}$距初始化${s_0}$的距离. 当剪枝率增加一步长时${{s}} = {{s}} + 1$, 否则, ${{s}} = {{s}} - 1$.

动作空间: 动作空间是动作的集合. 使用离散动作空间, 智能体拥有两种动作, 分别表示剪枝率增大或者减小. 设置每次动作的步长为0.05%, 以保证剪枝精度.

奖励函数: 在问题抽象的背景下, 奖励函数不再直接与泛化性相关, 使用式(5)计算奖励函数:

$ \begin{array}{*{20}{l}} {R\left( a \right) = } \end{array}\left\{ {\begin{array}{*{20}{l}} {r - 1}, \\ {r + 1}, \\ {r + a\times 0.5}, \end{array}\begin{array}{*{20}{l}} {s \notin \left[ {0, {\mathrm{uplimit}}} \right]} \\ {s = {\mathrm{end}}} \\ {{\mathrm{else}}} \end{array}} \right. $

(5)

其中, ${\text{uplimit}}$为设置的剪枝上限, ${\text{end}}$表示式(4)确定的剪枝终点. 使用此奖励函数鼓励智能体不断向右移动以提高剪枝率直到到达设定终点.

为了适应问题的要求并实现所提出的MDP, 本文选择DQN算法^[19]作为解决方案. RGP过程见算法1.

算法1. 基于DQN的RGP算法

1) 以容量N初始化经验池D;

2) 分别使用随机权重$\scriptstyle \theta $和$\scriptstyle {\theta ^ - }$初始化动作值函数Q和目标函数Q;

3) for episode=1 to M do

4) 　初始化探索策略, 获得初始状态$\scriptstyle {s_0}$

5)　　 for t=1 to T do

6)　　 执行动作$\scriptstyle {a_t}$, 对目标网络进行修剪和微调, 并根据学习距离确定是否终止

7)　　 计算奖励$\scriptstyle {r_t}$和新状态$\scriptstyle {s_{t + 1}}$

8) 　　将转移元组$\scriptstyle \left( {{s_t}, {a_t}, {r_t}, {s_{t + 1}}} \right)$存储到D

9)　　 令$\scriptstyle {s_t} = {s_{t + 1}}$

10) 　 随机从D中抽取minibatch个转移元组

11)　 for j =1 to minibatch do

　　　　　$\scriptstyle {y}_{j}= \left\{\begin{array}{l}\scriptstyle {r}_{j},\\ \scriptstyle {r}_{j}+\gamma \max Q\left({s}_{j+1}, {a}^{\prime }, {\theta }^{-}\right),\end{array}\begin{array}{l}\scriptstyle {s}_{j+1}\; {\mathrm{is}}\;{\mathrm{ terminal}}\\ \scriptstyle {\mathrm{others}}\end{array}\right. $

12) 　　　 在网络参数$\scriptstyle \theta $上执行梯度更新

　　　　　　　$\scriptstyle {\left( {{y_j} - Q\left( {{s_j}, {a_j}, \theta } \right)} \right)^2}$

13)　　 end for

14) 　　每C步令$\scriptstyle {\theta ^ - } = \theta $

15) 　end for

16) end for

算法1每次依据当前模型状态随机选择一个动作并执行剪枝操作, 评估奖励和状态, 并将转移元存储到经验池中. 随后智能体从经验池中随机抽取样本进行训练, 通过最小化预测的Q值与实际Q值之间的差距来更新网络参数, 直至其收敛.

2.3 稀疏模型聚合方法FedSA

传统模型聚合方法FedAVG使用加权平均聚合方式, 使用式(6)将局部模型参数聚合成全局模型参数.

$ \begin{array}{*{20}{c}} {{w_{t + 1}} = \displaystyle\mathop \sum \limits_{k = 1}^M \dfrac{{{m_k}}}{m}w_{t + 1}^k} \end{array} $

(6)

其中, ${w_{t + 1}}$为${{t}} + 1$轮聚合得到的全局模型参数, M代表参与聚合的客户端的数量, ${m_k}$为${{t}} + 1$轮聚合中客户端k的样本数量, m表示参与训练的M个客户端总样本数量, $w_{t + 1}^k$为${{t}} + 1$轮聚合中客户端k的本地模型参数.

在剪枝情境下, 联邦学习环境中模型的稀疏度存在差异. FedAVG方法简单地对模型参数进行平均, 而不考虑模型的稀疏性. 这意味着在聚合过程中, 零权重和非零权重都被平等地对待, 无法充分处理稀疏模型而产生负面影响. 本文提出FedSA以解决不同稀疏度模型聚合的问题.

FedSA方法的核心思想是只对非零权重进行加权平均, 避免对零权重进行无效计算, 确保聚合结果更加准确地反映全局模型的特征和结构.

具体来说, 在模型聚合过程中, FedSA首先对每个模型进行稀疏性分析, 得到其稀疏结构. 然后, 对非零权重进行加权和平均. 这种方法确保了聚合结果准确地反映了全局模型的特征和结构. 其公式如式(7)所示:

$ \begin{array}{c}{w}_{t+1}={\displaystyle \sum }_{k=1}^{M}\dfrac{\dfrac{{m}_{k}}{m}}{{{\displaystyle \sum }}_{k}^{M}\dfrac{{m}_{k}}{m} \left({w}_{t+1}^{k}\ne 0\right)}{w}_{t+1}^{k}\end{array} $

(7)

3 实验分析

本节首先评估所提出融合算法的有效性; 其次, 评估FRLP系统的泛化性; 最后评估系统的收敛速度.

3.1 实验设置

数据集: 本文使用CIFAR-10、MNIST和Fashion MNIST (FMNIST)数据集来评估FRLP. CIFAR-10是一个用于识别通用对象的数据集, 由10类RGB彩色图像组成, 包括50000张训练图像和10000张训练图像. MNIST是一个常用的手写数字识别数据集, 其中每个样本是一个28×28像素的灰度图像, 代表0–9之间的数字. FMNIST是一个类似于MNIST的服装图像分类数据集, 包含10个不同类别的服装图像.

模型: 本文使用VGG-19^[20]和ResNet-18^[21]. VGG-19由16个卷积层和3个完全连接层组成. ResNet-18由17个卷积层和1个线性层组成.

超参数: 本文使用相同的超参数进行试验. 建立了一个由1个中心服务器和100个客户端组成的FL系统. 在每一轮中, 随机选择10台设备参加训练.

3.2 基线

本节将我们提出的FRLP与几个最近提出的几种基线进行比较.

PruneFL^[13]: PruneFL 包括在选定的客户端进行初始修剪, 并进一步修剪作为 FL 过程的一部分.

PQSU^[22]: PQSU包括结构化剪枝、权重量化和选择性更新3部分, 并且只在初始轮次进行一次剪枝.

FedAVG^[2]: FedAVG是使用最广泛的FL算法之一. 本文使用FedAVG训练密集模型作为基线之一.

3.3 实验评估指标

本文使用的试验评估指标有模型泛化性、稀疏性以及损失.

模型的泛化性指的是模型对于新样本的适应能力, 即模型在未在训练集中出现过的数据上的预测能力. 准确率是分类模型最常用的评估指标之一, 它表示模型在测试集上正确预测的样本数与总样本数之比. 较高的准确率意味着模型在未见过的数据上的预测能力较强, 即模型具有较好的泛化性. 准确率计算公式见式(8):

$ \begin{array}{c}Accuracy=\dfrac{{{\displaystyle \sum }}_{i=1}^{N}T{P}_{i}}{\textit{Total}} \end{array} $

(8)

其中, $N$表示表示数据集中样本的类别数, $T{P_i}$表示第$i$类数据被正确分类的数量, ${\textit{Total}}$表示总的样本数.

稀疏性是指模型零权重的百分比, 较高的稀疏性可以减少模型的存储空间以及提高计算效率. 模型稀疏率的计算公式如式(9)所示:

$ \begin{array}{c}{\textit{Sparsity}}={{\displaystyle \sum }}_{i=1}^{m}\dfrac{{\tau }_{i}}{{M}_{i}{N}_{i}} \end{array} $

(9)

其中, $m$表示模型层数, ${\tau _i}$表示第$i$层模型参数中零权重数量, ${M_i}$, ${N_i}$分别表示第$i$层模型参数矩阵的行数和列数.

最后, 本文使用交叉熵损失函数计算损失, 计算公式见式(10):

$ \begin{array}{c}Loss=-\dfrac{1}{N}{\displaystyle \sum }_{i=1}^{N} \end{array}{y}_{i}\mathrm{log}\left({p}_{i}\right) $

(10)

其中, N为样本类别数, ${p_i}$表示样本属于第$i$类的概率, ${y_i}$表示真实标签的概率分布, 它是一个one-hot编码向量. 当样本属于第$ i $个类别, ${y_i}$= 1, 否则${y_i}$= 0.

3.4 融合算法FedSA评估

为了验证所提出中心聚合方法FedSA的有效性, 本节将FedSA与FedAVG进行比较. 仅改变FRLP框架内中心聚合方法以验证FedSA优越性. 实验结果见表1, 展示了不同模型及数据集下两种聚合方法产生全局模型的最佳准确率与稀疏性. 模型剪枝的目标是在保证准确率的情况下增加模型中零权重的比例.

实验结果可以看出, FedSA与FedAVG结果平均准确率相差0.57%, 但FedSA却能获得高平均18.9%的稀疏率, 证明了其在联邦学习剪枝任务中的有效性和可行性. FedSA方法可以更好地处理联邦学习环境中不同稀疏度模型的聚合问题, 避免了模型稀疏性对聚合结果的负面影响.

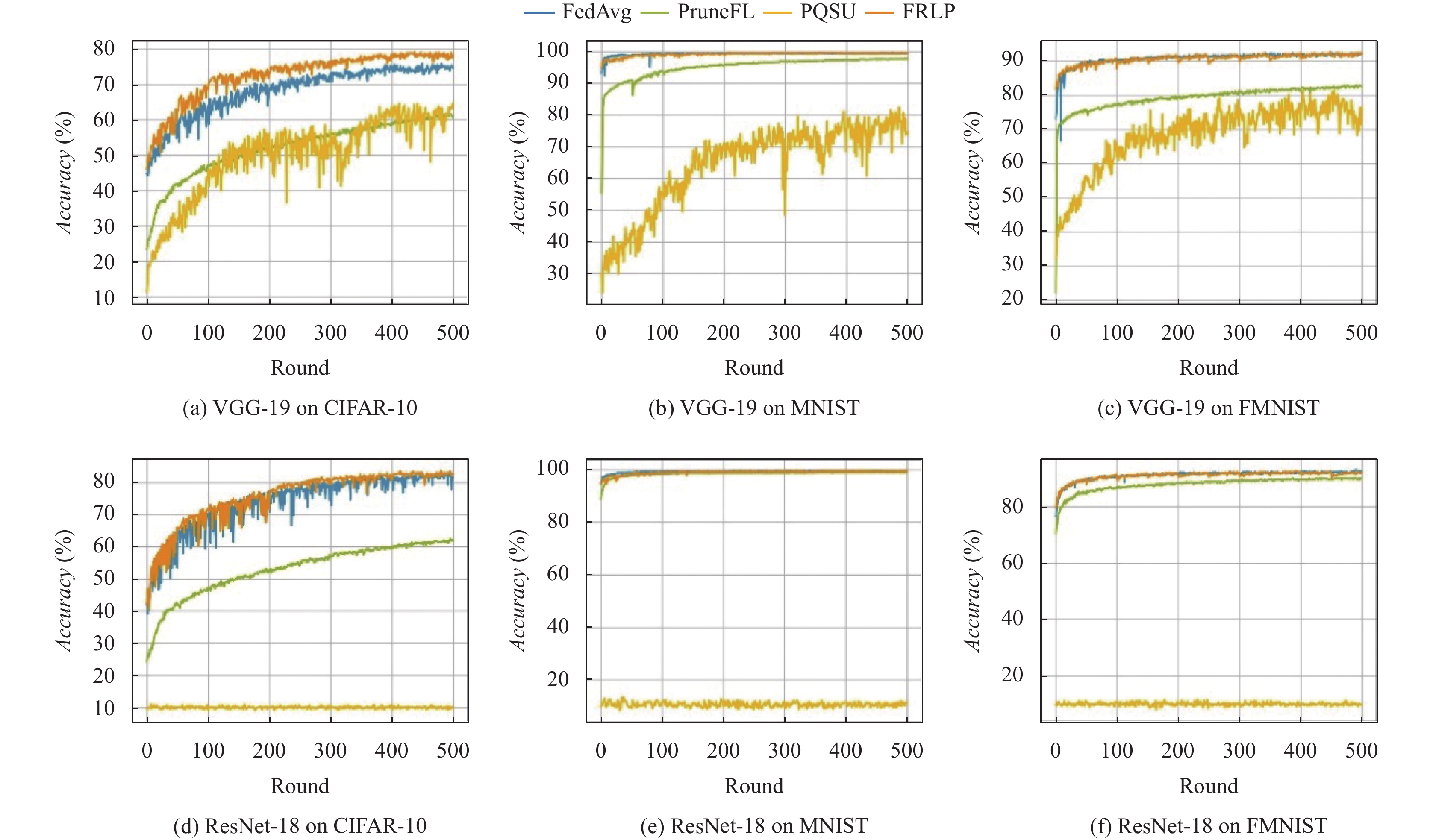
3.5 模型泛化性评估

本节使用模型准确率评估模型泛化性, 使用上述提出的数据集与基线验证全局模型准确率, PQSU基线参考FRLP结果设置成与其相同的剪枝率. 图2显示了不同数据集上FRLP与基线全局模型准确率的比较. 当剪枝模型为VGG-19时, FRLP的模型效果明显高于其他联邦剪枝基线, 与FedAVG训练密集模型保持相似的精度. 当剪枝模型为ResNet-18时, 基线PQSU进行的剪枝操作对模型造成巨大损伤, 使其因信息丢失严重以致存在较大的精度损失, 模型无法收敛. 并且由于ResNet-18模型在MNIST和FMNIST数据集上表现出色, PruneFL与FRLP精度差距减小, 但即使图2(e)表现出二者曲线几乎重叠, FRLP的准确率也始终高于PruneFL, 平均准确率相差0.43%.

3.6 收敛速度评估

实验结果如图3, 表2和表3所示. 图3显示了FRLP与基线方法在不同数据集上模型损失随训练轮次变化曲线. 除图3(a) PQSU获得最低损失的情况外, FRLP的损失始终低于其余联邦剪枝基线, 与未剪枝的联邦学习过程保持相似的水平. 表2和表3中Ra列显示了相应实验中模型准确率达到a×100%所需的最小轮数. 在表2和表3中, 与剪枝基线相比, FRLP总是以最快的速度达到指定准确率. 此外, FRLP还能达更高的准确率, 这是其他剪枝基线无法做到的. 因此, 我们可以得出结论, FRLP在剪枝方面具有显著的优势, 有效地提高模型的准确率和训练效率, 同时获得更低的训练损失.

4 结论与展望

为使联邦学习过程在资源受限的边缘端正常运行, 并解决传统联邦剪枝中人为设置固定剪枝率, 无法根据模型环境自适应剪枝的问题, 本文提出基于联邦强化学习的分布式模型剪枝方法FRLP. 首先构建中心剪枝-边缘微调的剪枝流程, 随后建立以模型泛化性为指标的通用强化学习剪枝方法RGP, 与自主选择最佳剪枝率. 其次设计稀疏模型聚合方法FedSA, 避免稀疏度不同的模型的无效加权. 本文使用多个数据集以及模型对FRLP进行广泛评估, 实验结果表明FRLP所得模型泛化性以及系统收敛速度相较于基线有明显提升.

为了减少强化学习训练及决策的时间, 本文已对剪枝过程抽象化, 形成通用模型. 但在系统运行过程中强化学习部分仍消耗大量时间, 下一步可继续进行时间优化.