2. 宁夏大学 经济管理学院, 银川 750021
2. School of Economics and Management, Ningxia University, Yinchuan 750021, China
在21世纪的互联网时代, 社交网络平台如Facebook、Twitter和微博已成为人们生活中不可或缺的一部分, 是信息交流和意见形成的关键平台. 这些平台允许用户自由分享和表达对各种事件、产品或观点的看法和情绪. 用户在社交网络上发布的内容不仅反映了个人态度, 还可能对其他用户的行为和观点产生深远的影响. 因此, 研究社交网络中的意见动态, 即人们在讨论特定话题时意见的变化和形成, 已经成为社会学和信息技术领域的研究焦点. 在这一研究中, 通常使用直接图来表示个体及其相互作用, 以探讨如何通过特定规则更新意见来达成共识, 以及意见形成过程中的复杂动态. 基于不同的意见更新规则, 其中包括DeGroot模型[1]、Friedkin-Johnsen (FJ)模型[2,3]、选民模型[4–6]和有界置信模型[7,8], 这些模型的提出揭示了研究意见动力学的必要性.
在意见动力学的研究中, 探讨如何在社交网络中达成共识[9]是一个核心挑战. 这一过程通常是由迭代和动态的讨论组成, 经常在leader的引导下进行. 在几轮讨论后, 参与者更新他们的意见, 直至最终达成共识. 关于共识达成的研究涉及多个方面[9–12]. 现有研究表明, 社交网络中的个体可以分为影响力较大的leader和跟随者的follower, 其中leader在意见形成过程中起着决定性作用[11]. 然而, 在现实中, 即使没有明显领导者的情况下, 如在形成道德价值观和是非观方面, 人们仍然能够自然而然地达成共识.
尽管已有研究对leader在意见形成中的作用进行了深入探讨, 但仍然存在一些未解之谜, 特别是在缺少中心化领导者的网络环境中, 共识是如何形成的? 探索这一问题不仅有助于深入理解社交网络的动力学, 也对理解人类社会决策过程中的群体行为有重要意义. 这提示着, 共识的形成可能不仅依赖于网络中的领导者, 而是受到更广泛的社会和心理因素的影响.
本文旨在通过深入分析社交网络中的个体邻域的意见, 调整与个体相似的意见权重以强化意见距离下的近距离意见影响力, 或调整与个体不太相似的意见权重增加与意见距离下的远距离意见影响力, 从而在没有全球领导人参与的情况下达成社会网络共识. 该研究的动机源于现实世界对特定需求的迫切需要, 例如在道德判断时, 个体常受到整个社会舆论的影响, 而忽略了邻域的观点. 此外, 该模型还具备预测公众共识在特定话题上的形成的潜力. 研究结果不仅可应用与社交媒体营销、公共政策制定等领域, 而且为理解和引导公众意见提供了新的独特视角.
在接下来的章节中, 将详细介绍研究的方法和分析过程, 并深入讨论所得到的结果.
2 相关工作近年来, 社会群体的研究呈现出一种跨学科的趋势, 将自然科学和计算机科学相结合, 形成了一个新兴的研究领域—观点动力学, 又称为舆论动力学. 该领域通过融合数学、物理以及计算机科学等技术, 特别是基于多智能体的建模和仿真方法, 探讨了社会群体中观点趋于一致、极化或者分裂现象的演化过程和规律.
在舆论动力学领域的研究中, 学者们提出了众多的舆论动力学模型. 其中, 最为经典的意见演化模型[13]是由美国心理学家French于1956年提出, 主要用于研究个体在社会群体中的社会影响力, 逻辑地解释了正式群体人际关系的影响过程. 1974年, DeGroot[1]扩展了French提出的模型并形成了DeGroot模型, 该模型提出了重复协商的沟通机制, 使用线性意见演化模型研究了群体达成共识的条件和场景. 随后, 学者们建立了基于离散意见的Voter模型[14,15]和Sznajd模型[16], 以及在有界置信度假设下考虑连续意见的Deffuant模型和Hegselmann-Kuarse模型[17]. 这些模型通过数学建模和仿真, 其传播规则为理解个体如何受到周围观点影响提供了重要线索.
由于在网络舆论环境中, 个体不仅与部分个体进行互动, 还会受到与之接触的其他各种观点的影响. 这种传播特征与DeGroot的传播规则非常相似, 因此我们将遵循DeGroot模型及其基本假设来构建模型.
意见动态系统的状态可分为多簇、极化和统一这3种[10]. 其中, 群体意见的统一是指整个群体达成一致的意见共识. 研究者们进一步关注了再舆论动力学中领导者共识的问题. Zino等人[18]提出了在DeGroot模型中, 通过一组异构性的领导者将整个网络引导到领导者的状态, 该领导者节点比其他节点更多地参与到信息共享过程. Ding等人[19]研究了前两个意见领袖的自信水平影响社交网络DeGroot的共识收敛速度. Zhao等人[20]研究了电子商务背景下两组不同目标意见的意见领袖对群体意见演变的影响. Tian等人[21]总结了顽固主体对意见形成的影响, 并提出了达成共识的标准. Jia等人[22]采用DeGroot-Friedkin (DF)模型以证明自我坚持、社会权利和人际影响在意见动态中的进化过程. 以上文献的研究内容表明, 在观点动力学中, 领导者的作用不可忽视, 其态度和影响力对整个群体形成共识具有重要影响.
然而, 在实际社交网络中, 通常不存在明确定义的领导者. 针对这一情景, 一些研究者着眼于无领导者共识的研究, 即在缺少中心化领导者的网络环境中, 共识是如何形成的. Yao等人[23]研究了固执节点影响其他非固执节点的观点以达成共识的演变过程. He等人[24]得到了在结构平衡和不平衡社交网络中, 固执个体对共识的收敛和稳定性的条件. Zhao等人[25]提出了调整固执代理的比例和网络连通性, 以产生更紧凑的最终意见空间的方法. Cho等人[26]将知情代理视为顽固代理, 试图解决在无领导者情景下的共识形成问题. 虽然研究中引入了顽固代理以促进共识形成, 但需要注意这一决策属于一种人为因素, 可能影响研究的普适性. 与此同时, 无领导共识在缺乏顽固代理时, 其形成速度相对较慢, 这引发了对研究方法的思考.
为了解决在缺乏中心化无领导者的情境下, 个体在共识形成中可能陷入演化过程较慢的这一问题, 本研究创新性地探讨了如何通过深入分析社交网络中邻域意见, 调整个体相似意见权重或个体不太相似意见权重, 以加速无领导者社会网络中的共识形成过程. 这一创新点旨在提高共识形成的效率, 为缺乏中心化领导者的社交网络共识研究提供新的视角. 在本研究中, 不仅考虑了个体的简单节点属性, 而是更为详细地设置了个体模型, 包括私人意见、表达意见、固执度以及偏好等多方因素. 这一创新点使研究更加贴近真实社交场景, 不再局限于对节点的简单描述, 而是全面描绘了个体对周围意见的更为丰富的接受程度.
3 预备知识在本节中, 引入了以下定义, 以便后续更容易阅读和理解.
3.1 表达意见和私人意见表达意见和私人意见[27]来自于社会心理学, 群体压力导致了从众行为, 导致社交网络中的个体表达的意见与私人意见并不一致. 表达的意见可能为了迎合大众而有意向其他个体所表达的意见靠拢, 私人意见也会通过说服或者其他暗示逐渐接近表达意见.
3.2 第一置信区间在社交网络中, 与agent i直接连接的邻居集合
| [Ni=j|i与j直接相连] | (1) |
当agent i的意见和第一置信区间
| [Si=j∈Ni | |O(i)−O(j)|⩽ε] | (2) |
本节首先阐述了社交网络构建的过程, 紧接着介绍了原始DeGroot模型的基础框架. 随后, 本节深入讲述了对DeGroot模型的改进, 重点在于引入个体的表达意见和私人意见, 并且融合了第二置信区间的概念. 基于这一改进, 构建了两种不同的模型: 一是 “近交” (far attack inbreeding, FAI)模型, 它通过增加第二置信区间的意见权重, 促使个体意见更多地与近似意见进行交互; 二是“远交” (outbred recent attack, ORA)模型, 该模型减少了第二置信区间的权重, 使得个体意见更倾向于与差异较大的观点进行交互. 最后, 通过仿真实验和分析比较, 深入探讨这两种模型的性能, 并对其进行评估.
4.1 社交网络在构建的社交网络中, 每个节点代表一个个体, 构成一个无向连通网络. 网络的特点是采用优先附加的方法生成, 更能真实地反映现实世界社交网络的特征和动态. 在这个网络中, 每个个体初始化时就会被赋予一个随机的固执度值
在介绍新模型时, 首先引入原始的DeGroot模型. 在原始DeGroot模型中, 网络中的所有个体在每个时间步仅通过加权邻居意见的平均值更新他们的观点. 式(3)表示了个体相互之间更新意见的算法.
| xi(t+1)=hixi(t)+(1−hi)m∑j=1wjyj(t)m∑j=1wj | (3) |
其中,
在原始DeGroot模型的基础上, 引入了表达意见和私人意见以及第二置信区间.
4.3.1 基准模型在初始模型的基础上融入了表达意见和私人意见, 进而构建了基准模型. 具体的更新规则如下:
| yi(t+1)=hixi(t)+(1−hi)∑mj=1wjyj(t)/wjyj(t)∑mj=1wj∑mj=1wj | (4) |
| xi(t+1)=peixi(t)+(1−pei)yi(t+1) | (5) |
其中,
在t时刻下, agent i 的第一置信区间
| Si=j∈Ni,|xi(t)−yj(t)|⩽ε | (6) |
其中,
那么总体模型如下所示:
| {Si,|xi(t)−yj(t)|⩽εRi,|xi(t)−yj(t)|>ε,j∈Ni | (7) |
| yi(t+1)=(1−hi)(b∑qk=1wkyk(t)/∑qk=1wk+(1−b)∑m−qu=1wuyu(t)/∑m−qu=1wu)+hixi(t) | (8) |
| xi(t+1)=peixi(t)+(1−pei)yi(t+1) | (9) |
其中,
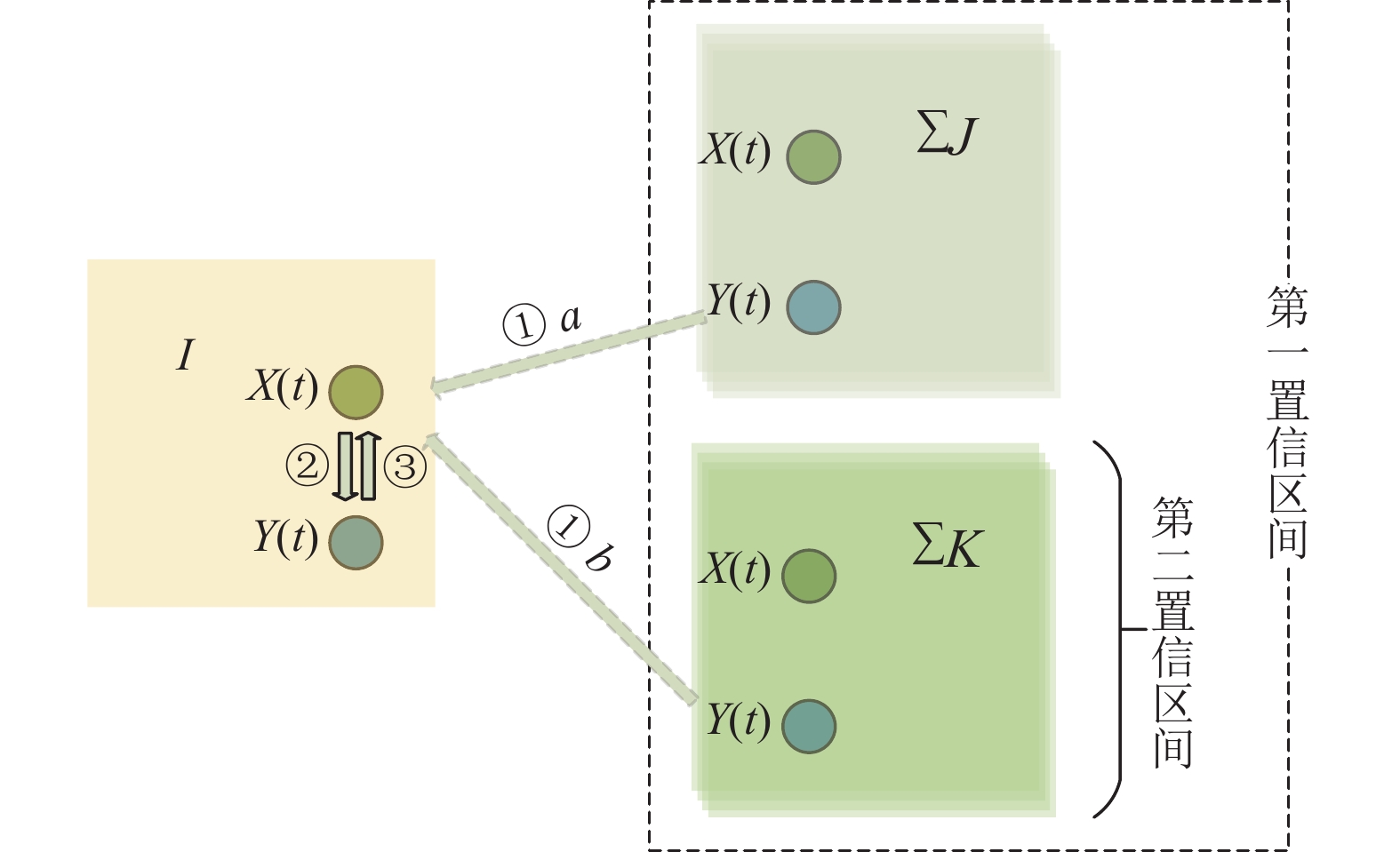
图1中展示的是以agent i为主, 其直接相连的邻居agent集合组成了第一置信区间. 然后, 通过应用式(6)对第一置信区间进行过滤, 形成了第二置信区间.
|
图 1 agent个体意见模型图 |
模型的动态过程如下所述.
● 在每个步骤的开始, agent i首先呈现自己的表达意见
● 随后, agent i获取第一置信区间内所有邻居的表达意见
● 最后, 在自我说服情况下, agent i依照式(9)调整自己的私人意见
本节中, 使用NetLogo软件进行仿真实验, 并基于实验结果进行分析. 实验考虑了一个包含76个个体的无标度网络. 在这个网络中, 个体的初始表达意见和私人意见均匀地分布在[0, 9]区间内, 代表各自不同的观点. 个体间的意见差异越小, 观点越相似. 个体仅与其邻域内的其他个体进行意见交流, 并通过表达意见与私人意见的相互作用来形成新的意见.
在研究中, 使用两个指标来评估模型的收敛速度和意见一致性: 收敛步长(衡量收敛速度)和意见相同率(衡量一致性程度). 在相同的初始条件下, 当意见相同率达到93%时, 认为达成了共识, 并以此确定模型的收敛步长.
实验中, 将基准模型与FAI模型和ORA模型分别比较, 以此分析两个改进模型的意见达成共识的性能.
接下来, 将介绍不同参数
参数
|
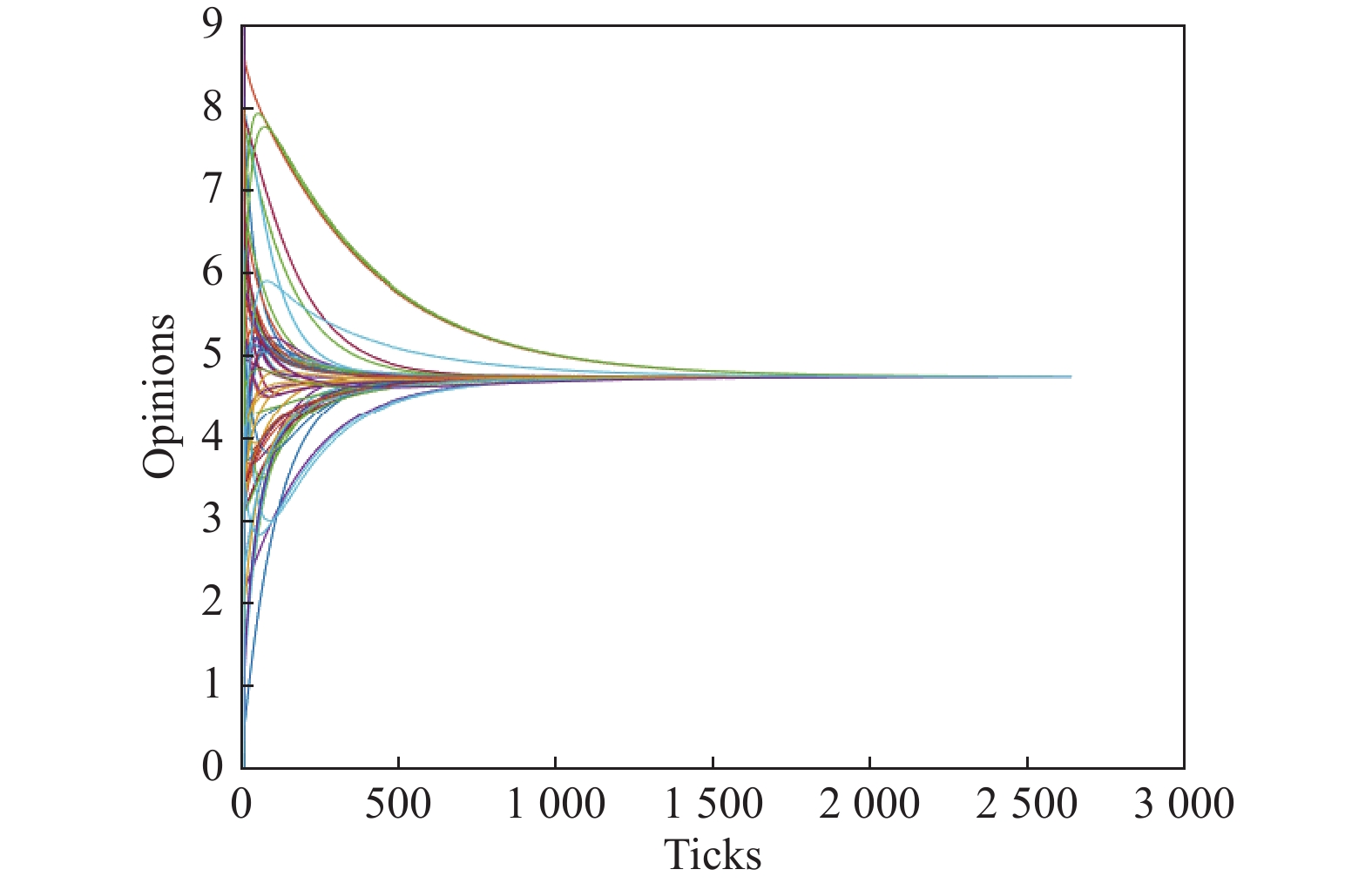
图 2 基准模型意见达成共识 |
图3是参数

|
图 3 n=76表达意见共识达成过程 |
在这次的仿真实验中, 参数
参数
如图4所示, 随着

|
图 4 |
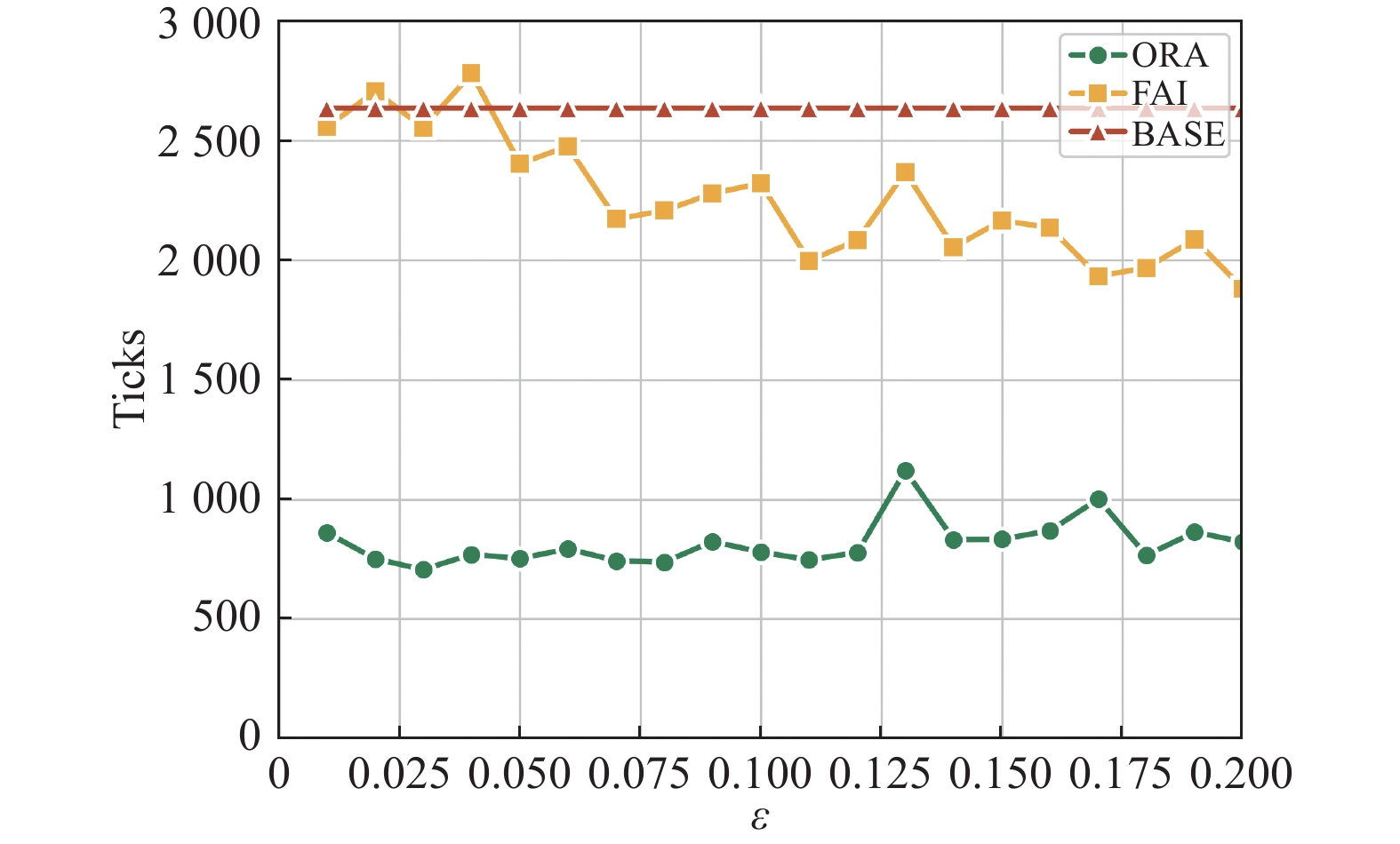
图5展示了
|
图 5 FAI模型和ORA模型的达成共识的收敛步长趋势 |
同时在图4中ORA模型下可以得到一个现象, 随着

|
图 6 ORA模型和FAI模型意见达成共识的收敛步长趋势 |
|
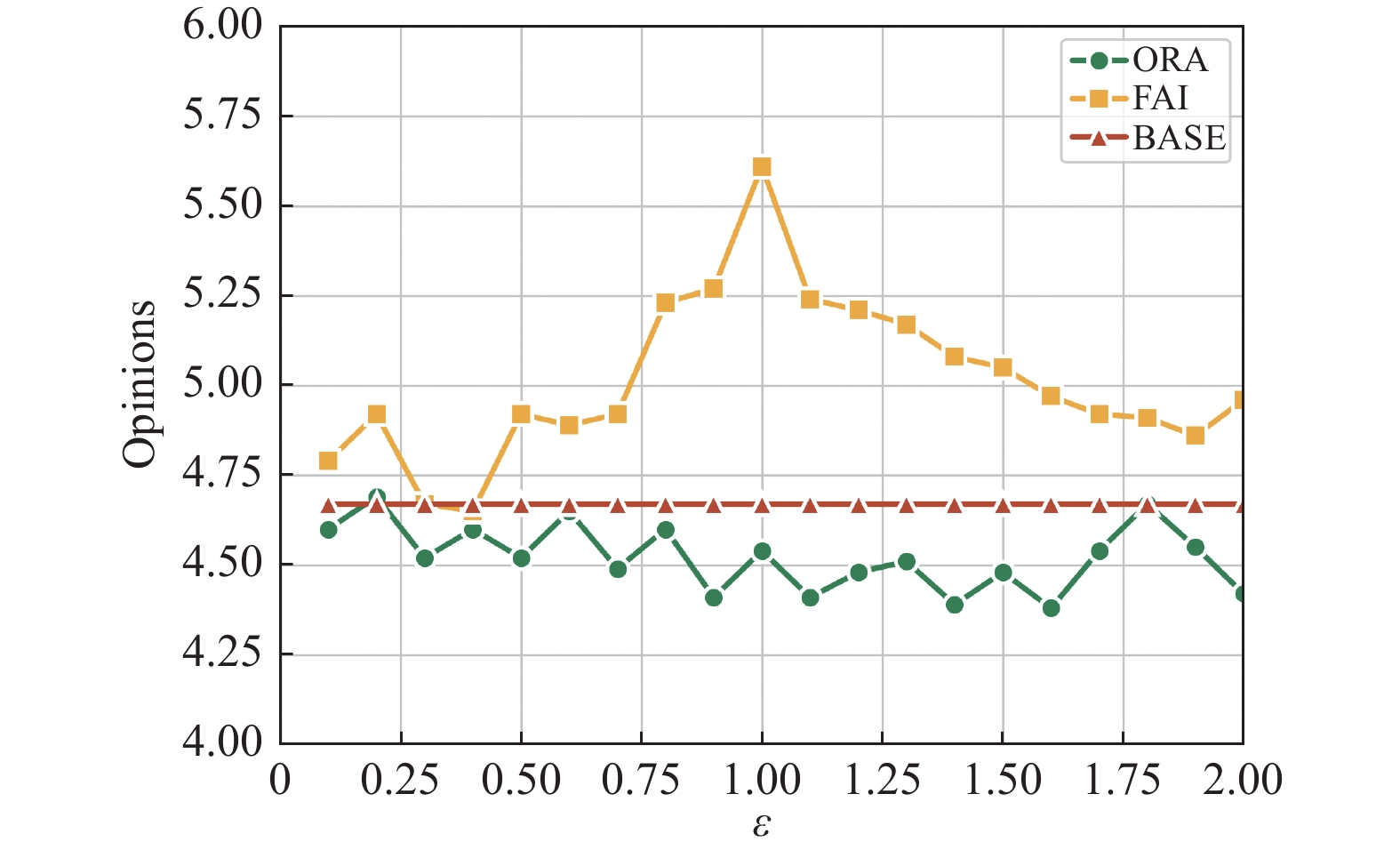
图 7 ORA模型和FAI模型的意见收敛随着 |
图7呈现了基准模型、FAI模型和ORA模型从
总的来说, FAI模型相较于基准模型, 仅在固定的参数值下更快达成共识, 但收敛意见值却呈现不稳定的趋势. 相反, ORA模型以更高的效率加速了达成共识的过程, 并成功保持了意见收敛之的稳定性, 接近基准模型的共识结果. 这一发现不仅强调了ORA模型在模拟现实世界共识形成过程中的潜力和有效性, 同时也呼应了对于在共识形成中取得更稳定结果的迫切需求.
5 总结与展望舆论形成是一个复杂的过程, 涉及个人心理和群体行为的交互. 本研究提出了一种新的意见更新规则策略, 旨在改进传统的共识模型. 此策略不仅考虑了个体的接受程度和对周围意见的重视程度, 还通过深入分析社交网络中的邻域意见, 对DeGroot模型进行了创新性改进. 在该策略中, 分别进行了两方面的改进, 一是对个体模型的详细设置, 涵盖了私人意见、表达意见、固执度以及偏好等多方因素, 使得个体内的意见传播更加符合现实中复杂场景. 二是将个体的邻域通过参数进行过滤, 当个体的私人意见与邻域中的表达意见的差值在参数的范围内, 那么这些邻域个体形成了第二置信区间. 通过增加第二置信区间的权重, 减少邻域剩余区间的权重, 形成了FAI模型; 通过减少第二置信区间的权重, 增加邻域剩余区间的权重, 形成了ORA模型.
在去中心化的社交网络中, 实验发现这两种模型在参数值固定的情况下, 能比原DeGroot模型更快地达成共识. 具体而言, 在初始条件相同的情况下, ORA模型在不同的参数值下的收敛速度基本稳定在700步长左右, 而FAI模型则随着参数值的增加, 其收敛速度逐步接近ORA模型. 此外, 就收敛意见值而言, ORA模型与基准模型的差异较小, 而FAI模型则表现出较大的波动. 这些发现突显了ORA模型在模拟现实世界共识形成过程中的潜力和有效性, 同时也符合在共识形成研究对稳定结果的迫切需求.
在未来的研究中, 考虑到人们交流次数的增加和社会环境的演变, 模型中的参数应当根据特定规律机制进行调整, 以更准确地反映现实生活中的变化. 因此, 引入学习算法(如强化学习)来使模型参数随时间动态调整, 可能是一个有价值的研究方向. 这样的学习算法不仅使模型更接近现实, 还能提供更深层次的理解, 探索不同条件下模型参数的优化策略.
| [1] |
DeGroot MH. Reaching a consensus. Journal of the American Statistical Association, 1974, 69(345): 118-121. DOI:10.1080/01621459.1974.10480137 |
| [2] |
Friedkin NE, Johnsen EC. Social influence networks and opinion change. Advances in Group Processes, 1999, 16(1): 1-29. |
| [3] |
Friedkin NE, Johnsen EC. Social influence and opinions. The Journal of Mathematical Sociology, 1990, 15(3–4): 193-206. DOI:10.1080/0022250X.1990.9990069 |
| [4] |
Galam S. The Trump phenomenon: An explanation from sociophysics. International Journal of Modern Physics B, 2017, 31(10): 1742015. DOI:10.1142/S0217979217420152 |
| [5] |
Majmudar JR, Krone SM, Baumgaertner BO, et al. Voter models and external influence. The Journal of Mathematical Sociology, 2020, 44(1): 1-11. DOI:10.1080/0022250X.2019.1625349 |
| [6] |
Pilyugin SY, Campi MC. Opinion formation in voting processes under bounded confidence. Networks & Heterogeneous Media, 2019, 14(3): 617-632. |
| [7] |
Deffuant G, Neau D, Amblard F, et al. Mixing beliefs among interacting agents. Advances in Complex Systems, 2000, 3(01n04): 87-98. DOI:10.1142/S0219525900000078 |
| [8] |
Hegselmann R, Krause U. Opinion dynamics and bounded confidence models, analysis and simulation. Journal of Artificial Societies and Social Simulation, 2002, 5(3): 1-33. |
| [9] |
Ding RX, Wang XQ, Shang K, et al. Social network analysis-based conflict relationship investigation and conflict degree-based consensus reaching process for large scale decision making using sparse representation. Information Fusion, 2019, 50: 251-272. DOI:10.1016/j.inffus.2019.02.004 |
| [10] |
Dong YC, Chen X, Herrera F. Minimizing adjusted simple terms in the consensus reaching process with hesitant linguistic assessments in group decision making. Information Sciences, 2015, 297: 95-117. DOI:10.1016/j.ins.2014.11.011 |
| [11] |
Dong YC, Ding ZG, Martínez L, et al. Managing consensus based on leadership in opinion dynamics. Information Sciences, 2017, 397–398: 187–205.
|
| [12] |
Liu BS, Zhou Q, Ding RX, et al. Large-scale group decision making model based on social network analysis: Trust relationship-based conflict detection and elimination. European Journal of Operational Research, 2019, 275(2): 737-754. DOI:10.1016/j.ejor.2018.11.075 |
| [13] |
Jr French JRP. A formal theory of social power. Psychological Review, 1956, 63(3): 181-194. DOI:10.1037/h0046123 |
| [14] |
Campbell A, Gurin G, Miller WE. The Voter Decides. Evanston: Row, Peterson, 1954.
|
| [15] |
Sood V, Redner S. Voter model on heterogeneous graphs. Physical Review Letters, 2005, 94(17): 178701. DOI:10.1103/PhysRevLett.94.178701 |
| [16] |
Sznajd-Weron K. Sznajd model and its applications. Acta Physica Polonica B, 2005, 36(8): 2537-2547. |
| [17] |
Hegselmann R, Krause U. Opinion dynamics and bounded confidence models, analysis and simulation. Journal of Artificial Societies and Social Simulation, 2002, 5(3): 2. [doi: 10.1111/1468-2451.00379]
|
| [18] |
Zino L, Rizzo A, Porfiri M. On consensus and collective behavior over heterogeneous temporal networks? Proceedings of the 21st IFAC World Congress. Berlin, 2020. 11221–11224.
|
| [19] |
Ding ZG, Chen X, Dong YC, et al. Consensus convergence speed in social network DeGroot model: The effects of the agents with high self-confidence levels. IEEE Transactions on Computational Social Systems, 2023, 10(5): 2882-2892. DOI:10.1109/TCSS.2022.3191468 |
| [20] |
Zhao YY, Kou G, Peng Y, et al. Understanding influence power of opinion leaders in e-commerce networks: An opinion dynamics theory perspective. Information Sciences, 2018, 426: 131-147. DOI:10.1016/j.ins.2017.10.031 |
| [21] |
Tian Y, Wang L. Opinion dynamics in social networks with stubborn agents: An issue-based perspective. Automatica, 2018, 96: 213-223. DOI:10.1016/j.automatica.2018.06.041 |
| [22] |
Jia P, MirTabatabaei A, Friedkin NE, et al. Opinion dynamics and the evolution of social power in influence networks. SIAM Review, 2015, 57(3): 367-397. DOI:10.1137/130913250 |
| [23] |
Yao LL, Xie DM, Zhang JL. Cluster consensus of opinion dynamics with stubborn individuals. Systems & Control Letters, 2022, 165: 105267. |
| [24] |
He G, Shen ZW, Huang TW, et al. Opinion dynamics with heterogeneous multiple interdependent topics on the signed social networks. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2023, 53(10): 6181–6193.
|
| [25] |
Zhou QY, Wu ZB. Multidimensional Friedkin-Johnsen model with increasing stubbornness in social networks. Information Sciences, 2022, 600: 170-188. DOI:10.1016/j.ins.2022.03.088 |
| [26] |
Cho JH. Dynamics of uncertain and conflicting opinions in social networks. IEEE Transactions on Computational Social Systems, 2018, 5(2): 518-531. DOI:10.1109/TCSS.2018.2826532 |
| [27] |
Ye MB, Qin YZ, Govaert A, et al. An influence network model to study discrepancies in expressed and private opinions. Automatica, 2019, 107: 371-381. DOI:10.1016/j.automatica.2019.05.059 |
 2024, Vol. 33
2024, Vol. 33



