在工业化和城市化的背景下, 空气污染已成为人们关注的焦点. 其中, PM_2.5 (指空气动力学直径小于或等于2.5 mm的大气颗粒物)是一种特别危险的因素, 可以直接进入人体并对健康造成危害^[1]. 许多研究表明, 高水平的PM_2.5暴露与呼吸系统和心血管疾病密切相关^[2,3]. 此外, PM_2.5还对出生率和婴儿健康产生不良影响^[4,5]. 然而, 控制雾霾需要更多实时的空气质量监测数据. 为了有效预防和控制空气污染, 并进行城市管理规划, 准确高效地预测近期PM_2.5浓度是必要的.

由于PM_2.5浓度预测的重要性, 近年来在该领域取得了显著进展^[6]. 主要的发展可以分为3个不同的阶段: (1)早期的研究将数据挖掘方法与统计分析相结合^[7,8]. Zhang等^[9]研究了美国东部天气研究与预报(WRF)/社区多尺度空气质量(CMAQ)系统的性能. 然而, 由于这些方法研究区域、研究数据的限制, 很难去拟合非线性特征, 从而导致预测准确性降低^[10]. (2)近年来, 深度学习的迅速发展, 为从输入数据中学习时空依赖关系提供了新的解决方案. 研究人员将整个城市视为图像并将其划分网格, 利用卷积神经网络(convolutional neural network, CNN)来提取序列内的空间相关性^[11,12]. 此外, 郭宇辰等^[13]利用将循环神经网络 (recurrent neural network, RNN)与CNN组合来捕捉序列内的时间依赖关系, 取得了不错的效果. 然而, 基于CNN的方法对空间上邻居的高效聚合使其对远距离依赖关系不敏感, 并且仅适用于欧几里德空间结构^[14]. Lin等^[15]基于门控递归单元(gated recurrent unit, GRU)及其变体, 设计了MLEGRU (multiple linear regression based GRU)对多站点数据进行预测. 但基于循环神经网络或其变体忽视了数据在空间上的依赖, 容易导致预测精度受影响. (3)图卷积网络(graph convolutional network, GCN)^[16]是CNN在图结构上的推广, 适用于处理非欧几里德空间数据. 由于空气质量监测站的拓扑结构, GCN已在PM_2.5浓度预测领域取得了成功且广泛的应用^[17,18]. 有研究者将GCN用于提取 PM_2.5 浓度预测中的空间依赖关系^[19]. 此外, 还尝试了将GCN与Bi-LSTM结合以捕捉时空依赖关系^[20]. Wang等^[21]将多图注意力图卷积与GRU结合, 将不同图之间相关站点的时空特征聚合, 有效提高了预测精度.

尽管GCN在PM_2.5预测中的有效性已得到验证, 但仍然存在4个重要问题尚未得到充分讨论: (1)邻接矩阵决定了图卷积网络中的聚合方法, 但通常是固定的, 并通过基于空间距离或图连接性的启发式方法生成. 这些方法无法捕捉真实的时空依赖. (2)现有方法忽视了空气质量预测中的层次依赖性. 空气质量受全球、区域和局部尺度上多种因素的影响. 这些因素以层次方式相互作用, 意味着一个层次上的预测或输入依赖于更高层次的预测. 例如, 周边地区的环境状况可能会受到意外事件(如工厂污染泄漏)的影响, 但这种干扰未必会对整个城市的空气质量产生影响. (3)当前的图卷积方法主要遵循图信号处理的观点, 倾向于平滑节点的输入信号. 在这种情况下, 只使用一个邻接矩阵的可叠加图卷积层难以有效获得多层次的数据高级表示. (4)不同层次表示对最终空气质量的贡献不应是静态的, 而应在时间上动态变化. 例如, 特定的天气异常(如雾霾天气)可能会增加低层次特征的影响. 这些问题可以用来改进当前的空气质量预测研究.

为了解决问题, 本文提出了一种新的深度学习框架, 自适应分层图卷积神经网络(adaptive hierarchical graph convolutional neural network, AHGCNN)用于PM_2.5预测. 具体而言, 为了解决主流图卷积网络在捕获多层次空间依赖方面的低效率和不准确性, 引入了自适应分层图卷积(hierarchical mapping graph convo-lution, HMGC). 通过自学习邻接矩阵, 该网络可以在每个层次上动态提取空间依赖. 此外, 对层次拓扑结构相关性进行建模, 提供了一种基于注意力的层次聚合机制, 以较小的计算成本实现了图卷积结构. 然后将GRU中的线性单元替换成HMGC, 构成自适应分层图卷积门控循环单元(adaptive hierarchical graph convolution gated recurrent unit, AHGC-GRU), 多层堆叠搭建网络主体结构, 输出预测结果.

1 理论基础 1.1 PM_2.5浓度预测问题定义

通常情况下, PM_2.5浓度预测被视为一个时空序列预测问题. 给定$N$个监测站的历史空气数据记录, 任务是预测每个监测站未来的PM_2.5浓度情况. 基于之前的研究, 本文将$N$个监测站及其两两连接定义为一个加权有向图$ G = (V, E, A) $, 其中$V$表示节点集合, $|V| = E$,$E$表示边的集合, $A \in {R^{N \times N}}$表示加权邻接矩阵, 描述了任意节点对之间的关系紧密程度. 在任意时间$t$, $G$的历史数据被编码为图信号${X_t} \in {R^{N \times C}}$, 其中$C$表示每个节点属性的维度. PM_2.5预测问题的核心在于学习一个函数$f$, 该函数能够利用$S$个历史图信号$x = [{X_{(t - S + 1)}}, \cdots, {X_t}] \in {R^{S \times N \times C}}$以及监测站网络的邻接矩阵$A \in {R^{N \times N}}$, 来预测$T$个未来的信号$\widehat y = [{\widehat X_{(t + 1)}}, \cdots, {\widehat X_{(t + T)}}] \in {R^{(T \times N \times C)}}$. 数学上可以表述为:

$ \widehat y = f(x, A) $

(1)

其中, $\widehat y$应尽可能接近$y$.

2 模型设计

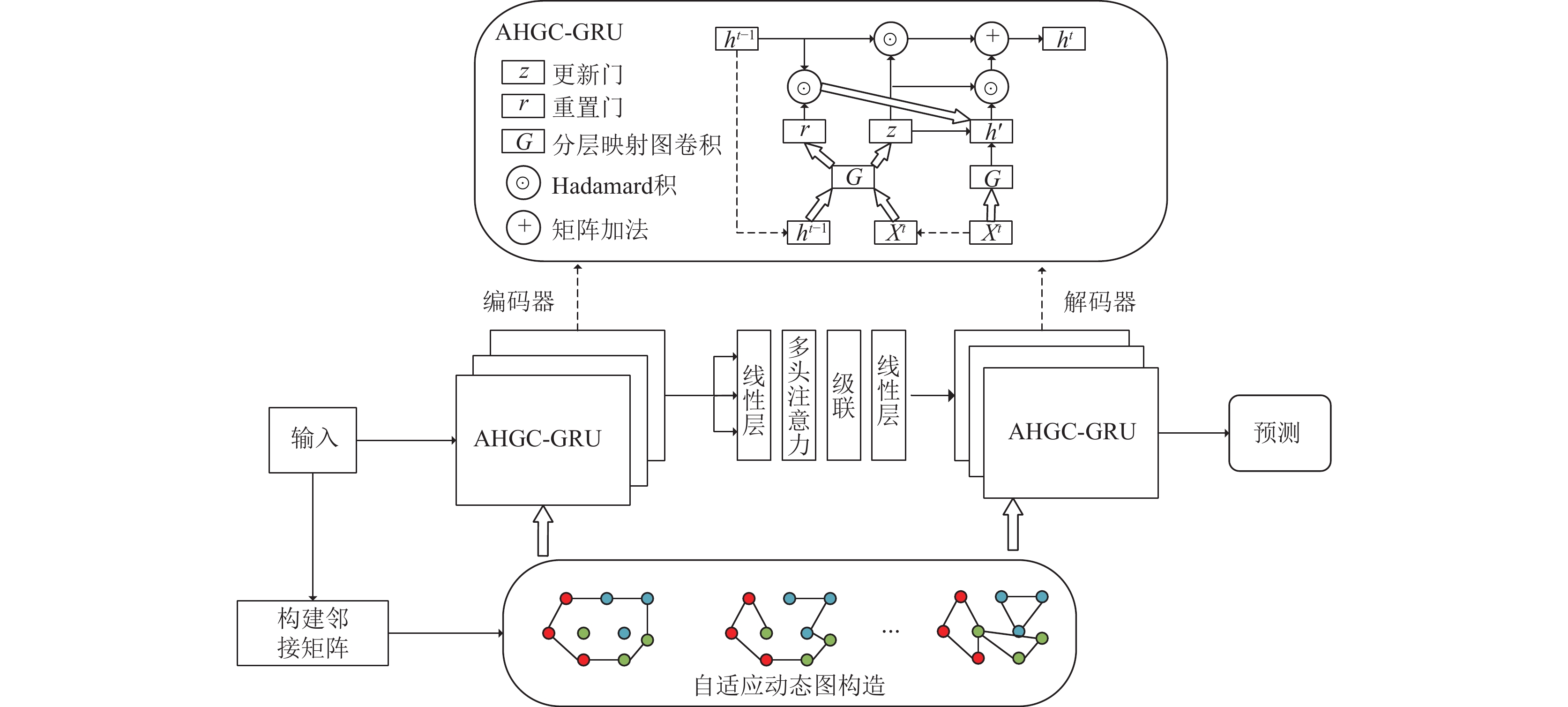
本节描述AHGCNN模型的基本组件. 如图1所示, 包含邻接矩阵生成、自适应动态图的构造、多层信息融合、AHGC-GRU多层堆叠形成的编码器和解码器. 下面详细介绍AHGCNN模型各个模块的具体实现.

2.1 构建邻接矩阵

邻接矩阵决定了在图卷积中节点及其邻居是如何被聚合的. 现有的研究依赖先验知识来事先构建图结构, 本文的方法是完全基于数据驱动的, 因此能够捕捉数据之间的时序依赖性.

对于给定的图信号集合${X_{{t_a}:{t_a} + \tau - 1}} \in {R^{\tau \times N \times d}}$, 将其转换为一个维度为$(\tau \times d) \times N$的二维矩阵${X^l}$. 为了有效地捕获不同站点之间的内部相似性, 并过滤掉站点之间的冗余信息. 本文使用奇异值分解(singular value decom-position, SVD)将${X^l}$分解为两部分. 即:

$ {\textit{SVD}}({X^l}) \to ({X^s}, {X^t}) $

(2)

其中, ${X^s}$和${X^t}$分别表示按时间维度和站点维度划分的矩阵.

矩阵${X^l}$包含大量的冗余信息. 通过使用SVD进行降维, 可以过滤掉这些冗余信息, 从而揭示出隐藏的模式. 矩阵${X^s} \in {R^{N \times \gamma }}$包含了每个站点特征的高级表示, 其中$\gamma $表示特征的维度. 本文采用基于高斯核的方法来计算矩阵${X^s}$中第$x$行和第$ y $列之间的相似性, 并将其用作生成的邻接矩阵中的边权重. 公式定义如下:

$ {A_{xy}} = {\textit{Similarity}}(X_x^s, X_y^s) = \exp \left( - \frac{{||X_x^s - X_y^s|{|^2}}}{{2{\beta ^2}}}\right) $

(3)

其中, ${A_{xy}}$指的是邻接矩阵$A$的第$x$行第$y$列的元素, $\;\beta $是标准偏差.

2.2 分层映射图卷积

为了高效准确地捕捉多层空间依赖关系, 本文引入了一种新的图卷积网络: 分层映射图卷积网络(HMGC). HMGC的特点在于每个层级都包含独特的邻接矩阵, 从而更灵活地建模底层图结构. 这种结构可以进行递归定义:

$ {Z^{(m + 1)}} = {Z^{(m)}}{ \star _G}g_\theta ^{(m)} = {A^{(m)}}{Z^{(m)}}{\theta ^{(m)}} $

(4)

${Z^{(m)}}$代表$m + 1$层的输入, 而${Z^{(m + 1)}}$不仅是第$m + 1$层的输出, 还是第$m + 2$层的输入. 参数$g_\theta ^{(m)}$和${\theta ^{(m)}}$表示第$m$层的图卷积滤波器参数, ${ \star _G}$表示图卷积操作.

节点之间的层级关系由${A^{(m)}}$建模, ${A^{(m)}}$的值取决于所处的层级. 利用分层映射函数$\varphi $构建第$m + 1$层的上层邻接矩阵:

$ {A^{(m + 1)}} = {\varphi ^{(m)}}({A^{(m)}}) $

(5)

对由式(3)生成的初始图结构进行标准化处理, 将其用于邻接矩阵的初始化, 并采用随机梯度下降进行优化. HMGC初始层的定义如下:

$ {A^{(0)}} = {D^{ - 1}}{A_{xy}} $

(6)

$ {Z^{(1)}} = {A^{(0)}}{Z^{(0)}}{\theta ^{(0)}} $

(7)

其中, $D$代表节点度的对角矩阵. ${Z^{(0)}} = X$, 在每个时间步中, 特征矩阵$X \in {R^{N \times d}}$作为HMGC初始层的输入.

2.3 自适应动态图构建

在现实中, 图结构并不总是可用的, 节点之间的关联性经常随着时间变化. 此外, PM_2.5浓度与天气条件密切相关. 在类似的天气条件下, 空气质量往往比不同的天气条件下更加均匀. 因此, 本文遵循模型训练过程来构建不同层之间的动态邻接矩阵. 天气数据的时间变化性使得动态邻接矩阵具有潜在的时间相关性.

首先, 节点的数量导致更新$N \times N$的邻接矩阵和映射函数$\varphi $在计算方面的代价很高, 从而在训练过程中导致过度参数化. 为了解决这个问题, 本文采用SVD将${A^{(0)}} \in {R^{N \times N}}$分解为两个小矩阵:

$ {\textit{SVD}}({A^{(0)}}) \to (E_1^{(0)}, E_2^{(0)}) $

(8)

$E_1^{(0)} \in {R^{N \times L}}$表示首层的源节点嵌入, 而$E_2^{(0)} \in {R^{N \times L}}$则代表目标节点嵌入. $L$表示维度. 值得注意的是, 可训练的参数数量从$N \times N$减少到了$2 \times N \times {{L}}\;(N \gg L)$.

函数$\varphi $通过全连接层进行实现, 以模拟层间相关性. 全连接层的参数在${E_1}$和${E_2}$之间共享.

$ \left\{\begin{gathered} {{E}}_1^{(m)} = E_1^{(m - 1)}{W^{(m - 1)}} + {b^{(m - 1)}} \\ {{E}}_2^{(m)} = E_2^{(m - 1)}{W^{(m - 1)}} + {b^{(m - 1)}} \\ \end{gathered}\right. $

(9)

在这种情况下, $E_1^{(m)}$和$E_2^{(m)}$分别代表第$m$层中的源节点嵌入和目标节点嵌入. 符号${W^{(m - 1)}}$和${b^{(m - 1)}}$分别表示权重矩阵和偏置向量. 为了简化模型, 不同层次的${E_1}$和${E_2}$的特征维度被设定为$L$, 从而将每个映射的参数数量减少到$L \times (L + 1)$.

基于式(4)和式(9), 对于分层映射图卷积(HMGC), 其数学表达式可以重新定义为:

$ {Z^{(m + 1)}} = (E_1^{(m)}E{_2^{(m)^{\mathrm{T}}}}){Z^{(m)}}{\theta ^{(m)}} $

(10)

2.4 基于注意力机制的分层信息融合

为了从所有图卷积层中汇集信息, 而不仅从一个固定的层中提取信息, 本文通过注意机制实现多层聚合策略, 以选择性地选取对当前预测任务准确性产生更大影响的信息.

通过HMGC获得的图信号的多层输出表示为$Z = \{ {Z^{(1)}}, {Z^{(2)}}, \cdots, {Z^{(M)}}\} , \; Z \in {R^{(M \times N \times \tau )}}$, 其中$M$表示图卷积层的总数, $\tau $表示特征维度. 本文使用多头注意力来调节各层间的权重比以此获得最终的特征向量$h$:

$ \left\{\begin{gathered} {Q_i} = W_i^QF(\widehat Z) \\ {K_i} = W_i^KF(\widehat Z) \\ {V_i} = W_i^VF(\widehat Z) \\ hea{d_i} = {{a}}ttention(({K_i}, {V_i}), {Q_i}) \\ h = Concat(hea{d_1}, \cdots, hea{d_i}){W_0} \\ \end{gathered}\right. $

(11)

其中, $F$表示线性转换, $\widehat {{Z}}$代表$Z$的扁平化输出, $W_i^Q, W_i^K, W_i^V$分别表示映射$Q, K, V$使用的3个线性层的权重, ${W_0}$表示注意力模块最后一个线性层的权重.

2.5 时间依赖建模

门控循环单元(GRU)是循环神经网络(RNN)的一种变体, 相对简单而又强大, 它解决了RNN中梯度消失和梯度爆炸的问题. 根据之前研究^[22], 本文将GRU中的线性变换替换为HMGC, 以获得更好的性能. 因此, 提出了自适应分层图卷积门控循环单元(AHGC-GRU).

$ \left\{\begin{gathered} {r^{(t)}} = \sigma ({\Theta _r}{ \star _G}[{h^{(t)}}, {H^{(t - 1)}}] + {b_r}) \\ {u^{(t)}} = \sigma ({\Theta _u}{ \star _G}[{h^{(t)}}, {H^{(t - 1)}}] + {b_u}) \\ {c^{(t)}} = \tanh ({\Theta _c}{ \star _G}[{h^{(t)}}, ({r^{(t)}} \odot {H^{(t - 1)}})] + {b_c}) \\ {H^{(t)}} = {u^{(t)}} \odot {H^{(t - 1)}} + (1 - {u^{(t)}}) \odot {c^{(t)}} \\ \end{gathered} \right.$

(12)

${h^{(t)}}$和${H^{(t)}}$分别代表时间步$t$处的注意力分数和门控循环单元(GRU)的输出, 对两者进行Hadamard乘积$ \odot $运算. $\sigma $表示Sigmoid激活函数, $\tanh $表示tanh激活函数, 重置门${r^{(t)}}$帮助网络遗忘不相关信息. 同时, 更新门${u^{(t)}}$控制着给定时间步的GRU输出. 符号${ \star _G}$表示图卷积操作, 而${\Theta _r}, {\Theta _u}, {\Theta _c}$则表示相应滤波器的参数.

在多步预测模型中, 编码器和解码器均由AHGC-GRU构成, AHGCNN模型的伪代码如算法1.

算法1. AHGCNN模型框架

输入: 图$\scriptstyle G = (V, E, A) $; 图卷积深度$\scriptstyle m$.

输出: 表征向量$\scriptstyle Z $.

1. $\scriptstyle {A^{(0)}} \leftarrow G(V, E, A)$

2. for $\scriptstyle m = 1, \cdots, m$ do

3.　 $\scriptstyle {{\text{Z}}^{(m)}}, E_1^{(m)}, E_2^{(m)} \leftarrow {\mathrm{AHGCGRU}}({Z^{(m - 1)}}, G, {A^{(m)}})$

4.　 $\scriptstyle {A^{(m + 1)}} \leftarrow ReLU(E_1^{(m)} \cdot E{_2^{(m)^{\mathrm{T}}}})$

5.　 $\scriptstyle Z \leftarrow \{ {Z^{(1)}}, \cdots, {Z^{(m)}}\} $

6.　 $\scriptstyle h \leftarrow mulatt(Z)$

7. for $\scriptstyle m = 1, \cdots, m$ do

8.　 $\scriptstyle {Z^{(m)}}, E_1^{(m)}, E_2^{(m)} \leftarrow {\mathrm{AHGCGRU}}(h, G, {A^{(m)}}) $

9. 　$\scriptstyle {A^{(m + 1)}} \leftarrow ReLU(E_1^{(m)} \cdot E{_2^{(m)^{\mathrm{T}}}})$

10. $\scriptstyle Z \leftarrow \{ {Z^{(1)}}, \cdots, {Z^{(m)}}\} $

3 实验设计与验证 3.1 数据集描述

为了评估模型捕捉时空依赖性的能力, 本文选择了位于中国北京市及周边地区的39个气象监测站作为研究对象. 通过考虑从这些监测站收集到的空气质量、气象数据的时空特性, 可以获得精确的预测结果. 这些预测结果可以显著地惠及易受影响的人群, 并有助于制定适当的空气污染控制政策.

依据之前的工作方式^[23], 本文使用了两种类型的数据: 空气污染物浓度数据和气象数据. 空气污染物浓度数据来源于北京市环境保护监测中心网站 (http://www.bjmemc.com.cn/), 其数据类型包括PM_2.5、PM₁₀、SO₂、NO₂、O₃、CO和AQI. 气象数据来自欧洲中期气象预报中心(ECMWF) (https://cds.climate.copernicus.eu/), 其中包含地面气压、气温、露点温度、风向和风速等参数.

从39个站点收集了为期3年的数据(2018年1月1日–2020年12月31日), 数据每小时采集一次. 鉴于数据的不完整性(例如缺失值), 本文采用线性插值技术填补短期的缺失值. 最终经过处理的数据根据7:1:2的比例被划分为训练集、验证集和测试集.

3.2 评价指标

本文采用两种评估指标来评估所提出模型在预测结果方面的性能, 包括均方根误差(RMSE)和平均绝对误差(MAE). 其定义如下:

$ MAE(y, \widehat y) = \frac{1}{n}\sum\limits_{i = 1}^n {|{y_i} - {{\widehat y}_i}|} $

(13)

$ {\textit{RMSE}}(y, \widehat y) = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{({y_i} - {{\widehat y}_i})}^2}} } $

(14)

其中, 变量$y$和$\widehat y$分别表示实际和预测的PM_2.5值, 而$n$表示测试数据的总数量. 较小的MAE和RMSE值意味着更好的最终预测结果. 值得注意的是, 在均方根误差(RMSE)的情况下, 每个误差都会被平方, 这意味着各个误差会呈二次增长, 并对最终RMSE值产生不同的影响. 因此, 通常会同时使用MAE和RMSE来综合评估所采用方法的性能.

3.3 基线模型

为了测试AHGCNN模型的预测效果, 本文与常见的深度学习网络模型进行了比较, 包括LSTM^[24]、GRU^[25]、RNN^[26]、Informer^[27]、FFTransformer^[28]; 同时为了说明图结构对于捕捉空气数据时空依赖的重要性, 与扩散递归神经网络(diffusion convolutional recu-rrent neural network, DCRNN)^[29]和Graph WaveNet^[30]等模型做实验对比.

3.4 实验参数

本次实验模型使用PyTorch 1.13.1实现, 并在单块GPU (NVIDIA RTX 3090, 24 GB显存)上进行训练, 操作系统为Ubuntu 22.04. 当预测模型各项参数设置如表1所示时, 模型的预测性能达到最佳.

模型使用 MSE 作为损失函数, 损失值的训练迭代情况如图2所示. 从图2中可以观察到, 在前10轮迭代中, 训练集和测试集的损失值迅速下降. 随着迭代次数的增加, 训练集的损失值持续缓慢下降. 在经过15轮迭代后, 模型基本完成拟合, 损失值趋于平稳, 训练精度达到0.1左右. 随后的20轮迭代中, 测试集的损失值基本稳定, 保持在0.4左右.

3.5 预测结果对比分析

如表2所示, RNN、LSTM和GRU模型表现最差. 这并不令人意外, 因为它们只能访问节点表示, 无法获取邻居信息. 说明在PM_2.5预测中捕获邻居信息的必要性.

AHGCNN模型在性能上优于现有的预测模型. 在短期预测方面, AHGCNN的改进效果更为显著. 与DCRNN相比, 在预测的1 h、3 h、6 h、12 h和24 h时间点, AHGCNN的MAE分别降低了5.56%、6.12%、5.91%、13.5%和3.18%, RMSE 分别降低了9.08%、5.38%、3.96%、8.49%和0.47%. 与Graph WaveNet相比, AHGCNN在预测的1 h、3 h、6 h、12 h和24 h时间点, 分别将MAE降低了1.9%、0.91%、1.59%、0.87%和0.52%, RMSE分别降低了1.13%、4.31%、4.09%、3.87% 和 3.35%. 这表明动态邻接矩阵能够有效地捕获随时间变化的时空依赖关系, 即使底层的图结构是未知的. 与长序列预测模型Informer相比, 在预测的1 h、3 h、6 h、12 h和24 h时间点, AHGCNN的MAE分别降低了10.95%、12.11%、9.76%、7.97%和3.73%, RMSE 分别降低了17.65%、9.46%、6.26%、3.25%和0.47%. 与FFTransformer相比, AHGCNN在预测的1 h、3 h、6 h、12 h和24 h时间点, 分别将MAE降低了11.51%、9.77%、13.24%、8.07%和3.16%, RMSE分别降低了4.9%、15.70%、10.43%、5.86% 和 2.39%. 这个结果证实了 AHGCNN在利用时空依赖知识方面的优势, 并展示了它可靠的预测能力.

图3展示了在多个监测站点中, AHGCNN、RNN、LSTM、GRU、DCRNN、Graph WaveNet、Informer和FFTransformer等多个模型之间的预测值与实际值之间的差异. 测试期间, RNN、LSTM 和GRU模型在预测值与实际值之间存在显著差异, 尤其是在空气质量数据发生明显波动的时期. 尽管DCRNN、Graph WaveNet、Informer和FFTransformer模型在稳定期间的性能有所提高, 但在突然变化时仍存在变化和与实际值的大偏差. 相反, AHGCNN模型表现出卓越的预测能力, 在各个时期表现出色. 这些发现说明其他模型无法充分利用监测站之间的非线性空间特性, 导致在数据剧烈变化时模型适应性不足. 然而, 通过多层信息的聚合, AHGCNN模型可以更有效地提取信息, 捕捉站点之间的异质空间和时间特征, 从而在空气质量数据突然变化时避免了其他模型中出现的显著预测误差.

我们对模型学习到的自适应邻接矩阵进行了分析和比较, 如图4所示. 与由数据生成的原始邻接矩阵相比, 学习到的邻接矩阵展现出更加丰富的站点之间的相关性, 为之前的邻接矩阵提供了补充. 这表明单个矩阵无法完全捕捉到随着时间变化而节点之间联系的变化.

4 结语

本文提出了一种基于自适应分层图卷积神经网络(AHGCNN)的PM_2.5浓度预测方法. 该模型能够在不需要预先确定图结构的情况下, 捕捉数据之间的隐式空间依赖关系. 具体而言, 为了捕捉多层次的空间依赖关系, 引入HMGC的图卷积结构. HMGC中的邻接矩阵是自学习的, 并且每一层都是独特的, 有助于处理随时间变化的潜在时空依赖关系. 此外, 本文采用分层映射机制, 将上层图结构与下层图结构连接起来. 这使得模型能够融合不同数据层次的信息, 同时减少模型参数的数量. 随后, 单元网络将这些组件综合起来形成最终的预测. 在真实世界数据集上进行的实验验证了AHGCNN在PM_2.5浓度预测任务中取得了良好的性能. 在未来的工作中, 将探索将更多外部知识纳入, 以构建动态邻接矩阵, 并引入更有效的注意机制来处理多层次信息.