在现实世界的场景中, 因为信息往往来自不同的角度或属性, 越来越多的数据是由多种视图产生的[1]. 如何快速分析数据并有效发现其中的信息, 已经成为一个热门话题. 聚类分析是探索性数据挖掘和所有行业的大数据价值发现的主要任务. 多视图聚类是一种新兴的聚类方法, 其将来自不同视图的数据融合起来进行聚类分析. 在实际应用中, 多视图数据往往更加全面、准确地反映了复杂系统的多方面信息. 因此, 多视图聚类方法在自然语言处理[2]、计算机视觉[3]和医疗领域[4]等领域都具有重要的应用价值.
目前, 主流的多视图聚类算法主要可以分为3类: 多视图核聚类、多视图子空间聚类和多视图谱聚类. Ren等人[5]在内核空间中保留了输入数据的全局和局部结构, 最大限度地保留了有益的图结构. Liu等人[6]增强了最优核的可表示性, 并加强了核学习和聚类之间的协商. Wang等人[7]开发了一种新的离散多核K均值模型, 该模型结合了一种优化算法来严格测量核之间的相关性. 该模型旨在通过减少冗余和提高多样性来增强内核融合. Liu等人[8]从预定义的一组核中学习一致核, 将样本逐渐分组到较少的聚类中, 并生成一系列大小递减的中间矩阵序列. Liu等人[9]构造了自适应局部核, 以充分考虑单个数据样本周围的局部密度, 其中在每个样本上明显选择不同数量的邻居. Liu等人[10]通过构建核矩阵, 然后将数据样本进行分组, 并删除输入中的冗余信息. 这些基于核矩阵的多视图聚类算法实用且应用广泛, 但是核聚类对核函数的选择和参数设置非常依赖, 核函数若不能有效捕捉数据特征, 则对聚类结果大打折扣.
子空间是数据的一个低维子集, 其中数据点在该子集内具有高度的相似性. 子空间聚类目的是识别所有视图的潜在子空间, 然后正确地对数据点进行聚类. Gao等人[11]同时对每个视图执行子空间聚类, 同时确保视图之间聚类结构的一致性. 张华伟等人[12]提出保持张量多视图子空间聚类算法用于保持视图内部及视图之间的结构信息. Gu等人[13]在统一优化模型中使用了无监督稀疏特征选择和鲁棒子空间提取以及统一图学习. Zhang等人[14]使用低维子空间表示数据点, 并利用自表示方法将每个数据点表示为数据本身的线性组合.
光谱聚类适用于任意形状的聚类. 尽管它在很大程度上依赖于图拉普拉斯矩阵构造的特征向量, 但它表现出了优异的性能. Wang等人[15]融合了来自多个视图的低维嵌入表示, 然后执行K-means算法来生成最终的聚类. Wu等人[16]通过基于张量奇异值分解的张量核参数化, 探索了多视图表示的高阶相关性. Gu等人[17]使用不同视图的视图特定和一致图比对作为输入到传统光谱聚类方法的信息统一图. 贺娜等人[18]利用L2,1范数正则项构造相似矩阵同时进行谱聚类. Shi等人[19]引入核范数从各种视图特征中捕获主成分, 可以有效地挖掘特定视图的信息. 但是在通过特征分解得到的特征向量进行降维的谱聚类算法中, 有一个共同假设, 即数据近似地来自一个共同的低维子空间, 该空间包含了所有特征, 这些特征向量被认为对应于数据的主要结构. 然而这个假设并不总是成立, 特别是在处理高维数据时, 因此要考虑算法的稳健性非常重要.
对于多视图数据, 每一个视图的数据特征都具有高维性以及冗余性. 高维性指的是每一个数据都是由多种特征组合而成的一个特征向量而且不同视图之间维度各不相同; 冗余性是指不同视图或数据之间存在重叠或重复的信息或特征, 它们可能不会为聚类算法提供足够多的独立信息与互补信息, 从而降低了聚类的效果. 因此原始数据中包含大量的冗余细节. 此外, 现有的多视图子空间聚类方法[20]是通过K-means算法对子空间进行后续处理获取聚类结果, 然而子空间聚类方法能够发现数据在不同子空间中的局部结构, 因此适合处理数据中的局部特征. 相比之下, K-means更倾向于发现全局聚类结构, 可能忽略了数据在不同子空间内的局部性.
与现有方法不同, 本文提出了具有鲁棒性的正交多视图子空间聚类算法, 以便准确地对多视图数据特征进行提取整合, 进而解决聚类问题. 首先, 为了获取多视图数据表示, 使用自适应领域的方法生成稀疏相似矩阵. 其次, 采用特征分解来获取低冗余的鲁棒数据表示, 紧接着构建潜在统一的子空间表示. 因为谱旋转能够通过改善子空间聚类的投影来提高算法对局部性结构的捕捉, 因此使用谱旋转作为基础, 对潜在子空间进行旋转生成离散型数据表示矩阵, 并优化划分矩阵. 算法中还利用迭代优化后的划分矩阵对子空间进行正交化, 确保子空间种簇内的强连通性和簇间的弱连通性. 聚类算法中使用了迭代优化来解决优化问题. 最后, 在多个真实数据集上研究了所提出的聚类算法的有效性, 并与现有的聚类方法进行比较.
2 本文方法本文所提出的方法主要包括3个部分, 自适应图学习、建立子空间和子空间正交约束和获取聚类结果, 整体算法模型如图1所示. 绿色实线表示相似图和鲁棒性表示矩阵的自适应学习过程, 黄色实线表示鲁棒性表示矩阵生成多视图联合子空间, 黑色实线表示划分矩阵通过谱旋转得到离散型指示矩阵并且通过正交化约束用于子空间学习.
2.1 具有鲁棒性的自适应图学习给定m个视图, n个数据的多视图数据集{Xv∈ Rd×n, v=1, 2, …, m}, d表示第v个视图的特征维度. 第v个视图对应的相似矩阵可以被表示为Sv=
| {min | (1) |

|
图 1 本文算法的模型图示 |
单个视图通常不能全面地描述数据之间的关联性且视图之间有一定的差异性, 因此利用参数α来表示每个视图的重要程度, 并确保每个视图都能赋予一定的权重比例. 其中第1项表示的是通过从原始数据矩阵Xv中自适应地为每一个数据分配距离较小的数据作为邻域, 以此学习聚类任务需要的相似图Sv, 这里本文约束Sv的每一行的和为1, 所有元素是非负的. 第2项作为一个先验项能够避免出现有且仅有1个数据点与xiv连接的情况, 其中μ是相似矩阵Sv的正则化参数, 本文设置为1. 第3项为谱嵌入项能够将相似图信息通过谱分解的方式传递到鲁棒性数据表示Uv, 在Uv上的正交约束保证了数据表示在低秩空间中, 有利于后续联合子空间的建立以及聚类过程, 其中
在实际应用中, 即使给定的数据是高维的, 实际问题的内在维度往往很低, 因为只需少数参数即可对数据进行描述. 数据可以从多个空间中采取, 而子空间聚类便是找到底层子空间, 然后根据识别出的子空间对数据进行正确聚类. 我们从多个视图的自适应图中提取到不同的鲁棒性表示具备了有利的数据特征信息. 因此, 通过联立表示矩阵然后建立联合子空间Z, 结合第2.1节的目标函数(1)可以表示为:
| \left\{\begin{split} & \mathop {\min }\limits_{\{ {S^v}\} _{v = 1}^m, \alpha , \beta , \{ {U^v}\} _{v = 1}^m, \{ L_S^v\} _{v = 1}^m, Z} \sum\limits_{i, j = 1}^n {||x_i^v} - x_j^v||_2^2s_{ij}^v \\ & {\text{ }} + \mu \sum\limits_{i, j = 1}^n {s{{_{ij}^v}^2}} + \sum\limits_{v = 1}^m {{\alpha _v}} {\mathrm{tr}}({U^v}L_S^v{U^v}^{\rm T}) \\ & {\text{ }} + \sum\limits_{v = 1}^m {{\beta _v}} ||{U^v} - {U^v}Z||_F^2 + \lambda ||Z||_F^2 \\ & {\mathrm{s.t.}} \left\{\begin{array}{l} \forall v{\text{, }}s_{ii}^v = 0, {\text{ }}s_{ij}^v \geqslant 0, {\text{ }}{{\text{1}}^{\rm T}}s_i^v = 1, {\text{ }}{U^v}{U^v}^{\rm T}{\text{ = }}{I} \\ {\text{ }}{\alpha ^{\rm T}}1 = 1, {\text{ }}\alpha \in \mathbb{R}_ + ^{{m}}, {\text{ }}{\beta ^{\rm T}}1 = 1, {\text{ }}\beta \in \mathbb{R}_ + ^{\text{m}} \\ {\text{ }}{\mathrm{diag}}(Z) = 0, {\text{ }}Z \in {\mathbb{R}^{n \times n}} \end{array}\right. \end{split} \right. | (2) |
其中, 参数β和参数α的作用性同样也是表示每个视图的权重. λ表示联合子空间正则化项||Z||F的权重, 在第4.3节进行讨论. 总之, 采用鲁棒性表示矩阵建立起来的联合子空间在迭代优化中能够产生反馈作用, 指导算法生成最优参数, 通过协作方式实现良好的聚类性能.
2.3 谱旋转框架以及正交化约束的子空间从联合子空间中获取划分矩阵, 接着通过谱旋转获取离散聚类指标矩阵得到最终聚类结果, 离散化的过程可以表示如下:
| \left\{\begin{split} & \mathop {\min }\limits_{Z, F, R, Y} {{{\mathrm{tr}}}}({F^{\rm T}}{L_Z}F) + \gamma ||FR - Y{({Y^{\rm T}}DY)^{ - \frac{1}{2}}}||_F^2 \\ & {\mathrm{s.t.}}{\text{ }}{F^{\rm T}}F = I,\; {R^{\rm T}}R = I, \;Y \in Ind \end{split}\right. | (3) |
其中, LZ表示联合子空间Z相对应的拉普拉斯矩阵, D矩阵表示LZ的度矩阵, F∈Rn×k表示聚类划分矩阵, R∈Rk×k表示旋转矩阵, Y表示仅有0和1的离散型指标矩阵, γ是平衡项参数, 这里设置为固定参数0.01. 紧接着可以通过将F和R作为单个变量积分来减少变量R, 用单一F替换FR的积, 因为F和R总是以这个积的形式一起出现, 得到如下表达式:
| \left\{\begin{split} & \mathop {\min }\limits_{Z, F, Y} {{{\mathrm{tr}}}}({F^{\rm T}}{L_Z}F) + \gamma ||F - Y{({Y^{\rm T}}DY)^{ - \frac{1}{2}}}||_F^2 \\ & {\mathrm{s.t.}}{\text{ }}{F^{\rm T}}F = I, \;Y \in Ind \end{split}\right. | (4) |
通过谱旋转, 将联合子空间相对应的划分矩阵F进行旋转操作, 得到最终的离散型聚类指标矩阵Y. 联合第2.1节和第2.2节, 形成了一个统一的多视图聚类算法目标函数, 如下:
| \left\{\begin{split} & \mathop {\min }\limits_{\{ {S^v}\} _{v = 1}^m, \alpha , \beta , \{ {U^v}\} _{v = 1}^m, \{ L_S^v\} _{v = 1}^m, Z, F, Y} \sum\limits_{i, j = 1}^n {||x_i^v} - x_j^v||_2^2s_{ij}^v \\ & {\text{ }} + \mu \sum\limits_{i, j = 1}^n {s{{_{ij}^v}^2}} + \sum\limits_{v = 1}^m {{\alpha _v}} {\mathrm{tr}}({U^v}L_S^v{U^v}^{\rm T}) \\ & {\text{ }} + \sum\limits_{v = 1}^m {{\beta _v}} ||{U^v} - {U^v}Z||_F^2 + \lambda ||Z||_F^2 \\ & {\text{ }} + {{{\mathrm{tr}}}}({F^{\rm T}}{L_Z}F) + \gamma ||F - Y{({Y^{\rm T}}DY)^{ - \frac{1}{2}}}||_F^2 \\ & {\mathrm{s.t.}} \left\{\begin{array}{l} \forall v{\text{, }}s_{ii}^v = 0, {\text{ }}s_{ij}^v \geqslant 0, {\text{ }}{{\text{1}}^{\rm T}}s_i^v = 1, {\text{ }}{U^v}{U^v}^{\rm T}{\text{ = }}{I} \\ {\text{ }}{\alpha ^{\rm T}}1 = 1, {\text{ }}\alpha \in \mathbb{R}_ + ^{\text{m}}, {\text{ }}{\beta ^{\rm T}}1 = 1, {\text{ }}\beta \in \mathbb{R}_ + ^{{m}} \\ {\text{ }}{\mathrm{diag}}(Z) = 0, {\text{ Z}} \in {\mathbb{R}^{n \times n}} \\ {\text{ }}{F^{\rm T}}F = I,\; Y \in Ind \end{array}\right. \end{split} \right. | (5) |
由于原始数据本身并不具备清晰的块状结构, 因此本文生成的联合子空间重构是学习结构化的一个优化过程. 本文利用划分矩阵正交约束进行子空间重建, 得到一个结构化的联合子空间, 以确保其内部具有鲁棒性的类内强连通性, 类间的弱连通性. 由于FTF约束为单位矩阵, 因此FFT所形成n维矩阵具有块状结构, 所以子空间重建可以表示为:
| \left\{\begin{gathered} \mathop {\min }\limits_{Z, F, R, Y} {{{\mathrm{tr}}}}(Z - F{F^{\rm T}}) \\ {\mathrm{s.t.}}{\text{ }}{F^{\rm T}}F = I, \;F \in \mathbb{R}_ + ^{{{n}} \times {{k}}} \\ \end{gathered} \right. | (6) |
由于Z约等于FFT是式(6)的解, 且经过迭代优化后的划分矩阵可以作为正反馈对联合子空间进行优化, 因此本文算法令Z=FFT进对其重构.
3 优化第2节形成的目标函数(5)由于有多个变量需要优化较为复杂, 因此采用交替优化算法对其进行迭代优化.
3.1 更新Y固定划分矩阵F来更新Y. 目标函数可转换为:
| \mathop {\max }\limits_{Y \in Ind} {\text{ }}{{{\mathrm{tr}}}}({F^{\mathrm{T}}}DY{({Y^{\mathrm{T}}}DY)^{ - \frac{1}{2}}}) | (7) |
可以参照文献[21]中提出的更新指标矩阵算法来解决优化问题.
3.2 更新F固定离散指示矩阵Y来更新F, 目标函数可转换为:
| \mathop {\max }\limits_{{F^{\rm T}}F = I} {\text{ }}{{{\mathrm{tr}}}}({F^{\mathrm{T}}}ZF + 2\gamma {F^{\mathrm{T}}}C) | (8) |
其中, C=Y(YTDY)–0.5可以使用拉格朗日乘积法来处理该目标函数, 并且其满足KKT条件, 因此可以进一步表示为:
| \mathop {\max }\limits_{{F^{\rm T}}F = I} {{{\mathrm{tr}}}}({F^{\mathrm{T}}}G) | (9) |
其中, G=2ZF+2γC, 对G进行SVD分解分别得到左奇异矩阵P和右奇异矩阵Q, 因此获得最优解:
| F = P{Q^{\rm T}} | (10) |
固定其他变量, 关于Z的最小目标函数为:
| \left\{\begin{split} & \mathop {\min }\limits_Z \sum\limits_{v = 1}^m {{\beta _v}} ||{U^v} - {U^v}Z||_F^2 + \lambda ||Z||_F^2 \\ & {\mathrm{s.t.}}{\text{ }}{\mathrm{diag}}(Z) = 0,\; {{ Z}} \in {\mathbb{R}^{n \times n}} \end{split} \right. | (11) |
式(12)给出了Z的最优解, 证明见文献[10].
| {Z^*} = - D{{\text{(diag(}}D{\text{))}}^{ - 1}}, {\text{ diag(}}{Z^*}{\text{) = 0}}{} | (12) |
固定其他变量, 关于Uv的最小目标函数为:
| \left\{\begin{split} & \mathop {\min }\limits_{{U^v}} \sum\limits_{v = 1}^m {{\alpha _v}} {{{\mathrm{tr}}}}({U^v}L_S^v{U^v}^{\rm T}) + \sum\limits_{v = 1}^m {{\beta _v}} ||{U^v} - {U^v}Z||_F^2 \\ & {\mathrm{s.t.}}\;{U^v}{U^v}^{\rm T} = {I}, \;{U^v} \in {\mathbb{R}^{c \times n}} \end{split}\right. | (13) |
其可以进一步转化为:
| \left\{\begin{split} & \mathop {\max }\limits_{{U^v}} {{{\mathrm{tr}}}}({U^v}{Q^v}{U^v}^{\rm T}) \\ & {\mathrm{s.t.}} \left\{\begin{array}{l} {\text{ }}{Q^v} = 2{\beta _v}{Z^{\rm T}} - {\beta _v}Z{Z^{\rm T}} - {\alpha _v}L_S^v \\ {U^v}{U^v}^{\rm T} = {I},\; {U^v} \in {\mathbb{R}^{c \times n}} \end{array}\right. \end{split} \right. | (14) |
可以通过特征分解有效地求解, 其中Uv是c个最大特征值对应的特征向量矩阵.
3.5 更新Sv固定其他变量, 关于Sv的最小目标函数为:
| \left\{\begin{split} & \mathop {\min }\limits_{{s^v}} \sum\limits_{i, j = 1}^n {||x_i^v} - x_j^v||_2^2s_{ij}^v + \mu \sum\limits_{i, j = 1}^n {s{{_{ij}^v}^2}} + \sum\limits_{v = 1}^m {{\alpha _v}} {{{\mathrm{tr}}}}({U^v}L_S^v{U^v}^{\rm T}) \\ & {\mathrm{s.t.}}{\text{ }}s_{ij}^v = 0, \;s_{ij}^v \geqslant 0, \;{1^{\rm T}}s_i^v = 1 \end{split} \right. | (15) |
显然地, 为每个视图更新Sv是独立的. 因此, 我们可以一个接一个地更新Sv, 可以表述为:
| \left\{\begin{split} & \mathop {\min }\limits_{{S^v}} ||x_{\text{i}}^v - x_j^v||_2^2s_{ij}^v + \mu \sum\limits_{i, j = 1}^n {s{{_{ij}^v}^2}} - \sum\limits_{v = 1}^m {{\alpha _v}} {{{\mathrm{tr}}}}({U^v}{S^v}{U^v}^{\rm T}) \\ & {\mathrm{s.t.}}{\text{ }}s_{ij}^v = 0, \;s_{ij}^v \geqslant 0,\; {1^{\rm T}}s_i^v = 1 \end{split} \right. | (16) |
| \left\{ \begin{split} & \min ||s_j^v + \frac{{g_j^v}}{{2\mu }}||_2^2 \\ & {\mathrm{s.t.}}{\text{ }}s{_j^{v\rm T}}1 = 1,\; s_j^v \geqslant 0 \end{split}\right. | (17) |
由向量概率单形欧氏投影算法能够解决上述表达式.
3.6 更新α固定其他变量, 关于α的最小目标函数:
| \left\{ \begin{split} & \mathop {\min }\limits_\alpha \sum\limits_{v = 1}^m {{\alpha _v}} {{{\mathrm{tr}}}}({U^v}L_S^v{U^v}^{\rm T}) \\ & {\mathrm{s.t.}}{\text{ }}\forall v{\text{, }}{\alpha ^{\rm T}}1 = 1, {\text{ }}\alpha \in \mathbb{R}_ + ^{{m}} \end{split} \right. | (18) |
对上函数式求关于α的导数, 并令其为0, 得到下面的优化公式:
| {\alpha _v} = \frac{{{{{\mathrm{tr}}}}({U^v}L_S^v{U^v}^{\rm T})}}{{\displaystyle\sum\limits_{v = 1}^m {\sqrt {{{{\mathrm{tr}}}}{{({U^v}L_S^v{U^v}^{\rm T})}^2}} } }} | (19) |
固定其他变量, 关于β的最小目标函数:
| \left\{\begin{split} & \mathop {\min }\limits_\beta \sum\limits_{v = 1}^m {{\beta _v}} ||{U^v} - {U^v}Z||_F^2 \\ & {\mathrm{s.t.}}{\text{ }}{\beta ^{\rm T}}1 = 1, {\text{ }}\beta \in \mathbb{R}_ + ^{{m}} \end{split}\right. | (20) |
与第3.6节类似, 对上函数式求关于β的导数, 并令其为0, 得到下面的优化公式:
| {\beta _v} = \frac{{||{U^v} - {U^v}Z||_F^2}}{{\displaystyle\sum\limits_{v = 1}^m {||{U^v} - {U^v}Z||_F^2} }} | (21) |
基于上述优化过程, 步骤如算法1所示, 各个变量依次交替优化, 在循环中该算法的收敛准则是指当指示矩阵Y稳定不再变化时或者obj(t)–obj(t+1)<10–5算法终止并达到收敛状态, obj(t)为第t次迭代过程中目标函数(5)的值, 此时算法终止并达到收敛状态.
算法1. 优化过程
输入: 多视图数据集X, 类别数k, 超参数c和λ, 最大迭代数max=50, μ=1, γ=0.01.
1) 用KNN近邻算法初始化Sv, 计算
2) WHILE 不收敛 DO
3) 通过求解式(12)更新Z;
4) FOR任意的v=1, …, m DO
4) 通过式(19)更新αv;
5) 通过式(21)更新βv;
6) 通过求解式(14)更新Uv;
7) 通过求解式(17)更新Sv;
8) END FOR
9) 通过求解式(7)更新Y.
10) 通过式(10) F=PQT更新F.
11) END WHILE
输出: 离散型聚类指示矩阵Y.
4 实验 4.1 数据集及比较算法数据集包括3source数据集, 100leave数据集, BBC数据集, Wiki数据集, HW数据集. 表1展示了数据集的具体数值, 简要介绍如下.
| 表 1 本文所使用数据集的统计表 |
3source: 数据集包含BBC、Reuters和Guardian的3个源的新闻数据, 共169条分为6个类别.
100leave: 这是一个UCI数据集. 它由1600个样本和100种植物组成.
BBC: 是由单一视角的体育语料库组成, 将新闻文章分割成4个片段. 共有685条数据, 5个类别.
Wiki: 来自维基百科的特色文章, 用于检索的数据集, 包含2866个样本、10个类, 其中词汇和SIFT直方图分别用于文本、图像两个模态.
HW: 由荷兰实用地图集合中提取的手写数字(0–9)的特征组成, 其中包含2 000条数据, 10个类别.
为了证明我们提出的算法的聚类性能, 我们在5种不同类型的数据集上, 将本文提出的算法与4种基线算法进行了比较. 所考虑的4种基线算法分别是基于图的多视图聚类(GMC)[22]、通过协同训练鲁棒数据表示进行的多视图子空间聚类(COMSC)[10]、同时进行谱嵌入和离散化的大图聚类(GCSED)[21]、一致的一步多视图子空间聚类(COMVSC)[14]. GMC算法将所有视图的数据图矩阵进行融合, 生成一个统一的图矩阵并利用图的连通性得出最终的聚类; COMSC算法对样本进行分组并消除数据冗余, 同时聚类结果将指导特征分解生成更有区别的数据表示; GCSED算法针对单视图数据建立了一种同时进行谱嵌入和谱旋转的新框架, 在对比实验中, 本文将数据集中每一个视图都运行在该算法上, 取最优数据作为该算法的最终结果; COMVSC算法建立了一个统一的多视图子空间聚类框架, 该框架联合优化了相似度学习、聚类划分和最终的聚类标签, 避免了现有的两步方法的次优解.
在接下来的实验中, 对于这4种比较算法, 我们使用了它们的原始参数设置. 所有的程序都在Matlab平台上运行, 在一台带有Intel(R) Core(TM) i7-7700 CPU @ 3.60 GHz四核处理器, RAM 16.0 GB和Windows 10操作系统. 每个算法实现10次, 然后取它们的平均值作为所有算法的最后结果. 我们采用了精度(ACC)、归一化互信息(NMI)和纯度(Purity)这3个评价指标来衡量该算法的性能. ACC表示与节点的真实标签相比的预测的正确率. NMI反映了聚类结果和基本事实标签之间的一致性. Purity表示正确聚集的数量与总数的比率.
4.2 比较实验及讨论实验结果见表2, 本文用粗体标记最优的结果, 并使用下划线标记次优结果. 实验结果表明, 本文提出的算法在5个数据集上都能获得最好的聚类性能, 证明了该算法的有效性. 其中评估指标ACC值在5个数据集上的优势分别为7.69%、3.06%、8.03%、2.48%、2.05%; NMI值在5个数据集上的优势分别为8.99%、0.68%、14.14%、0.79%、4.03%; Purity值在5个数据集上的优势分别为7.69%、1.63%、8.03%、2.20%、2.05%. 这表明该算法是一种有价值的多视图聚类算法. 本文算法表现提升最大的是在3source数据集和BBC数据集上, 因为这两个数据集特征维度最高分别达到3631、4684, 显然本文算法在高维数据上更具有鲁棒性和有效性.
| 表 2 各算法在5个公开数据集上的ACC、NMI和Purity值 |
与图聚类算法(GMC)和一步多视图子空间聚类算法(COMVSC)相比, 本文算法具有鲁棒性, 能很好地提升聚类效果. 与核算法(COMSC)相比, 这验证了自适应图学习和子空间正交化的有效性. 与单视图聚类算法(GCSED)比较, 说明多视图数据特征要比单视图数据特征更加丰富, 可以提供更多信息, 有助于发现隐藏在数据中的结构和关系, 聚类效果更佳.
4.3 参数敏感性分析本文算法中使用了c和λ两个超参数, 为了研究参数的敏感性, 本文使用网格搜索方式来选择最优参数组合. 其中超参数c表示本文算法使用c个最大特征值对应的特征向量作为鲁棒性数据表示矩阵, 超参数λ表示子空间Z的正则化项权重, 用与控制子空间Z的大小, 提高算法的稳定性和泛化性能. 具体而言c的取值范围设置为[k, 2k, …, 20k], 其中k是指数据集的类别; λ的取值范围设置为[2−10, 2−8, …, 210]. 图2和图3分别记录了不同参数在5个数据集上的3个评估指标的变化曲线.
从图2中可以观察到超参数c在给定的范围内对应的评估指标变化, 具体而言, 在3source数据集上评估指标的值浮动较大, 在3k时达到最优值, 是因为其视图是由不同数据源组成, 过多的特征信息会提高聚类的难度, 以及导致其对应的最大特征向量也不一定包含最佳聚类信息, 因此每个视图的鲁棒性表示矩阵的建立是必要的. 对于数据集100leave, 由于其类别达到100, 因此超参数最多达到15k数据量, 可以观察到, ACC、NMI和Purity随着c值的增加也在显著增加, 在7k左右评估指标达到最大值, 然后下降. 在BBC和Wiki数据集上, 随着c的增大, 评估指标的值逐渐增大, 当c取值在10k左右, 模型取得最佳效果, 之后变化趋势趋于平稳. 说明在一定程度上扩大c的范围能够让模型充分利用更多的数据信息, 增强聚类的鲁棒性. 而对于HW数据集c的取值对其影响并不大, 是由于该数据集特征维度较少, 冗余性特征相对较少因此对聚类效果影响不大.

|
图 2 超参数c对算法的影响性 |
|
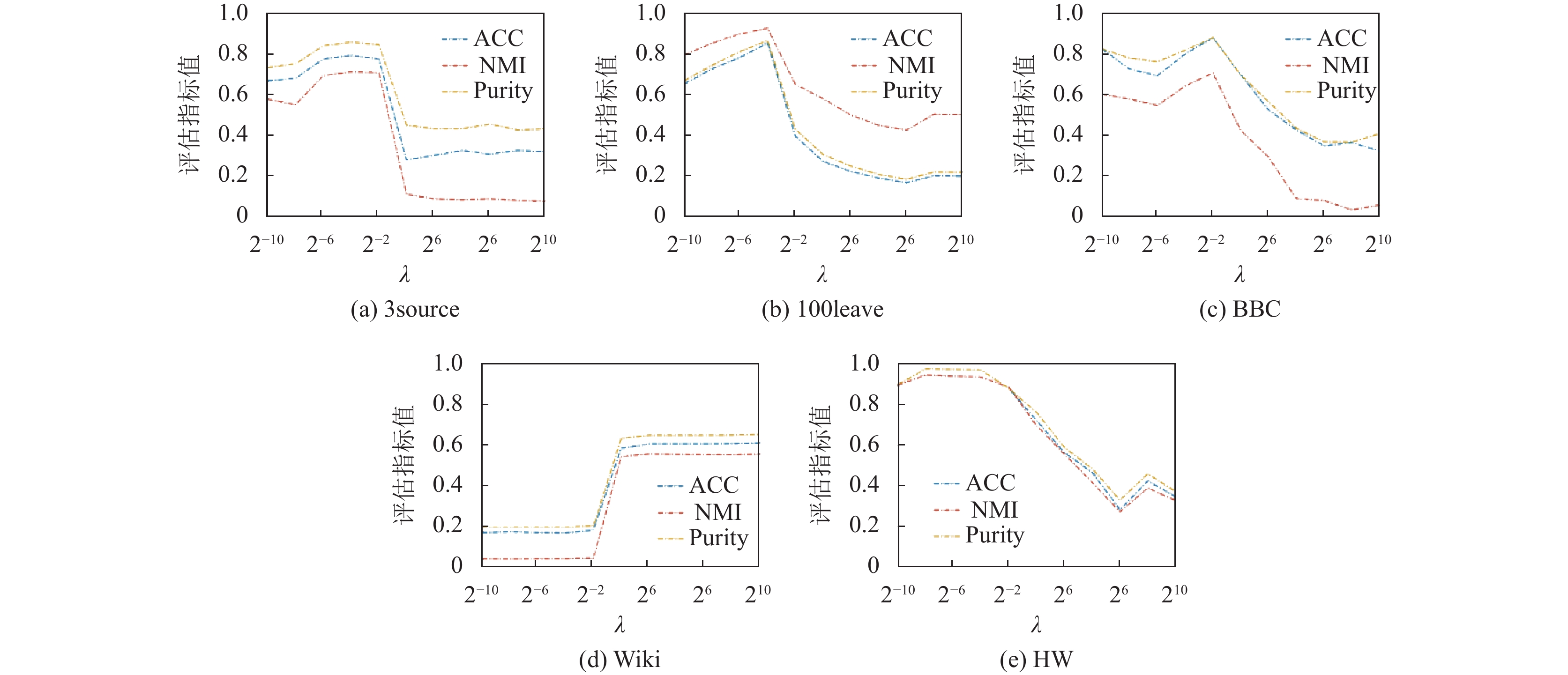
图 3 超参数λ对算法的影响性 |
在图3中, 对于3source、BBC数据集, 随着超参数λ数值的增加, 评估指标值也在增加, 分别在2−4和附近时达到最优; 而100leave、HW数据集在2−2达到最优, 然后都开始下降. 但Wiki数据集在20达到最优后趋于平衡. 由于λ过大正则化项的影响过于显著, 对算法中的其他优化项或约束条件产生抑制作用, 导致算法无法充分利用其他优化目标, 忽略了其他特征. λ过小正则化项的影响几乎可以忽略, 这会导致子空间更易受到数据中冗余信息和局部变化的影响, 但本文利用了划分矩阵对子空间Z进行正交化处理, 因此本文算法生成的联合子空间能够形成明显的块对角结构, 可以改善后续的聚类性能.
5 结论为了更好地探索多视图数据特征, 本文提出了一种具有鲁棒性的正交约束多视图子空间聚类算法, 该算法利用特征分解获取鲁棒的数据表示, 并通过多视图潜在子空间表示和谱旋转步骤, 实现了更为准确和鲁棒的聚类结果. 划分矩阵利用正交化对子空间进行重构, 进一步保证了子空间的连通性, 从而提升了聚类质量. 通过实验证明, 在多个基准数据集上, 该算法的性能优于现有方法, 证实了其有效性. 这一研究为多视图数据的聚类提供了一种新颖有效的解决方案, 对于实际应用具有重要意义.
| [1] |
胡傲然, 陈晓红. 基于多样性与一致性的单步多视图聚类. https://doi.org/10.19678/j.issn.1000-3428.0067660. [2023-09-07].
|
| [2] |
代劲, 胡艳. 混合粒度多视图新闻数据聚类方法. 小型微型计算机系统, 2021, 42(4): 719-724. |
| [3] |
于晓, 刘慧, 林毓秀, 等. 一致性引导的自适应加权多视图聚类. 计算机研究与发展, 2022, 59(7): 1496-1508. |
| [4] |
Khan A, Maji P. Approximate graph Laplacians for multimodal data clustering. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 43(3): 798-813. DOI:10.1109/TPAMI.2019.2945574 |
| [5] |
Ren ZW, Sun QS. Simultaneous global and local graph structure preserving for multiple kernel clustering. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(5): 1839-1851. DOI:10.1109/TNNLS.2020.2991366 |
| [6] |
Liu XW, Zhou SH, Wang YQ, et al. Optimal neighborhood kernel clustering with multiple kernels. Proceedings of the 31st AAAI Conference on Artificial Intelligence. San Francisco: AAAI, 2017. 2266–2272.
|
| [7] |
Wang R, Lu JT, Lu YH, et al. Discrete multiple kernel k-means. Proceedings of the 30th International Joint Conference on Artificial Intelligence. Montreal: IJCAI, 2021. 3111–3117.
|
| [8] |
Liu JY, Liu XW, Wang SW, et al. Hierarchical multiple kernel clustering. Proceedings of the 35th AAAI Conference on Artificial Intelligence. AAAI, 2021. 8671–8679.
|
| [9] |
Liu J, Liu X, Xiong J, et al. Optimal neighborhood multiple kernel clustering with adaptive local kernels. IEEE Transactions on Knowledge and Data Engineering, 2020, 34(6): 2872–2885. [doi: 10.1109/TKDE.2020.3014104]
|
| [10] |
Liu JY, Liu XW, Yang YX, et al. Multiview subspace clustering via co-training robust data representation. IEEE Transactions on Neural Networks and Learning Systems, 2022, 33(10): 5177-5189. DOI:10.1109/TNNLS.2021.3069424 |
| [11] |
Gao HC, Nie FP, Li XL, et al. Multi-view subspace clustering. Proceedings of the 2015 IEEE International Conference on Computer Vision. Santiago: IEEE, 2015. 4238–4246.
|
| [12] |
张华伟, 陆新东, 朱小明, 等. 基于t-SVD的结构保持多视图子空间聚类. 计算机科学, 2022, 49(S2): 210800215. |
| [13] |
Gu ZB, Feng SH, Hu RT, et al. ONION: Joint unsupervised feature selection and robust subspace extraction for graph-based multi-view clustering. ACM Transactions on Knowledge Discovery from Data, 2023, 17(5): 70. |
| [14] |
Zhang P, Liu XW, Xiong J, et al. Consensus one-step multi-view subspace clustering. IEEE Transactions on Knowledge and Data Engineering, 2022, 34(10): 4676-4689. DOI:10.1109/TKDE.2020.3045770 |
| [15] |
Wang Y, Wu L, Lin XM, et al. Multiview spectral clustering via structured low-rank matrix factorization. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(10): 4833-4843. DOI:10.1109/TNNLS.2017.2777489 |
| [16] |
Wu J, Lin Z, Zha H. Essential tensor learning for multi-view spectral clustering. IEEE Transactions on Image Processing, 2019, 28(12): 5910–5922. [doi: 10.1109/TIP.2019.2916740]
|
| [17] |
Gu ZB, Feng SH. Individuality meets commonality: A unified graph learning framework for multi-view clustering. ACM Transactions on Knowledge Discovery from Data, 2023, 17(1): 7. |
| [18] |
贺娜, 马盈仓, 张丹, 等. 基于谱聚类和L2,1范数的多视图聚类算法. 计算机与数字工程, 2021, 49(11): 2335-2341. |
| [19] |
Shi SJ, Nie FP, Wang R, et al. Self-weighting multi-view spectral clustering based on nuclear norm. Pattern Recognition, 2022, 124: 108429. DOI:10.1016/j.patcog.2021.108429 |
| [20] |
潘振君, 梁成, 张化祥. 基于一致图学习的鲁棒多视图子空间聚类. 计算机应用, 2021, 41(12): 3438-3446. |
| [21] |
Wang Z, Li ZQ, Wang R, et al. Large graph clustering with simultaneous spectral embedding and discretization. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 43(12): 4426-4440. DOI:10.1109/TPAMI.2020.3002587 |
| [22] |
Wang H, Yang Y, Liu B. GMC: Graph-based multi-view clustering. IEEE Transactions on Knowledge and Data Engineering, 2020, 32(6): 1116-1129. DOI:10.1109/TKDE.2019.2903810 |
 2024, Vol. 33
2024, Vol. 33



