柔性作业车间调度问题(flexible job shop scheduling problem, FJSP)是制造企业实际生产中经常遇到的一类问题, 它是作业车间调度问题(JSP)的扩展^[1], 去除了各工序存在唯一指定机器的限制, 考虑了工序的加工柔性, 更能适应当前动态的车间环境^[2]. 在过去的几十年中, 专家学者对FJSP进行了大量的研究, 提出了许多有效的解决方案^[3]. 这些解决方案主要可以分为集中式的调度方法和分布式多Agent的调度方法.

在复杂的实际作业生产车间中, 集中式的调度方法, 如遗传算法(genetic algorithm, GA)、模拟退火算法(simulated annealing, SA)、禁忌搜索算法(tabu search, TS)等由于其计算时间长, 往往无法很好地应用^[4]. 多Agent方法由于其实时性好、处理扰动能力强, 能够很好地解决实际车间中的调度问题^[5]. 然而, 传统的多Agent方法一般采用单一的调度规则, 忽略了调度过程中的环境变化影响, 存在Agent自适应能力和调度优化效果较差的缺点.

为了克服多Agent方法的这些缺点, 许多文献对其进行了研究. 郭剑等^[6]提出了一种SP-MCTS搜索方法, 利用马尔科夫决策过程对生产调度过程进行建模, 实现了自适应调度, 提高了调度的性能, 但仅适用于混流车间. 刘亚辉等^[7]提出了一种双环深度Q网络方法, 利用知识图谱实现对车间知识的表示, 并通过感知-认知双系统来对调度进行驱动, 但优化性能一般. 胡晓阳等^[8]将调度规则与贪心算法融合, 扩大了调度结果解的搜索空间, 实现了调度结果的优化, 但牺牲了一定实时性能. 贺俊杰等^[9]利用多智能体强化学习对纺织面料染色车间调度问题进行了调度优化, 克服了单一调度规则的缺点, 但仅适用于特定的并行调度问题. Qu等^[10]采用强化学习方法来根据环境状态自适应地生成调度规则, 但也仅适用于JSP.

在某一场景下, 调度规则选择与此场景的特征密切相关, 不同的特征下需要的调度规则也是各异的. FJSP比JSP更加复杂, 调度过程中的变化因素更多, 相应需要的调度规则也更为多变. 如果仅使用单一调度规则而不依据调度场景特征来个性化的选择, 那么将无法获得优异的调度方案. 本研究针对该问题, 将FJSP以机器选择和缓冲区工件调度两阶段来表示^[11], 利用上下文赌博机(contextual bandits)来类比建模. 上下文赌博机在若干回合的训练后, 能够识别场景特征与所需调度规则的模式关系. 利用该模式, 工件Agent在不同的场景下会应用上下文赌博机模型的计算结果制定调度策略, 实现整体调度结果的优化. 这种调度方式相比原始的单一调度规则, 具有更强的自适应性, 能够满足FJSP复杂场景的需求.

1 问题描述

本研究以最大完工时间(Makespan)为优化目标. 最大完工时间是所有加工工件最后完成时刻, 反映所有加工任务的整体完成速度, 体现了车间生产效率. 对最大完工时间目标进行优化, 可以实现对车间生产效率的提高.

同时, 依据实际车间场景作出如下假设^[12].

(1) 工件分批抵达生产车间, 每批抵达的工件数量是随机的.

(2) 工序加工机器不唯一, 有若干台机器可供使用.

(3) 每台机器在同一时刻仅可以加工一个工件.

(4) 准备时间包含在加工时间当中, 运输时间不予考虑.

(5) 工序一旦开始加工, 直到加工完成前都不能被打断.

1.1 符号定义

根据以上假设, 定义符号如下.

$ J $: 所有工件组成的集合

$ M $: 所有机器组成的集合

$ {C_i} $: 工件$ {J_i} $的完工时间

$ {O_{ij}} $: 工件$ i $的第$ j $道工序

$ s{t_{ij}} $: 工件$ i $的第$ j $道工序的开始加工时间

$ o{t_{ij}} $: 工件$ i $的第$ j $道工序的加工结束时间

$ s{m_{mi}} $: 机器$ m $加工第$ i $道工序的开始时间

$ o{m_{mi}} $: 机器$ m $加工第$ i $道工序的结束时间

$ {t_{ijm}} $: 工件$ i $的第$ j $道工序对应机器$ m $的加工时间

$ {X_{ijm}} = \left\{ \begin{array}{l} 1, \quad {O}_{ij}在机器m上加工 \\ 0, \quad 否则 \end{array} \right. $

1.2 FJSP优化模型

根据以上假设及符号定义, 可以建立FJSP数学模型如下.

优化指标选择Makespan, 记为$ C $.

$ C = \mathop {\max }\limits_{1 \leqslant i \leqslant N} \left( {{C_i}} \right) $

(1)

目标函数为:

$ \min \left( C \right) $

(2)

约束函数为:

$ \sum\limits_{m = 1}^M {{X_{ijm}}} = 1 $

(3)

$ s{t_{i\left( {j + 1} \right)}} \geqslant o{t_{ij}} $

(4)

$ s{m_{m(i + 1)}} - o{m_{mi}} \geqslant 0 $

(5)

$ o{t}_{ij}-s{t}_{ij}={\displaystyle \sum _{m=1}^{M}({X}_{ijm}\cdot{t}_{ijm}}) $

(6)

其中, 式(3)表示工件工序加工机器选择的唯一性约束; 式(4)表示工艺路线顺序约束; 式(5)表示工件工序加工先后顺序约束; 式(6)表示工序加工时间与机器加工时间需要具备一致性.

2 调度策略 2.1 自适应实时调度方法

在经济全球化的浪潮下, 市场需求变化不断加快, 生产制造企业亟需一个具有高柔性、高实时性、高敏捷性的制造系统来迎接这种挑战. 在该种需求下, 多Agent车间调度方法崭露头角, 以其独有的智能性、实时性、可重构性为现代制造系统应对挑战提供了可能. 然而, 传统的多Agent调度方法一般采用单一的调度规则, 忽略了调度过程中场景变化影响, 使得调度结果及Agent的自适应能力较差. 本研究通过上下文赌博机对车间调度过程建模, 利用场景特征进行规则选择, 从而改善了整体的表现.

2.1.1 上下文赌博机基本原理

上下文赌博机是一种强化学习模型, 每个回合包含一个状态, 并且能够影响即时奖励^[13]. 可以将上下文赌博机模型由$ \left\{ {A, S, R} \right\} $三元素构成, 其中, 元素$ A $表示模型具备的行为空间, 元素$ S $表示模型具备的状态空间, 元素$ R $表示模型所获得的奖励. 图1描述了上下文赌博机运行的逻辑, 在回合$ e $, Agent会依据此刻所处的环境$ {s_e} $通过计算值从行为空间$ A $中选择行为$ {a_e} $. 当Agent将行为$ {a_e} $作用于环境$ {s_e} $后, 环境$ {s_e} $将反馈给它奖励$ {r_e} $. 奖励$ {r_e} $是与环境状态$ {s_e} $和行为$ {a_e} $都相关的变量^[14], 这也意味着变化的环境状态被量化为上下文信息, 以帮助在上下文相关的、高度动态的、复杂的系统中进行决策^[15]. Agent通过若干回合的学习, 可以识别到环境状态与奖励之间的模式, 利用该模式即可制定使奖励值最大的策略.

2.1.2 车间调度决策过程建模

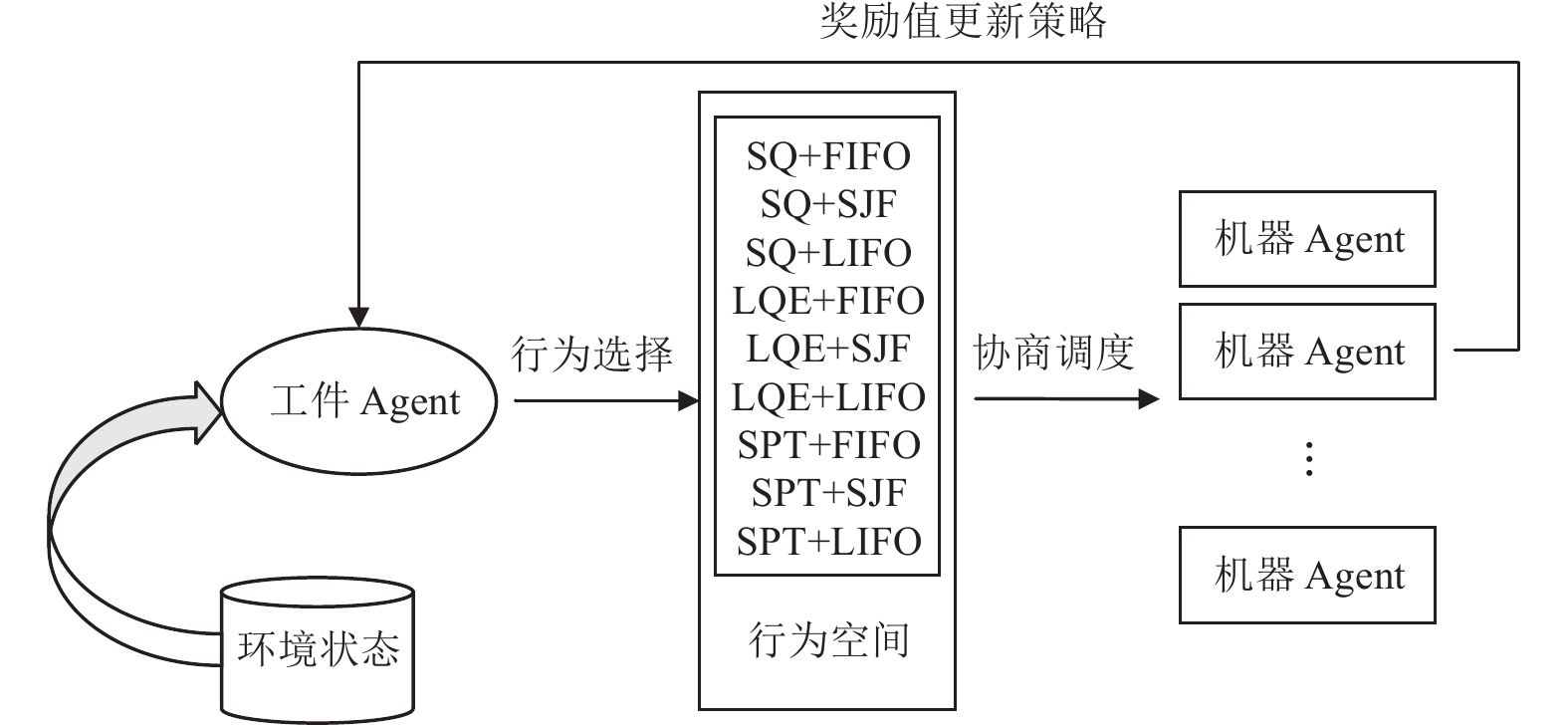
柔性作业车间调度问题比较复杂, 涉及工件、加工工序、加工机器, 是一个三元组合优化问题并已被证明为NP-hard. 对于该问题, 直接使用上下文赌博机模型进行优化势必会导致状态空间爆炸而无法收敛. 但是, 在采用多Agent车间调度方法的FJSP中, 工件Agent的决策是单步决策, 并且仅包含两个阶段: 机器选择阶段和缓冲区调度阶段. 如图2所示, 在每一决策回合, 工件Agent仅需要选择对应的机器选择规则和缓冲区调度规则, 随后便可基于该类规则实施加工进程. 在这种情形下, 上下文赌博机只需对工件Agent的单步决策过程进行优化, 仅涉及单道工序与多个调度规则组合的优化问题, 大大降低了状态空间维度并使得模型优化能够收敛.

车间调度决策过程建模为上下文赌博机的描述如下.

(1) 状态空间

状态空间包含从生产场景中提取的关键特征, 在Agent进行调度时, 上下文赌博机模型会依据这些特征实时计算每个行为收益并进行选择. 本研究提取的场景关键特征如下: 同时调度的各工序数量, 加工机器缓冲区的工件数量, 加工机器缓冲区的总加工时间, 加工机器所需加工时间.

(2) 行为空间

行为空间由机器选择规则和缓冲区调度规则的组合构成. 机器选择规则包括: 最短队列优先(shortest queue, SQ), 队列工件最少优先(less queued element, LQE), 处理时间最短优先(shortest processing time, SPT). 缓冲区调度规则包括: 先入先出(first in first out, FIFO), 工件加工时间最短优先(shortest job first, SJF), 后入先出(last in first out, LIFO). 通过将以上各机器选择规则和缓冲区调度规则进行两两组合, 形成包含9种行为的自适应实时车间调度行为空间, 分别为SQ+FIFO, SQ+SJF, SQ+LIFO, LQE+FIFO, LQE+SJF, LQE+LIFO, SPT+FIFO, SPT+SJF, SPT+LIFO. 在工件需要调度时, 上下文赌博机会基于实时环境状态从调度规则构成的行为空间中选择最合适的规则用于当前工件的调度, 从而是实现了对调度规则的个性化选择.

(3) 奖励

在Agent进行了行为选择后, 奖励值通过平均等待时间(mean wait time, MWT)变化量来计算, 计算方法见式(7)和式(8). 若当前平均等待时间较决策前变小, 计算的奖励将为正值, 表示这是一个好的决策; 否则给予负奖励值, 表示这是一个坏的决策. 策略学习算法将根据奖励值不断地进行学习, 最后获得能使奖励值最大的策略. 奖励值计算公式如下:

$ MW{T_t} = \frac{{\displaystyle\sum\limits_{j = 1}^n {W{T_{j, t}}} }}{n} $

(7)

$ {r_t} = MW{T_{t - 1}} - MW{T_t} $

(8)

其中, $ W{T_{j, t}} $为$ t $时刻工件$ j $到完成加工还需等待的时间, $ n $为当前工件的总数量.

2.1.3 策略学习算法LinUCB

本研究采用LinUCB算法对上下文赌博机进行训练, 该算法使用一维线性模型拟合环境状态和奖励两者潜在的模式关系, 实现高准确、高泛化的预测目标. 该算法在每一回合$ t $会计算行为集合中所有行为的期望奖励值, 并选择期望奖励值最大的行为作为Agent本轮的决策, 计算公式如下:

$ E\left[ {{r_{t, a}}\left| {{x_{t, a}}} \right.} \right] = x_{t, a}^{\rm{T}}\theta _a^ * $

(9)

其中, $ {r_{t, a}} $是回合$ t $选择行为$ a $的期望奖励值, $ \theta _a^ * $是行为$ a $的线性规划参数, $ {x_{t, a}} \in {R^d} $是状态空间设定的关键特征向量.

在线性模型中, $ \theta _a^ * $决定了模型预测的准确度. LinUCB算法通过在每一回合中的学习, 可以不断地对$ \theta _a^ * $进行在线优化, 使其符合当前的环境状态. 具体而言, LinUCB算法会记录$ m $回合的$ {x_{t, a}} $与$ {r_{t, a}} $, 构造历史经验矩阵$ {G_a} \in {R^{m \times d}} $和$ {c_a} \in {R^m} $, 然后使用岭回归^[16]对当前的$ \theta _a^ * $进行优化, 计算公式如下:

$ {\hat \theta _a} = {\left( {G_a^{\rm{T}}{G_a} + {I_d}} \right)^{ - 1}}{b_a} $

(10)

其中, 为简化公式的表示, 记${b_a} = G_a^{\rm{T}}{c_a}$.

此外, 为了防止陷入局部最优, LinUCB在上述计算值的基础上设置了置信区间. 在模型进行行为选择时, 将会选择置信区间上界最大的行为. 即在回合$ t $, 选择:

$ {a_t}: = \mathop {\arg \max }\limits_{a \in A} {\hat \mu _a} = \mathop {\arg \max }\limits_{a \in A} \left( {x_{t, a}^{\rm{T}} {{{\hat {\theta}} _a}} + {{{\hat {\sigma}} _a}} } \right) $

(11)

其中, ${\hat \sigma _a} = \alpha \sqrt {x_{t, a}^{\rm{T}}{A_a}{x_{t, a}}}$, ${A_a}: = G_a^{\rm{T}}{G_a} + {I_d}$, $ \alpha $是控制探索程度的参数.

算法1介绍了LinUCB算法的计算流程.

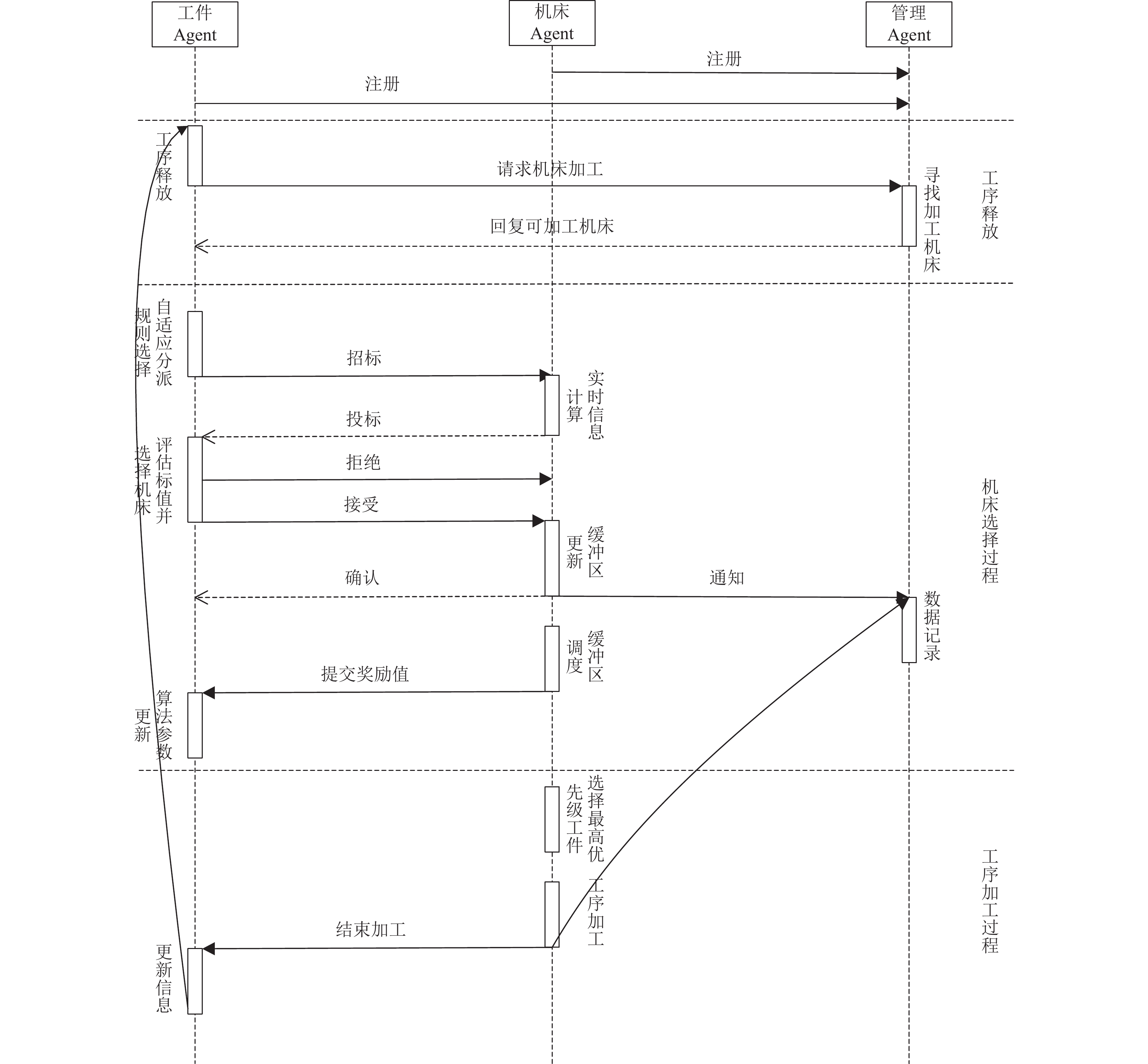
2.1.4 自适应实时车间调度策略

图3详细描述了本研究提出的基于上下文赌博机的自适应实时车间调度方法. 其详细描述如下.

(1) 机床Agent和已到达的工件Agent在管理Agent处进行注册.

(2) 有工件释放工序时, 工件Agent向管理Agent提出加工请求, 管理Agent发送可供选择的加工机床清单.

(3) 根据设定的状态空间关键特征, 工件Agent使用LinUCB算法, 计算出当前最优的机器选择规则和缓冲区调度规则.

算法1. 在线LinUCB

初始化参数$\scriptstyle \alpha \in {{\mathbb{R}}_{+}} $

for $\scriptstyle e=1\to E $ do

　观察所有行为的状态特征向量$\scriptstyle {{x}_{e,a}}\in {{R}^{d}} $, $\scriptstyle a\in A $

　for all $\scriptstyle a\in A $ do

　if $\scriptstyle a $ 第1次被选 then

　　$\scriptstyle {{A}_{a}}\leftarrow {{I}_{d}} $ (d维单位矩阵)

　　$\scriptstyle {{b}_{a}}\leftarrow {{0}_{d\times 1}} $ (d维零向量)

　end if

　$\scriptstyle {{{\hat{\theta }}\,}_{a}}\leftarrow A_{a}^{-1}{{b}_{a}}$

　$\scriptstyle {{{\hat{\mu }}\,}_{a}}\leftarrow {\hat{\theta }}\,_{a}^{{\rm{T}}}{{x}_{e,a}}+\alpha \sqrt{x_{e,a}^{{\rm{T}}}A_{a}^{-1}{{x}_{e,a}}}$

　end for

　选择行为$\scriptstyle {{a}_{e}}=\underset{a\in A}{\mathop{\arg \max }}\,{{{\hat{\mu }}\,}_{a}}$并观察真实的奖励$\scriptstyle {{r}_{e,{{a}_{e}}}} $

　$\scriptstyle {{A}_{{{a}_{e}}}}\leftarrow {{A}_{{{a}_{e}}}}+{{x}_{e,{{a}_{e}}}}x_{e,{{a}_{e}}}^{{\rm{T}}}$

　$\scriptstyle {{b}_{{{a}_{e}}}}\leftarrow {{b}_{{{a}_{e}}}}+{{r}_{e,{{a}_{e}}}}{{x}_{e,{{a}_{e}}}} $

end for

(4) 工件Agent向清单中所有机床Agent发起招标.

(5) 机床Agent向工件Agent投标, 提供选出的机器选择规则需要的信息.

(6) 工件Agent根据选出的机器选择规则计算标值, 选择标值最大的机床, 并向对应的机床Agent发送“接受”消息.

(7) 被接受的机床Agent回应确认, 如果当前机床空闲则直接进行加工; 否则存入缓冲区, 并使用选出的缓冲区调度规则对自己的缓冲区进行优先级排序; 最后, 计算平均等待时间的变化值, 作为奖励值提交给工件Agent.

(8) 工件Agent根据收到的奖励值, 更新对应工序算法的参数.

(9) 机床加工完成后, 如果工件完成所有加工则存入仓库并注销工件Agent, 否则工件Agent释放下一道工序, 重复步骤(2)–步骤(8); 之后, 空闲的机床从缓冲区中选择优先级最高的工件继续加工.

3 实验与分析

本节描述了验证基于上下文赌博机的自适应实时车间调度方法有效性的仿真实验. 实验环境为: Windows 10 64位操作系统, 主频3.10 GHz的Intel Core i9-9900 CPU、128 GB内存, 编程语言为Python, 开发环境为PyCharm.

3.1 算例设计

本研究设计的算例共包含10台机床, 编号为M1到M10. 同时包含10种类型的工件, 编号为${J_1}$到${J_{10}}$, 详细加工信息如表1所示. 表1中的数字是工序在对应机器上的加工时间, 而“—”代表此道工序不可以在此机器上加工.

在许多离散型制造企业中, 尤其是在面向订单的离散型制造企业中, 工件通常是成批地、间断地投放到车间的^[17]. 因此, 在本研究的模拟算例中, 工件成批地到来, 每批工件的数量从数值5–10中随机产生, 工件的类型从表1的10种工件中随机选择, 各批次工件组成如表2所示. 为了更好地比较调度的Makespan指标, 选择5批随机产生的工件, 到达时间间隔设定为5, 然后采用单一调度规则和自适应调度规则分别计算完成5批工件加工的Makespan进行比较.

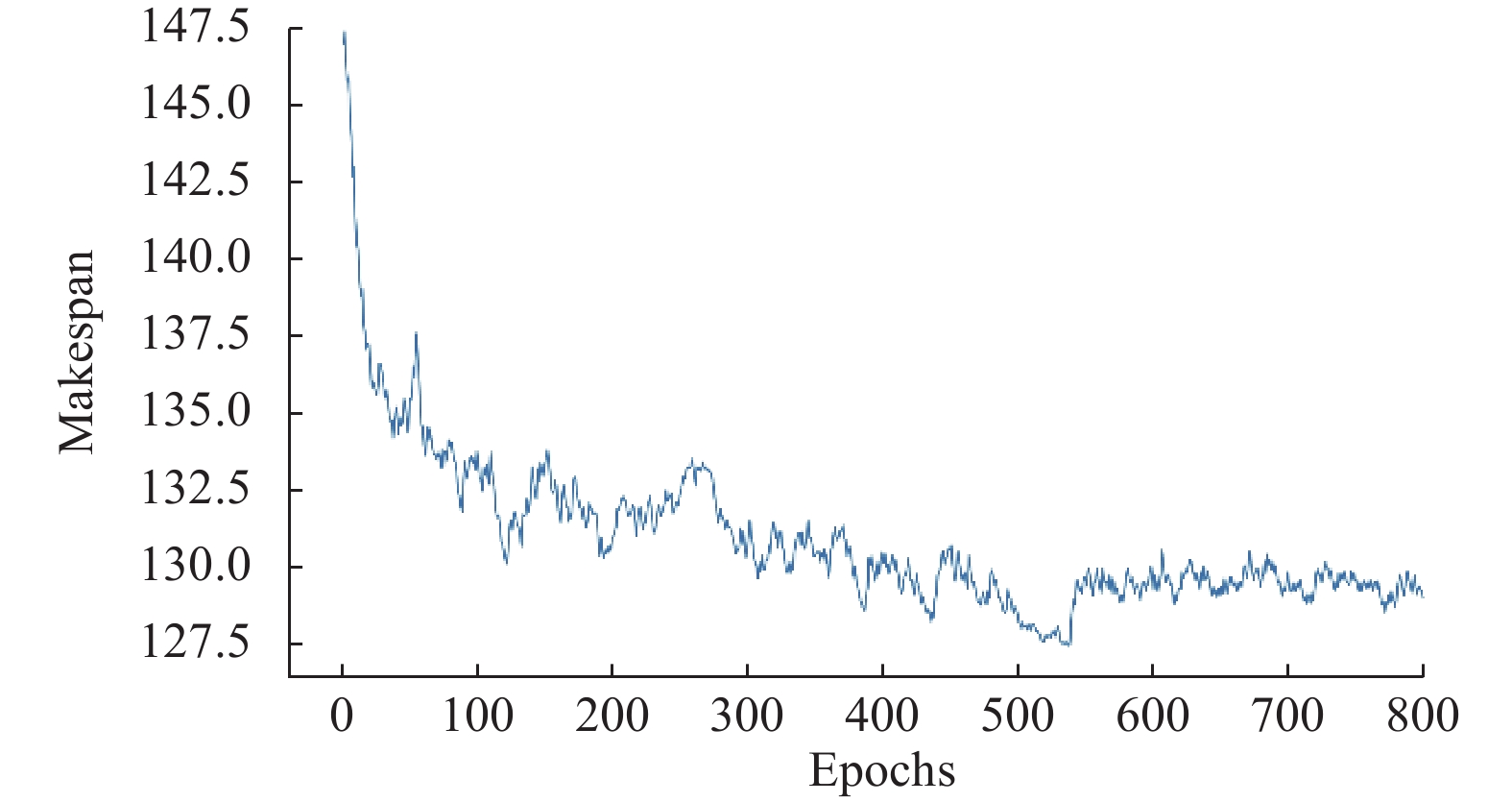
3.2 仿真结果与分析

针对随机产生的5批工件进行调度, 调度的规则包括9种单一的调度规则以及采用上下文赌博机的自适应实时车间调度方法. 自适应实时车间调度方法首先进行800个回合的学习, 图4显示了最大完工时间的变化趋势. 从图4可见, 通过不断地学习, 最大完工时间逐渐下降, 最终稳定在127.5–130之间. 因此, 上下文赌博机模型使用LinUCB算法能够识别到环境状态与规则选择之间的映射关系, 并能够利用该模型优化调度结果.

自适应实时车间调度方法的结果采用平均值计算, 并与9种单一调度规则方法获得的调度结果进行对比. 由图5可见, 采用本研究基于上下文赌博机的自适应实时车间调度方法能够获得比所有单一调度规则方法更好的调度结果. 可见, 利用上下文赌博机模型在不同环境下选择不同的调度规则, 比使用单一调度规则更优. 该结果证明了采用自适应实时车间调度方法的有效性.

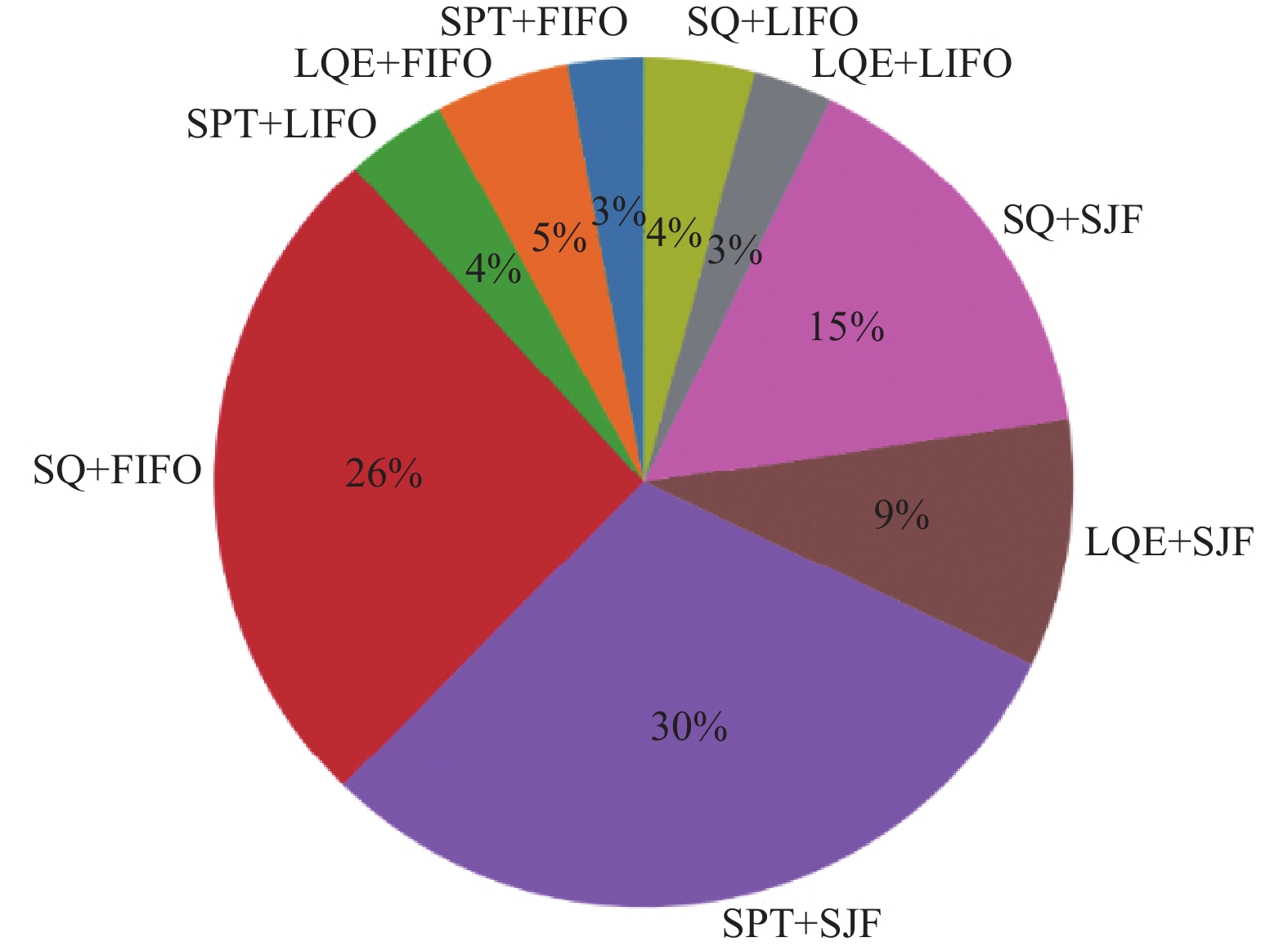
在整个仿真实验中, 当工件需要生产调度时, 上下文赌博机会基于生产车间环境特征从调度规则库中选择合适的调度规则, 从而使得不同调度时刻所使用的调度规则不同. 图6对各种调度规则的使用频次进行了统计, 显示了在采用自适应实时车间调度方法时各种调度规则被选取的分布, 与采用单一调度规则方法不同, 每种调度规则都在生产调度过程中被选用. 可见, 规则集合中的各元素在上下文赌博机模型的决策下, 适应了动态变化的环境状态, 最终实现了性能更加优秀的调度结果.

4 结论

传统的多Agent车间调度方法使用单一调度规则, 难以适应复杂FJSP的动态变化, 引起调度结果的欠优化. 本研究针对该问题提出了一种新的自适应实时车间调度方法, 采用强化学习中上下文赌博机对工件的调度过程进行类比建模, 并使用LinUCB算法进行策略学习, 使得工件Agent能够根据环境状态自主选择调度规则, 增强了工件Agent的自适应能力, 获得了更好的优化性能.