海运是国际贸易和全球经济的基础, 在国际货物运输中使用最为广泛. 国际贸易总运量中的2/3以上, 中国进出口货运总量的约90%都是利用海上运输. 随着对海运交通需求的增加, 船舶安全问题受到行业和学术界越来越多的关注. 其中, 准确的船舶轨迹预测在避免碰撞、异常轨迹检测、导航安全保障、港口管理等方面发挥着至关重要的作用. 船舶自动识别系统(automatic identification system, AIS)作为船舶航行信息的主要载体, 包含本船和他船的精确船位、航向、航速、转向速度等动态信息, 提供了大量的数据用于轨迹预测. 通过多层神经网络挖掘 AIS 数据中蕴含的轨迹信息, 分析船舶的活动规律和轨迹特征, 实现精准预测航行过程, 具有重要研究意义, 同时也能够为海上交通和海事监督提供可靠的技术支持.

近些年的船舶轨迹预测研究通常利用深度学习方法, 如循环神经网络(RNN)^[1]、门控循环单元(GRU)^[2]、长短期记忆(LSTM)^[3]和Transformer^[4]. 其中因为LSTM对比RNN解决了长序列训练过程中的梯度消失问题, 能够让LSTM具有更好的记忆性能, 这使得LSTM和它的变体被广泛运用于轨迹预测问题. 文献[5]提出一个双向LSTM (Bi-LSTM)网络的LSTM变体对比LSTM在收敛速度和预测准确性都有提高. 还有部分研究^[4]采用了深度学习模型中基于注意力的LSTM编码器-解码器框架. 这一框架融合了空间和时间的注意力机制, 并对空间和时间的权重进行了结合, 从而能够更精准地关注信息的特定区域.

由于Transformer的自注意力机制的引入, 使得它在捕捉长期依赖上有着出色表现. 已经有一些Transformer变体用于轨迹预测, 例如: TrAISformer^[6]提出一种新的AIS数据表示方法用于解决异质性问题, 其方法是将特征空间扩展到更高维度并克服过拟合的问题; MSTFormer^[7]提出一种具有动态感知注意力结构. 在这个研究中, 提出了多头动态感知自注意力机制, 这使得模型更有效地关注长期轨迹依赖和运动状态变化.

综上, 目前进行的大多数船舶轨迹预测研究^[8]主要聚焦于过去坐标位置上, 即仅使用AIS数据作为数据源. 但在复杂的海事环境中, 仅通过坐标信息很难全面地反映船舶的实际行驶状态. 对此, 文献[9]的研究对AIS数据与电子航海图(ENC)的融合进行了探讨, 强调了在路径规划和碰撞风险分类等方面将AIS数据与电子航海图结合使用的重要性. 此外, 越来越多轨迹预测研究不仅使用历史轨迹信息. 如在行人轨迹预测领域的研究中^[10–12], 部分学者将轨迹与环境的相互作用进行建模; 通常是通过鸟瞰图来捕捉行人在静态场景中的环境信息, 并在相关数据集上进行了评估.

在本研究中, 从AIS数据和ENC图像这两个信息源互相补充的特性中获得启发, 提出了一个新颖的多模态船舶轨迹预测网络——S-Transformer. 它集成了船舶的特定模态: AIS数据和ENC图像, 以预测未来船舶坐标的序列.

1 基于S-Transformer的船舶轨迹预测 1.1 问题定义

本文旨在解决海上船舶轨迹预测问题. 给定一个数据集$ R = \{ {X^{(i)}}, C\} _{i = 1}^K $, 有K个样本, 每个样本由历史轨迹X、ENC图像C组成. 其中历史轨迹AIS数据是使用一个由船舶的位置和速度组成的4维实值向量: ${X_i} \triangleq {[lat, lon, {\textit{SOG}}, {\textit{COG}}]^i}$ . lat、lon、Sog、Cog 分别为纬度、经度、航速、航向数据. 对于海图图像, 本文采取固定的视角, 视角下的图像能包括船舶的所有轨迹.

在本文中, 船舶轨迹预测问题被视为时间序列预测任务. 因此, 在本文中, 预测框架可以被表示为: $\widehat {{Y}} = \mathcal{F}({{X}}, {{M}};\mathbb{C})$. 其中, $ \mathcal{F} $表示网络; $\widehat {{Y}}$为预测轨迹; X为历史轨迹; M为海图图像; $ \mathbb{C} $为网络参数. 目标是预测未来t个时间步长的船舶轨迹.

1.2 网络结构

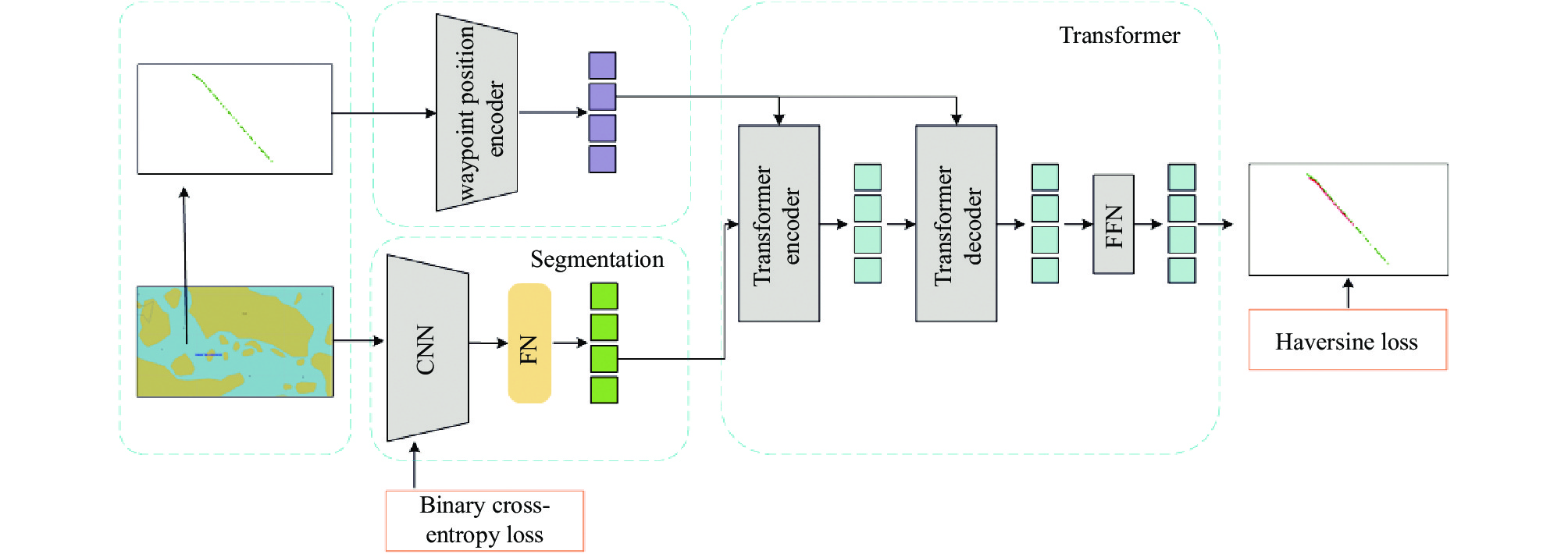
为解决船舶轨迹预测问题, 本文提出基于S-Transformer的轨迹预测方法. S-Transformer的网络结构如图1所示, 整体可以分成两个模块: 分割模块(segmentation)与Transformer .

1.2.1 分割模块

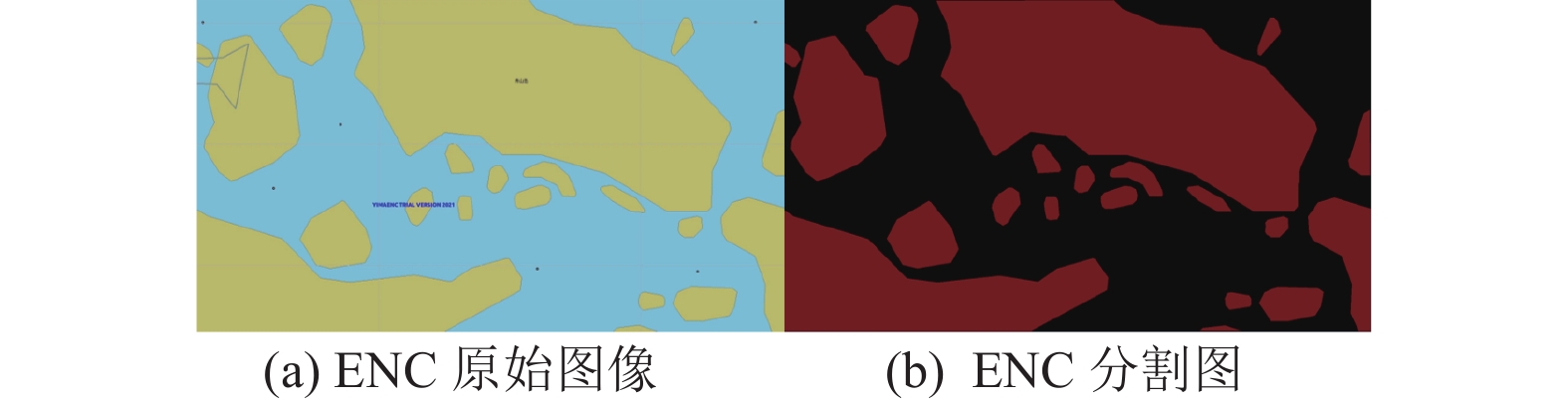
考虑到ENC图像与AIS数据相结合在船舶轨迹预测中的重要作用, 本文旨在通过对ENC图像进行分割, 为船舶定义可达区域. 为了实现这一目标, 本研究引入了一个分割模块. 该模块的核心任务是生成ENC图像的二值分割掩码, 以有效划分出船舶的可行区域. 在分割模块中, 本文采用了U-Net^[13]网络结构. 在网络的上采样层, 生成了二进制分割掩码, 并在分割后添加全连接层, 以将其转换为与坐标具有相同维度的表示. 最后, 采用串联方式将两种表示在每个时间步骤上进行组合. 分割结果如图2所示.

1.2.2 Transformer

为了挖掘AIS历史数据中可能存在的长期依赖关系, 本文选择采用了遵循Transformer^[14]的网络结构. 该网络结构包括Transformer编码器、解码器以及前馈网络(FFN). 具体而言, Transformer编码器包括6个编码器层, 每个编码器层都采用标准架构, 由多头自注意力模块和前馈网络(FFN)组成. 解码器与编码器具有相似的结构.

由于Transformer没有LSTM和RNN的循环性, 因此它使用位置编码(position encoder)对序列信息进行建模Transformer中, 对于每个位置pos, 都会有一个固定的位置编码.

$ P{E_{(pos, n)}} = \left\{ {\begin{array}{*{20}{l}} {\sin \left( {pos/{{10000}^{2n/{d_{{\rm{model}}}}}}} \right), }&{n{\text{%}} 2 = 1} \\ {\cos \left( {pos/{{10000}^{2n/{d_{{\rm{model}}}}}}} \right), }&{n{\text{%}} 2 = 0} \end{array}} \right. $

(1)

其中, n为维度, ${d_{{\rm{model}}}}$为令牌嵌入后的特征维度. 这个函数可以编码绝对位置和相对位置.

在训练网络时, 为了提高并行效率, 通常采用批处理(batch-size)的训练方式, 这导致AIS数据被分成多个小部分进行训练. 尽管这些小部分的AIS数据之间存在依赖关系, 但批处理的运算方式使得这些小部分之间缺乏联系, 从而难以学习更长范围内的AIS数据依赖关系. 为了解决这一问题, 引入了文献[15]中提到的segment recurrence的概念, 以便捕捉AIS数据的长期依赖关系. 通过引入分段循环机制, 可以更好地捕捉AIS数据之间的时序关系, 使得模型能够更准确地理解和预测船舶的轨迹. 这在船舶轨迹预测任务中尤为重要, 因为长期依赖关系往往对于准确的预测具有关键性影响.

在训练过程中, 对前一段计算得到的隐藏状态序列进行固定并缓存, 当模型处理下一个新段时, 将其作为扩展的上下文进行重用. 尽管梯度仍然保留在一个段中, 但是这个额外的输入允许网络利用历史信息, 从而能够对长期依赖关系建模并避免上下文碎片化.

分段之间的实现如下, 两个长度为L的连续片段表示为${{{S}}_\tau } = [{X_{\tau, 1} } , \cdots, {X_{\tau, L} }]$和${{{S}}_{\tau + 1}} = [{X_{\tau + 1, 1}} , \cdots, {X_{\tau + 1, L}}]$. ${S_\tau }$的隐层节点的状态表示为$h_\tau ^n \in {R^{L \times d}}$, 其中d是隐层节点的维度. ${S_{\tau + 1}}$的隐层节的状态$h_{\tau + 1}^n$的计算过程为:

$ {\tilde{h}}_{\tau +1}^{({n-1})}=[SG({h}_{\tau }^{(n-1)})\circ {h}_{\tau +1}^{(n-1)}] $

(2)

$ {{Q}}{\kern 1pt} _{\tau + 1}^{(n)}, K{\kern 1pt} _{\tau + 1 }^{(n)} ,V{\kern 1pt} _{\tau + 1}^{(n)} = h{\kern 1pt} _{\tau + 1}^{(n - 1)}{{{W}}^q}, \tilde h{\kern 1pt} _{\tau + 1}^{(n - 1)}{{{W}}^k}, \tilde h{\kern 1pt} _{\tau + 1}^{(n - 1)}{{{W}}^v} $

(3)

$ h_{\tau + 1}^{(n)} = {\text{Transformer-layer}}(Q_{\tau + 1}^{(n)}, K_{\tau + 1}^{(n)}, V_{\tau + 1}^{(n)}) $

(4)

其中, $\tau $表示第几段, n表示第几层, h表示隐层的输出; $ SG( \cdot ) $即stop-gradient, 表示这一部分不参与BP计算; $[{h_u} \circ {h_v}]$表示沿两个隐藏序列在 length 维度上拼接; W是模型需要的学习参数; 与传统Transformer相比关键在于key和value矩阵的计算上, 即$K_{\tau + 1}^n$和$V_{\tau + 1}^n$使用的是扩展了上个片段的隐层状态的$ \tilde h_{\tau + 1}^{n - 1} $. 因此上一段的$ h_\tau ^{n - 1} $被缓存.

在模型处理每个数据片段时, 它会充分利用上一个片段的隐藏状态, 以提供关于上下文的重要信息. 这样的设计使得在处理当前片段时, 不仅可以利用当前片段内的信息, 还可以利用前一个片段的信息, 从而更好地捕捉AIS序列中的依赖关系.

1.3 损失函数

本文采用多任务损失来训练整个网络. 对于辅助的语义分割任务, 文本使用二元交叉熵损失函数. 损失函数如下:

$ {\mathcal{L}_{{\rm{road}}}} = - \sum\nolimits_{i = 1}^{{H{'}}} {\sum\nolimits_{j = 1}^{{W{'}}} {[{y_{i, j}}\log ({x_{i, j}}) + (1 - {y_{i, j}})\log ({x_{i, j}})]} } $

(5)

在以往研究中, 船舶轨迹预测损失函数一般采用均方差公式. 由于地球近似一个球体, 因此在计算地球上的距离时, 需要考虑地球的曲率, 而不是简单计算平面的坐标差. 所以本文使用Haversine公式作为模型的损失函数, 能够更准确地捕捉到实际距离的影响:

$ \begin{gathered} dis = 2r\arg \sin \sqrt {{{\sin }^2}\left(\frac{{lat2 - lat1}}{2}\right) + \cos (lat2)\cos (lat1){{\sin }^2}\left(\frac{{lon2 - lon1}}{2}\right)} \end{gathered} $

(6)

$ {\mathcal{L}_{{{\rm{waypoint}}} }} = \frac{{\displaystyle\sum {_{n = 1}^N} }}{N} $

(7)

其中, r为地球半径; (lat1, lon1)为真实坐标; (lat2, lon2)为预测坐标.

上述介绍了二元交叉熵损失函数与Haversine损失. 根据文献[16]中的组合损失结合这两种损失. 将每个任务添加一个可学习的噪声参数$ \sigma $, 从而得到以下损失:

$ {\mathcal{L}_{{\rm{total}}}} = \frac{1}{{2\sigma _1^2}}{\mathcal{L}_{{{\rm{waypoint}}} }} + \frac{1}{{2\sigma _2^2}}{\mathcal{L}_{{\rm{road}}}} + \log {\sigma _1}{\sigma _2} $

(8)

通过将这些参数添加到损失函数中, 可以在优化过程中学习任务权重. 使用这种设置使得可以在实时学习中确定这些参数.

2 实验细节 2.1 数据集

数据集包括以下两个数据源.

AIS数据: 本次实验选取了船舶在中国最大港口宁波舟山港与其他周围港口之间的通行的AIS数据, 数据收集于船达通. 这个数据集包括从2023年1月1日–2023年3月1日期间的船舶上的AIS数据, 经度范围为121°9.20'E–122°23.05'E , 纬度范围为29°50.70'N–30°7.30'N.

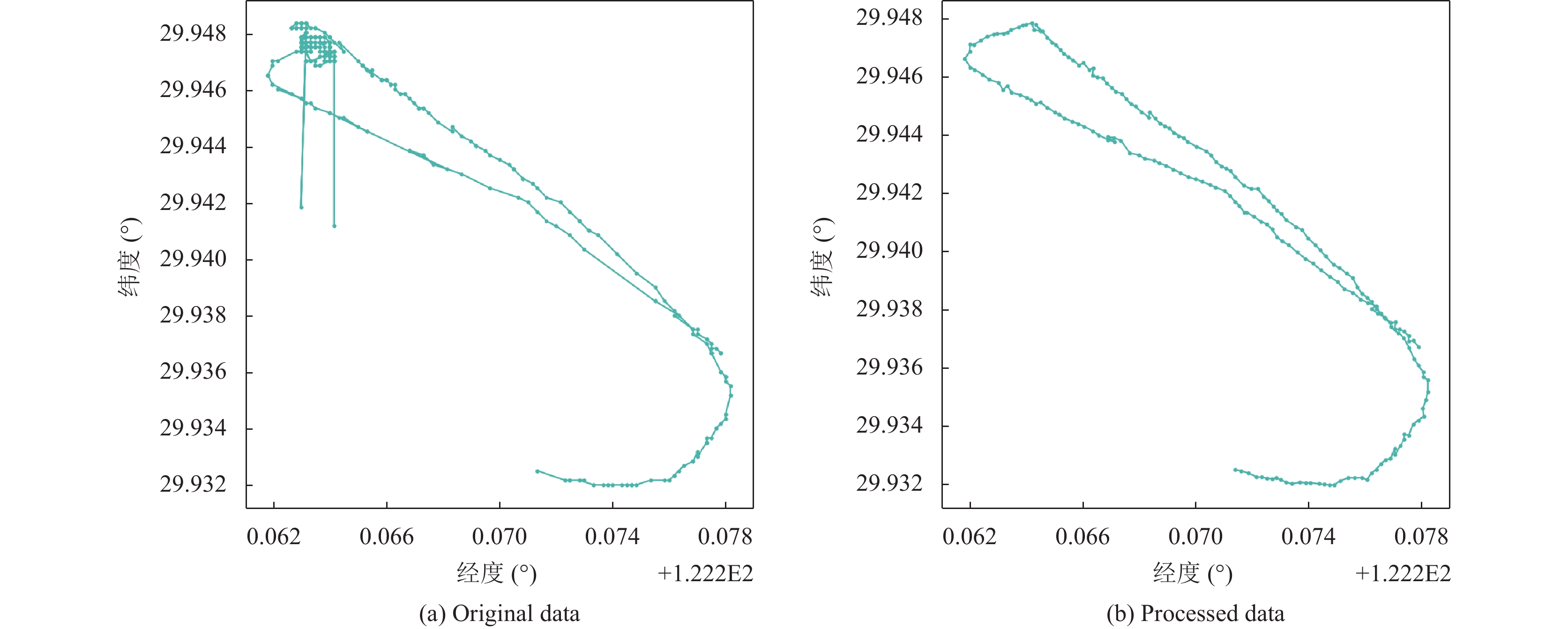
原始AIS数据存在各种问题. 首先是由于距离太远, 无法接收到准确的数据; 其次是人为因素, 比如船只操纵员按下错误的键或输入错误的数据也会导致数据误差. 所以这会导致原始数据有测量尺度不均匀、数据缺失、数据不标准等问题. 因此本文进行了必要的数据预处理^[6,17], 如图3所示.

◇ 删除具有速度异常的数据(速度>25节)的AIS数据.

◇ 删除航行长度小于20的AIS数据.

◇ 删除连续两个轨迹为停泊的AIS数据.

◇ 删除靠岸小于1 km的AIS数据.

◇ 删除不在经纬度范围内的AIS数据.

ENC图像: 电子导航图包含安全导航所需的信息. 在本次研究中, 使用陆地和水域信息的ENC. ENC图像有多个尺寸, 本文使用常见的1920×1080分辨率, 比例尺为1:70000.

2.2 实验设置

本文中的实验均在相同硬件条件下进行, 传统模型部分采用CPU进行计算, 处理器为Intel Core i7-11800H CPU @ 2.30 GHz, 8 核 16 线程. 深度学习部分使用12 GB的NVIDIA3060 GPU 计算, 运算平台为 CUDA 11.6 和 cuDNN. 主要利用Python 3.9完成, 使用TensorFlow框架构建模型. 初始学习率为0.001, 训练周期为100.

2.3 评判标准

本研究采用以下指标来评估S-Transformer模型.

均方误差(MSE), 表示船舶真实轨迹坐标与预测轨迹坐标之差的平方. 公式如下:

$ {\textit{MSE}} = \frac{1}{N}\sum\limits_{t = 1}^N {{{(rea{l_t} - predictio{n_t})}^2}} $

(9)

终点位置误差(FDE), 表示船舶真实轨迹终点坐标与预测终点坐标之间距离, 使用式(6)计算.

两误差指标的值越小, 说明轨迹预测模型描述实验数据的精确度越高.

3 实验与结果分析 3.1 对比实验

本文将S-Transformer与一些传统方法与几种最先进的机器学习方法进行比较, 以说明模型的优秀预测能力. 对比模型包括: SVR^[18]、LSTM、LSTM Seq2Seq^[19], attention-based LSTM^[20]、Transformer. 下面是具体实验结果.

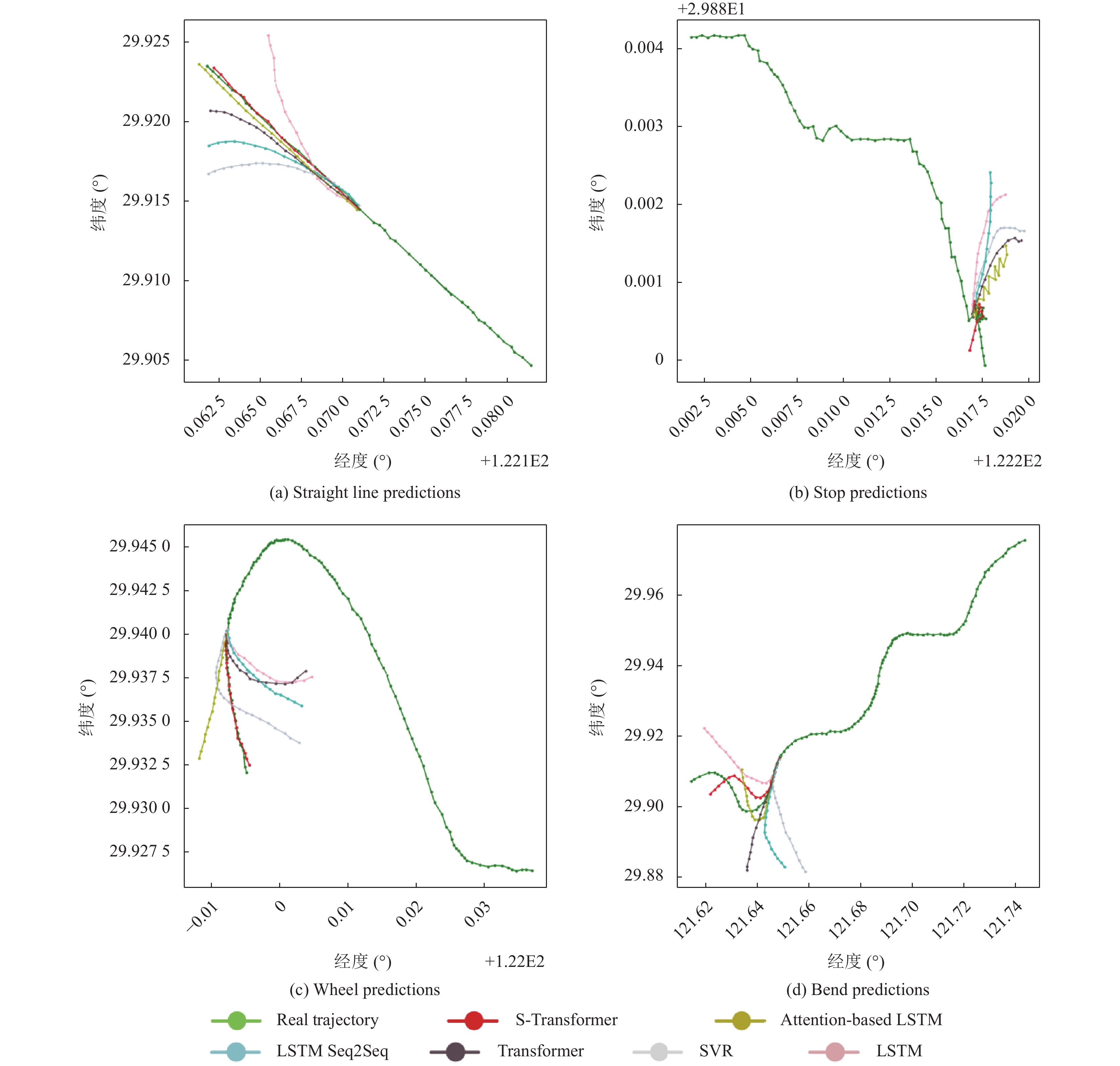
3.1.1 预测精度

为了评估S-Transformer的预测能力, 本文挑选了几个有代表性的船舶行驶情况作为比较场景并进行了可视化. 在图4可以看到更多各个模型预测能力的细节.

图4(a)展示了船舶直线航行场景的预测结果. 基准模型的最终位置明显偏离了真实位置. 这是因为一旦在预测起点出现误差, 模型的预测误差往往会显著累积. 而S-Transformer通过引入分段循环结构(segment recurrence), 能够捕捉AIS数据中的长期依赖关系, 使得预测结果保持在一定范围内的偏差.

在图4(b)中是船舶驶入港口后停下然后再次启航的情景. 这对于各个模型而言都是一个巨大的挑战, 大多数基准模型难以对这种场景进行准确预测. 然而, S-Transformer通过引入分割模块, 使得最终预测位置更接近真实位置.

在图4(c)中, S-Transformer在船舶转弯预测方面表现出色. 相比之下, 其他模型由于转弯时曲率的剧烈变化, 预测出现偏差.

此外, 图4(d)展示了连续弯曲船舶航行路径的情景, 在这种情况下, 不同模型的预测准确性都有所降低. 虽然该模型能够预测轨迹的大致趋势, 但预测结果与真实位置仍存在差距.

总之, 在各个情况的预测中, S-Transformer适用于常见的主要航运路线.

3.1.2 长期预测

为了验证模型在不同长度时间的预测效果, 本文进行对比实验, 在实验中分别列出了0.5 h、1 h、2 h、4 h的不同时间段的各个模型的MSE和FDE效果. 其对比实验如表1所示.

随着预测时间不断增加, 船舶轨迹呈现出复杂的行驶路径, 这导致模型对预测结果有很多的不确定性. 在这种情况下, 基线模型SVR在2 h与4 h的MSE分别为5.135×10⁻³和14.354×10⁻³, 整体升高9.219×10⁻³; 而在相同条件下, S-Transformer在2 h与4 h的MSE分别为1.745×10⁻³和4.17×10⁻³, 整体升高2.362×10⁻³. 同样情况下, SVR在2 h和4 h的FDE从5.135 km提高到14.354 km, 增加了9.219 km; 而S-Transformer在2 h和4 h的FDE升高仅为SVR的25.62%.

在长期船舶轨迹预测任务中, 传统方法(如SVR)和深度学习方法(如LSTM)在表现上明显不如S-Transformer. S-Transformer通过提取相关的长期依赖性, 显著提升了在长期预测方面的船舶轨迹预测能力. 此外, 与基准Transformer模型相比, 本文所提出的S-Transformer模型还引入了分割模块, 进一步提升了预测精度. 根据表1中的数据, 可以看出优化后的S-Transformer模型的FDE仅为Transformer的58.56%, 而MSE减小了33.79%. 这表明在长距离轨迹预测方面, 本文引入的segment recurrence和分割模块在模型性能提升方面具有重要的意义.

综上所述, S-Transformer在短期和长期预测精度方面优于其他模型. 然而, 在超过2 h的时间跨度下的轨迹预测方面, 仍有提升的空间.

3.2 消融实验

为了进一步评估S-Transformer架构的不同组成部分的重要性, 本文进行了消融研究, 使用MSE与FDE进行比较评估.

首先, 给Transformer添加分割模块, 以评估ENC提供船舶行驶的环境信息的重要性. 根据表2所示的结果, 与传统的Transformer相比, S-Transformer在MSE上降低了11.71%, 在FDE上减少了0.187 km.

其次, 本文引入了segment recurrence机制到Transformer中, 以捕捉AIS数据的长期依赖关系. 结果显示, S-Transformer的MSE降低了20.19%, FDE减少了0.318 km.

最后, 为证明Haversine损失函数的优势, 本文使用了该损失函数, 结果表明, 与使用${\mathcal{L}}_{{{\textit{MSE}}}}$的S-Transformer对比MSE降低了3.86%, FDE减少了0.014 km. 这些消融实验有助于说明S-Transformer模型中各个组件的作用和贡献. 总体而言, 当所有结构一起使用时, 模型可以实现更好的预测准确性.

4 结论与展望

本文提出了一种名为S-Transformer的多模态船舶轨迹预测模型, 并在真实的公开AIS数据和ENC图像上进行了实验. 根据实验结果, S-Transformer在性能方面明显优于基准方法. 通过结合ENC图像分割掩码的辅助训练和引入segment recurrence机制, S-Transformer在不同的船舶行驶情况下都表现出优越性能. 此外, 采用Haversine公式作为损失函数也进一步提升了模型的性能.

最后, 虽然本文提出的模型在一些方面优于其他模型, 但是在长期预测上的准确性还是有巨大挑战. 多模态轨迹预测涉及不同的数据源, 目前的研究只涉及AIS数据与ENC图像, 未来工作中可以更加深入研究一些激光、雷达^[21]、电子卫星图像等数据信息, 使船舶轨迹预测变得更加准确可靠.