基于混合数据类型相关性度量的非正态数据合成

引用本文

王春东, 张世鹏. 基于混合数据类型相关性度量的非正态数据合成. 计算机系统应用, 2024, 33(3): 195-205.http://www.c-s-a.org.cn/1003-3254/9441.html

Wang CD, Zhang SP. Non-normal Data Synthesis Based on Mixed Data Type Correlation Measurement. Computer Systems and Applications, 2024, 33(3): 195-205(in Chinese).http://www.c-s-a.org.cn/1003-3254/9441.html

基于混合数据类型相关性度量的非正态数据合成

王春东, 张世鹏

天津理工大学计算机科学与工程学院, 天津 300384

收稿日期：2023-09-23; 修改日期：2023-10-20; 采用时间：2023-11-03; csa 在线出版时间：2024-01-19

基金项目：国家自然科学基金联合基金(U1536122); 天津市科委重大专项(15ZXDSGX00030)

通讯作者：王春东, E-mail: michael3769@163.com.

摘要：数据在机器学习、人工智能等领域的研究和开发工作中占据了极其重要的地位. 然而现实中存在的一些因素导致数据需求者无法获得符合工作要求的真实数据集, 例如隐私问题、数据稀缺和数据质量较差等. 针对此现状, 在 SI (sampling-iteration) technique的基础上改进出一种非正态数据合成算法(KMSI). 该算法使用混合类型相关系数矩阵以减小SI technique在目标设定、控制循环等步骤中的度量误差, 通过替换Bootstrap采样法为核密度估计采样法以避免使用真实数据. 实验结果表明, KMSI相较SI technique能够应对复杂分布和混合类型的数据集, 且在合成结果中不包含真实数据; 相较于其他改进方法, KMSI在合成数据集样本量上能够给予使用者更大的自定义空间.

关键词: 合成数据集隐私保护相关系数核密度估计

Non-normal Data Synthesis Based on Mixed Data Type Correlation Measurement

WANG Chun-Dong, ZHANG Shi-Peng

School of Computer Science and Engineering, Tianjin University of Technology, Tianjin 300384, China

Abstract: Data plays an extremely important role in research and development in fields such as machine learning and artificial intelligence. However, some real-world factors prevent data consumers from obtaining real datasets that meet their work requirements, such as privacy issues, data scarcity, and poor data quality. In response to this situation, this study develops a non-normal data synthesis algorithm (KMSI) as an improvement to the sampling-iteration (SI) technique. This algorithm utilizes a mixed-type correlation coefficient matrix to reduce measurement errors in various steps of the SI technique, including target setting and control loops. It replaces Bootstrap sampling with kernel density estimation sampling to avoid using real data. Experimental results show that, compared to the SI technique, KMSI is capable of handling complex and mixed-type datasets and does not include real data in the synthetic results. Furthermore, compared to other enhancement methods, KMSI offers users more customization options for the sample size in synthetic datasets.

Key words: synthetic dataset privacy protection correlation coefficient kernel density estimation

机器学习与人工智能领域的研究工作方兴未艾, 能否构建出以更高性能和准确度实现预测、分类、识别等模仿人类器官机能的数学模型, 极大程度上依赖着数据的质量, 因此愈发凸显其重要地位^[1].

但是, 在现实中总是存在着各种因素, 使得数据需求者不能自由获取到满足自己实验或开发需求的真实数据集, 常见因素有以下3种: 第一, 数据集涉及法律限制的隐私问题或保密领域; 比如数据集中包含真实的姓名、住址、职业等信息; 不同国家和区域的法律出于保护公民隐私权的严格规定是此类障碍出现的直接原因. 第二, 数据集比较稀缺; 当研究人员对一些有偿数据集存在需求, 或者数据集的建立需要耗费超过研究人员能够承担的精力与时间成本时, 该因素是不可忽视的^[2]. 第三, 数据集中的数据质量较差; 通常表现为数据不平衡、数据量少、特征冗余等问题, 这些问题的存在会直接影响模型的性能, 导致表现下降^[3]. 当这些因素单独或叠加出现时, 使用真实数据集对研究工作将难以起到积极作用. 因此, 合成数据生成方法成为一个重要的研究方向, 旨在实现合成数据集与真实数据集的分布与相关性高度相近的目标.

目前关于多元非正态数据的合成方法, 已经有一些工作对该领域进行整理^[4]与研究. Fleishman提出的解决方案^[5]基于三阶多项式变换并通过对方程组的求解把一个正态分布单变量转换为自定义非正态分布单变量. 在此基础之上, Vale等人提出的VM-transform^[6]通过计算中间相关系数矩阵以调整算法对各个变量之间相关关系的影响将其成功运用于生成多变量数据上. VM-transform确立了以“变换-计算”方式生成多元非正态数据集的基本框架, 之后沿用该框架并做出改进分布描述方式的工作例如文献[7–13]. “采样-迭代”框架即SI technique, 是由Ruscio等人^[14]提出并完善的^[15]. “采样-迭代”框架对真实数据采样以实现对分布的描述, 并以迭代试错的方式逐步确定最优中间相关系数矩阵; 这消除了“变换-计算”框架对于分布矩的限制, 更有利于处理未定义矩和同矩不同分布的情况. Amatya等人^[16]提出的方法旨在合成混合类型数据集, 并强调了序数、连续型数据分别符合广义泊松分布与正态分布; Humski等人^[17,18]使用插值矩阵的方法进一步扩大了“变换-计算”框架合成样本的生成上限, 并将其应用到社交图谱等复杂数据集上. Foster^[19]提出的模型能够以更简单的方式使用因子分析方法构建合成数据集; 该模型与Bartholomew等人^[20]描述的较为相似.

现有工作对SI technique的改进集中在优化对变量分布的描述上, 但鲜有工作具体讨论数据相关性与隐私保护问题. 因此, SI technique 依旧存在改进空间: 第一, 单一相关系数矩阵难以准确度量多类型混合数据的相关性, 多类型混合、非线性数据等现象在真实数据中十分常见^[21,22]. 第二, 采样方式无法在隐私保护的前提下重现真实特征列分布. SI technique中的采样法有两种: Bootstrap采样法和预定义分布采样法. 对真实数据集使用Bootstrap意味着采样结果均为真实数据, 增加了隐私暴露的风险, 且Bootstrap极大限制了采样数据量, 这对于使用者是不利的. 使用预定义分布采样虽然能够降低隐私暴露风险, 但预定义的分布并不总是能够符合真实分布的所有情况.

综上所述, SI technique在应对合成多元非正态数据问题上具有更高的灵活度, 但在一些存在隐私保护要求的场景下有不足. 本文改进的KMSI算法在SI technique的基础上应用两项改进措施以弥补缺点: 1)替换Bootstrap采样法为核密度估计采样法, 使其在采样结果无真实数据的条件下完成自定义样本量的采样, 且复现真实数据集的分布. 2)替换原版算法中的皮尔逊相关系数矩阵为混合类型相关系数矩阵, 减小算法在应对混合类型数据集时的度量误差, 提高算法鲁棒性.

1 方法 1.1 核密度估计采样法

核密度估计(kernel density estimation)是一种非参数概率密度估计方法, 通常用于在给定数据的情况下估计未知概率密度函数^[23]. 假设$X = \{ {x_1}, \cdots , {x_n}\}$ 是一组独立同分布的特征值, 取自某未知的概率密度曲线 $f$, 拟合该组数据的概率密度函数为:

$ f'(x) = \frac{1}{{nh}}\sum\limits_{i = 1}^n {K\left(\frac{{x - {x_i}}}{h}\right)} $

(1)

其中, K代表核函数, h代表窗宽. 拟合不同类型数据的核密度函数需要选取不同的核函数. 窗宽h对拟合结果亦影响较大, 窗宽决定了拟合函数曲线的形态. Botev等人^[24]提出的确定最优窗宽的方法ISJ (improved Sheather-Jones)在复杂分布的情况下被认为比Scott经验法则^[25]拥有更高精度和健壮性, 在实践中取得了较好的效果. 在获得了每一列对应的拟合概率密度函数后使用反函数变换法来获得采样值. 相较Bootstrap, 核密度估计采样法的采样值不直接来自原始数据, 降低了隐私泄露的可能; 其次, 它无需重复采样, 能够产生更多样的数值; 最后, 使用概率密度函数可以采样任意数量的合成数据, 这使得使用者能够自定义合成数据集大小.

1.2 混合类型相关系数矩阵

相关系数矩阵是SI technique算法过程中衡量特征变量之间相关性极为重要的工具. KMSI中使用的混合类型相关系数矩阵是由斯皮尔曼秩相关系数、克莱姆相关系数和CMCD (correlation measure between continuous and discrete features)相关性度量法共同构成的. 斯皮尔曼秩相关系数适用于度量连续型和连续型数据之间的相关性, 并且对于序数型数据亦有良好表现; 其计算公式如下:

$ {\rho _{{\rm{Spearman}}}} = 1 - \frac{{6 \cdot \displaystyle\sum {d_i^2} }}{{n({n^2} - 1)}} $

(2)

其中, ${d_i}$表示第i个位次对的差值, n表示样本数. 克莱姆相关系数适合用来度量离散型变量之间的相关性, 其计算公式如下:

$ {\phi _{{\rm{Cramer}}}} = \sqrt {\frac{{{\chi ^2}}}{{n(k - 1)}}} $

(3)

其中, ${\chi ^2}$表示样本的卡方检测量, n代表样本量, k代表任意变量的较少类别数. CMCD相关性度量法是由Jiang等人^[26]基于类分离^[16]理论提出的, 该理论相较离散化方法能够减少信息丢失并提高效率. 混合类型相关系数矩阵的完整计算方式如算法2所示; 由于相关系数适用的数据类型不尽相同, 因此需要输入数据集中每列特征的具体类型Type.

算法1. CMCD相关性度量法

输入: 连续特征$\scriptstyle {X}=\left(x_{1}, x_{2} , \cdots , x_{n}\right)$, 离散特征$\scriptstyle {Y}=\left(y_{1}, y_{2}, \cdots , y_{n}\right)$

输出: 相似度$\scriptstyle \operatorname{Sim}(X, Y) $

1) 组合两列特征$\scriptstyle (X, Y) = \{ ({x_1}, {y_1}), ({x_2}, {y_2}), \cdots , ({x_n}, {y_n})\}$

2) 根据Y中元素不同取值, 把$\scriptstyle (X, Y)$划分为r组

3) 计算每组连续变量的均值$\scriptstyle {U_1}, {U_2} , \cdots , {U_i} , \cdots , {U_r}$, $\scriptstyle {U_i} = \frac{1}{{{n_i}}}\sum\limits_{j = 1}^{{n_i}} {{x_{ij}}} $

4) 计算全部连续变量的均值$\scriptstyle {M_0} = \frac{1}{n}\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^{{n_i}} {{x_{ij}}} } $

5) 计算各组中连续数据与对应$\scriptstyle {U_i}$差值平方和$\scriptstyle {S_{{\rm{ithintra}}}} = \sum\limits_{j = 1}^{{n_i}} {{{({x_{ij}} - {U_i})}^2}}$

6) 计算$\scriptstyle {U_i}$与$\scriptstyle {M_0}$差值的平方和$\scriptstyle {S_{{\rm{inter}}}} = \sum\limits_{i = 1}^r {{n_i}{{({U_i} - {M_0})}^2}}$

7) 计算$\scriptstyle {S_{{\rm{inter}}}}$与各个$\scriptstyle {S_{{\rm{ithintra}}}}$ 的总和$\scriptstyle {S_T}$

8) 计算结果$\scriptstyle {\textit{Sim}}(X, Y) = \left\{ \begin{gathered}\scriptstyle \frac{{{S_{{\rm{inter}}}}}}{{{S_T}}}, {\; \rm{if}}\;{S_T} \ne 0 \\\scriptstyle 0{},\quad \;\;\;{}{\; \rm{if}}\;{S_{{\rm{intra}}}} = {S_{{\rm{inter}}}} = {S_T} = 0 \\ \end{gathered} \right.$

算法2. 混合类型相关系数矩阵计算法

输入: 数据集$\scriptstyle D = \{ {X_1}, {X_2} , \cdots , {X_n}\}$, 数据类型$\scriptstyle Type = [{t_1}, {t_2} , \cdots , {t_n}]$

输出: 混合类型相关系数矩阵M

1) i=0, M=array[n][n]

2) WHILE (i<n) DO

3) 　WHILE (j=i, j<n) DO

4)　　 IF (Type[i]==Type[j]) DO

5) 　　　IF (Type[i]==“continue”) DO

6) 　　　　$\scriptstyle M[i][j]=M[j][i]=\operatorname{Spearman}\left(X_{i}, X_{j}\right) $

7) 　　　END IF

8)　　　 IF (Type[i]==“discrete”) DO

9)　　　　 $\scriptstyle M[i][j]=M[j][i]=\operatorname{Cramer}(X_{i}, X_{j}) $

10)　　 END IF

11) 　ELSE

12) 　　 $\scriptstyle M[i][j]=M[j][i]=\operatorname{CMCD}(X_{i}, X_{j})$

13)　 END IF

14) END WHILE

15) END WHILE

16) RETURN M

1.3 KMSI

SI technique的核心理念是通过迭代的方式试错最优中间相关系数矩阵, 从而不断提高当前合成数据集和目标相关系数矩阵之间的相似程度, 直到两者之间的差距没有明显缩小为止, 最终使得合成数据集拥有与真实数据集高度一致的相关性表达. 在应用了核密度估计采样法与混合类型相关系数矩阵后, KMSI具体计算方法如算法3所示.

算法3. KMSI

输入: 核密度估计概率密度函数组$\scriptstyle P\left(f_{1}, f_{2} , \cdots , f_{k}\right)$, 因子数量$\scriptstyle {N}\_ {{\textit{factors}}}$, 最大循环次数$\scriptstyle { max\_trials } $, 初始乘数init_multi, 特征列数据类型data_type, 合成数据集样本量$\scriptstyle {N}\_{ {desire }} $, 目标相关系数矩阵$\scriptstyle {M}_{ {target }} $

输出: 合成数据集$\scriptstyle F^{\prime}\left(X'_1, X'_2 , \cdots , X'_m, C' \right)_{N \times k}$

1) $\scriptstyle M_{\text {distribution }}=\mathrm{KDE} \_\operatorname{sampling}(P) $ //核密度估计采样

2) $\scriptstyle {M_{{\rm{intermediate}}}} = {M_{{\rm{target}}}}$

3) IF ($\scriptstyle {N}\_ {{\textit{factors}}}$==Null||$\scriptstyle {N}\_ {{\textit{factors}}}$==0) DO

4)　 $\scriptstyle N\_{\textit{factors}} = {{\text{Parallel}}} \_{\text{analysis}}({M_{{\rm{intermediate}}}}, {M_{{\rm{distribution}}}}, data\_type)$

5) END IF

6) $\scriptstyle {M_{{\rm{shared}}\_{\rm{comp}}}}, {M_{{\rm{unique}}\_{\rm{comp}}}} = {\rm{Normal}}\_{\rm{sampling}}(\mu = 0, {\sigma ^2} = 1)$

7) $\scriptstyle \text {trials\_without\_improvement }=0$

8) WHILE ($\scriptstyle { {\rm{trials}}\_{\rm{without}}\_{\rm{improvement}} }\lt { {\rm{max}}\_{\rm{trials}} }$) DO

9)　 $\scriptstyle M_{\text {shared\_load }}= { {\rm{Factor}}\_{\rm{analysis}} }\left(M_{\text {intermediate}}, N\_ {{\textit{factors}} }\right)$

10)　 $\scriptstyle M_{\text{unique\_load }}= {{\rm{Unique}}\_{\rm{load}}\_{\rm{calculation}}}\left(M_{\text{shared\_load}}\right)$

11) 　$\scriptstyle M_{ {{\rm{combin}} }}={{\rm{Combin}}}(M_{\text {shared\_comp}}, M_{\text {shared\_load}}, M_{\text {unique\_comp}},$$\scriptstyle M_{\text {unique\_load }}) $

12)　 $\scriptstyle F_{\text {middel\_result }}^{\prime}= { {\rm{Data}}\_{\rm{replace}} }\left(M_{\text {combin}}, M_{\text {distribution}}\right)$

13) 　$\scriptstyle rmsr = {\text{RMSR}} \_{\rm{calculation}}({M_{{\rm{target}}}}, F{'_{{\rm{middle}}\_{\rm{result}}}}, data\_type)$

14) 　IF (rmsr is the lowest) DO

15) 　　$\scriptstyle M_{\text {best\_corr }}=M_{\text {intermediate }}$

16)　　 $\scriptstyle {\rm{trials}}\_{\rm{without}}\_{\rm{improvement}} = 0$

17) 　ELSE DO

18) 　　Update $\scriptstyle M_{\text {intermediate }}$ by using $\scriptstyle { {\rm{init}}\_{\rm{multi}} }$

19)　　 $\scriptstyle { {\rm{trials}}\_{\rm{without}}\_{\rm{improvement}} }++$

20) 　END IF

21) END WHILE

22) 使用$\scriptstyle M_{\text {intermediate }}$和$\scriptstyle N_{-} \text {factors }$按照步骤9)–步骤12)得到最终结果$\scriptstyle F'$

23) return F'

KMSI首先使用核密度估计采样法和混合类型相关系数矩阵以提取数据的分布与相关性信息, 保存在Distribution矩阵和target矩阵中, 分别对应步骤1)和步骤2). 在步骤4)、步骤9)、步骤15)、步骤21)对应的平行分析、因子分析、循环控制、数据生成步骤中也需要使用了混合类型相关系数矩阵. 此外, 在步骤13)中使用了均方根残差(root mean square residual, RMSR)来监控中间相关系数矩阵与真实相关系数矩阵之间差距, 以实现循环控制. RMSR的计算方法如式(4)、式(5)所示.

$ {r_{{\rm{residual}}}} = {({C_{{\rm{real}}}} - {C_{{\rm{magnify}}}}{\text{ }}{\rm{or}}{\text{ }}{C_{{\rm{redual}}}})_{{\rm{UnderTriangularElements}}}} $

(4)

$ {\textit{RMSR}} = \sqrt {\frac{{\displaystyle\sum {r_{{\rm{residual}}}^2} }}{{k(k - 1)/2}}} $

(5)

2 实验与评价

本节实验首先在若干UCI数据集上检验改进方式的有效性, 再使用两种机器学习算法在不同的训练集和测试集上构建模型, 以模型性能指标为基准完成对合成数据集质量和KMSI鲁棒性的评测.

2.1 改进点测试 2.1.1 核密度估计采样

本节实验旨在测试核密度估计采样法生成的Distribution矩阵对真实数据集分布的复现程度. 表1展示了这些数据集的相关信息, 其中C/D features表示各个数据集中连续与离散型特征列的数量, sampling proportion表示本节实验中对各个数据集的采样比例.

表 1 数据集信息

分别对4个数据集的各个特征列使用核密度估计法拟合其概率密度函数, 并使用拟合得来的概率密度函数进行随机采样以得到不同采样比例的Distribution矩阵. 对于连续型特征, 采用高斯核函数赋予权重、ISJ algorithm计算窗宽; 对于离散型特征, 采用Delta核函数赋予权重、Silverman经验法则计算窗宽. 图1–图4展示了一部分特征列与真实特征列的对比结果, 纵坐标P表示概率密度. 图1对应Adult数据集连续型特征“age”和离散型特征“marital-status”的分布情况, 图2对应Bank数据集连续型特征“duration”和离散型特征“job”的分布情况, 图3和图4则分别对应Credit和Heart两个数据集中不同类型特征列的分布情况. 真实特征列在其定义域范围内表现出多峰、长尾、偏移等现象, 这既表明真实情况下的数据分布较难满足正态分布的假设, 也证明了原版算法使用预定义的概率密度函数采样的做法存在不合理性. 相比较于核密度估计采样法得到的结果, 黄色直方图代表的采样数据与蓝色直方图代表的真实数据在分布上是基本一致的, 这证明核密度估计法具备还原真实数据集分布的能力.

图 1 Adult特征分布对比

此外, 对于Petricioli等人^[18]提出的使用分位数矩阵插值法生成 Distribution矩阵同样进行了测试, 在上述数据集上计算了合成数据特征列与真实数据特征列之间的KS-test值, 以考察分位点数量q与Distribution矩阵复现分布效果之间的关系. 设定各个合成数据集的样本量与对应真实数据集相等以统一采样比例并消除样本数量带来的影响; 为优化展示效果, 仅对部分结果绘制成图, 如图5–图7所示. 随着分位点数量q的增加, 两种不同类型特征列的KS-test值均逐渐下降到较低水平并不断震荡, 伴随着p值逐渐上升到0.05以上, 这代表了两个分布的相似程度在不断增加并趋于稳定, 总体Distribution矩阵的分布情况越来越接近真实数据集.

图 2 Bank特征分布对比

图 3 Credit特征分布对比

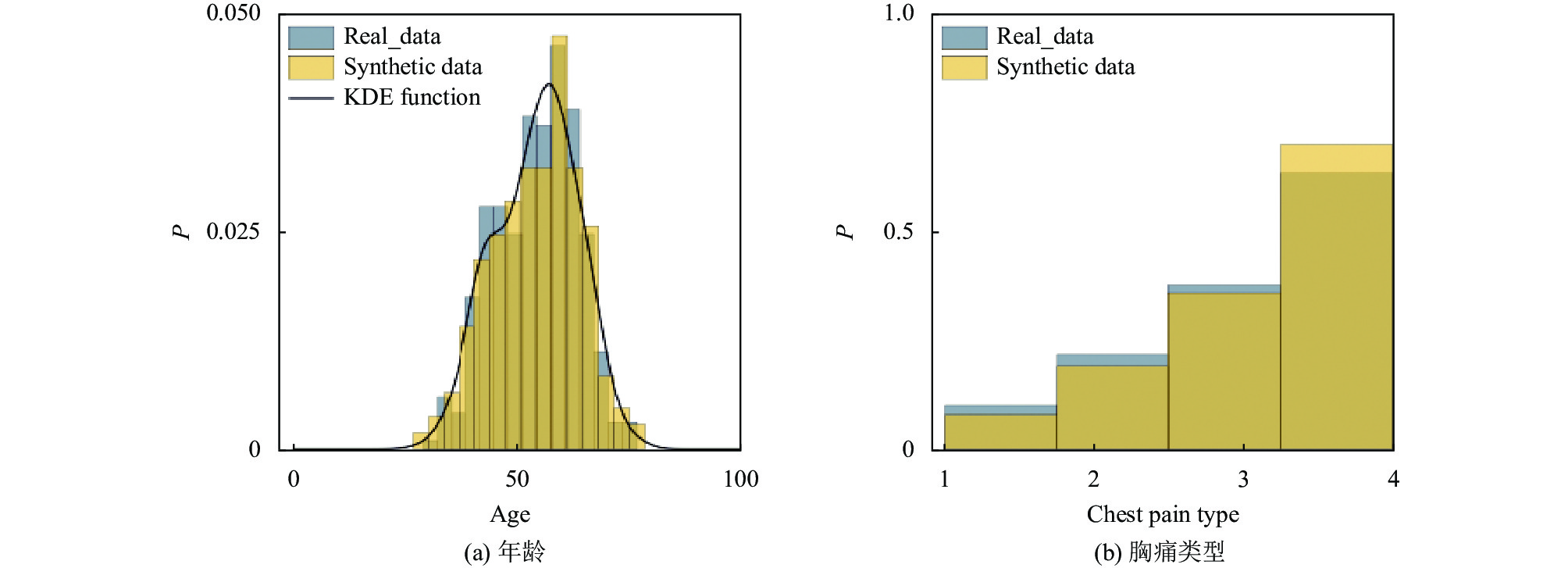
图 4 Heart特征分布对比

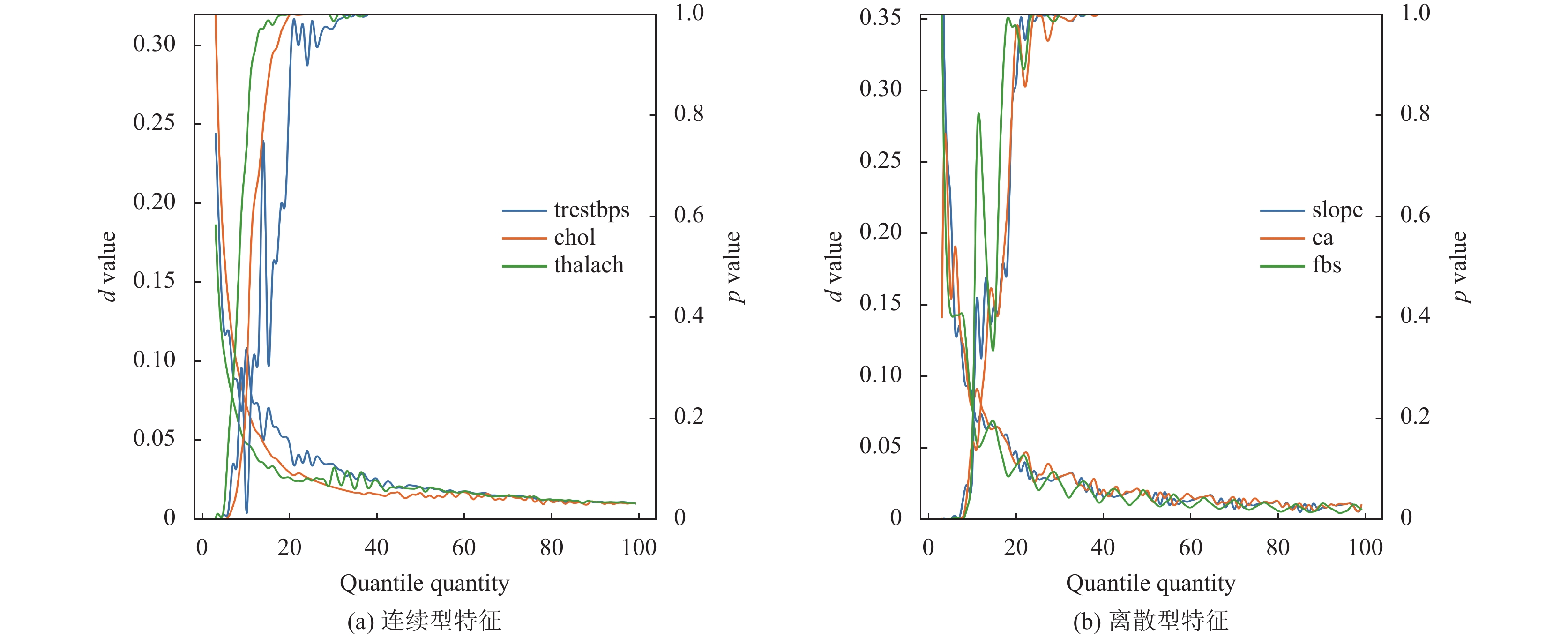
图 5 Heart K-S检验

图 6 Credit K-S检验

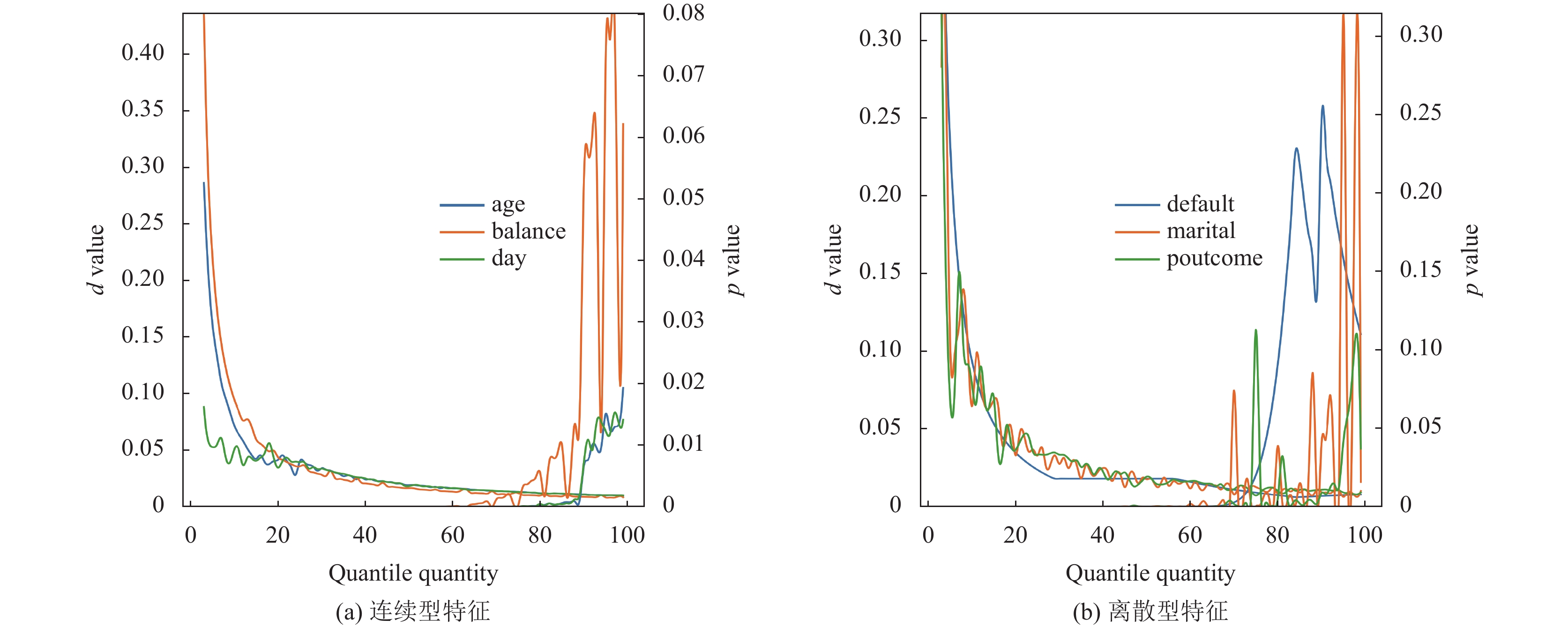
图 7 Bank K-S检验

虽然该方法在获取扩大的 Distribution矩阵上的确有良好表现, 但当希望得到一个缩小的Distribution矩阵时, 分位点数量q必须谨慎选择. 设定以Adult数据集为基础的合成数据量为原数据集的0.1% (32例样本), 测试q取值范围为[2, 500]时 KS-test 的变化; 如图8所示, 当q值超过所需样本量时, KS-test值出现了明显的宽幅波动, 在个别取值点甚至出现了高于起始值的现象, 这代表着该方法生成的合成数据无法稳定还原真实数据的分布. 此外, 当q值超过所需样本量时, 论文中用于扩大样本量的插值模块将被跳过, 使得 Distribution矩阵里将只包含来自真实数据集的样本, 隐私安全问题也就成为该算法的致命缺点.

图 8 Adult K-S检验

2.1.2 混合类型相关系数矩阵

为了检验KMSI在生成不同大小Distribution矩阵时的鲁棒性, 模拟实验设置如下: 首先按照算法2计算数据集的混合类型相关系数矩阵${C_{{\rm{real}}}}$, 再使用核密度估计采样法得到不同比例放大和缩小的Distribution矩阵${D_{{\rm{magnify}}}}$和${D_{{\rm{reduce}}}}$, 然后分别计算二者的混合类型相关矩阵${C_{{\rm{magnify}}}}$、${C_{{\rm{reduce}}}}$, 最后使用可视化工具讨论${C_{{\rm{real}}}}$和${C_{{\rm{magnify}}}}$、${C_{{\rm{reduce}}}}$之间均方根残差的稳定性.

考虑到4个数据集的样本量不尽相同, 故 Adult和Bank数据集重点测试${C_{{\rm{reduce}}}}$的变化; Credit和Heart数据集重点测试${C_{{\rm{magnify}}}}$的变化. 表2列出了该模拟实验中各个数据集的测试点.

表 2 模拟实验设置

图9、图10展示了这4个数据集在各个测试点的RMSR变化, 可以看出, 在扩大和缩小情况下真实数据集和Distribution矩阵的混合类型相关系数矩阵之间的差距并没有发生较大变动, 总体上维持在±0.1范围内; 这说明混合类型相关系数矩阵在数据充足和稀缺的条件下具有健壮性, 与核密度估计采样法结合后无不良表现.

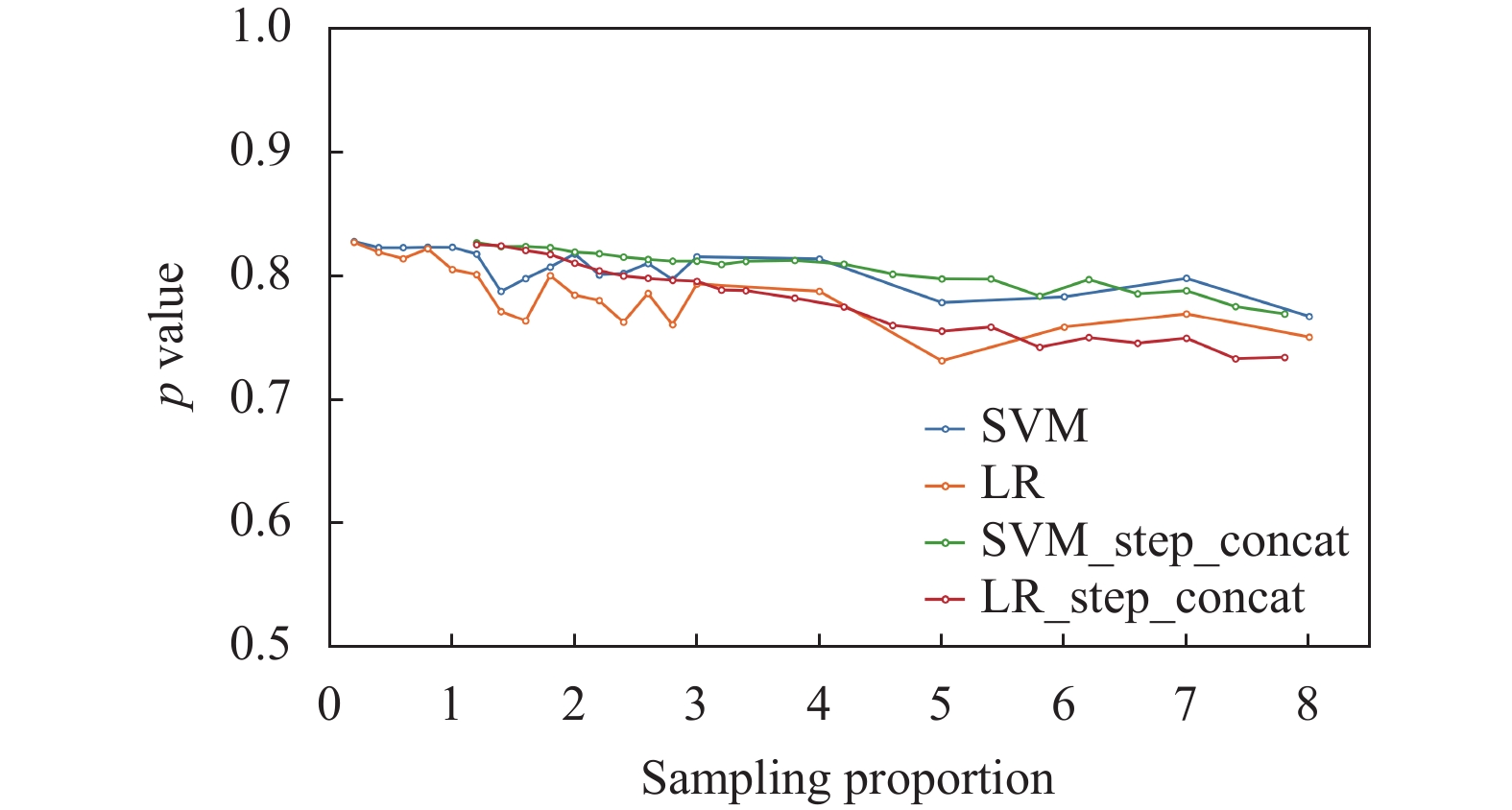
图 9 “步进式合并”模型表现

图 10 Credit与Heart数据集的RMSR波动

2.2 总体测试

本节实验通过检验合成数据的质量来展示KMSI算法的总体表现.

2.2.1 相关信息

该部分实验使用Adult数据集, 为了检验改进算法在数据不平衡情况下的性能, 本节实验在数据预处理阶段采用了文献[27]中构建的数据划分工具FedLab对真实数据集划分出4种不同类型的子数据集; 通过使用合成数据集构建的分类模型性能来讨论算法效果. 对于在生成合成数据阶段的数据集不对离散型特征进行特殊编码, 仅用自然数表示不同类别; 在模型验证阶段则需要对离散特征进行特殊编码以获得较高的模型性能. 实验代码使用Golang和Python共同编写完成.

2.2.2 实验评估

在完成数据预处理等步骤后, KMSI以一个从真实数据集中计算得来的目标相关系数矩阵${C_{{\rm{target}}}}$和使用核密度估计采样法得来的初始Distribution矩阵为算法输入. KMSI的超参数iter_without_improvement限定了算法在得到新的最小值的最大步数, ${\rm{init}}\_{\rm{multi}}$则起到学习率的作用. 在实际实验中发现iter_without_improvement取5左右, ${\rm{init}}\_{\rm{multi}}$取2左右比较合适.

实验使用真实数据集训练逻辑回归和支持向量机分类模型, 以分类模型的准确度作为评价数据质量的标准. 使用机器学习指标判断更加客观具体, 且借助高准确度的机器学习模型有利于判别合成数据集的总体质量. 表3–表7展示了机器学习分类器在各个合成数据集上的表现, 为探究用户自定义样本量对算法的影响, 表4中的合成数据子集样本数量等同于对应的真实数据子集, 其他表格对应的合成数据子集样本数量均为500. 使用真实数据集训练的支持向量机模型与逻辑回归模型的准确度分别是0.837、0.828; 从实验数据可以看出, 两种分类模型在真实数据集上的准确度整体上明显高于在合成数据集上的准确度, 这说明合成数据集中的确存在不符合真实特征关系的样本. 但通过对比不同子集划分方式(表3, 表5–表7)和不同样本数量(表3, 表4)的结果, 可以看出分类模型在合成数据集上的准确度并没有出现明显变化, 始终保持在0.7左右. 这种现象说明KMSI在生成任意大小的合成数据集时能够保持性能稳定, 具备了在满足数据隐私的前提下应对特征列复杂分布和数据不平衡问题的鲁棒性, 能够给予使用者在样本量上更大的自定义空间.

表 3 基于Dirichlet分布的标签偏移子集在模型上的表现

表 4 基于Dirichlet分布的数量偏移子集在模型上的表现

表 5 基于Dirichlet分布的数量偏移子集在模型上的表现

表 6 独立同分布子集在两种模型上的表现

表 7 基于样本量的标签偏移子集在两种模型上的表现

为了探究这部分不符合真实特征关系的样本对模型的具体影响, 实验把合成数据子集和对应的真实数据子集合并, 分别用合并前后的数据集训练分类模型, 在完整数据集上测试准确度, 结果如表8所示; 为了更直观地展示KMSI在产生更宽样本量范围的合成数据集上的能力, 以第13号真实数据子集为例生成不同比例的合成数据子集, 使用上述方式测试了分类模型的准确度, 结果如图11所示. 从表格和折线图中观察到在生成缩小和扩大的合成数据集时, 模型的准确度分别维持在80%和75%左右. 结合前一部分的实验结果可以推断出, 若进一步扩大合成数据在合并后数据集中的比例, 模型准确度将维持在70%左右, 接近表3–表7所示的结果. 鉴于KMSI在生成缩小的合成数据集上拥有较好表现, 本实验也尝试用“步进式合并(step-merging)”的方法, 即用数个合成样本比例为20%的合成数据集与真实数据集合并来产生不同大小的扩大数据集; 结果展示在图12中. 同样以第13号真实数据子集为材料, “步进式”方法在整体稳定性上有了明显优化, 尤其是在合成样本比例为[1.1, 3.0]范围内表现出优于直接合成方法的稳定性. 因此, 在应对生成扩大合成数据集任务时, 使用步进式合并的方式是更具鲁棒性的方式.

表 8 使用合并前后数据子集训练的两种模型在真实数据集上的表现

No.	Dir label skew quantity=500				Dir label skew equal quantity				Dir quantity skew quantity=500				IID quantity=500				Quantity skew quantity=500
	Before		After		Before		After		Before		After		Before		After		Before		After
	SVM	LR	SVM	LR	SVM	LR	SVM	LR	SVM	LR	SVM	LR	SVM	LR	SVM	LR	SVM	LR	SVM	LR
0	0.825	0.825	0.822	0.816	0.824	0.826	0.801	0.789	0.820	0.783	0.761	0.728	0.825	0.826	0.826	0.824	0.827	0.826	0.826	0.824
1	0.812	0.823	0.811	0.810	0.813	0.825	0.811	0.808	0.831	0.828	0.831	0.828	0.832	0.827	0.830	0.820	0.827	0.826	0.824	0.817
2	0.823	0.826	0.820	0.822	0.824	0.825	0.808	0.799	0.829	0.827	0.828	0.826	0.827	0.827	0.825	0.825	0.834	0.828	0.831	0.825
3	0.825	0.825	0.817	0.807	0.823	0.823	0.818	0.804	0.817	0.809	0.733	0.720	0.821	0.826	0.817	0.816	0.826	0.825	0.824	0.812
4	0.804	0.807	0.804	0.770	0.804	0.808	0.810	0.760	0.813	0.827	0.788	0.770	0.837	0.829	0.831	0.819	0.832	0.828	0.831	0.826
5	0.822	0.817	0.806	0.788	0.822	0.819	0.818	0.810	0.833	0.828	0.832	0.828	0.831	0.828	0.827	0.822	0.819	0.826	0.812	0.818
6	0.810	0.821	0.759	0.752	0.806	0.820	0.770	0.754	0.821	0.824	0.818	0.813	0.827	0.825	0.827	0.823	0.832	0.827	0.830	0.821
7	0.831	0.826	0.831	0.827	0.827	0.827	0.821	0.804	0.816	0.826	0.796	0.798	0.828	0.827	0.827	0.828	0.829	0.827	0.825	0.817
8	0.833	0.827	0.833	0.821	0.833	0.828	0.827	0.805	0.824	0.828	0.812	0.803	0.830	0.825	0.830	0.820	0.829	0.825	0.828	0.820
9	0.826	0.826	0.825	0.818	0.828	0.828	0.826	0.806	0.831	0.828	0.829	0.825	0.830	0.828	0.828	0.827	0.826	0.825	0.819	0.816
10	0.833	0.830	0.825	0.826	0.833	0.828	0.824	0.805	0.824	0.827	0.823	0.818	0.825	0.827	0.825	0.823	0.829	0.828	0.828	0.826
11	0.826	0.825	0.826	0.821	0.828	0.827	0.825	0.812	0.826	0.824	0.827	0.822	0.830	0.828	0.826	0.824	0.826	0.828	0.821	0.821
12	0.825	0.824	0.819	0.815	0.823	0.824	0.819	0.809	0.832	0.827	0.831	0.825	0.830	0.828	0.829	0.823	0.832	0.828	0.830	0.825
13	0.822	0.828	0.820	0.807	0.823	0.828	0.817	0.794	0.827	0.826	0.823	0.819	0.832	0.826	0.828	0.827	0.829	0.824	0.820	0.809
14	0.829	0.827	0.827	0.822	0.827	0.826	0.822	0.807	0.828	0.825	0.827	0.820	0.828	0.830	0.824	0.823	0.832	0.828	0.829	0.824
15	0.830	0.828	0.829	0.826	0.826	0.828	0.818	0.801	0.817	0.826	0.818	0.796	0.823	0.827	0.822	0.816	0.824	0.827	0.816	0.807
16	0.827	0.829	0.823	0.822	0.828	0.829	0.818	0.800	0.829	0.828	0.822	0.814	0.831	0.824	0.832	0.820	0.828	0.827	0.825	0.824
17	0.795	0.822	0.769	0.766	0.795	0.822	0.781	0.745	0.823	0.824	0.819	0.798	0.829	0.827	0.827	0.822	0.826	0.826	0.824	0.814
18	0.831	0.828	0.832	0.828	0.833	0.828	0.824	0.808	0.831	0.828	0.829	0.826	0.829	0.826	0.824	0.819	0.827	0.827	0.826	0.823
19	0.830	0.825	0.825	0.818	0.832	0.825	0.818	0.800	0.810	0.813	0.806	0.786	0.829	0.828	0.827	0.818	0.826	0.824	0.819	0.805

表 8 使用合并前后数据子集训练的两种模型在真实数据集上的表现

3 总结与展望

SI technique是一种基于概率统计学构建的合成数据生成算法, 它以迭代的方式不断缩小采样数据与真实数据相关系数矩阵之间的距离, 进而找到合适的中间相关矩阵以合成数据. KMSI对原版采样方法和相关性度量方法做出调整, 使其能够应对复杂分布特征列和混合数据类型数据集; 其合成结果不包含真实数据, 并降低了原版算法对合成样本量的限制. 通过对机器学习模型准确度的观察, KMSI在获得较真实数据集更小的合成数据集上有良好表现, 实验数据也佐证了使用“步进式”方法是获得扩大的合成数据集的较优选择.

图 11 合并后模型表现

图 12 Adult与Bank数据集的RMSR波动

生成合成数据的意义不仅在于其本身, 也在于它暗示了另一条改进数据集不平衡问题的道路, 即有针对性地对一个数据集中的少数类数据使用合成数据生成方法, 通过产生少数类合成数据扩充数据集来达到平衡类别的目的. 后续工作将按照该思路把KMSI与联邦学习相结合, 以探索新的应用场景.

参考文献

[1]	Lu YZ, Shen MJ, Wang HZ, et al. Machine learning for synthetic data generation: A review. arXiv:2302.04062, 2023.
[2]	Babbar R, Schölkopf B. Data scarcity, robustness and extreme multi-label classification. Machine Learning, 2019, 108(8–9): 1329-1351. DOI:10.1007/s10994-019-05791-5
[3]	Pipino LL, Lee YW, Wang RY. Data quality assessment. Communications of the ACM, 2002, 45(4): 211-218. DOI:10.1145/505248.506010
[4]	Olvera OL. Issues, problems and potential solutions when simulating continuous, non-normal data in the social sciences. https://conferences.lnu.se/index.php/metapsychology/article/view/2117. (2020-07-31).
[5]	Fleishman AI. A method for simulating non-normal distributions. Psychometrika, 1978, 43(4): 521-532. DOI:10.1007/BF02293811
[6]	Vale CD, Maurelli VA. Simulating multivariate nonnormal distributions. Psychometrika, 1983, 48(3): 465-471. DOI:10.1007/BF02293687
[7]	Headrick TC. Fast fifth-order polynomial transforms for generating univariate and multivariate nonnormal distributions. Computational Statistics & Data Analysis, 2002, 40(4): 685-711.
[8]	Nagahara Y. A method of simulating multivariate nonnormal distributions by the Pearson distribution system and estimation. Computational Statistics & Data Analysis, 2004, 47(1): 1-29.
[9]	Foldnes N, Olsson UH. A simple simulation technique for nonnormal data with prespecified skewness, kurtosis, and covariance matrix. Multivariate Behavioral Research, 2016, 51(2-3): 207-219. DOI:10.1080/00273171.2015.1133274
[10]	Fialkowski A, Tiwari H. SimCorrMix: Simulation of correlated data with multiple variable types including continuous and count mixture distributions. The R Journal, 2019, 11(1): 250-286. DOI:10.32614/RJ-2019-022
[11]	Ferrari PA, Barbiero A. Simulating ordinal data. Multivariate Behavioral Research, 2012, 47(4): 566-589. DOI:10.1080/00273171.2012.692630
[12]	Demirtas H, Gao R. Mixed data generation packages and related computational tools in R. Communications in Statistics—Simulation and Computation, 2022, 51(8): 4520-4563. DOI:10.1080/03610918.2020.1745841
[13]	Foldnes N, Grønneberg S. Non-normal data simulation using piecewise linear transforms. Structural Equation Modeling: A Multidisciplinary Journal, 2022, 29(1): 36-46. DOI:10.1080/10705511.2021.1949323
[14]	Ruscio J, Ruscio AM, Meron M. Applying the bootstrap to taxometric analysis: Generating empirical sampling distributions to help interpret results. Multivariate Behavioral Research, 2007, 42(2): 349-386. DOI:10.1080/00273170701360795
[15]	Ruscio J, Kaczetow W. Simulating multivariate nonnormal data using an iterative algorithm. Multivariate Behavioral Research, 2008, 43(3): 355-381. DOI:10.1080/00273170802285693
[16]	Amatya A, Demirtas H. Concurrent generation of multivariate mixed data with variables of dissimilar types. Journal of Statistical Computation and Simulation, 2016, 86(18): 3595-3607. DOI:10.1080/00949655.2016.1177530
[17]	Humski L, Pintar D, Vranić M. Analysis of Facebook interaction as basis for synthetic expanded social graph generation. IEEE Access, 2019, 7: 6622-6636. DOI:10.1109/ACCESS.2018.2886468
[18]	Petricioli L, Humski L, Vranić M, et al. Data set synthesis based on known correlations and distributions for expanded social graph generation. IEEE Access, 2020, 8: 33013-33022. DOI:10.1109/ACCESS.2020.2970862
[19]	Foster R. Simulating factor structures from continuous and discrete distributions using mixture of means within a hierarchical model. https://osf.io/b43yq. (2022-11-28).
[20]	Bartholomew D, Knott M, Moustaki I. Latent variable models and factor analysis: A unified approach. 3rd ed., Chichester: John Wiley & Sons, Ltd., 2011.
[21]	Kairouz P, McMahan HB, Avent B, et al. Advances and open problems in federated learning. Foundations and Trends® in Machine Learning, 2021, 14(1–2): 1-210.
[22]	Solorio-Fernández S, Carrasco-Ochoa JA, Martínez-Trinidad JF. A survey on feature selection methods for mixed data. Artificial Intelligence Review, 2022, 55(4): 2821-2846. DOI:10.1007/s10462-021-10072-6
[23]	Kamalov F, Elnagar A. Kernel density estimation-based sampling for neural network classification. Proceedings of the 2021 International Symposium on Networks, Computers and Communications (ISNCC). Dubai: IEEE, 2021. 1–4.
[24]	Botev ZI, Grotowski JF, Kroese DP. Kernel density estimation via diffusion. The Annals of Statistics, 2010, 38(5): 2916-2957.
[25]	Scott DW. Multivariate density estimation: Theory, practice, and visualization. 2nd ed., Hoboken: John Wiley & Sons, Ltd., 2015.
[26]	Jiang SY, Wang LX. Efficient feature selection based on correlation measure between continuous and discrete features. Information Processing Letters, 2016, 116(2): 203-215. DOI:10.1016/j.ipl.2015.07.005
[27]	Li QB, Diao YQ, Chen Q, et al. Federated learning on non-IID data silos: An experimental study. Proceedings of the 38th IEEE International Conference on Data Engineering (ICDE). Kuala Lumpur: IEEE, 2022. 965–978.