知识图谱, 最初由谷歌公司于2012年提出^[1], 旨在使用实体、概念及其关系形成的巨大语义网络描述真实世界. 目前, 已经有许多大型知识图谱被构建, 如由谷歌、维基百科等公司开源的DBpedia^[2], YAGO^[3]等通用知识图谱, 以及特定领域如医疗^[4]、科学^[5]领域知识图谱. 然而, 不同知识图谱之间的质量和覆盖领域存在差异, 为了增强知识图谱完整性和知识覆盖度, 并融合多个异构图谱之间的知识, 实体对齐方法(entity alignment, EA)被提出^[6,7], 用于整合来自不同知识图谱的信息, 以补充和扩展现有的知识图谱.

传统的实体对齐方法基于特征工程, 即通过实体的文字信息(如实体名称、实体描述等)来判断实体是否一致. 然而, 由于重名、别名、跨语种等多种因素, 基于特征的方式缺乏鲁棒性和可扩展性. 基于深度学习的方法一般分为基于翻译的方法和基于图神经网络(graph neural network, GNN)的方法^[8], 它们将不同图谱采用表示学习方法嵌入到低维向量空间^[9], 并通过两个实体向量之间的距离来确定它们是否匹配. 基于这种思想, MTransE、BootEA^[10]、MuGNN^[11]等被提出用于解决实体对齐问题. 随着多模态知识图谱得到广泛应用, 多模态实体对齐任务(multi-modal entity alignment, MMEA)也被进一步提出, 如图1所示.

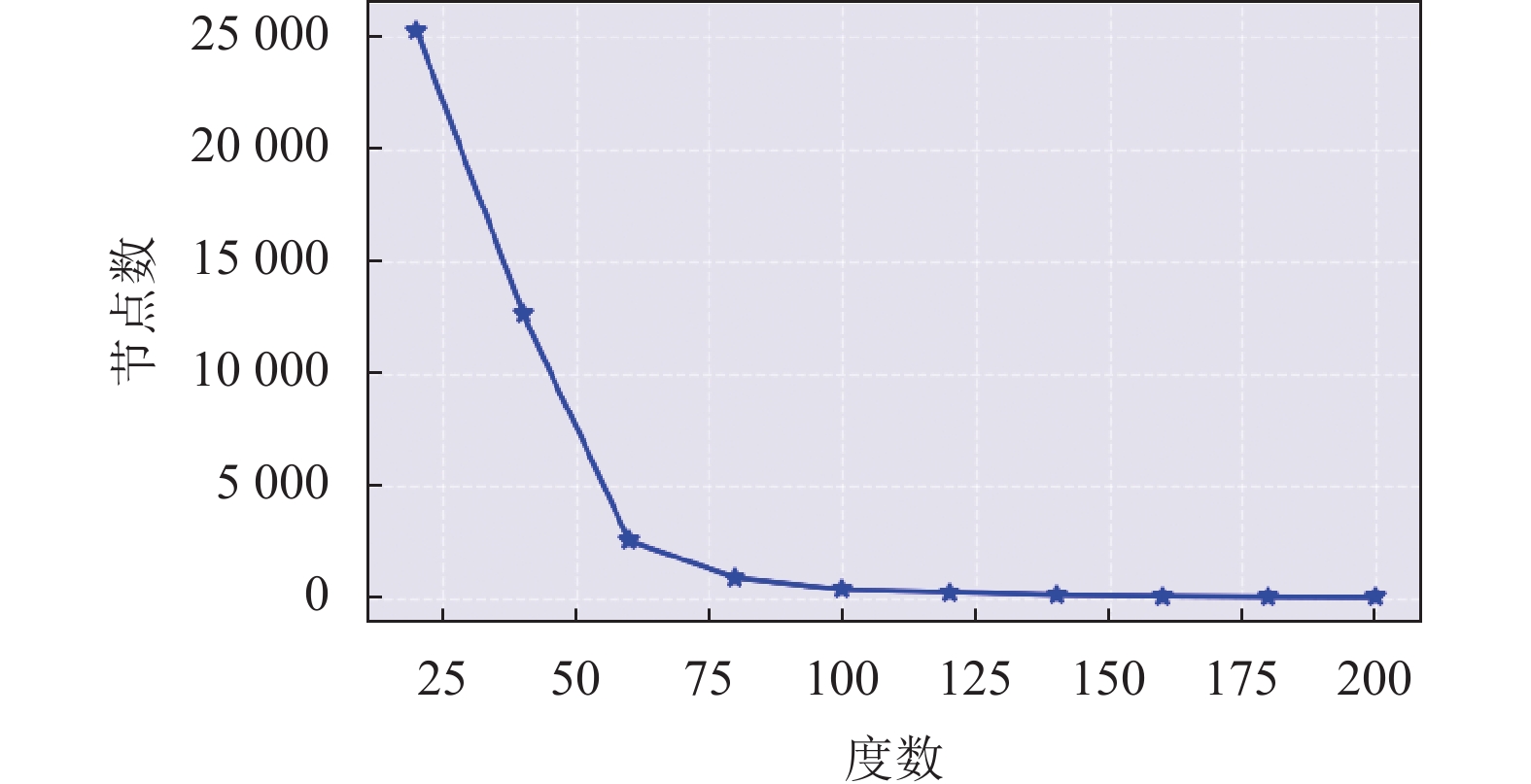
以DBP15k (ZH-EN)为例, 统计数据集内各度数区间的节点数量, 如图2所示, 大部分节点的度数在0–20之间, 只有少数节点包含丰富的边信息. 这些度数较低的中心节点往往特征表达能力较差, 因而属于实体对齐任务中较难被对齐的节点, 其对齐效果显著低于高度数区间^[12].

另一方面, 在引入了图像信息的DBP15k数据集中, 除了约60%–85%的实体外, 仍然存在很多实体缺乏图像表征, 如表1所示. 在多模态实体对齐中, 这部分实体的图像表征往往被直接地以正态分布中采样的随机向量来表示, 由于缺少对邻居实体图像信息的引入而缺乏准确性^[13].

尽管大多数模型已经在一些公开数据集如DBP15k^[14]、DWY100K^[10]、SRPRS^[15]上实现了80%以上的准确率, 但许多方法只是直接地使用了预训练模型编码多模态表征, 使邻域较少或图像模态特征缺失的节点获得的是图结构无关或弱关联的特征.

基于以上分析, 本文提出一种端到端的多模态实体对齐方法(relation-aware multi-subgraph graph neural network, RAMS), 通过图神经网络实现模态信息与图结构信息的融合, 通过多子图实现不同模态间的信息交互, 并通过基于关系注意力的子图采样平衡节点特征表达. 在开源数据集上的实验表明, 本文所提出的方法在效果、运行效率、鲁棒性、长尾节点等多个方面均具有优异表现.

1 实体对齐相关工作 1.1 基于深度学习的实体对齐方法

现有的知识图谱实体对齐方法通常采用先编码后对齐的思想. 首先, 模型学习图谱内实体的表征, 然后通过映射矩阵或实体交换等策略对齐两个图谱的语义空间, 并最终通过余弦相似度、曼哈顿距离、欧几里得距离等来判断实体之间的相似性.

基于深度学习的实体对齐方法可以分为TransE系列方法和GNN系列方法. 基于TransE的图谱编码方法通常将关系视作从头实体到尾实体的平移, 即h+r≈t. MTransE^[6]是TransE的一种变体, 它用于编码不同语言的图谱, 并对齐这两个语义空间. COTSAE^[16]引入了属性对比联合学习模块来编码实体的语义信息. JAPE^[14]引入了负样本学习, 并联合学习属性预测任务和对齐任务.

TransE系列方法只在单个三元组上进行训练, 缺乏对全局信息的利用能力, 而这一点在基于GNN的图谱编码方法中得到了改善. GCN-Align^[17]是第1个将GNN应用于实体对齐任务的方法, 然而由于普通图卷积网络在建模中的缺陷, 该方法无法有效地利用图谱中丰富的关系信息. MuGNN^[11]认为图谱间的结构差异会影响对齐效果, 因此首先通过规则补全来调和异构图谱之间的结构差异, 然后通过多通道GNN对图谱进行编码. NAEA^[18]和MRAEA^[19]根据实体之间的关系类型赋予实体不同的权重系数, 使模型能够定义有用的邻居节点用于消息传递. 此外, 还有一些GNN方法^[11,20,21], 如MuGNN等在变换矩阵的设计中采用了反直觉的约束, 即强迫矩阵为单位或对角, 这样可以保证在线性转换后异构图谱之间的距离分布不会发生改变.

1.2 基于深度学习的多模态实体对齐方法

与常规实体对齐任务相比, 多模态实体对齐涉及额外的步骤, 即多模态特征融合. 在多模态嵌入阶段, 实体具有多种模态的特征, 这样可以产生相对应的实体向量表示. 然后, 使用收敛或加权级联等方法将这些表示进行组合, 生成实体的多模态融合特征. 利用得到的实体表示来计算要对齐的实体之间的相似性得分, 从而预测实体的对齐结果.

PoE (product of experts)^[22]最早被提出, 通过结合多个专家模型的预测来获得实体对齐的置信度. 为了表征实体不同模态的信息, MMEA^[23]正式提出了多模态实体对齐任务, 并采用TransE、VGG16和RBF模型分别表征图结构、图像、属性特征, 通过强制各模态特征与融合特征相似来对齐实体. HMEA^[24]采用GCN和DenseNet, 并在双曲空间完成了MMEA任务. EVA^[13]提出了一种无监督的方法来生成视觉中枢, 并使用加权级联的方法组合实体的多模态特征. MCLEA^[25]使用类似的嵌入器编码实体, 并设计了模态间和模态内的损失来实现模态融合和对齐. 此外, MEAformer^[26]引入了Transformer结构, 以增强模态融合的效果.

上述方法^[13,23–25]通过直接地采用预训练的图像模型, 如VGG16、DenseNet、ResNet等, 较快地实现了实体多模态信息的表征. 然而, 这些方法大多更关注于单一模态的表达, 通过预训练和前馈层获得的模态特征往往直接通过强制嵌入相似或加权级联的方法得到实体的最终表征, 而忽略了多模态特征与图的结构及其邻域间的相关性, 这限制了实体对齐任务的发展.

尽管MSNEA^[27]在向多模态表征中引入图结构信息方面做出了尝试, 即将实体的多模态信息与TransE型的图结构表征方法相结合, 通过令实体在每个模态下的表征满足h+r≈t的约束, 实现模态信息与图结构信息的融合. 但TransE在复杂关系处理方面具有局限性, 这限制了模型的表现.

2 多子图信息融合的多模态实体对齐方法

规定一个多模态知识图谱G={E, R, I, T^R, T^V}, 包括实体集E, 关系集R, 图像集I, 及关系三元组集T^R, 实体图像对T^V. 每个三元组t^R=(e_i, r_ij, e_j)$\in $T^R表示头实体e_i能够通过关系r_ij$\in $R连接至e_j. 每个实体图像对t^V=(e_i, v_i)$\in $T^V表示图像v_i能够作为实体e_i的描述.

给定两个图谱G₁和G₂, 有已知的对齐种子实体S={(e₁, e₂)$\in $E₁×E₂|e₁$ \leftrightarrow $e₂}. 实体对齐的任务就是通过S、G₁和G₂找到未在S中的对齐种子实体.

我们所提出的方法的框架如图3所示. 对输入的图谱, 通过采样生成子图, 并使用多视图聚合编码的方式将各模态信息输入多子图正交图神经网络. 具体而言, 采样后的子图经邻域聚合、关系聚合和图像聚合, 得到各节点的表征. 这些表征经过正交映射图神经网络编码后, 进行多跳拼接形成节点向量表示. 编码后的关系被用于计算关系注意力, 并支持子图采样过程, 最后进行联合学习预测对齐节点.

2.1 多子图增强的节点特征编码方法

多子图增强的特征编码网络如图4所示.

(1)邻域聚合编码

对输入的图谱G={E, R, I, T^R, T^V}, 从三元组(e_i, r_ij, e_j)中保留实体对(e_i, e_j), 则节点的初始邻域特征按式(1)进行计算:

$ {\mathbf{h}}_{{e_i}}^{(0)} = \left[ {\frac{1}{{\left| {N_{{e_i}}^e} \right| + 1}}\sum\limits_{{e_j} \in N_{{e_i}}^e \cup \left\{ {{e_i}} \right\}} {{{\mathbf{h}}_{{e_j}}}} } \right] $

(1)

其中, e_i$\in $E表示当前节点, $ N_{{e_i}}^e $表示节点e_i的所有邻居节点, $ {\mathbf{h}}_{{e_i}}^{(0)} $表示汇聚了邻域信息的节点特征向量. $ {{\mathbf{h}}_{{e_j}}} $为节点e_j参数化的特征, 将在迭代中不断更新.

将$ {\mathbf{h}}_{{e_i}}^{(0)} $拼接得到邻域聚合的初始节点特征矩阵H⁽⁰⁾, 用于输入至关系敏感型正交GNN网络中. 每层GNN网络更新过程如式(2)所示:

$ {{\mathbf{H}}^{(l)}} = {{GNN}}({{\mathbf{H}}^{(l - 1)}}) $

(2)

其中, H^(l–1)代表输入第l层GNN的节点特征矩阵; H^(l)代表第l层GNN输出的节点特征矩阵(同时作为第l+1层GNN的输入).

为了得到全局特征表示, 对多层GNN的输出特征进行拼接, 多跳拼接的邻域聚合节点特征表示为$ {\mathbf{h}}_{{e_i}}^{{\mathrm{entity}}} $, 如式(3)所示:

$ {\mathbf{h}}_{{e_i}}^{{\mathrm{entity}}} = [{\mathbf{h}}_{{e_i}}^{(0)}||{\mathbf{h}}_{{e_i}}^{(1)}|| \cdots ||{\mathbf{h}}_{{e_i}}^{(l)}] $

(3)

其中, $ {\mathbf{h}}_{{e_i}}^{(l)} $代表邻域子图下, 第l层GNN输出的e_i特征, $ {\mathbf{h}}_{{e_i}}^{(0)} $为初始的邻域表征.

(2)关系聚合编码

与邻域聚合编码相类似, 从三元组(e_i, r_ij, e_j)中保留实体-关系对(e_i, r_ij)和(e_j, r_ij), 模仿空间域图神经网络传递方式, 将边信息也以聚合方式传递给关联节点, 如式(4)所示:

$ {\mathbf{h}}_{{e_i}}^{(0)} = \left[ {\frac{1}{{\left| {N_{{e_i}}^r} \right|}}\sum\limits_{{r_j} \in N_{{e_i}}^r} {{{\mathbf{h}}_{{r_j}}}} } \right] $

(4)

其中, e_i$\in $E表示当前节点, $ {r_j} \in N_{{e_i}}^r $表示节点e_i的相邻边, $ h_{{e_i}}^{(0)} $表示汇聚了邻边信息的节点特征向量. 边特征$ {{\mathbf{h}}_{{r_j}}} \in {{\mathbf{H}}^R} $为边r_j的参数化表示, 将在迭代中不断更新.

同上, 将边子图信息输入正交GNN网络, 并多跳链接生成关系聚合节点特征$ {\mathbf{h}}_{{e_i}}^{{\mathrm{relation}}} $.

(3)图像聚合编码

本文选取在ImageNet^[28]的目标识别任务上预训练的ResNet-152作为图像特征提取器, 取该模型最后一层全连接层及Softmax层前的输出特征作为图像表征, 如式(5)所示:

$ {h}_{{e}_{i}}^{V}={W}_{V}\cdot ResNet({v}_{i})+{b}_{V} $

(5)

其中, v_i代表输入图像, $ h_{{e_i}}^V $代表图像特征输出, W_V、b_V为可训练参数. 对于没有图像的实体, 本文分配一个从正态分布中采样的随机向量, 由其他图像的平均值和标准偏差进行参数化.

其次, 同“节点聚合特征编码”步骤相同, 从三元组(e_i, r_ij, e_j)中保留实体对(e_i, e_j), 并构建(v_i, v_j)对应二元组关系, 进行如式(6)所示的图像聚合节点特征:

$ {\mathbf{h}}_{{e_i}}^{(0)} = \left[ {\frac{1}{{\left| {N_{{e_i}}^v} \right|}}\sum\limits_{{v_j} \in N_{{e_i}}^v} {{{\mathbf{h}}_{{v_j}}}} } \right] $

(6)

其中, e_i表示当前节点, $ {{\mathbf{h}}_{{v_j}}} $代表节点e_j的图像特征, $ N_{{e_i}}^v $表示e_i节点的所有相邻图像节点.

同上, 将视觉子图信息输入正交GNN网络生成最终图像特征传递节点表示. 由于图像特征与图结构特征不同, 两跳以上的节点聚合可能会引入过多的噪声与不相似图像, 因此, 图像聚合编码仅使用一层GNN, 并以该层输出作为图像聚合的节点特征$ {\mathbf{h}}_{{e_i}}^{{\mathrm{visual}}} $.

节点$ {e}_{i} $经每个子图信息聚合后所得特征分别为$ {\mathbf{h}}_{{e_i}}^{{\mathrm{entity}}},\; {\mathbf{h}}_{{e_i}}^{{\mathrm{relation}}},\; {\mathbf{h}}_{{e_i}}^{{\mathrm{visual}}} $. 3类特征经可训练权重平衡得到用于对齐的实体表征$ {f_{{e_i}}} $, 如式(7)所示:

$ {f_{{e_i}}} = \left[ {{w_1} \cdot {\mathbf{h}}_{{e_i}}^{{\mathrm{entity}}}||{w_2} \cdot {\mathbf{h}}_{{e_i}}^{{\mathrm{relation}}}||{w_3} \cdot {\mathbf{h}}_{{e_i}}^{{\mathrm{visual}}}} \right] $

(7)

其中, 可训练权重w₁、w₂、w₃在运算前进行了Softmax, 以保证权重和为1.

2.2 基于关系注意力的知识图谱子图采样方法

受GraphSAGE^[29]启发, 本文采用一种小批量mini-batch的子图采样方式, 将知识图谱训练节点切分为多个子块进行训练. 更进一步, 由于三元组包含信息的质量不一, 对当前节点的影响程度也不一, 本文采用基于关系注意力计算的子图采样方法取代了平均随机采样, 实现非均匀概率采样.

对中心节点$ {{e}}_{i} $进行采样时, 三元组(e_i, r_k, e_j)的路径采样概率记为P((e_i, r_k, e_j)|e_i), 令其等同于路径的注意力值α_ijk. 对每个中心节点, 其采样期望为各路径权重与被采样概率相乘的加权和(也可以用作衡量模型的选择能力), 如式(8):

$ E\left[ {{\alpha _{{e_i}}}} \right] = \sum\limits_{{e_j} \in \mathcal{N}_{{e_i}}^e} {\sum\limits_{{r_k} \in {R_{ij}}} P \left( {\left( {{e_i}, {r_k}, {e_j}} \right)|{e_i}} \right){\alpha _{ijk}}} = \sum\limits_{{e_j} \in \mathcal{N}_{{e_i}}^e} {\sum\limits_{{r_k} \in {R_{ij}}} {\alpha _{ijk}^2} } $

(8)

如果使用固定的采样次数t或简单地设定t与节点的度成反比, 这会导致部分节点与路径被过度采样或忽视, 进一步造成信息的冗余与不足. 因此, 我们期望对任一中心节点e_i, 其注意力期望值之和在实验结束后应保持一定的稳定性, 那么在每个训练周期内采样次数$ {t_{{e_i}}} $应符合如下公式:

$ {t_{{e_i}}} = \left\lceil {\frac{\tau }{{E\left[ {{\alpha _{{e_i}}}} \right]}}} \right\rceil $

(9)

其中, $ \tau $为控制采样率的超参数, $ \left\lceil {x} \right\rceil $为向上取整操作.

基于期望加权计算的子图采样方法通过使采样次数与节点注意力期望成反比, 平衡了模型对各节点的学习效果, 并减少了由于对部分中心节点多次采样所造成的信息冗余.

2.3 联合学习损失函数 2.3.1 多子图特征融合损失函数

受NCA^[30]文本-图像匹配方法启发, 本文在融合实体的邻域、结构、图像信息时, 采用了一个与NCA损失类似的函数, 以增加对样本的区分能力.

新的多模态融合损失函数使用了局部和全局的统计数据衡量样本的重要程度, 为解决嵌入时的枢纽度问题, 采用软加权方案. 如式(10)所示:

$ \begin{split} {L_{{\text{NCA}}}} =& \frac{1}{N}\sum\limits_{{{i}} = 1}^N {\left( {\frac{1}{\alpha }\log \left( {1 + \sum\limits_{{{m}} \ne {{i}}} {{{\mathrm{e}}^{\alpha {S_{mi}}}}} } \right)} \right.} \\ &+\left. {\frac{1}{\alpha }\log \left( {1 + \sum\limits_{{{n}} \ne {{i}}}^{\text{ }} {{{\mathrm{e}}^{\alpha {S_{in}}}}} } \right) - \log \left( {1 + \beta {S_{ii}}} \right)} \right) \end{split} $

(10)

其中, $ \alpha $、$ \;\beta $为超参数, 本文中选取$ \alpha$为15, $ \;\beta $为10, N为每个batch中的枢轴数. S_xy代表其下标两个向量的余弦相似度, 如S_ii为实体i两种模态表征的相似度, S_mi与S_in为实体i的某个模态表征与另一实体的另一模态表征. 对实体i的两种模态表征, 预期该实体的每个表征与其他实体在另一模态的表征尽可能有差异, 同一实体的两种模态表征尽可能相似.

2.3.2 无负样本对比损失函数

两图谱间的对齐采用无负样本对比损失函数^[12]. 具体而言, 图谱经过RAMS前向传播得到图谱特征f, 同时记录一个无梯度的副本, 记为f ^init. 在编码后, 双方互相向对方的特征f ^init进行学习, 计算式(11)所示损失:

$ {L_{{\text{NFC}}}} = \sum\limits_{\left( {{e_i}, {e_j}} \right) \in S} {( - {\text{sim}}({f_{{e_i}}}, f_{{e_j}}^{{\mathrm{init}}}) - {\text{sim}}({f_{{e_j}}}, f_{{e_i}}^{{\mathrm{init}}}))} $

(11)

实体对齐的置信度采用式(11)的形式进行计算:

$ {{score}}({e_i}, {e_j}) = {\text{sim}}({f_{{e_i}}}, f_{{e_j}}^{{\mathrm{init}}}) + {\text{sim}}({f_{{e_j}}}, f_{{e_i}}^{{\mathrm{init}}}) $

(12)

2.3.3 联合学习损失函数

联合学习损失函数如下:

$ {L_{{\text{Joint}}}} = \sum\limits_i^n {{L_{{\text{NCA}}}} + {L_{{\text{NFC}}}}} $

(13)

其中, $ \displaystyle\sum\limits_{{i}}^{{n}} {{L_{{\text{NCA}}}}} $代表所有模态的多模态融合损失相加结果, $ {L_{{\text{NFC}}}} $代表无负样本损失. 由于无负样本损失在编码过程中已经将所有模态进行融合, 因此无需进行模态间的求和计算.

2.3.4 跨域相似度计算

通过两个实体间的相似度直接地判断对齐可能性是较为粗暴的方法. 因为最近邻关系是不对称的: y是x的最近邻K个实体并不意味着x是y的最近邻K个实体.

受CSLS^[31]启发, 我们令两个实体间的相似度受它们与其他实体间的相似度影响. 具体地, 考虑一个二分图, 分别为源图谱KG_S和目标图谱KG_T. N_T(x_i)表示目标图谱中与源图谱实体$ {x}_{i} $相似度最高的K个实体集合. 类似地, N_S(y_j)表示源图谱中与目标图谱实体y_j相似度最高的K个实体集合. 对于源图谱中的实体x_i, 其与目标图谱中K个近邻间的平均相似度计算如式(13):

$ {{av}}{{{g}}_{{T}}}\left( {{x_i}} \right) = \frac{1}{K}\sum\limits_{{y_j} \in {N_T}\left( {{x_i}} \right)} {\cos \left( {{{\mathbf{h}}_{{x_i}}}, {{\mathbf{h}}_{{y_j}}}} \right)} $

(14)

其中, cos计算的是向量余弦相似度. 如果实体x_i和另一个图谱中的K近邻实体都较为相似, 那么avg_T(x_i)就会具有较高的值, 并会因此影响它与待对齐实体间的相似程度. 源图谱实体x_i与目标图谱实体y_j的跨域相似度计算如式(14):

$ {\text{sim}}\left( {{x_i}, {y_j}} \right) = 2\cos \left( {{x_i}, {y_j}} \right) - {{av}}{{{g}}_{{T}}}\left( {{x_i}} \right) - {{av}}{{{g}}_{{S}}}\left( {{y_j}} \right) $

(15)

此外, 本文采用了双向迭代策略来构造高质量的半监督对齐对. 根据RAMS跨域相似度计算获得的新的对齐节点, 当且仅当实体e_i和e_j是彼此最近的邻居时, (e_i, e_j)将被视为新的半监督对齐实体.

3 实验分析 3.1 评价指标及实验设置

遵循现有的实体对齐方法, 本文采用Hits@k (k=1, 10)和平均倒数排名(MRR)作为评价指标. 在预测阶段, 对于每个源实体, 目标实体将按其与源实体的距离分数进行升序排列. Hits@k反映前k个预测对齐实体中正确对齐实体的比例. MRR表示正确对齐实体排名的倒数的平均值. Hits@k和MRR分数越高表明性能越好.

对于所有数据集, 本文都设置了相同的默认配置: 嵌入维度d=300, GNN层数l=2, 采样率$ \tau$=1, 相似性阈值$ \epsilon $=0.05, 扩散系数α=15, β=10, 批量大小为512, dropout率设定为30%, 采用RMSprop对模型进行优化, 学习率设置为0.005.

3.2 多模态实体对齐实验结果与分析

为验证模型有效性, 本文选择近几年表现出色的公开模型进行对比. 为了保证模型之间比较的公平性, 将模型分为两组, 基础组(Basic)和数据增强组(itera-tive learning, IL), 其中基础组仅使用了数据集原本的信息且并未使用任何数据增强方法, 数据增强组通过无监督或半监督方法获取了额外信息进行训练. 实验结果表2所示.

从实验结果中可以看出:

1)考虑不使用迭代的模型, RAMS (Basic)明显优于以往的神经网络模型, 并在Hits@1指标上都超越了次优模型10%–20%的水平. 相比于GCN-Align、MuGNN等GNN模型, RAMS融合了多模态特征, 在未经迭代的情况下具有很好的冷启动特征优势, 说明了子图特征融合的有效性.

2)考虑使用迭代模型的情况下, RAMS (IL)同样优于所有基线模型, 在Hits@1上超越了次优模型4%–5%的水平. 相比于BootEA、NAEA等使用了负采样方式的模型, RAMS采用对比无负采样损失进行训练, 提升了模型效率也同时保证了模型的准确率; 相比于EVA、MRAEA等多模态实体对齐模型, 本文方法采用了多模态子图方式编码, 效果均优于普通单独编码融合方法.

3)对比所有方法, 使用迭代对齐策略的模型整体优于上半部分模型的表现, 本文方法中使用了迭代数据增强策略后, 整体Hits@1水平也上升了将近10%, 验证了在实体对齐任务中使用迭代对齐等数据增强方式对模型的提升较大. 在MRAEA与本文方法中, 都使用了双向迭代策略或无监督数据增强策略, 可以看出模型准确率有进一步的提升.

3.3 模型鲁棒性实验结果与分析

本文从3个角度测试实验参数对模型稳定性的影响.

(1)预对齐种子比率

预对齐种子占比率指训练集种子在所有标注实体对中的占比. 实验采用10%、20%、30%、40%这4个占比率进行实验. 预对齐种子占比率实验对比结果如图5所示.

本文选取RREA、MuGNN、MRAEA这3种表现较为出色的基线模型作为RAMS的对比. 从图5中可以看出, 本文模型在各种预对齐种子占比率的表现都十分优秀, 在仅有10%对齐种子的情况下, 模型表现也能够达到73%–75%的Hits@1值, 这相比于RREA、MuGNN、MRAEA这3种模型在40%对齐种子的情况还要出色, 验证了本文即使在少量样本的情况下也可以获得出色的表现, 在数据输入方面的鲁棒性较高.

(2)子图采样大小

子图采样大小指每个批次输入模型的子图采样节点数. 从图6中可以看出, 在128–1024的采样大小情况下, RAMS (IL)的Hits@1水平波动较小, 验证了模型在不同采样率情况下的鲁棒性. 而模型运行时间则随着采样数量增加而大幅度减小, 一方面由于随着采样子图增长, 训练轮次随之减小, 模型处理时间下降, 另一方面, 子图采样增加了模型并行性, 在显存的负担能力以内能够增强运行效率.

(3)网络层数大小

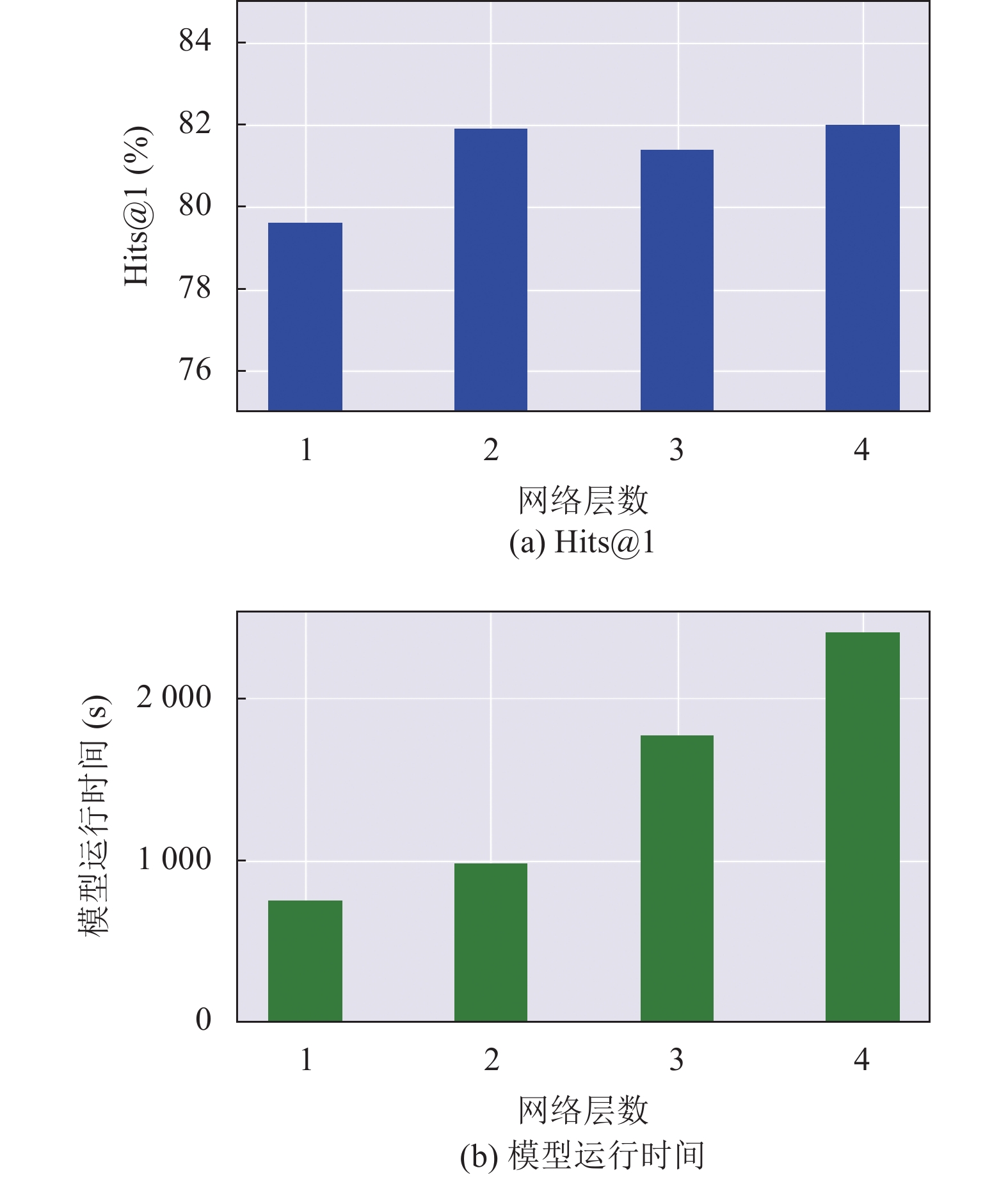
网络层数指邻域、结构子图中GNN神经网络层数. 图7展示了随着网络层数加深, Hits@1水平波动也相对较小, 只有在一层时由于消息传递不足, 使得模型表现较弱, 验证模型在图神经网络层数方面的鲁棒性. 此外, 随着层数增加, 由于模型复杂度上升, 模型运行时间也随之增加, 因此本文仅选用两层深度网络, 在较少的时间内, 保障模型的准确率.

3.4 模型效率实验结果与分析

本文进一步验证了RAMS在运行效率上的优势, 与各基线方法的对比结果如表3所示.

从未使用迭代策略的基础组看, 本文方法仅次于GCN-Align, 且时间差距不大. 但由于GCN-Align仅使用了图谱结构信息, 且仅由双层基础GCN编码, 而本文考虑多子图多模态信息, 在同一量级的时间内, 本文方法的准确率远超前者. 对比其他复杂模型, 本文方法在保证准确率的同时, 时间花费上大幅减小, 验证了本文方法对模型效率的提升.

从使用了迭代策略的数据增强组来看, RAMS同样在时间上大幅超越所有基线模型, 对比NAEA、TransEdge、MRAEA等使用了多模态信息的模型, 本文方法在低时间复杂度的情况下获得了较高的实体对齐准确率表现.

3.5 长尾节点实验结果与分析

将DBP15k (ZH-EN)中所有节点按照节点度数进行划分, 大部分节点的度数在0–25之间, 仅有少数节点包含丰富边信息. 这些邻居节点较少的中心节点往往特征表达能力一般较差. 分别计算所划分的各度区间内Hits@1值, 实验结果如图8所示.

可以看出, 模型在各区间内都具有良好的表现. 在度数小于20的稀疏节点区间, 本文模型的表现能达到79.3%, 高于表2中部分方法的最终实验结果. 而在信息丰富的区间, 如度数高于120的节点区间, 模型的Hits@1值超过了90%, 甚至在180–200的区间里达到了接近完美的水平. 这与图神经网络消息传递机制的规律相符: 邻域信息越丰富, 当前节点所能获得的信息越充足, 而领域相似信息越多, 对应实体的对齐置信度越高.

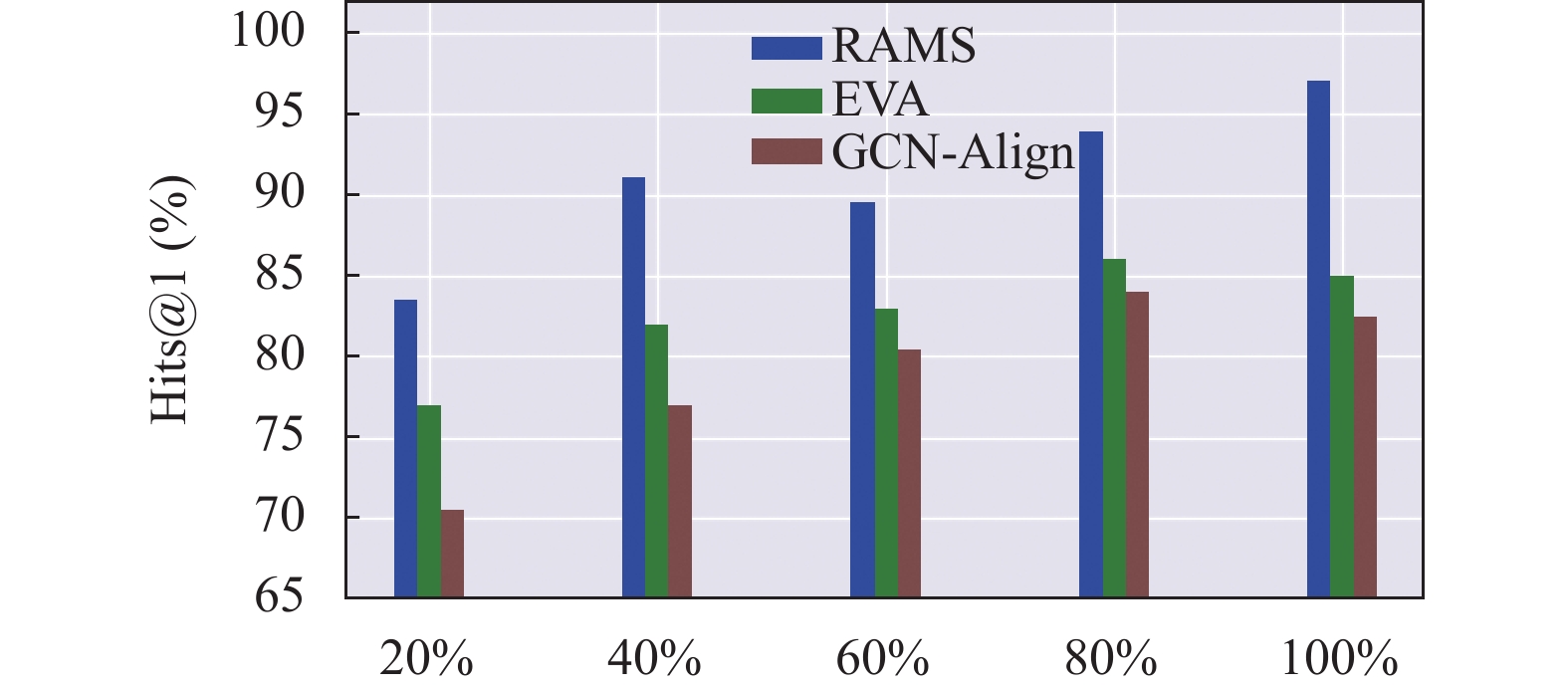
为了进一步比较本文在长尾节点上的表现, 本文选取多模态基线模型EVA与仅使用结构信息的基线模型GCN进行比较, 实验结果如图9所示.

将节点按度数从小到大排列, 划分为5个区间, 统计各区间内模型的表现. 仅使用结构信息的GCN模型在各度数区间都表现不佳, 随度数增加模型效果有所改善. 相比GCN, 加入了图像等多模态信息的EVA模型在效果上有较大提升, 这验证了多模态信息能够起到特征补充的作用. 最后, 由于本文模型额外在多模态特征编码阶段引入了关系敏感型多子图图神经网络, 使模态信息与图结构信息充分融合, 因此相比基线模型在各度数区间都获得了进一步提升, 验证了本文模型的有效性.

4 结论与展望

针对模态特征缺失问题, 本文提出了一种多模态多视图的关系敏感型正交图神经网络. 该网络通过多视图特征编码和模态融合损失来补足模态间的信息差异, 并借助期望控制的采样方法和矩阵约束方法增强模型效果. 广泛的对比实验表明, 本文提出的模型超越了所有的基线模型, 并验证了本文模型在鲁棒性、运行效率、长尾节点准确率等多个维度保持优势.

在未来的工作中, 我们计划在子图编码模块引入差异化的网络结构, 以进一步改进多子图消息传递机制, 从而平衡模态间信息差异并增强模态表征能力. 同时, 考虑到现实中的知识图谱可能更加稀疏, 并且图像等额外信息的分布更加不均匀, 我们还将针对长尾节点和稀疏图进行研究与优化.