2. 中国科学技术大学 数学科学学院, 合肥 230026;
3. 中国科学院 吴文俊数学重点实验室, 合肥 230026;
4. 合肥国家实验室, 合肥 230088
2. School of Mathematical Sciences, University of Science and Technology of China, Hefei 230026, China;
3. Wu Wen-tsun Key Laboratory of Mathematics, Chinese Academy of Sciences, Hefei 230026, China;
4. Hefei National Laboratory, Hefei 230088, China
网络(或图)的代数连通度是其拉普拉斯矩阵的第二最小特征值[1]. 航空运输网络[2,3], 电子物流网络[4], 电流回路网络[5]以及其他网络都可以从代数连通度中受益. 这对于多智能体系统的一致性研究也是至关重要的. 对于一阶协议, 代数连通度越大, 收敛速度越快[6]. 对于二阶协议, 代数连通度仍然是影响收敛速度的关键因素. 此外, 网络结构中边的数量越多, 表明代数连通度越大, 对应的多智能体系统更加稳健且高效.
然而, 系统中存在过多的通信链路也是浪费的, 因为它会导致能源消耗、多余的链路维护和重复计算成本的问题[7]. 特别是在大规模多智能体系统中, 当每对可通信智能体之间都保持通信时, 通信链路的数量与小规模多智能体系统相比呈指数级增长, 由此产生的多余资源消耗更为显著. 然而, 一些链路的存在对于系统来说是不必要的, 删除它们对代数连通度几乎没有影响[8]. 因此, 如何去除一些相对冗余的链路, 同时保持尽可能大的代数连通度是多智能体系统领域非常感兴趣的问题. 这实际上也是图论中最大化代数连通度的问题. 我们感兴趣的是如何删除指定数量的通信链路以减少消耗, 同时使代数连通度尽可能大.
在学习可适用于最大化代数连通度问题的配置时, 选择适当的模型架构至关重要. 最大化代数连通度问题是优化图的拓扑结构问题. 普通的神经网络模型使用向量或者矩阵表示输入数据, 并且通过线性变换或者非线性激活函数来处理数据, 无法捕捉到图中节点之间的关系以及边的权重, 更无法进行图层面的计算. 另外普通神经网络只能接受固定维度的输入和输出, 这使得模型只能适用于同一种规模的任务场景, 一旦图中的节点数量增加或减少, 原来训练的模型将无法使用, 只能重新训练.
相比普通的神经网络, 图神经网络可以借助图结构的信息并且在图上进行卷积操作, 还能灵活处理不同大小和形状的图结构数据. 这一点是非常重要的, 因为我们希望通过小规模任务场景训练得到的模型可直接使用在大规模任务场景中, 以克服最大化代数连通度问题随着图规模的增加带来的计算时间急剧增加的问题. 另外, 图神经网络的计算图和多智能体系统之间的收敛协议有一定程度的类似. 多智能体系统可以表述为图的形式, 智能体对应图中的节点, 通信链路对应图中的边. 多智能体系统的收敛协议涉及信息的传递和交流, 每个智能体信息的迭代更新是基于能与之通信的智能体进行的, 即相邻的智能体. 图神经网络中每个节点的信息传递与更新也是基于邻居节点的信息. 两者的信息更新均是基于邻居信息, 每个节点或智能体的状态都会影响网络或系统中的其他节点或智能体, 进而影响整个网络或系统的性能.
因此, 我们考虑利用图神经网络模型来解决最大化代数连通度问题. 我们的模型设计旨在衡量系统中每条通信链路的存在对于整个网络的连通能力的贡献大小, 再根据模型的输出删去贡献较小的链路的同时尝试避开关键的通信链路. 基于此, 本文提出了一种基于图神经网络(GNN)模型的最大化代数连通度方法. 借助传统的优化算法, 我们生成了一系列的样本. 通过学习这些样本, 我们训练得到的模型能够快速推理出相对冗余的链路. 与现有方法相比, 我们的方法在保证代数连通度尽可能大的同时克服了随着智能体数量增长带来的巨大计算成本, 可以直接应用于大规模的多智能体系统中.
1 相关工作 1.1 最大化代数连通度最大化代数连通度问题是NP难的问题[9], 目前还没有高效的方法可以精确地求解. Kim等人考虑了加权图的最大化代数连通度问题[10]. 他们设定每条边的距离大于或等于一个常数, 并且边的权重由这个距离的函数决定. 针对这一约束优化问题, 他们提出了一种基于半正定规划(SDP)求解器的迭代算法. Rafiee等人考虑了多智能体系统中的网络拓扑结构的两个问题[11]. 一是在限定的通信链路数量下使网络结构尽快收敛, 二是在最低成本下找到恰当的网络拓扑结构可以使网络满足所需的基本性能. 他们将这两个关于寻找最佳通信图的问题表述为一个混合整数半正定规划(MISDP)问题. Dai等人将动态网络的最优拓扑设计问题分为3类[12]. 一是无权图的网络设计, 二是边的权重为两个端点位置相关的函数的网络设计, 三是需要保持连接的移动网络系统的设计. 他们将上述3类问题转化为MISDP问题和混合整数二次约束规划(MIQCP)问题, 采用求解器进行求解. 上述文献对于代数连通度问题的求解都是基于求解器进行的, 受求解器的限制, 只能用于小规模任务场景的求解.
有很多关于最大化代数连通度的启发式算法被提出. Ghosh等人考虑的是向给定图中添加一条边使得代数连通度最大化的问题[13]. 他们提出了一个基于费德勒向量的贪婪扰动启发式算法. Kim考虑了向给定的图中添加一条边使得代数连通度最大化的问题[14], 针对这个问题给出了一个基于长期方程的高效二分算法. Sydney等人考虑了如何重新布置网络中的一条边来提高网络的代数连通度问题[15], 即从原图中删除一条边之后再重新添加一条边. Wei等人向航空运输网络中引入了加权的代数连通度[3], 并且使用了禁忌搜索算法对最大化代数连通问题求解. Wei等人通过最大化代数连通度的方法优化了航空运输网络结构[16]. 他们首先建立了一个有约束的SDP问题, 然后为解决这个问题提出了舍入技术. Li等人提出了通过添加图中的最小度的顶点和与这个顶点相距最远的顶点之间的边来最大化代数连通度[17]. 上述算法经常应用于各种网络的结构优化中. Trimble等人使用贪婪扰动算法、二分法、禁忌搜索法和SDP方法构建了无人机网络连通性跟踪算法[18]. Cheung等人采用最大化代数连通度方法解决了受损电子网络的恢复问题[4], 并使用了贪婪扰动算法、禁忌搜索算法和舍入技术.
贪婪扰动算法作为一种基于费德勒向量的求解算法, 求解速度快, 但是性能相对较差. 而最小度最远距离算法作为改进的贪婪扰动算法, 对于图结构的要求更加严格. 除了这两种算法, 上面提及的启发式算法相较于基于求解器的方法计算时间有所提升, 但是随着任务规模的增大, 求解问题花费的时间仍然是十分可观的. 因此, 我们希望找到一种可以快速解决最大化代数连通度问题的方法, 在面对大规模任务场景时有着高效的求解速度以及可靠的性能.
1.2 图神经网络图神经网络首次由Scarselli等人提出[19], 在最近几年发展出了很多不同图神经网络架构. Kipf等人提出了图卷积神经网络以从图中提取特征结构[20], 完成各种基于图的任务, 包括链接预测、节点分类和图分类等任务. 然而图卷积神经网络无法计算训练过程中没有出现的顶点的嵌入. Hamilton等人提出了图采用与聚合模型[21], 这是一种能够利用顶点的信息高效产生未知顶点的嵌入的方法. Veličković等人提出了图注意力网络[22], 它利用了掩码自注意力层, 获取每个节点的领域特征的同时给该领域中的每个节点分配了不同的权重, 这种模型的优点在于不需要提前知晓图的结构信息的同时运算成本减少了. You等人提出了一个通用的图神经网络设计空间[23]. 借助于这个设计空间, 可以快速找到适合具体任务的图神经网络模型的学习架构. 这些图神经网络架构也被应用到了很多领域, 包括社交网络[24,25]、交通工程[26]和生物领域[27,28]等.
图神经网络在这些领域的应用出现了颠覆传统方法的性能和表现. 通过建立多层的神经网络和设计不同的模型架构, 图神经网络能够从多种多样的数据中提取出模型需要的特征, 使得许多难以解决的问题变得可能. 然而目前还没有利用图神经网络模型来解决最大化代数连通度算法的工作. 因此, 本文提出了一种监督式图神经网络模型来求解此问题. 为了保证模型生成解集的质量, 本文选择了基于松弛半正定规划的舍入技术来生成大量小规模任务场景的解作为训练标签. 另外, 随着规模的增长, 图神经网络模型的求解时间几乎不变. 也就是说, 该方法既保证了在大规模任务场景中的求解速度, 也兼顾了求解质量.
2 问题定义代数连通度随着图中边的数量的增加而增加. 然而对于多智能体系统而言, 有一部分通信链路的存在对于代数连通度的提升贡献不大, 删除这些冗余链路还可以降低系统的损耗. 因此, 在本文中要考虑的问题是, 对于一个多智能体系统而言, 如何在删除指定数量的边的同时以使得代数连通度尽可能地大.
2.1 多智能体系统的图表述考虑这样一个有n个智能体的多智能体系统, 每个智能体i的位置表示为
| wij=w(xi,xj)=f(dij) | (1) |
其中,
| f(y)={1,y⩽ρ1ϵρ1−yρ1−ρ2,y>ρ1 | (2) |
其中,
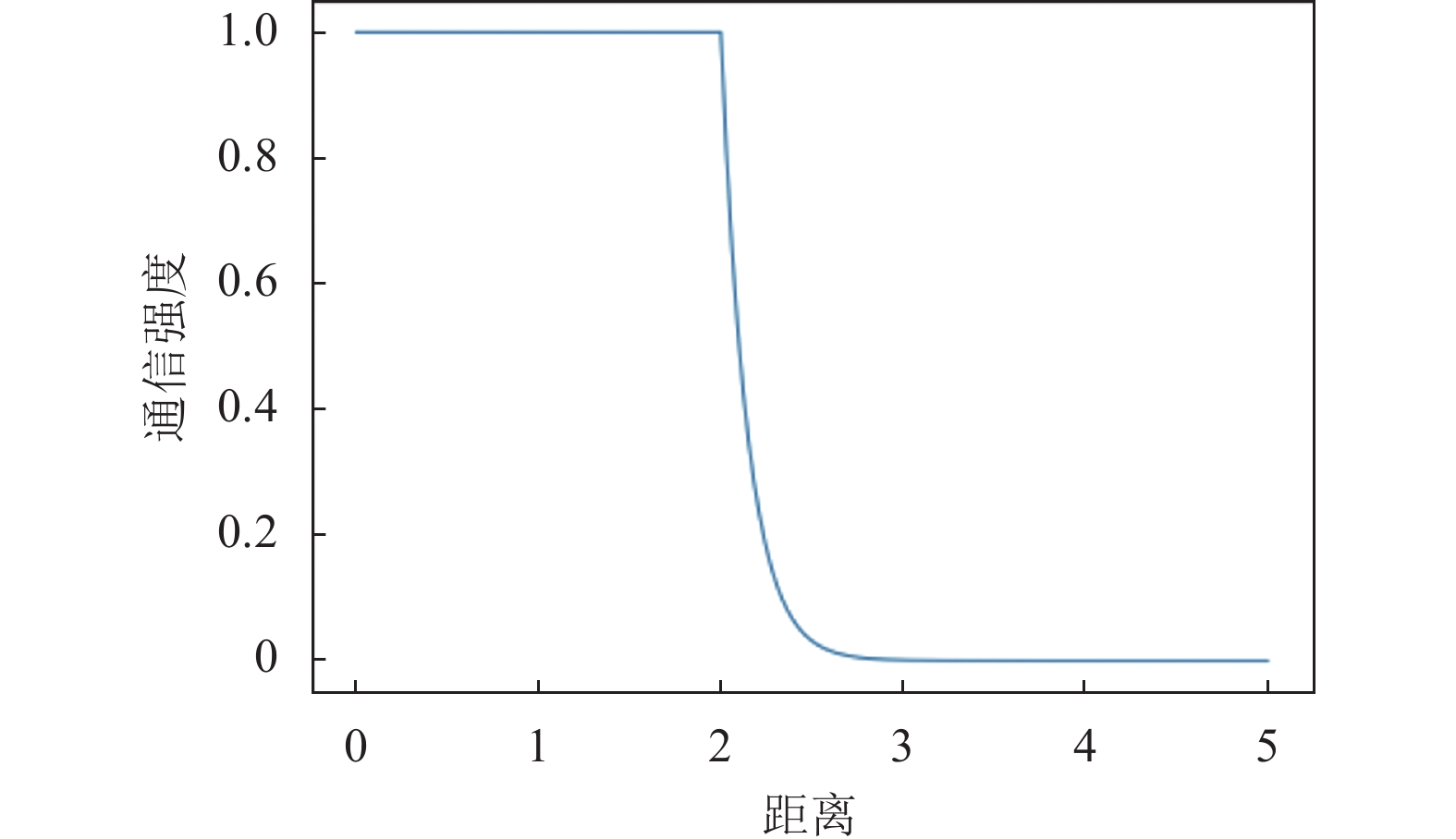
|
图 1 函数 |
这样的一个多智能体系统可以用一个加权的无向图来表示. 系统中的每个智能体对应于图中的一个节点. 对于任意一对智能体, 如果它们之间可以通信, 那么这对智能体对应的顶点之间存在边, 否则边不存在. 对应的图可以表示为
此外, 拉普拉斯矩阵还可以表示为边向量的外积和[13]. 对于边集E中的每条边
图G的代数连通度是拉普拉斯矩阵的第2小特征值, 用
在此框架下, 我们需要考虑的问题是:
| {maxλ2(L0−∑e∈ExewehehTe)s.t.{∑e∈Exe=bx∈{0,1}|E| | (3) |
其中, b是给定的正整数,
我们所使用的GNN模型是通过监督学习获得的. 因此一个完整的GNN模型需要明确定义的任务场景和相应的解集作为输入. 每一组这样的输入构成一个样本, 而我们需要大量的样本来进行模型训练, 以达到较好的效果. 然而问题(3)是一个有
对于问题(3), 第1步是将该问题转化为松弛问题, 即将每条边是否存在的二元变量扩展为在[0, 1]上的连续变量. 问题(3)的松弛问题为:
| {maxλ2(L0−∑e∈ExewehehTe)s.t.{∑e∈Exe=bx∈[0,1]|E| | (4) |
显然问题(4)比问题(3)拥有更大的可行集, 因此问题(4)的解是问题(3)的上界. 这个松弛问题可以重新写成以下的松弛半正定规划问题:
| {maxss.t.{L0−∑e∈ExewehehTe≽ | (5) |
这里的松弛半正定规划问题(5)和松弛问题(4)是等价关系, 其中s为移除边之后的代数连通度[30]. 使用MOSEK求解器可以求解松弛半正定规划问题(5). 在这个松弛的SDP问题中, 解是在[0, 1]之间的连续值, 因此需要进一步选择边.
3.2 样本生成我们采取文献[16]中提到的舍入技术中的逐步法来选择边. 即每次选择一条解向量中值最大的边, 从边集E中删除, 存入有序集合S中, 并更新拉普拉斯矩阵和约束b, 然后再对问题(6)进行求解, 重复以上步骤直到约束b为0. 最后, 我们获得了一个包含了b条边的有序集合S. 在这里, 对于给定的约束b, 问题(5)求解得到的边集合只能针对一个约束. 一旦约束b发生改变, 标签不再正确, 训练的模型失效. 为了模型的可扩展性, 我们在此处设定
算法1. SDP-Step[16]
输入:
输出: 有序集合S
1)
2) while b > 0 且
3) 求解问题(5)得到解向量x
4)
5)
6) 移除
7)
8)
9) end while
我们使用算法1中的优化专家来计算边的删除次序. 在这个算法的基础上, 我们可以生成大量的随机任务场景, 并且根据算法1对问题进行求解, 从而生成训练模型需要的标签.
图2(a)显示了在大小为
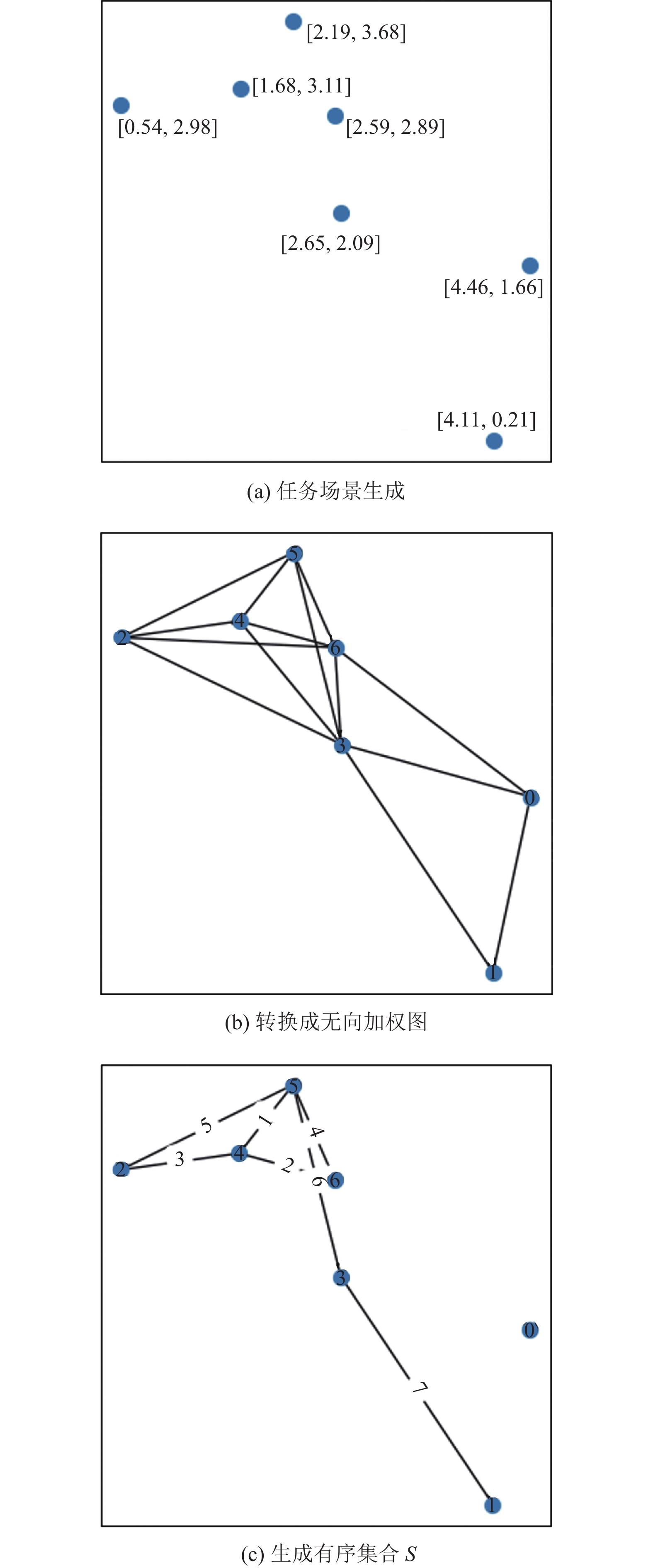
|
图 2 单个样本的生成示例 |
4 模型框架
本文提出的模型是基于文献[23]中提出的图神经网络设计空间构建的. 整个模型框架如图3所示, 首先通过第3节的方法生成大量的任务场景以及对应的有序集合. 据此训练好我们的模型, 然后根据模型的边选择策略来移除边. 在本节中, 首先, 我们对该设计空间进行简要的阐述. 然后, 我们给出了图的初始节点特征设定. 在此设计空间的基础上, 我们给出了模型的具体模型架构. 之后, 根据每个样本中的无向图

|
图 3 GNN模型框架 |
4.1 图神经网络设计空间
图神经网络设计空间有3个维度, 即层内设计、层间设计以及训练配置[23]. 层内设计是图神经网络架构的核心, 是整个模型中的消息传递层. 对于层内设计, 第k个图神经网络层可以被定义为:
| \left\{ {\begin{array}{*{20}{l}} {h_{u, {\mathrm{mid}}}^{(k)} = {\textit{Dropout}}\left( {BN\left( {{W^{(k)}}\left( {{w_{uv}}h_u^{(k)} + {b^{(k)}}} \right)} \right)} \right)} \\ {h_v^{(k + 1)} = AGG\left( {\left\{ {ACT\left( {h_{u, {\mathrm{mid}}}^{(k)}} \right), u \in \mathcal{N}(v)} \right\}} \right)} \end{array}} \right. | (6) |
其中,
层间设计包括预处理层、后处理层和信息传递层的数量的选择. 训练配置方面包括批大小、学习率、优化器和训练周期. 更详细的说明可以参考文献[23].
4.2 节点的初始特征设定在设计GNN模型的过程中, 需要输入的主要变量是节点特征和边的权重. 边的权重由两个相邻智能体之间的通信强度决定. 根据任务场景, 多智能体系统通常规模不定, 因此必须确保当智能体数量在一定范围内时模型是有效的. 为了使GNN模型可扩展, 节点的初始特征维度必须与图中的节点数量无关. 在本文中, 我们将每个节点u的初始特征向量的第v个元素定义为:
| {h}_{u, v}^{(0)}=\left\{\begin{array}{ll}1, & (u, v)\in E\\ \text{0}\text{, }& (u, v)\notin E\;{\mathrm{or}}\;v > n\end{array}\right. | (7) |
其中, E是图的边集, n是图的顶点数量. 当节点u与节点v之间有边连接时, 特征向量的第v个元素为1, 如果没有连接, 则为0. 特征向量中第n个元素之后都用0进行填充, 以确保模型对一定规模内的图都可以计算. 那么向GNN模型输入的整体的特征矩阵为
在使用图神经网络对节点特征进行处理时, 一种有效的方法是在GNN模型之前和之后添加多层感知机(MLP)层进行处理. 通过这种方式, 在保持输入特征的基本信息的同时, 可以降低GNN模型中需要学习的参数数量, 减少模型的复杂度, 并且减轻模型训练的压力. 因此, 预处理层和后处理层的引入是必要的. 分别设定为两个MLP层, 每个MLP层的参数不是共享的. 通过实验, 我们发现GNN模型层数设定为3层是比较合适的, 每一层GNN模型中的线性层参数不一致,
| 表 1 层内设计的参数设定 |
| 表 2 训练配置的参数设定 |
4.4 预测层
经过上述模型我们只能计算出每个节点的最终节点特征. 然后, 我们的目标是在避开比较关键的通信链路的同时选择出一些不那么重要的通信链路. 因此, 我们还需要通过预测层来选择出这些边.
针对图中已经存在的每一条边
| scor{e_e} = {{h}}_u^{\mathrm{T}}{{{h}}_v} | (8) |
其中,
损失函数主要包括两个部分, 一部分是针对有序集合S中的每条边. 另一部分是针对不在有序集合S中但在边集E中的边. 对于有序集合S中的边, 从第2节中我们知道越是排在前面的边, 相对于整个图来说相对没那么重要, 是可以先舍弃的. 相反, 对于那些相对靠后的边, 我们越是需要谨慎删除. 对于那些不在有序集合S中但在边集E中的边, 哪怕只是删除一条都对代数连通度的影响都很大.
首先, 我们将有序集合S中的每条边的次序都对应到一个标签, 对应关系定义为:
| labe{l_e} = 1 - \frac{{ran{k_e}}}{b} | (9) |
其中, b是问题中的约束,
我们将均方误差损失函数作为其优化目标函数, 定义为:
| Los{s_S} = \sum\limits_{e \in S} {{{\left( {\left(1 - \frac{{ran{k_e}}}{b}\right) - scor{e_e}} \right)}^2}} | (10) |
然后, 对于那些不在有序集合S中但在边集E中的边, 我们希望模型预测出来的贡献度得分的绝对值越小越好, 因此, 我们将这部分损失函数定义为:
| Los{s_{E\backslash S}} = \sum\limits_{e \in E\backslash S} {score_e^2} | (11) |
综合损失函数如下:
| Loss = \;Los{s_S}\; + Los{s_{E\backslash S}} | (12) |
在本节中, 我们将对训练得到的GNN模型进行仿真实验, 并将实验结果与传统算法进行对比. 任务场景限制在[0, 5]×[0, 5]的平面上. 首先在平面上随机生成一个智能体, 之后每一个智能体都生成在当前所有智能体的可通讯范围内, 从而保证多智能体系统对应的图一定是连通的. 根据式(1)的通信模型计算边的权重. 设定
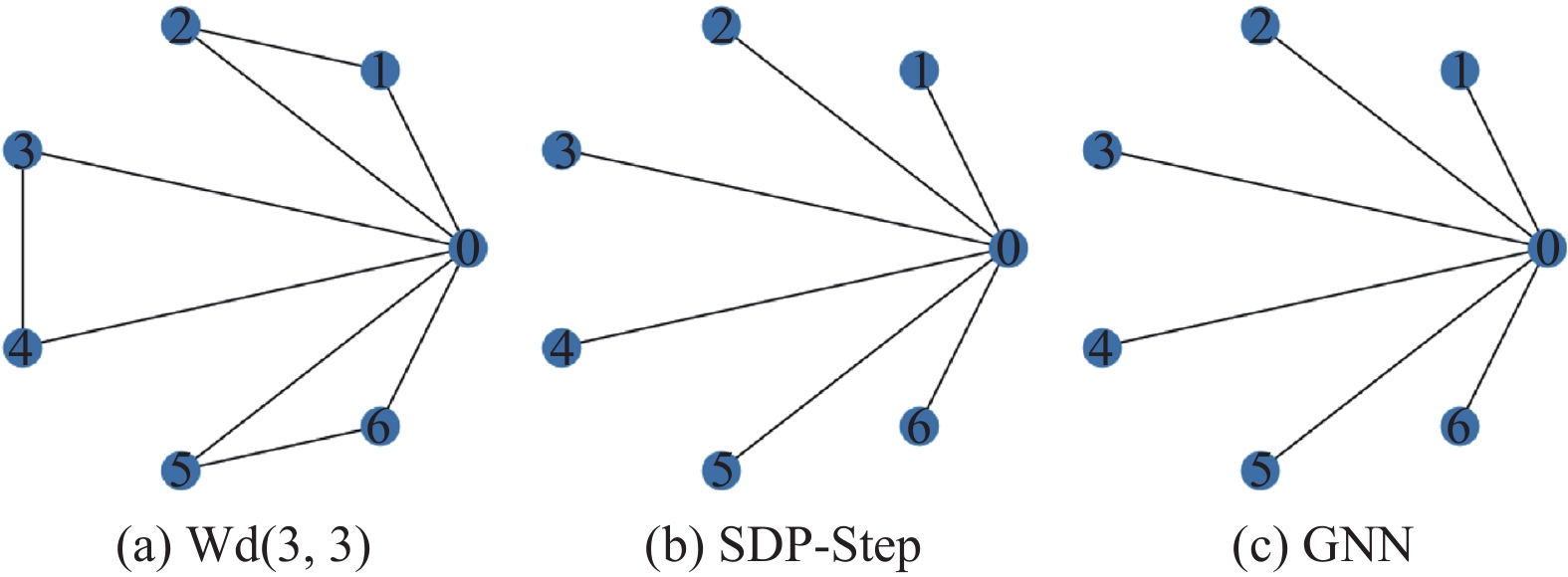
首先, 我们利用风车图对GNN模型的性能进行了简单的测试, 并对GNN模型的预测结果进行了解释. 风车图是一个包含n个团的图, 每个团共享一个节点, 每个团中有k个相互连接的节点. 我们用符号Wd(n, k)来表示这种图的结构特征. 风车图有许多冗余边. 在删除与中心节点无关的边时, 风车图的代数连通度保持不变[32,33]. 这为我们直接评估GNN模型的性能提供了便利.
对于图4(a)中的风车图Wd(3, 3), 当需要删除3条边时, SDP-Step算法得到的结果为{(1, 2), (3, 4), (5, 6)} (图4 (b)), 与GNN模型的输出相同(图4(c)). 然而, 在对图5(a)中的Wd(3, 4)进行测试时, 可以看出, 当需要删除4条边时, SDP-Step算法选择删除{(4, 5), (7, 8), (1, 3), (2, 3)} (图5(b)), GNN模型选择删除{(1, 2), (2, 3), (1, 3), (4, 6)} (图5(c)). 虽然我们的GNN模型给出的边删除方案与SDP-Step算法不太一致, 但两者的代数连通度都是1.0. 因此, 从代数连通度的角度来看, GNN模型的表现并不逊色于SDP-Step算法. GNN模型的输出与SDP-Step算法的结果存在差异, 这是因为在给定的任务空间中, 可能存在多种不同的优化策略. 相较于对比解集的差异性, 采用代数连通度作为指标能更客观地判断GNN模型的性能.
5.2 泛化性在本节中, 我们采用相同的方式随机生成了100个拥有20个智能体的任务场景, 并将GNN模型的结果与这些传统算法的结果进行了比较. 为了评估删除边的数量对GNN模型性能的影响, 我们将可删除边的数量b设置为1, 2, …, 15. 表3描述了GNN模型和其他算法在预算限制下的平均代数连通度和平均计算时间. 对于每个算法, 第1行是代数连通度, 第2行是计算时间. 对于代数连通度表现, 我们将最佳结果以加粗和下划线标明, 次好的结果以加粗标明.
|
图 4 风车图Wd(3, 3)对比 |

|
图 5 风车图Wd(3, 4)对比 |
| 表 3 GNN模型与其他算法的代数连通度和平均计算时间对比(n=20) |
显然, SDP-Step算法的求解效果是最佳的. 在这种较小规模的任务场景中, 进行了3000次迭代搜索的禁忌搜索算法表现和SDP-Step算法表现几乎一致. 可以发现GNN模型的表现不俗, 和性能极佳的SDP-Step算法和禁忌搜索算法的表现相差不大, 甚至是比贪婪扰动启发式算法和二分法算法表现更好. GNN模型的表现没有超越SDP-Step算法而是始终略差于它, 这是很自然的. 因为在小规模任务场景中, 随着更多的边被移除, 剩余的边中关键边的比例稳步增长, 这无意中给模型的性能带来更大的挑战. 在这个过程中, 不经意间可能会破坏网络的更多关键边, 从而对模型的性能造成更大的压力.
另外, 我们可以观察到GNN模型和其他算法在计算时间上随着要移除的边的数量增加时的变化情况. 与SDP-Step算法相比, 禁忌搜索算法需要更多的计算时间, 而二分法算法的计算时间也不可忽视. 只有贪婪扰动算法的计算时间与GNN模型相当; 然而, 该算法的性能表现明显不及GNN模型.
因此, 我们的模型是具有一定的泛化能力的, 即便在没有见过的任务场景中, 表现也相对出色. 另外, 在小规模的任务场景中, GNN模型表现出两个优势: 相对较强的性能和几乎可以忽略的计算时间.
5.3 可扩展性当任务场景中的智能体的数量增加时, 为GNN模型生成新的样本数据以重新训练模型参数成本很高. 此外, SDP-Step算法是一种基于求解器的方法, 然而随着智能体的数量增加, 求解器的执行时间会显著增加, 从而导致生成新标签的代价变得异常昂贵且不切实际. 因此, 我们旨在通过在小规模任务场景中训练GNN模型, 实现其在大规模场景中的泛化应用. 禁忌搜索算法和贪婪扰动算法随着智能体的数量增多需要花费大量时间, 而传统算法(包括二分法)的性能都不及SDP-Step算法. 因此, 在这种情况下, 我们仅使用SDP-Step算法评估GNN模型的性能. 将GNN模型的代数连通度记为
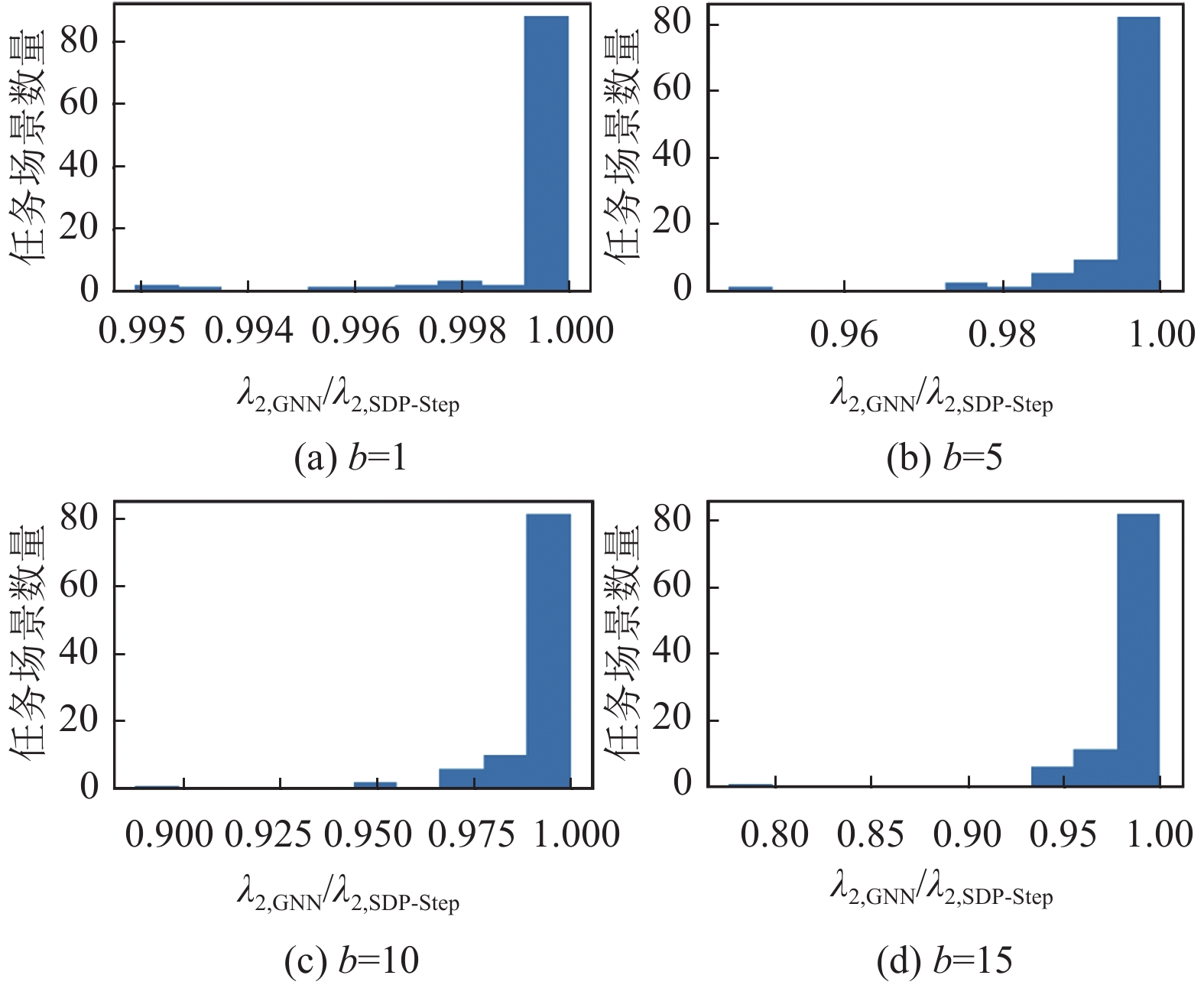
图6给出了在拥有30个智能体的100个随机任务场景下分别删除1、5、10、15条边的实验结果分布. 横坐标为
同样, 图7给出了在拥有50个智能体的100个随机任务场景下分别删除1、5、10、15条边的实验结果分布. 在去除1、5、10和15条边后, GNN模型的平均性能分别达到了SDP-Step的99.95%、99.66%、99.23%和98.63%. 从图7中, 我们可以看到, GNN模型没有再超越SDP-Step, 但在移除10条边的范围内, GNN模型几乎在所有情况下都能达到97%以上的性能. 当移除15条边时, 它的性能几乎达到95%以上. 此外, 我们观察到在其中一个任务场景中, 当移除10或15条边时, GNN模型的性能略低于90%. 但是需要注意的是, 与总计100个任务场景相比, 这个特定任务场景所占的比例极小, 因此对整体结果的影响非常有限.

|
图 6 b=1, 5, 10, 15时 |
|
图 7 b=1, 5, 10, 15时 |
从这两个实验可以看出, 当任务场景中智能体的数量较大时, GNN模型的性能同样非常稳定. 在经过小规模任务场景中最大化代数连通度方案的学习之后, GNN模型能够有效地推理出更大规模任务场景中的最大化策略. 这表明GNN模型具备了处理大规模任务场景的能力, 并且对于不同规模的任务场景具有一定的可扩展性.
5.4 大规模任务场景计算时间对比我们建立GNN模型不是为了小规模的任务场景, 而是为了更大规模的任务场景. 尽管SDP-Step算法总是能够给出优秀的解决方案, 但随着任务场景中智能体数量的增加, SDP-Step算法产生解决方案所需的时间变得漫长, 不适合实时的应用. 相比之下, GNN模型的计算时间与智能体的数量无关, 可以推广到更大规模的场景. 图8比较了SDP-Step和GNN模型在智能体的数量逐渐增加的情况下, 去除特定数量的边所需的平均计算时间. 与SDP-Step的计算时间相比, GNN模型的计算时间基本上可以忽略不计. 这是因为在SDP-Step中, 我们必须重复求解SDP问题, 而重复的次数是由要去除的边的数量决定的. 此外, 当工作场景的规模增长时, 解决SDP问题需要更长的时间. 然而, 随着智能体数量的增加, GNN花费的时间几乎没变, 可以推广到实时应用中去.

|
图 8 n=15–50时GNN与SDP-Step的计算时间 |
5.5 参数实验
本文提出的图神经网络的模型框架主要是参考设计空间的架构建立的. 根据实验尝试, 模型的部分参数设定对模型本身的性能没有太大的影响. 但是有些参数对模型的性能影响较大, 包括图神经网络层数、聚合函数、学习率、随机失活和批标准化. 在本节中, 我们通过实验来分析批标准化和随机失活这两个参数的设定与否对模型性能的影响, 以及图神经网络层数、聚合函数和学习率这些参数取不同的值时模型结果的变化. 实验中默认的参数设置为: GNN层数为3层, 聚合函数为MEAN, 学习率为0.01, 随机失活为0.3以及批标准化为True. 实验仍然以SDP-Step的解作为基准, 即每个模型的代数连通度与SDP-Step的代数连通度的比值作为指标衡量模型性能好坏, 测试的任务场景规模为n=20.
5.5.1 批标准化与随机失活批标准化和随机失活都是可以有效减少模型过拟合的一种方式. 批标准化是模型对每层的输入都进行了归一化处理, 随机失活则是随机舍弃一部分邻点传递过来的信息. 这里批标准化参数取值范围为{True, False}, 即采用批标准化和不采用批标准化, 随机失活参数取值范围为{False, 0.3, 0.6}, 即不采用随机失活、采用并设为0.3和设为0.6. 为了综合测试这两个参数的设定对模型效果的影响, 对这两组参数取值两两组合, 共进行了6次实验. 实验结果如图9所示. 横轴标签中“-”左侧是批标准化的取值, T对应True, F对应False. 右侧对应随机失活的取值, F对应False, 0.3和0.6对应本身的值. 纵坐标为模型的代数连通度与SDP-Step的代数连通度的比值. 可以看出, 虽然批标准化对模型性能的提升非常有限, 但是采用批标准化比不采用表现确实更好一些. 另外, 一定的随机失活可以使模型的泛化能力更强表现更稳定可靠, 但是取值较大时无法充分获取图上的信息, 模型性能表现较差.

|
图 9 批标准化与随机失活参数分析 |
5.5.2 图神经网络层数
当图神经网络层数为一层时, 意味着每个节点只获取了其一阶邻点的信息. 随着图神经网络层数的增加, 每个节点能由近及远获取到图中更多节点的信息. 此处层数取值范围为{1, 2, 3, 4, 5, 6, 7}, 实验结果如图10所示. 横坐标为图神经网络的层数, 纵坐标为模型的代数连通度与SDP-Step的代数连通度的比值. 从图10中可以看出, 图神经网络层数为1层时模型效果差很多, 2层时相对较差. 当层数为3层以上时, 模型表现逐渐变差, 但比1–2层要好一些. 因此图神经网络层数选择3层是合适的.
5.5.3 聚合函数本文考虑的聚合函数的取值范围为{MAX, SUM, MEAN}. 实验结果如图11(a)所示. 横坐标为聚合函数的取值, 纵坐标为模型的代数连通度与SDP-Step的代数连通度的比值. 可以看出, 选择MEAN作为聚合函数模型的性能会优于MAX和SUM, 分别高了5.54%和2.55%. 可以推测MEAN优于MAX是因为本文的问题虽然是链接预测任务, 但是连通度的衡量是基于整个图的, 相比之下MEAN获取的邻点的信息更加全面一些. 根据实验结果来看, 聚合函数推荐使用MEAN.

|
图 10 图神经网络层数参数分析 |

|
图 11 聚合函数和学习率参数分析 |
5.5.4 学习率
本文考虑的学习率的取值范围为{0.0001, 0.001, 0.01, 0.1}. 实验结果如图11(b)所示. 横坐标为学习率参数的取值, 纵坐标为模型的代数连通度与SDP-Step的代数连通度的比值. 可以发现当学习率较小和较大时, 模型的性能均表现不佳. 当学习率过小时, 模型每次更新的步长更小, 收敛速度慢, 而当学习率过大时, 模型参数在训练过程中波动较大, 难以收敛. 从实验结果来看, 学习率设置为0.01是更合适的.
6 结论本文提出了一种基于图神经网络的最大化代数连通度算法. 该算法学习如何在大量潜在通信链路中去除一部分链路以降低系统损耗的同时保持尽可能大的代数连通度. 传统的优化和启发式算法随着智能体的数量的增加消耗的时间骤增, 而GNN模型消耗的时间和计算成本几乎不变. 该GNN模型是一种监督模型, 需要使用传统算法生成参考解集. 然而, 对于组合优化问题, 好的解集不是唯一的, 甚至相同性能的两种解集完全不同. 对于一个有监督的模型, 解集中发生一两个边的偏差也可能会导致更糟糕的结果. 一个自然的问题是, 我们是否能找到一个更好的模型, 可以自发地探索最大化代数连通度的问题, 更智能地适应更大规模的任务场景, 同时表现更好. 这是我们未来尝试要解决的问题.
| [1] |
Fiedler M. Algebraic connectivity of graphs. Czechoslovak Mathematical Journal, 1973, 23(2): 298-305. DOI:10.21136/CMJ.1973.101168 |
| [2] |
Lumbanraja EMU, Sugeng KA, Hariadi N. Algebraic connectivity optimization in flight routes addition problem using tabu search method. AIP Conference Proceedings, 2017, 1862(1): 030137. DOI:10.1063/1.4991241 |
| [3] |
Wei P, Sun DF. Weighted algebraic connectivity: An application to airport transportation network. IFAC Proceedings Volumes, 2011, 44(1): 13864-13869. DOI:10.3182/20110828-6-IT-1002.00486 |
| [4] |
Cheung KF, Bell MGH. Improving connectivity of compromised digital networks via algebraic connectivity maximisation. European Journal of Operational Research, 2021, 294(1): 353-364. DOI:10.1016/j.ejor.2021.01.015 |
| [5] |
Goddet E, Retière N, Stojanović V, et al. Maximizing the algebraic connectivity of meshed electrical pathways used as current return network. Mathematics and Computers in Simulation, 2019, 158: 18-31. DOI:10.1016/j.matcom.2018.05.002 |
| [6] |
Zhu JD. On consensus speed of multi-agent systems with double-integrator dynamics. Linear Algebra and Its Applications, 2011, 434(1): 294-306. DOI:10.1016/j.laa.2010.08.024 |
| [7] |
Fang C, Yu FR, Huang T, et al. Distributed energy consumption management in green content-centric networks via dual decomposition. IEEE Systems Journal, 2017, 11(2): 625-636. DOI:10.1109/JSYST.2015.2454231 |
| [8] |
Chen XZ, Zhang SG, Zhang LJ, et al. Determining redundant links of multiagent systems in keeping or improving consensus convergence rates. IEEE Systems Journal, 2022, 16(4): 6153-6163. DOI:10.1109/JSYST.2021.3130591 |
| [9] |
Mosk-Aoyama D. Maximum algebraic connectivity augmentation is NP-hard. Operations Research Letters, 2008, 36(6): 677-679. DOI:10.1016/j.orl.2008.09.001 |
| [10] |
Kim Y, Mesbahi M. On maximizing the second smallest eigenvalue of a state-dependent graph Laplacian. IEEE Transactions on Automatic Control, 2006, 51(1): 116-120. DOI:10.1109/TAC.2005.861710 |
| [11] |
Rafiee M, Bayen AM. Optimal network topology design in multi-agent systems for efficient average consensus. Proceedings of the 49th IEEE Conference on Decision and Control. Atlanta: IEEE, 2010. 3877–3883.
|
| [12] |
Dai R, Mesbahi M. Optimal topology design for dynamic networks. Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference. Orlando: IEEE, 2011. 1280–1285.
|
| [13] |
Ghosh A, Body SP. Growing well-connected graphs. Proceedings of the 45th IEEE Conference on Decision and Control. San Diego: IEEE, 2006. 6605–6611.
|
| [14] |
Kim Y. Bisection algorithm of increasing algebraic connectivity by adding an edge. IEEE Transactions on Automatic Control, 2010, 55(1): 170-174. DOI:10.1109/TAC.2009.2033763 |
| [15] |
Sydney A, Scoglio C, Gruenbacher D. Optimizing algebraic connectivity by edge rewiring. Applied Mathematics and Computation, 2013, 219(10): 5465-5479. DOI:10.1016/j.amc.2012.11.002 |
| [16] |
Wei P, Chen L, Sun D. Algebraic connectivity maximization of an air transportation network: The flight routes’ addition/deletion problem. Transportation Research Part E: Logistics and Transportation Review, 2014, 61: 13-27. DOI:10.1016/j.tre.2013.10.008 |
| [17] |
Li G, Hao ZF, Huang H, et al. Maximizing algebraic connectivity via minimum degree and maximum distance. IEEE Access, 2018, 6: 41249-41255. DOI:10.1109/ACCESS.2018.2857411 |
| [18] |
Trimble J, Pack D, Ruble Z. Connectivity tracking methods for a network of unmanned aerial vehicles. Proceedings of the 9th IEEE Annual Computing and Communication Workshop and Conference. Las Vegas: IEEE, 2019. 440–447.
|
| [19] |
Scarselli F, Gori M, Tsoi AC, et al. The graph neural network model. IEEE Transactions on Neural Networks, 2009, 20(1): 61-80. DOI:10.1109/TNN.2008.2005605 |
| [20] |
Kipf TN, Welling M. Semi-supervised classification with graph convolutional networks. arXiv:1609.02907, 2017.
|
| [21] |
Hamilton WL, Ying Z, Leskovec J. Inductive representation learning on large graphs. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 1025–1035.
|
| [22] |
Veličković P, Cucurull G, Casanova A, et al. Graph attention networks. Proceedings of the 6th International Conference on Learning Representations. Vancouver: ICLR, 2018.
|
| [23] |
You JX, Ying R, Leskovec J. Design space for graph neural networks. Proceedings of the 34th International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2020. 1427.
|
| [24] |
Ying R, He RN, Chen KF, et al. Graph convolutional neural networks for Web-scale recommender systems. Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. London: Association for Computing Machinery. 2018. 974–983.
|
| [25] |
You JX, Liu BC, Ying R, et al. Hierarchical temporal convolutional networks for dynamic recommender systems. Companion Proceedings of the 2019 World Wide Web Conference. San Francisco: ACM, 2019. 2236–2246.
|
| [26] |
Qu ZG, Liu XZ, Zheng M. Temporal-spatial quantum graph convolutional neural network based on Schrödinger approach for traffic congestion prediction. IEEE Transactions on Intelligent Transportation Systems, 2023, 24(8): 8677-8686. DOI:10.1109/TITS.2022.3203791 |
| [27] |
Gao JL, Lyu T, Xiong F, et al. Predicting the survival of cancer patients with multimodal graph neural network. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2022, 19(2): 699-709. DOI:10.1109/TCBB.2021.3083566 |
| [28] |
Aslan Hİ, Ko H, Choi C. Classification of vertices on social networks by multiple approaches. Mathematical Biosciences and Engineering, 2022, 19(12): 12146-12159. DOI:10.3934/mbe.2022565 |
| [29] |
Zavlanos MM, Egerstedt MB, Pappas GJ. Graph-theoretic connectivity control of mobile robot networks. Proceedings of the IEEE, 2011, 99(9): 1525-1540. DOI:10.1109/JPROC.2011.2157884 |
| [30] |
Nagarajan H, Rathinam S, Darbha S, et al. Algorithms for synthesizing mechanical systems with maximal natural frequencies. Nonlinear Analysis: Real World Applications, 2012, 13(5): 2154-2162. DOI:10.1016/j.nonrwa.2012.01.010 |
| [31] |
Glover F. Tabu search—Part I. ORSA Journal on Computing, 1989, 1(3): 190-206. DOI:10.1287/ijoc.1.3.190 |
| [32] |
Jafarizadeh S. Fastest mixing reversible Markov chain on friendship graph: Trade-off between transition probabilities among friends and convergence rate. Systems & Control Letters, 2019, 130: 13-22. |
| [33] |
Jafarizadeh S. Fastest mixing reversible Markov chain: Clique lifted graphs and subgraphs. IEEE Transactions on Signal and Information Processing over Networks, 2020, 6: 88-104. DOI:10.1109/TSIPN.2020.2964211 |
 2024, Vol. 33
2024, Vol. 33



