2. 辽宁石油化工大学 人工智能与软件学院, 抚顺 113001
2. School of Artificial Intelligence and Software, Liaoning Petrochemical University, Fushun 113001, China
在带钢热镀锌生产线中, 受到退火炉内各段温度、张力的影响, 带钢的长度会不断变化, 这对获取退火炉内各辊的转速造成了很大困扰, 也因此难以计算两卷带钢之间的焊缝到达气刀处的准确时间, 而这会威胁气刀的安全. 为了得到焊缝的实时位置, 王超提出使用优化支持向量机[1]、极限学习机算法[2]对带钢进入退火炉后的延伸量进行预测以计算焊缝的位置, 冯兴隆[3]分别提出多元线性回归、支持向量机和改进支持向量机对焊缝通过退火炉的时长进行预测. 但这些作者都对问题进行了简化, 没有直接使用原始数据, 而是将焊缝进出退火炉这段时间内测得的一组原始数据求平均值后压缩成一条记录. 基于压缩后的数据提出的模型虽然在退火炉的设定参数变化不大的情况下表现良好, 但却无力应对实际生产过程中退火炉的设定参数有较大调整的情况. 与此同时, 区别于Autoformer[4]、FEDformer[5]和Informer[6]等模型适用的连续性长时间序列, 带钢焊缝原始数据是分组式的, 时间上不连续且长度不大, 因此一般性的时间序列预测模型难以直接应用于退火炉内分组式辊速序列预测.
原始Transformer模型存在容易忽略局部依赖关系、时间和空间复杂度高的缺点[7]. 为了增强自注意力捕获局部依赖关系的能力, Gao等人[8]提出基于自注意力的时变网络SATVNN模型, 并分别测试了在自注意力中加入基于相对位置计算的高斯分布权重值、拉普拉斯分布权重值、柯西分布权重值, 用于提高相邻输入序列的重要程度, 帮助模型更快地捕捉时间序列的局部依赖关系. 而为了降低Transformer模型中自注意力的复杂度, Ainslie 等人[9]提出的ETC模型、Zaheer 等人[10]提出的Big Bird模型利用自注意力矩阵在大多数数据点上都非常稀疏的特点, 采用了随机注意、滑动窗口注意、全局注意相结合的方式[11], 将自注意力的复杂度由二次方降低为线性, 克服了Transformer模型时间和空间复杂度高的缺点.
本文结合带钢生产数据的实际特点, 在Transformer模型的基础上提出了使用带状稀疏的柯西自注意力的BSCWEformer模型, 成功地将Transformer模型应用于分组式辊速序列预测任务. BSCWEformer模型仅使用Transformer模型的解码器部分, 并在自注意力中加入基于相对位置计算的柯西分布权重值, 增强了模型捕捉时间序列动态变化的能力. 与此同时, 根据生产数据具有天然的局部相关性的特点, 模型采用了带状稀疏的自注意力, 在不影响模型预测准确度的前提下, 极大地降低了模型的时间和空间复杂度, 并且实现简单, 避免了ETC等模型需要特殊的库支持、实现复杂且在分组式辊速序列预测任务中的有效性难以估计的缺点.
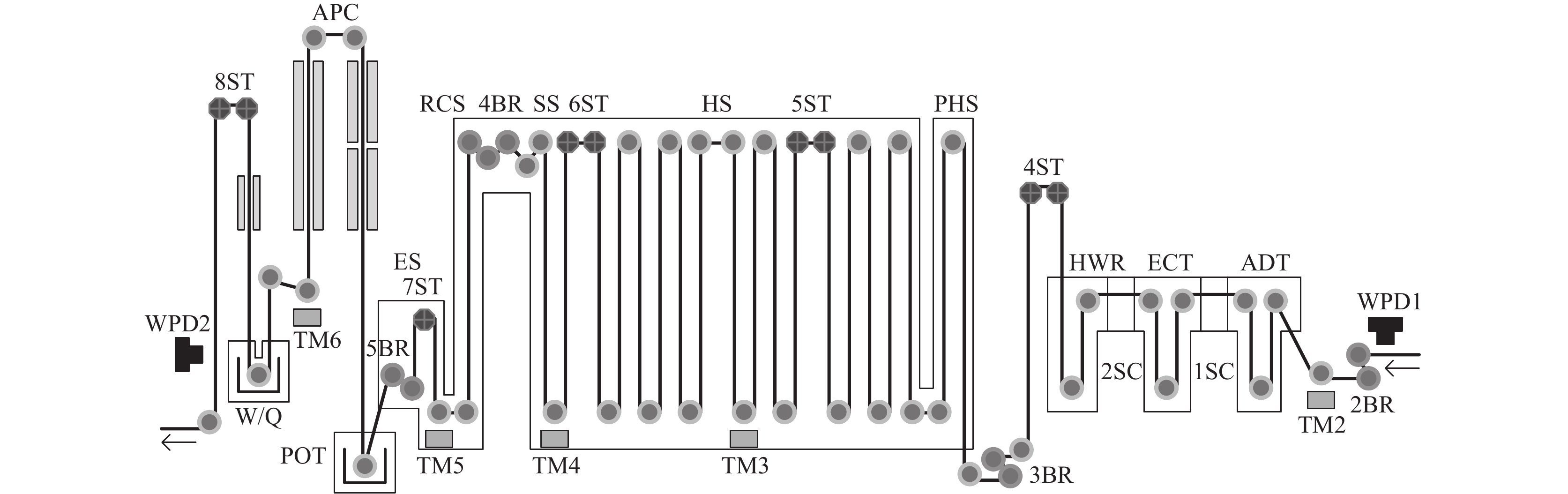
1 退火炉内辊速预测问题简介退火炉的结构可分为预热段(PHS)、还原加热段(HS)、还原均热段(SS)、冷却段(RCS)、均衡段(ES)、锌锅(POT)等, 如图1所示, 锌锅(POT)后 1.7 m 左右为气刀所在位置, 用于控制带钢表面镀锌的厚度, 平时关闭, 在带钢焊缝经过时打开[12,13]. 带钢进入退火炉后, 在各段温度和张力作用下, 其长度会发生变化, 导致2BR、3BR、4BR、5BR处各辊的转速发生改变, 带钢焊缝也将难以准确定位, 从而无法确定焊缝到达气刀处的准确时间, 可能造成气刀的损坏.
|
图 1 退火炉内带钢热镀锌工艺流程图 |
退火炉内的设备记录了带钢焊缝从WPD1处到WPD2处这段时间内各段温度、张力的时序数据. 需要根据这一组时序数据预测图1中2BR、3BR、4BR、5BR处的辊的转速, 从而计算带钢焊缝经过WPD1后多久到达气刀处.
可以将各段温度、张力数据视为输入序列
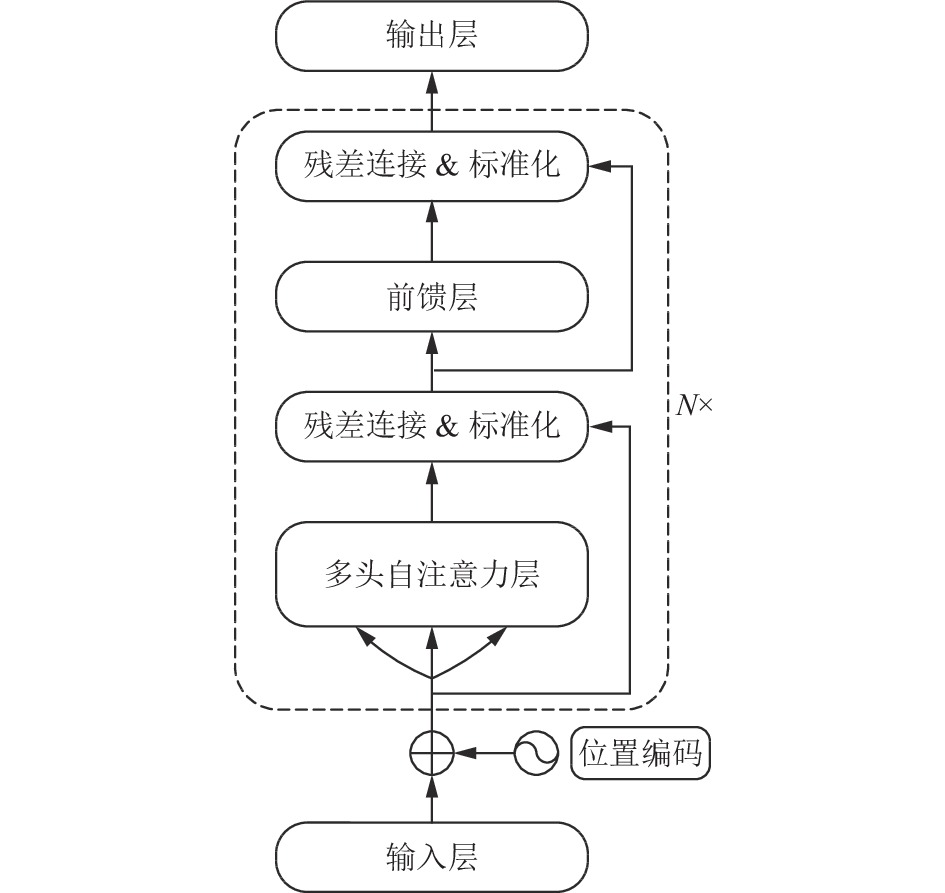
为了能够将温度、张力等分组式输入序列映射成对应的辊速目标序列, BSCWEformer模型仅采用Transformer模型的解码器部分, 如图2所示, 并且使用带状稀疏的柯西自注意力代替Transformer模型中的自注意力. 通过在自注意力中加入基于输入序列之间的相对位置计算的柯西分布权重值, 增强模型捕捉输入序列动态变化的能力, 同时通过对原始自注意力进行带状的稀疏化, 降低模型的时间和空间复杂度.
|
图 2 模型的总体结构 |
2.1 自注意力实现带状稀疏的过程
与Transformer模型的自注意力不同, 带状稀疏的自注意力限制了目标序列预测需要关注的输入序列的范围. 在保证模型预测准确度的前提下, 通过将关注范围限制在较小的范围内, 避免了计算全部自注意力矩阵的时空开销, 从而降低自注意力的复杂度. 其实现方法是将原始自注意力中的查询、键和值先按规则进行分块, 然后再逐块计算分块自注意力, 避免了在Transformer模型中每个自注意力得分的计算都需要所有输入序列参与的复杂性, 其具体过程如下.
步骤1. 将温度、张力序列
步骤2. 设置自注意力层多头数量为
步骤3. 将
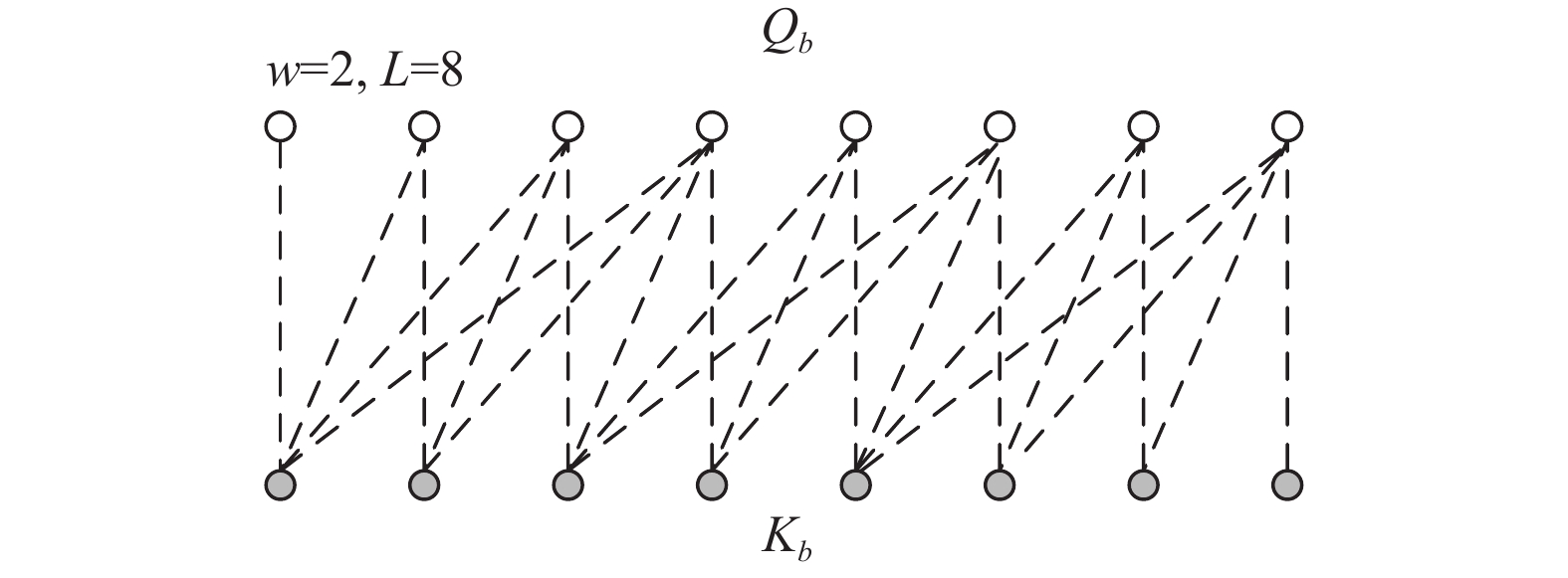
步骤4. 设置带状稀疏自注意力的分块大小为
|
图 3 分块后的Q、K关联示意 |
步骤5. 将
步骤6. 与
步骤7. 与
与原始自注意力中直接计算
为了克服原始自注意力不易捕获局部依赖关系的缺点, BSCWEformer模型在自注意力中加入了柯西权重值, 提高了相邻序列的重要性, 称为柯西自注意力. 通过将温度、张力序列的相对距离信息加入到自注意力中, 提高最近的温度、张力序列的信息比重, 即越新的数据越重要, 保留的信息越多. 输入序列的重要性也会随着相对距离的增加而缓慢降低, 使模型能够更好地捕捉时序数据的动态变化.
柯西权重矩阵
| $ C = \left( {\begin{array}{*{20}{c}} {{c_{11}}}& \ldots &{{c_{1\left( {2w} \right)}}} \\ \vdots & \ddots & \vdots \\ {{c_{w1}}}& \cdots &{{c_{w\left( {2w} \right)}}} \end{array}} \right) $ |
其中,
| $ {c_{ij}} = \frac{\gamma }{{1 + \lambda {{\left| {i - j} \right|}^2}}} $ |
其中,
BSCWEformer模型柯西自注意力的计算过程如下:
| $ {S_1} = \frac{{{Q_b}{{\left( {{K_b}} \right)}^{\rm{T}}}}}{{\sqrt {{d_x}} }} $ | (1) |
其中,
| $ {S_2} = {S_1} + C $ | (2) |
其中,
| $ {S_3} = {S_2} + M $ | (3) |
其中,
| $ O = {\textit{Softmax}}\left( {{S_3}} \right){V_b} $ | (4) |
其中,
| $ O'' = {\textit{Linear}}\left( {O'} \right) $ | (5) |
其中,
观察生产数据的分布规律, 正常的一组生产数据中应该包含数百条连续的记录, 并且只有两个卷号的交替, 而且两组之间的时间间隔十几分钟或几十分钟不等, 然后通过以下步骤预处理数据并划分训练集和测试集.
1) 清除时间上孤立的异常数据, 即一段时间内只有一条或几条记录的数据.
2) 对数据进行分组, 只保留包含两个卷号的正常分组.
3) 剔除与预测任务无关的特征, 如卷号等.
4) 将所有分组数据随机打乱先后顺序后, 按照7:3的比例划分训练集和测试集.
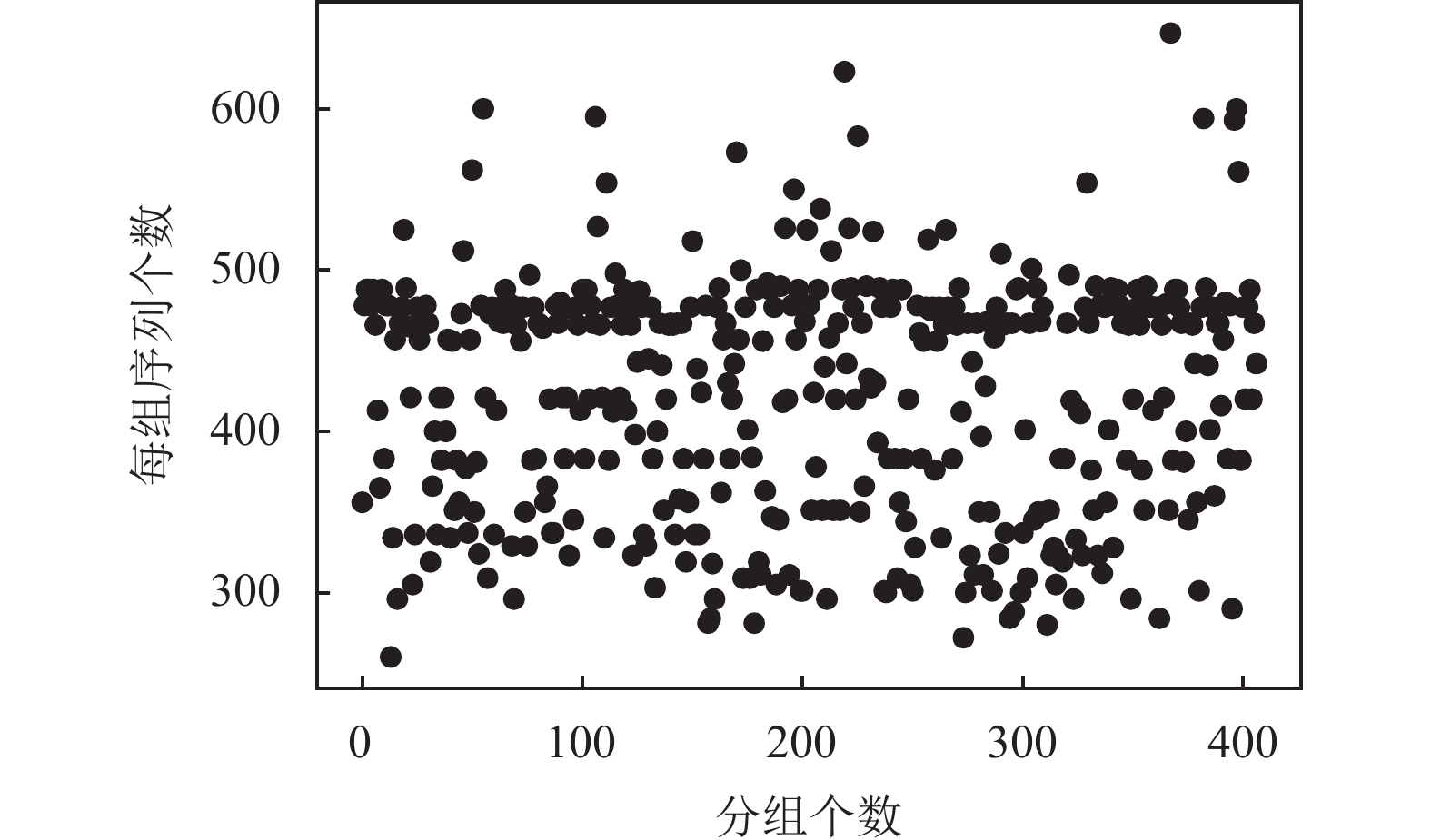
经过上述步骤处理后, 得到训练集数据949组, 测试集数据407组, 每组序列长度300–700不等, 如图4所示. 输入序列
|
图 4 测试集各组序列的长度 |
| 表 1 生产数据整理后的属性 |
3.2 参数设置与模型对比
BSCWEformer模型的超参数设置: 除输入、输出层外, 共有
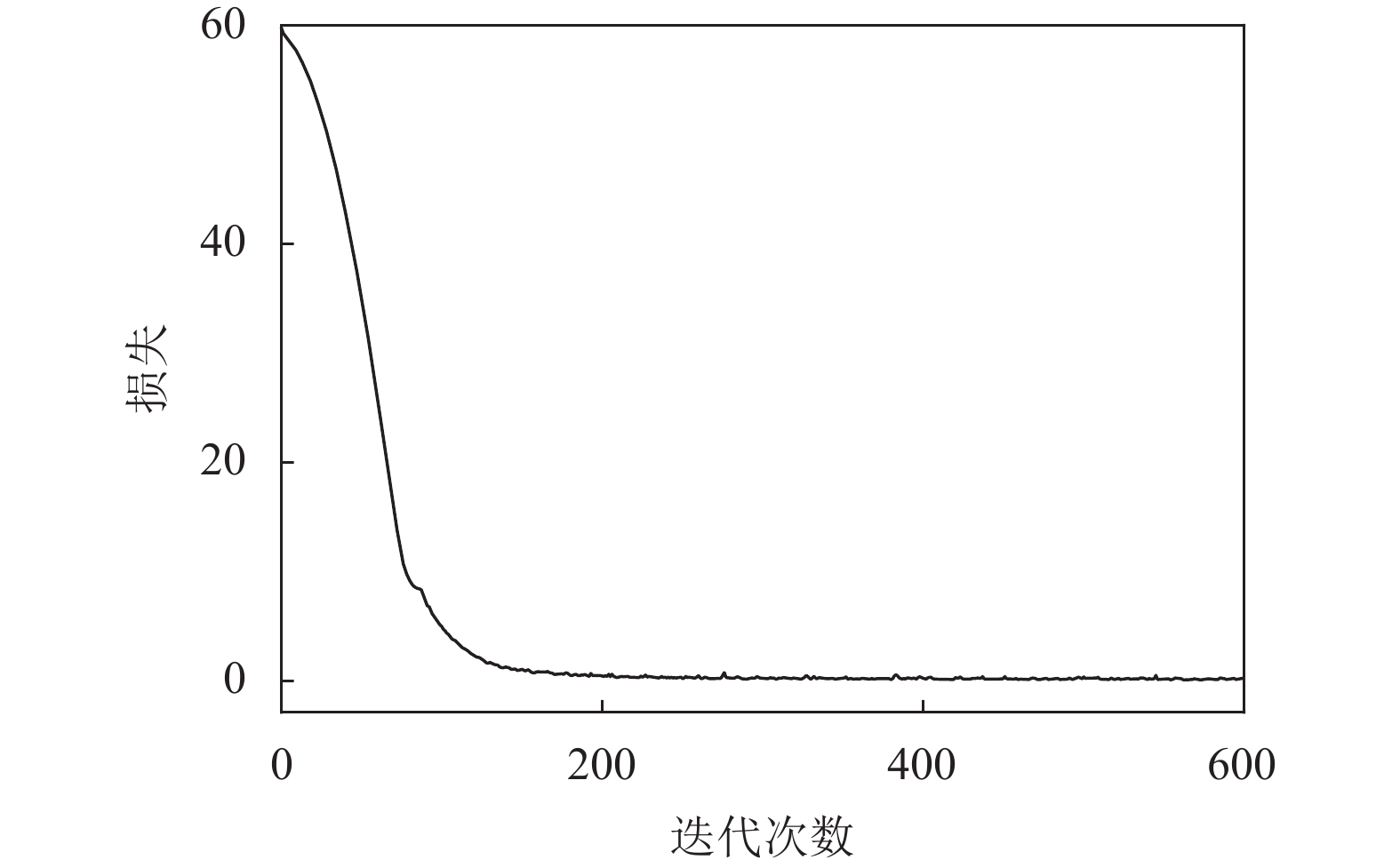
|
图 5 损失收敛曲线 |
与此同时, 本文选择了几个适用于分组式时间序列预测任务的模型作为基准模型, 包括前馈神经网络(FNN)、LSTM[14]、LSTMa[15]、RNMT+[16]、Transformer[17]、LogSparse Transformer[18]. 其中, LSTMa模型使用Luong注意力; RNMT+由LSTM和多头自注意力堆叠而成, 常用于机器翻译; LogSparse Transformer模型使用因果卷积获取查询和键, 简写为LogTrans, Transformer简写为Trans.
此外, 本文比较了所有模型的时间和空间复杂度, 以及在生产过程中实际预测必需的迭代次数, 如表2.
得益于带状稀疏的自注意力, BSCWEformer模型拥有线性的时间和空间复杂度, 对比原始Transformer等模型复杂度大大降低. 并且在实际生产过程中, FNN、RNMT+、Transformer模型需要完全实时地根据每一条输入序列预测辊速输出序列以计算焊缝在退火炉内的位置, 因此实际预测时的时间复杂度为
| 表 2 各模型复杂度对比 |
3.3 结果与分析
通过407组测试数据对所有模型进行测试, 并将平均绝对误差(MAE)、平均绝对百分比误差(MAPE)作为评价指标, 各模型在所有分组测试数据上的MAE损失如图6所示.
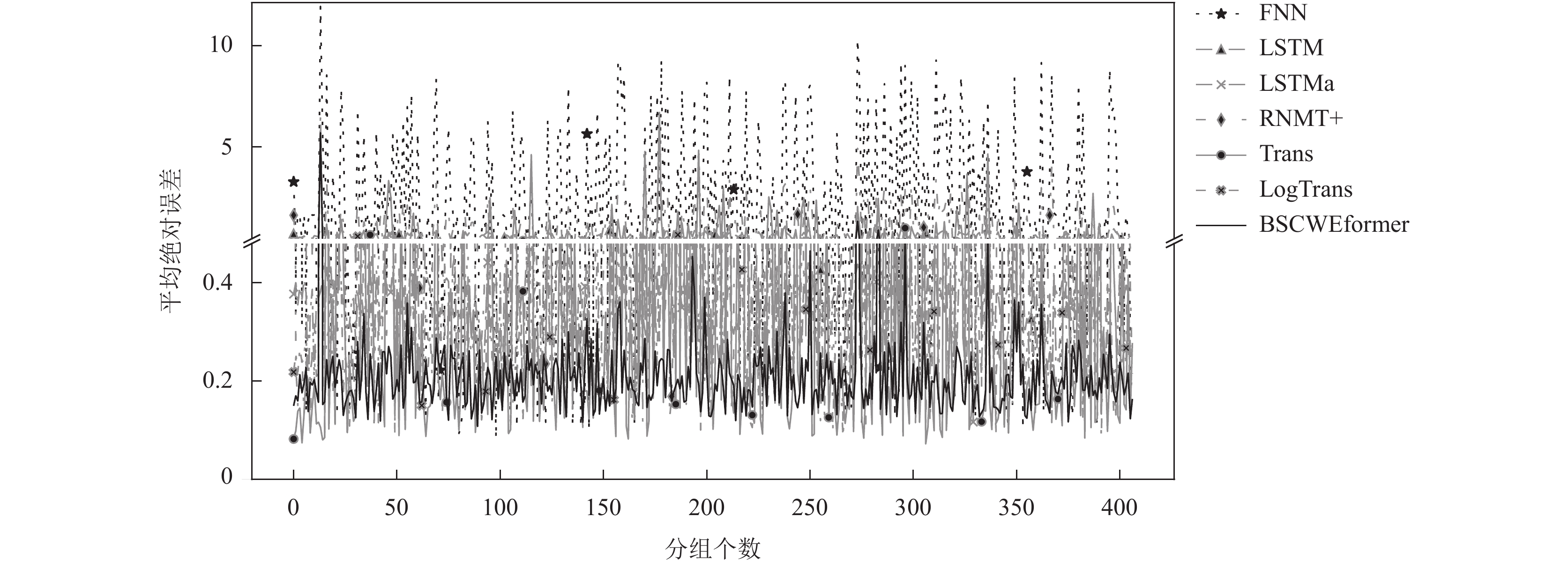
|
图 6 所有模型在测试集上每组测试数据的MAE |
图6中较大的波动, 主要由于某组温度、张力序列中的机组速度、温度、张力等属性的突然变化, 导致预测损失的剧烈波动. 从图6可以看出, FNN模型在测试集上的MAE预测损失波动最为剧烈, 其次是RNMT+和Transformer模型. 而LSTM、LSTMa、LogTrans、BSCWEformer模型的MAE预测损失明显更加平稳, 并且LSTMa和LogTrans、BSCWEformer模型的MAE预测损失始终处于LSTM之下. 其中, BSCWEformer模型的MAE预测损失显著低于其他模型, 其折线始终处于最底端, 并且波动不大, 证明了模型的准确性和稳定性.
各模型在所有测试数据上的总体MAE损失如图7所示. 与图6显示的结果相对应, BSCWEformer模型的总体MAE最低, 在分组式辊速序列预测任务上的表现最好. 各模型在所有评价指标上的测试结果, 如表3所示.
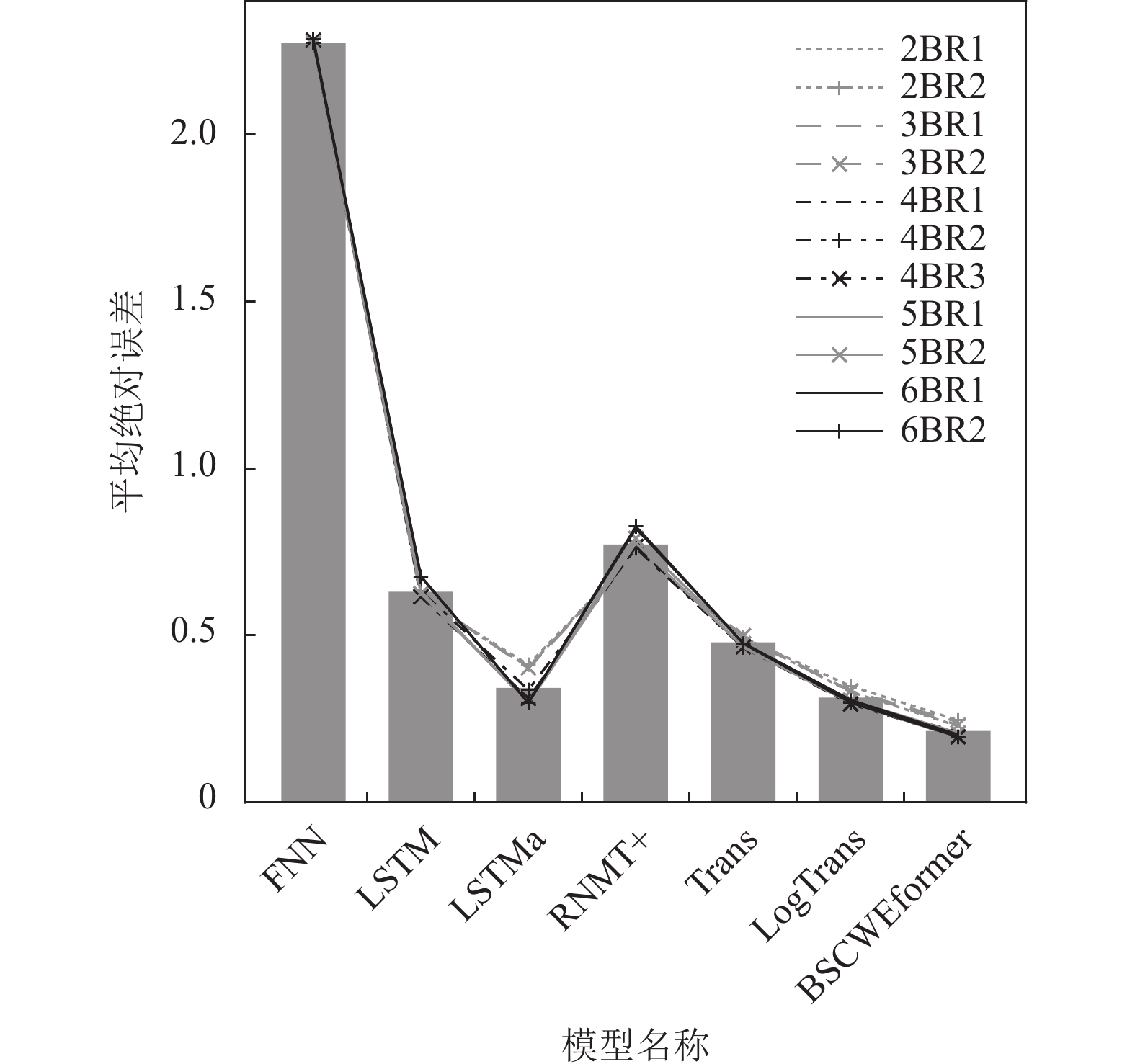
|
图 7 各模型总体MAE |
| 表 3 各模型在所有测试数据上的详细MAE和MAPE |
从表3中的测试结果可以看出, 前馈神经网络(FNN)在完全不关注之前多个温度、张力序列对当前辊速序列预测的累积作用的情况下的预测结果最差; 而结构复杂、参数众多的RNMT+模型的预测损失虽然相对于FNN大幅降低, 但预测结果也比较差, 说明复杂的模型未必适合于分组式辊速序列的预测; LSTM模型的MAE预测损失相较于RNMT+模型降低约18%, 加上Luong式点积注意力后MAE预测损失再次降低了45%; Transformer模型的MAE预测损失虽然相对于LSTM降低了24%, 但内存占用高, 只能以较小的批量进行训练, 训练时间长; LogSparse Transformer模型的预测效果相对于Transformer模型提升明显, 其MAE预测损失降低了34%, 但是其采用的是对数形式的稀疏自注意力, 在分组式辊速序列预测任务中节省的空间很有限, 却需要复杂的额外实现. 本文提出的BSCWEformer模型预测效果最好, 其MAE预测损失相对于Transformer模型降低了55%, 且内存占用少, 可以设置较大的批量进行训练.
4 结论与展望本文提出的BSCWEformer模型成功地将Transformer模型应用于分组式辊速序列预测, 具有模型结构简单、复杂度低、善于捕获局部依赖关系的优点. 经过实际生产数据的测试, 对比其他多种模型, 验证了本文提出的BSCWEformer模型的性能和准确度. 针对生产现场无法安装焊缝检测设备的实际情况, BSCWEformer模型利用现有设备的测量数据, 能够准确地预测连续热镀锌工艺过程中退火炉内各个辊的转速, 为计算焊缝到达气刀处的准确时间提供了依据, 从而可以精准地控制气刀的开合, 对提高带钢镀锌的成品率并保障气刀的安全具有重要意义.
| [1] |
王超, 王建辉, 顾树生, 等. 基于优化支持向量机的带钢延伸量软测量研究. 东北大学学报(自然科学版), 2015, 36(8): 1084-1088. DOI:10.3969/j.issn.1005-3026.2015.08.005 |
| [2] |
Wang C, Wang JH, Gu SS, et al. Elongation prediction of steel-strips in annealing furnace with deep learning via improved incremental extreme learning machine. International Journal of Control, Automation and Systems, 2017, 15(3): 1466-1477. DOI:10.1007/s12555-015-0463-7 |
| [3] |
冯兴隆. 镀锌生产线退火炉焊缝跟踪的数学模型研究 [硕士学位论文]. 沈阳: 东北大学, 2016.
|
| [4] |
Wu HX, Xu JH, Wang JM, et al. Autoformer: Decomposition Transformers with auto-correlation for long-term series forecasting. Proceedings of the 35th International Conference on Neural Information Processing Systems. 2021. 22419–22430.
|
| [5] |
Zhou T, Ma ZQ, Wen QS, et al. FEDformer: Frequency enhanced decomposed Transformer for long-term series forecasting. Proceedings of the 2022 International Conference on Machine Learning. Baltimore: Proceedings of Machine Learning Research, 2022. 27268–27286.
|
| [6] |
Zhou HY, Zhang SH, Peng JQ, et al. Informer: Beyond efficient Transformer for long sequence time-series forecasting. Proceedings of the 35th AAAI Conference on Artificial Intelligence. Palo Alto: AAAI Press, 2021. 11106–11115.
|
| [7] |
Huang SZ, Tang EH, Li S, et al. Hardware-friendly compression and hardware acceleration for Transformer: A survey. Electronic Research Archive, 2022, 30(10): 3755-3785. DOI:10.3934/era.2022192 |
| [8] |
Gao CX, Zhang N, Li YR, et al. Self-attention-based time-variant neural networks for multi-step time series forecasting. Neural Computing and Applications, 2022, 34(11): 8737-8754. DOI:10.1007/s00521-021-06871-1 |
| [9] |
Ainslie J, Ontanon S, Alberti C, et al. ETC: Encoding long and structured inputs in Transformers. Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing. Punta Cana: Association for Computational Linguistics, 2020. 268–284.
|
| [10] |
Zaheer M, Guruganesh G, Dubey A, et al. Big Bird: Transformers for longer sequences. Proceedings of the 34th International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2020. 1450.
|
| [11] |
Lin TY, Wang YX, Liu XY, et al. A survey of Transformers. AI Open, 2022, 3: 111-132. DOI:10.1016/j.aiopen.2022.10.001 |
| [12] |
王超. 极限学习机算法及其在热镀锌生产过程建模中的应用研究 [博士学位论文]. 沈阳: 东北大学, 2016.
|
| [13] |
刘明达. 基于模糊自适应的锌层厚度预测控制研究 [硕士学位论文]. 沈阳: 东北大学, 2015.
|
| [14] |
王菲. LSTM循环神经网络的研究进展与应用 [硕士学位论文]. 哈尔滨: 黑龙江大学, 2021.
|
| [15] |
Luong T, Pham H, Manning CD. Effective approaches to attention-based neural machine translation. Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing. Lisbon: Association for Computational Linguistics, 2015. 1412–1421.
|
| [16] |
Chen MX, Firat O, Bapna A, et al. The best of both worlds: Combining recent advances in neural machine translation. Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics. Melbourne: Association for Computational Linguistics, 2018. 76–86.
|
| [17] |
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 6000–6010.
|
| [18] |
Li SY, Jin XY, Xuan Y, et al. Enhancing the locality and breaking the memory bottleneck of Transformer on time series forecasting. Proceedings of the 33rd International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2019. 471.
|
 2024, Vol. 33
2024, Vol. 33


