2. 贝尔法斯特女王大学 电子学、电气工程与计算机科学学院, 贝尔法斯特 BT9 5BN
2. School of Electronics, Electrical Engineering and Computer Science, Queen’s University Belfast, Belfast BT9 5BN, UK
高光谱图像(hyperspectral image, HSI)包含了数百个连续波段, 具有非常高的光谱分辨率, 这其中包含了大量的光谱和空间信息. 这些物理特性, 可以使分类时的“同谱异物”和“同物异谱”的现象减少, 可以应用于精准区分相似的地物分辨识别. 如今, HSI分类已广泛应用于诸多领域, 例如环境监测、林业监测、灾害防治、环境评价等[1,2].
在过去的几十年里, HSI分类通过机器学习[3]得到了很大的发展. 在机器学习中, 有许多分类方法是通过利用HSI丰富的光谱特征来进行HSI分类, 包括主成分分析(PCA)[4]、支持向量机(SVM)[5]和随机森林(RF)[6]等方法. 然而, 机器学习方法的网络层次往往数量较少, 网络结构深度不够, 从而限制了模型对HSI特征提取能力以及模型在不同场景下的泛用性, 这使得机器学习方法可能会在高光谱图像分类这一领域的进一步探索受到阻碍.
近年来, 深度学习(deep learning, DL)被广泛应用于HSI分类[7], 相较于机器学习算法, 深度学习能够更好地完成分类任务. 深度学习典型的框架有卷积神经网络(CNN)[8]、图卷积网络(GCNs)[9]、循环神经网络(RNN)[10]和Transformer[11]等, 这些框架均被大量应用于高光谱图像分类领域的研究.
由于HSI人工标注困难, 样本量少的特性, 少样本学习(few-shot learning, FSL)的研究逐渐成为高光谱分类领域研究者们的目标. 虽然深度学习在HSI分类任务上成效显著, 但是如果在训练样本数量过少的情形下, 深度学习模型很容易面临过拟合的困境. 并且根据数据集包含的种类信息, 有部分种类样本数量存在显著差异, 若选取过少的样本会使模型出现过拟合现象, 难以正确分类. 而FSL可以减少模型所需的标注样本量, 满足HSI标记样本量较少的情况, 从而降低标记困难带来的不利影响, 还能够通过轻量级的模型结构降低模型训练所需要的时间. 因此, 在HSI分类领域中对FSL方法的深入研究具有十分重要的意义.
2 研究现状目前, 已经有很多研究人员对HSI分类领域中的FSL方法展开研究[12]. Xue等人[13]提出了一个端对端的基于注意力的二阶池化网络, 通过设计了一个基于注意力的池化算子, 用于模拟判别特征和代表性特征. Zhang等人[14]采用残差三维卷积神经网络(CNN)作为特征提取网络, 引入contrast learning以学习更多的HSI判别性表示. Manifold等人[15]提出了一种新型的U-Net网络, 通过嵌套分别对高光谱图像进行空间学习和光谱学习, 可应用于多种领域. 但以上的FSL方法都是直接对样本进行训练分类, 并没有通过数据增强等方法增加训练样本量, 所以少样本带来的负面影响依旧存在.
除去上述的使用CNN的FSL方法, Siamese network也是FSL领域中一个常用的方法. Siamese network具有双分支结构, 传统的Siamese network就被用于人脸识别的场景, 比对两个输入图片的特征并返回一个相似度结果, 属于度量模型. 通过计算特征相似度来确定输入中一对样本是否匹配. 在这几年不断发展下, Siamese network可以实现多分类的任务, 即确定样本对属于哪个类别. 通过计算每个样本的交叉熵损失进行分类, 产生类概率能够在测试阶段直接获得分类结果, 并且具有鲁棒性. 在标记样本有限的情况下, 能够通过构建任意数量的样本对来进行数据增强. Siamese network与上述方法的不同之处在于能够通过将两个样本进行样本对配对, 从而实现训练样本的数据增强效果, 降低样本数量少带来的不利影响, 并且在通过编码后将样本映射到样本空间中, 通过contrast loss对拉近同类样本的类内距离, 拉远不同类样本的类间距离, 更好地提升模型的分类能力.
虽然已有大量的研究人员对Siamese network在HSI分类领域上进行了探索, 但在标记样本较少的情况下提高分类性能仍然是一个值得进一步探究的方向. Cheng等人[16]提出了一个具有原型自校准(SC)和互校准(IC)的Siamese原型网络(SPNet), 利用两个额外的损失函数来校准模型, 有助于模型学习到更具代表性的原型, 并做出更准确的预测. Cao等人[17]设计了一个端对端的三维卷积组成的Siamese network, 并加入了对比训练提升类间分类和类内分类的能力. Xue等人[18]采用了将一维卷积和二维卷积组合的方法降低了参数量, 并考虑了使用不同大小的空间窗口大小输入可以提供更多的特征以及设计加权损失优化模型. 但以上的算法在样本对构建时, 都是选择直接在原HSI上进行随机选取获取训练样本. 但经过调查大量公开遥感数据集后, 可以得出高光谱遥感图像的各个种类在空间上的分布大多是块状的结论. 上述算法没有考虑到在HSI空间上的分布情况, 存在出现随机选取的样本点之间的间距过小的可能性, 从而导致模型在进行空间上的特征提取时导致信息冗余. 针对高光谱遥感图像的分布规律, 我们采用了间隔选取和边缘样本选取相结合的方法进行样本选取, 再在这个基础上进行两两配对, 极大程度的获取该种类的信息, 实验结果表明, 在这个样本选取方法能够比随机选取的算法得到的分类结果更好.
近年来, 注意力机制的运用也逐渐灵活, 有很多研究者不断提出新的想法. Liu等人[19]提出了一种使用多维CNN结合注意力机制模型, 在该模型中, 通过使用三维卷积层从HSI的3D数据中提取空间光谱特征. 之后再通过二维卷积层和一维卷积层在抽象水平上进一步学习空间和光谱特征. Feng等人[20]提出一种新型混合空谱特征级联融合网络(MSSFN), 利用三维残差模块和二维可分离空间残差模块提取混合空间光谱特征, 增强特征提取能力.
对于以上使用了注意力机制的算法, 大多都没有考虑作为训练样本的中心像素与邻域像素之间的相关性. 为此, 我们考虑了邻域像素与中心像素的相关性, 通过计算向量的余弦距离, 来生成二者之间的相似度, 并通过该相似度来判断邻域像素的重要性分布, 从而使得模型能够在训练时效果更好.
本文设计了一种基于注意力的Siamese network. 它首先利用一维卷积和二维卷积提取HSI的光谱空间信息, 然后利用全局平均池化(GAP)进行分类, 进一步降低网络参数和模型复杂度. 其次, 通过样本对的差异化输入, 能够获取更多的样本对, 并通过设置伪标签对每一类的训练样本对数量进行控制, 避免了部分类别样本数过多或过少带来的过拟合或欠拟合影响, 同时平衡了每类的正负样本对, 有利于更好地实现类内分类和类间分类. 最后, 添加了光谱注意力机制和空间相似度度量模块, 分别对光谱维度进行权重分布, 从而更高效地提取光谱信息特征, 同时对空间维度进行约束, 考虑中心向量与相邻向量之间存在的关系, 以达到更好的特征提取. 通过实验结果表明, 我们的工作与在部分数据集上随机选择的方法相比取得了较好的实验效果.
综上所述, 本文的主要创新点可以概括为以下几点.
1) 对训练样本的选取方法的改进. 综合考虑HSI中的信息样本分布规律, 减少冗余特征选取, 从而提升模型分类性能.
2) 采用了差异化输入. 我们选择的Siamese network在构建样本对时, 相较于采用相同大小补丁构建样本对, 采用差异化输入能够获得更多的样本对, 降低样本不足的影响.
3) 添加空间相似度度量模块. 以往的研究对样本邻域间的研究较少, 我们采用余弦相似度对中心向量及邻域向量进行相似度度量, 获得邻域像素的相关性分布, 利于模型训练.
3 基于注意力的Siamese network我们主要的想法是设计一个添加注意力机制的Siamese network用于少样本高光谱遥感图像分类任务. 下面主要介绍我们设计的模型结构以及添加的注意力模块.
3.1 模型结构我们构建了一个Siamese network框架, 其模型结构如图1所示, 其中Ws1表示大补丁的空间窗口大小, Ws2表示小补丁的空间窗口大小. 在该框架训练开始之前, 对原高光谱图像进行PCA处理, 降低维数至K, 再通过样本对配对来进行数据增强. 首先, 将大小两个补丁送入网络中进行特征提取. 在经过4层一维卷积层后, 采用光谱注意力模块对光谱特征进行重标定, 再将光谱维度与通道进行合并, 通过1层二维卷积层获得全局的光谱信息. 之后对提取到的特征, 我们选取中心的特征向量与相邻的特征向量进行相似度度量, 获得空间维度的权重图, 将权重与原特征图进行相加后, 再进行3层二维卷积层操作进行进一步空间特征提取. 最后通过全局平均池化层来获取分类的结果.
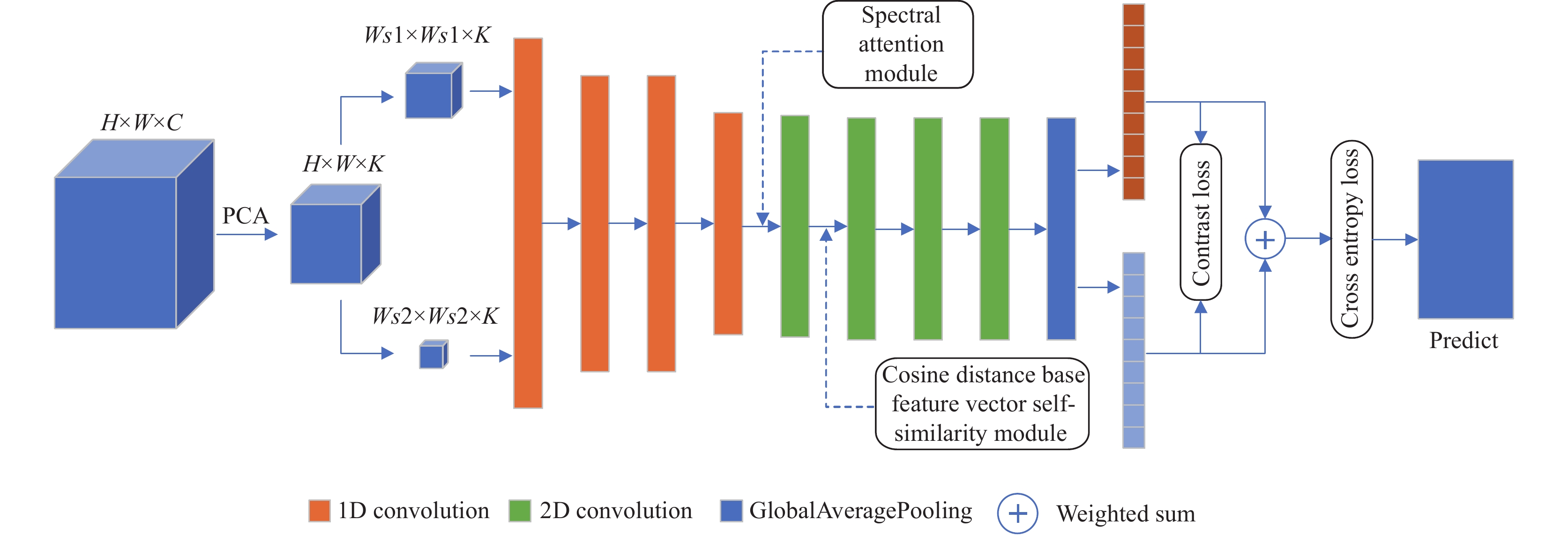
|
图 1 网络结构图 |
在分类任务中, 对于距离远的正样本和距离近的负样本往往被认为是困难样本, 会对实验结果带来较大的影响. 为此, 在训练过程中, 我们选择将输出的结果进行对比训练, 通过对比训练能够拉近类内距离, 增大类间距离, 有利于降低困难样本对实验结果的干扰. 同时, 我们在最后一层二维卷积后选取特征图中的中心向量来计算其欧氏距离作为权值, 有利于对比损失函数的拟合.
对于模型训练时的调优, 我们通过contrast loss和cross entropy loss对模型进行优化. 其中, 对比损失函数contrast loss, 我们添加了两个补丁块的中心向量之间的欧氏距离作为权值, 通过加权可以使得模型更加关注硬样本, 促使模型向正确的方向拟合. 交叉熵损失函数cross entropy loss是常用的多分类损失函数, 主要是用来判定实际的输出与期望的输出的接近程度.
算法1. 模型算法
输入: 整个epochs为N, PCA处理后的HSI图像中的补丁块X1, X2.
输出: 对整个图像的预测标签结果.
训练阶段:
1) 通过间隔采样与边缘采样相结合的取样方法, 选取训练样本作为训练集, 剩余样本作为测试集.
2) 根据训练样本索引选取补丁块, 将每个大补丁块与所有小补丁块进行两两配对, 获得训练样本对{P1, P2}.
3) for epoch from 1 to N do:
4) 将P1, P2输入模型中, 得到特征向量y1, y2
5) 根据y1, y2计算contrast loss
6) if {P1, P2}的中心为同一样本 then
7) 计算交叉熵损失cross entropy loss
8) 通过contrast loss和cross entropy loss和 Adam优化器对模型进行调优
9) end if
10) end for
测试阶段:
1) 根据测试样本索引选取补丁块, 将每个大补丁块与所有小补丁块进行两两配对, 获得训练样本对{P3, P4}
2) for epoch from 1 to N do:
3) 将P3, P4输入模型中, 得到特征向量y3, y4
4) 使用arg max(α×y3+β×y4)获得预测标签
5) end for
3.2 光谱注意力机制为提升模型性能, 让模型能够更好地关注光谱信息, 我们设计了一个光谱注意力机制, 如图2所示. 模型的输入为补丁 , 通过AveragePool3D进行池化操作, 将原大小为Ws×Ws×k的补丁池化为1×1×k, 通过池化操作后, 可以获得全局的感受野. 再通过两个全连接操作, 将光谱维度的信息进行激励操作, 通过全连接层和激活函数之后, 获得光谱维度上的权重信息w, 最后将权重信息w与原输入的补丁进行相乘操作, 从而得到每个光谱维度信息的重要性分布, 完成对光谱特征的重标定.

|
图 2 网络结构图 |
3.3 邻域相似度模块
根据高光谱图像本身的特性可知, 每一类样本在空间上大多以块状聚集在一起, 但是以前的工作大多没有考虑到特征空间中的中心光谱向量与相邻光谱向量之间的联系. 为此, 我们添加了一个基于余弦距离的特征向量自相似模块, 用于探索原始输入空间中不同相邻光谱像元的空间互补信息的贡献.
如图3所示, 将进行降维后的特征映射作为输入, 首先通过一个一维卷积层来将原本的通道数映射为3倍, 再进行切分生成Q、K、V. 之后在Q中选取其中心向量与K中的所有相邻向量通过计算向量之间的余弦距离得到它们之间相似度, 再将生成的结果通过Softmax函数后可以得到一个拥有权重分布的特征图, 之后将生成的特征图与V进行重新加权, 最后与原输入进行相加从而得到中心向量与相邻向量之间的相关度关系.

|
图 3 网络结构图 |
4 实验分析
下面实验部分将介绍实验使用的公开数据集, 数据预处理方法, 实验的相关设置以及实验的结果与分析.
4.1 数据集介绍为了公平地证明所提出的网络的有效性和效率, 我们在3个流行的公开HSI数据集上进行了广泛的实验, 即Salinas (SA)、Indian Pines (IP)和Pavia Centre and University (PU). 表1列出各数据集包含的类别和对应的数量, 并且在数据集后的括号中标注了实验所选取的样本比例. 从表1可知, SA有16个类别, 共计54129个样本. IP有16个类别, 共计10249个样本. PU共有9个类别, 共计42776个样本.
| 表 1 3个数据集包含的各个种类及对应数量 |
4.1.1 Salinas (SA)数据集
第1个HSI是在1992年由AVIRIS传感器在美国加利福尼亚州的Salinas山谷上空获得的, 具有3.7 m的高空间分辨率, 图像尺寸为512×217个像素点, 采集图像的通道数共有224个波段. 在去除了20个含有噪声和吸水波段之后, 共有204个波段用于实验中. SA数据集图像及ground-truth图如图4所示.

|
图 4 SA数据集图像及ground-truth图 |
4.1.2 Indian Pines (IP)数据集
第2个HSI是由AVIRIS传感器在美国印第安纳州的西北部的Indian Pines地区获得的. 图像尺寸为145×145个像素点, 采集图像的通道数共有220个波段. 在去除了覆盖吸水区域的波段之后, 共有104个波段用于实验中. IP数据集图像及ground-truth图如图5所示.
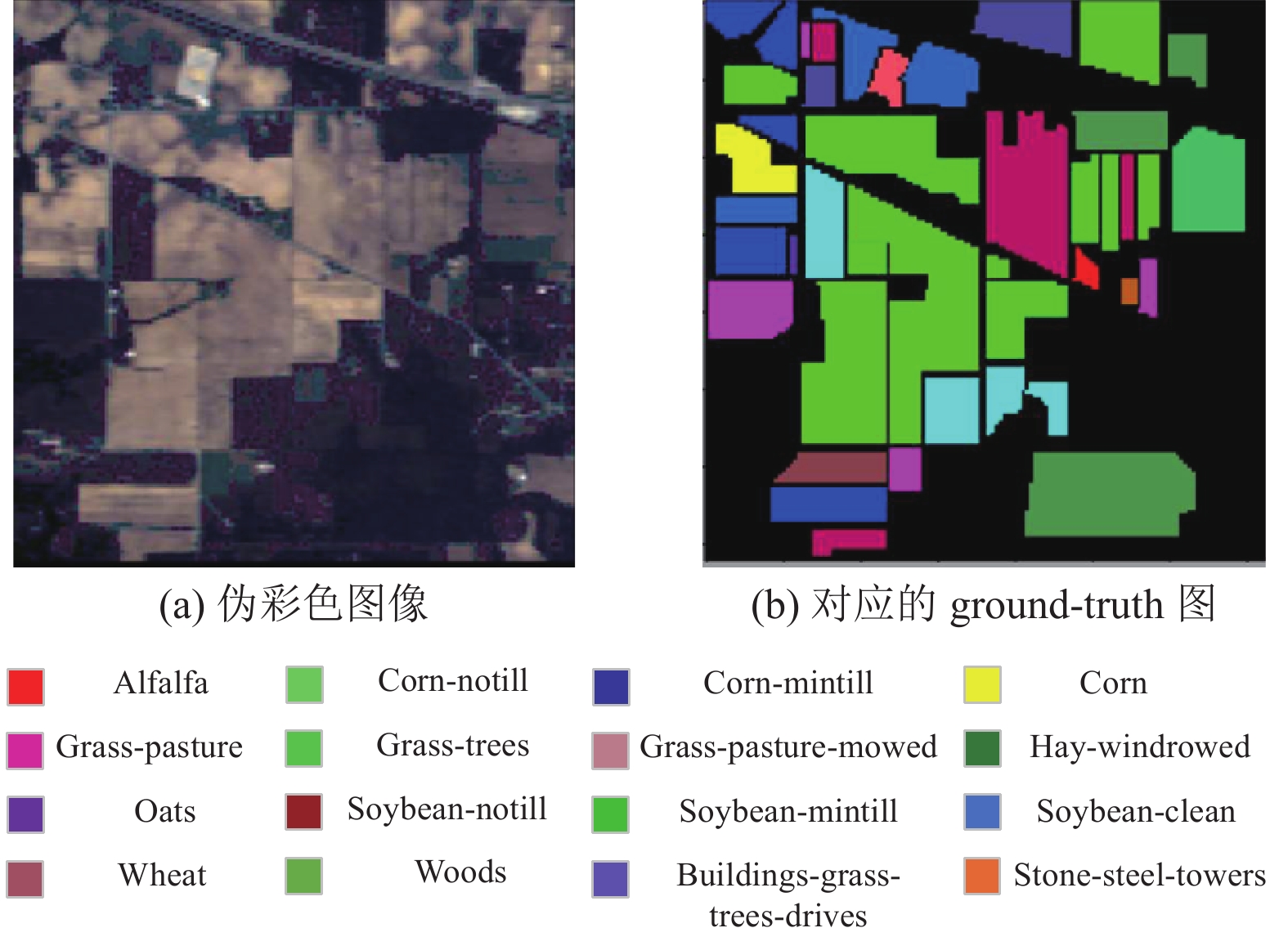
|
图 5 IP数据集图像及ground-truth图 |
4.1.3 Pavia Centre and University (PU)数据集
第3个HSI是由ROSIS传感器在意大利北部的Pavia Centre and University上空获得的, 具有1.3 m的空间分辨率, 图像尺寸为610×340个像素点, 采集图像的通道数共有103个波段. PU数据集图像及ground-truth图如图6所示.

|
图 6 PU数据集图像及ground-truth图 |
4.2 数据预处理
在数据输入模型之前, 我们对原始形状为H×W×C的HSI进行预处理. 首先对光谱维度进行PCA的降维操作, 将原始图像形状变为H×W×K, 其中H为空间维度的高度, W为空间维度的宽度, C为原高光谱图像的光谱带数, K为PCA处理后图像的通道数. 通过多次实验, 我们选择将高光谱图像的通道数降低至60, 即K=60. 这样可以有效减少数据维度, 降低计算复杂度.
高光谱分类任务的目的是通过已有的标记样本去预测未标记的样本, 为每一个未标记的样本分配一个语义标签. 从高光谱数据的形式上看, PCA处理后的高光谱图像的像素集
| Zi,j={0,yi≠yj1,yi=yj |
通过样本对的构建, 我们能够获取大量的训练样本对, 达到了数据增强的目的, 有利于模型的训练. 为推进模型的进一步拟合, 防止某类的样本对数量过多, 我们选择设置一个假标签flag, 将每一个样本对都使用假标签作为索引, 可以利用假标签来从中选取部分样本对.
为减少训练时间, 我们选择在每类的正样本对中通过假标签按10%的比例确定最终的训练正样本数. 但由于正负样本对的数量上存在极大的不平衡, 因此选择随机选取总数等同于正样本对的负样本对, 将正负样本对共同组合成训练集, 避免了样本对数量不平衡导致模型对类间分类的潜在影响.
构建好样本对之后, 我们选择以patch的形式进行输入, 将以样本对中对应的像素点作为patch的中心, 每个像素对应一个补丁, 边缘像素使用零填充来构建补丁, 生成一组补丁对, 其中每个小块
(1) Patch的窗口大小: 3D补丁块的空间窗口大小决定该补丁块空间相邻信息的数量, 窗口尺寸越大则其包含的信息越多, 在特征提取时就能挖掘出更多的信息, 从而提升模型的分类性能. 因此, 我们做了相应的实验来确定最合适的窗口大小, 并考虑针对Siamese network输入的补丁对策略选择采用不同大小的窗口尺寸, 原因在于相邻像素大多数是某一类的情况下, 其中心像素大概率为相同类别, 就不需要控制过大的窗口进行判断, 以减少冗余信息和训练时间.
为验证该想法的有效性, 我们设置了间隔为2的窗口大小分别从5到13进行组合, 其分类评估的OA值如图7所示. 可以看出在使用差异化输入方法后, 结果会略高于采用相同大小输入的补丁对.

|
图 7 3个数据集在不同窗口大小下OA值 (%) |
(2)网络性能表现: 为了比较提出的方法以及网络的性能和效率, 我们将所提出的网络与两个传统的机器学习算法进行比较, 即带有高斯核函数的支持向量机(SVM)和随机森林(RF). 同时也与5个先进的深度学习模型进行比较, 即SSTN[21]、SSAN[22]、SSSAN[23]、CVSSN[24]、S3Net[18]. 所选择的对比算法覆盖了传统的机器学习算法、基于Transformer的算法、基于三维CNN的算法、基于注意力的算法和Siamese network的算法. 在我们的实验中, 会根据不同的算法输入调整训练集, 具体的配置在第4.4.3节.
(3)评价指标: 为比较不同方法和模块的分类性能, 我们采用总体精度(overall accuracy, OA)、平均精度(average accuracy, AA)和Kappa系数这3个指标来评价不同模型的性能. 其中, OA是正确分类的标记样本数量与测试集中总样本数量的比值. AA是所有土地覆盖等级精度的平均值. Kappa综合衡量分类结果与基础真值之间的一致性. 在所有实验中选择进行10次独立运行, 并将返回各指标计算的结果取平均值作为最终结果.
(4)运行平台: 所有实验均在Windows 11、Intel i7-8750u、NVIDIA GeForce RTX 3090、64 GB内存硬件下进行. 不同的深度学习框架是在Python 3.6环境下基于PyTorch 1.14构建的.
4.4 消融实验 4.4.1 样本对构建对比实验我们选择采用间隔采样和边缘采样的方式选取一定比例的训练样本, 并将训练样本组合生成样本对输入到模型中. 为验证该方法的有效性, 我们进行了两个对比实验. 由于样本的选择大多是按比例或者按固定样本数量进行选取, 第1个对比实验我们验证采用比例进行选取优于按固定样本数进行选取, 我们将与按固定样本选取的方式进行对比, 在SA数据集中, 将统一按照11×9的窗口大小进行训练, 分别选择采用2%的比例进行选取和固定样本数量为每类40样本的方法进行对比实验, 从表2中可以看到, 按照比例选取的方法能够对结果有进一步的提升. 比例选取可以避免对某一类数量较多的类训练不足导致的分类效果不好, 从而提升整体的分类结果.
| 表 2 样本选取对比实验的OA值 (%) |
第2个实验我们在比例选取样本的基础上, 通过添加间隔采样和边缘采样的方法进行对比实验, 实验结果如表3所示, 表中勾选则说明采用了该种方法. 可以看到采用二者结合的方法能够提升整体的性能.
| 表 3 SA数据集上的间隔选取与边缘选取对比实验 (%) |
4.4.2 不同窗口大小输入
为验证该方法的有效性, 我们在每类选择10个样本的基础上, 按照窗口大小{5, 7, 9, 11, 13}分别对两个样本进行设置, 再将两个样本构建成样本对的形式输入到网络中, 设置epoch为50训练10次, 取其对应的平均OA值. 从结果上看, 该方法相对于采用相同窗口大小的输入, 准确率OA能够有一定提升.
如图7所示, 在SA数据集中, 当WindowSize大小分别为9和7时能获得最好的分类结果. 因此在后续的实验中我们将继续设置WindowSize大小分别为9和7. 同理, 在IP数据集中, 我们则选择采取WindowSize大小分别为13和7进行后续实验, 在PU数据集中采取WindowSize大小分别为13和5进行后续实验.
4.4.3 实验结果与分析表现在SA和PU的实验中, 实验参数都设置为按2%比例选取样本构建训练集, 并在需要构建验证集的算法(SVM、RF、SSTN、SSAN、SSSAN、CVSSN)中, 采用0.2%的比例构建验证集, 其余样本均用于测试. 而IP数据集由于样本数量较少, 我们选择设置10%的比例进行构建, 同样在以上算法中, 我们采用1%的比例构建验证集, 其余样本用于测试.
在我们的网络和S3Net中是采取使用样本对的形式输入, 而其余算法的输入均为单个样本输入, 为保证实验的准确性, 我们将采用单个样本输入的对比算法中的输入patch大小设置与样本对中的较大patch一致. 其次, S3Net在数据选择上是使用每类固定样本数进行训练集的构建, 我们每类选择设置为40, 与我们2%比例选取的样本数大致相同, 确保算法之间能够正常比较.
表4中是模型运行10次统计出的OA、AA和Kappa在SA、IP和PU这3个数据集上的结果. 从表4中可以看出, 深度学习的算法效果远远强于传统的机器学习算法, 因此我们的对比主要关注在深度学习算法上.在同样采取比例选取样本构建训练集的算法(SSTN、SSAN、SSSAN、CVSSN)中, 我们的算法取得了最优的性能. 在SA数据集上与次优的CVSSN相比, OA、AA和Kappa分别提升了1.53%、0.85%和1.71%. 对IP数据集而言, 与CVSSN相比, OA、AA和Kappa分别提升了0.6%、1.3%和0.7%. 同样, 在PU数据集中与CVSSN相比, OA、AA和Kappa分别提升了0.44%、0.34%和0.58%.
| 表 4 各算法在3个数据集上的分类结果 |
对于同样采用了Siamese network构建模型的S3Net, 我们的模型在选取训练集上采取的方法不同, 从结果上看, 我们的模型在相同的数据集上所采用的间隔采样和边缘样本采样的方法能够比S3Net算法所使用的按每类固定数量的选取方法得到的结果更优, 在SA数据集上, OA、AA和Kappa分别提升了1.79%、0.5%和1.99%. 在IP数据集上, OA、AA和Kappa分别提升了3.67%、0.91%和4.22%. 在PU数据集上, OA、AA和Kappa分别提升了2.04%、0.65%和2.72%. 对于其他按比例选取样本的深度学习算法, 我们的模型在面对少样本的情况下能够取得更好的结果.
4.4.4 注意力模块和相似度度量模块消融实验为验证模型中所添加的注意力模块和相似度度量模块的有效性, 我们在SA数据集上进行了消融实验. 其结果如表5所示.
| 表 5 添加的模块的消融实验 |
在表5中, 勾选表示添加了对应的模块, Attention表示光谱注意力模块, Similarity表示空间邻域相似度度量模块, Model 列中的“1”表示没有添加注意力模块, “1-A”表示添加了Attention模块, “1-S”表示添加了Similarity模块, “1-AS”表示两者都添加. 最后一栏表示在对应的模块选择上所得到的分类结果评测指标. 由于样本对是按照比例进行随机选取, 我们进行了多次重复的训练, 选取各类中得到的最好结果作为最终结果. 从结果上看, 添加模块后的模型各评测指标均比未添加的模型各评测指标高出一些, 在二者都添加之后可以获得最优的分类结果. 因此, 上述实验验证了添加这两个注意力模块的有效性.
5 结论与展望本文采用了比例选取方式确定训练样本数总数, 并通过间隔采样和边缘采样的方法对样本点进行选取, 两两组合构建样本对实现数据增强, 有效削弱了样本量不足带来的过拟合问题, 再以样本对的形式输入到设计的孪生网络中去. 我们的算法按照以上方式进行样本选取, 相对于其他算法按随机选取样本的方式选取, 训练结果在各个指标上都有着提升. 在实际的高光谱分类的实验中, 其分类结果证明了本文采取的样本选取方法以及算法的有效性. 我们同时也进行了光谱注意力模块和空间相似度度量模块的消融实验, 实验结果表明, 添加两个模块之后模型性能有些许提升, 证明了模块的有效性.
Siamese network能够以样本对的形式实现数据增强的效果, 相较于常规以单个样本为输入的算法, 能够拥有大量可供训练的样本, 适用于少样本的情景中进行分类. 同时, 我们添加了注意力机制和相似度度量模块, 分别作用于高光谱图像的光谱维度和空间维度, 关注光谱间的相关性和空间上中心向量与相邻向量之间的联系, 可以对模型的分类带来提升.
当前我们的方法采用比例选取的方法生成训练集, 并两两组合生成样本对, 但是存在正负样本对数量不平衡的情况, 目前我们采取随机选取10%的正样本对, 并随机选取相同数量的负样本对共同组成训练集输入模型中进行实验. 今后, 我们可以考虑结合主动学习对样本对进行更高效的选取, 从而进一步提升分类性能. 另外, 对于负样本对的选取仍是一项值得进一步探索的工作.
| [1] |
Fauvel M, Tarabalka Y, Chanussot JA, et al. Advances in spectral-spatial classification of hyperspectral images. Proceedings of the IEEE, 2013, 101(3): 652-675. DOI:10.1109/JPROC.2012.2197589 |
| [2] |
Lei JJ, Li XY, Peng B, et al. Deep spatial-spectral subspace clustering for hyperspectral image. IEEE Transactions on Circuits and Systems for Video Technology, 2021, 31(7): 2686-2697. DOI:10.1109/TCSVT.2020.3027616 |
| [3] |
Jordan MI, Mitchell TM. Machine learning: Trends, perspectives, and prospects. Science, 2015, 349(6245): 255-260. DOI:10.1126/science.aaa8415 |
| [4] |
Kang XD, Xiang XL, Li ST, et al. PCA-based edge-preserving features for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(12): 7140-7151. DOI:10.1109/TGRS.2017.2743102 |
| [5] |
Tarabalka Y, Fauvel M, Chanussot J, et al. SVM- and MRF-based method for accurate classification of hyperspectral images. IEEE Geoscience and Remote Sensing Letters, 2010, 7(4): 736-740. DOI:10.1109/LGRS.2010.2047711 |
| [6] |
Du PJ, Bai XY, Tan K, et al. Advances of four machine learning methods for spatial data handling: A review. Journal of Geovisualization and Spatial Analysis, 2020, 4: 13. DOI:10.1007/s41651-020-00048-5 |
| [7] |
Paoletti ME, Haut JM, Plaza J, et al. Deep learning classifiers for hyperspectral imaging: A review. ISPRS Journal of Photogrammetry and Remote Sensing, 2019, 158: 279-317. DOI:10.1016/j.isprsjprs.2019.09.006 |
| [8] |
Yu CY, Han R, Song MP, et al. A simplified 2D-3D CNN architecture for hyperspectral image classification based on spatial-spectral fusion. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2020, 13: 2485-2501. DOI:10.1109/JSTARS.2020.2983224 |
| [9] |
Hong DF, Gao LR, Yao J, et al. Graph convolutional networks for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(7): 5966-5978. DOI:10.1109/TGRS.2020.3015157 |
| [10] |
Mou LC, Ghamisi P, Zhu XX. Deep recurrent neural networks for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(7): 3639-3655. DOI:10.1109/TGRS.2016.2636241 |
| [11] |
Hong DF, Han Z, Yao J, et al. SpectralFormer: Rethinking hyperspectral image classification with Transformers. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5518615. |
| [12] |
Jia S, Jiang SG, Lin ZJ, et al. A survey: Deep learning for hyperspectral image classification with few labeled samples. Neurocomputing, 2021, 448: 179-204. DOI:10.1016/j.neucom.2021.03.035 |
| [13] |
Xue ZH, Zhang MX, Liu YF, et al. Attention-based second-order pooling network for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(11): 9600-9615. DOI:10.1109/TGRS.2020.3048128 |
| [14] |
Zhang SH, Chen ZK, Wang D, et al. Cross-domain few-shot contrastive learning for hyperspectral images classification. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 5514505. |
| [15] |
Manifold B, Men S, Hu RQ, et al. A versatile deep learning architecture for classification and label-free prediction of hyperspectral images. Nature Machine Intelligence, 2021, 3(4): 306-315. DOI:10.1038/s42256-021-00309-y |
| [16] |
Cheng G, Cai LM, Lang CB, et al. SPNet: Siamese-prototype network for few-shot remote sensing image scene classification. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5608011. |
| [17] |
Cao ZY, Li XR, Jiang JF, et al. 3D convolutional siamese network for few-shot hyperspectral classification. Journal of Applied Remote Sensing, 2020, 14(4): 048504. |
| [18] |
Xue ZH, Zhou YY, Du PJ. S3Net: Spectral-spatial Siamese network for few-shot hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5531219. |
| [19] |
Liu JX, Zhang KF, Wu SQ, et al. An investigation of a multidimensional CNN combined with an attention mechanism model to resolve small-sample problems in hyperspectral image classification. Remote Sensing, 2022, 14(3): 785. DOI:10.3390/rs14030785 |
| [20] |
Feng F, Zhang YS, Zhang J, et al. Small sample hyperspectral image classification based on cascade fusion of mixed spatial-spectral features and second-order pooling. Remote Sensing, 2022, 14(3): 505. DOI:10.3390/rs14030505 |
| [21] |
Zhong ZL, Li Y, Ma LF, et al. Spectral-spatial Transformer network for hyperspectral image classification: A factorized architecture search framework. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5514715. |
| [22] |
Sun H, Zheng XT, Lu XQ, et al. Spectral-spatial attention network for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(5): 3232-3245. DOI:10.1109/TGRS.2019.2951160 |
| [23] |
Mei XG, Pan ET, Ma Y, et al. Spectral-spatial attention networks for hyperspectral image classification. Remote Sensing, 2019, 11(8): 963. DOI:10.3390/rs11080963 |
| [24] |
Li MS, Liu YK, Xue GK, et al. Exploring the relationship between center and neighborhoods: Central vector oriented self-similarity network for hyperspectral image classification. IEEE Transactions on Circuits and Systems for Video Technology, 2023, 33(4): 1979-1993. DOI:10.1109/TCSVT.2022.3218284 |
 2024, Vol. 33
2024, Vol. 33



