社会网络是指个人或组织所构成的社会结构, 构成主体是一些人或社会实体, 在这些人或社会实体之间, 存在一些关系或互动模式, 如个人之间的友情关系、公司之间的合作关系、国家之间的贸易关系等. 社会网络可以建模为一个图数据类型, 其中节点映射到个人或社会实体, 节点之间的连边对应于相应的人或社会实体之间的关联. 个人或社会实体之间的关系在不断变化, 因此会发生多个连边和顶点的添加或删除, 这种变化导致社会网络呈现高度的动态性和复杂性. 社会关系是对个人之间人际关系的描述, 它可以看作是一对节点之间的定义. 具有社会关系的两个节点不仅存在稳定长期的联系, 而且这一对节点要具有更多相同的兴趣爱好. 人们经常根据自己的社会属性来互相接触, 并且与兴趣相似、行为相似和经常见面的人交朋友. 因此, 社会网络局部会出现一些内部连接比外部连接更紧密的子图, 这也是社会网络社会性和高聚集性的一种体现.

近年来, 许多学者开始关注社会网络的信息挖掘, 主要包括链路预测、社团检测、聚类分析等. 其中, 链路预测可用于提取缺失信息、识别虚假交互、评估网络演化机制等, 具有广泛的应用场景和重要的现实意义, 成为近期的研究热点. 在社交网络平台中, 链路预测可以帮助用户在社交平台中寻找感兴趣的朋友, 并进行相应的推荐, 节约用户的社交成本; 对社交平台而言, 链路预测增加个人用户的朋友关系有利于增加网络用户的在线率, 提高用户黏性, 增加社交平台的影响力. 在电子商务领域, 链路预测可以基于个人及其朋友以往的购买信息和相关的属性信息, 预测用户的下次购买行为并进行相应推荐. 在引文网络和科研合作方面, 链路预测可以评估一篇论文是否可以成为一篇高影响力论文, 以及帮助科研工作者找到高水平的科研合作者, 从而促进学术产出. 在生物分子网络中, 链路预测可以利用给定的蛋白质相互作用网络, 从网络结构中挖掘不同的信息, 设计不同的拓扑相似度度量方法, 根据已知的相互作用预测未知的相互作用, 高效挖掘潜在的蛋白质相互作用关系. 在社会网络隐私控制领域, 由于许多用户将个人帖子、音频、视频和其他敏感信息分享到社交网站, 社交平台对用户的隐私保护非常重要, 链路预测可以根据连接权重形式的信任来确定两个用户之间关系的强度, 计算用户之间的信任级别来识别种子用户的所有可能的可信用户. 到目前为止, 在社会网络链路预测的研究中, 基于节点相似性的链路预测算法通过测量两个节点的相似性来进行预测, 具有较强的可扩展性, 应用领域也较为广泛, 长期以来一直受到学者的青睐.

Chai等^[1]考虑如何选择合适的基矩阵以及重建网络的结构特征对链接预测的影响, 提出采用全连接网络的邻接矩阵作为低秩表示的基矩阵, 将重构网络邻接矩阵的核规范作为惩罚项. Zhao等^[2]利用元路径投影和语义图聚合, 提出可以从不同的元路径中学习节点对的嵌入, 用于异构网络的端到端链路预测方法. 李巧丽等^[3]提出将节点间最优路径应用于网络中的节点传输能力问题, 将6阶范围内最优路径数和最优路径长度进行融合, 定义节点紧密中心性函数来构建相似度传输矩阵. Mishra等^[4]发现多种类型的链路可以被编码到不同的层中, 节点本身及其本质关系得以保留, 由此在考虑各个层相对密度的同时, 将高阶路径和不同的层进行关系融合. Orzechowski等^[5]考虑到社交网络中的交互表现出不对称性, 提出一种新的局部连边聚类指标, 使用不对称邻域重叠对有关社会关系不对称的信息进行提取. Liu等^[6]通过局部信息对单纯分解权重和闭合比率权重进行相似性度量, 提出基于局部特征的高阶链路预测算法, 并捕获局部高阶路径信息以预测网络中未来可能出现的交互作用. 上述方法作为基于路径信息相似性的链路预测方法, 依据近似完整的网络拓扑结构信息, 链路预测准确率较高, 但是算法的计算过程复杂度过大, 不适合应用于大规模的数据集, 并且在实际应用场景中完整的网络拓扑结构信息较难获取.

Mishra等^[7]基于合并节点和连边相关性的概念, 利用边的邻近信息计算边相关性, 而根据节点对图形整体结构的重要性并综合局部和全局的属性计算节点相关性. Liu等^[8]考虑源节点和目的节点之间的中间节点的平均度, 量化节点的初始信息贡献, 应用节点之间通过3种信息传输方式接收的总信息量来衡量它们之间的相似性. 郁湧等^[9]将节点的共同邻居聚类系数和度融合作为局部信息的指标, 并且使用节点中心性对在网络中节点的重要性进行表示. Sarhangnia等^[10]提出一种新的二分网络中链路预测的相似性度量方法, 基于节点的邻域结构对现有经典方法进行修改并重新定义. Ghasemi等^[11]考虑将网络的拓扑特征与节点的动态特征进行结合, 并提出将子空间聚类算法应用于社会对象的聚类, 有效区分聚类的强度. Zhu等^[12]考虑无向未加权网络邻接矩阵的对称性, 进一步分析不同中心性对链路的影响, 提出一种结合节点重要性和网络拓扑属性的链路预测算法, 说明了节点度中心性和邻近中心性对链路预测精度的重要性. 以上基于节点信息相似性的链路预测方法主要考虑网络拓扑中的节点信息, 算法复杂度较低, 所适用的网络数据集范围更广, 但在考虑单一指标的情况下预测精度受限, 易受到网络拓扑结构变化的影响.

许多现实世界网络中节点之间的平均路径长度较短, 同时网络的拓扑结构又具有高聚集性, 因此网络内部会出现局部的高度连接. 上述方法并未同时对节点间的路径特征和局部信息进行分析, 容易丢失重要的网络拓扑结构信息, 影响预测精度. 本文通过对网络拓扑信息进行挖掘, 充分考虑社会网络结构的社会性和高聚集性, 根据节点的局部信息和路径特征并将其作为节点相似性的衡量依据, 提出一种基于节点交互度的社会网络链路预测方法. 为了验证该方法的预测性能, 本文针对6个真实的网络数据集进行了链路预测实验. 结果表明, 与其他方法相比, 本文方法在AUC和Precision两个评价指标上均表现出更优的预测性能, 预测结果平均分别提升22%和54%, 结果证明节点交互度在社会网络链路预测方面的可行性和有效性, 可以在各种真实世界的网络中获得更好的准确性.

1 链路预测概述 1.1 问题描述

一个无向网络可以被具体表示为$ G = (V, E) $, 其中$ V = \left\{ {{v_1}, {v_2}, {v_3}, \cdots , {v_N}} \right\} $表示网络中节点的集合, 共包含$ N $个节点, 即$ |V| = N $; $ E = \left\{ {{e_1}, {e_2}, {e_3}, \cdots , {e_M}} \right\} $表示网络中节点连边的集合, 共有$ M $条连边, 即$ |E| = M $. 令网络中所有的节点对可能组成边的全集为$ U $, 则全集$ U $为所有$ N\times(N - 1)/2 $个节点对可能组成所有边的集合. 链路预测问题即利用网络的已知结构和节点属性等信息, 计算尚未形成连边的一对节点之间形成连边的概率. 基于节点相似性的链路预测算法对于每个未连接的节点对$ (x, y) $计算节点相似度, 计算的相似性分数越高, 那么节点对在未来形成链路的概率就越大. 按照该链路预测分数值从大到小进行排序, 排序越靠前的节点对之间就越可能产生链接, 即当计算出的相似性度量$ {S _{xy}} $越大, 那么节点之间出现连边的可能性就越大.

1.2 基准算法

本文所使用到的符号及其说明如表1所示. 本文所对比的链路预测方法如表2所示.

在以上基于相似性的链路预测算法的指标中, CN指标和JAC指标考虑节点之间共同邻居的数量; AA指标、RA指标和ERA指标考虑共同邻居节点度的影响, 认为度小的共同邻居节点对连边影响要更大; PA指标将待预测节点对的度作为相似性的衡量指标; CCLP指标利用共同邻居节点的聚类系数定义节点间的相似性; NDCC指标和TNDCC指标在共同邻居算法的基础上, 考虑节点聚类系数和度这两种重要的拓扑属性; CN2D指标利用节点的度分布以及共同邻居数量, 对节点间的相似性进行估计.

2 基于节点交互度的社会网络链路预测方法

在本节我们提出一种新的链路预测方法. 根据小世界网络的特性, 本方法从路径特征的角度对节点间信息交换的效率进行评估, 充分考虑社会网络的社会性和高聚集性, 并在没有公共邻居的节点之间的链路预测方面得到成功应用. 除此之外, 本方法从节点间拓扑结构的角度对公共邻居的局部信息进行分析, 将共同邻居节点的聚类系数和度作为计算节点交互度的重要信息, 提高对局部信息的有效利用, 达到提高预测精度的目的. 由于不同规模数据集中路径特征和局部信息的不同, 本方法基于网络数据集规模大小使用定义的参数$ \alpha $控制路径特征和局部信息的权重构成零和条件, 将计算得到的节点交互度作为链路预测相似性的衡量指标, 从而有效地提高了预测精度. 基于节点交互度的链路预测方法的基本原理是如果两个节点之间的交互度越大, 那么这两个节点之间的关系更为亲密, 则存在连边的可能性也就越大. 社会网络的网络拓扑结构复杂, 节点本身蕴含着丰富的属性特征, 依据节点间的路径特征和局部信息可以有效地挖掘社会网络中节点间的交互度. 基于以上分析, 本文融合路径特征和局部信息对社会网络节点交互度进行定义, 并分别从上述两个角度对节点间的相似性进行度量.

2.1 小世界网络下的节点效率

小世界网络模型在图像上介于规则网络和随机网络之间, 其特点是节点之间特征路径长度小, 接近随机网络, 而聚合系数依旧相当高, 接近规则网络. 在社会网络这种图结构中, 绝大多数节点之间并不相邻, 但任意给定节点的邻居们却很可能彼此相邻, 并且大多数任意节点, 都可以用较少的步数访问到其他节点. 其次社会网络内部存在聚集的子网络, 这种子网络的特点是网络内部几乎任意两个节点之间都存在连接. 具体体现在一些彼此并不相识的人, 却可以通过一条很短的熟人链条被联系在一起; 具有相同社会背景的人形成小团体, 团体内部彼此关系紧密. 这说明社会网络中同样存在小世界现象.

Latora等^[23]用小世界网络的效率概念衡量了网络信息交换的效率, 认为图中一对节点的效率是节点间最短路径距离的乘积倒数, 图的全局平均效率是所有节点对的平均效率. 显然, 若两节点间最短路径长度越短, 只需经过较少节点就能相互访问, 说明节点间的效率越高, 交互关系也更为密切.

2.2 节点交互度的分析与量化

在社会网络的结构中, 两个节点之间的共同邻居节点会充当信息载体的角色, 源节点的信息在共同邻居节点的传递下发送到目的节点. 因此节点之间的公共邻居是衡量两个节点相似性的重要依据, 并且公共邻居的聚类系数和度也可以表达节点之间链路结构的信息.

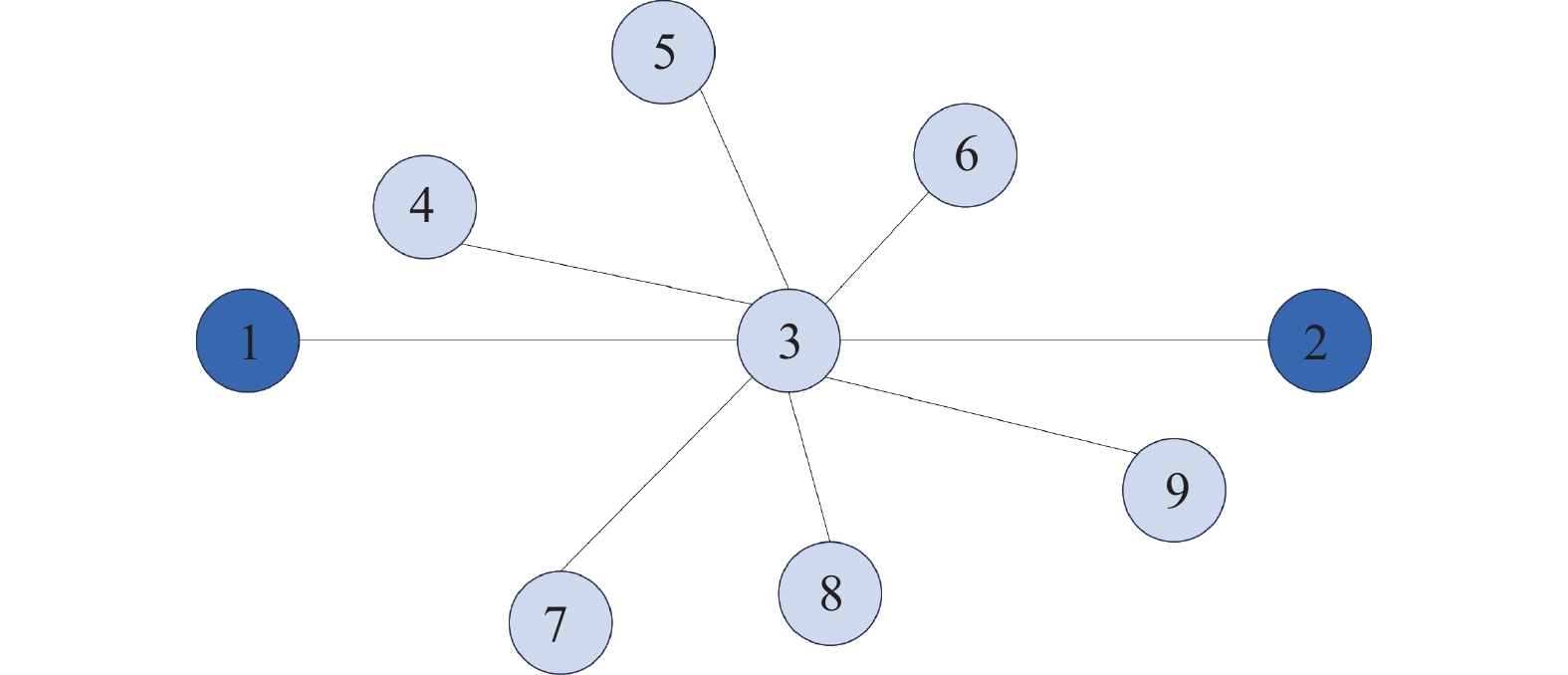
图1中, 节点1和节点2是一组待预测的节点对, 节点3是它们的共同邻居节点. 从图1中可以看出, 与节点3相邻的节点彼此之间没有任何连边, 是相互独立的, 此时节点3的邻居节点彼此相互联系的程度处在较低水平.

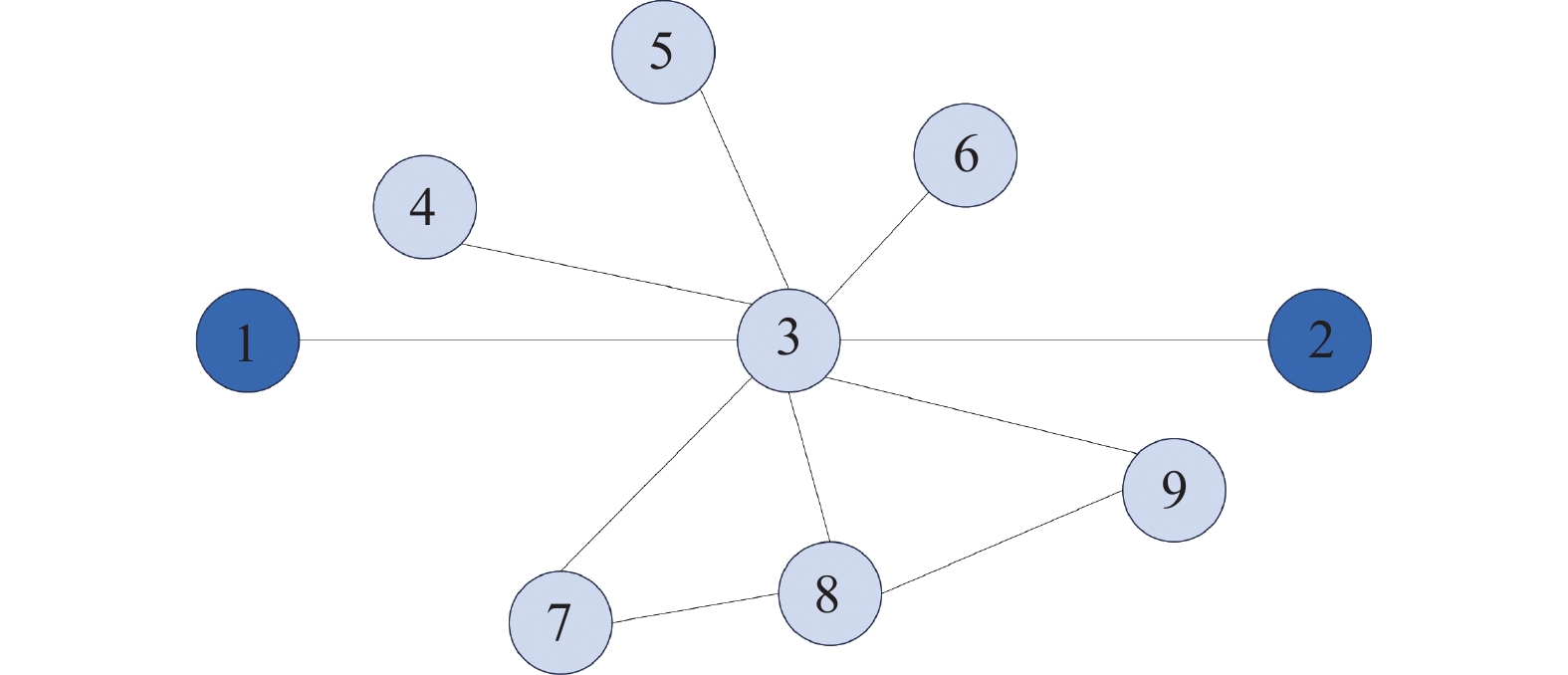
图2中, 节点7和节点8建立连接, 以及节点8和节点9也形成连边, 此时节点3作为节点对的共同邻居节点发挥联系作用, 让节点对彼此建立连接. 那么作为共同邻居节点, 节点3使得待预测节点之间交互度更大, 从而相邻节点之间产生连接的可能性更高.

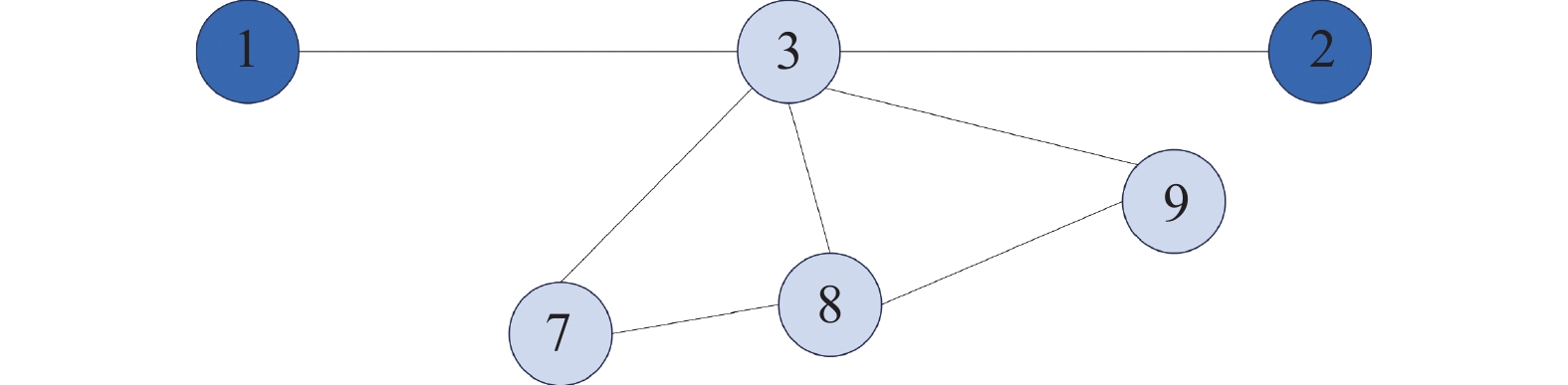
图3中, 节点3的度相较于图2中节点3的度有所减少, 在以节点3为共同邻居的节点对之间, 彼此产生连接的数量比例显著增加. 另一方面, 节点3作为共同邻居节点承担传递信息的作用, 在节点3的度减少的同时, 节点3的邻居节点得到的信息会相应增加. 这说明节点3作为待预测节点对的共同邻居节点, 对待预测节点之间的交互度的贡献上升, 连接可能性也会更大.

节点的聚类系数使用了共同邻居的邻居节点之间的连接, 描述了该节点的相邻节点之间也相互连接的可能性, 并且这些连接和链路预测的连边概率具有相同的拓扑结构^[18]. 节点的度描述了与该节点相关联的节点个数, 由于节点通过邻居节点作为信息载体来传递信息, 那么经由邻居节点传递的这个信息将会在接下来的信息传递再均匀分布给它的所有邻居^[15]. 基于以上分析, 待预测节点之间共同邻居节点的聚类系数越大或节点的度越小, 那么待预测节点之间的交互关系会更强, 彼此之间更为相似, 存在连接的概率也就越高.

显然, 仅考虑节点局部信息而忽视路径特征难以应用于没有公共邻居的节点之间的链路预测. 基于上述分析, 对于节点相似性的度量可以从共同邻居的拓扑属性和节点效率两个方面进行考察. 节点间共同邻居的信息可作为待预测节点对的局部信息, 而节点效率是通过分析节点间路径特征得到的. 因此, 本文用路径特征和局部信息描述节点间相似性定义节点交互度.

定义 1. 节点交互度. 对社会网络中的任意两节点$ x $和节点y, 节点交互度可用于对节点之间的相似性进行度量, 考虑路径特征和局部信息后并通过归一化处理使得前后量纲统一, 计算表达式如下:

$ {S_{xy}} = \alpha \frac{1}{{{d_{xy}}}} + (1 - \alpha )\sum\limits_{{\textit{z}} \in \Gamma (x) \cap \Gamma (y)} {\frac{1}{{1 + {{\mathrm{e}}^{ - \frac{{C{C_{\textit{z}}}}}{{{k_{\textit{z}}}}}}}}}} $

(1)

其中, $ {d_{xy}} $为节点$ x $和节点$ y $之间的最短路径长度; $ \Gamma (x) $为节点$ x $的邻居节点; $ C{C_{\textit{z}}} $为节点$ x $和节点$ y $的共同邻居节点$ {\textit{z}} $的聚类系数; $ {k_{\textit{z}}} $为节点$ x $和节点$ y $的共同邻居节点$ {\textit{z}} $的度; $ \alpha $为可调节参数, 用于根据网络具体拓扑结构的不同进行调节.

本文将上述所提方法命名为节点交互度(interacting degree of nodes, IDN), 节点交互度可作为节点$ x $和$ y $形成连边的可能性, 实现社会网络的链路预测. 此方法相较于传统基于相似性的链路预测指标, 适用于较大规模网络, 通过路径特征和局部信息更为全面地考量节点相似性. 对于小规模网络数据集, 本算法在考虑节点间局部信息的同时, 会优先考虑完整的网络拓扑结构信息和路径特征, 进而克服在小规模数据集上预测精度受限的问题. 对于较大规模数据集而言, 本算法则是主要对节点间局部信息进行充分利用, 减少路径特征信息在节点交互度所占的权重, 在一定程度上降低了计算复杂度. 本算法创新性地整合了路径特征和局部信息, 基于数据集规模的不同提出社会网络节点交互度的定义, 对节点间相似度进行准确刻画, 在预测精度和计算复杂度两个方面实现了有效的平衡, 从而增强对不同网络链路的预测能力, 降低了计算复杂度.

2.3 算法流程

在算法1中, $ \alpha $是可调节参数, 并且取值范围为(0, 1). 由于$ \alpha $的最佳取值受到不同网络拓扑结构的影响, 这里将取值范围内的取不同值的$ \alpha $值代入算法1, 不同的$ \alpha $取值会生成不同的链路预测结果, 本文从不同预测结果中选择结果最优时的参数值, 将其作为该网络的最优参数. 此时把参数$ \alpha $的最优取值代入到IDN算法中, 得到节点的相似性分数矩阵. IDN算法的具体步骤如算法1所示.

算法1. 基于节点交互度的链路预测算法

输入: 无向网络$\scriptstyle G = (V, E) $, 参数$\scriptstyle \alpha $;

输出: 节点相似性分数矩阵S=[s_ij].

1) 初始化节点相似性分数矩阵S=[s_ij], 节点间最短距离矩阵D=[d_ij];

2) 计算每两个节点之间最短路径长度, 并更新节点间最短距离矩阵D=[d_ij];

3) 通过数据预处理, 得到每个节点的聚类系数和度;

4) 根据式(1)计算节点之间的相似性分数;

5) 更新并生成节点相似性分数矩阵S=[s_ij].

3 实验设置

本实验将来自不同领域的6个网络将分为两部分, 分别是训练集E_Training和测试集E_Test, 两部分的比例为8:2, E=E_Training∪E_Test, E_Training∩E_Test =$\varnothing $. 本文介绍的算法和基准方法将应用于这些训练集, 获得链路预测的相似性分数矩阵.

3.1 实验数据

在本实验中, 我们将使用从公共学术网站下载的6个真实世界网络数据来验证我们的算法, 并将结果与上面介绍的基准算法进行比较. 这些网络通常用于链路预测研究, 分别包括: Dolphins^[24], Polbook^[25], FWFW^[26], Jazz^[27], USAir^[28], Polblogs^[29], 每个数据集的简要描述如下.

(1) Dolphins网络: 这是海豚种群中成员关系构建的网络, 节点表示海豚, 节点之间的连边表示种群成员之间的联系.

(2) Polbook网络: 这是亚马逊商城的买者购买图书情况的网络, 节点表示出售的有关美国政治的图书, 节点之间的连边表示同一买家频繁共同购买图书.

(3) FWFW网络: 这是佛罗里达海湾雨季的食物链网络, 节点表示生物, 节点之间的连边则表示生物之间的捕食关系.

(4) Jazz网络: 这是爵士音乐家合作网络, 节点表示爵士音乐家, 节点之间的连边则表示音乐家之间是朋友关系.

(5) USAir网络: 这是美国航空网络, 节点表示机场, 节点之间的连边表示机场之间有直飞航线.

(6) Polblogs网络: 这是博客网页之间的超链接关系构成的网络, 节点表示博客网页, 节点之间的连边则表示博客网页之间的包含有超链接.

本文使用到的上述网络数据集主要参数如表3所示, 其中N表示网络中节点数, M表示网络中连边数, <d>表示网络平均路径, <k>表示网络中节点的平均度, <c>表示网络平均聚类系数, D表示网络密度.

3.2 评价指标

AUC是一种在链路预测中最常用的评价指标, 可以解释为在测试集中随机选择的缺失链路被分配的相似性高于在未知链路集中随机选择的链路的概率^[30]. 当在随机情况下, AUC≈0.5, 一个链路算法的性能越好, 那么它的AUC会越接近于1. 在实验中, 我们独立地比较$ n $次, 其中有$ {n_1} $次测试集中的边的分数值大于不存在的边的分数值, 有$ {n_2} $次两者分数相等, 则AUC的计算公式为:

$ AUC = \frac{{{n_1} + 0.5{n_2}}}{n} $

(2)

Precision同样是链路预测中常见的评价指标, 相比于对预测整体准确性进行评价的AUC, 它更侧重于关心前$ L $个预测节点对中预测正确的比例^[31]. 在本文中, 我们设置$ L $=100, 即在实验中若排在前100个预测节点对中有$ m $个节点对在测试集中, 则Precision的计算公式为:

$ Precision = \frac{m}{L} $

(3)

4 实验与结果分析 4.1 AUC评价方法

首先我们对所提出的IDN算法在AUC评价指标下的性能与基准算法进行比较. 图4给出了不同网络中IDN算法与其他算法的 AUC 值. 从图4中可以看出, 与其他基准算法相比, IDN算法在Dolphins、Polbook、Jazz、USAir、Polblogs这5个不同的网络数据集上都取得了AUC的最大值, 预测结果平均提升比例为22%, 这也验证了考虑节点交互度的IDN算法在链路预测中能更有效地挖掘网络拓扑结构. 需要注意的是在FWFW数据集上, 各算法的AUC表现都不理想, 而除PA算法外其他算法AUC值均小于0.7, 本文算法并未发挥出优势. 造成此现象的原因在于PA算法不需要节点的邻域信息, 仅考虑待预测节点对的度, 而该数据集网络密度较大, PA算法得以发挥优势, 这说明网络中节点的度对预测结果有很大的影响.

图5给出了不同的链路预测方法在各数据集中的 AUC 值的堆积柱形图. 从图5中可以看出, IDN算法每种颜色的面积几乎均匀, 说明该算法对各个网络数据集能够较为稳定地预测. 而 CN算法、AA算法、JAC算法每种颜色面积差别很大, 表明这些算法的稳定性相对较差. 虽然在FWFW数据集上IDN算法的AUC值要低于PA算法, 但IDN算法的 AUC 累计值最大, 相反PA算法和JAC算法的累计值要处于劣势, 这也验证了本文基于节点交互度的链路预测算法有效性.

4.2 Precision评价方法

为了进一步验证我们提出的IDN算法的性能, 本文在Precision评价指标下将本文算法与其他基准算法进行比较. 图6给出了不同链路预测算法在各网络中的 Precision值. 可以看出, 与其他基准算法相比, IDN算法在Dolphins、Polbook、FWFW、Jazz、USAir这5个不同的网络数据集的Precision值都是最高的, 在Precision评价指标下平均提升比例为54%. 值得注意的是, JAC算法和TNDCC算法在个别数据集中的Precision为0, 这是因为JAC算法的原理是计算节点间公共邻居占彼此邻居数量的比例, 在遇到大规模数据集时, 比例急剧减小从而导致性能不佳; 而TNDCC算法结合两层节点度进行预测, 在遇到小规模数据集时, 也会导致预测效果不理想的情况. 而PA算法的思想是基于网络模型中新加入节点会倾向于和度大的节点相连的优先连接机制而提出的, 在这种机制的链路预测中, 节点链路预测的概率就正比于节点之间度的乘积, 在遇到网络密度较大数据集时有一定优势, 相反, 对一般数据集的预测性能较差.

图7给出了不同的链路预测方法在各数据集中的Precision值的堆积柱形图. 从图7中可以明显看出, JAC算法、PA算法、TNDCC算法在部分颜色的面积上有缺失且每种颜色之间的面积差别较大, 说明算法在不同数据集上的稳定性较差. 从整体看来, 各个算法在Jazz数据集上整体预测效果较好, 而在Dolphins数据集上的预测效果普遍较差. 相比于其他算法, 本文提出的IDN算法Precision累计值最大, 算法的预测结果也较为稳定. 这也进一步证明本文引入节点交互度作链路预测的性能优越性.

4.3 参数$ \alpha $对实验结果的影响

本文为了确定$ \alpha $的最优参数值, 分别设置了$ \alpha $={0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9}的平均结果. 通过6个网络数据集对链接预测AUC和Precision评价指标进行计算, 本文方法的实验结果如图8和图9所示. 可以看出, 在不同的网络中, IDN算法的性能对参数的敏感程度较低, 原因在于本文通过归一化处理统一量纲, 使得算法在保证性能的同时兼顾了稳定性. 实验还发现, 本文方法对每个网络取得最佳预测性能对应的参数值并不相同. 在对实际网络应用中, 本文方法可根据网络拓扑结构适当调节$ \alpha $值, 提高链路预测的性能.

4.4 实验结果分析

从上述实验结果来看, 在6个不同的网络数据集中, 本算法对比其他10个基准算法, AUC和Precision指标最好的各有5个网络, 且在AUC和Precision两个评价指标上预测结果平均分别提升22%和54%, 这些都进一步证明了IDN算法的优越性. 通过分析本算法的优势, 主要有以下3个方面. 首先, 与传统基于局部信息相似性的方法相比, 本算法考虑了节点在网络中信息交换的效率; 其次, 基于全局相似性方法通过考虑网络中的所有路径来预测链路的存在, 本算法使用较少的路径信息来降低算法的计算复杂度; 第三, 本算法在衡量节点间相似性时考虑了共同邻居节点的拓扑信息, 并使用归一化处理统一量纲, 本算法在与其他算法的稳定性比较中表现最佳.

5 结语

本文通过分析网络拓扑结构中节点间的交互关系, 提出了一种基于节点交互度的社会网络链路预测方法. 与传统的基于相似性的链路预测方法不同, 该方法不仅引入了共同邻居的相关局部信息, 而且考虑了节点效率在节点交互所起到的作用, 对节点局部信息和路径特征进行分析, 达到深度挖掘节点信息的目的, 在相似性的计算中更具有准确性和稳定性, 充分考虑社会网络结构的社会性和高聚集性. 本文借助6个真实网络数据集对该方法进行了验证, 结果表明本文提出的方法在AUC和Precision两个评价指标上均表现出更优的预测性能, 证明了节点交互度在社会网络链路预测方面的可行性和有效性. 本文在接下来的研究中, 可以不局限于静态网络的链路预测方法, 通过挖掘时序性特征来研究动态网络的演化趋势, 对本文的方法作进一步改进.