2. 安徽大学 计算机科学与技术学院, 合肥 230601
2. School of Computer Science and Technology, Anhui University, Hefei 230601, China
观察样本的数据信息往往可以取自多个视图, 来获得不同特征描述. 例如, 一件艺术作品的价值可以从审美、思想和技巧等不同的角度进行分析, 而技巧又包含多种不同的表现手法. 这些分析结果都可以被称为多视图数据. 多视图数据通常具有一致性和互补性, 因而可以通过尝试在不同视图间寻找共享的类簇结构, 实现比单一视图聚类更加准确的聚类方式, 这样的聚类被称为多视图聚类[1].
由于多视图数据来源的多样性, 多视图数据通常表现为高维数据, 这意味着计算时需要面临成倍增加的时间与空间复杂度. 同时, 由于客观噪声与采样误差, 多视图数据在聚类时的准确性会受到极大的影响. 子空间聚类可以将高维数据映射到低维的子空间中, 该聚类算法假设所有高维数据可以看作是低维子空间的并集, 通过对子空间分配类簇, 可以解决高维数据的聚类难题[2]. 由于高维数据点分布较为任意且稀疏, 传统的基于质心分布假设的算法在子空间聚类的结果上往往表现不佳[3]. 谱聚类[4,5]是一种解决子空间聚类问题的有效方法, 它因在任意形状类簇上的良好聚类表现, 受到了广泛关注. 在谱聚类过程中, 如何构建合适的相似度矩阵是主要的难题. 其中, 低秩稀疏子空间聚类[6]被认为是一种有效可靠的解决方案. 该方案结合了低秩子空间聚类[7,8]与稀疏子空间聚类[9]. 通过低秩约束来捕获数据的全局结构, 在假设子空间相互独立且采样数据充分的情况下, 保证了聚类的精度, 使得对象能被同一子空间中的其他对象线性表示. 同时, 借助稀疏表示, 对象能够被表示为其他对象的稀疏线性组合. 相比“纯低秩表示”, 稀疏约束的假设相对宽松, 但该方法受数据点维度的影响较大, 存在对子空间过分割的可能性. 因此, 对于子空间聚类来说, 结合低秩表示与稀疏约束来捕捉对象的全局结构与局部结构是必要的. 低秩稀疏子空间聚类被众多学者拓展研究, 应用在不同的领域. 其中, 多视图数据处理领域是许多学者研究的热点之一. Brbić等[3]将低秩稀疏子空间聚类推广到多视图领域, 用基于成对与基于质心两种正则化方法对多视图数据进行了处理, 并尝试通过解决核希尔伯特空间中的相关优化问题, 将算法扩展到非线性子空间中; Tian等[10]将基于成对正则化的多视图低秩稀疏子空间聚类应用于高光谱图像分类, 在非重叠的三维块上实现了该算法在大尺度遥感图像上的应用, 进一步证明了MLRSSC算法巨大的发展前景. 王丽娟等[11]将视图多样性概念应用于多视图低秩稀疏子空间聚类算法中. 通过挖掘多视图特征的多样性信息, 确保了不同视图下子空间表示矩阵的多样性.
聚类的目的是对相似的对象进行划分归类. 在聚类算法中, 若每个对象只属于单一类簇, 则被称为硬聚类; 若每个对象可归属于多个类簇, 则被称为软聚类. 从决策角度讲, 硬聚类是一种非黑即白的二支决策聚类; 软聚类虽然存在归属多个类簇的可能, 但这种聚类的表达方式模糊了对象与类簇间的不确定性. 为了区分出对象与类簇间“是”“否”“不确定”的关系, 需要引入Yao提出的三支决策[12]的思想, 用核心域与边缘域的组合结构来表示类簇, 将确定的对象存入核心域中, 将不确定的对象存入边缘域中. 这种聚类表示方式被称为三支聚类, 由Yu等[13–15]首次提出. 三支决策的核心思想是在没有把握作出决策的情况下, 延迟决策的进行, 等至有足够把握再执行决策. 在聚类过程中, 该决策可以在一定程度上避免高风险决策的发生, 以此来达到提高聚类性能的目的. 自提出三支聚类后, 许多学者进行了拓展研究. 于洪等[16]将三支决策应用于传统的K-means算法, 提出了一种考虑q近邻的分离性指数来作为决策的主要依据进行三支聚类. 夏月月等[17]将网格聚类算法中划分网格的思想加入三支决策下的K-means聚类, 用网格密度来快速确定核心域与边缘域, 有效解决K-means算法初始聚类中心随机选择导致的聚类结果不准确问题; 徐天杰等[18]将人工蜂群与三支K-means算法结合来解决聚类中心初始化的问题, 通过人工蜂群算法寻求最优蜜源的位置, 将其作为初始聚类中心, 并在此基础上重复迭代聚类算法. Yu等[19]将三支决策与主动学习策略相结合, 引入多视图聚类. 在基于熵概念测量对象的不确定性之后, 学习重要信息的成对约束, 来提高高维多视图数据的聚类精度.
在通过谱聚类获得数据点隶属度的过程中, K-means聚类作为其中一环, 将被应用于对图拉普拉斯矩阵的特征向量[3]进行聚类, 而K-means聚类是一种硬聚类算法, 只考虑了对象属于类簇或者不属于类簇这两种关系, 直接对所有样本进行了一次性划分. 因此, 多视图稀疏子空间聚类得到的是二支聚类的结果. 这种聚类结果没有反映出类簇与对象的不确定性关系[19]. 对此, 本文提出了一种基于投票的三支决策聚类, 将其与谱聚类算法结合, 进一步反映聚类过程中对象和类簇的不确定性关系. 通过优先对确定对象进行聚类, 并修正相关参数, 来逐步完善各类簇的主体结构与内部信息. 投票制度保证了尽可能多的可靠数据点参与聚类时的划分决策, 在减弱聚类随机性的同时, 降低了错误决策带来的负面影响.
因此, 本文引入三支决策思想, 提出了一种基于三支决策的多视图稀疏子空间聚类方法. 该方法对多视图稀疏子空间聚类进行了拓展, 在一些数据集中, 表现出了更优的聚类性能.
1 相关理论基础本节主要介绍了多视图低秩稀疏子空间聚类(MLRSSC)与三支决策聚类(TWDC). 低秩稀疏子空间聚类的主要任务是借助数据在低维子空间中的稀疏表示, 为一组给定的数据集构造出合适的亲和矩阵, 最后通过谱聚类的方法得到基于子空间的聚类结果. 三支决策聚类则是通过构造一种新的类簇内部结构, 对样本对象重新进行了划分, 筛选出核心对象与边缘对象, 从而挖掘出样本对象潜在的不确定性. 在一定范围内, 借助三支决策可以更新相似度矩阵, 继而迭代谱聚类过程, 以此获得更加准确聚类结果.
1.1 低秩表示与稀疏约束考虑一个样本数量为n的数据集
低秩表示[7,8]的思想是寻找数据集的最低秩表示, 试图从数据集中找到一个低秩表示矩阵
| $ \mathop {\min }\limits_{\mathbf{C}} {\text{ }}rank({\mathbf{C}}), {\text{ }}{\rm{s.t.}}{\text{ }}{\mathbf{X}} = {\mathbf{XC}} $ | (1) |
由于秩函数的离散性质, 上述公式的优化是NP难问题. 一个有效的方法是引入核范数代替秩函数, 将其转化为凸优化问题. 考虑到细微噪声(如高斯噪声)的影响, 一个相对合理的策略是加入一个松弛约束系数来放宽等式约束, 将目标函数转化为:
| $ \mathop {\min }\limits_{\mathbf{C}} \| {\mathbf{C}}{\| _ * }{\text{ + }}\lambda \| {\mathbf{E}}{\| _{{\text{ }}F}},\; \; {\rm{s.t.}} {\text{ }}{\mathbf{X}}{\text{ = }}{\mathbf{XC}} + {\mathbf{ E}} $ | (2) |
其中,
稀疏子空间聚类[9]的思想是将数据表示为同一子空间中其他数据的线性组合, 在子空间彼此独立的条件下, 通过引入了
| $ \mathop {\min }\limits_{\mathbf{C}} \| {\mathbf{C}}{\| _{ 1}} , \;\; {\rm{s.t.}} \; {\mathbf{X}} = {\mathbf{XC}}, {\rm{diag}}({\mathbf{C}}) = 0 $ | (3) |
类似地, 在受到噪声污染的情况下, 重新考虑目标函数为:
| $ \begin{gathered} \mathop {\min }\limits_{\mathbf{C}} \| {\mathbf{C}}{\| _{ 1}}{\text{ + }}\lambda \| {\mathbf{E}}{\| _{{\text{ }}F}}, \;\; {\rm{s.t.}} \; {\mathbf{X}} = {\mathbf{XC}} + {\mathbf{E}}{\text{, }}{\rm{diag}}({\mathbf{C}}) = 0 \\ \end{gathered} $ | (4) |
其中,
在受到噪声污染的情况下, 低秩稀疏子空间聚类的目标函数如下:
| $ \left\{\begin{gathered} \mathop {\min }\limits_{\mathbf{C}} {\beta _1}\| {\mathbf{C}}{\| _ * } + {\text{ }}{\beta _2}\| {\mathbf{C}}{\| _{ 1}} + {\text{ }}\lambda \| {\mathbf{E}}{\| _{{\text{ }}F}} \\ {\text{ }}{\rm{s.t.}}{\text{ }}{\mathbf{X}} = {\mathbf{XC}} + {\text{ }}{\mathbf{E}}{\text{, }}{\rm{diag}}({\mathbf{C}}) = 0 \\ \end{gathered} \right.$ | (5) |
当通过低秩稀疏子空间聚类求解出矩阵C后, 可以通过式(6)求得相似度矩阵:
| $ {\bf W} = \left| {\bf C} \right| + {\left| {\bf C} \right|^{\rm{T}}} $ | (6) |
利用谱聚类的方法, 对得到的相似度矩阵W进行聚类, 可以得到数据集X内部对象的初步划分.
1.2 三支决策聚类一般来说, 聚类即是对n个待划分的样本对象
三支决策的思想是用一组三元集合{CoreArea, FriArea, TriArea}来表示类簇Zi的内部结构, 其中CoreArea为类簇的核心域, 其间的元素对象明确属于该类簇. FriArea为类簇的边缘域, 其间的对象暂时不确定是否属于该类簇. TriArea为类簇的琐碎域, 表达式为U – (CoreArea ∪ FriArea), 其间的对象不属于该类簇. 同时, 3个域之间互不相交, 且它们的并集为样本对象的全集. 我们分别用Co(Zi)与Fr(Zi)来分别指代某一具体类簇Zi的核心域与边缘域, 将类簇Zi简化为一个二元集合{Co(Zi), Fr(Zi)}. 核心域与边缘域满足如下性质: (1)每个类簇的核心域内至少有一个对象, 不能为空; (2)任一对象无法存在于多个核心域内, 但可以同时存在于多个边缘域; (3)所有对象都必须划入某个类簇中; (4)任一对象一旦进入某个类簇的核心域, 则无法存在于其他类簇的边缘域.
三支聚类的结果将表示为: {(Co(Z1), Fr(Z1)), …, (Co(ZK), Fr(ZK))}.
当边缘域的结果全部划入核心域, 则聚类结果以二支的方式呈现: {Co(Z1), …, Co(ZK)}.
2 多视图低秩稀疏子空间的三支聚类 2.1 多视图聚类模型对一个有n个视角的多视图数据进行子空间聚类, 首先需要对不同视图的数据表示矩阵进行正则化. 而在聚类时所选择的正则化方式往往对最终聚类结果有重要影响. 本文将以基于质心的正则化方式进行多视图子空间聚类, 在无噪声的情况时, 其目标函数如下:
| $\left\{\begin{split} & \mathop {\min }\limits_{{{\mathbf{C}}^{(1)}}, \cdots ,{{\mathbf{C}}^{({n_v})}}} \sum\limits_{v = 1}^{{n_v}} ( {\beta _1}\parallel {{\mathbf{C}}^{(v)}}{\parallel _ * } + {\beta _2}\parallel {{\mathbf{C}}^{(v)}}{\parallel _{{\text{ }}1}} + {\lambda ^{(v)}}\parallel {{\mathbf{C}}^{(v)}} - {{\mathbf{C}}^*}\parallel _F^2) \\ & {\rm{s.t.}}{\text{ }}{{\mathbf{X}}^{(v)}} = {{\mathbf{X}}^{(v)}}{{\mathbf{C}}^{(v)}}, {\text{ }}{\rm{diag}}({{\mathbf{C}}^{(v)}}) = 0{\text{, }} {\text{ }}v = 1, 2, \cdots , {n_v} \end{split} \right.$ | (7) |
其中,
基于质心正则化的目标函数中包括多个变量, 同时求解难度很大. 因此, 需要通过交替最小化各视图的表示矩阵
(1)固定一致性变量
(2)固定各视图
式(7)的求解是一个受线性约束的凸优化问题, 所有子问题都能被精确求解[3], 文献[24]保证了ADMM算法的全局收敛性. 根据文献[3], 当迭代次数到达最大值T或迭代的变量符合收敛条件时, 迭代停止. 迭代停止时, 需要将C*带入式(6)得到相似度矩阵W, 最后对相似度矩阵W应用谱聚类的方法完成多视图部分的聚类.
(1) 固定
当固定除某一特定视图
| $ \left\{\begin{split} & \mathop {\min }\limits_{{{\mathbf{C}}^{(v)}}} {\beta _1}{\left\| {{{\mathbf{C}}^{(v)}}} \right\|_ * } + {\beta _2}{\left\| {{{\mathbf{C}}^{(v)}}} \right\|_1} + {\lambda ^{(v)}}\left\| {{{\mathbf{C}}^{(v)}} - {{\mathbf{C}}^*}} \right\|_F^2 \\ & {\rm{s.t.}}{\text{ }}{{\mathbf{X}}^{(v)}} = {{\mathbf{X}}^{(v)}}{{\mathbf{C}}^{(v)}}, {\text{ }}{\rm{diag}}({{\mathbf{C}}^{(v)}}) = 0 \end{split}\right. $ | (8) |
通过引入辅助变量
| $ \left\{\begin{split} & \mathop {\min }\limits_{{{\mathbf{A}}^{(v)}}, {\mathbf{C}}_1^{(v)}, {\mathbf{C}}_2^{(v)}, {\mathbf{C}}_3^{(v)}} {\beta _1}{\left\| {{\mathbf{C}}_1^{(v)}} \right\|_ * } + {\beta _2}{\left\| {{\mathbf{C}}_2^{(v)}} \right\|_1} + {\lambda ^{(v)}}\left\| {{\mathbf{C}}_3^{(v)} - {{\mathbf{C}}^ * }} \right\|_F^2 \\ & {\rm{s.t.}}{\text{ }}{{\mathbf{A}}^{(v)}} = {\mathbf{C}}_2^{(v)} - {\rm{diag}}({\mathbf{C}}_2^{(v)}), {\text{ }}{{\mathbf{X}}^{(v)}} = {{\mathbf{X}}^{(v)}}{{\mathbf{A}}^{(v)}} \\ & {{\mathbf{A}}^{(v)}} = {\mathbf{C}}_1^{(v)}, {{\mathbf{A}}^{(v)}} = {\mathbf{C}}_3^{(v)} \end{split}\right. $ | (9) |
将式(9)写为拉格朗日增广形式:
| $ \begin{split} & L({{\mathbf{A}}^{(v)}}, \{ {\mathbf{C}}_i^{(v)}\} _{i = 1}^3, \{ {{\mathbf{\Lambda }}_i}\} _{i = 1}^4) = {\beta _1}{\left\| {{\mathbf{C}}_1^{(v)}} \right\|_ * } \\ &\qquad + {\beta _2}{\left\| {{\mathbf{C}}_2^{(v)}} \right\|_1} + \lambda \left\| {{\mathbf{C}}_3^{(v)} - {{\mathbf{C}}^ * }} \right\|_F^2 \\ &\qquad + \frac{{{\mu _1}}}{2}\left\| {{{\mathbf{X}}^{(v)}} - {{\mathbf{X}}^{(v)}}{{\mathbf{A}}^{(v)}}} \right\|_F^2 \\ &\qquad + \frac{{{\mu _2}}}{2}\left\| {{{\mathbf{A}}^{(v)}} - {\mathbf{C}}_2^{(v)} + {\rm{diag}}({\mathbf{C}}_2^{(v)})} \right\|_F^2 \\ &\qquad + \frac{{{\mu _3}}}{2}\left\| {{{\mathbf{A}}^{(v)}} - {\mathbf{C}}_1^{(v)}} \right\|_F^2 + \frac{{{\mu _4}}}{2}\left\| {{{\mathbf{A}}^{(v)}} - {\mathbf{C}}_3^{(v)}} \right\|_F^2 \\ &\qquad + {\rm{tr}}\left[ {{{({\mathbf{\Lambda }}_1^{(v)})}^{\rm{T}}}({{\mathbf{X}}^{(v)}} - {{\mathbf{X}}^{(v)}}{{\mathbf{A}}^{(v)}})} \right] \\ &\qquad + {\rm{tr}}\left[ {{{({\mathbf{\Lambda }}_2^{(v)})}^{\rm{T}}}({{\mathbf{A}}^{(v)}} - {\mathbf{C}}_2^{(v)} + {\rm{diag}}({\mathbf{C}}_2^{(v)}))} \right] \\ &\qquad + {\rm{tr}}\left[ {{{({\mathbf{\Lambda }}_3^{(v)})}^{\rm{T}}}({{\mathbf{A}}^{(v)}} - {\mathbf{C}}_1^{(v)})} \right] + {\rm{tr}}\left[ {{{({\mathbf{\Lambda }}_4^{(v)})}^{\rm{T}}}({{\mathbf{A}}^{(v)}} - {\mathbf{C}}_3^{(v)})} \right] \\ \end{split} $ | (10) |
其中,
为了解决式(9)的凸优化问题, 需要用ADMM算法进行求解, 分别更新各个辅助变量.
将式(10)中关于
| $ \begin{split} {{\mathbf{A}}^{(v)}} = &{[{\mu _1}{({{\mathbf{X}}^{(v)}})^{\rm{T}}}{{\mathbf{X}}^{(v)}} + {\mu _2}{\mathbf{I}} + {\mu _3}{\mathbf{I}} + {\mu _4}{\mathbf{I}}]^{ - 1}} \\ & \times {\text{ }}[{\mu _1}{({{\mathbf{X}}^{(v)}})^{\rm{T}}}{{\mathbf{X}}^{(v)}} + {\mu _2}{\mathbf{C}}_2^{(v)} + {\mu _3}{\mathbf{C}}_1^{(v)} + {\mu _4}{\mathbf{C}}_3^{(v)} \\ & + {({{\mathbf{X}}^{(v)}})^{\rm{T}}}{\mathbf{\Lambda }}_1^{(v)} - {\mathbf{\Lambda }}_2^{(v)} - {\mathbf{\Lambda }}_3^{(v)} - {\mathbf{\Lambda }}_4^{(v)}] \end{split} $ | (11) |
其中,
在更新
| $ \left\{\begin{split} &{{\mathbf{A}}^{(v)}} + \frac{{{\mathbf{\Lambda }}_3^{(v)}}}{{{\mu _3}}} = {\mathbf{U\Sigma }}{{\mathbf{V}}^{\rm{T}}}{\text{ }}rank\left({{\mathbf{A}}^{(v)}} + \frac{{{\mathbf{\Lambda }}_3^{(v)}}}{{{\mu _3}}}\right) = r \\ &{\eta _s}\left({\mathbf{\Sigma }}, \frac{{{\beta _1}}}{{{\mu _3}}}\right) = {\rm{diag}}\left(\left\{ {sgn} (\sigma_i){\left(\left| {\sigma_i} \right| - \frac{{{\beta _1}}}{{{\mu _3}}}\right)_ + }\right\} \right) \\ &{\mathbf{\Sigma }}{\text{ }} = {\text{ }}{\rm{diag}}\left( {\left\{ {\sigma_i} \right\}1 \leqslant i \leqslant r} \right) \end{split}\right. $ | (12) |
其中,
| $ {\mathbf{C}}_1^{(v)} = {\mathbf{U}}{\eta _s}\left({\mathbf{\Sigma }}, \frac{{{\beta _1}}}{{{\mu _3}}}\right){{\mathbf{V}}^{\rm{T}}} $ | (13) |
在文献[3]中, 将该过程表述为式(14):
| $ {\mathbf{C}}_1^{(v)} = {\pi _{\frac{{{\beta _1}}}{{{\mu _3}}}}}\left({{\mathbf{A}}^{(v)}} + \frac{{{\mathbf{\Lambda }}_3^{(v)}}}{{{\mu _3}}}\right) $ | (14) |
根据文献[26,27], 类似地,
| $ \left\{\begin{gathered} {\mathbf{C}}_2^{(v)} = {\pi _{\frac{{{\beta _2}}}{{{\mu _2}}}}}\left({{\mathbf{A}}^{(v)}} + \frac{{{\mathbf{\Lambda }}_2^{(v)}}}{{{\mu _2}}}\right) \\ {\mathbf{C}}_2^{(v)} = {\mathbf{C}}_2^{(v)} - {\rm{diag}}\left({\mathbf{C}}_2^{(v)}\right) \\ \end{gathered}\right. $ | (15) |
通过将式(9)中关于
| $ {\mathbf{C}}_3^{(v)} = {(2{\lambda ^{(v)}} + {\mu _4})^{ - 1}}(2{\lambda ^{(v)}}{{\mathbf{C}}^ * } + {\mu _4}{{\mathbf{A}}^{(v)}}{\text{ + }}{\mathbf{\Lambda }}_4^{(v)}) $ | (16) |
其中,
对偶变量
| $ \left\{\begin{gathered} {\mathbf{\Lambda }}_1^{(v)} = {\mathbf{\Lambda }}_1^{(v)} + {\mu _1}({{\mathbf{X}}^{(v)}} - {{\mathbf{X}}^{(v)}}{{\mathbf{A}}^{(v)}}) \\ {\mathbf{\Lambda }}_2^{(v)} = {\mathbf{\Lambda }}_2^{(v)} + {\mu _2}({{\mathbf{A}}^{(v)}} - {\mathbf{C}}_2^{(v)}) \\ {\mathbf{\Lambda }}_3^{(v)} = {\mathbf{\Lambda }}_3^{(v)} + {\mu _3}({{\mathbf{A}}^{(v)}} - {\mathbf{C}}_1^{(v)}) \\ {\mathbf{\Lambda }}_4^{(v)} = {\mathbf{\Lambda }}_4^{(v)} + {\mu _4}({{\mathbf{A}}^{(v)}} - {\mathbf{C}}_3^{(v)}) \\ {\mu _i} = \min (\rho {\mu _i}, {\mu _{\max }}), \; i = 1, \cdots , 4 \\ \end{gathered}\right. $ | (17) |
其中,
在噪声影响下, 式(9)的目标函数修改为:
| $ \left\{\begin{split} & \mathop {\min }\limits_{{{\mathbf{C}}^{(1)}}, \cdots {\text{, }}{{\mathbf{C}}^{({n_v})}}} \sum\limits_{v = 1}^{{n_v}} \left( \frac{1}{2}\left\| {{{\mathbf{X}}^{(v)}} - {{\mathbf{X}}^{(v)}}{{\mathbf{A}}^{(v)}}} \right\|_F^2 + {\beta _1}\parallel {{\mathbf{C}}^{(v)}}{\parallel _ * }\right. \\ &\qquad\quad \left.+ {\beta _2}\parallel {{\mathbf{C}}^{(v)}}{\parallel _{{\text{ }}1}} + {\lambda ^{(v)}}\parallel {{\mathbf{C}}^{(v)}} - {{\mathbf{C}}^*}\parallel _F^2\right) \\ & {\rm{s.t.}}{\text{ }}{{\mathbf{X}}^{(v)}} = {{\mathbf{X}}^{(v)}}{{\mathbf{C}}^{(v)}}, {\text{ }}{\rm{diag}}({{\mathbf{C}}^{(v)}}) = 0{\text{, }}v = 1, 2, \cdots , {n_v} \end{split}\right. $ | (18) |
在被噪声污染时,
| $ \begin{split} {{\mathbf{A}}^{(v)}} = &{[{({{\mathbf{X}}^{(v)}})^{\rm{T}}}{{\mathbf{X}}^{(v)}} + {\mu _2}{\mathbf{I}} + {\mu _3}{\mathbf{I}} + {\mu _4}{\mathbf{I}}]^{ - 1}} \\ & \times {\text{ }}[{({{\mathbf{X}}^{(v)}})^{\rm{T}}}{{\mathbf{X}}^{(v)}} + {\mu _2}{\mathbf{C}}_2^{(v)} + {\mu _3}{\mathbf{C}}_1^{(v)} + {\mu _4}{\mathbf{C}}_3^{(v)} \\ & + {\text{ }}{({{\mathbf{X}}^{(v)}})^{\rm{T}}}{\mathbf{\Lambda }}_1^{(v)} - {\mathbf{\Lambda }}_2^{(v)} - {\mathbf{\Lambda }}_3^{(v)} - {\mathbf{\Lambda }}_4^{(v)}] \end{split} $ | (19) |
(2)固定
更新完每一个视图的自表示矩阵后, 将
| $ {{\mathbf{C}}^ * } = \frac{{\displaystyle\sum {_{v = 1}^{{n_v}}{\lambda ^{(v)}}{{\mathbf{C}}^{(v)}}} }}{{\displaystyle\sum {_{v = 1}^{{n_v}}{\lambda ^{(v)}}} }} $ | (20) |
算法1. 基于质心的正则化多视图低秩稀疏子空间聚类
输入: 各视图矩阵
输出: 各视图间的一致性相似矩阵W
步骤:
1. 初始化各系数:
2. 未收敛时或未超过迭代次数上限T时循环执行:
3. 遍历各视图
4. 固定其他变量, 根据式(11)更新
5. 固定其他变量, 根据式(14)更新
6. 固定其他变量, 根据式(15)更新
7. 固定其他变量, 根据式(16)更新
8. 固定其他变量, 根据式(17)更新对偶变量
9. 结束遍历
10. 根据式(17)更新惩罚系数
11. 固定各视图变量, 根据式(20)更新
12. 判断收敛条件:
13. 结束循环
14. 将
通过谱聚类对得到的相似度矩阵W进行分割求解, 可以初步得到多视图聚类的解. 但获得的初步解是一种二支聚类解, 没有考虑到类簇与对象间的不确定性, 聚类结果存在一定的误差. 因此, 本文引入三支决策, 设计了一种基于投票的三支聚类, 将其应用于多视图聚类求解的谱聚类环节, 对得到的二支聚类的解作进一步的修正.
三支决策聚类的主要思想为: 对于确定的解将其纳入核心域, 对于不确定的解将其纳入边缘域. 通过优先构造出由确定性较高的对象组成的核心域, 可以尽可能多地增加掌握的聚类信息, 提升对不确定样本成功聚类的可能性. 聚类基于k近邻与投票制度, 一定程度上降低了聚类过程中噪声的干扰. 同时, 考虑到错误划分样本带来的连锁效应, 我们设定了基于原始样本数量动态变化的迭代上限Q, 通过控制其大小来取得相对较优的聚类解.
本文基于一些评价性指标将三支聚类结果与原来直接通过谱聚类得到的结果进行比对, 来验证其有效性.
3.1 算法框架图图1为三支聚类算法的主要框架流程图. 框架以循环迭代的形式呈现, 其主要包括3个模块: 初始化域模块, 扩展域模块以及边缘域对象重划分模块. 其中, 初始化域模块只在第1次迭代时启动, 该模块的目的是将可信度较高的聚类结果作为各类簇的基本依据; 扩展域模块则会根据当前候选区情况选择性启动, 其主要思想是通过不断完善各类簇核心域内的主体信息, 重新考虑之前的未划分对象, 决定是否将其归入类簇; 而重划分模块在每轮迭代时都会启动. 这是考虑到聚类过程中各类簇的特征信息是实时变化的, 一些早先被划入边缘域的样本可能会因这些信息变动, 获得进入核心域的资格; 同时, 某些边缘域样本的重划分, 可能导致一些无法得到划分的对象重新获得划入某一类簇的资格. 重划分的目的就是在于尽可能谨慎地、及时地更新这些可能存在的变动.
三支决策聚类迭代结束条件为循环次数大于设定值Q或者无可划分目标对象, Q值需要视具体数据样本对象的复杂度设定.

|
图 1 算法框架图 Fig. 1 Algorithm Framework Diagram |
3.2 算法思想
为了得到一个三支聚类的结果, 需要经历初始、扩展、重划分3个主要阶段. 本文的三支决策思想基于文献[19]与文献[28]做出改进, 在初始化部分, 核心域基于原有的二支聚类结果进行重塑; 在扩展与重划分部分, 引入基于k近邻标准的投票制度, 在尽可能保证对聚类性能不产生负提升的情况下, 一定程度上对其结果进行部分修正, 提高聚类效率.
算法2. 基于投票的三支决策算法
输入: 相似度矩阵W, 类簇数量K
输出: 三支表示最终的聚类结果{(Co(Z1), Fr(Z1)), …, (Co(Zi), Fr(Zi)), …, (Co(ZK), Fr(ZK))}
步骤:
1. 相似度矩阵W执行谱聚类过程, 得到初始二支解
2. 判断是否为第1次迭代. 若是, 则在原二支聚类解中, 选取距离聚类中心最近的样本点与其周围样本点初始化核心域{Co(Z1), …, Co(ZK)}; 否则进入步骤3.
3. 判断当前待分类区是否划分完毕. 若未划分完毕, 则遍历每一个候选区的待分类样本, 使其参与投票. 对于某个待分类样本x, 所有类簇的核心域样本
4. 判断当前边缘域有无划分完毕. 若未划分完毕, 则通过式(24)–式(27), 在边缘域中选出重划分候选对象
5. 依据式(29)执行投票决策, 得出最终划分对象, 将其划入指定类簇的核心域, 同时删除存在于其他类簇边缘域的该对象.
6. 式(31)更新相似度矩阵, 判断迭代次数是否超过设定最大值Q, 若超过则结束算法; 否则跳转至步骤1.
3.2.1 初始化核心域得到相似度矩阵后, 利用谱聚类可以得到一个原始的二支解. 三支聚类将原有的n个类簇的二支解
初始化的核心域对象的选择依据为: 谱聚类过程中, 所有目标对象关于各自K-means聚类中心的距离. 其主要分为两个部分: 中心对象群与近中心对象群. 中心对象群由若干距离聚类中心最近的样本点组成, 其任务主要负责吸引核心样本点. 近中心对象群则由若干围绕聚类中心对象的样本点组成, 其主要负责吸引介于核心与边界域之间特征较为模糊的样本点.
3.2.2 扩展核心域与边缘域本节将介绍扩展核心域与边缘域部分. 定义核心近邻IC(x, cn), 边缘近邻IF(x, fn)分别为样本x在范围cn与fn个近邻的集合, voteCo为1×K的矩阵, 用于储存各个类簇内对象的投票结果. 其中cn<fn, 两个变量基于类簇个数K与样本总数M动态分配, 我们通过两个参数θ1与θ2来控制他们, 其定义主要如下:
| $ cn = \left\lfloor {\left\lfloor {\frac{M}{K}} \right\rfloor \times \frac{1}{{{\theta _1}}}} \right\rfloor , \; fn = \left\lfloor {\left\lfloor {\frac{M}{K}} \right\rfloor \times \frac{1}{{{\theta _2}}}} \right\rfloor $ | (21) |
对于待划分样本x与已划分样本
| $ \left\{\begin{gathered} (1){\text{ }}{\rm{if}}{\text{ }}({\mathbf{x}} \in IC({{\mathbf{x}}_j}, fn)\; \& \&\; {\mathbf{x}} \notin IC({{\mathbf{x}}_j}, cn) , \\ {\rm{then}}{\text{ }}{\mathbf{voteCo}}(1, k) = {\mathbf{voteCo}}(1, k) \\ (2){\text{ }}{\rm{if}}{\text{ }}({\mathbf{x}} \in IC({{\mathbf{x}}_j}, cn) \; \& \& \; {{\mathbf{x}}_j} \notin IC({\mathbf{x}}, cn)), {\text{ }} \\ {\rm{then}}{\text{ }}{\mathbf{voteCo}}(1, k) = {\mathbf{voteCo}}(1, k) \\ (3){\text{ }}{\rm{if}}{\text{ }}({\mathbf{x}} \in IC({{\bf{x}}_j}, cn) \; \& \& \; {{\mathbf{x}}_j} \in IC({\mathbf{x}}, cn)), {\text{ }} \\ {\rm{then}}{\text{ }}{\mathbf{voteCo}}(1, k) = {\mathbf{voteCo}}(1, k) + 1 \\ \end{gathered}\right. $ | (22) |
其中, 若符合条件(1)或条件(2), 则将进入边缘域, 符合条件(3)将进入核心域, 均不符合者将在该阶段不作划分, 等待至下一轮再作划分.
该阶段将遍历所有类簇的核心域样本, 对当前待划分对象x进行投票决策. 对于某一类簇, 若其核心域内的任意对象投出正票, 则视为该类簇参与对当前待划分对象的竞争, 划分对象便有机会进入该类簇的核心域. 当多个类簇同时对某一待划分对象竞争时, 将依据类簇Zk与待划分对象的投票分数函数Sc(Zk)来确定样本对象的划分:
| $ \left\{\begin{array}{l} {\textit{Sc}}({Z_k}) = \dfrac{1}{{\left| {Co({Z_k})} \right|}}\displaystyle\sum\nolimits_{{x_j} \in Co({Z_k})} {\dfrac{{{W_{ \cdot j}} - \min ({W_{ \cdot j}})}}{{\max ({W_{ \cdot j}}) - \min ({W_{ \cdot j}})}}} \\ {x_j} \in \displaystyle\bigcup _{k = {k_1}}^{{k_n}}Co({Z_k}) \end{array} \right.$ | (23) |
其中, W·j为待划分对象xi与核心域样本xj的相似度, |Co(Zk)|为类簇Zk核心域样本数量, {k1, …, kn}为参与竞争的多个类簇的编号. 待分类对象将被划入投票分数最高的类簇.
3.2.3 边缘域对象的重新划分在本节我们将讨论如何对位于边缘域的对象进行重新划分. 挑选合适的边缘域样本是该部分的关键. 其中, 考虑边缘域中最有可能隶属于核心域的对象, 即相似度最大的对象, 是一种常见的选择方案. 但基于最大相似度的采样策略存在局限性, 随着边缘域样本的逐渐减少, 最大相似度的有效性会逐渐下降. 基于不确定性的采样是一种适用性广泛的采样策略, 通过优先划分不确定性最大的样本来减少整体模型的熵, 从而得到相对优的解. 本文提出一种基于相似度判别与不确定性判别交替采样的方法, 同时继续通过投票来确定每轮迭代中的采样模式.
考虑边缘域样本
| $ p({{\mathbf{x}}_t} \in Co({Z_k})) = \frac{{\dfrac{1}{{\left| {Co({Z_k})} \right|}}\displaystyle\sum\nolimits_{{{\mathbf{x}}_j} \in Co({Z_k})} {{W_{ \cdot j}}} }}{{\displaystyle\sum\nolimits_{n = 1}^K {\dfrac{1}{{\left| {Co({Z_n})} \right|}}\displaystyle\sum\nolimits_{{{\mathbf{x}}_j} \in Co({Z_k})} {{W_{ \cdot j}}} } }} $ | (24) |
通过排序求解式(25)得到隶属某一类簇概率最大的边缘域样本xs.
| $ {{\mathbf{x}}_s} = \mathop {\arg \max p({\mathbf{x}} \in Co({Z_k}))}\limits_{{\mathbf{x}} \in \cup _{i = 1}^KFr({Z_i})} , \; k \in [1, K] $ | (25) |
得到每个边缘域样本的隶属概率后, 通过不确定性熵计算公式计算出其不确定度:
| $ H({\mathbf{x}}) = - \frac{1}{K}\sum\limits_{k = 1}^K {(p({\mathbf{x}} \in Co({Z_k}))} {\log _2}p({\mathbf{x}} \in Co({Z_k}))) $ | (26) |
通过排序求解式(27)得到隶属某一类簇概率最大的边缘域样本xe.
| $ {{\mathbf{x}}_e} = \mathop {\arg \max H({\mathbf{x}})}\limits_{{\mathbf{x}} \in \cup _{i = 1}^KFr({Z_i})} $ | (27) |
至此, 当前拥有了两个候选对象Xe与Xs. 同时, 根据式(24)结果, 按照隶属类簇概率p的降序排列, 记录Xe与Xs隶属类簇的序列E与序列S:
| $ E = \{ {Z_{{e_1}}}, {Z_{{e_2}}}, \cdots , {Z_{{e_n}}}\} , \; S = \{ {Z_{{s_1}}}, {Z_{{s_2}}}, \cdots , {Z_{{s_n}}}\} $ | (28) |
按照序列的顺序, 通过对每个核心域的对象进行问询投票, 来确定候选对象的选择. 引入一个1×2大小的投票统计矩阵reVote, 其中reVote{1, 1}部分为正票统计数, reVote{1, 2}部分为负票统计数, 对于候选对象x, 定义核心近邻RC(xj , rn)为核心域Ak样本xj在范围rn个近邻的集合, 投票问询的规则为:
| $ \left\{\begin{gathered} {\rm{if}}{\text{ (}}{\mathbf{x}} \in RC({{\mathbf{x}}_j}, rn){\text{) , then }}{\mathbf{reVote}}\{ k, 1\} = {\mathbf{reVote}}\{ k, 1\} + 1 \\ {\rm{if}}{\text{ (}}{\mathbf{x}} \notin RC({{\mathbf{x}}_j}, rn){\text{) , then }}{\mathbf{reVote}}\{ k, 2\} = {\mathbf{reVote}}\{ k, 2\} + 1 \\ \end{gathered}\right. $ | (29) |
其中,
当xe与xs都被所有类簇否定时, 即:
| $ {\mathbf{reVote}}\{ k, 1\} < {\mathbf{reVote}}\{ k, 2\} , 1 \leqslant k \leqslant K $ | (30) |
当该情况出现时, 意味着当前边缘域内最大相似度指标的有效性已经完全丧失, 不再值得信任. 为了尽可能减少错误决策带来的影响, 将选择不确定性最大的候选样本Xe, 划入其隶属度最高的类簇
基于文献[19], 当边缘域的样本划入核心域后, 需要重新更新相似度矩阵. 将同类簇内的两个样本间的关系定义ML, 非同类簇内的两个样本间的关系定义为CL, 给出更新规则:
| $ \left\{\begin{gathered} {\rm{if}}\;({x_i}, {x_j}) \in ML, \; {\rm{then}}{\text{ }}{{\mathbf{w}}_{ij}} = {{\mathbf{w}}_{ji}} = 1 \\ {\rm{if}}\;({x_i}, {x_j}) \in CL, \; {\rm{then}}{\text{ }}{{\mathbf{w}}_{ij}} = {{\mathbf{w}}_{ji}} = 0 \\ \end{gathered}\right. $ | (31) |
为了验证本算法的性能, 我们采用5个真实数据集来验证, 分别是Prokaryotic, 3-sources, Reuters, UCI Digits与Citeseer. 表1展示了这些数据的详细信息. 其中, 3-sources与Reuters具备特征数量多, 样本数量少且数据稀疏的特点; 相反, UCI Digits与Prokaryotic的样本数量较多但特征向量维度低; Citeseer数据集拥有着数量相对近似的特征与样本数量. 通过对不同类型与特点的数据集进行实验测试, 可以更全面评估各算法的表现性能.
| 表 1 测试数据集 Table 1 Testing datasets |
Prokaryotic数据集: 包含551种原核生物的数据集, 由数据文本与基因组[29]构成. 最大聚类样本数为313个, 最小聚类样本数为35个.
3-sources数据集: 同时被BCC, Reuters和Guardian这3家报社刊登的新闻组成的数据集. 一共169个样本, 分属商业、政治、运动、健康、娱乐、科技6类领域.
Reuters数据集: 由5种不同语言组成的文档功能数据集. 共分为6个类, 本文参照文献[3]选取标准, 选取了共600个数据样本.
UCI Digits数据集: 取自荷兰公共服务地上0–9手写数字组成的数据集. 从10个类别中选取了200个样本, 由3个视图组成. 分别为76个字符形状的傅里叶系数、216个轮廓相关的特征和Karhunen-Love系数.
Citeseer数据集: 各类科学文章组成的数据集. 由两个视图组成, 分别是文本信息与文章引用关系.
基于上述数据集分别与如下对比算法进行比较.
(1) 基于协同正则化的多视图谱聚类(co-regularized multi-view spectral clustering, Co-Reg)[30], 该算法通过两种正则化方法得到视角.
(2) 基于鲁棒的多视图谱聚类(robust multi-view spectral clustering, RMSC)[31], 该算法通过构建低秩转移概率矩阵作为马尔科夫链的关键输入, 降低了各个视图数据中噪点对聚类性能的影响.
(3) 凸稀疏多视图谱聚类(convex sparse multi-view spectral clustering, CSMSC)[32]. 该算法利用稀疏性对谱聚类进行了优化.
(4) 基于低秩稀疏约束的自权重多视角子空间聚类(self-weighted multi-view subspace clustering with low-rank sparse constraint, SWMSC)[2], 一种新的基于低秩约束的自权重多视角聚类算法.
(5) 多视图稀疏子空间聚类(centroid multi-view low-rank sparse subspace clustering, MLSSC)[3], 该算法通过低秩与稀疏约束, 构建共享各个视图的一致性矩阵来学习联合子空间表示的子空间聚类.
其中, 为了保证与本文正则化方案的一致性, 算法1与算法4均基于质心进行正则化. 通过对比原始算法, 传统算法与近几年最新的算法, 可以更加直观地体现出本文算法的性能表现.
4.2 评价指标文本采用两个常见的指标来评价算法的性能, 分别是精确度(accuracy, ACC)与归一化互信息(normalized mutual information, NMI).
ACC表示聚类的准确度. N表示样本数, Pi是第i个样本聚类产生的标签, 其真实标签是yi. 当且仅当x=y时,
| $ ACC = \frac{1}{N}\sum\limits_i^N {\delta ({y_i}} , map({P_i})) $ | (32) |
NMI表示两个聚类成果的相近程度.
| $ {\textit{NMI}}(Y, C) = \frac{{2 \times I(Y;C)}}{{H(Y) + H(C)}} $ | (33) |
其中, Y表示数据真实的类别, C表示聚类结果, H(·)表示交叉熵.
4.3 参数设置多视图低秩稀疏子空间聚类中, 低秩参数β1, 稀疏参数β2, 视图间一致性参数λ与惩罚系数μ对于不同的数据集, 需要做出相应调整. 其中, 其针对UCI Digits, 3-sources, Reuters这3个数据集的参数调整在文献[5]中给出, 分别设定为: {0.9, 0.1, 0.7, 10}, {0.1, 0.9, 0.7, 102}, {0.5, 0.5, 0.3, 104}.
在三支决策中, 初始核心域系数ω, 核心近邻系数θ1, 边界近邻系数θ2以及最大迭代次数Q依据数据集Prokaryotic, 3-sources, Reuters设定为: {15, 0.8, 1.6, 15}, {30, 2.2, 2.6, 20}, {8.8, 2, 10, 100}.
初始核心域系数ω影响着初始聚类空间与原低秩稀疏聚类算法结果的相似度. 最大迭代次数Q在一定程度上影响着核心域样本与边缘域样本在算法结束时的数量. 核心近邻系数θ1控制进入核心域的严苛程度, 当其较大时, 会提高算法的运行时间. 边缘近邻系数θ2影响着算法过程中边缘域的数量, 在一定程度上影响着算法结果的波动程度.
4.4 实验结果与分析对每一组数据的测试, 本文的算法(TW-MLSSC)与多视图稀疏子空间聚类算法都将参数调整至表现性能最好, 运行10次获得评价指标, 并计算各个评价指标的平均值以及方差.
从表2与表3可以看出, 在3-sources与Reuters这类特征向量多且样本数据较为稀疏的数据集上, 本文算法的性能相较于原算法有所提升. 但在UCI Digits与Prokaryotic这些特征数量相对样本数量较少的数据集上, 性能表现反而有所下降; 相较于RSCM与CSMSC算法, 本算法总体表现出了更好的性能. 与目前较新的多视图聚类算法相比, 在部分数据集上有着更优异的表现.
从整体结果进行分析, 本文设计的基于投票的三支决策聚类在特征向量、样本数量稀疏的实验测试数据集上, 对原算法会有较大的正向提升; 但当特征向量数量相对样本数量较少时, 提升效果并不理想. 这一结果也符合实际情况: 三支决策聚类的思想是在缺乏足够信息的情况下, 延迟决策的进行, 来避免高风险决策的发生. 若延迟决策后依旧无法有足够的信息支撑, 算法的实际效果便会大打折扣, 在实验中的具体表现为实验数据集样本特征数量相对样本数量较少的情况. 反之, 在样本特征向量较多时, 延迟决策所带来的收益便会相对明显, 这是因为有了足够且有效的信息为聚类提供决策支持.
| 表 2 对比算法在不同数据集上的ACC Table 2 The ACC of different algorithms on five multi-view datasets |
| 表 3 对比算法在不同数据集上的NMI Table 3 The NMI of different algorithms on five multi-view datasets |
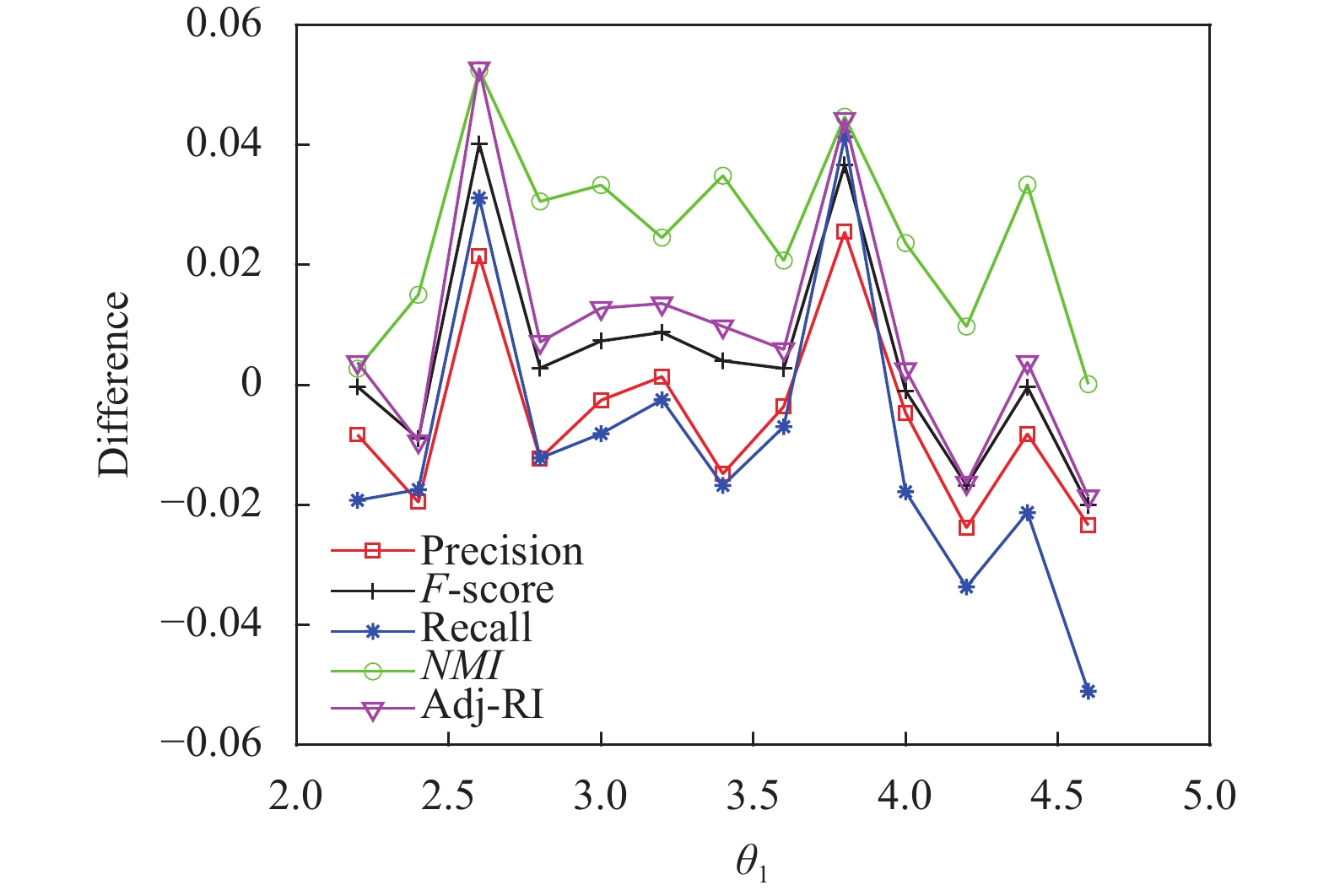
图2和图3给出了不同边缘近邻参数θ2参数设定下3-sources中核心近邻参数θ1对3-sources算法性能的影响, Y轴为本文算法与二支决策的多视图稀疏子空间算法在评价指标上的差值. 可以看出, 本文算法性能对参数θ1与θ2的设置较为敏感. 算法不同参数的设置下, 在某些局部区间均出现较好算法表现. 同时, 也在某些区间表现出截然不同的算法性能, 说明了不恰当的参数设置会对算法的性能带来负提升.
|
图 2 3-sources核心近邻参数θ1对算法性能的影响{ω=30, Q=20, θ2=2.2} |
5 结论与展望
为处理高维多视图数据, 本文采用一种低秩表示的稀疏子空间聚类算法. 稀疏子空间聚类保证了在其子空间内每个聚类视角用尽可能少的数据点来线性表示, 低秩表示用来减少数据冗余, 降低噪声的干扰问题. 此外, 本文采用三支决策思想, 设计了一种基于投票的三支决策方法, 将其应用于多视图低秩稀疏子空间聚类. 从实验结果来看, 本文提出的算法在一些特定数据集上有效提高了聚类的性能, 证明了“延迟决策”这一三支决策的主要思想应用在聚类领域的可行性与积极作用.
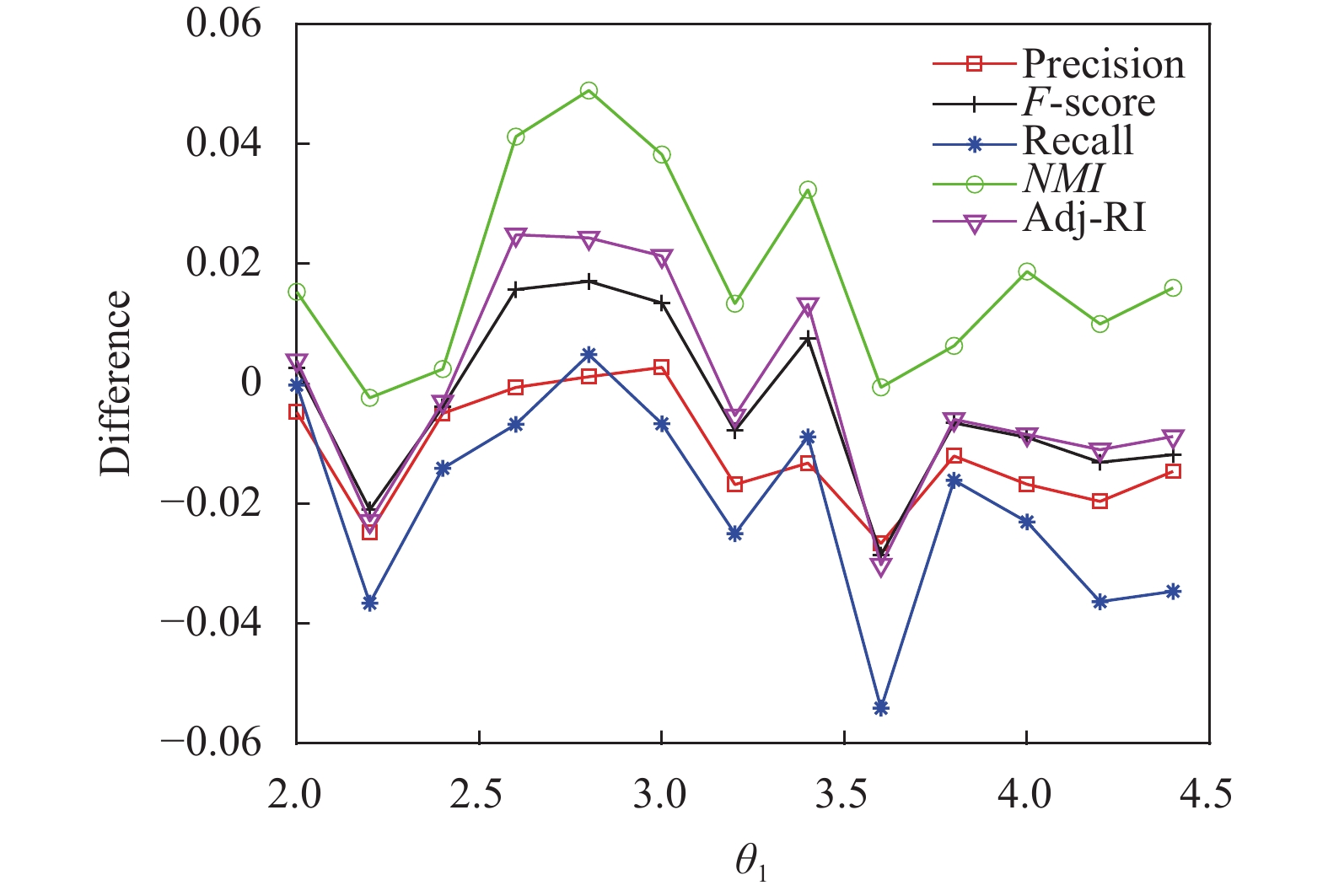
|
图 3 3-sources核心近邻参数θ1对算法性能的影响{ω=30, Q=20, θ2 =2} |
该算法也存在着缺陷, 例如在特征向量较少的数据集中表现较差, 甚至造成了性能的负提升; 参数选取的区间不稳定等. 在未来的工作中, 我们将侧重于提高算法的效率, 同时借鉴其他多视图聚类算法的思想, 对现有的算法模型进行优化. 此外, 尝试探究近邻系数对于三支决策聚类更深层次的影响与其背后的运行机制.
| [1] |
Chao GQ, Sun SL, Bi JB. A survey on multiview clustering. IEEE Transactions on Artificial Intelligence, 2021, 2(2): 146-168. DOI:10.1109/tai.2021.3065894 |
| [2] |
夏菁, 丁世飞. 基于低秩稀疏约束的自权重多视角子空间聚类. 南京大学学报(自然科学), 2020, 56(6): 862-869. DOI:10.13232/j.cnki.jnju.2020.06.008 |
| [3] |
Brbić M, Kopriva I. Multi-view low-rank sparse subspace clustering. Pattern Recognition, 2018, 73: 247-258. DOI:10.1016/j.patcog.2017.08.024 |
| [4] |
Ng AY, Jordan MI, Weiss Y. On spectral clustering: Analysis and an algorithm. Proceedings of the 14th International Conference on Neural Information Processing Systems: Natural and Synthetic. Vancouver: MIT Press, 2001. 849–856.
|
| [5] |
Shi JB, Malik J. Normalized cuts and image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(8): 888-905. DOI:10.1109/34.868688 |
| [6] |
Wang YX, Xu H, Leng CL. Provable subspace clustering: When LRR meets SSC. Proceedings of the 26th International Conference on Neural Information Processing Systems. Lake Tahoe: Curran Associates Inc., 2013. 64–72.
|
| [7] |
Liu GC, Lin ZC, Yu Y. Robust subspace segmentation by low-rank representation. Proceedings of the 27th International Conference on International Conference on Machine Learning. Haifa: Omnipress, 2010. 663–670.
|
| [8] |
Vidal R, Favaro P. Low rank subspace clustering (LRSC). Pattern Recognition Letters, 2014, 43: 47-61. DOI:10.1016/j.patrec.2013.08.006 |
| [9] |
Elhamifar E, Vidal R. Sparse subspace clustering: Algorithm, theory, and applications. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(11): 2765-2781. DOI:10.1109/TPAMI.2013.57 |
| [10] |
Tian L, Du Q. Parallel multi-view low-rank and sparse subspace clustering for unsupervised hyperspectral image classification. Proceedings of the 2018 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference. Honolulu: IEEE, 2018. 618–621.
|
| [11] |
王丽娟, 丁世飞, 夏菁. 基于多样性的多视图低秩稀疏子空间聚类算法. 智能系统学报, 2023, 18(2): 399-407. DOI:10.11992/tis.202110026 |
| [12] |
Yao YY. Three-way decision: An interpretation of rules in rough set theory. Rough Sets and Knowledge Technology. Berlin: Springer, 2009. 642–649.
|
| [13] |
Yu H, Jiao P, Yao YY, et al. Detecting and refining overlapping regions in complex networks with three-way decisions. Information Sciences, 2016, 373: 21-41. DOI:10.1016/j.ins.2016.08.087 |
| [14] |
Yu H, Zhang C, Wang GY. A tree-based incremental overlapping clustering method using the three-way decision theory. Knowledge-based Systems, 2016, 91: 189-203. DOI:10.1016/j.knosys.2015.05.028 |
| [15] |
Yu H. A framework of three-way cluster analysis. Proceedings of the 2017 International Joint Conference on Rough Sets. Olsztyn: Springer, 2017. 300–312.
|
| [16] |
于洪, 毛传凯. 基于K-means的自动三支决策聚类方法. 计算机应用, 2016, 36(8): 2061-2065, 2091. DOI:10.11772/j.issn.1001-9081.2016.08.2061 |
| [17] |
夏月月, 张以文. 一种融合三支决策理论的改进K-means算法. 小型微型计算机系统, 2020, 41(4): 724-731. DOI:10.3969/j.issn.1000-1220.2020.04.009 |
| [18] |
徐天杰, 王平心, 杨习贝. 基于人工蜂群的三支K-means聚类算法. 计算机科学, 2023, 50(6): 116-121. DOI:10.11896/jsjkx.220800150 |
| [19] |
Yu H, Wang XC, Wang GY, et al. An active three-way clustering method via low-rank matrices for multi-view data. Information Sciences, 2020, 507: 823-839. DOI:10.1016/j.ins.2018.03.009 |
| [20] |
Yu H, Zhou QF. A cluster ensemble framework based on three-way decisions. Proceedings of the 8th International Conference on Rough Sets and Knowledge Technology. Halifax: Springer, 2013. 302–312.
|
| [21] |
Yao YY. Three-way decisions and cognitive computing. Cognitive Computation, 2016, 8(4): 543-554. DOI:10.1007/s12559-016-9397-5 |
| [22] |
Yu H, Zhang C, Hu F. An incremental clustering approach based on three-way decisions. Proceedings of the 9th International Conference on Rough Sets and Current Trends in Computing. Granada: Springer, 2014. 152–159.
|
| [23] |
Boyd S, Parikh N, Chu E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends® in Machine Learning, 2011, 3(1): 1-122. DOI:10.1561/2200000016 |
| [24] |
Hong MY, Luo ZQ. On the linear convergence of the alternating direction method of multipliers. Mathematical Programming, 2017, 162(1): 165-199. DOI:10.1007/s10107-016-1034-2 |
| [25] |
Cai JF, Candès EJ, Shen ZW. A singular value thresholding algorithm for matrix completion. SIAM Journal on Optimization, 2010, 20(4): 1956-1982. DOI:10.1137/080738970 |
| [26] |
Donoho DL. De-noising by soft-thresholding. IEEE Transactions on Information Theory, 1995, 41(3): 613-627. DOI:10.1109/18.382009 |
| [27] |
Daubechies I, Defrise M, De Mol C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Communications on Pure and Applied Mathematics, 2004, 57(11): 1413-1457. DOI:10.1002/cpa.20042 |
| [28] |
胡凌超, 于洪. 一种基于投票的三支决策聚类集成方法. 计算机应用, 2016, 37(8): 1741-1745. |
| [29] |
Brbić M, Piškorec M, Vidulin V, et al. The landscape of microbial phenotypic traits and associated genes. Nucleic Acids Research, 2016, 44(21): 10074-10090. DOI:10.1093/nar/gkw964 |
| [30] |
Kumar A, Rai P, Daumé H. Co-regularized multi-view spectral clustering. Proceedings of the 24th International Conference on Neural Information Processing Systems. Granada: Curran Associates Inc., 2011. 1413–1421.
|
| [31] |
Xia RK, Pan Y, Du L, et al. Robust multi-view spectral clustering via low-rank and sparse decomposition. Proceedings of the 28th AAAI Conference on Artificial Intelligence. Québec: AAAI Press, 2014. 2149–2155.
|
| [32] |
Lu CY, Yan SC, Lin ZC. Convex sparse spectral clustering: Single-view to multi-view. IEEE Transactions on Image Processing, 2016, 25(6): 2833-2843. DOI:10.1109/TIP.2016.2553459 |
 2024, Vol. 33
2024, Vol. 33


