异常检测(anomaly detection)[1], 又称离群点检测(outlier detection), 是检测不匹配预期模式或与大多数数据实例显著不同的数据点, 这些被检测出的数据点被称为异常点.
随着物联网和传感器数据在物理系统(cyber physical systems, CPS)中的快速增长, 例如工业系统和数据中心, 需要监视这些设备以防止受到攻击. 异常检测在计算机视觉[2]、数据挖掘[3]、自然语言处理等实际应用领域发挥着越来越重要的作用, 已成为许多研究人员和从业者感兴趣的领域, 现在是数据挖掘和质量保证的主要任务之一[4].
在该领域中, 异常检测技术可分为基于线性模型的方法[5]、基于距离的方法[6]、支持向量机的方法[7]、基于密度的方法[8]. 然而, 这些方法通常以相对简单的方式建模传感器数据之间的相互关系. 例如, 仅捕获线性关系, 这对于许多现实世界的复杂、高度非线性关系是不足够的.
近年来, 基于深度学习的技术已经使得在高维数据集中进行异常检测变得更加容易, 相较于其他方法其性能有较大提升. 例如, 自编码器[9]是一种流行的用于异常检测的方法, 它基于反向传播算法与最优化算法, 将输入数据在神经网络中进行特征学习映射, 从而得到一个重构的输出数据. 深度自编码高斯混合模型(deep autoencoding Gaussian mixture model for unsupervised anomaly detection, DAGMM)[10]可以处理高维数据、非线性数据以及自动学习数据的分布. 无监督异常检测(unsupervised anomaly detection, UASD)[11]的组成包括基于自编码方法和基于生成对抗网络(generative adversarial network, GAN)[12]的方法. 基于LSTM (long short-term memory)[13]的方法在公开的数据集上测试均表现出良好性能. 但是, 大多数方法忽略了传感器数据彼此之间的相关性.
利用多元时间序列中传感器数据之间的复杂关系学习特征来提高异常检测的性能. 图神经网络(graph neural network, GNN)[14]利用图结构数据来进行异常检测取得了良好的成效. 图卷积网络(graph convolutional network, GCN)[15]是图神经网络和卷积神经网络结合的异常检测模型, 卷积核在图上进行局部连接和信息传播, 有效地利用图结构的拓扑信息和节点信息, 提高图数据的表征能力且具有较强的泛化能力. 图注意力网络(graph attention network, GAT)[16]是一种基于注意力机制的图神经网络, 可以动态地计算每个节点对其邻居节点的注意力权重, 从而捕捉节点之间的非均匀性. 但是, 这一类检测模型在时间序列异常检测过程中并没有考虑不同的传感器具有非常不同的行为. 例如, 一个传感器可能测量水压, 而另一个传感器可能测流量, 典型的GNN使用相同的模型参数来模拟每个节点的行为. 图偏差网络[17]能够学习到不同传感器之间的不同行为, 从而捕捉传感器数据之间的依赖性和相互作用, 并且再将数据送入到图注意力模型学习, 能够提供异常检测的可解释性. 但是图偏差网络缺少对时间依赖性的学习以及对异常数据的不稳定性的处理.
综上所述, 本文提出了一种基于图偏差网络的外部自编码器时间序列异常检测模型, 该模型将时间序列数据分别送入由外部注意力机制、自动编码器组成的时间依赖性学习模块学习时间依赖性以及送入图结构学习模块学习传感器数据依赖性, 经过不同角度的特征提取, 再送入图预测网络进行训练预测, 同时考虑到时间异常数据可能会随着时间的改变而发生推移, 引入自适应学习机制帮助网络更好地适应异常数据的变化, 从而提高时间序列异常检测的准确率. 本文的主要贡献如下: (1)提出了基于图偏差网络的外部自编码器时间序列异常检测方法, 将时间依赖性特征和传感器依赖性特征结合学习; (2)对于时间异常数据的不稳定性, 采用自适应学习机制提高网络的准确性; (3)对3个数据集进行了实验, 本文提出的模型相较于其他异常检测模型拥有更好的结果, 均提升了时间序列异常检测准确率.
1 相关模型和技术 1.1 图偏差网络GDN模型2005年, Gori等人[18]首次提出图神经网络GNN, 这种网络是基于深度学习的, 旨在直接对图结构数据进行学习, 以揭示图中节点和边的内在规律以及更深层次的语义特征. 该模型的主要理念是通过学习一个映射函数来实现这一目标, 通过该映射图中的节点可以聚合它自己的特征与它的邻居特征生成节点的新表示. 一般来说, GNN假设一个节点的状态受到其邻居节点状态的影响. 基于CNN的图卷积网络GCN通过聚合其一步邻居的表示来建模一阶节点的特征表示. 相关的变体在时间依赖的问题中表现出成功, 例如, 基于GNN的模型可以在交通预测[19]任务中表现良好. 在推荐系统[20]和相关应用[21]中验证了GNN建模大规模多关系数据的有效性. 然而, 这些方法使用相同的模型参数来建模每个节点的行为, 在表示不同传感器不同的行为时面临限制. 此外, GNN通常需要图结构作为输入, 而在模型的设置中, 图结构最初是未知的, 需要从数据中学习.
2021年, Deng等人[17]提出的图偏差网络GDN是一种基于图神经网络的多元时间序列异常检测方法. 该模型包括4个部分: 传感器数据编码模块、图结构学习模块、基于图注意力预测模块、计算图偏差分数模块. 算法的具体步骤: 首先对每个传感器获取到数据进行初始化, 即图1中传感器数据编码模块, 可用来在图结构学习中判断传感器数据之间的相关性; 该模型考虑除了自身与其他传感器均存在依赖性, 经过图结构的学习得到该节点与其他节点的依赖性数据, 归一化后, 选择这样的归一化点积, 以此组成邻接矩阵并认为该传感器与其他传感器存在较强的关联性, 并用邻接矩阵来存储邻接关系; 将得到的邻接关系和初始化的数据结合送入图注意力预测网络预测某时刻的传感器数据的值; 最后利用观测值和预测值计算得到异常分数, 并和阈值进行比较, 判断异常. 该模型的具体流程如图1所示.

|
图 1 图偏差网络模型 |
1.2 自编码器
1986年, Rumelhart等人[22]提出自编码器, 它利用输入数据本身作为监督, 来学习一种数据的压缩表示, 被称为神经网络的预训练方法. 该方法依赖于反向传播算法和优化技巧(如梯度下降法), 利用输入数据本身作为监督信号, 引导神经网络试图学习一种映射关系, 从而实现重构输出的生成. 在时间序列异常检测场景下, 异常对于正常来说是少数, 使用自编码器重构出来的输出跟原始输入的差异超出一定阈值的话, 原始时间序列即存在了异常.
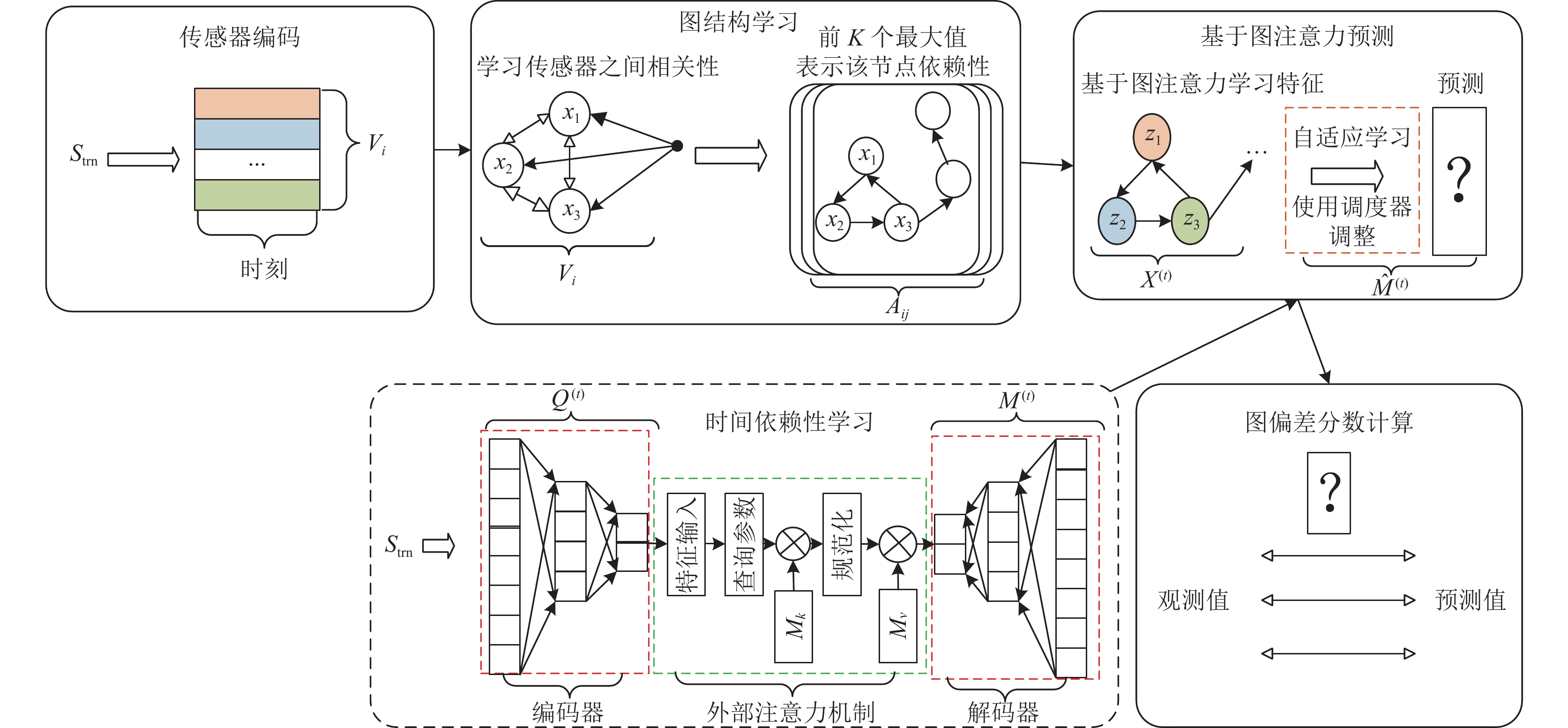
算法模型由两个核心组成部分组成: 编码器(encoder)和解码器(decoder). 编码器旨在将高维输入转化为低维隐变量, 从而引导神经网络学习最富信息的特征; 解码器旨在把隐藏层的隐变量还原到初始维度, 最好的状态就是解码器的输出能够完美地或者近似恢复出原来的输入. 考虑到时间序列异常检测的时效性, 本文采用全连接层来架构自编码器. 在图2中以红色虚线框表示.
1.3 外部注意力机制2017年, Vaswani等人[23]提出自注意力机制, 它能够捕捉长距离依赖关系, 有助于提高各种自然语言处理[24]和计算机视觉[25]任务的性能. 该算法的原理是: 对于每个输入向量, 都计算它与其他输入向量的点积(或者加上一个可学习的权重矩阵), 然后通过一个Softmax激励函数得到一个概率分布, 这个概率分布表示每个输入向量对当前输出向量的贡献程度. 然后, 将这个概率分布与输入向量相乘, 得到输出向量. 但是这导致了样本中位置数量的二次计算复杂度. 此外, 自注意力集中在单个样本内不同位置之间的自相关性上, 而忽略了与其他样本的潜在相关性, 并且只考虑数据样本中元素之间的关系, 而忽略了不同样本中元素间的潜在关系, 这可能会限制自注意的能力和灵活性.
2022年, Guo等人[26]提出的外部注意力机制, 建立在一对独立的、可训练共享内存单元之上, 通过两个级联的线性层和两个归一化层的简单组合, 就可以落实. 外部注意力机制的优点是, 它可以减少计算复杂度, 并且也可以捕捉不同样本之间的联系, 而不是只关注同一个样本内部的相关性. 在图2中以绿色虚线框表示.
1.4 自适应学习自适应学习是深度学习中的一种技术, 可以自动调整学习率和其他超参数, 并减少手动调整超参数的工作量. 在深度学习中, 学习率是一个非常重要的超参数, 它控制着模型在每次迭代中更新权重的速度. 如果学习率太小, 模型将需要更多的迭代才能收敛; 如果学习率太大, 模型可能会在训练过程中发生震荡或不收敛.
在本文代码中, 使用了Adam优化算法和ReduceLROnPlateau调度器来自动调整学习率. ReduceLROnPlateau调度器会监控验证损失, 并在损失停止下降时降低学习率, 因子参数决定要降低多少学习率, 耐心参数决定在降低学习率之前等待多少个周期. 这种方法可以自动调整学习率, 以提高模型的性能. 在图2中以橘色虚线框表示.
|
图 2 图偏差网络的外部自编码器异常检测模型 |
2 AEEA-GDN异常检测模型
在本文中, 训练数据来自
GDN网络在没有先验信息的情况下, 学习某个传感器除了自身之外与其他传感器之间的关系, 得到不同传感器之间的不同行为, 从而捕捉传感器之间的依赖性和相互作用, 并且将学习特征送入到图注意力模型学习, 能够提供异常检测的可解释性. 但是, 该模型未考虑在同一时刻下, 各个传感器呈现的特征以及异常点的特征, 所以引入时间依赖性学习模块来学习检测异常. 例如, 如果一个时间序列中的时间数据点之间存在某种周期性关系, 则可以使用这种关系来检测异常. 此外, 在现实环境中, 异常数据是罕见的, 会受到时间变化的影响, 使用同一参数训练模型是不合理的, 为此引入自适应学习监控验证损失, 并在损失停止下降时降低学习率, 因子参数决定要降低多少学习率, 耐心参数决定在降低学习率之前等待多少个周期, 这种方法可以自动调整学习率, 以提高模型的性能.
基于图偏差网络的外部自编码器模型结构如图2所示. 该模型由5个部分组成: 传感器数据编码模块、图结构学习模块、时间依赖性学习模块、基于图自适应注意力预测模块、图偏差分数计算模块, 其中虚线部分属于本文的创新点模块, 实线部分属于GDN模块.
2.2 传感器数据编码模块在工业环境中, 不同的传感器可能具有不同的特性, 并且这些特性可以以复杂的方式关联. 例如, 假设在两碗水中放置了检测水质和水温的传感器, 那么, 这两个水质、水温传感器的行为可能相似. 但是, 同样有可能的是, 同一碗水中的传感器会表现出很强的相关性. 因此, 本文为了灵活表示每个传感器, 采用多维的方式描述每个传感器的特性.
在训练数据集
| $ {V_i} \in {R^d}, \; i \in \{ 1, 2, \cdot \cdot \cdot , N\} $ | (1) |
其中,
因为每个传感器之间的相似关系不同, 也可能两个传感器之间不存在相似关系, 所以本文采用有向图来表示传感器之间的不对称依赖关系, 考虑到传感器之间的依赖关系存在先验信息的情况下, 本文假设除了自身节点与其他传感器节点均存在依赖关系, 通过式(2)表示传感器之间的候选关系:
| $ {C_i} \subseteq \{ 1, 2, \cdots, N\} \backslash \{ i\} $ | (2) |
其中,
通过式(3)计算得到传感器
| $ e_{j i}=\frac{V_i^{\rm{T}} V_j}{\left\|V_i\right\| \cdot\left\|V_j\right\|} $ | (3) |
其中,
选择
| $ {A_{ji}} = 1\{ j \in {\textit{TopK}}(\{ {e_{ki}}:k \in {C_i}\} )\} $ | (4) |
其中,
对
| $ F_{ {{\rm{Encoder}}\_{\rm{out}} }}=\textit{Encoder}\left(Q^{(t)}\right) $ | (5) |
其中,
通过式(6)提取重要的时间序列数据特征:
| $ H = {(\partial )_{i, j}} = Norm({F_{{\rm{Encoder}}\_{\rm{out}}}}M_k^{\rm{T}}) $ | (6) |
| $ {F_{{\rm{exattn}}\_{\rm{out}}}} = H{M_v} $ | (7) |
其中,
将
| $ {M^{(t)}} = Decoder(Z) $ | (8) |
其中,
在时刻
| $ X_i^{(t)}: = [{M^{(t - k)}}, {M^{(t - k + 1)}}, \cdot \cdot \cdot , {M^{(t - 1)}}] $ | (9) |
其中,
考虑到传感器之间的关系, 采用图注意力机制来融合传感器特征
| $ Z_i^{(t)}={\textit{ReLU}}\left(\alpha_{i, i} D X_i^{(t)}+\sum_{j \in N(i)} \alpha_{i, j} D X_j^{(t)}\right) $ | (10) |
注意系数计算如下:
| $ g_i^{(t)}=V_i \oplus D X_i^{(t)} $ | (11) |
| $ \pi(i, j)= {\textit{LeakyReLU}} \left(a^{\rm{T}}\left(g_i^{(t)} \oplus g_j^{(t)}\right)\right) $ | (12) |
| $ N(i)=\left\{j, A_{j i}>0\right\} $ | (13) |
| $ \alpha_{i, j}=\frac{\exp (\pi(i, j))}{\displaystyle\sum_{k \in N(i) \cup(i)} \exp (\pi(i, k))} $ | (14) |
其中,
经过以上公式得到
| $ {\hat M^{(t)}} = Linear([{V_1} \circ Z_1^{(t)}, \cdots, {V_N} \circ Z_N^{(t)}]) $ | (15) |
其中,
由于本文的数据集都是数值型, 所以采用smooth_l1_loss作为损失函数:
| $ L_{ {{\rm{smooth}}\_{\rm{l}}1\_{\rm{loss}} }}=\frac{1}{T_{\text {train }}-w} \sum_{t=w+1}^{T_{\text {train }}}\left\|\hat{M}^{(t)}-M^{(t)}\right\|_2^2 $ | (16) |
通过式(17)得到传感器
| $ Er{r_i}(t) = |M_i^{(t)} - {\hat M_i}^{(t)}| $ | (17) |
其中,
不同的传感器的偏差可能存在一定的差距, 通过式(18)对每个传感器的偏差做归一化处理:
| $ {a}_i(t)=\frac{{Err}_i(t)-\tilde{u}_i}{\tilde{\omega}_i} $ | (18) |
其中,
因为异常只会影响一小部分传感器, 甚至是单个传感器, 所以为了计算时刻的整体异常情况, 使用函数对传感器进行聚合:
| $ y(t)= \max _{i}\, {{{a}}_{i}}(t) $ | (19) |
如果
| $ \varepsilon={ave}\left(\sum_{t \in T} y(t)\right) $ | (20) |
其中,
根据图2所示, 步骤1: 传感器数据编码模块对训练数据
算法1. AEEA-GDN模型构建
1) 样本数据Strn中用Vi表示每个传感器用嵌入向量;
2) 根据特征和特征数
3)
4) 将图结构特征
5) 根据观测值和预测值得到偏差分数, 将偏差分数聚合得到异常分数, 如果异常分数高于阈值, 则判定为异常, 输出二分类结果
为了验证本文所提出模型的有效性, 将在时间序列数据集上进行实验. 在文本数据集方面, 选取了3个公开可用的数据集, 详见表1. 这些数据集均来源于真实世界, 涵盖了不同领域的时间序列数据. 下面对这些时间序列数据集进行简要描述.
| 表 1 异常检测数据集 |
安全水处理(SWaT)[27]: 从水处理试验台(一个小型网络物理系统)收集的11天多变量时间序列数据. 最近4天的数据包含36次攻击. 这些攻击的目标和持续时间各不相同.
配水(WADI)[28]: 从配水管道收集的16天多变量时间序列数据. 每个系列包括各种网络流量, 传感器和执行器测量. 16天中, 正常情况下有14天有数据, 攻击场景下有2天有数据.
火星科学实验室漫游车(MSL)[29]: 从火星科学实验室漫游车记录的多变量时间序列数据. 训练试验台和测试试验台是分开的, 测试试验台的异常都被标记.
3.2 模型设置及评价指标本文的AEEA-GDN模型, 由PyTorch 1.7.0架构, 使用CUDA 10.1版本和PyTorch几何库1.7.0版本, 在2个NVIDIA RTX 2080Ti显卡的服务器上训练数据集, 使用Adam优化器. 对于WADI (SWaT、MSL)数据集, 本文模型使用嵌入向量长度为128 (64、64)、批量大小为128 (128, 128)、滑动窗口大小为30 (15、15)和128 (64、64)神经元的隐藏层. 自编码器由全连接层架构, 隐藏层节点的个数设置为前一层神经元数量的1/2. 此外, 本文ReduceLROnPlateau调度器中的因子参数是0.1, 耐心参数是10.
对于性能评估, 由于本文的数据集是二分类的, 所以本文采用3个标准的评估指标精确率(P)、召回率(R)、F1分数(F1):
| $ \left\{\begin{array}{l} {P}=\dfrac{T P}{T P+F P} \\ {R}=\dfrac{T P}{T P+F N} \\ F 1=2 \cdot \dfrac{P \times {R}}{P+R} \end{array}\right. $ | (21) |
其中, TP是真阳性, FP是假阳性, FN是假阴性,
为了评估本研究所提出方法的实际效果, 选择了3种典型异常检测算法进行比较, 并以精确率(P)、召回率(R)、F1分数(F1), 作为异常检测性能的评判指标. 在3组真实数据集上, 7个模型的测试结果详见表2.
| 表 2 异常检测性能比较 (%) |
为了研究每个组件的必要性, 采用逐渐排除这些组件的方法来检测模型的性能, 可以直观地看到在缺少相关组件时, 性能是如何下降的. 消融实验对比结果如表3所示.
| 表 3 消融实验对比结果 (%) |
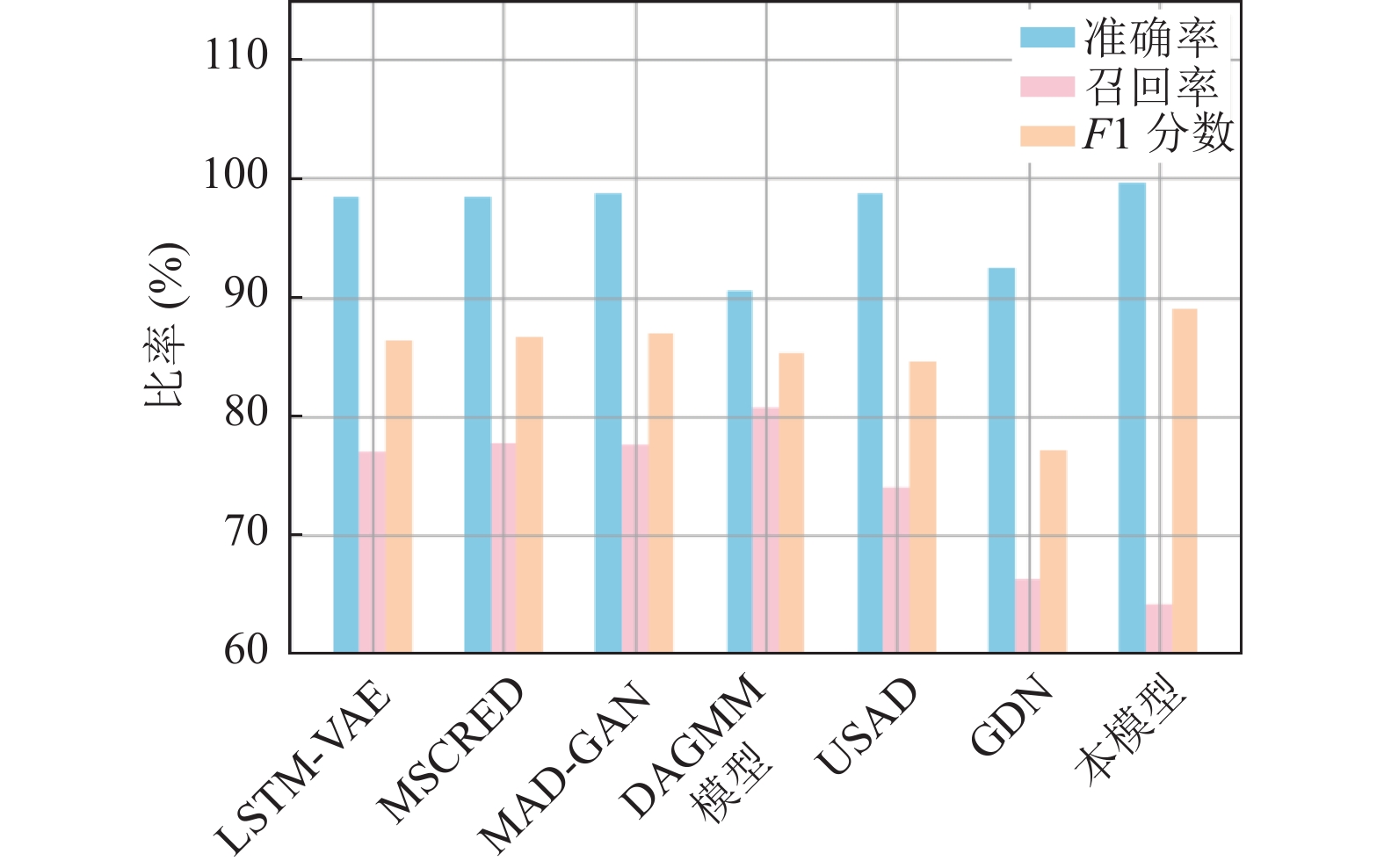
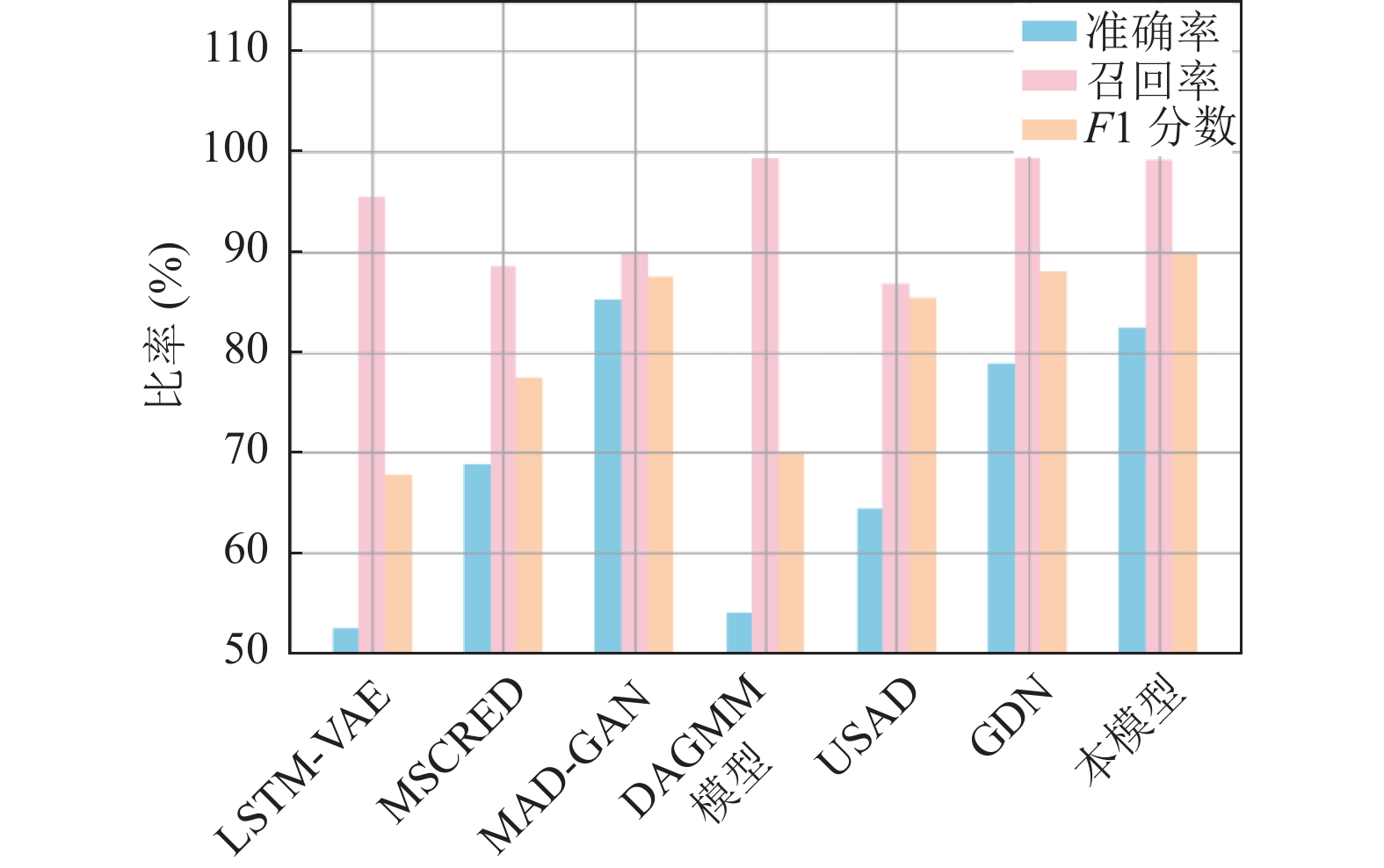
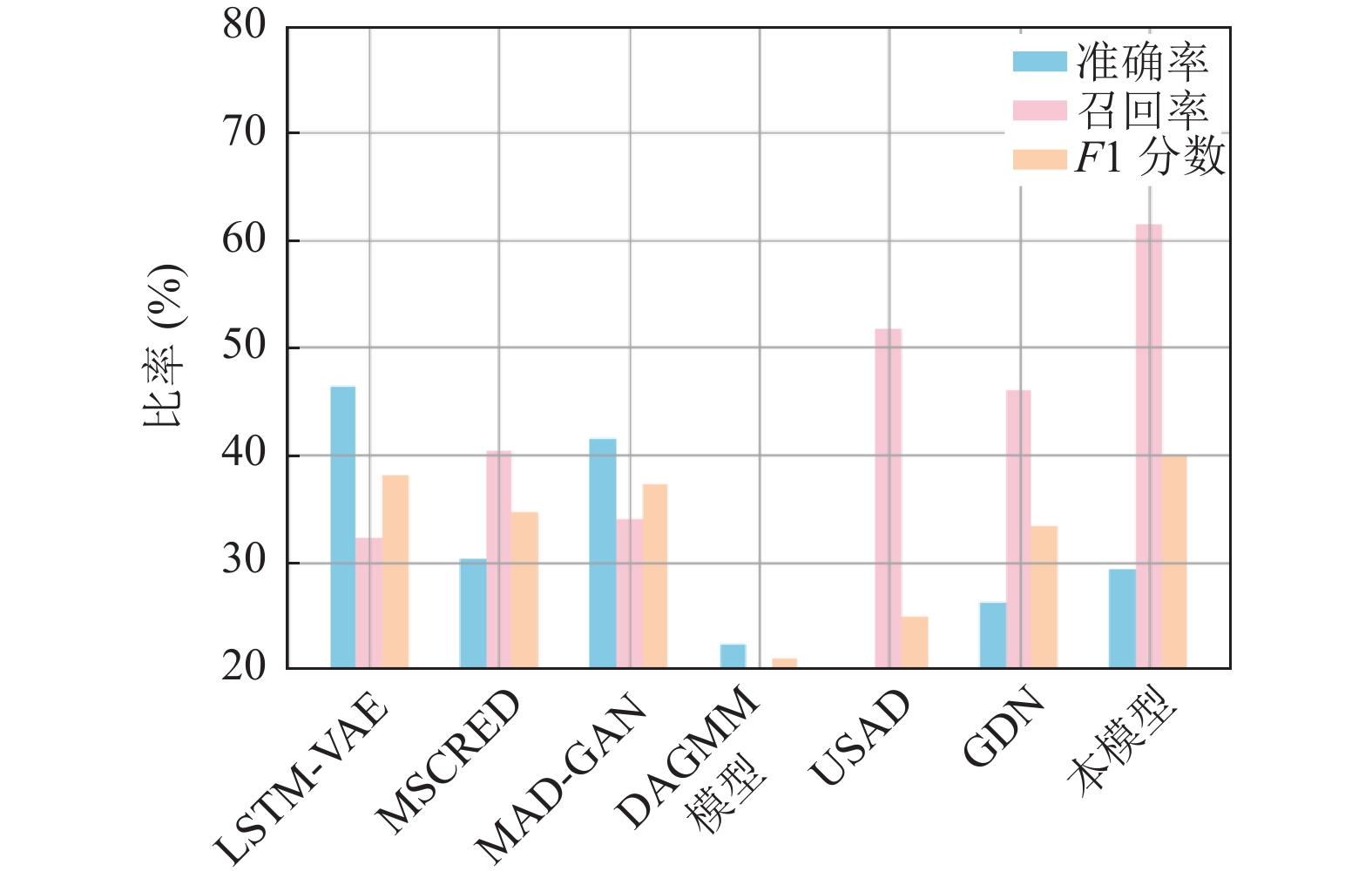
为了直观展示本文AEEA-GDN模型的整体性能, 分别在SWaT、MSL、WADI数据集上将P、R、F1结果对比, 比较结果如图3–图5所示.
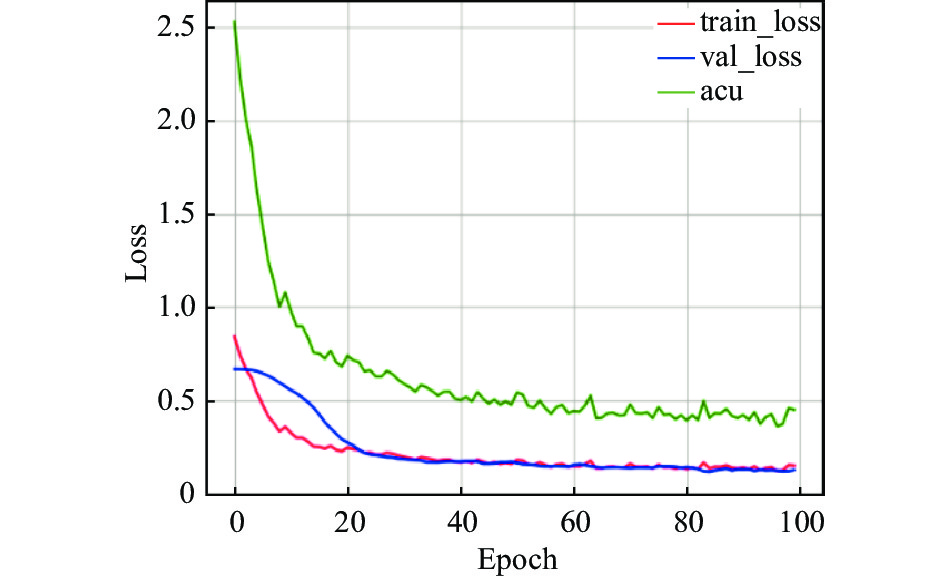
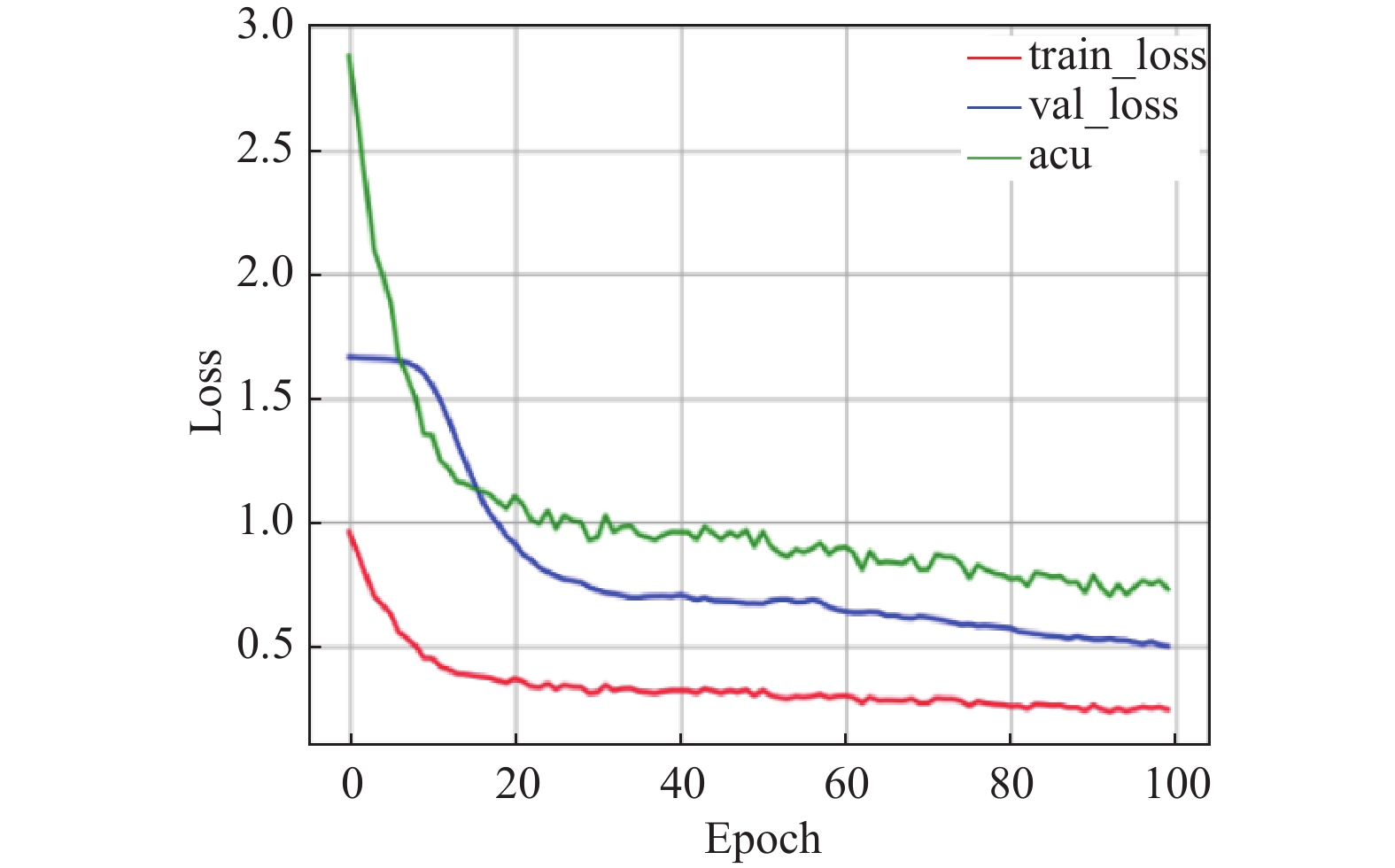
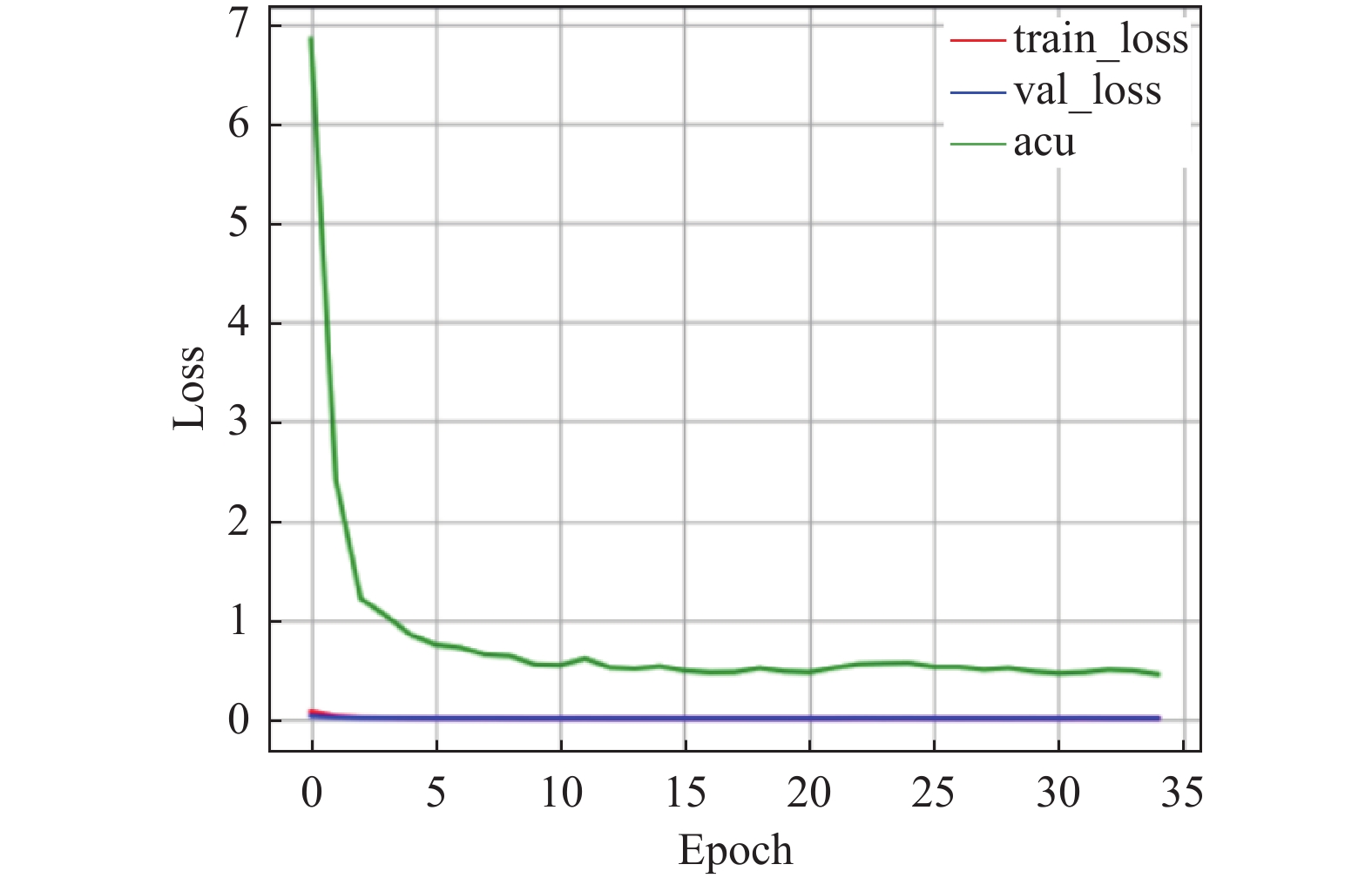
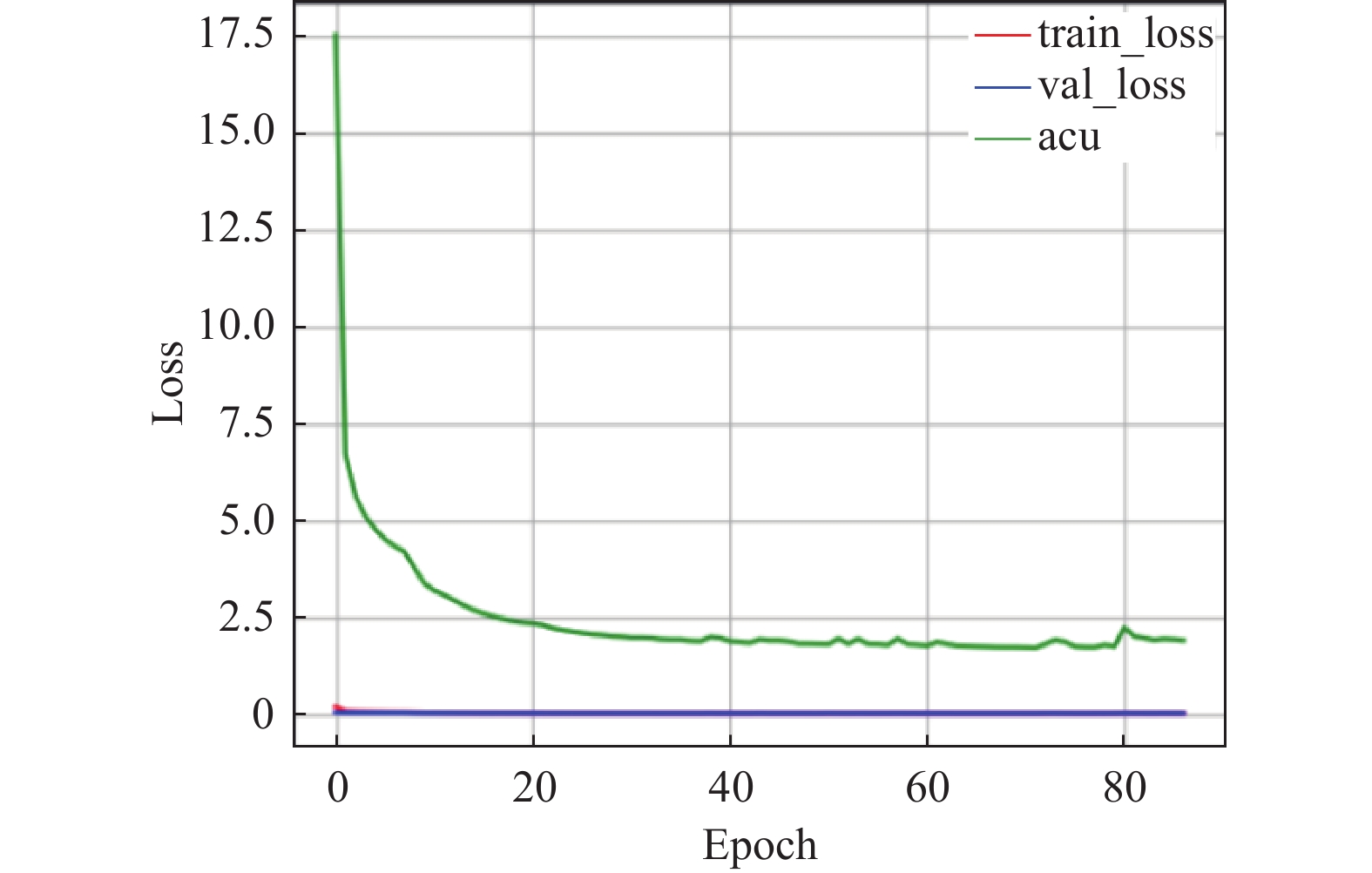
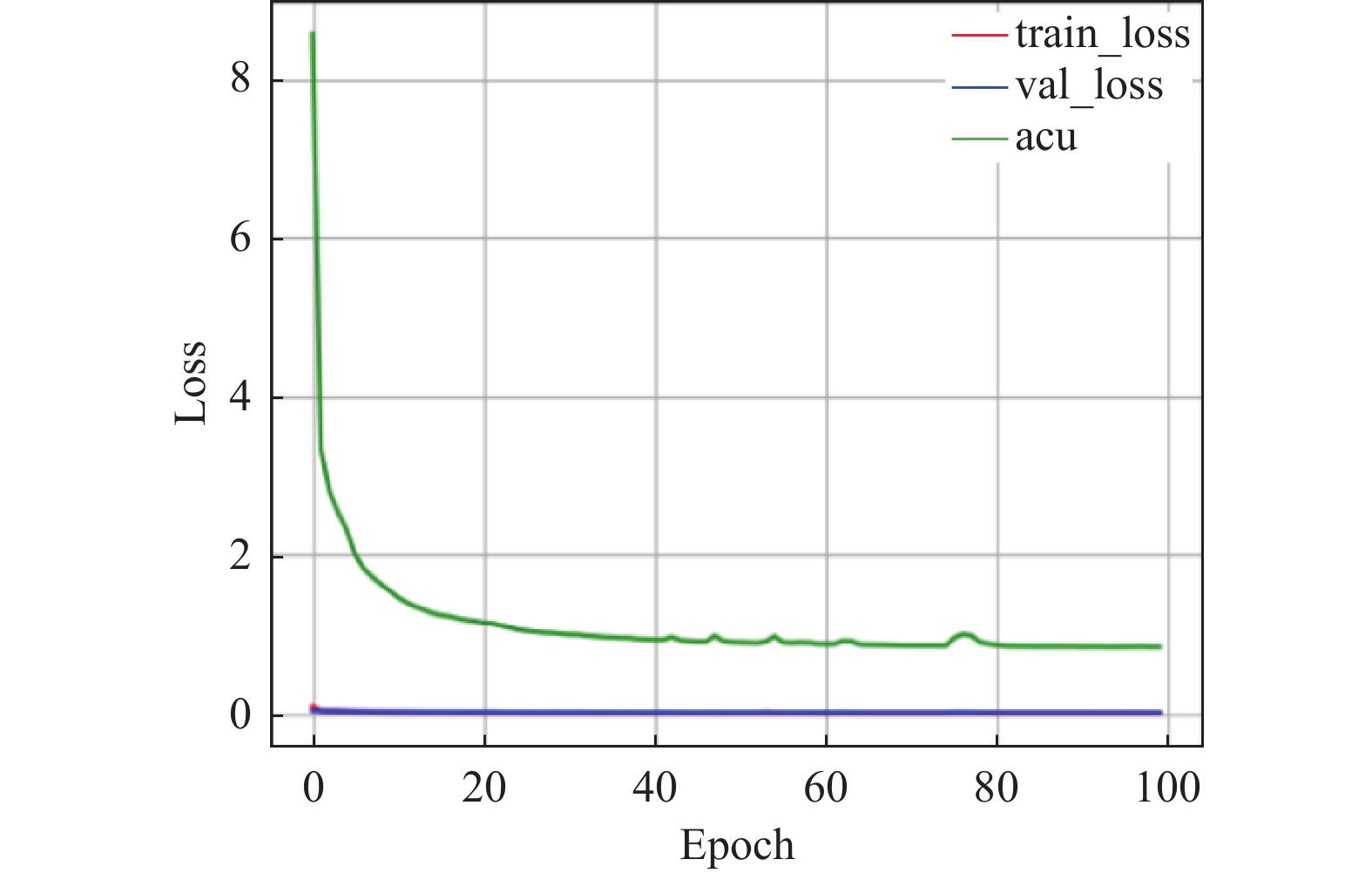
对于AEEA-GDN的训练过程, 探寻每个组件对模型的影响, 尤其在加入自适应学习组件后, 模型的训练迭代次数能够达到100轮次, 得到充分训练. 分别在3个数据集上测试, 测试结果如图6–图14所示. 在模型中引入自适应学习之后, 能够改善模型中的分类效果不佳的问题. 图8、图11、图14中能够看出acu逐渐偏向1, 表示分类效果逐渐改善. 其中, acu表示分类效果评价指标.
|
图 3 SWaT上模型性能比较 |
|
图 4 MSL上模型性能比较 |
|
图 5 WADI上模型性能比较 |
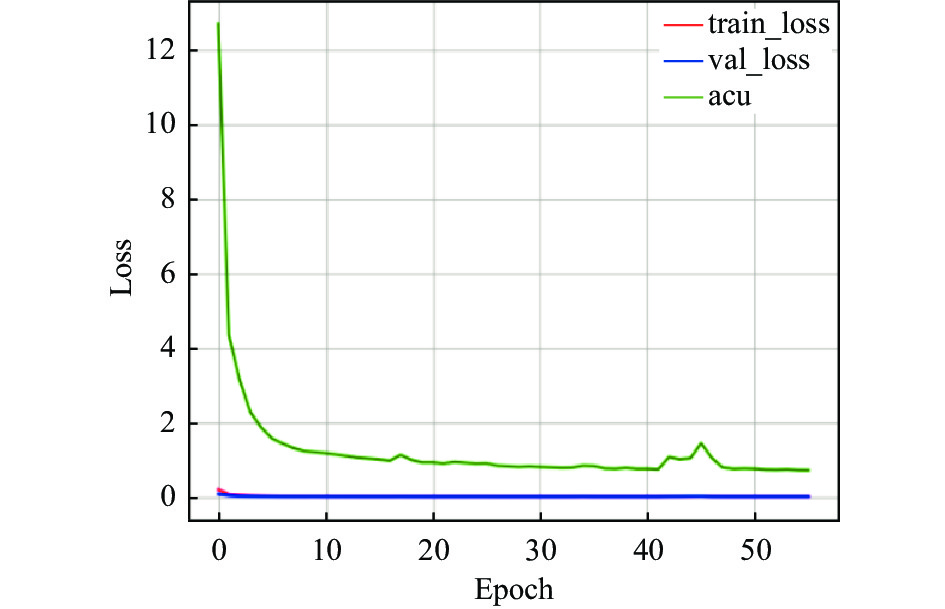
|
图 6 SWaT在GDN模型变化曲线 |
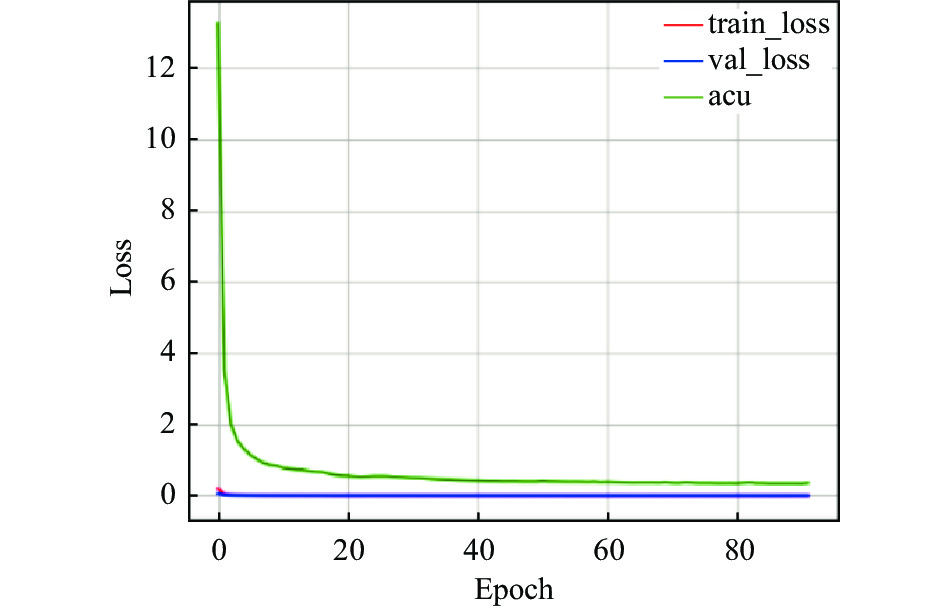
|
图 7 SWaT自编码器和外部注意力机制变化曲线 |
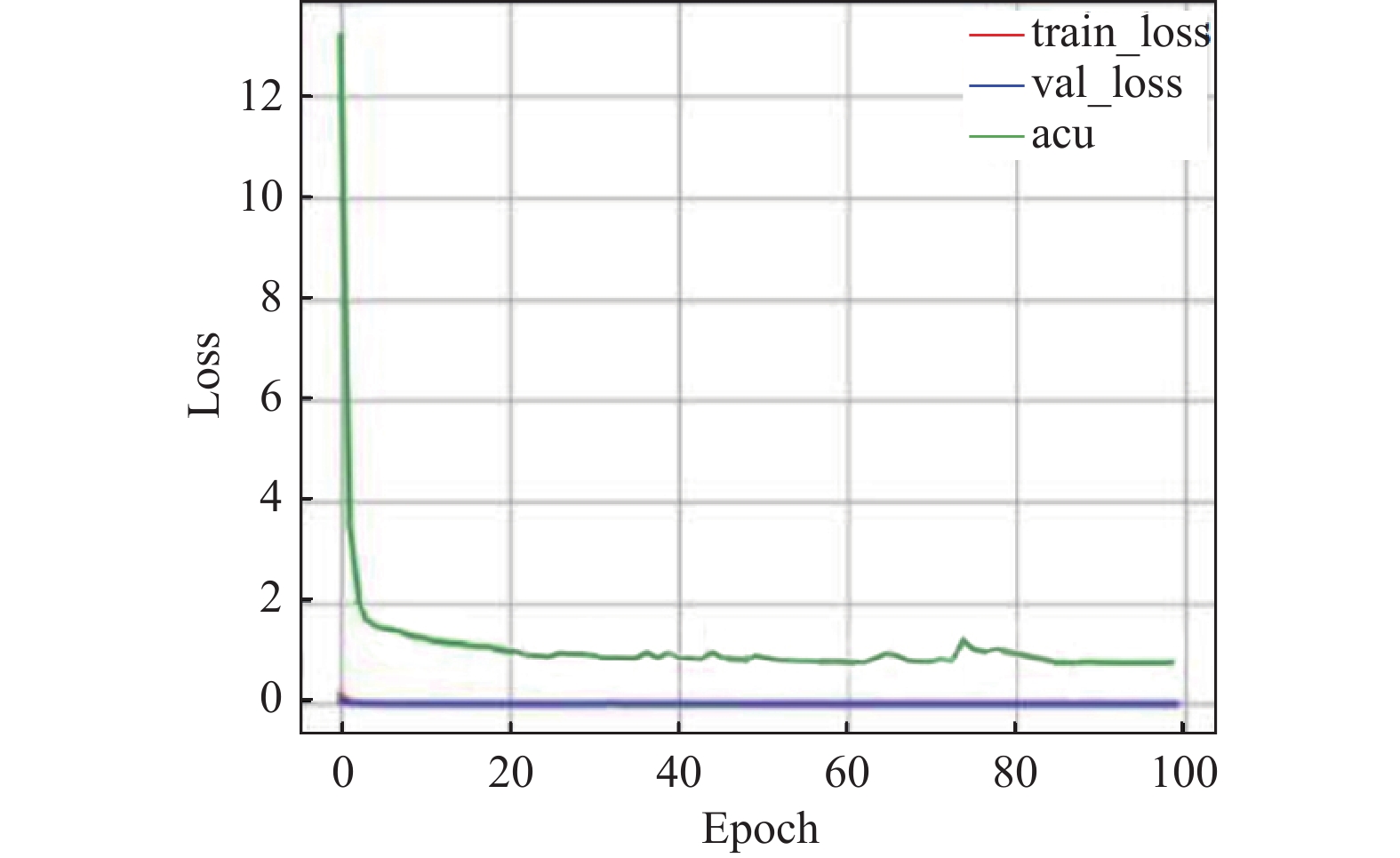
|
图 8 SWaT引入自适应学习变化曲线 |
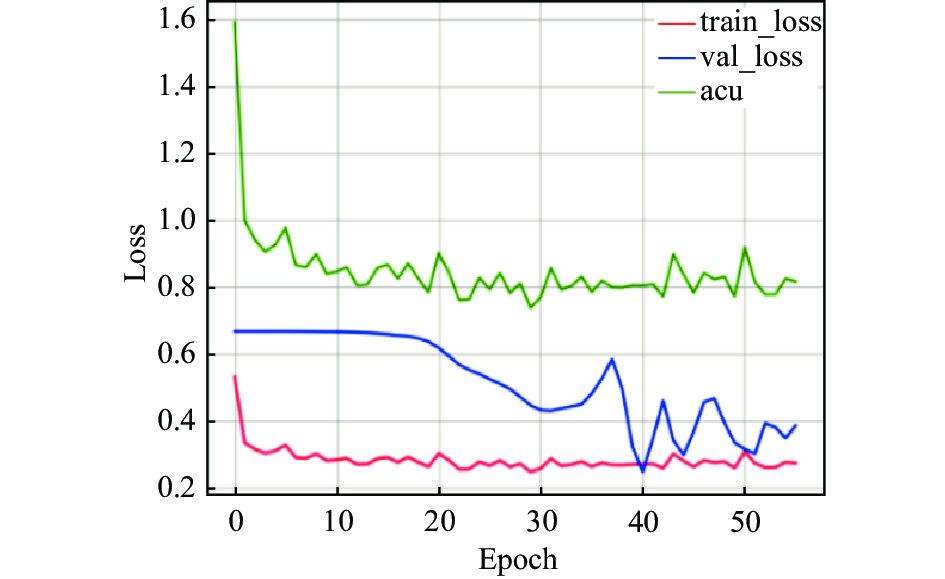
|
图 9 MSL在GDN模型变化曲线 |
|
图 10 MSL自编码器和外部注意力机制变化曲线 |
|
图 11 MSL自适应学习变化曲线 |
|
图 12 WADI在GDN模型变化曲线 |
|
图 13 WADI自编码器和外部注意力机制 |
|
图 14 WADI数据集引入自适应学习变化曲线 |
4 结论与展望
针对基于图偏差网络的时间序列异常检测模型, 本文提出将传感器的依赖性和时间依赖性结合送入图预测网络训练, 并且在模型训练时, 加入自适应学习帮助网络更好地适应异常数据的变化, 根据异常数据的变化调整网络的学习率, 在多个公共数据集上的实验结果表明本文模型在异常检测领域的有效性. 在WADI数据集上, 本模型训练结果并不很好, 主要是WADI数据集涵盖了众多传感器数据, 导致数据维度较高, 这给模型性能带来了挑战. 在未来工作中, 考虑维数超过100的情况下, 如何提升本文的异常检测模型的准确率.
| [1] |
Pang GS, Shen CH, Cao LB, et al. Deep learning for anomaly detection: A review. ACM Computing Surveys, 2022, 54(2): 38. |
| [2] |
Elsken T, Metzen JH, Hutter F. Neural architecture search: A survey. The Journal of Machine Learning Research, 2019, 20(1): 1997-2017. |
| [3] |
Blázquez-García A, Conde A, Mori U, et al. A review on outlier/anomaly detection in time series data. ACM Computing Surveys (CSUR), 2021, 54(3): 1–33.
|
| [4] |
Blázquez-García A, Conde A, Mori U, et al. A review on outlier/anomaly detection in time series data. ACM Computing Surveys, 2022, 54(3): 56. |
| [5] |
Shyu ML, Chen SC, Sarinnapakorn K, et al. A novel anomaly detection scheme based on principal component classifier. Proceedings of the 2003 IEEE Foundations and New Directions of Data Mining Workshop. IEEE, 2003. 172–179.
|
| [6] |
Angiulli F, Pizzuti C. Fast outlier detection in high dimensional spaces. Proceedings of the 6th European Conference on Principles of Data Mining and Knowledge Discovery. Helsinki: Springer, 2002. 15–27.
|
| [7] |
Schölkopf B, Platt JC, Shawe-Taylor J, et al. Estimating the support of a high-dimensional distribution. Neural Computation, 2001, 13(7): 1443-1471. DOI:10.1162/089976601750264965 |
| [8] |
Breunig MM, Kriegel HP, Ng RT, et al. LOF: Identifying density-based local outliers. ACM SIGMOD Record, 2000, 29(2): 93-104. DOI:10.1145/335191.335388 |
| [9] |
Aggarwal CC. An introduction to outlier analysis. Outlier Analysis. 2nd ed., Cham: Springer, 2017. 1–34.
|
| [10] |
Zong B, Song Q, Min MR, et al. Deep autoencoding Gaussian mixture model for unsupervised anomaly detection. Proceedings of the 6th International Conference on Learning Representations. Vancouver: OpenReview.net, 2018. 1–19.
|
| [11] |
Audibert J, Michiardi P, Guyard F, et al. USAD: Unsupervised anomaly detection on multivariate time series. Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. ACM, 2020. 3395–3404.
|
| [12] |
Li D, Chen DC, Jin BH, et al. MAD-GAN: Multivariate anomaly detection for time series data with generative adversarial networks. Proceedings of the 28th International Conference on Artificial Neural Networks. Munich: Springer, 2019. 703–716.
|
| [13] |
Lample G, Ballesteros M, Subramanian S, et al. Neural architectures for named entity recognition. Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies. San Diego: Association for Computational Linguistics, 2016. 260–270.
|
| [14] |
Defferrard M, Bresson X, Vandergheynst P. Convolutional neural networks on graphs with fast localized spectral filtering. Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona: Curran Associates Inc., 2016. 3844–3852.
|
| [15] |
Kipf TN, Welling M. Semi-supervised classification with graph convolutional networks. Proceedings of the 5th International Conference on Learning Representations. Toulon: OpenReview.net, 2016.
|
| [16] |
Veličković P, Cucurull G, Casanova A, et al. Graph attention networks. Proceedings of the 6th International Conference on Learning Representations. Vancouver: OpenReview.net, 2018.
|
| [17] |
Deng AL, Hooi B. Graph neural network-based anomaly detection in multivariate time series. Proceedings of the 35th AAAI Conference on Artificial Intelligence. AAAI, 2021. 4027–4035.
|
| [18] |
Gori M, Monfardini G, Scarselli F. A new model for learning in graph domains. Proceedings of the 2005 IEEE International Joint Conference on Neural Networks. IEEE, 2005. 729–734.
|
| [19] |
Yu B, Yin HT, Zhu ZX. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting. Proceedings of the 27th International Joint Conference on Artificial Intelligence. Stockholm: IJCAI.org, 2017. 3634–3640.
|
| [20] |
Lim N, Hooi B, Ng SK, et al. STP-UDGAT: Spatial-temporal-preference user dimensional graph attention network for next POI recommendation. Proceedings of the 29th ACM International Conference on Information & Knowledge Management. ACM, 2020. 845–854.
|
| [21] |
Wang YW, Wang W, Ca YJ, et al. Detecting implementation bugs in graph convolutional network based node classifiers. Proceedings of the 31st IEEE International Symposium on Software Reliability Engineering (ISSRE). Coimbra: IEEE, 2020. 313–324.
|
| [22] |
Rumelhart DE, Hinton GE, Williams RJ. Learning representations by back-propagating errors. Nature, 1986, 323(6088): 533–536.
|
| [23] |
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. Proceedings of the 31st International Conference on Neural Information Processing Systems. Red Hook: Curran Associates Inc., 2017. 6000–6010.
|
| [24] |
Bahdanau D, Cho K, Bengio Y. Neural machine translation by jointly learning to align and translate. Proceedings of the 3rd International Conference on Learning Representations. San Diego: ICLR, 2015.
|
| [25] |
Wang XL, Girshick R, Gupta A, et al. Non-local neural networks. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 7794–7803.
|
| [26] |
Guo MH, Liu ZN, Mu TJ, et al. Beyond self-attention: External attention using two linear layers for visual tasks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 45(5): 5436–5447.
|
| [27] |
Mathur AP, Tippenhauer NO. SWaT: A water treatment testbed for research and training on ICS security. Proceedings of the 2016 International Workshop on Cyber-physical Systems for Smart Water Networks. Vienna: IEEE, 2016. 31–36.
|
| [28] |
Ahmed CM, Palleti VR, Mathur AP. WADI: A water distribution testbed for research in the design of secure cyber physical systems. Proceedings of the 3rd International Workshop on Cyber-physical Systems for Smart Water Networks. Pennsylvania: ACM, 2017. 25–28.
|
| [29] |
Hundman K, Constantinou V, Laporte C, et al. Detecting spacecraft anomalies using LSTMs and nonparametric dynamic thresholding. Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. London: ACM, 2018. 387–395.
|
 2024, Vol. 33
2024, Vol. 33


