2. 贝尔法斯特女王大学 电子学、电气工程与计算机科学学院, 贝尔法斯特 BT9 5BN
2. School of Electronics, Electrical Engineering and Computer Science, Queen’s University Belfast, Belfast BT9 5BN, UK
数据分析被广泛用于提取有用的信息和做出决策. 数据的预处理对数据分析至关重要, 因为真实数据往往受到环境或其他因素的影响, 导致数据中出现异常点(也称为离群点, outliers)[1,2]. 如果不对存在异常点的数据进行处理, 将会直接影响决策. 为避免这种情况的发生, 通常在进行数据分析之前必须清除数据中的异常点, 以确保其不会影响决策. 然而, 如何高效准确地发现数据中的异常点是关键之一[3]. 随着大数据时代的到来, 数据变得越来越多, 越来越复杂, 维度也越来越高[4]. 因此, 我们需要一种能够处理大数据, 从复杂、高维的数据中提取有用信息并识别特征之间相关性的模型. 这正成为一个基础性的研究问题[5].
异常点偏离正常点, 通常表现为离散的数据点[6]. 通常情况下, 异常点位于概率分布的低密度区域[7,8], 因此常使用密度估计来识别异常点. 在起初数据量较少且维度较低的情况下, 引入基于密度估计的方法, 例如 LOF[9], 和基于距离的方法, 例如 KNN[10]. LOF能够同时考虑数据集的局部和全局属性, 但需要计算数据点两两之间的距离, 造成整个算法的时间复杂度为O(n2). 为改进这一问题, Goldstein[11]提出了FastLOF改进方法.
而基于距离的方法, 除了计算数据点两两之间的距离, 带来高复杂度问题外[12,13], 算法的优劣还依赖于距离度量方法的选取. 为避免距离计算带来的困难, 逐渐转向基于统计学方法的研究, 例如 HBOS[14]、KDE[15]、GMM[16]. 尽管它们取得了一定的进展, 但仍存在一些限制, 例如, HBOS会受到bin取值的影响, 当bin取值较大时可能导致概率密度函数的不连续. 然而, Pavlidou等人[15]提出KDE, 使用邻域的信息可以很大程度上解决概率密度函数的不连续问题. 由于数据往往呈现多个分布, GMM是最合适的模型. GMM将多个高斯分布加权叠加来拟合数据分布, 分布外围的数据点概率密度低通常被视为异常点.
在处理小型低维特征数据时, 上述方法都具有一定的优势. 但当处理大型高维特征数据时, 它们的处理变得非常困难. 例如, 基于距离的方法在数据量大、维度高时会导致高昂的计算成本. 而在处理大型高维数据时, GMM会受到维度灾难的影响[17,18]. 大型高维数据主要存在两个问题, 即数据量大和维度高[5]. 为了解决这些问题, 可以将其拆分为两个子问题: 首先, 如何处理大数据; 其次, 如何处理高维数据. 对于大型数据, 模型需要具有较低的计算成本. Liu等人[19]提出的孤立森林(isolation forest, iForest)能够有效处理大型数据, 它是一种基于集成的方法, 并且具有线性时间复杂度. 然而, iForest仅对全局异常点敏感, 不太适合处理局部相对稀疏的点[20]. 为了解决这一问题, Bandaragoda等人[20]提出了名为iNNE的模型, 它仍然采用数据孤立的思想, 并引入最近邻距离算法来考虑数据的局部分布特性. 然而, iNNE模型中的最近邻距离算法需要计算样本之间的距离, 导致计算复杂度较高.
其次, 对于高维数据, 首选的方法是使用降维技术, 以减少数据的维度. 例如, PCA[21]、Autoencoder[22]和DAGMM[23]都是解决维度灾难和计算成本问题的有效方法. 传统异常检测方法是通过PCA降维, 然后将数据输入高斯混合模型(GMM). 然而, 这种方法使用了两阶段的训练和标准的期望最大化(EM)算法. 通过降低维度, 可以降低密度估计的计算复杂度, 也间接降低了模型的复杂性, 使得降维模型能够有效处理大型数据. DAGMM采用端到端的方式联合优化深度自编码器和高斯混合模型的参数. 这种联合优化有效地平衡了自编码重建、潜在表示的密度估计和正则化[23]. 但DAGMM仍然存在一些限制, 例如评价网络的输入引入噪声(重构误差), 此外, 低维潜在空间分布与GMM分布之间的相关性仅依赖于各分量的权重估计.
除了通过降维来处理高维数据外, Goldstein等人[14]提出了HBOS, Li等人[24]提出了ECOD, 它们采用了另一种方法来处理高维数据, 即假设维度之间是相互独立的, 因此分别对每个特征维度进行建模, 大大降低了模型的计算复杂度. HBOS独立计算每个特征维度的直方图, 而ECOD单独计算每个特征维度的经验累积分布, 将经验累积密度函数较小的点视为异常点. 尽管它们能够解决维度灾难问题并取得了显著的进展, 但它们都无法对特征之间的依赖关系进行建模.
上述统计模型表明它们具有卓越的能力, 但根据模型是否需要训练参数, 可以将统计模型分为两类: 非参数方法和参数方法[25]. 不同方法各有优缺点. KDE、HBOS、ECOD等属于非参数方法, 非参数方法的优势在于不需要考虑数据的分布[1]以及超参数的调整, 可以很方便地应用. 但非参数方法需要将以前的样本与候选样本进行比较, 以评估候选样本是否为异常点. 每次添加新数据进行预测时, 都需要重新拟合以前的数据. 对于大型数据来说, 以前的数据较多会导致非参数方法进行冗余计算, 进而带来高昂的计算成本.
相反, 参数方法可以在已有的数据上拟合后固定模型参数, 直接用于候选样本的评估, 例如: GMM. 除了基于统计模型的参数方法可以解决过度冗余计算问题. 基于学习的方法也能够有效解决这一问题. 例如: 基于学习(深度学习) 的方法可以在训练好模型参数后, 直接对新样本进行预测, 例如: OC-SVM[26]、DCN[27]、DAGMM、EM3[28]、EGBADen[29]. 并且基于学习的方法能够解决传统参数方法的一些限制, 例如在面对高维数据时, GMM处理成本高, 难以推广. DAGMM将降维模块 (Autoencoder)和评估网络(GMM)进行端到端的联合优化训练, 能够解决传统GMM的这一限制. 但是在联合优化时, 低维潜在空间分布与GMM分布之间的相关性仅依赖于估计每个分量的权重. 这导致评价网络对潜在空间映射的反馈有限. 虽然基于学习的无监督异常检测已经取得一些进展. 但是近几年在这个方向的研究在减少[30].
现有的无监督异常检测方法在处理大型高维数据时面临一些挑战[31]. 其中最主要的挑战之一是算法的可扩展性, 即是否适用于大多数数据. 例如, LOF、iNNE和OC-SVM等方法在处理高维大数据时往往缺乏扩展性, 通常需要对高维大数据进行预处理. 此外, 像HBOS和ECOD等方法虽然在特定数据集上有效, 但难以扩展到具有高度特征相关性的数据集. 然而, 基于学习的方法不仅仅是针对单独的特征, 而是能够综合考虑所有特征以学习数据中的关键特性. 面对新领域的数据时, 模型只需重新训练以学习新的数据特性, 而不需要重大改动. 这突显了基于学习方法具有强大的表征学习能力[32], 使其成为解决实际问题的便捷选择. 随着数据量和维度的不断增加, 首要问题在于模型必须有效地处理高维大数据. 其次, 模型必须能够准确地识别数据的特征. 考虑到这些因素, 我们认为采用基于学习的方法最适合处理高维大数据, 并且易于扩展. 尽管基于学习的方法表现出强大的竞争力, 但像DAGMM这样出色的模型仍然存在一些限制, 比如需要为特定数据集设计相应的模型. 因此, 本文希望针对DAGMM的局限性提出改进方案, 以使基于学习的模型更具竞争力.
为了解决上述限制, 本文提出了一种基于学习的异常检测模型, 被称为深度自动编码器标准化流(DANF). 其动机是为了高效地处理大型高维数据, 进行密度估计, 并解决已有模型(例如DAGMM)存在的限制. DANF使用自动编码器将原始数据映射到低维潜在空间, 并且通过标准化流来自动调整分布的变换参数. 本文的目标是确保自动编码器的输出能够通过标准化流将低维潜在空间分布转换为高斯分布, 从而使得密度估计和异常点识别更加容易.
2 深度自编码标准化流模型本节将详细展示本文提出的方法, 主要分为以下3个部分进行阐述. 首先, 在第2.1节中, 阐述了DANF的设计; 其次, 在第2.2节中, 详细介绍了DANF每个组件的技术细节; 最后, 在第2.3节中, 讨论了涉及优化模型的损失函数.
2.1 DANF的设计根据离群点的定义, inliers密度高, 而outliers密度低[8]. 因此, 使用GMM评估具有一定的合理性, 它通常被视为评估样本是否为异常点的关键组成部分. 因为高斯分布中心具有较高的概率密度, 而周围散点的概率密度低. 然而, 在处理高维大数据时, GMM容易受到维度灾难的影响[17,18]. 本文采用了DAGMM的方法, 通过使用Autoencoder对输入数据进行预处理(将原始数据嵌入到低维潜在空间), 以减轻GMM的计算负担. DAGMM通过潜在空间分布计算高斯分布的均值和协方差, 并使用评估层来确定每个分布的权重. 但其优化过程需要保证协方差是正定矩阵. 与此不同, normalizing flow (NF)能够将复杂的低维潜在空间分布映射成高斯分布, 并使用基于单调有理二次样条的完全可微模块, 保持可逆性的同时增强了耦合和自回归变换的灵活性[33]. 这有助于解决DAGMM在优化密度估计模块时需要确保协方差矩阵为正定矩阵的问题, 而且无需直接计算潜在空间的均值和协方差. 因此, 本文基于NF的特点将其作为模型的密度估计模块. 然而, 如何有效地联合优化Autoencoder和NF仍然具有挑战性. 接下来, 我们将在第2.2节中详细描述这些技术细节.
2.2 网络结构根据前述讨论, 为了处理大型高维数据, 本文选择了将Autoencoder和NF结合使用. 希望Autoencoder能够将原始数据映射到低维潜在空间并保留关键信息, 同时NF能够将复杂的低维分布映射为高斯分布. 然而, 如何充分利用不同模块之间的协同作用以及发挥它们各自的优势是需要深入探讨的问题. 如果采用解耦的两阶段训练, 不同模块之间可能只会发挥各自的优势. 在这种情况下, Autoencoder仅用于简单的降维, 而未必有利于NF将低维空间分布映射成高斯分布; 反之, NF只负责将低维空间分布映射成高斯分布, 而未能引导Autoencoder嵌入适合且易于转换的低维潜在空间分布. 这可能导致各模块之间协同不足. 因此, 我们采用联合优化的端到端训练策略, 以充分发挥它们之间的协同作用.
图1 通过Encoder将样本X映射到潜在空间分布Z, 并根据Decoder重构Z得到
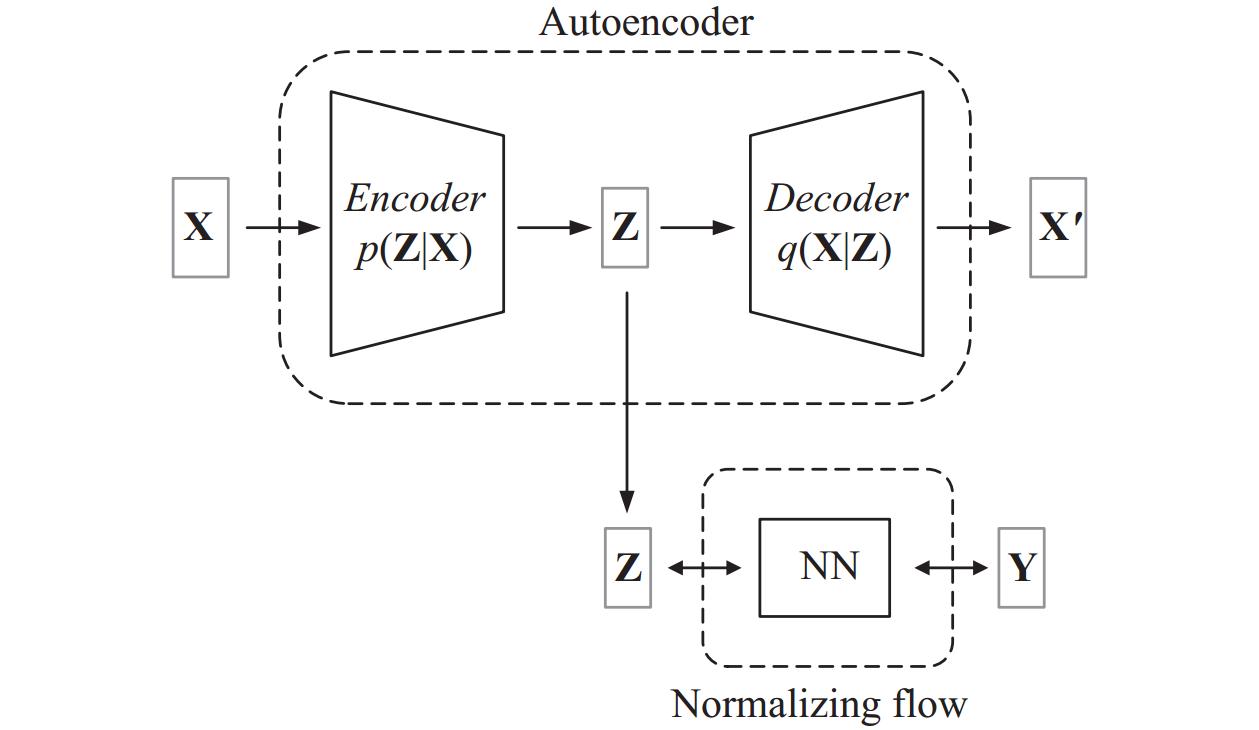
|
图 1 DANF模型结构图 |
DANF之所以使用Autoencoder而不是传统的降维技术, 例如PCA[21], 是因为它不仅可以将数据降维, 还能通过联合优化参数的梯度反向传播, 接收来自NF映射的反馈, 从而调整数据在低维空间中的映射. 通过联合优化, 将这两个模块紧密联系在一起, 充分发挥它们之间的协同作用和各自的优势. DANF的整体结构图如图1所示, 具体的计算公式如下:
| $ {{\bf Z}}= Encoder({\bf X}), \quad {\bf X}' = Decoder({\bf{Z}}) $ | (1) |
其中, X代表给定的数据样本,
编码器和解码器的设计: DAGMM针对不同的数据集需要设计特定的模型, 因为这些数据集具有不同的特征维度, 这限制了其灵活性和扩展性. 与此不同, DANF不需要为每个数据集设计特定的编码器. 尽管它并没有采用完全相同的模型来处理所有数据集, 而是在处理不同数据集时遵循一定的规律, 从而比DAGMM具有更好的灵活性和扩展性. 实际上, 现实世界中的各领域数据不尽相同, 数据特征从几个到数百甚至数千个, 如果对这些差异很大的数据使用相同的固定模型, 显然是不合理的, 这可能导致模型的无效性. 因此, DANF根据自动编码器对输入数据的处理需求设计了两种编码器方式, 以适应高维特征数据和低维特征数据.
本文设计了两种不同形式的网络架构(编码器), 用于将具有不同特征数量的数据映射到低维潜在空间. 对于高维数据, 直接对数据进行降维处理. 对于低维数据, 采用先扩维后降维的两步策略将其嵌入到合适的子空间中. 关于编码器设计的详细信息如下.
对于高维数据的编码器:
| $ Linear(d, {\text{ }}d/2) - Linear(d/2, {\text{ }}d/4) - Linear(d/4, {\text{ }}d') $ | (2) |
对于低维数据的编码器:
| $ Linear(d, {\text{ }}d \times 2) - Linear(d \times 2, {\text{ }}d \times 5) - Linear(d \times 5, {\text{ }}d') $ | (3) |
其中, d表示输入信号的维数, d' 表示映射的低维空间分布的维数. 解码则是编码的逆过程.
图2 通过一序列的变换f (f1,
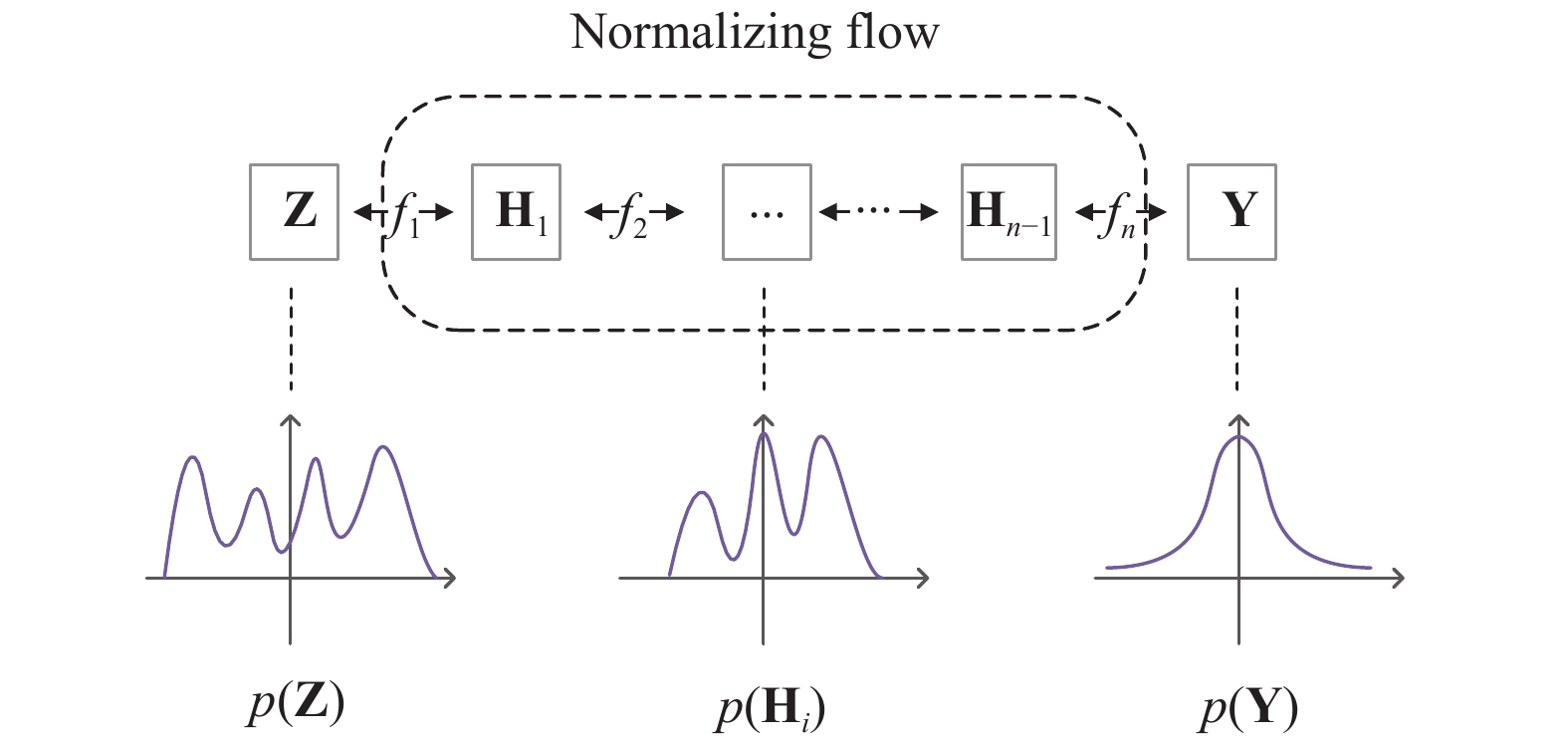
|
图 2 Normalizing flow |
如图2所示, 本文采用NF将复杂的低维潜在空间分布映射成高斯分布来进行分布评估. 我们希望NF能够学习一种将复杂的低维潜在空间映射到高斯分布的变换
| $ p({\bf{Z}}) = p(f({\bf{Z}}))\left|\det \left(\frac{{\partial f({\bf{Z}})}}{{\partial {\bf{Z}}}}\right)\right| $ | (4) |
其中, Jacobian矩阵
| $ \begin{gathered} p({\bf Y}) = N({\bf Y};\mu , \Sigma ) \\ \;\;\;\;\;\;\; = \frac{1}{{{{(2 {\text{π}} )}^{d/2}}{{\left| \Sigma \right|}^{1/2}}}}\exp \left\{ { - \frac{1}{2}{{({\bf Y} - \mu )}^{\rm{T}}}{\Sigma ^{ - 1}}({\bf Y} - \mu )} \right\} \\ \end{gathered} $ | (5) |
其中, d表示数据维度;
为了优化本文提出的方法, 使非线性变换f能够将低维潜在空间分布Z映射到一个更为简单的高斯分布, 本方法需要最大化分布的对数似然. 根据式(4)可以计算分布的对数似然:
| $ \log (p({\bf{Z}})) = \log (p(f({\bf{Z}}))) + \log \left(\left|\det \left(\frac{{\partial f({\bf{Z}})}}{{\partial {\bf{Z}}}}\right)\right|\right) $ | (6) |
本文将分布的对数似然作为评估样本是否为异常点的重要依据. 根据所选的阈值, 我们将对数似然小于阈值的样本标记为异常点. 然而, 关于阈值的选择, 本文采用了DAGMM的方法, 根据数据集中异常点的占比来选择异常值分数中的百分位数. 在优化模型参数时, 需要最大化分布的对数似然. 在本文中, 我们将对数似然取反, 将最大化分布的对数似然变为最小化, 记为L2. 根据上述过程, 本节提供了DANF用于预测样本的伪代码. 在模型训练结束后, 固定模型参数. 然后, 将测试集的数据按批量大小输入模型, 拟合好的模型会对测试集的批量样本计算出异常值分数. 最终, 我们获得测试集所有样本的异常值分数. 通过将异常值分数与阈值进行比较, 我们可以判断样本是否为异常点. 具体如算法1所示.
算法1. DANF预测算法
Input: 输入数据X =
Output: 离群值的分数 O :=
PREDICT(X):
for sampled mini-batch x_batch =
# 1. 通过自动编码器的编码器将数据映射到低维潜在空间, 然后通过解码器将低维潜在分布Z重构为
# 2. 通过一系列变换f, 将低维潜在空间分布Z映射到目标高斯分布, 并计算目标分布的高斯密度函数.
# 3. 给定Z, 计算函数f的Jacobian矩阵的行列式. 计算
# 4. 通过步骤2中的高斯分布概率密度函数和步骤3中的Jacobian矩阵的行列式来计算低维潜在空间分布Z的对数似然.
end for
Return 离群值的分数O=
为了充分发挥每个模块的优势, 希望能够为它们设计最优化的参数, 因此需要定义它们的优化目标. 目标函数主要由两个部分组成, 每个部分的作用将在接下来的部分详细描述. 具体的损失函数公式如下:
| $ {L_1} = \frac{1}{N}\sum\limits_{i = 1}^N {{{({{\boldsymbol x}_i} - {{\boldsymbol x}'_i})}^2}} $ | (7) |
| $ loss = {L_1} + {L_2} $ | (8) |
其中,
实验中, 我们根据数据集的特征数量选取不同的编码器设计, 用于将原始数据映射到低维潜在空间. 对于高维数据, 直接对数据进行降维处理. 对于低维数据, 采用了一种先升高维度, 然后再降低维度的方法. 这是因为直接对低维数据进行降维会导致模型参数较少, 可能无法充分学习数据之间的特性, 从而使模型不稳定. 在第3.5节的实验中, 实验验证了这一点. 具体使用哪种编码器方式, 请参考6个基准数据集的实验部分.
对于DANF的训练设置, 实验采用了DAGMM的设置, 其中KDDCUP、Thyroid、Arrhythmia、Satimage-2、HandOutlines和KDDCUP-Rev数据集的批量大小分别设置为1024、1024、128、1024、128、1024. 关于训练的epoch数, 与DAGMM不同, DANF不需要进行太多的训练迭代. 因此, 除了Thyroid数据集的训练epoch数设置为2000, 其余5个数据集的训练epoch数均设置为200. 另外, 为了优化DANF的参数, 本文采用了广泛使用的Adam[36]优化器. 学习率统一设置为0.0001.
3.2 数据集实验使用6个基准数据集, 其中前5个是公开的基准数据, 分别是KDDCUP99 10 percent (KDDCUP)、Thyroid、Arrhythmia、Satimage-2和HandOutlines, 第6个数据集被称为KDDCUP-Rev的数据集, 它是KDDCUP的一个子集, 通过某种采样比例在KDDCUP数据集中进行采样而来. 每个数据集的详细信息请参见表1. 其中, KDDCUP数据集来源于UCI存储库( http://archive.ics.uci.edu/ml), 而Thyroid、Arrhythmia和Satimage-2数据集来源于ODDS存储库( http://odds.cs.stonybrook.edu/), HandOutlines来源于UCR 存储库(https://www.cs.ucr.edu/~eamonn/time_series_data_2018/).
| 表 1 实验数据集的相关信息 |
表1列出了6个基准数据集的详细信息, 包括每个数据集的样本数量、特征数量以及异常样本占比.
需要注意的是, KDDCUP数据集中的7个分类字段都是字符类型数据, 包括protocol_type、service、flag、land、logged_in、is_host_login、is_guest_login. 实验需要将这些字段转换为数值类型以便输入模型, 我们按照DAGMM的方法, 使用了一种称为one-hot编码的方法, 对KDDCUP数据集中的这7个分类字段进行了转换, 从而得到了一个具有121维特征的数据集. KDDCUP-Rev作为本实验的第6个数据集, 是通过保留了KDDCUP数据集中的所有正常样本, 并根据正常样本和异常样本的比例(4:1)进行采样得到的.
3.3 模型训练策略实验使用一类数据作为训练数据(inliers或outliers), 并遵循DAGMM的设置, 将数据集划分为训练集和测试集, 其中6个数据集中的所有正常样本的50%被用作训练数据, 而其余的正常样本和所有异常样本被用作测试数据[23]. 需要注意的是, KDDCUP数据集中的正常样本数量远小于异常样本数量, 因此, 本文将异常样本标记为正常样本, 将正常样本标记为异常样本.
3.4 实验结果在本节, 我们根据上述的设置以及模型的训练策略, 在6个公开的基准数据集上进行了实验. 在仅使用inliers或outliers作为训练集的情况下, 我们进行了DANF与GMM、DAGMM、OC-SVM、EM3、GOAD[37]、EGBADen等模型的比较实验, 以验证DANF的有效性. 对于模型的评估指标, 本实验遵循了DAGMM[23]中的平均Precision、Recall和F1-score.
在实验中, 由于6个数据集的特征维度存在差异, 我们采用了不同的编码器设置, 具体根据特征是高维数据还是低维数据来决定使用第2.2节讨论的两种编码器中的一种.
对于KDDCUP、Arrhythmia、KDDCUP-Rev和HandOutlines这4个数据集, 它们的特征维度较高, 因此DANF将原始数据空间嵌入到低维潜在空间的编码器只进行降维处理, 具体设置参见式(2).
然而, 对于Thyroid、Satimage-2数据集, 分别只包含6、36个特征, 我们采用的编码器首先将原始空间的数据映射到高维空间, 然后再映射到低维潜在空间, 编码器具体形式参见式(3).
编码器设置根据数据集的特征维度的不同进行灵活选择, 其目的是确保在处理高维和低维数据时都能够有效地嵌入潜在空间.
表2是不同的方法在6个公开的基准数据集上, 平均Precision、Recall和F1-score的结果. 最佳评估指标用加粗表示, “—”表示没有数据. 由于在Satimage-2、HandOutlines数据集上, OS-CVM、DAGMM、GOAD和EGBADen的实验结果来自文献[38], 然而, 在文献[38]中未展示Precision和Recall, 因此这两个数据集只使用F1-score来比较模型的性能. 显然, 在仅使用inliers或outliers作为训练集的实验中, DANF在KDDCUP、Arrhythmia、KDDCUP-Rev和Thyroid这4个基准数据集上的平均Precision、Recall和F1-score这3个评价指标都优于DAGMM和OC-SVM. 特别值得注意的是, 在Thyroid和Arrhythmia数据集上, DANF的F1-score相对于DAGMM分别提高了26.43%和8.71%. 即使与自监督的GOAD相比, DANF在无监督的情况下也达到了可比的性能, 在Satimage-2和HandOutlines数据集上, DANF在F1-score上优于GOAD, 分别提高了 3.69%和2.28%, 成为最佳模型. 在KDDCUP数据集上, DANF的F1-score超越了EM3的2.34%.
| 表 2 实验结果比较 |
这些结果表明, 在无监督的异常检测任务中, DANF相对于其他模型在多个评价指标上表现出更好的性能, 尤其在特定数据集上取得了显著的提升.
本文在图3中展示了DANF在Satimage-2数据集上的结果, 即NF拟合低维潜在空间的结果. 在图3中, “Normal”表示正常样本, “Outlier”表示异常样本, 而“Flow”表示通过NF经过高斯分布反变换生成的数据点. 通过图3的分析, 可以看出DANF能够很好地拟合Satimage-2的数据并区分异常样本.
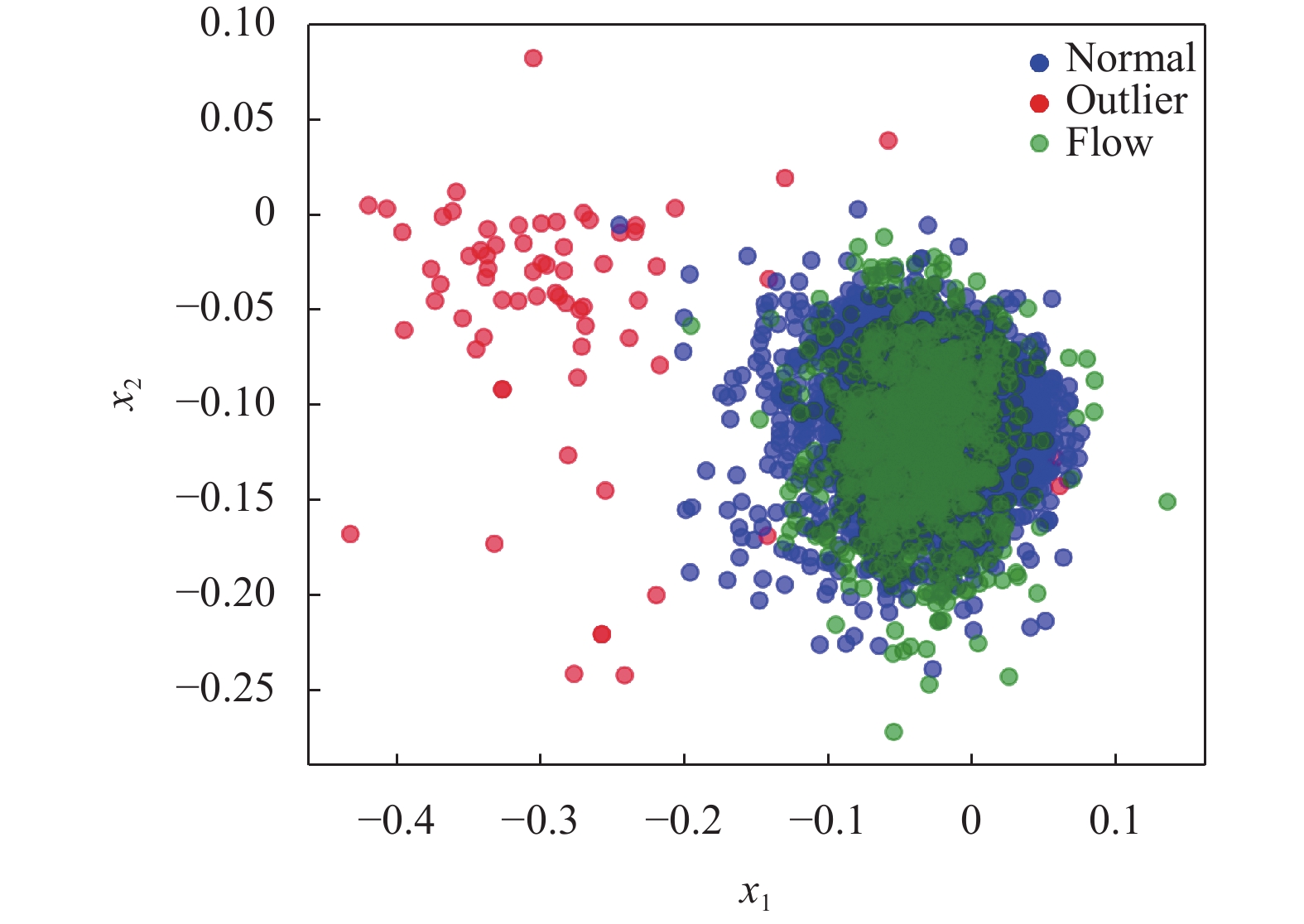
|
图 3 Latent space |
3.5 消融实验
在本节中, 尝试使用一个模型来扩展到所有数据集上. 在Thyroid、Satimage-2数据集上, 进行了与其他4个数据集上使用相同模型的实验, 即Autoencoder的编码器直接对原始数据进行降维. 表3展示了明显的对比结果. 对于低维数据, 直接降维在很大程度上影响了模型的建模有效性. 这也验证了在第3.1节中, 采用两种编码器来应对不同数据的选择是正确的.
| 表 3 DANF在Thyroid、Satimage-2数据集上使用不同编码器对模型建模的影响 |
表3中, 降维表示模型的编码器只对数据降维, 而先升后降表示模型的编码器对数据进行先升高维度, 再降低维度. 实验结果显示, 对于Thyroid、Satimage-2数据集, 采用先升高维度再降低维度的编码器设置可能更适合, 因为这两个数据集分别只包含6、36个特征, 直接降维可能会丧失数据的信息, 而通过先升高维度再降低维度可以更好地保留和利用数据的信息.
4 结论与展望本文关注一个在无监督异常检测研究领域普遍被忽略的重要问题, 即如何有效处理大型高维数据. 以往的研究通常直接对复杂的分布建模, 而忽略了将复杂的数据分布转换成已知的简单分布的方法. 本文研究如何有效地对复杂数据分布进行建模并关注数据的特性. 其解决方案是使用可学习的模型: Autoencoder将高维空间映射到低维空间, NF将其转换成简单的高斯分布, 并使用密度估计来评估数据点是否为异常点. 可学习模型的优势在于它们能够根据不同领域数据的独特属性进行自适应学习.
本文设计了一个网络(DANF)用于无监督的异常点检测, 通过将原始数据映射到低维空间, 进行异常点的有效检测. 该模型使用 NF 克服了直接使用 GMM 去拟合复杂的低维潜在空间分布的问题. 它将复杂的低维潜在空间映射到简单的高斯分布, 从而简化了对复杂数据的建模.
实验结果表明, 在选择的6个公开基准数据集上, 在仅使用inliers 或 outliers建模的情况下, 本文所提出的DANF在多个评估指标上显著超越了直接使用GMM进行建模的性能, 并且在平均Precision、Recall和F1-score这3个评估指标上均优于DAGMM. 在KDDCUP数据集上, DANF的F1-score超越了EM3 模型2.34%.
| [1] |
Chander B, Kumaravelan G. Outlier detection strategies for WSNs: A survey. Journal of King Saud University-computer and Information Sciences, 2022, 34(8): 5684-5707. DOI:10.1016/j.jksuci.2021.02.012 |
| [2] |
方正, 高岑, 田月, 等. 数据整合中异常检测算法研究. 计算机系统应用, 2017, 26(7): 200-203. DOI:10.15888/j.cnki.csa.005936 |
| [3] |
Liu SH, Zhou B, Ding Q, et al. Time series anomaly detection with adversarial reconstruction networks. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(4): 4293-4306. DOI:10.1109/TKDE.2021.3140058 |
| [4] |
周茂袁, 伍小双. 基于深度学习的异常检测模型综述. 中国民航大学学报, 2023, 41(4): 1-7, 36. |
| [5] |
Thudumu S, Branch P, Jin J, et al. A comprehensive survey of anomaly detection techniques for high dimensional big data. Journal of Big Data, 2020, 7: 42. DOI:10.1186/s40537-020-00320-x |
| [6] |
Aggarwal CC. An introduction to outlier analysis. Outlier Analysis. Cham: Springer International Publishing, 2017.
|
| [7] |
Lazarevic A, Kumar V. Feature bagging for outlier detection. Proceedings of the 11th ACM SIGKDD International Conference on Knowledge Discovery in Data Mining. Chicago: ACM, 2005. 157–166.
|
| [8] |
Pokrajac D, Lazarevic A, Latecki LJ. Incremental local outlier detection for data streams. Proceedings of the 2007 IEEE Symposium on Computational Intelligence and Data Mining. Honolulu: IEEE, 2007. 504–515.
|
| [9] |
Breunig MM, Kriegel HP, Ng RT, et al. LOF: Identifying density-based local outliers. Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data. Dallas: ACM, 2000. 93–104.
|
| [10] |
Ramaswamy S, Rastogi R, Shim K. Efficient algorithms for mining outliers from large data sets. Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data. Dallas: ACM, 2000. 427–438.
|
| [11] |
Goldstein M. FastLOF: An expectation-maximization based local outlier detection algorithm. Proceedings of the 21st International Conference on Pattern Recognition (ICPR2012). Tsukuba: IEEE, 2012. 2282–2285.
|
| [12] |
Chandola V, Banerjee A, Kumar V. Anomaly detection: A survey. ACM Computing Surveys, 2009, 41(3): 1-58. DOI:10.1145/1541880.1541882 |
| [13] |
卓琳, 赵厚宇, 詹思延. 异常检测方法及其应用综述. 计算机应用研究, 2020, 37(S1): 9-15. |
| [14] |
Goldstein M, Dengel A. Histogram-based outlier score (HBOS): A fast unsupervised anomaly detection algorithm. KI-2012: Poster and Demo Track. Springer, 2012. 59–63.
|
| [15] |
Pavlidou M, Zioutas G. Kernel density outlier detector. Topics in Nonparametric Statistics: Proceedings of the 1st Conference of the International Society for Nonparametric Statistics. New York: Springer, 2014. 241–250.
|
| [16] |
Yang XW, Latecki LJ, Pokrajac D. Outlier detection with globally optimal exemplar-based GMM. Proceedings of the 9th SIAM International Conference on Data Mining. Sparks: Society for Industrial and Applied Mathematics, 2009. 145–154.
|
| [17] |
Zhang TY, Chen W, Liu YX, et al. An intrusion detection method based on stacked sparse autoencoder and improved Gaussian mixture model. Computers & Security, 2023, 128: 103144. DOI:10.1016/j.cose.2023.103144 |
| [18] |
Zhu PY, Zhang CW, Li XF, et al. A high-dimensional outlier detection approach based on local Coulomb force. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(6): 5506-5520. DOI:10.1109/TKDE.2022.3172167 |
| [19] |
Liu FT, Ting KM, Zhou ZH. Isolation forest. Proceedings of the 8th IEEE International Conference on Data Mining. Pisa: IEEE, 2008. 413–422.
|
| [20] |
Bandaragoda TR, Ting KM, Albrecht D, et al. Isolation-based anomaly detection using nearest-neighbor ensembles. Computational Intelligence, 2018, 34(4): 968-998. DOI:10.1111/coin.12156 |
| [21] |
Bro R, Smilde AK. Principal component analysis. Analytical Methods. 2014, 6(9): 2812–2831.
|
| [22] |
Tsai DM, Jen PH. Autoencoder-based anomaly detection for surface defect inspection. Advanced Engineering Informatics, 2021, 48: 101272. DOI:10.1016/j.aei.2021.101272 |
| [23] |
Zong B, Song Q, Min MR, et al. Deep autoencoding Gaussian mixture model for unsupervised anomaly detection. Proceedings of the 6th International Conference on Learning Representations. Vancouver: OpenReview.net, 2018.
|
| [24] |
Li Z, Zhao Y, Hu XY, et al. ECOD: Unsupervised outlier detection using empirical cumulative distribution functions. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(12): 12181–12193.
|
| [25] |
卢梦茹, 周昌军, 刘华文, 等. 基于二阶近邻的异常检测. 计算机系统应用, 2023, 32(2): 160-169. DOI:10.15888/j.cnki.csa.008968 |
| [26] |
Schölkopf B, Platt JC, Shawe-Taylor J, et al. Estimating the support of a high-dimensional distribution. Neural Computation, 2001, 13(7): 1443-1471. DOI:10.1162/089976601750264965 |
| [27] |
Yang B, Fu X, Sidiropoulos ND, et al. Towards K-means-friendly spaces: Simultaneous deep learning and clustering. Proceedings of the 34th International Conference on Machine Learning. Sydney: JMLR.org, 2017. 3861–3870.
|
| [28] |
An P, Wang ZY, Zhang CJ. Ensemble unsupervised autoencoders and Gaussian mixture model for cyberattack detection. Information Processing & Management, 2022, 59(2): 102844. DOI:10.1016/j.ipm.2021.102844 |
| [29] |
Han X, Chen XH, Liu LP. GAN ensemble for anomaly detection. Proceedings of the 35th AAAI Conference on Artificial Intelligence, the 33rd Conference on Innovative Applications of Artificial Intelligence, IAAI 2021, the 11th Symposium on Educational Advances in Artificial Intelligence. AAAI, 2021. 4090–4097.
|
| [30] |
Han SQ, Hu XY, Huang HL, et al. Adbench: Anomaly detection benchmark. Proceedings of the 36th Conference on Neural Information Processing Systems. 2022. 32142–32159.
|
| [31] |
Pang GS, Shen CH, Cao LB, et al. Deep learning for anomaly detection: A review. ACM Computing Surveys, 2022, 54(2): 38. DOI:10.1145/3439950 |
| [32] |
邓华伟, 李喜旺. 基于深度学习的网络流量异常识别与检测. 计算机系统应用, 2023, 32(2): 274-280. DOI:10.15888/j.cnki.csa.008989 |
| [33] |
Durkan C, Bekasov A, Murray I, et al. Neural spline flows. Proceedings of the 33rd International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2019. 675.
|
| [34] |
Dinh L, Krueger D, Bengio Y. Nice: Non-linear independent components estimation. Proceedings of the 3rd International Conference on Learning Representations. San Diego: ICLR, 2015.
|
| [35] |
Kingma DP, Dhariwal P. Glow: Generative flow with invertible 1×1 convolutions. Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montréal: Curran Associates Inc., 2018. 10236–10245.
|
| [36] |
Kingma DP, Ba J. Adam: A method for stochastic optimization. Proceedings of the 3rd International Conference on Learning Representations. San Diego: ICLR, 2015.
|
| [37] |
Bergman L, Hoshen Y. Classification-based anomaly detection for general data. Proceedings of the 8th International Conference on Learning Representations. Addis Ababa: OpenReview.net, 2020.
|
| [38] |
Xi L, Liang CC, Liu H, et al. Unsupervised dimension-contribution-aware embeddings transformation for anomaly detection. Knowledge-based Systems, 2023, 262: 110209. DOI:10.1016/j.knosys.2022.110209 |
 2024, Vol. 33
2024, Vol. 33


