路径规划是一个典型的大规模全局优化问题. 由于其节点数量众多、搜索空间广阔, 传统的动态规划求解方法常受到求解时间的限制. 虽然智能优化方法能够在可接受的时间范围内找到次优解, 但是往往容易陷入局部最优或搜索停滞等问题^[1]. 在机器人领域中, 路径规划是研究的热点问题之一^[2]. 如何使移动机器人能够自主寻找长度最短、平稳性最佳的路径是实现自主导航的关键问题. 机器人能否成功地自主导航, 取决于其智能能力. 通过让机器人学习周围环境的信息, 并引导它运用智能技术从一个起始点安全地移动到指定地点, 完成避障、寻优等一系列子任务, 最终找到一条无碰撞的优化路径^[3].

移动机器人的单/多目标路径规划问题可转化为多目标优化问题(MOP)进行研究. 近年来, 许多研究者已经认识到各种多目标进化算法(multi-objective evolu-tionary algorithm, MOEA)是解决MOP的有效途径.

目前, 已经发展出许多进化算法, 包括遗传算法(genetic algorithm, GA)、粒子群算法(particle swarm optimization, PSO)、蚁群算法(ant colony optimization, ACO)等一系列算法. 研究者们对这些算法进行了改进, 尝试解决移动机器人的单/多目标路径规划问题. 例如, Singh等人^[4]利用多目标NSGA-II启发式算法优化无人机的飞行轨迹, 开发的NSGA-II模型演变为最优的无人机飞行轨迹, 同时实现了无人机能耗最小化、节点能耗最小化、平均RSSI最大化的目标. Ajeil等人^[5]使用一种新颖的自然启发式算法实现的点生成, 该算法是将粒子群优化和改进频率蝙蝠算法(PSO-MFB)进行有效结合, PSO-MFB生成并选择满足条件的点, 将不可行解转化为可行解, 最后通过避障算法形成一条无碰撞路径. Gul等人^[6]是通过灰狼优化器与粒子群优化算法(PSO-GWO)的结合来优化路径, 将PSO-GWO算法生成的所有最优可行解与局部搜索技术相结合, 将所有不可行解转换为可行解, 最后使用防撞检测和避障算法, 避免机器人碰撞障碍物. 上述研究者采用智能仿生算法让机器人智能化的躲避障碍物, 完成自主导航任务. 然而, 这些算法仍然存在一些缺陷. 例如, 当算法参数设置不合理时, 算法性能将会受到较大影响, 甚至无法找到一条有效路径; 当算法陷入局部最优时, 无法跳出; 算法的全局搜索与局部搜索平衡性的问题等.

随着深度强化学习(deep reinforcement learning, DRL)的兴起, 强化学习在多目标路径规划中也得到广泛应用. 在现实世界中, 移动机器人需要在考虑多个目标的情况下进行路径规划, 如最短路径、最小能耗、最大效率等. 多目标强化学习算法, 例如NSGA-II和SPEA2等的应用, 使得机器人能够在不同目标之间进行权衡和优化. 现实环境中的路径规划在某些情况下, 机器人可能处于部分可观测环境中, 即无法直接观测到完整的状态信息. 针对这种情况, 研究者们通过将历史观测信息纳入决策, 提高了路径规划的性能, 例如刘晓峰等人^[7]提出一种基于记忆启发的强化学习方法, 不需要植入先验知识, 利用启发式回报函数改造Q学习方法, 提高搜索效率. 当涉及大规模的状态空间和复杂的动作空间, 这使得算法训练过程非常耗时, 王楷文等人^[8]提出一种将深度强化学习与状态预测相结合的多智能体动态避碰路径规划方法, 将多障碍物避碰问题转换为时序单障碍物避碰问题, 提高了训练效率与避碰能力. 对于超参数难以设置的缺点, Kiran等人^[9]提出了一种分布式可变长度遗传算法框架, 可以系统地调整各种强化学习应用的超参数, 通过进化改进训练时间和架构的稳健性. 对于复杂的路径规划问题, 算法的收敛和稳定性也是一个难点, Dong等人^[10]提出一种自适应双记忆经验回放结构, 利用双记忆库结构拆分经验数据, 调整 HER 机制比例, 提高了算法的成功率, 并保证训练效率.

综上所述, 目前路径规划算法依然存在一些问题, 例如, 如何更好地避免陷入局部最优解, 如何更好地平衡全局搜索和局部搜索的效率问题等.

针对这些问题, 本文提出了一种融合强化学习的多目标路径规划算法(RLAP-NSGA-II), 不仅提出了两种不同的交叉算子: SARSA算子和tanh-SBX算子, 而且设计了一种基于Metropolis准则的SA进化策略, 平衡算法的探索与利用能力. 本文主要贡献如下.

(1) 为了提升算法在迭代前期的全局搜索能力, 提出了SARSA算子, 将强化学习中的SARSA算法融入NSGA-II的迭代过程中, 在线学习种群的基因特征与动作空间并不断更新策略, 引导子代种群的进化方向, 加快了算法在迭代前期的探索效率, 避免了较多无效路径的探索.

(2) 防止算法在逼近全局最优解的过程中, 出现振荡现象, 提出了tanh-SBX算子. 该算子通过引入tanh函数, 使其局部搜索具备动态调整能力, 快速逼近全局最优, 提高了算法在迭代后期的利用效率, 使优化后的近似最优路径尽可能地逼近全局最优.

(3) 在平衡全局搜索与局部搜索的效率问题上, 提出了一种SA进化策略. 将种群分为两种不同性质的子种群: 精英种群和非精英种群, 不同的算子作用于不同性质的种群, 得到4种进化策略. 通过模拟退火算法(SA)的Metropolis准则计算策略更新概率, 设计一种衰减函数, 基于该函数调整Metropolis准则中的温度系数, 使概率不断趋于零. 最终, 更新策略的概率趋于零, 使得搜索过程逐渐稳定, 在平衡算法探索与利用效率的同时有效平衡了路径的长度和平稳度并实时更新策略, 找到更优的安全路径.

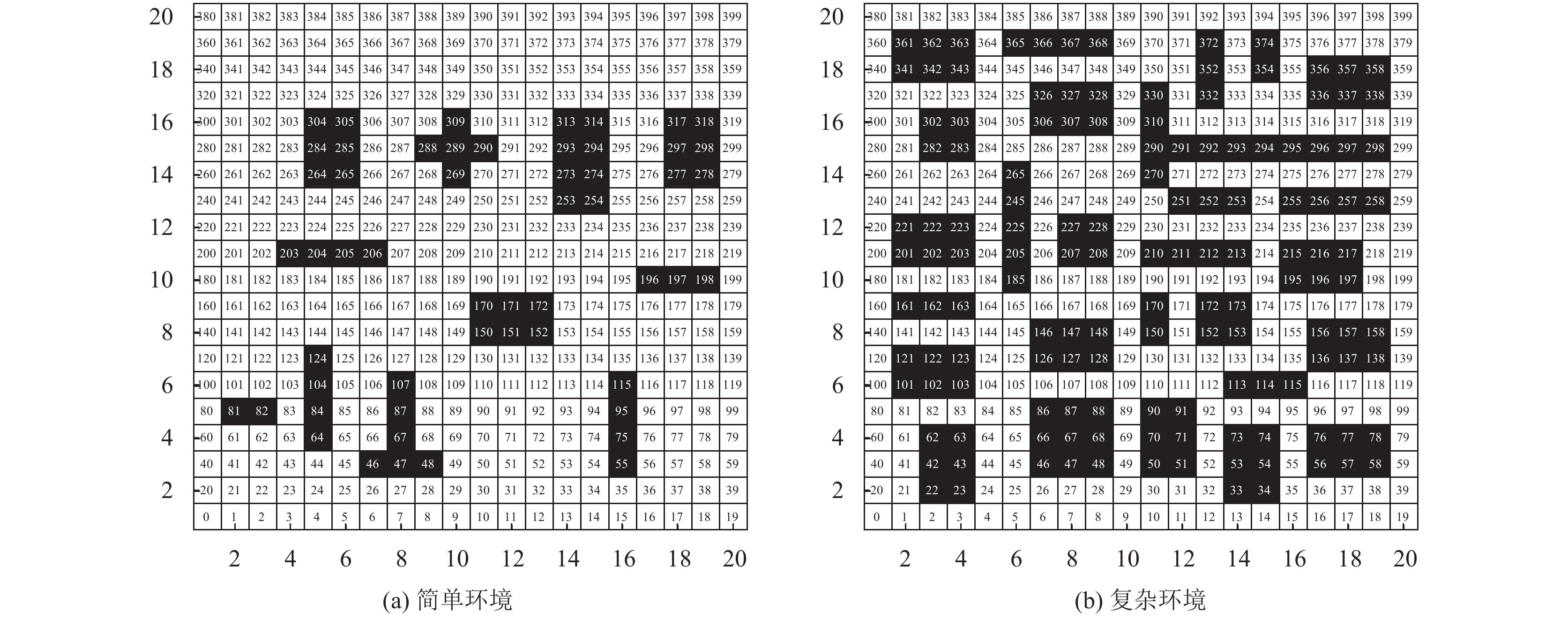
1 移动机器人路径优化的数学模型 1.1 障碍物环境模型

为了简化障碍物的外观, 将采用路径规划中常用简化环境的方法——栅格法, 它不仅可以快速建立环境模型, 而且简化的障碍物对模型的影响很小. 该方法是将环境以矩阵的形式分割成若干矩形块, 障碍物所在区域为不可行区域, 所在的矩形块用黑色填充, 在矩阵中对应的值为1. 其余部分均为可行区域, 所在的矩形块用白色填充, 在矩阵中对应的值为0. 同时结合矩阵坐标系和序号法, 建立障碍物环境模型. 图1为20×20障碍物环境模型, 将坐标(1, 1)的序号定为0, 从左至右, 从下至上标号.

该序号具有唯一性, 可通过式(1)计算序号对应的坐标值, 其中${x^n}$表示序号$n$的横坐标, ${y^n}$表示序号$n$的纵坐标, ${G^x}$表示地图$G$的横坐标上限, ${G^y}$表示地图$G$的纵坐标上限, $\text{mod} ( \cdot )$表示取模运算, $fix( \cdot )$表示取整运算, 即四舍五入为最近的整数.

$ \left\{ \begin{gathered} {x^n} = \text{mod} \left( {n, {G^x}} \right) + 1 \\ {y^n} = fix\left(\dfrac{n}{{{G^y}}}\right) + 1 \\ \end{gathered} \right. $

(1)

1.2 优化问题的数学模型

移动机器人在进行路径规划任务时, 首先需要解决的问题是如何在避障的同时, 使路径最短和平稳度最佳. 将路径长度和平稳度作为优化目标, 路径长度即路径的长度, 平稳度使用角度改变量(平滑度)和转弯次数(拐点数)进行量化. 例如, $A$由$n$个序号$s$组成的一条路径, 即$A = \{ {s^1}, {s^2} ,\cdots, {s^n}\} $, 那么路径$A$的长度、平滑度和拐点数可用式(2)计算:

$ \left\{ {\begin{array}{*{20}{l}} {{L_A} = \displaystyle\sum\limits_{i = 2}^n {\left| {{s^i} - {s^{i - 1}}} \right|} } \\ {{E_A} = \displaystyle\sum\limits_{i = 3}^n e \left( {{s^i}, {s^{i - 1}}, {s^{i - 2}}} \right)} \\ {{P_A} = \displaystyle\sum\limits_{i = 3}^n p \left( {{s^i}, {s^{i - 1}}, {s^{i - 2}}} \right)} \end{array}} \right. $

(2)

其中, $L$表示路径$A$的长度, $E$表示平滑度, $P$表示拐点数, $e( \cdot )$是计算直线(sⁱ, s^i–1)与直线(s^i–1, s^i–2)组成的夹角, $p( \cdot )$是判断路径(sⁱ, s^i–1, s^i–2)是否存在拐点, 若存在, $p({s^i}, {s^{i - 1}}, {s^{i - 2}}) = 1$, 反之为0. 综上所述, 目标函数可用式(3)表示如下:

$ \left\{ {\begin{array}{*{20}{l}} {{\text{ min }}L = \displaystyle\sum\limits_{i = 2}^n {\left| {{s^i} - {s^{i - 1}}} \right|} } \\ {{\text{ min }}E = \displaystyle\sum\limits_{i = 3}^n e \left( {{s^i}, {s^{i - 1}}, {s^{i - 2}}} \right)} \\ {{\text{ min }}P = \displaystyle\sum\limits_{i = 3}^n p \left( {{s^i}, {s^{i - 1}}, {s^{i - 2}}} \right)} \end{array}} \right. $

(3)

2 RLAP-NSGA-Ⅱ 2.1 tanh-SBX算子

SBX算子是Deb等人^[11]提出的一种模拟单点二进制交叉的交叉算子, 该算子是主要针对解决实数编码方式在进行单点交叉时, 前后个体的基因信息差别较大, 无法体现出子代继承父代基因信息的特点. 例如, 当两个父代基因信息分别为${X^a}(x_1^a, \cdots , x_p^a, \cdots , x_n^a)$、${X^b} (x_1^b, \cdots , x_p^b, \cdots , x_n^b)$, 若交叉位点在p处, 通过单点交叉算子得到两个子代${X^c}(x_1^a, \cdots , x_p^b, \cdots , x_n^b)$、$ {X^d}(x_1^b, \cdots, x_p^a, \cdots, x_n^a) $, 由于编码方式为实数编码, 父代与子代相似度大幅减小, 导致子代与父代的适应度值变化过大, 并不是期待的结果. 为了使子代保留父代的部分基因信息, 父代可通过SBX算子得到子代${X^e}(x_1^e, \cdots, x_p^e, \cdots, x_n^e)$、${X^f}(x_1^f, \cdots, x_p^f, \cdots, x_n^f)$, 可根据式(4)计算得到:

$ \left\{ {\begin{array}{*{20}{l}} {x_i^e = 0.5 \times \left[ {(1 + \gamma ) \cdot x_i^a + (1 - \gamma ) \cdot x_i^b} \right]} \\ {x_i^f = 0.5 \times \left[ {(1 - \gamma ) \cdot x_i^a + (1 + \gamma ) \cdot x_i^b} \right]} \end{array}} \right. $

(4)

其中, $\gamma $是根据交叉分布指数$\eta $依据式(5)随机生成得到:

$ \gamma = \left\{ \begin{gathered} {(2\lambda )^{^{\frac{1}{{1 + \eta }}}}},\qquad\; \lambda < 0.5 \\ {\left(\frac{1}{{2 - 2\lambda }}\right)^{^{\frac{1}{{1 + \eta }}}}},\;\; {\mathrm{else}} \\ \end{gathered} \right. $

(5)

交叉分布指数$\eta $是用户定义的参数, $\eta $值越大则产生子代与父代相似度越高, 子代能保留部分父代基因信息, $\eta $值越小则产生子代与父代的差距越大, 建议$\eta = 20$, 可使算子达到较好的效果. SBX算子在局部优化搜索上表现较佳, 同时也容易陷入局部最优, 由于$\eta $值是人为设置的固定参数, 当种群搜索至局部最优区域时, 为了保留父代基因信息, 生成子代均与局部最优点高度相似, 从而无法摆脱局部最优. 文献[12]指出让交叉分布指数$\eta $动态变化, 可使算法得到更优的解, 因此本文将设计一种具备自适应能力的tanh-SBX算子, 使种群在面临局部最优时能有一定能力跳出局部最优.

为了使算子具备跳出局部最优的能力, 首先需要解决两个核心问题: 第一, 如何识别是否陷入局部最优. 第二, 陷入局部最优时, 如何跳出局部最优. 针对上述问题, 有两种解决思路: 第一, 可根据当代种群与上一代种群的目标函数值在迭代的过程中是否变化极小, 并且与全局最优解仍有较大差距判断是否陷入局部最优, 当陷入局部最优时, 可将交叉分布指数$\eta $设置一个较小的数, 使种群尽可能生成多样性较高且保留较少局部最优解基因信息的子代, 从而跳出局部最优. 第二, 由于局部最优的目标空间距离全局最优的目标空间较远, 初始种群与全局最优的目标空间也具有较远的距离, 因此在算法的迭代前期应该快速锁定全局最优的大致方位, 并朝向全局最优方向逼近, 即迭代前期尽可能生成多样性较高的子代, 去搜索全局最优的大致方位, 而不是不断保留父代的部分基因信息去局部搜索, 不仅花费过多的计算资源, 搜索效率也会大大降低; 迭代中期种群易陷入局部最优的原因是算子的局部搜索能力太强, 子代与父代差距较小且多样性较差, 无法跨越局部最优区域, 可将交叉分布指数$\eta $设置为一个较小的值削弱局部搜索能力, 提高子代的多样性; 迭代后期种群应该收敛至全局最优区域, 此时算法的收敛性依赖于全局最优区域的局部搜索能力, 为了提高收敛速度, 可将交叉分布指数$\eta $设置为一个较大的值, 增强局部搜索能力, 不断逼近全局最优. 综上所述, 可根据种群的迭代过程动态调整交叉分布指数$\eta $实现算法在不同阶段的搜索任务.

对于第1个解决思路, 需要已知全局最优的信息, 同时在搜索过程中消耗过多计算资源, 影响搜索效率. 因此采用第2个解决思路, 为了使算法更好地完成不同阶段的搜索任务, 交叉分布指数$\eta $将根据式(6)计算得到:

$ \eta (n) = \frac{{\theta (\exp (n) - \exp ( - n))}}{{2(\exp (n) + \exp ( - n))}} + \frac{\theta }{2} $

(6)

式(6)是由tanh函数改进而来, 保留了tanh函数的饱和性, 其中$\theta $是由用户定义的交叉分布指数$\eta $的上界值$(0 < \eta < \theta )$, 定义域$n \in ( - m, + m)$. 为了使tanh函数正常工作, 需要将种群的代数$N$根据式(7)映射到tanh函数的定义域中:

$ n = \frac{N}{{{N_{\max }}}} \times 2m $

(7)

其中, ${N_{\max }}$表示最大迭代次数, $m$是根据用户需求设置定义域范围, 由于$\eta $值的微小变化对算法搜索效率影响不大, 因此$m$值没必要取的过大, 同时必须要覆盖$\eta $值的上下界, 建议设置$m = 5$.

2.2 SARSA算子

优化算子不仅主导着算法的优化方向, 而且决定着结果的质量, 因此大部分学者通过改进算子改善算法的性能, 文献[13]提出的一种自适应交叉变异算子, 通过自适应调节交叉概率和变异概率确保优质解的保存和对劣质解的破坏. 文献[14]利用指数函数对传统遗传算法的交叉、变异算子自调整公式进行改进, 使自适应策略更加符合实际情况, 同时能够避免算法陷入局部最优解. 文献[15]改进传统遗传算法的选择、交叉、变异算子, 采用分层法对种群个体进行选择操作, 采用单点交叉法对种群个体进行交叉操作, 采用八邻域单点变异法对变异算子种群个体进行变异操作, 提高了算法的收敛速度. 上述改进方法弥补了传统算法的一些缺陷, 但鲁棒性较弱, 原因在于算子缺乏自主学习能力, 因此引入了SARSA算子. 在强化学习算法中, SARSA算法是一种使用时序差分求解强化学习控制问题的方法, 该算法一直使用同一个策略$\pi $更新价值函数和选择新的动作. 该算法的名称是由${\mathrm{S, \;A, \;R, \;S,\; A}}$几个字母组成, 其中${\mathrm{S}}$代表状态(state), ${\mathrm{A}}$代表动作(action), ${\mathrm{R}}$代表奖励(reward), 在迭代过程中, 该算法严格按照策略$\pi $选择两个动作, 但只执行第1个动作$A$, 通过第3个动作$A'$更新价值函数, 更新规则表示为式(8):

$ q(s, a) = q(s, a) + \alpha \left[ {r + \gamma q\left( {s', a'} \right) - q(s, a)} \right] $

(8)

其中, $\alpha $表示学习率, $\gamma $表示折扣因子.

策略: 在遗传算法中, 将策略$\pi (a|s)$表示为个体$s$采取交叉动作$a$后, 根据子代的排序等级确定动作$a$被选中的概率, 具体表示为式(9):

$ \pi (a|s)=\left\{ {\begin{array}{*{20}{l}} {1 - \varepsilon + \dfrac{\varepsilon }{{|A(s)|}}, \;a = \arg {{\max }_a}{rank} \left( {{X_j}, a} \right)} \\ {\dfrac{\varepsilon }{{|A(s)|}}, \qquad\;\;\;\;\;a \ne \arg {{\max }_a}{rank} \left( {{X_j}, a} \right)} \end{array}} \right. $

(9)

种群初始化后, 将$\varepsilon $贪心策略与初始种群(环境)进行交互, 得到初始策略.

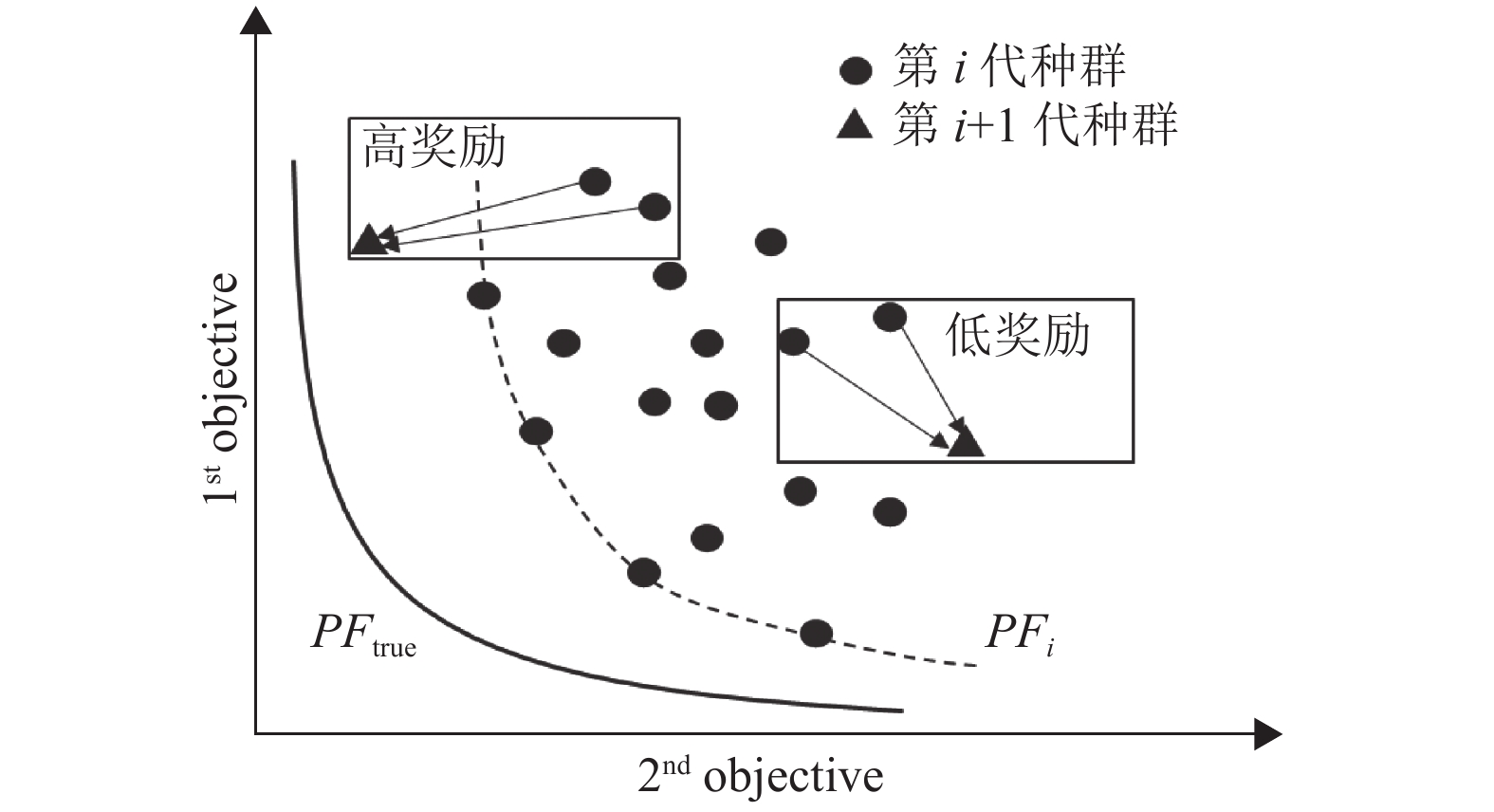
奖励机制: 在强化学习中, 除了策略以外, 还需要引入一些必不可少的概念, 强化学习的核心在于如何进行奖励, 合理的奖励机制会引导种群的交叉方向, 促进种群生成优良子代.

在遗传算法优化任务中, 采用$\varepsilon $贪心策略后, 假设父代${S_i}\;(i = 1, 2, \cdots, m)$随机选定母代${S_r}$ (r = randperm(m))进行交叉, 选择的交叉位点(动作) ${A_j}\;(j = 1, 2, 3, \cdots, n)$不同, 将会产生不同的子代${X_j}\;(j = 1, 2, 3, \cdots, n)$, 其中$n$为个体基因段个数, 如图2所示,计算子代${X_j}$在种群中的排序等级$rank({X_j})$来确定该交叉动作${A_j}$的奖励${R_j}$, 其中${X_{{\mathrm{merge}}}} = {X_j} \cup {X_{rank = 1}}$, ${X_{rank = 1}}$表示种群中的非支配解. 遗传算法的优化过程是可行解逐渐逼近理论${\mathrm{pareto}}$前沿$ (P{F_{{\mathrm{true}}}}) $的过程, 因此只需要让可行解集不断向理论${\mathrm{pareto}}$前沿的方向进化即可, 交叉动作得到排序等级高的子代, 奖励${R_j}$理应更大(见图3).

因此将$1/rank({X_j})$作为交叉动作${A_j}$的奖励, 可表示为式(10):

$ \left\{ {\begin{array}{*{20}{l}} {rank({X_j}) = g({X_j}, {X_{{\mathrm{merge}}}})} \\ {{R_j} = \dfrac{1}{{rank({X_j})}}} \end{array}} \right. $

(10)

其中, $g( \cdot )$表示执行非支配算法的函数.

回报: 当智能体采用策略$\pi $确定第2个动作$a'$后, 可根据式(11)计算回报的估计值.

$ U = R + \gamma q(s', a') $

(11)

其中, $\gamma $表示折扣因子.

动作价值函数: 通过式(11)计算回报的估计值更新动作价值, 可用式(12)表示如下:

$ q(s, a) = q(s, a) + \alpha [U - q(s, a)] $

(12)

其中, $\alpha $表示学习率, 通过动作价值函数量化策略引导种群的优化效果, 学习率$\alpha $可以缩小动作价值和实际回报之间的差距, 不断更新策略, 始终选择更优的策略引导种群迭代, 确保种群优化方向的准确性. 综上所述, SARSA算子的伪代码如算法1所示.

算法1. SARSA算子伪代码

输入: 迭代次数$\scriptstyle T$, 状态集(种群基因) $\scriptstyle S$, 动作集$\scriptstyle A$, 学习率$\scriptstyle \alpha $, 折扣因子$\scriptstyle \gamma $, 探索率ϵ.

输出: 最优策略$\scriptstyle \pi (a|s)$和最优动作价值函数$\scriptstyle q(s, a)$.

(1) 随机初始化动作价值$\scriptstyle q(s, a)$, 终止状态的$\scriptstyle q$值初始化为0.

(2) for i = 1:T

1) 初始化个体$\scriptstyle s$作为当前状态序列的第1个状态, 根据策略$\scriptstyle \pi $确定动作$\scriptstyle a$.

2) if $\scriptstyle s' \ne {s_{{\mathrm{end}}}}$

① 执行动作$\scriptstyle a$, 得到奖励$\scriptstyle R$和新种群$\scriptstyle s'$

② 采用策略$\scriptstyle \pi $确定动作$\scriptstyle a'$

③ 计算回报的估计值$\scriptstyle U = R + \gamma q\left( {s', a'} \right)$

④ 更新动作价值函数$\scriptstyle q(s, a) = q(s, a) + \alpha [U - q(s, a)]$

⑤ 根据$\scriptstyle q(s, a)$修改策略$\scriptstyle \pi (a|s)$的ϵ值

⑥ $\scriptstyle s = s'$, $\scriptstyle a = a'$

3) else 转到步骤②

2.3 SA进化策略

启发式算法在求解问题的最优解时, 可以将算法的搜索行为分为: 探索与利用. 如何平衡探索与利用是应该解决的核心问题, 文献[16]表明在AGLDPSO中, 采用主从多亚种群分布模型, 将整个种群划分为多个亚种群, 这些亚种群共同进化, 最后实验证明与其他单种群进化或集中式机制的大规模优化算法相比, 多亚种群分布式协同进化机制将充分交换不同亚种群之间的进化信息, 进一步增强种群多样性. 受到该文献的启发, 将种群划分为两个子种群: 精英种群和非精英种群, 并设计了4种策略, 最后通过模拟退火算法的Metropolis准则更新概率.

在每个迭代步骤中, 根据Metropolis准则计算更新策略的概率, 根据衰减函数来调整Metropolis准则中的温度参数, 以使概率随着时间的推移而逐渐降低. 最终, 更新策略的概率趋于零, 使得搜索过程逐渐趋于稳定, 伪代码如算法2.

算法2. SA进化策略伪代码

输入: 策略集$\scriptstyle M$, 初始种群$\scriptstyle pop$, 初始温度$\scriptstyle {T_0}$, 终止温度$\scriptstyle {T_f}$, 降温速度$\scriptstyle K \in (0, 1)$.

输出: 当前种群$\scriptstyle pop'$.

(1) 令$\scriptstyle T = {T_0}$, 任取初始策略$\scriptstyle {m_1}$

(2) if $\scriptstyle T > {T_f}$, 对当前温度$\scriptstyle T$, 执行以下步骤:

1) 采用当前的策略$\scriptstyle {m_1}$进化种群$\scriptstyle pop$, 根据精英率$\scriptstyle {r_1}$评估当前策略的优劣, $\scriptstyle r = {{{N_{{\mathrm{elite}}}}} / {{N_{pop}}}}$, 其中$\scriptstyle {N_{{\mathrm{elite}}}}$为精英个体数量, $\scriptstyle {N_{pop}}$为总个体数量.

2) 对当前策略进行随机扰动, 得到另一个策略$\scriptstyle {m_2}$

3) 根据$\scriptstyle {m_2}$策略进化种群, 计算精英率$\scriptstyle {r_2}$

4) 计算精英率的增量$\scriptstyle {\mathrm{d}}r = {r_2} - {r_1}$

5) 根据Metropolis准则进行判断, if $\scriptstyle {\mathrm{d}}r > 0$

　接受策略$\scriptstyle {m_2}$作为新的当前策略, $\scriptstyle {m_1} = {m_2}$.

6) else

① 计算$\scriptstyle {m_2}$接受的概率$\scriptstyle p = \exp ( - {{{\mathrm{d}}r} / T})$

② if $\scriptstyle \exp ( - {{{\mathrm{d}}r} \mathord{\left/ {\vphantom {{dr} T}} \right. } T}) > rand(0, 1)$, 接受策略$\scriptstyle {m_2}$, $\scriptstyle {m_1} = {m_2} $.

③ else保留策略$\scriptstyle {m_1}$

④ 根据策略$\scriptstyle {m_1}$进化种群$\scriptstyle pop$, 得到子代种群$\scriptstyle pop'$

7) 根据衰减函数进行降温: $\scriptstyle T = T \times K$, 转到步骤(2)

(3) else输出当前种群

全局探索策略${m_1}$: 全局探索策略旨在探索全局空间, 让种群在有限的迭代次数中尽可能逼近全局最优区域. 由于传统全局搜索算子的效率十分缓慢, 将采用SARSA算子解决这个问题. SARSA算子是一个在全局搜索的效率和范围上进行折中的全局搜索算子. 该算子对精英种群和非精英种群的基因信息进行学习, 得到一个最优策略以指导种群的搜索方向, 减少无效搜索, 为了尽可能使搜索范围覆盖全局, 策略初始定义为柔性策略.

潜力挖掘策略${m_2}$: 潜力挖掘策略是针对非精英种群设计的, 旨在将普通个体的转化为精英个体, 从而扩充精英种群的数量. 非精英种群和精英种群均是由整个种群中划分而来, 对于全局空间而言, 它们处于同一个或相邻的局部子空间, 基因信息具有一定的联系, 因此使用局部搜索算子可以充分挖掘普通个体之间的基因信息, 使其转化为精英个体. tanh-SBX算子作为该策略的局部搜索算子.

加速收敛策略${m_3}$: 精英种群占比不断快速提升, 并占据主导地位, 非精英种群数量越来越少, tanh-SBX算子逐渐失去效用. 精英种群通过SARSA算子逼近全局最优的效率较低, 这是因为SARSA算子的搜索范围和步长较大, 只能在全局最优附近振荡, 无法快速逼近全局最优, 因此通过tanh-SBX算子在全局最优区域进行局部搜索, 使种群快速逼近全局最优, 加快算法的收敛速度.

脱离局部最优策略${m_4}$: 加速收敛策略结束后, 种群有两种状态: 陷入局部最优和无限逼近全局最优. 针对第1种状态, 本文设计了脱离局部最优策略, 该策略是使非精英种群通过SARSA算子增加非精英种群的多样性, 让非精英种群尽可能地找到全局最优解空间, 最后通过tanh-SBX算子在全局最优区域内局部搜索, 带领种群无限逼近全局最优.

在算法的迭代前期, 初始解集随机分散于解空间的任意位置, 需要确定全局最优解的大致方向, 由于初始解空间过大, 需要消耗大量的计算资源和时间成本, 因此采用全局探索策略, 而SARSA算子是针对该问题被设计而来的. 采用全局探索策略之后, 精英个体会缓慢增加, 此时将会采用潜力挖掘策略, 是为了提高非精英个体转化为精英个体的效率, 精英种群占据主导地位之后, 此时将会出现两种情况, 第1种是处于全局最优解附近. 第2种是处于局部最优解附近. 针对这两种情况, 采用两种策略去应对, 第1种情况会采用加速收敛策略, 快速逼近全局最优解, 得到优化结果; 第2种情况会采用脱离局部最优策略, 让非精英种群尽可能地找到全局最优解空间, 脱离局部最优.

图4是RLAP-NSGA-II的流程图, 其中策略集$ M = \{ {m_i}|i = 1, 2, 3, 4\} $, 上述4种策略均是以图5的流程作为基础框架, 不同之处在于交叉的对象不同和交叉算子不同, 其他设置均与文献[17]保持一致.

2.4 编码方式

根据第2节建立的数学模型可知, 一段序号可以表示一条路径, 例如, $A$由$n$个序号$s$组成的一条路径, 即$ A = \{ {s^1}, {s^2}, \cdots, {s^n}\} $. 由于该编码方式高效简洁, 在进行交叉和变异算子时更容易操作, 将地图环境与种群基因建立联系, SARSA算子可直接通过种群基因与地图环境进行交互, 因此采用该编码方式表示路径.

2.5 避障处理

首先, 对环境中的障碍物进行静态建模和识别, 然后, 将这些障碍物的信息存储在地图中, 最后, 在地图的可行区域随机生成若干条初始路径, 在遗传操作生成新路径时, 还需对路径进行碰撞检测, 判断路径是否与障碍物相交, 如果存在碰撞, 则对路径进行变异操作生成新路径.

2.6 适应度值

适应度值是衡量个体在适应度函数下的优劣程度的指标. 适应度函数的设计应该基于问题的特性和目标, 以便使得算法能够在合理的时间内找到最优解或次优解, 因此将适应度值与优化目标建立数学关系, 如式(13)所示:

$ F = \frac{1}{L} + \frac{1}{E} + \frac{1}{P} $

(13)

其中, L、E和P可根据式(2)计算.

2.7 算法理论性分析

算法的理论性分析将从3个方面进行: 收敛速度、收敛精度和时间复杂度.

算法的收敛速度和收敛精度与每次迭代的更新步长有直接关系, 当算法处于探索状态时, 如果算法的更新步长过小, 那么需要更多的迭代次数才能接近最优解. 这一阶段采用具有全局搜索能力的SARSA算子, 通过学习率$\alpha $更新策略的参数, 实际上就是通过学习率$\alpha $逐渐加大了父代与子代的差距, 让每次迭代的更新步长逐渐增加, 算法可能会更快地接近最优解, 那么算法的收敛速度更快. 当算法处于利用状态时, 过大的更新步长会导致算法始终在最优解附近振荡, 此时全局探索策略无法完成优化任务, 通过模拟退火算法更新优化策略, 选择更新步长较小的优化策略达到逼近最优解的目的. 这一阶段采用具有局部搜索能力的tanh-SBX算子, 将迭代次数通过tanh函数引入到计算交叉分布指数$\eta $的公式中, 通过迭代次数的线性增长实现交叉分布指数$\eta $的非线性增长, $\eta $值越大, 更新步长越小, 越接近最优解, 那么算法的收敛精度越高.

RLAP-NSGA-II的时间复杂度由以下部分组成: 非支配排序和SARSA算子. 假如待优化目标为$M$个, 种群规模为$N$, 在开始非支配排序时, 每个个体的${n_p} = 0$, ${S_p} = \varnothing $. 在第1轮排序后, 每个个体$p$会记录${n_p}$和${S_p}$, 故第1轮时间复杂度为${\mathrm{O}}(M{N^2})$, 在后续的排序中, 只需要对上一轮排序的非支配解集取一个个体$p$, 在$p$的${S_p}$中取出个体$q$, 此时${n_q} = {n_q} - 1$, 若${n_q}$为0, 则个体$q$进入下一轮排序的非支配解集. 若每轮都只有一个个体被选出, 每次需要花费${\mathrm{O}}(N)$, 所以非支配排序的时间复杂度为${\mathrm{O}}(M{N^2})$. 假如SARSA算子需要训练$N$次收敛, 每次训练的时间步数量为$M$, 可根据算法1计算出SARSA算子的时间复杂度:

$ \begin{split} T(episode, t) =& {t_1} + ({t_2} + {t_{2.1}} + ({t_{2.2}} + {t_{2.2.1}} + {t_{2.2.2}} \\ & +{t_{2.2.3}} + {t_{2.2.4}} + {t_{2.2.5}} + {t_{2.2.6}}) \times M) \times N \\ =& {t_1} + ({t_{a1}} + {t_{a2}} \times M) \times N \\ =& {t_1} + {t_{a1}} \times N + {t_{a2}} \times M \times N \\ =& {t_{a2}} \times M \times N \\ = &M \times N \end{split} $

(14)

其中, ${t_1}$表示算法1步骤(1)所花费的时间, 当训练次数和时间步数量足够大时, ${t_1}$、${t_{a1}}$和${t_{a2}}$对$M$和$N$的影响很小, 因为$M \times N$的增长速度明显快于$N$, 所以函数$T$的主要影响因素是$M \times N$, SARSA算子的时间复杂度为${\mathrm{O}}(MN)$. 综上所述, RLAP-NSGA-II的时间复杂度为$ {\mathrm{O}}(M{N^2}) $.

3 实验结果和性能分析

实验平台的计算机操作系统是Windows 10 (64位), 仿真实验将在AMD-RYZEN7-5800H CPU @ 3.2 GHz的环境下进行. 本文从以下几个方面进行分析: 1)不同环境下路径规划的仿真与对比分析. 2) RLAP-NSGA-II的多样性分析.

3.1 不同环境下路径规划的对比分析

环境的复杂性主要由环境中障碍物的比例和密度来定义, 分为简单环境和复杂环境. 在简单环境中障碍物的比例和密度比在复杂环境中要小. 在本节中, 为了验证RLAP-NSGA-II的性能, 将采用2张不同障碍覆盖率的地图环境与NSGA-II、Q-learning^[18]和IACO^[19]进行对比实验, 地图分别为障碍覆盖率为13.5%的简单环境和障碍覆盖率为34.5%的复杂环境如图6.

3.2 简单环境下的路径规划对比实验

在20×20的简单环境下, RLAP-NSGA-II、NSGA-II、Q-learning和IACO的路径规划结果由图7可知, RLAP-NSGA-II的拐点数为5个, 且路径角度变化较小, 均小于90°; NSGA-II的拐点数也为5个, 整体路径和前者十分相似; Q-learning的拐点数有8个, 路径存在一些不必要的拐点; IACO的拐点数有6个, 其中有两处直角拐弯. 为了更直观地比较算法之间的性能, 计算了路径长度和平滑度(见表1), 从表1数据可知, RLAP-NSGA-II的路径长度和平滑度均优于IACO和Q-learning, 与NSGA-II的性能持平. 同时为了避免实验结果的偶然性, 将RLAP-NSGA-II、NSGA-II、Q-learning和IACO这4种算法在简单环境下进行15次独立实验, 仿真结果见表2可知, RLAP-NSGA-II和NSGA-II均能收敛至全局最优解, 而Q-learning和IACO容易陷入局部最优解, 且无法跳出, RLAP-NSGA-II与NSGA-II相比, 前者收敛至最优解所需的迭代次数更小, 图8也更好的验证了这一结论.

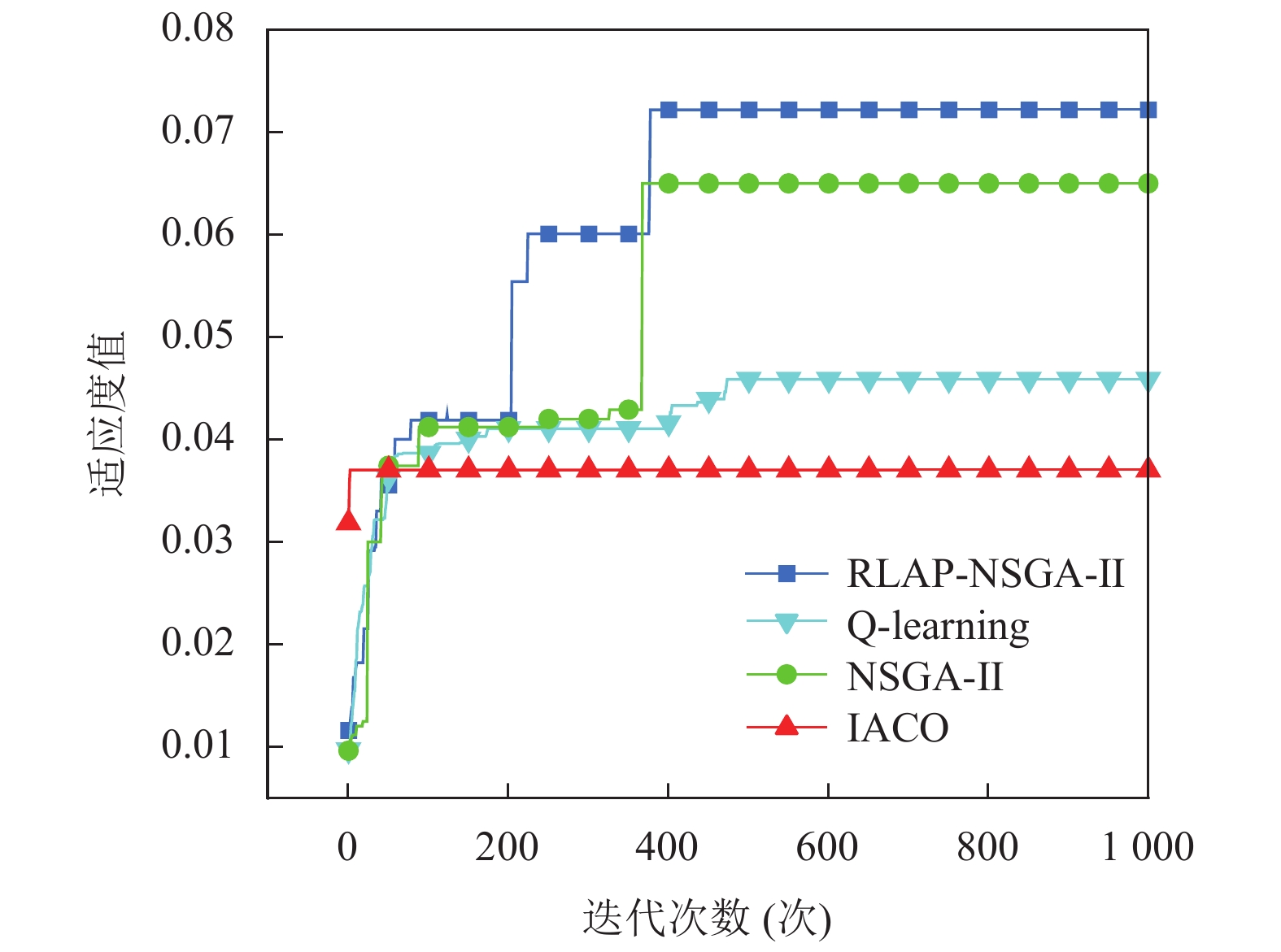
3.3 复杂环境下的路径规划对比实验

在20×20的复杂环境下, RLAP-NSGA-II、NSGA-II、Q-learning和IACO的路径规划结果由图9可知, RLAP-NSGA-II有8个拐点, 均为小角度拐弯; NSGA-II有10个拐点, 与前者相比路径更曲折; Q-learning有19个拐点, 路径存在较多的小角度拐弯, 导致整体路径不平滑; IACO有8个拐点, 且路径出现较多直角拐弯. 从表3的数据可知, 在路径长度方面, RLAP-NSGA-II优于Q-learning和IACO, 但略输于NSGA-II; 在路径平滑度方面, RLAP-NSGA-II均优于其余的算法. 同时为了避免实验结果的偶然性, 将RLAP-NSGA-II、NSGA-II、Q-learning和IACO这4种算法在复杂环境下进行15次独立实验, 仿真结果见表4可知, RLAP-NSGA-II的最佳适应度值均优于NSGA-II、Q-learning和IACO, 与NSGA-II相比, RLAP-NSGA-II完全收敛所需的平均迭代次数更小, 且更加稳定. 值得注意的是, 仔细观察可发现RLAP-NSGA-II与NSGA-II的路径较为相似, 区别在于躲避第1个障碍物(左下3×2长方形)的选择不同, 前者牺牲了路径长度, 选择道路更为宽阔的路径空间, 避免更多的拐弯, 在路径长度与平滑度之间做了更好的妥协, 后者则更趋向于路径长度, 但增加了两个拐点, 因此在实际应用中, 前者的路径更可能被决策者选择. 总体来说, RLAP-NSGA-II在路径长度、平滑度和拐点个数上均优于Q-learning和IACO, 在处理路径长度与平滑度这对矛盾上, RLAP-NSGA-II能找到更好的妥协方案, 图10也正好验证了上述结论, 在0–100代期间, RLAP-NSGA-II不断更新最优路径, 与NSGA-II相比, 在相同的迭代次数中, RLAP-NSGA-II的适应度值大部分高于NSGA-II. 在100–300代期间, NSGA-II最优路径的适应度值变化不明显, 可能陷入局部最优, 而RLAP-NSGA-II在200代左右适应度值发生明显变化, 脱离局部最优, 且适应度值始终高于NSGA-II. 在300–1000代期间, NSGA-II和RLAP-NSGA-II均在400代左右适应度值发生明显变化, 但RLAP-NSGA-II的适应度值更高, 在路径长度与平稳度之间做了更好的妥协. 与RLAP-NSGA-II相比, Q-learning和IACO在迭代过程中均陷入局部最优且无法跳出, 无法较好地平衡路径长度和平稳度, 虽然Q-learning在迭代中后期, 适应度值发生略微提升, 但适应度值仍然较低. 综上所述, 在算法收敛后, RLAP-NSGA-II的适应度值高于NSGA-II和IACO, 因此RLAP-NSGA-II平衡路径长度和平稳度的能力更强.

3.4 不同算法的多样性分析

本节是比较不同算法之间解的多样性, 以路径规划为例, 由于复杂地图的可行解数量较少, 导致解的搜索空间较小和多样性较低, 很难体现出算法之间的差异, 因此选择简单地图进行实验, Q-learning算法不适用多样性分析, 不参与该分析实验. 本文采用Deb等人^[17]设计的只衡量分布性的多样性指标∆和Miao等人^[20]提出的多样性指标DIV, ∆值越小代表算法获得最优解集的分布性越好, 当DIV值处于波动状态时说明算法搜索最优解能力较强. 实验结果如图11、图12, 在迭代前期, 算法全局搜索可行解, 此时搜索空间较大, ∆值和DIV值均会大幅波动. 从图11可知, RLAP-NSGA-II在130代左右∆值趋近于0, 且后续迭代过程中∆值保持不变, 而NSGA-II和IACO在400代之后, ∆值才逐渐稳定趋近于0.

从图12可知, 在200代之后, NSGA-II的DIV值保持不变, 说明该算法处于停滞状态, 种群的多样性较差, 容易陷入局部最优, 而RLAP-NSGA-II的DIV值在区间内依然保持小幅波动且大于0, 说明算法依然在搜索新解, 搜索最优解能力较强, 不易陷入局部最优. 值得注意的是, 在迭代过程中IACO的DIV值一直处于大幅波动状态, 即使是在迭代后期种群的多样性依然有较大的变化, 说明算法一直在搜索新解, 但搜索的效率过低.

4 结 论

本文设计了一种融合强化学习的多目标路径规划算法(RLAP-NSGA-II), 来弥补智能仿生算法在路径规划中的一些不足. 与其他算法不同的是该算法采用SARSA算子提高了算法在前期全局搜索的效率, 通过tanh-SBX算子加快了后期的收敛速度, 将种群划分为性质不同的子种群保持了种群多样性, 为了平衡算法探索与利用的效率问题, 设计了4种不同性质的进化策略, 通过模拟退火算法的Metropolis准则计算更新策略的概率, 使算法始终保持最适合的策略进行优化, 并有一定概率接受较差的策略, 随着时间的增加, 接受较差策略的概率趋于零, 算法的搜索过程逐渐稳定. 最后对Q-learning、IACO、NSGA-II和RLAP-NSGA-II进行不同环境地图的路径规划对比实验, 实验结果验证了, RLAP-NSGA-II在多目标路径规划问题上的有效性. 实验研究表明, 在更为复杂的环境地图中, RLAP-NSGA-II在处理路径长度与平稳度这对矛盾目标上, 能找到更好的妥协方案, 且在多种环境地图下均能找到近似最优解. 相比传统智能仿生算法, 在更加复杂的环境中, 所提出的算法能有效平衡优化目标, 找到更优的安全路径.

随着后续研究的深入, 将RLAP-NSGA-II应用于更加复杂的动态环境下的多目标路径规划, 以验证所提出算法的性能, 或结合最新的强化学习理论范式提升算法性能, 也是值得深入研究的方向之一.