目前, 随着网络通信技术的发展, 尤其是5G技术的逐渐普及, 相较于传统的文本信息, 图像因其包含内容广泛、生动易理解的特点, 已成为信息载体的主要形式. 图像被广泛应用于社交媒体网络、军事应用、交通检查、天气预报、医疗事业等各个领域, 覆盖了社会的方方面面. 这些图像中通常包含一些机密信息, 因此图像的安全问题引起了广大学者的广泛关注. 为了防止图像内容被非法窃取和利用, 数字图像加密技术成为当前保护图像数据最常用的方法.
研究之初, 图像加密技术主要针对单幅图像进行, 随着数据总量的爆炸式增长, 人们在网络中交流信息增多, 通常需要一次传输多张图片. 为了保护这些图像的安全, 可以重复使用单图像加密算法进行加密, 然而它们降低了加密效率[1]. 为了提高加密效率, 研究者们将研究重点从单图像加密转移到多图像加密. 在过去的几年里, 多图像加密算法发展于不同领域, 如光学[1–3]、变换域[4–6]、混沌[7]、混沌和DNA域[8,9]的组合, 研究者们提出了各种有效的多图像加密方法. 例如: 文献[10]提出了一种基于二维码密钥的光学方法, 在联合变换相关器(JTC)系统下对多幅图像进行加密. 文献[11]将多分辨率奇异值分解(MSVD)技术和Gyrator域变换相结合实现多图像加密. 文献[12]提出了一种基于三维置乱和超混沌系统的多图像加密算法. 文献[13]将DNA序列和元胞自动机(CA)相结合, 使多图像加密算法足够强大, 能够抵御图像加密的常见攻击. 随着时间的推移, 图像的加密技术日益发展. 研究者们发现如果仅使用单一的混沌系统, 图像的安全性有待提高[14]. 因此, 许多研究者设计将多种混沌系统应用到多图像加密算法中. 文献[15]设计了一种基于三维混沌映射的动态混沌库, 采用Haar小波变换和三维混洗置乱的方法实现多图像加密. 文献[16]提出了一种基于三维排列模型和混沌系统的多图像加密对称算法, 具有较高的安全性.
在前人工作的启发下, 针对多图像加密算法效率低、抗攻击性差等问题, 提出了一种基于离散小波变换和多混沌系统的多图像加密算法. 首先, 利用离散小波变换提取原始图像的低频子带, 达到压缩图像的效果, 有效减少待加密数据量, 提高加密效率; 其次, 通过混沌序列生成的矩阵对图像进行全局置乱, 打乱所有图像中像素点的位置; 最后, 通过混沌序列对图像进行双向扩散和行列置乱, 改变每一个像素值, 提高算法抵抗攻击的能力.
1 相关知识 1.1 logistic-sine-cosine映射将一维映射logistic映射和sine映射作为种子映射, 将他们与移位常数结合, 然后执行余弦变换以生成结果[17]. 组合运算可以有效地搅乱两个种子映射的混沌动力学, 余弦变换有复杂的非线性特征. 其表达式如式(1)所示:
| {xi+1=cos(π(F(r,xi)+G(1−r,xi)+β))F(r,xi)=4rxi(1−xi)G(1−r,xi)=(1−r)sin(πxi) | (1) |
其中,
超混沌Lorenz系统在Lorenz系统的基础上引入一个非线性控制器 w, 可以生成4个各不相同的混沌序列, 系统维度高, 结构复杂[18]. 它是一个发展成熟的混沌系统, 有助于提高加密方案的安全性能. 表达式如下:
| {.x=a(y−x)+w.y=cx−y−xz.z=xy−bz.w=−yz+rw | (2) |
其中,
离散小波变换的主要原理是将高频边缘细节信息舍弃, 提取低频分量得到原始图像的近似图[19]. 离散小波变换可将图像进行二维分解得到4个子带图像, 分别为低频分量(LL)、水平高频分量(LH)、垂直高频分量(HL)以及对角线高频分量(HH). 其中低频分量为图像内容的缩略图, 包含了原图中大部分内容信息, 剩余3个分量包含不同方向的高频边缘信息. 若还想对缩略图进行进一步压缩, 还可对其进行二级甚至多级分解, 最终得到与原始图像相似但能量更低的子图像. 如图1所示为离散小波变换的一级和二级分解图.
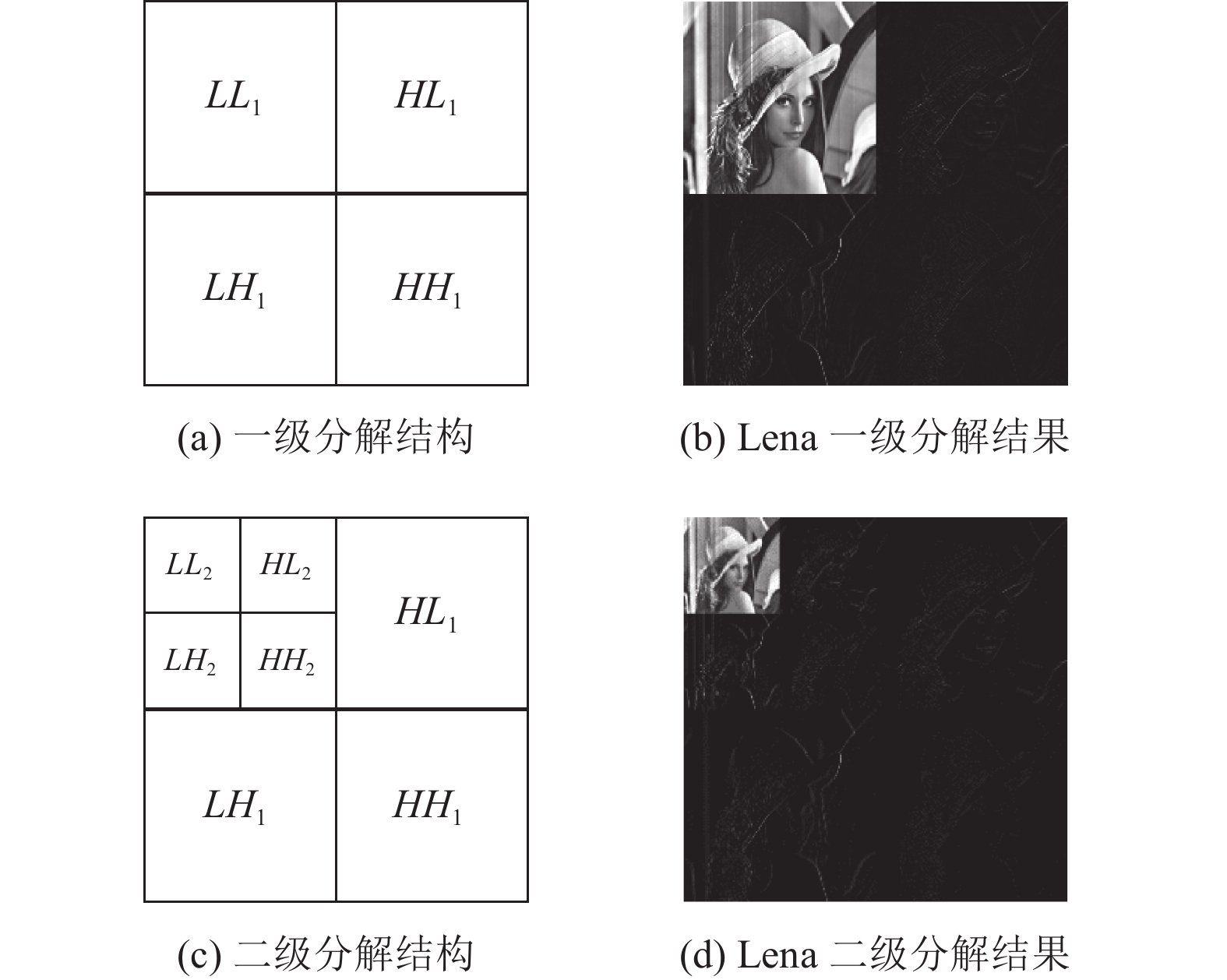
|
图 1 离散小波变换分解图 |
2 多图像加密算法
本文提出的算法主要包括以下几个步骤, 第1步, 对原始图像进行离散小波变换; 第2步, 运用LSC映射生成混沌序列, 进而生成矩阵O, 利用矩阵O对图像像素坐标位置进行置乱; 第3步, 运用超混沌Lorenz系统生成混沌序列对图像进行双向扩散, 从而提高图像数据信息的保密性; 第4步, 对经过扩散的图像进行行列置乱, 获得最终的密文图像. 这一步骤是加密过程的最后一步, 它有助于进一步混淆原始图像. 算法的加密流程图如图2所示.

|
图 2 加密流程图 |
2.1 图像预处理
步骤1. 使用离散小波变换函数分别对
| [CAk,CHk,CVk,CDk]=dwt2(Ik,‘db1') | (3) |
其中,
步骤2. 通过对每幅图像进行步骤1的操作, 得到
步骤3. 将
密钥决定了LSC映射的初始状态, 长度设置为256位. 图3显示了安全密钥的结构. 可以观察到, 它由6个部分组成. 其中
| FN=48∑i=1Bini×2−i | (4) |
系数
| IN=32∑i=1Bini×2i−1 | (5) |
此后, 加密的初始状态可以使用如下公式计算:
| {x0=f1×(x0+H1)mod1p=f2×(p+H2)mod1 | (6) |
其中,
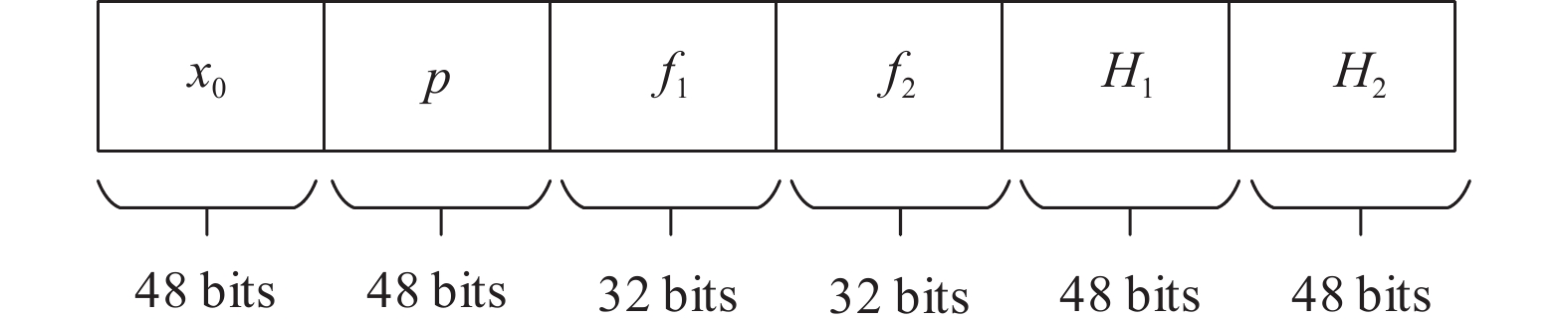
|
图 3 LSC映射的密钥结构图 |
2.3 置乱算法
本文采用具有初始状态
步骤1. 将初始状态
步骤2. 分别对序列
步骤3. 初始化大小为
步骤4. 使用
步骤5. 初始化列索引
步骤6. 找到明文图像P中位置为
步骤7. 将这些像素看成连接在一起的一个串, 并将它们向上移动
步骤8. 对于
如图4所示, 为了更好地演示置乱过程, 我们以一个4×4大小的明文图像作为示例来进行说明. 由于矩阵O的第1列是

|
图 4 置乱示意图 |
2.4 混沌序列的产生
在我们的方案中, 混沌系统初始值的生成过程与用户随机输入的整数和明文图像的像素值有关, 详细过程描述如下.
步骤1. 由用户随机输入一个整数
步骤2. 将图像P的像素的所有灰度值相加, 求和后记为
步骤3. 将
步骤4. 将
步骤5. 式(2)中给出的超混沌Lorenz系统的初始条件
| {Qx0=(mod(fix(k1/100),40))+(k1/1014−fix(k1/1014))Qy0=(mod(fix(k2/100),40))+(k2/1014−fix(k2/1014))Qz0=(mod(fix(k3/106),80))+(k3/1014−fix(k3/1014))Qw0=(mod(fix(k4/106),80))+(k4/1014−fix(k4/1014)) | (7) |
其中,
步骤6. 在初始条件
| {E=mod(fix(ei×105),256)G=mod(fix(gi×105),256)U=mod(fix((ui+100)×1010),256)+1V=mod(fix((vi+100)×1010),256)+1 | (8) |
其中,
为了加强算法的安全性, 本文对置乱后的图像进行双向扩散处理, 目的在于让图像的每一个像素都发生变化, 从而使得图像中的信息难以被外部攻击者读取. 具体的扩散步骤如下.
步骤1. 将置乱后图像的像素值按列优先转化成长度为
| di′=((di+d′i−1)mod256)⊕ei | (9) |
其中,
步骤2. 利用序列
| li=((d′i+li+1)mod256)⊕gi | (10) |
将得到的一维序列
本文采用行列置乱进一步扰乱图像像素的位置, 增强加密算法的随机性和安全性, 得到最终密文图像C. 具体步骤如下.
步骤1. 利用序列
步骤2. 对经过行移位处理后的像素矩阵, 利用序列
加密算法和解密算法使用的密钥相同, 故解密过程是加密过程的逆运算. 对于密文图像, 首先输入超混沌Lorenz系统的初始值, 生成四维混沌序列, 利用混沌序列先将其进行逆行列置乱, 然后再将其拉伸为一维序列; 利用逆向扩散的初始值解除逆向扩散, 利用正向扩散的初始值解除正向扩散, 将一维序列还原为二维矩阵; 接着输入LSC映射的密钥, 迭代式(1), 获得一维序列; 运用第2.3节中的方法结合一维序列生成用于置乱的矩阵O, 从而恢复出像素位置置乱前的矩阵, 解除像素灰度值的位置变换, 恢复出组合图像P. 最后, 对组合图像按合并关系进行分割得到原始图像的近似内容, 解密过程结束.
4 实验结果及安全性分析为了验证所提算法的可行性和有效性, 采用Matlab 2020a 进行仿真测试, 实验的主机环境是Intel Core i7-7500U的CPU, 8 GB的机带RAM, 2.90 GHz的处理器, 以及64位Windows 10操作系统.
4.1 加解密结果图选取图像Lena、Elaine、Cameraman、Baboon作为测试图像, 其均为源自CVG-UGR (computer vision group, University of Granada)数据库大小为256×256的灰度图像, 如图5(a)–图5(d)所示. Lena是一种标准的测试图像, 广泛应用于图像加密领域. 图5(e)为密文图像, 图5(f)–图5(i)为解密结果. 密文图像形态类似于噪声, 其不再包含明文图像中的相关信息. 由于通过解密算法得到的是原始图像的低频子带, 即明文图像的近似内容, 故解密结果与原始图像不完全一致, 但其结果不影响接收方正确接收传输内容.

|
图 5 加解密仿真结果图 |
4.2 直方图
图6为明文图像和密文图像的像素值直方图, 可以直观地看到它们的像素值分布情况. 其中加密后图像的直方图分布非常接近均匀分布, 即攻击者无法通过对密文图像的直方图统计获得明文图像的直方图信息, 说明我们提出的算法具有很好的扩散性和抵抗统计攻击的能力.
4.3 相邻像素相关性明文图像通常具有很强的相邻像素相关性, 一个好的图像加密算法需要具备有效地减弱像素值相关性的能力[20]. 当相关系数的绝对值接近于1时说明两者高度相关, 反之相关系数的绝对值越接近于0时, 说明两者的相关性越弱. 计算相关系数的公式如下:
| rxy=cov(x,y)√D(x)√D(y) | (11) |
| cov(x,y)=1NN∑i=1(xi−E(x))(yi−E(y)) | (12) |
| E(x)=1NN∑i=1xi | (13) |
| D(x)=1NN∑i=1(xi−E(x))2 | (14) |
其中,
信息熵是衡量图像信息随机性的重要标准, 表2所示为本文方法与其他文献信息熵的对比结果. 当密文图像的信息熵越接近于8时, 说明图像的混乱程度越高, 加密效果越好. 从表2中可以看出, 加密后本文方法的信息熵非常接近理想值8, 说明本文算法基本可以满足抵抗熵攻击的性能. 同时也可以看出本文方法的信息熵比文献[22]略高, 比文献[21]略低. 表明本文采用离散小波变换合成大图像并采用随机生成的矩阵置乱整幅图像的方法比文献[22]中基于猫映射的像素值扰乱的方法效果更好, 比文献[21]中应用混沌序列替换组合图像的子块, 再对其进行像素值置乱的方法效果略差, 在以后的研究中还有待提高.

|
图 6 明文和密文图像直方图 |
| 表 1 相邻像素相关系数 |
| 表 2 不同算法信息熵对比 |
4.5 密钥空间
基于混沌的密码系统的密钥空间必须达到2100的大小才能抵御各种攻击. 本文方法中LSC映射的密钥是256位, 满足密钥大小的要求, 另外4个超混沌系统的初始值也作为密钥输入. 且本方案是在灰度级为256、双精度和64位Windows 10操作系统下进行的. 根据IEEE浮点标准, 64位双精度计算精度为1015, 整个系统的密钥空间大小经叠加后达到2256×1014×1015, 由此可以得出本文算法所拥有的密钥空间远远大于2100, 对穷举攻击具有足够的抵御能力.
4.6 密钥敏感性分析密钥敏感性是指当解密密钥仅发生微小变化, 却对密文图像的解密造成了非常严重的影响[24]. 由于混沌系统本身具有极高的初值敏感性, 所以实验选择通过改变超混沌Lorenz系统的初始值来验证方案对于密钥的敏感性. 在解密时对超混沌Lorenz系统的第一个初始值密钥进行更改, 更改后的初始值密钥与原先的初始值密钥相差0.000 000 000 1.
使用与正确密钥不同的密钥进行解密, 4个原始图像都无法正确重建. 如图7所示, 以Lena图像的解密结果为例, 虽然密钥仅产生了极其微小的变化, 却也无法得到正确的解密图像. 由此证明了算法对于密钥的敏感性, 说明了算法的安全性.
4.7 差分攻击分析原始图像和密文图像之间的差异通常采用两个标准来测量, 即NPCR (number of pixels change rate)和UACI (unified average changing intensity)[24], 其相应的理想值分别为NPCR=99.6094%, UACI=33.4635%. 越接近理论值, 说明发生微小的变化所得到的密文图像与原明文所得到的密文图像差别越大, 则算法抵抗差分攻击的性能越好. 计算公式如下:
| NPCR=1m×n∑i,jD(i,j)×100% | (15) |
| UACI=1m×n[∑i,j|C1(i,j)−C2(i,j)|255]×100% | (16) |
其中,

|
图 7 不同密钥的解密结果 |
| 表 3 明文敏感性实验结果(%) |
4.8 鲁棒性
图像在传输期间不可避免会受到噪声污染或剪切攻击, 为了测试所提算法的鲁棒性, 通过在密文图像中添加不同噪声和切割部分密文再对其进行解密来模拟图像在传输期间受到的干扰. 图8显示了不同噪声攻击和剪切攻击下的Lena图像的解密结果. 通过观察解密后的图像可以发现, 虽然图像中存在明显的斑点和噪声, 但是仍然能够清晰地看出图像的基本特征和信息. 同时, 本文算法对剪切过的密文图像仍然可以解密大部分图像信息, 这说明了所提出的算法具有一定的抗噪声攻击和抗剪切攻击的能力.

|
图 8 不同干扰后Lena的加密图像及其对应的解密图像 |
5 结语
本文提出基于多混沌系统的多图像加密算法, 总体基于传统的置乱扩散方法, 实现了对多幅图像进行加密. 算法结合了LSC映射和超混沌Lorenz系统, 克服了单一混沌系统的缺陷. 算法包括图像预处理、密钥的生成、像素点位置置乱、双向扩散以及行列置乱等模块. 加密方案利用图像的明文信息和用户输入的整数来确定超混沌Lorenz系统的初始值, 增加了明文与密文的联系, 增强了算法抵御选择明文攻击的能力, 增加了混沌序列的不可预测性.
通过以上仿真实验分析, 本文提出的加密算法密钥空间足够大, 相邻像素的相关性小, 能够抵抗差分攻击. 此外, 本算法也具有较强的抵抗统计攻击的能力, 可以有效地防止攻击者从密文中获取大量的有效信息. 相较于文献[21]方法, 所提算法抵抗熵攻击的性能较弱, 在以后的研究过程中应不断加以改进. 另外, 本文算法仅适用于灰度图像, 未来针对彩色多图像的加密算法还有待研究.
| [1] |
Gan ZH, Chai XL, Zhang MH, et al. A double color image encryption scheme based on three-dimensional Brownian motion. Multimedia Tools and Applications, 2018, 77(21): 27919-27953. DOI:10.1007/s11042-018-5974-9 |
| [2] |
郑伟, 席思星, 王桂林, 等. 结合计算全息和频移的JTC系统多图像光学加密方法. 红外与激光工程, 2022, 51(5): 20220175. |
| [3] |
王雪光, 李明, 于娜娜, 等. 基于空间角度复用和双随机相位的多图像光学加密方法. 物理学报, 2019, 68(24): 240503. |
| [4] |
Pan SM, Wen RH, Zhou ZH, et al. Optical multi-image encryption scheme based on discrete cosine transform and nonlinear fractional Mellin transform. Multimedia Tools and Applications, 2017, 76(2): 2933–2953.
|
| [5] |
佟晓筠, 毛宁, 张淼, 等. 基于Henon映射与改进的提升小波变换图像加密算法. 信息网络安全, 2022, 22(9): 31-39. |
| [6] |
Bian ZX, Zhang LH, Ye HL, et al. Multiple-image encryption based on Toeplitz matrix ghost imaging and elliptic curve cryptography. Laser Physics Letters, 2021, 18(5): 055206. DOI:10.1088/1612-202X/abf5cc |
| [7] |
Zhang L, Zhang XQ. Multiple-image encryption algorithm based on bit planes and chaos. Multimedia Tools and Applications, 2020, 79(29): 20753-20771. DOI:10.1007/s11042-020-08835-4 |
| [8] |
Haq TU, Shah T. Algebra-chaos amalgam and DNA transform based multiple digital image encryption. Journal of Information Security and Applications, 2020, 54: 102592. DOI:10.1016/j.jisa.2020.102592 |
| [9] |
Zhang XQ, Wang XS. Multiple-image encryption algorithm based on DNA encoding and chaotic system. Multimedia Tools and Applications, 2019, 78(6): 7841-7869. DOI:10.1007/s11042-018-6496-1 |
| [10] |
Chen Q, Shen XJ, Cheng Y, et al. Joint-transform correlator multiple-image encryption system based on quick-response code key. Current Optics and Photonics, 2019, 3(4): 320-328. DOI:10.3807/COPP.2019.3.4.320 |
| [11] |
王丰, 邵珠宏, 王云飞, 等. Gyrator变换域的高鲁棒多图像加密算法. 中国图象图形学报, 2020, 25(7): 1366-1379. DOI:10.11834/jig.190344 |
| [12] |
Sahasrabuddhe A, Laiphrakpam DS. Multiple images encryption based on 3D scrambling and hyper-chaotic system. Information Sciences, 2021, 550: 252-267. DOI:10.1016/j.ins.2020.10.031 |
| [13] |
Enayatifar R, Guimãraes FG, Siarry P. Index-based permutation-diffusion in multiple-image encryption using DNA sequence. Optics and Lasers in Engineering, 2019, 115: 131-140. DOI:10.1016/j.optlaseng.2018.11.017 |
| [14] |
刘海峰, 周雪飞, 梁星亮, 等. 基于多混沌系统的图像加密算法. 陕西科技大学学报, 2022, 40(1): 188-195. |
| [15] |
Zhong HY, Li GD. Multi-image encryption algorithm based on wavelet transform and 3D shuffling scrambling. Multimedia Tools and Applications, 2022, 81(17): 24757-24776. DOI:10.1007/s11042-022-12479-x |
| [16] |
Zhang XQ, Wang XS. Multiple-image encryption algorithm based on the 3D permutation model and chaotic system. Symmetry, 2018, 10(11): 660. DOI:10.3390/sym10110660 |
| [17] |
Hua ZY, Zhou YC, Huang HJ. Cosine-transform-based chaotic system for image encryption. Information Sciences, 2019, 480: 403-419. DOI:10.1016/j.ins.2018.12.048 |
| [18] |
Li Z, Peng CG, Li LR, et al. A novel plaintext-related image encryption scheme using hyper-chaotic system. Nonlinear Dynamics, 2018, 94(2): 1319-1333. DOI:10.1007/s11071-018-4426-4 |
| [19] |
白牡丹, 李珊珊, 张泽坤. 基于超混沌系统的多权限多图像加密算法. 计算机系统应用, 2023, 32(5): 141-148. DOI:10.15888/j.cnki.csa.009061 |
| [20] |
李珊珊, 赵莉, 张红丽. 基于猫映射的图像灰度值加密. 计算机应用, 2021, 41(4): 1148-1152. |
| [21] |
Zarebnia M, Pakmanesh H, Parvaz R. A fast multiple-image encryption algorithm based on hybrid chaotic systems for gray scale images. Optik, 2019, 179: 761-773. DOI:10.1016/j.ijleo.2018.10.025 |
| [22] |
Bisht A, Dua M, Dua S. A novel approach to encrypt multiple images using multiple chaotic maps and chaotic discrete fractional random transform. Journal of Ambient Intelligence and Humanized Computing, 2019, 10(9): 3519-3531. DOI:10.1007/s12652-018-1072-0 |
| [23] |
Yu CY, Li JZ, Li X, et al. Four-image encryption scheme based on quaternion Fresnel transform, chaos and computer generated hologram. Multimedia Tools and Applications, 2018, 77(4): 4585-4608. DOI:10.1007/s11042-017-4637-6 |
| [24] |
Patro KAK, Soni A, Netam PK, et al. Multiple grayscale image encryption using cross-coupled chaotic maps. Journal of Information Security and Applications, 2020, 52: 102470. DOI:10.1016/j.jisa.2020.102470 |
| [25] |
Wei JJ, Zhang M, Tong XJ. Multi-image compression-encryption algorithm based on compressed sensing and optical encryption. Entropy, 2022, 24(6): 784. DOI:10.3390/e24060784 |
| [26] |
Nan SX, Feng XF, Wu YF, et al. Remote sensing image compression and encryption based on block compressive sensing and 2D-LCCCM. Nonlinear Dynamics, 2022, 108(3): 2705-2729. DOI:10.11071-022-07335-4 |
 2024, Vol. 33
2024, Vol. 33



