1 引言

随着车联网的发展, 主动式的交叉路口车辆调度方式开始涌现, 其中“无信号交叉路口”的概念被提出, 相较于传统信号灯交叉路口车辆调度方式, 遵循特定通行规则的无信号交叉路口车辆调度方式更能适应实时的交通流, 而无信号交叉路口的通行效率问题是交叉路口车辆调度的热点问题.

麻雀搜索算法(sparrow search algorithm, SSA)是根据麻雀种群觅食行为而提出的智能搜索算法^[1], SSA调节参数少、局部寻优能力强, SSA已成功应用于CT图像检测^[2]、电池堆参数优化领域^[3]、机器学习参数优化^[4]和无人机路线规划^[5,6]等领域, 但SSA仍存在易陷入局部最优解、全局搜索能力弱等不足.

为提升SSA的性能, 国内外学者对其进行改进. 张伟康等^[7]引入Circle映射、蝴蝶优化算法以及逐维变异方法, 在初始化种群、发现者位置更新策略以及扰动个体位置方面对SSA进行优化. 吕鑫等^[8]引入Tent混沌序列初始化种群, 通过高斯变异和Tent混沌扰动对个体进行扰动, 克服SSA易陷入局部极值点的缺陷; Liu等^[4]引入重心反向学习机制、学习系数以及变异算子, 在初始化种群、发现者位置更新策略、跟随者位置更新策略方面提高种群多样性以及算法的全局搜索能力; Yuan等^[9]通过引入混沌策略以及自适应惯性权重来增加种群的多样性和提高SSA的收敛速度和全局搜索能力; 王海瑞等^[10]引入Tent混沌映射、Levy飞行策略以及柯西高斯变异来提高SSA的全局搜索能力. 毛清华等^[11]引入柯西变异算子和反向学习策略在算法得到最优解时进行扰动, 从而提高算法跳出局部最优解的能力. 除上述对SSA的理论研究外, 还用来解决工程上的问题. 例如, 韩统等^[12]在求解多无人机协同航迹规划的问题上, 引入对数螺旋策略和自适应步长; 贺航等^[13]在解决森林火灾图像多阈值分割问题上, 引入精英反向学习策略与Levy飞行机制增强算法全局寻优搜索能力; 杨玮等^[14]运用SSA解决冷链物流企业库存-配送的路径问题.

根据以上描述, 如直接用SSA来解决无信号交叉路口的车辆通行效率问题则可能会取得不太理想的效果. 故提出自适应参数和等级反向学习的改进策略提高SSA的全局搜索寻优能力以及寻优精度, 应用到无信号交叉路口的车辆调度问题上, 从而提高无信号交叉路口车辆通行效率.

本文第2节介绍无信号交叉路口的基本规则和麻雀算法基本理论; 第3节提出基于自适应参数和等级反向学习策略的麻雀算法(ALSSA)并分别介绍其基本原理; 第4节将ALSSA与SSA以及其他5个算法在多个基准测试函数进行性能测试, 并对ALSSA进行Wilcoxon秩和检验P值, 进一步验证改进策略的有效性, 然后进行消融实验验证每一种改进措施的有效性; 第5节首先介绍无信号交叉路口车辆编码规则, 然后进行仿真实验计算多种类型的车道在多种车流量的情况下的最优通行时间.

2 无信号交叉路口与麻雀算法基本理论

本节依次介绍无信号交叉路口仿真模型、交叉路口离散化数学模型、无信号交叉路口约束条件、麻雀算法的构成部分及其所对应的公式.

2.1 无信号交叉路口概况

无信号交叉路口管理系统由5部分组成, 分别为总控制中心以及4个子控制中心, 4个子控制中心分别管理交叉路口东、西、南、北路段的车辆, 各路段车辆到达交叉路口外部缓冲区WIN_i时会把本车信息发送给相应的子控制中心, 各子控制中心处理车辆发送来的信息, 周期性地将车辆信息传输给总控制中心, 总控制中心将信息处理后生成调度策略发送给4个子控制中心, 由4个子控制中心再将调度策略发送给相应的车辆, 车辆无信号交叉路口模型如图1所示.

图1中, 将交叉路口内部区域离散化, 离散化后的交叉路口由多个长宽相同的小单元格组成, 离散化后的单元格为“路权点”. IN_i表示交叉路口内部区域入口处, L表示WIN_i到IN_i的距离, L_C表示路权点的长度. 为方便表示和计算, 本文用离散事件过程描述车辆接收调度策略后通过交叉路口的一系列动作.

以双向两车道交叉路口内部区域为例, 其离散化模型如图2所示, 交叉路口内部区域每个路权点编号用C_i, i=1, 2, 3, 4表示. 车辆的直行、左转以及右转车辆按照图3所示规定路线行驶, car_inten表示车辆行驶路径, car_inten=<C₁, C₂, …, C_i>, 其中通过路权点C_i后表示车辆驶出交叉路口, 例如图3中车辆左转弯表示为car_inten=<C₂, C₁, C₄>, 通过C₄后就驶离了交叉路口.

车辆通过离散化的交叉路口时满足以下约束.

1) 各路权点同一时刻只能容纳一辆车, 前一辆车进入路权点后该路权点不允许下一辆车进入, 且通过路权点的时间忽略不计.

2) 车辆进入交叉路口入口区域时已经调节好速度, 且同一方向的车辆要按照到达顺序依次进入交叉路口路权点.

3) 每辆车需要通过多个路权点且通过路权点的先后次序不能改变, 即每辆车按照指定的行驶路线通过交叉路口.

4) 多个路权点之间是连续的, 相邻的路权点之间没有额外的空间.

5) 机动车右转弯时容易造成视野盲区导致交通事故, 一旦发生交通事故为避免二次事故的发生将该路权点设置为“故障点”且在故障期间所在路权点不可用.

6) 右转弯发生交通事故后会在一定时间内处理完毕.

根据以上描述, 无信号交叉路口在右转弯行驶路线的路权点都可能发生交通事故成为“故障点”, 以无信号交叉路口双向两车道为例, 其故障模型如图4所示, 红色区域代表可能会发生故障的“路权点”.

2.2 麻雀算法基本原理

麻雀种群分为发现者、跟随者、警戒者, 算法的基本思想、公式参数解释等, 前人已有详细介绍, 本文不做过多赘述, 可参考文献[1], 下面引入本文用到的重要公式.

在D维解空间内种群规模为N的每只麻雀的位置表示为:

$ X = \left( {\begin{array}{*{20}{c}} {{x_{1, 1}}}& \cdots &{{x_{1, D}}} \\ \vdots &{{x_{i, d}}}& \vdots \\ {{x_{N, 1}}}& \cdots &{{x_{N, D}}} \end{array}} \right) $

(1)

麻雀觅食的位置适应度值表示为:

$ F\left( X \right) = \left( {\begin{array}{*{20}{c}} {f\left( {\left[ {{x_{1, 1}}, \cdots , {x_{1, D}}} \right]} \right)} \\ {f\left( {\left[ {{x_{2, 1}}, \cdots , {x_{2, D}}} \right]} \right)} \\ \vdots \\ {f\left( {\left[ {{x_{N, 1}}, \cdots , {x_{N, D}}} \right]} \right)} \end{array}} \right) $

(2)

每代发现者的位置更新公式如下:

$ {x}_{i, d}^{t+1}=\left\{\begin{array}{l} {x}_{i, d}^{t}\cdot\mathrm{exp}\left\{\dfrac{-i}{\alpha \cdot ite{r}_{\mathrm{max}}}\right\}, {\rm{if}} \; {R}_{2} \lt {\textit{ST}}\\ {x}_{i, d}^{t}+Q \times L, \qquad\qquad\;\;{\rm{if}} \; {R}_{2}\geqslant {\textit{ST}}\end{array}\right. $

(3)

每代跟随者的位置更新公式如下:

$ {x}_{i, d}^{t+1} = \left\{ \begin{array}{l}Q\cdot\mathrm{exp}\left\{\dfrac{x{w}_{d}^{t}-{x}_{i, d}^{t}}{{i}^{2}}\right\}, \qquad\qquad\qquad\;\;\;\;{\rm{if}} \; i \gt \dfrac{N}{2}\\ x{b}_{d}^{t}+\dfrac{1}{D}{\displaystyle \sum _{d=1}^{D}\left(\left|{x}_{i, d}^{t}-x{b}_{d}^{t}\right|\cdot rand\left\{-1, 1\right\}\right)}, \; {\rm{else}} \; \end{array}\right. $

(4)

警戒者位置更新公式如下:

$ {x}_{i, d}^{t+1}=\left\{\begin{array}{l}x{b}_{d}^{t}+\beta \cdot\left|{x}_{i, d}^{t}-x{b}_{d}^{t}\right|, \quad\;\;\;\; {\rm{if}} \; {f}_{i}\ne {f}_{g}\\ {x}_{i, d}^{t}+{ K}\cdot\left\{\dfrac{\left|{x}_{i, d}^{t}-x{w}_{d}^{t}\right|}{\left|{f}_{i}-{f}_{w}\right|+\varepsilon }\right\}, \; {\rm{if}} \; {f}_{i}={f}_{g}\end{array}\right. $

(5)

3 基于自适应参数和等级反向学习策略的麻雀算法(ALSSA)

根据上述对麻雀算法基本理论的介绍, 针对SSA寻优精度不足、易陷入局部最优等缺陷. 本节依次引入自适应收敛因子和等级反向学习策略提高SSA的寻优精度和全局搜索能力, 最后给出ALSSA的步骤.

3.1 基于自适应参数的麻雀算法(ASSA)

在SSA中, 麻雀种群中的发现者只受到上代发现者的位置的影响, $\exp \left\{ {\dfrac{{ - i}}{{\alpha {\text{ }} \cdot {\text{ }}ite{r_{\max }}}}} \right\}$的值在迭代过程中不断降低, 个体的每一维都在变小, 搜索空间也随之逐渐减小, 增大陷入局部空间的概率, 为解决这一问题以及提高算法的寻优精度, 提出自适应收敛因子η.

$ \eta = {\eta _0} \cdot {\lambda ^{t + 1}} $

(6)

其中, η₀为权重因子初始值为1, λ为自适应因子, 是一个[0, 1]之间的随机数, t为当前的迭代次数, 所以在式(6)的基础上, 发现者的位置更新公式为:

$ {x}_{i, d}^{t+1}=\left\{\begin{array}{l}{x}_{i, d}^{t}\cdot\mathrm{exp}\left\{\dfrac{-i}{\alpha \cdot \eta \cdot ite{r}_{\mathrm{max}}}\right\}, {\rm{if}} \; {R}_{2} \lt {\textit{ST}}\\ {x}_{i, d}^{t}+Q \times L, \qquad\qquad\quad\;{\rm{if}} \; {R}_{2}\geqslant {\textit{ST}}\end{array}\right. $

(7)

此外, 在觅食过程中避开捕食者, 选择一定数量的麻雀作为警戒者. 当警戒者数量SN较大时, 有利于提高SSA全局优化能力, 但是, 当SN较小时, 有利于加快收敛速度. 警戒者数量的自适应更新公式为:

$ {\textit{SN}} = {{\textit{SN}}_{\max }} - round\left[({{\textit{SN}}_{\max }} - {{\textit{SN}}_{\min }}) \cdot \frac{{g \cdot t}}{{ite{r_{\max }}}}\right] $

(8)

3.2 基于等级反向学习策略的麻雀算法(LSSA)

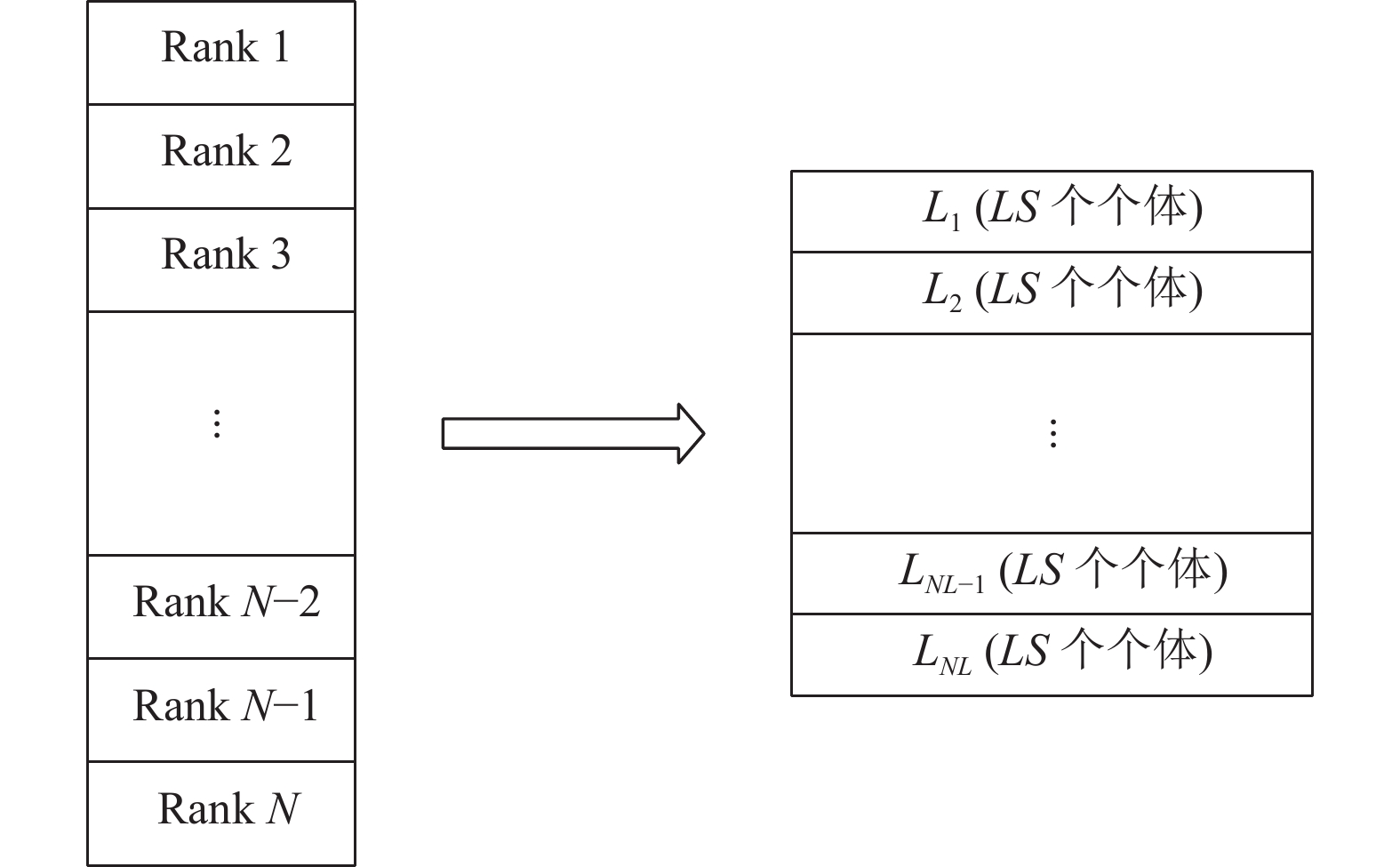
首先等级反向学习策略需要计算种群中每个个体的适应度值, 适应度值按从小到大排序为(Rank 1, Rank 2, Rank 3, …, Rank N), 将N个个体划分为NL个等级, 每个等级有LS个个体, L₁表示个体最好的等级, L_NL表示个体最坏的等级, 等级示意如图5所示.

生成反向个体的概率P_i随等级降低而逐渐升高, P_i的计算公式如下所示:

$ {P_i} = \frac{{(i - 1) \times NL}}{{N + i}} $

(9)

反向个体优于当前个体的概率高于50%, 考虑到仍有部分个体在反向学习之后个体质量有所降低^[15], 为减少这种现象发生的概率并保持种群多样性, 将求得的反向个体和上一等级的最优个体进行凸组合, 得到趋优反向个体.

$ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{x'} }_j = \lambda \cdot {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{x} _j} + \left( {1 - \lambda } \right) \cdot {x_{lb}} $

(10)

其中, $ \lambda $为[0, 1]之间的随机数, $ {x_{lb}} $表示上一等级的最优个体.

通过实施该策略, 即使最初求得的反向个体相较于当前个体有所退化, 但与上一等级的最优个体进行凸组合后, 反向解还会接受一部分来自最优个体的特征, 进一步提升反向个体的质量, 同时算法的勘探能力、种群多样性和算法的寻优精度也得到提高.

3.3 基于自适应参数和等级反向学习策略的麻雀算法的步骤

步骤1. 导入相关参数, 初始化种群.

步骤2. 计算每个麻雀个体的适应度值并对其排序, 找出最优和最差适应度值的个体及其位置.

步骤3. 根据发现者式(7)更新发现者位置.

步骤4. 根据式(4)更新追随者位置.

步骤5. 根据式(5)和式(8)更新警戒者位置.

步骤6. 更新麻雀个体适应度值, 根据个体的适应度值从优到劣重新排序.

步骤7. 按照更新后的适应度值将麻雀种群划分为NL个等级, 每个等级有LS个体以及生成反向个体的概率P_i.

步骤8. 根据每个等级生成反向个体的概率P_i生成对应的反向个体.

步骤9. 判断是否达到算法结束条件, 若达不到, 则跳转到步骤3, 否则, 进入步骤10.

步骤10. 记录最优结果, 结束运行.

根据上述步骤可以得到基于自适应参数和等级反向学习策略的麻雀算法(ALSSA), 提高了SSA的全局搜索能力以及寻优精度, ALSSA流程如图6所示.

4 算法性能测试

为检验ALSSA算法在全局搜索能力、收敛速度、寻优精度等方面的性能, 将ALSSA与SSA、IGWO、IGOA、GTO、EWOA、ALO算法同时在CEC的13个基准函数^[16]上进行对比测试, 结果表明ALSSA在全局搜索能力、收敛速度、寻优精度等方面性能均有提升. 接下来, 使用Wilcoxon秩和检验和统计分析方法对ALSSA算法进行性能评估, 对比结果表明ALSSA的性能是优越的. 最后, 进行消融实验验证是每一种改进策略的有效性.

4.1 基准测试函数测试

在Matlab R2020a环境下进行仿真实验, 种群大小设置为300, 最大迭代次数为500, 独立运行30次之后, 取运行结果的平均运行时间(Time)、最优值(Best)、最差值(Worst)、平均值(Mean)和标准差(Std)以及成功查找到最优值的次数(NOS), 各算法的寻优对比结果如附录表A1所示.

从表A1可以得出, ALSSA和SSA平均运行时间基本相同, 远小于其他5个算法. ALSSA和SSA在f1–f4、f9、f11测试函数上可以找到理论最优解0, 除GTO算法在f1、f3、f11上可以找到理论最优值, 其他算法均不能找到理论最优值; 在f5、f6测试函数上ALSSA可以寻到理论最优值, SSA则未能找到理论最优值, 除EWOA、GTO在f6上可以寻到理论最优值, 其他算法均不能找到理论最优值; 在f7、f8、f10、f12、f13上ALSSA虽未寻到最优值, 但是其平均寻优值是这些算法中最靠近最优解的. 由上可见ALSSA具有较好的全局搜索能力、寻优能力以及寻优精度, 结合寻优所耗费的时间, 综合性能是突出的. 各个基准函数的收敛曲线图如附录图A1所示.

图A1的13个收敛曲线图中可以清晰地看到各算法在寻优过程中适应度值的变化情况. 除第12个基准函数, ALSSA的收敛速度均是最快的, 这是因为加入自适应参数的结果, 而引入等级反向学习策略后ALSSA的寻优精度高于其他算法. 再结合表A1可以看出ALSSA算法能跳出局部极值点进行全局搜索, 而且从寻优结果来看大部分测试函数ALSSA算法均能找到理论最优值, 或者ALSSA寻优结果比其他算法的结果更接近理论最优值, 所以算法性能是优异的.

4.2 Wilcoxon秩和检验分析

对于改进算法性能的评估, 应该进行统计检验^[17]. 换而言之, 仅基于平均值和标准偏差值来比较算法优劣还不够, 需要进行统计检验以证明ALSSA比其他算法具有显著的改进优势. 通过对每一次的结果进行独立比较, 来体现算法的稳定性和公平性. 本文采用 Wilcoxon秩和检验在P值为5%的显著性水平下进行检验, 当P值小于5%时, 拒绝假设, 说明ALSSA比其他算法具有显著性差异, 反之接受假设, 表明对比算法的寻优能力整体上相同. 表1给出13个基准函数下 ALSSA 与其他五种算法之间的秩和检验P值, 因为当两个对比算法都达到最佳值时, 无法进行比较, 用 NaN 表示, 即不能进行显著性判断, R为显著性判断的结果, “+”“–”“=”分别表示 ALSSA 性能好于、劣于和等于所对比的算法.

从表1可以得出, 大部分P值远远小于5%, 这说明ALSSA的优越性比其他6种算法在统计上是显著的, 而且ALSSA在基准测试函数测试上大部分优于SSA性能, 小部分是等同于SSA的性能, 但在部分基准测试函数上要劣于或者等于其他5种算法的一个. 基于上述得出对SSA的性能提升还是比较明显的.

4.3 消融实验

由于ALSSA的各种改进措施导致其寻优性能比较好, 但具体哪一种改进措施起作用, 是否有某一种改进措施不起作用还未知, 为表明各种改进措施的作用, 使实验更具说服力, 需要ALSSA的消融实验, 分别以SSA、ASSA、LSSA与ALSSA在13个基准函数上作对比实验, 因为当迭代次数过大的时候, SSA和ALSSA在很多情况下都会找到最优解, 故看不出是哪种改进措施起到的效果比较明显, 所以这里种群数量为200, 迭代次数为30次, 最终结果如表2所示.

从表2可得, 在基准测试函数f1–f4、f7上ASSA对SSA的提升效果比较大, f6、f8、f12、f13则是LSSA对SSA的提升效果比较明显, 在其他的基准函数情况上则是都找到了最优解, 故看不出是哪个措施的提升效果更显著, 是两者相结合的共同作用的结果.

5 无信号单交叉路口场景实验

本节对无信号交叉路口实际通行情景进行仿真实验, 为更接近车辆通过交叉路口的真实情况, 提出车辆编码规则并进行初始化, 最后对每种车道进行多种车流量仿真实验, 得到最优通行时间.

5.1 编码规则

在一段时间T内通过的一组车辆, 其编号组成一条位置码, 表示即将到达交叉口的一组车辆, 其中车辆编号由所在的道路编号和车辆优先级组成. 在双向两车道的交叉路口, 道路编号为1, 2, 3, 4, 而双向四车道的道路编号为1, 2, 3, 4, 5, 6, 7, 8. 车辆优先级用数字1, 2, 3,…, n表示, 优先级依次递减. 结合上述所述, 车辆编号12表示在1车道到达交叉口入口处的第2辆车, 33表示在3车道到达交叉口入口处的第3辆车.

一条位置码由一组车辆编号随机排列组成, 但优先级高的编号需要在优先级低的编号之前. 如一条位置码[23, 13, 12, 21, 31, 42, 11, 22, 32, 41]不符合规则, 21要在22和23之前, 22也要在23之前, 其他顺序同理. 因为本文设定右转弯的车辆可能会发生故障, 将发生故障的车辆所在的那条位置码称为“坏”位置码.

5.2 位置码初始化

在车辆调度优化中, 随机的初始化可能会存在“坏”的位置码, 为得到“好”的初始位置码, 提高算法的收敛速度, 本文引入结合优先级思想的初始位置码生成算法. 基于优先级的位置码初始化的具体步骤如算法1.

算法1. 基于优先级的位置码初始化

输入: 种群大小n, m个车辆编号

输出: n条“好”位置码

Step 1. 将m个车辆编号按从小到大重新排序

Step 2. 创建n个容量为m的数组, 每个数组代表一条位置码, 数组每个元素存放的位置称为位置座Locus.

Step 3. 初始化数组, 遍历每个数组, 将m个车辆编号随机放在数组位置座上, 数组的初始化需要满足位置码编码规则.

(1)根据车辆编号判断车辆类型type及车辆优先级priority.

(2)如果车辆优先级priority = 1, 随机选择位置座将车辆编号存放在该位置座位Locus上.

(3)如果车辆优先级priority > 1, 获取type1 = type并且priority1= priority–1车辆编号的位置座Locus, 如果Locus < m, 随机选择位置座Locus1, 且Locus1 > Locus, 将该车辆编号存放在位置座Locus1.

(4)如果Locus > m, 扩容数组原来的长度的一倍, 再随机选择位置座Locus1, 且Locus1 > Locus, 将该车辆编号存放在位置座Locus1.

Step 4. 删除每个数组中非车辆编号的位置座.

Step 5. 输出n个容量为m的数组.

算法1中同类型位置按照优先次序由高到低排列且每个位置都为随机选取, 保证位置码的多样性及位置码的正确性.

算例: 一组车辆编号为[11, 21, 12, 22, 23, 31]的车到达交叉路口, 编码过程如下.

(1)排序

将[11, 12, 21, 22, 23, 31]车辆编号按从小到大的顺序排列.

(2)随机选择对应的位置座

1)车辆编号为11, 对应type = 1, priority = 1, 随机选择位置座.

2)车辆编号为12, 对应type = 1, priority = 2, 获取type = 1, priority1 = 1, 车辆编号为11的位置座Locus = 4, 随机选择车辆编号为12的位置座且Locus1 > Locus. 同种类型的编号需要遵循优先级原则, 不同类型的编号不需要遵循优先级原则. 如Locus1 = 8.

3)车辆编号为21, 对应type = 2, priority = 1, 随机选择位置座.

4)按照上述方法依次选择位置座, 数组长度不够时, 扩展数组.

5)删除多余的位置座, 得到最终的位置码序列.

5.3 仿真实验

车辆在通过交叉路口时规定最低时速为20 km/h, 最高时速为40 km/h. 在《2022年国民经济和社会发展统计公报》指出我国2022年事故发生率为0.000088%, 这里设定故障发生的概率为0.00001%, 当发生故障时, 车辆所在的路权点不可通行, 需要等待故障修复, 故设定平均故障修复时间为1 h, 因事故而导致的延误时间用T_delay表示, 每个路权点的长度设置为18 m, 每一组车辆时间间隔T_gap为5 s, 车辆正常行驶通过的时间为T_usual. 利用ALSSA、SSA、IGWO这3个算法分别对双向两车道、双向四车道以及双向八车道的车流量进行设置, 其中双向两车道的车流量分别设置100、300、500辆车, 双向四车道的车流量分别设置600、800、1000辆车, 双向八车道的车流量分别设置2000、4000、6000辆车, 对以上3种车道的不同车流量求解总通过时间T_total=T_delay+T_gap+T_usual, 每个车流量独立运行测试30次, 求其平均值.

表3–表5中不同车道不同车流量的通过时间是求解30次最优通过时间的平均值, 而ALSSA各种情况的通过时间均优于其他两种算法, 进而反映出ALSSA寻优精度是优于其他两个算法的; 当为表3的车流量时, 3种算法的标准差值相差不大, 3个算法的标准差最大值和最小值之差约为0.5, 例如, 车流量为500时ALSSA、SSA、IGWO (后面都按此算法顺序)标准差依次为0.87、1.15、1.35. 当为表4的车流量时, 最大标准差和最小标准差之差约为2, 例如, 车流量为1000时, 标准差依次为1.13、2.80、3.42. 当车流量为2000、4000、6000时最大标准差和最小标准差之差均大于3, 其中车流量为6000时, 标准差依次为1.36、6.16、5.94. 上述标准差的变化说明, 当车流量较小时, 各个算法都能找到全局最优值, 但是当车流量逐渐增大时, 除ALSSA外, 其他两个算法在寻优过程极易陷入局部最优点, 导致多次测试过程中寻优值有较大变化, 而ALSSA随着车流量的增大标准差虽有一定程度增大, 但属于可接受的波动范围内, 说明ALSSA是比较稳定的, 提高了SSA跳出局部最优的能力, ALSSA全局搜索能力是优异的.

从表3–表5得出首先ALSSA所有车道所有车流量的总通过时间均是小于SSA和IGWO算法的总通过时间, 而且随着车道数的增加以及车流量多倍数增加总通过时间反而不是相应倍数的增长, 说明当车道越多车流量越多时本文的方法是适用且高效的.

6 结论

本文在麻雀搜索算法的基础上, 引入自适应发现者——警戒者调整策略以及等级反向学习策略, 提出自适应参数和等级反向学习策略的麻雀算法. 自适应发现者—警戒者调整策略加快种群初始化的收敛速度而且使算法前期着重寻找全局最优, 后期着重局部寻优整体上提高寻优精度. 等级反向学习策略可以增强算法的全局寻优搜索能力使得算法跳出局部极值点, 这使得 ALSSA 算法相较于SSA算法寻优精度更高, 全局寻优能力更强. 选取13个基准测试函数与其他5种算法进行比较, 并进行Wilcoxon 秩和检验对算法显著性水平进行验证. 实验表明, ALSSA寻优性能提升较明显, 具有良好的扩展能力, 鲁棒性强, 表现出优异的性能.