2. 湖北大学 计算机与信息工程学院, 武汉430062;
3. 智慧政务与人工智能应用湖北省工程研究中心, 武汉 430062
2. School of Computer Science and Information Engineering, Hubei University, Wuhan 430062, China;
3. Engineering Research Center of Hubei Province in Intelligent Government Affairs and Application of Artificial Intelligence, Wuhan 430062, China
克隆选择算法是人工免疫算法中的一种以高突变来解决复杂问题的元启发式搜索算法[1], 具有结构新颖、收敛速度快等特点, 在目前主流的智能优化算法中具有明显的优势. 近些年来, 在函数优化[2]、路径规划[3]、故障诊断[4]、参数识别[5]等领域得到广泛应用, 如多任务分配调度优化、城市物流选址配送、机电线路故障诊断、电机高精度参数识别等.
当前的克隆选择算法流程主要包括克隆、变异、选择、更新等步骤. 传统的克隆选择算法在种群初始化阶段使用随机初始化生成的抗体种群稳定性与均匀性不强, 导致算法搜索速度变慢. 同时在变异阶段, 如果采用随机变异算子也会使算法的不确定性增加导致收敛速度降低. 因此传统的克隆选择算法在解决实际问题时, 存在算法搜索速度慢, 收敛速度慢, 而且容易陷入局部最优, 与全局最优相差过大的问题[6].
针对上述问题, 众多学者也对克隆选择算法提出各种改进思路. 2019年, Zhou等人建立了双目标函数模型, 并且引入了精英策略, 提高了算法的寻优精度, 但是算法的收敛速度和全局搜索能力并没有得到有效的提升[7]; 2020年, Liu等人针对抗体选择阶段, 将可变邻域搜索运算符嵌入克隆选择算法中, 使用由亲和力值和约束设施索引值组成的序列双索引进行抗体重新选择, 提高算法的局部寻优的准确性, 加快算法的收敛速度, 但是该算法没有解决易陷入局部最优的问题[8]; 2021年, 王丽丽等人使用云模型产生变异因子和反向学习策略相结合对变异抗体改进, 提高了算法的寻优能力[9]; 2023年, 戴迎春等人将全局搜索与局部搜索结合改进提出一种采用自适应的差分变异算子与全交叉操作来扩大搜索范围, 提高算法跳出局部最优的能力[10].
从上述文献可以看出, 众多学者将改进重点大都放在算法的变异阶段中, 虽然能提高算法的寻优能力, 但无法平衡算法不同时期的全局搜索与局部搜索能力, 并且忽视了初始种群位置不均匀对算法整体稳定性的影响, 无法兼顾种群多样性与搜索能力. 因此, 本文为解决这两个阶段存在的问题, 尝试研究出新的方案替代克隆选择算法目前的初始化和变异两个阶段的操作.
本文提出一种基于定向变异策略的改进克隆选择算法(directed mutation strategy clone selection algorithm, DMSCSA), 使用Halton序列来初始化抗体种群, 使生成的抗体能均匀地分布在整个解空间中, 以此来保证抗体种群的多样性. 使用黄金正弦算法来对部分抗体进行定向变异更新位置, 后用柯西变异对部分抗体进行随机变异, 提高算法的收敛精度和速度.
2 基础理论 2.1 Halton序列原始的克隆选择算法使用Random函数随机初始化种群, 所得到的抗体群随机性虽高, 但均匀性较差, 导致种群搜索速度变慢. 因此本文引入Halton序列来“伪均匀”地初始化种群, 使生成的抗体能更加均匀地分布在整个解空间, 加快算法发现优质解的速度, 提高算法的收敛速度.
二维Halton序列的生成原理如下所示: 任选一个素数p, 对于任意的非负整数k, 可得到如下分解:
| $ k = {a_0} + {a_1} + {a_2}{p^2} + \cdots + {a_r}{p^r} $ | (1) |
得到k的p进制表示
| $ {\Phi _p}:k \to {a_0}{p^{ - 1}} + {a_1}{p^{ - 2}} + \cdots + {a_r}{p^{ - r - 1}} $ | (2) |
| $ \varphi (k) = \left( {{\Phi _{p1}}\left( k \right), {\Phi _{p2}}\left( k \right)} \right) $ | (3) |
其中, p1, p2表示不同大于等于2的任意素数,
图1和图2分别为使用Random函数与Halton序列所生成的初始化种群分布图.

|
图 1 Random初始化种群 |

|
图 2 Halton初始化种群 |
由图1和图2的对比可以得知, 同样随机生成1000个点的情况下, 使用Halton序列生成的种群可以更加均匀地分布在整个空间中, 抗体无明显拥挤现象, 因此可以得出Halton序列产生的初始化种群效果更好.
2.2 黄金正弦算法2017年, Tanyildizi等人提出一种新型元启发式算法[1]——黄金正弦算法(golden sine algorithm, Gold-SA)[11]. 算法核心原理是利用正弦函数与单位圆的关系来迭代寻优. Gold-SA算法通过引入两个黄金分割系数
| $ {x_1} = a \times \left( {1 - \tau } \right) + b \times \tau $ | (4) |
| $ {x_2} = a \times \tau + b \times \left( {1 - \tau } \right) $ | (5) |
其中,
随着迭代次数增加, Gold-SA算法通过式(6)进行位置更新, 如下所示:
| $ V_i^{t + 1} = V_i^t\left| {\sin \left( {{R_1}} \right)} \right| - {R_2}\sin \left( {{R_1}} \right)\left| {{x_1}D_i^t - {x_2}V_i^t} \right| $ | (6) |
其中,
本文引入柯西变异来提高算法跳出局部最优的能力[12]. 柯西变异因其两端分布的特性可以在抗体附近产生较大的扰动从而扩大算法的搜索空间. 使用柯西变异计算公式如下:
| $ {X}_{{\mathrm{new}}}={X}_{{\mathrm{best}}}+{X}_{{\mathrm{best}}}\cdot Cauchy\left(0, 1\right) $ | (7) |
其中,
传统的克隆选择算法在初始化阶段使用Random函数随机初始化种群, 所生成的种群稳定性差, 且对随机程度敏感, 抗体寻优存在盲目性, 易陷入局部最优导致算法收敛速度慢. 其次, 算法在变异阶段使用随机变异的效果不确定, 会出现抗体不均衡有极好或极差的情况. 最后, 算法随机变异后抗体多样性不足, 会出现变异后的抗体相似度过高而产生拥挤现象导致算法搜索速度与收敛精度降低[13].
因此本文针对以上3个问题, 在初始化阶段引入Halton序列生成均匀稳定的种群, 以解决种群稳定性差、抗体盲目寻优的问题, 在保证种群稳定性的同时提高算法搜索速度. 在变异阶段, 对亲和力较高的部分抗体使用黄金正弦定向变异来解决随机变异时的效果极端且不可控的问题, 对亲和力较低的部分抗体使用柯西变异来解决抗体相似度过高而拥挤且多样性不足的问题. 两种变异策略结合, 能够在保证种群多样性与稳定性的前提下, 提高算法的寻优精度与寻优能力.
3.2 算法流程描述DMSCSA流程如图3所示, 具体描述如算法1.
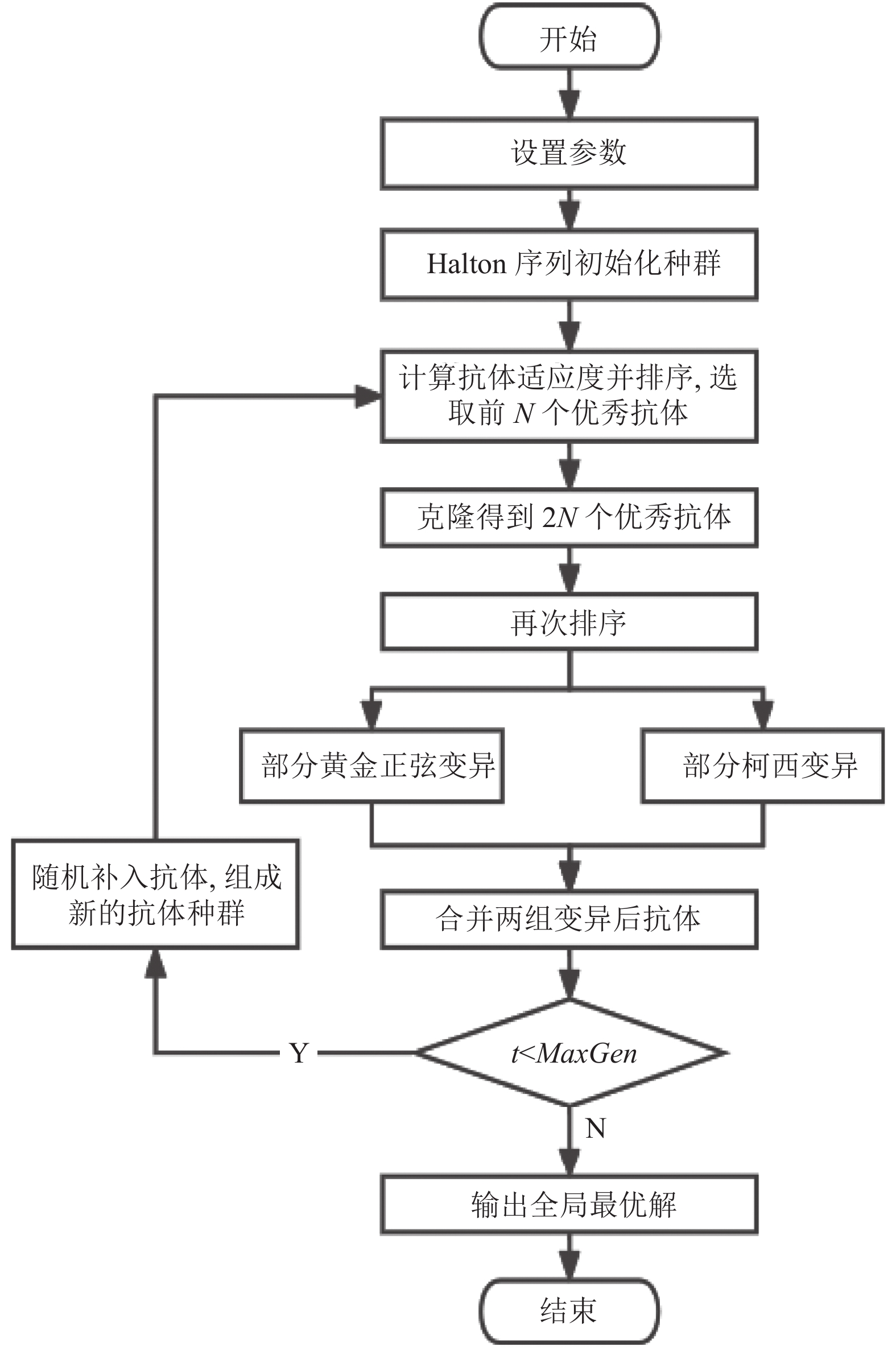
|
图 3 算法流程图 |
算法1. DMSCSA
输入: 种群规模D, 优秀抗体规模N, 维度dim, 抗体值的上下边界lb, ub, 最大迭代次数MaxGen;
输出: 全局最优解BestAns.
1. 目标函数
2. 初始化参数: 种群规模D, 优秀抗体规模N, 维度dim, 抗体值的上下边界lb, ub, 最大迭代次数MaxGen, 当前迭代次数t.
3. 使用Halton序列初始化抗体种群:
4. WHILE(t<MaxGen)
5. 调用目标函数, 计算本轮抗体的亲和力并按照亲和力高低进行排序.
6. 选择亲和力高的前N个优秀抗体, 进行克隆操作, 得到2N个优秀抗体.
7. 对2N个优秀抗体再次计算亲和力并排序, 得到亲和力较高的N'个抗体和剩下亲和力较低的N''个抗体 (N'+ N''=2N).
8. 对N'进行黄金正弦定向变异, 对N''进行柯西算子随机变异.
9. 将变异后的两组抗体组合成抗体群D', 并随机补入X个抗体(X=D–2N), 组成新的种群D'' (D''= D'+X).
10. t++
11. WHILE(t>MaxGen)
12. 输出全局最优解BestAns.
13. END
3.3 算法性能分析DMSCSA算法主要包括种群规模D、抗体的维度dim、优秀抗体规模N、最大迭代次数MaxGen等参数, 算法主要包括以下6个操作步骤: (1)使用Halton序列初始化种群; (2)计算抗体亲和力; (3)选择优秀抗体; (4)克隆; (5) 黄金正弦与柯西变异结合的变异操作(6)种群更新.
设Halton序列初始化每一个抗体的时间为
| $ {\mathrm{O}}\left( {\left( {D{t_1} + f\left( D \right)} \right)} \right) = {\mathrm{O}}\left( {D + f\left( D \right)} \right) $ | (8) |
设对抗体种群
| $ \begin{split} & {\mathrm{O}}\left( {MaxGen\left( {f\left( D \right){t_2} + N{t_3} + N{t_4} + D{t_5}} \right)} \right) \\ &\;\;\; = {\mathrm{O}}\left( {D + f\left( D \right)} \right) \end{split} $ | (9) |
则DMSCSA算法的总时间复杂度为:
| $ \begin{gathered} T\left( D \right) = {\mathrm{O}}\left( {D + f\left( D \right)} \right) + {\mathrm{O}}\left( {D + f\left( D \right)} \right) = {\mathrm{O}}\left( {D + f\left( D \right)} \right) \end{gathered} $ | (10) |
同理, 按上述方法分析传统克隆选择算法的时间复杂度同样为
本实验选取CEC2019测试集中8种测试优化算法的函数作为实验的测试函数, 这些函数计算复杂, 难度较高, 常用于检验算法综合性能. 利用这些测试函数分别对本文提出的算法(DMSCSA)、混合变异克隆选择算法(HMCSA)[14]、精英克隆选择算法(ECSA)[15]进行测试.
4.1 测试函数本文所选取的测试函数如表1所示, f1–f4采用单峰测试函数, 它们的共同特点是具有全局最小值, 且函数图像复杂, 具有多个局部极小值. f5–f8采用多峰测试函数, 用于检测算法在高维复杂函数下的寻优性能.
4.2 寻优速度与精度分析对于单峰测试函数, 记录DMSCSA算法、HMCSA算法、ECSA算法在相同测试环境中各执行50次后的平均值以及标准差, 实验结果如表2所示.
对于多峰测试函数, 分别设置维度dim=10, dim=50, dim=100, 记录DMSCSA算法、HMCSA算法、ECSA算法在相同测试环境中各执行50次后的平均值如表3所示.
由表2分析可知, 4个单峰测试函数中, DMSCSA算法的寻优精度与标准误差都要好于HMCSA算法与ECSA算法.
由表3数据分析可知, Ackley’s function测试函数的结果中, 3个算法的寻优精度都随着维度的增加而有所降低, 而HMCSA算法的收敛稳定性和寻优精度受维度的影响较小, 且收敛精度最高. Rastrigin’s function、Levy function、Griewank’s function测试函数的结果中, 3个算法的寻优精度均随着维度的增加而降低, 但DMSCSA算法的寻优精度和收敛稳定性相较于HMCSA算法和ECSA算法所受影响更小、效果更好.
综上所述, DMSCSA算法与另外两个算法相比, 算法的收敛精度与稳定性更高. 说明本文提出的改进策略是有效的.
4.3 消融实验分析为了验证本文提出的改进策略的效果, 本文设置DMSCSA1算法不含Halton序列初始化种群、DMSCSA2算法不含黄金正弦变异、DMSCSA3算法不含柯西变异. 对10维的8个标准测试函数各执行50次计算平均值, 实验结果如表4所示.
由表4可知, 本文提出的Halton序列、黄金正弦变异、柯西变异策略都对标准CSA的性能有一定的提升. 其中, DMSCSA1的算法效果较DMSCSA2与DMSCSA3算法更明显, 说明黄金正弦变异与柯西变异同时作用提高了算法的寻优精度. 由DMSCSA2与DMSCSA3以及ECSA这3种算法对比可知, 使用Halton序列初始化抗体种群在可行域区间均匀分布对算法寻优精度的提高是有效的. 同时, 本文提出的综合3种改进策略的DMSCSA算法比不含某一改进策略的算法均具有更优的精度和更稳定的效果, 表明本文策略的有效性.
| 表 1 CEC2019测试函数 |
| 表 2 单峰测试函数寻优性能比较 |
| 表 3 多峰测试函数寻优性能比较 |
| 表 4 消融实验性能比较(dim=10) |
4.4 收敛曲线分析
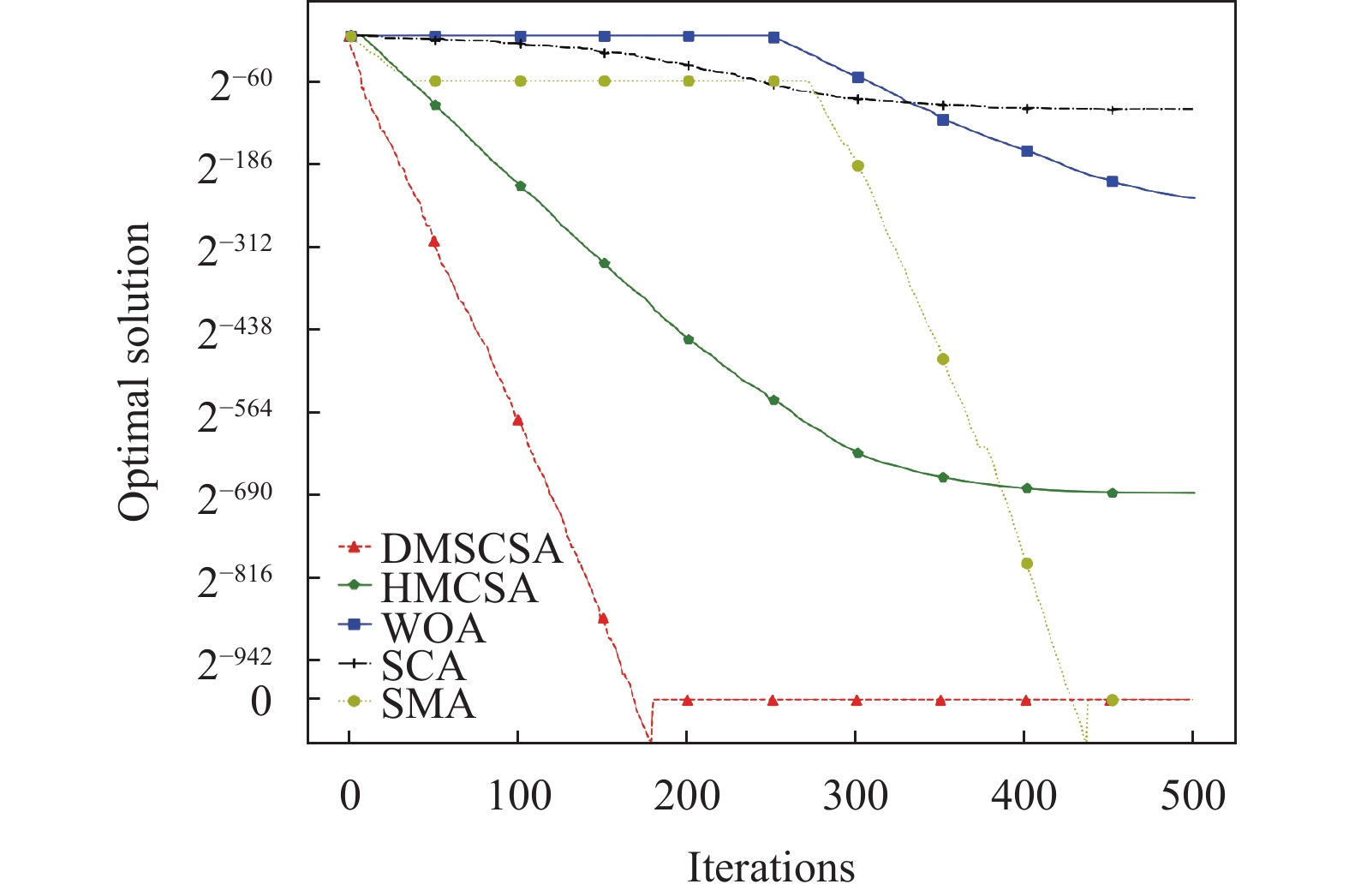
通过收敛曲线图可以更加直观地反映算法的寻优性能. 本文选取混合变异克隆选择算法(HMCSA)[14]、鲸鱼优化算法(WOA)[16]、黏液霉菌算法(SMA)[17]、正余弦算法(SCA)[18]共计4个近几年提出的、寻优效果好的智能搜索算法来进行收敛曲线对比.
图4–图9给出了DMSCSA算法与混合变异克隆选择算法(HMCSA)[14]、鲸鱼优化算法(WOA)[16]、黏液霉菌算法(SMA)[17]、正余弦算法(SCA)[18]对于6个测试函数的收敛曲线对比图. 其中横纵坐标分别表示算法的总迭代次数和算法寻优值.
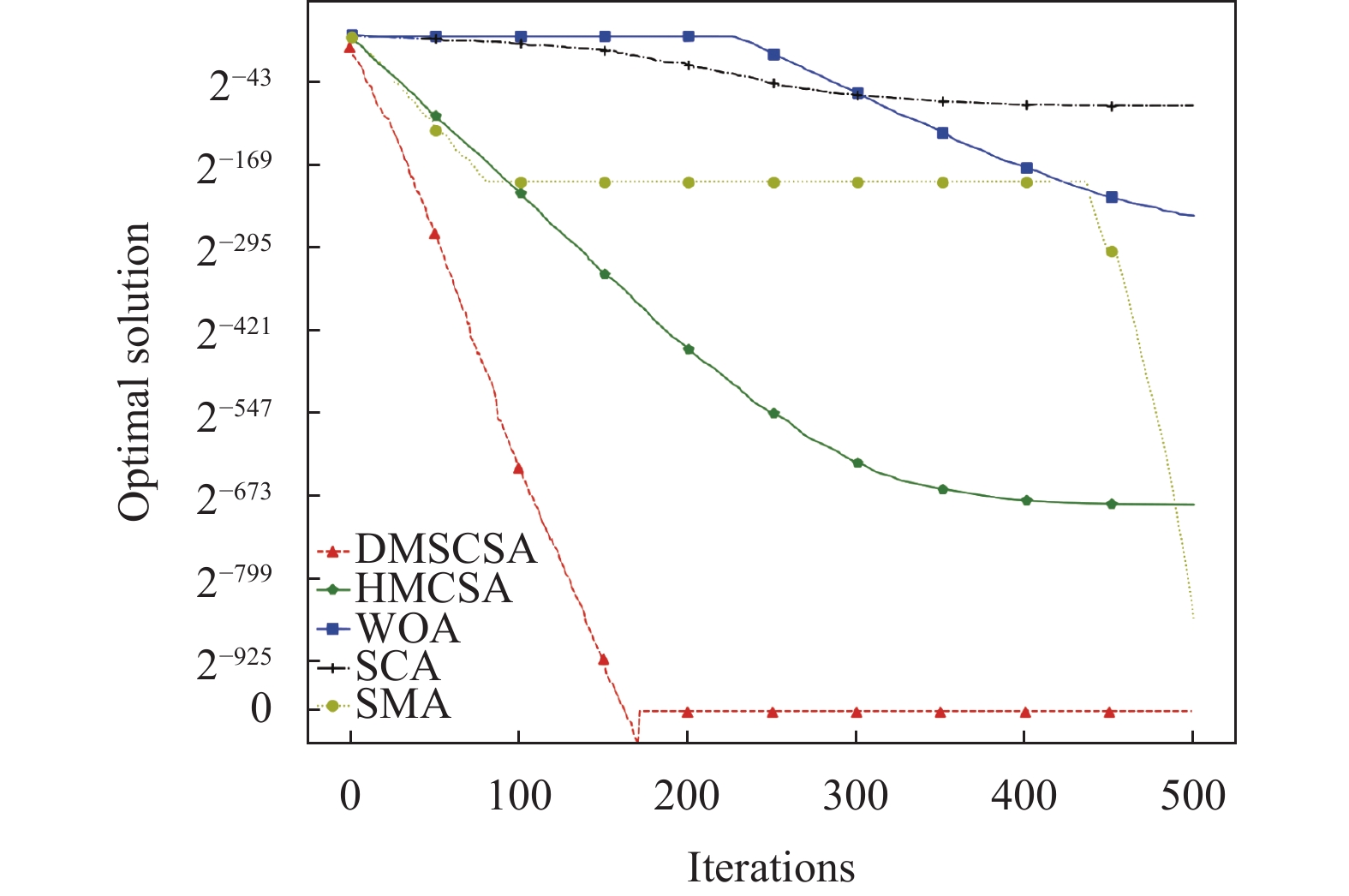
|
图 4 |
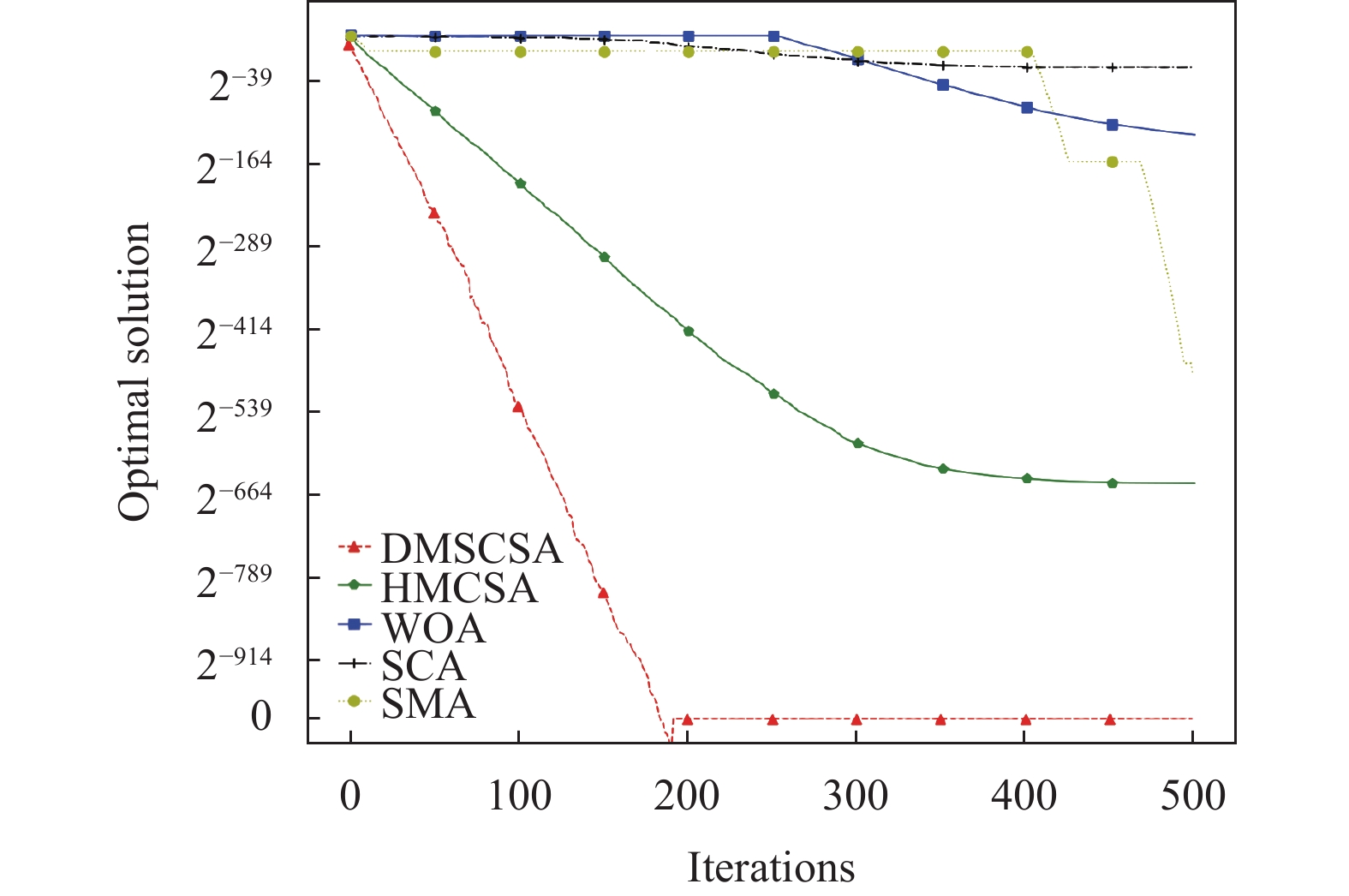
|
图 5 |
以上6个测试函数的收敛曲线对比图清晰地展现出DMSCSA算法与其他4个算法在迭代次数和维度都相同的情况下的寻优结果、寻优速度以及收敛曲线变化趋势. 其中f1–f4这4个单峰函数中, DMSCSA算法收敛速度与精度均表现最好. 在多峰函数测试情况下,
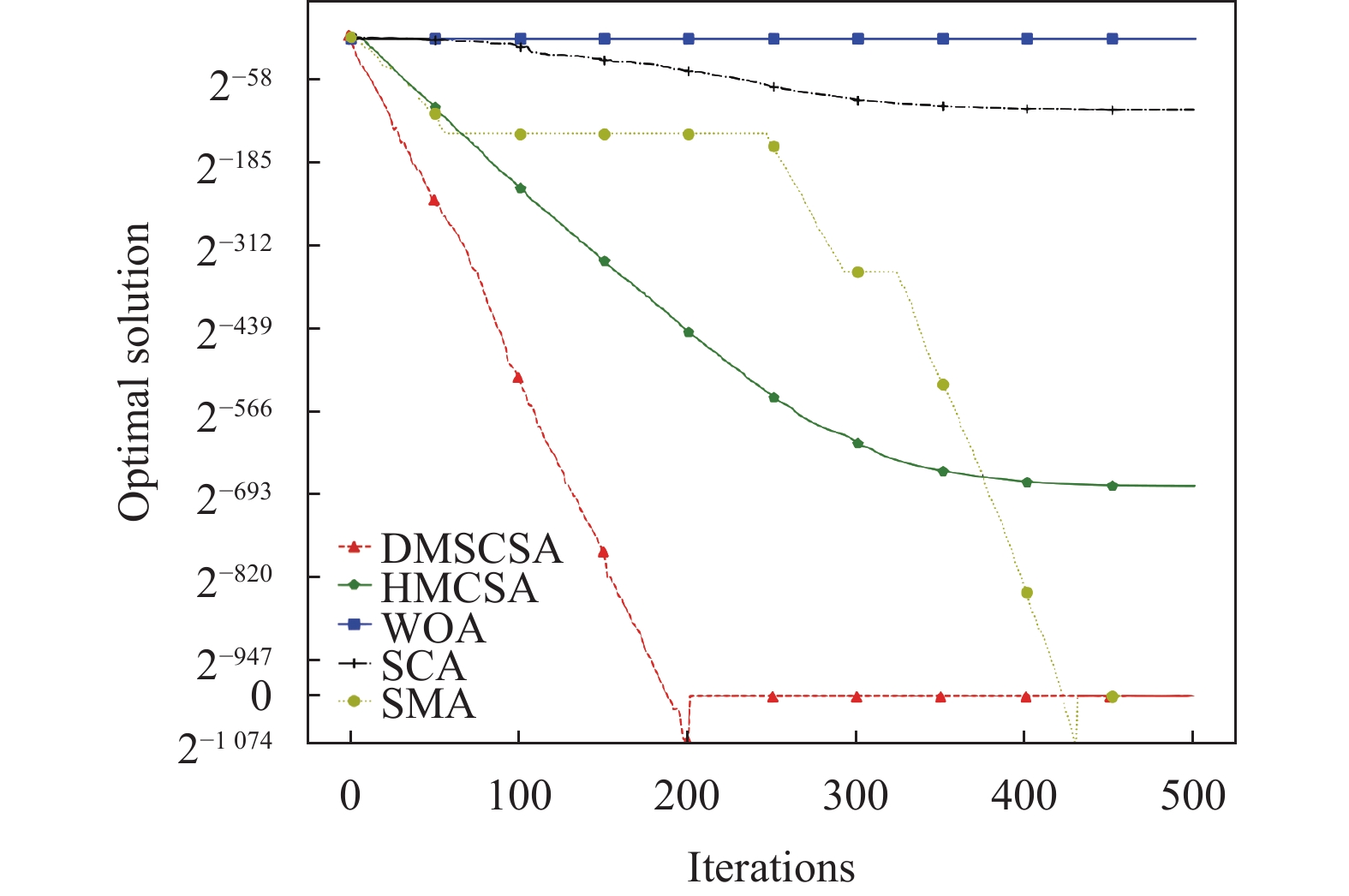
|
图 6 |

|
图 7 |

|
图 8 |
5 总结与展望
针对传统的克隆选择算法在初始化阶段, 使用随机性初始化生成较为分散的种群而导致算法搜索时间增大的问题, 本文采用Halton序列来伪随机地初始化种群, 使产生的抗体都能均匀地分布在整个解空间中. 针对算法在变异阶段随机变异可能导致收敛速度降低问题, 本文采用黄金正弦算法来进行定向变异, 使算法一直往最优解的方向正向变异. 引入柯西变异来扩大搜索范围以解决算法容易陷入局部最优的问题.
|
图 9 |
改进的算法在初始化阶段以及变异阶段中进行定向生成与定向更新, 弥补了克隆选择算法在这两个阶段的不足. 与其他同类型算法的对比实验结果表明, 改进后的算法能在兼顾种群多样性与搜索能力的前提下, 提高算法的寻优精度和收敛速度. 因此, 本文提出的改进是一种有效的改进策略.
| [1] |
王其涛. 元启发式算法在离散选址中的应用 [硕士学位论文]. 南京: 南京航空航天大学, 2010. ]
|
| [2] |
全燕鸣, 何一明. 多机器人任务分配调度的克隆选择算法. 华南理工大学学报(自然科学版), 2021, 49(5): 102-110. DOI:10.12141/j.issn.1000-565X.200300 |
| [3] |
孙欣, 王宇嘉, 林炜星. 均匀克隆选择算法在城市配送中心选址中的应用. 制造业自动化, 2022, 44(9): 86-90. DOI:10.3969/j.issn.1009-0134.2022.09.019 |
| [4] |
孔德健, 史其宁, 白佳琦, 等. 免疫克隆算法在500 kV输电线路故障识别中的应用. 电气自动化, 2019, 41(5): 38-40, 102. DOI:10.3969/j.issn.1000-3886.2019.05.012 |
| [5] |
陈强, 傅煜, 蔡琦盼. 基于克隆选择差分进化算法的永磁同步电机参数辨识. 传感器与微系统, 2022, 41(1): 135-137, 141. DOI:10.13873/J.1000-9787(2022)01-0135-03 |
| [6] |
舒万能, 丁立新. 克隆选择算法的优化和品质因数. 软件学报, 2016, 27(11): 2763-2776. DOI:10.13328/j.cnki.jos.004911 |
| [7] |
Zhou BH, Wu Q. An improved immune clonal selection algorithm for bi-objective robotic assemble line balancing problems considering time and space constraints. Engineering Computations, 2019, 36(6): 1868-1892. DOI:10.1108/EC-11-2018-0512 |
| [8] |
Liu JQ, Zhang ZQ, Gong JH, et al. A novel hybrid clonal selection algorithm for the corridor allocation problem with irregular material handling positions. Computers & Industrial Engineering, 2022, 168: 108118. DOI:10.1016/J.CIE.2022.108118 |
| [9] |
王丽丽, 申燚, 徐玉松, 等. 融合云模型和反向学习的克隆选择算法. 计算机工程与应用, 2021, 57(17): 68-74. DOI:10.3778/j.issn.1002-8331.2007-0327 |
| [10] |
戴迎春, 徐子瑞, 蔡明明, 等. 差分克隆选择算法在多机器人任务分配中的应用. 江苏海洋大学学报(自然科学版), 2023, 32(1): 18-26. DOI:10.3969/j.issn.2096-8248.2023.01.003 |
| [11] |
Tanyildizi E, Demir G. Golden sine algorithm: A novel math-inspired algorithm. Advances in Electrical and Computer Engineering, 2017, 17(2): 71-78. DOI:10.4316/AECE.2017.02010 |
| [12] |
李爱莲, 全凌翔, 崔桂梅, 等. 融合正余弦和柯西变异的麻雀搜索算法. 计算机工程与应用, 2022, 58(3): 91-99. DOI:10.3778/j.issn.1002-8331.2106-0148 |
| [13] |
Yang C, Chen BQ, Jia L, et al. Improved clonal selection algorithm based on biological forgetting mechanism. Complexity, 2020, 2020: 2807056. DOI:10.1155/2020/2807056 |
| [14] |
石建平, 代天军, 周章渝, 等. 混合变异克隆选择算法及其在机械臂逆运动学问题中的应用. 计算机集成制造系统, 2023, 29(5): 1539-1549. DOI:10.13196/j.cims.2023.05.012 |
| [15] |
Gálvez A, Iglesias A, Avila A, et al. Elitist clonal selection algorithm for optimal choice of free knots in B-spline data fitting. Applied Soft Computing, 2015, 26: 90-106. DOI:10.1016/j.asoc.2014.09.030 |
| [16] |
Mirjalili S, Lewis A. The whale optimization algorithm. Advances in Engineering Software, 2016, 95: 51-67. DOI:10.1016/j.advengsoft.2016.01.008 |
| [17] |
Li SM, Chen HL, Wang MJ, et al. Slime mould algorithm: A new method for stochastic optimization. Future Generation Computer Systems, 2020, 111: 300-323. DOI:10.1016/j.future.2020.03.055 |
| [18] |
Mirjalili S. SCA: A sine cosine algorithm for solving optimization problems. Knowledge-based Systems, 2016, 96: 120-133. DOI:10.1016/j.knosys.2015.12.022 |
 2024, Vol. 33
2024, Vol. 33


