时间序列数据, 又称时序数据, 是按照时间顺序进行排列的一组集合[1]. 当研究者们通过观察时序数据发现其中一个数据和其他数据相差过大时, 则认为该时间点发生了异常, 根据异常点数量的不同, 可以将异常数据分为点异常和集合异常[2], 不同的异常情况带来的安全隐患不同, 如果不进行及时处理, 那么最后有可能带来重大的经济损失, 因此, 研究者们通过各种方法检测出时序数据的异常部分, 这个过程被称为时序数据异常检测[3]. 时序数据异常检测作为数据分析领域的一个重要研究方向, 它常被应用于各种工程应用, 例如城市车辆轨道运行情况[4]、航天器遥测数据[5]和大气排污[6]等, 工程师们通过对时序数据发生异常的片段进行处理, 从而提高系统的可靠性和准确性.
随着互联网和物联网的发展, 越来越多的传感器数据被实时采集和存储, 这些数据往往是多维庞杂的. 所以如何从这些数据中提取有价值的信息, 现已成为数据分析领域的重要研究问题之一.
早期研究人员使用统计分布的方法对时序数据进行异常检测, 例如K-means模型[7]将相似点聚集成簇, 多数点形成的簇被视为正常, 远离正常簇的点被视为异常, 尽管K-means计算高效, 但它难以处理多维数据. 经典方法自回归求和滑动平均模型(autoregressive integrated moving average model, ARIMA)的变体也常被用于检测异常数据[8], 但很少用于多维时序数据的异常检测, 并且异常检测的准确率仍需提高. Nakamura等人[9]提出的MERLIN模型通过改进时间序列不一致的方法解决了用户选择子序列长度敏感性问题, 并在大量的时序数据中有效地找到所有可能的结果, 但是子序列的排列容易受到其他维度的影响, 以至于在多维时序数据上表现不佳. 为了解决传统方法难以处理多维时序数据的问题, 研究者们引入深度学习的方法.
相比传统方法, 深度学习方法更适用于大量多维数据. 其中, Hundman等人[10]提出长短期记忆无参阈值异常检测(long short term memory and no parameter exception detection threshold, LSTM-NDT). 该方法利用LSTM得到重建误差, 并通过无参阈值的方法判断该点是否为异常. LSTM-NDT不需要人工干预, 节省了大量人力成本, 但LSTM-NDT单一的架构难以关注到时序数据其余特征. 为了让模型关注到更多的时序特征, 丰富时序预测结果, 研究者们将多种深度学习模型进行融合, 其中Su等人[11]提出一种多模型融合的模型OmniAnomaly, OmniAnomaly将门控循环单元(gated recurrent unit, GRU)和变分自动编码器(variational auto-encoders, VAE)相结合, 它可以处理变量之间显式的时间关联, 从而提高数据重建的鲁棒性, 同时, OmniAnomaly使用一种新的阈值自动检测方法: 阈值峰值(peak of threshold, POT), POT可以高效准确地检测异常. 虽然OmniAnomaly利用GRU关注到时序数据之间的时间特性[12], 但往往会忽视时序数据的全局特性. 为了捕获时序数据的全局特征, Tuli等人[13]提出一种基于Transformer的异常检测(Transformer networks for anomaly detection, TranAD)模型, TranAD采用Tansformer和GAN相结合的方式, 将Transformer作为判别器和生成器进行对抗式训练以提高模型特征提取的稳定性, 同时TranAD使用对抗训练一阶段的焦点得分作为外部知识, 增强了模型对异常点的关注度, 提高模型对时序数据局部趋势的建模能力, 得益于Transformer模型的结构, TranAD在众多数据集上表现良好, 但因为TranAD是以Transformer为主的深度模型, 所以TranAD不容易关注到时序数据的时间特征.
为了使模型能够同时关注到时序数据的多种特征, 研究者们将目光投向Stacking集成学习, Stacking集成学习[14]是指结合所有基模型的一种训练方式, 先训练不同的基模型, 然后所有基模型的输出使用投票法或全连接等方式生成最终结果. 使用Stacking集成学习可以让不同的基模型学习到不同的时序特征, 降低过拟合风险, 从而提高模型的整体性能. 陈仲磊等人[15]提出一种基于集成学习的异常检测框架, 使用预训练生成式转换器(generative pre-trained Transformer, GPT)、GRU、随机森林作为集成学习的基模型, 基模型GRU作为预测的主要网络, GPT利用注意力机制提高模型预测准确率, 两个基模型共同关注时序数据的全局和时间特征, 提高模型异常检测能力, 随机森林对整体输出进行宏观调控提升模型稳定性. 但是过于复杂的集成模型难以训练大规模数据, 并且计算开销大.
综合以上研究存在的问题, 本文提出一种基于PSO和外部知识的时序数据异常检测模型(anomaly detection of time series based on PSO and external knowledge, PEAD), 其中为了提高基模型对时序数据局部趋势的建模能力, PEAD将快速傅里叶变换(fast Fourier transform, FFT)生成的外部知识引入基模型, 另外, 为了使得PEAD模型可以同时关注时序数据时间特征和全局特征, PEAD使用PSO[16]对基模型进行Stacking集成学习, 通过减少基模型数量和使用传统方法集成, 保证模型结构简洁高效的同时能够有效处理大规模数据.
1 理论基础 1.1 粒子群优化算法Kennedy等人[17]受到鸟类觅食规律的启发, 经过多年研究最终形成粒子群优化算法, 又称粒子群算法, 粒子群算法的本质在于集体的信息共享机制.
如图1所示, 假设森林中的鸟类进行随机移动, 目的是为了搜索整个森林中最大食物, 每个鸟类通过初始方向进行随机搜索, 在第1次搜索结束后, 鸟类可能会接近最大食物, 也可能会接近少量食物, 又或者偏离食物, 搜索结束后鸟类会记录当前搜索到的最大食物和位置, 然后通过共享机制将食物和位置共享给整个鸟类群, 这样鸟类群就知道哪个位置的食物最多, 鸟类在随后的每一次搜索通过自身记录的最大食物位置和全体最大食物位置进行移动, 从而使整个鸟类群向最大食物的位置聚拢.

|
图 1 鸟类捕食过程 |
将上述鸟类捕食过程对应到粒子群算法中, 鸟类表示粒子, 食物表示适应值, 鸟类位置表示一个局部解, 鸟类当前搜索到的最大食物表示局部最大适应值, 最大食物表示全局最大适应值, 鸟类当前搜索到的最大食物位置表示局部最优解, 最大食物位置表示全局最优解. 本研究的目的是通过粒子群算法, 找到两个模型输出的最优权重, 也就是最大食物位置, 通过加权求和的方式给不同的模型分配权重, 让模型可以同时关注到时序数据的不同特征.
1.2 快速傅里叶变换快速傅里叶变换是离散傅里叶变换的一种快速计算方法, 本质上是使用分治策略, 将数据规模为
本研究使用FFT算法, 将时序数据从时域映射到频域, 然后保留高频的数据, 最后使用逆FFT生成高频时序数据, 高频时序数据将作为外部知识和原始数据结合, 最后生成带有高频信息的输入数据, 相比原始数据, 带有高频信息的输入数据更加关注时序数据中变化明显的区域, 从而增强基模型对局部趋势的建模能力.
2 基于PSO和外部知识的异常检测模型本文基于PSO和外部知识的异常检测模型算法流程如算法1所示.
算法1. 基于PSO和外部知识的异常检测模型
1) 输入: 训练集
2) 数据预处理: 对
3) FFT生成外部知识: 对
4) 基模型Transformer生成重构数据
5) 基模型LSTM生成重构数据
6) for i=1 to n: 步骤4)和步骤5)经过迭代训练后分别得到
7) PSO生成最终重构数据
8) 输出: 对
本文基于PSO和外部知识的异常检测模型PEAD结构图如图2所示, 整体结构分为6个部分, 首先对原始时序数据
第2节剩下部分将会详细介绍模型的具体实现.
2.1 数据预处理在进行异常检测之前, 首先对时序数据进行预处理操作. 以多维时序数据为例, 假设时间长度为N, 时序数据可以表示如下:
| $ T = \{ {x_1}, {x_2}, \cdots, {x_N}\} $ | (1) |
其中,
接下来对数据进行归一化处理, 并且设置滑动窗口, 归一化如下:
| $ {x_n} = \frac{{{x_n} - \min (T)}}{{\max (T) - \min (T) + \varepsilon }} $ | (2) |
其中, min(T)、max(T)分别表示时序数据T的最小值和最大值,
滑动窗口经常被用于处理时序数据[13], 具体地, 使用滑动窗口对归一化时序数据进行切片, 切片大小取决于窗口大小q.
| $ {W_N} = \{ {x_{N - q + 1}}, \cdots, {x_N}\} $ | (3) |
滑动窗口
| $ {f_j} = \sum\limits_{n = n - q + 1}^N {{x_n}{{\rm{e}}^{ - i\omega n}}} $ | (4) |
FFT内部生成频率
| $ {f'_j} = \left\{ {\begin{array}{*{20}{l}} {{f_j},\;\;\;\;\;\;\;\;\;\;j \in \max ({f_j}, k)} \\ {0,\;\;\;\;\;\;\;\;\;\;\;j \notin \max ({f_j}, k)} \end{array}} \right. $ | (5) |

|
图 2 PEAD模型结构图 |
最后,
| $ {W'_N} = \sum\limits_{j = 0}^{n/2 + 1} {{f_j}{{\rm{e}}^{i\omega j}}} $ | (6) |
新的时序数据
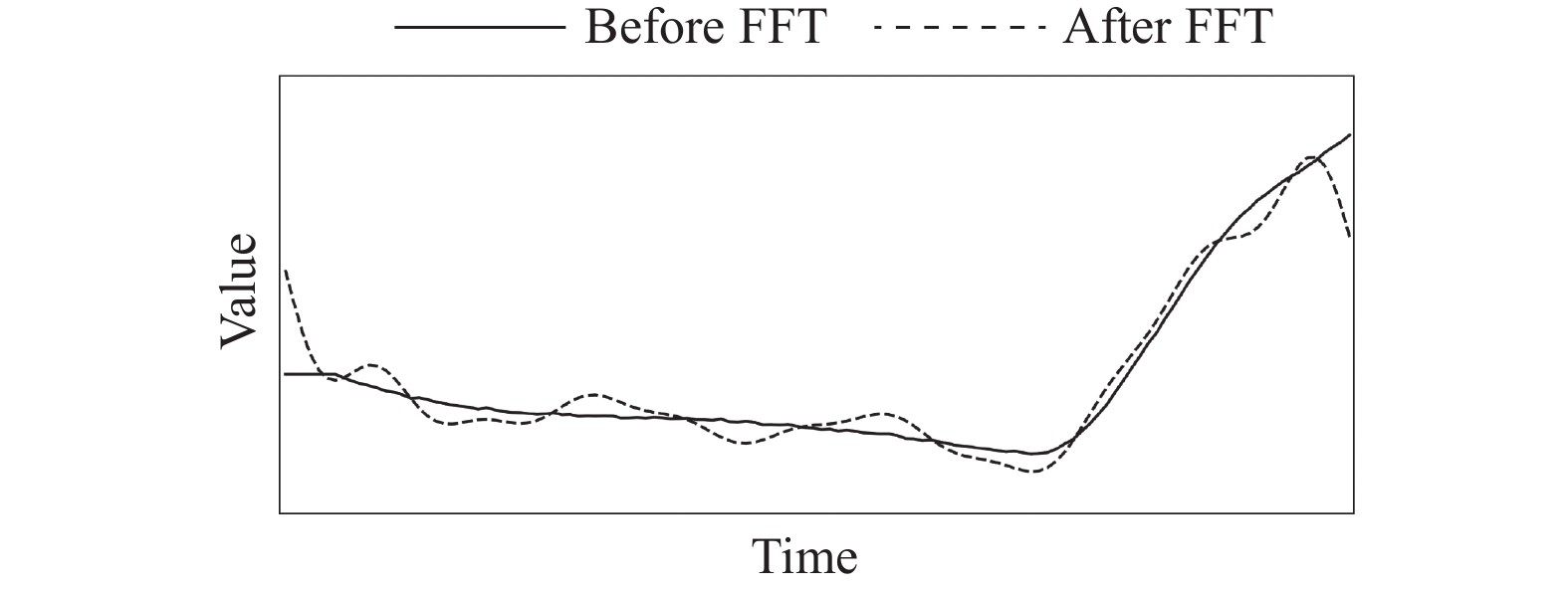
|
图 3 时序数据FFT前后对比 |
2.3 集成模型训练部分 2.3.1 基模型Transformer生成重构数据1
实验使用的基模型之一是Transformer, 它常被用于各种自然语言处理任务[19], 由于时序数据属于文本数据的一种, 因此可以使用Transformer处理时序数据. 如图4所示, 基模型Transformer分为两个部分, 一个是编码层Encoder, 另一个是解码层Decoder. 外部知识

|
图 4 Transformer模型结构图 |
| $ I = {W_N} \oplus {W'_N} $ | (7) |
| $ I' = Norm(I + MultiHeadAtt(I, I, I)) $ | (8) |
| $ I'' = Norm(I' + FeedForward(I')) $ | (9) |
其中, “
对于Decoder, 直接将原始数据T输入Decoder.
| $ T' = Norm(T + MultiHeadAtt(T, T, T)) $ | (10) |
| $ T'' = Norm(T' + MultiHeadAtt(T', I'', I'')) $ | (11) |
其中, Encoder的输出
| $ {O_1} = {\textit{Sigmoid}}(FeedForward(T'')) $ | (12) |
激活函数Sigmoid的作用主要是生成[0, 1]范围内的输出, 并使结果标准化.
对基模型Transformer 使用梯度下降算法优化模型权重, 误差函数使用均方误差, Transformer经过迭代训练后得到重构数据
| $ {L_1} = ||{O_1} - T|{|_2} $ | (13) |
另一个基模型使用LSTM, 原始数据T作为输入. LSTM和Transformer不同, 它主要是对
LSTM有3个门控机制, 利用不同的权重来过滤过去的信息, 首先是用来更新输入门的模块:
| $ {{\textit{z}}_n} = g({W_{\textit{z}}}{x_n} + {R_{\textit{z}}}y{}_{n - 1} + {b_{\textit{z}}}) $ | (14) |
其中, g是激活函数, 使用tanh进行激活, 它可以将数值规定到[−1, 1]的范围内;
输入门: 当前时间点输入
| $ {i_n} = \sigma ({W_i}{x_n} + {R_i}{y_{n - 1}} + {P_i} \otimes {c_{n - 1}} + {b_i}) $ | (15) |
其中,
遗忘门: 时序数据并非每个点都息息相关, 这时就需要遗忘门有选择地遗忘一部分数据, 从而达到更鲁棒的效果[12].
| $ {f_n} = \sigma ({W_f}{x_n} + {R_f}{y_{n - 1}} + {P_f} \otimes {c_{n - 1}} + {b_f}) $ | (16) |
其中,
隐藏状态: 隐藏状态c记录之前所有时间点的所有信息[12], 它保存了每个时间点的时间特征.
| $ {c_n} = {{\textit{z}}_n} \otimes {i_n} + {c_{n - 1}} \otimes {f_n} $ | (17) |
利用更新模块
输出门: LSTM块利用当前时间点
| $ {o_n} = \sigma ({W_o}{x_n} + {R_o}{y_{n - 1}} + {P_o} \otimes {c_n} + {b_o}) $ | (18) |
其中,
LSTM输出: 对
| $ {y_n} = g({c_n}) \otimes {o_n} $ | (19) |
一个时间点使用一个LSTM块预测

|
图 5 LSTM模型结构图 |
| $ {O_2} = FeedForward(Y) $ | (20) |
对基模型LSTM使用梯度下降算法优化模型权重, 误差函数使用均方误差, LSTM经过迭代训练后得到重构数据
| $ {L_2} = ||{O_2} - T|{|_2} $ | (21) |
PSO是一种启发式寻优算法, 它通过粒子群不断地迭代优化函数, 最终寻找到函数取得最小或最大值时的最优位置[16].
假设在2维空间有N个粒子, 每个粒子代表一个解.
| $ {W_i} = \{ {w_{i1}}, {w_{i2}}\} $ | (22) |
其中,
| $ f = ||({w_{i1}}O'_1 + {w_{i2}}{O'_2}) - T|{|_2} $ | (23) |
其中,
| $ {V_i} = \{ {v_{i1}}, {v_{i2}}\} $ | (24) |
其中,
| $ V_i^{k + 1} = \omega V_i^k + {c_1}{r_1}(P_{il}^k - W_i^k) + {c_2}{r_2}(P_w^k - W_i^k) $ | (25) |
其中, k表示当前时刻, k+1表示下一时刻,
速度更新完成后再对粒子的位置进行更新, 更新公式如下:
| $ W_i^{k + 1} = W_i^k + V_i^{k + 1} $ | (26) |
更新后的
算法2. PSO算法
1) 初始化粒子群;
2) 计算每个粒子的适应值
3) 对于每个粒子, 将当前适应值和局部最优适应值进行比较, 如果当前适应值小于局部最优适应值, 那么更新局部最优适应值, 并且更新局部最优位置
4) 对于每个粒子, 将当前适应值和全局最优适应值进行比较, 如果当前适应值小于全局最优适应值, 那么更新全局最优适应值, 并且更新全局最优位置
5) 迭代更新粒子速度
6) 根据终止条件判断迭代次数是否达到最大, 或者粒子全局最优适应值是否小于给定阈值, 若是, 结束算法并输出全局最优适应值和对应最优位置
PSO算法得到的
| $ {P_w} = \{ {p_1}, {p_2}\} $ | (27) |
| $ O = {p_1}{O'_1} + {p_2}{O'_2} $ | (28) |
经过PSO模块得到最优权重
实验使用POT方法自动选择异常的阈值[20], 对重构数据
| $ L = ||O - T|{|_2} $ | (29) |
| $ {y_i} = 1 \; ({\rm{if}}{\text{ }}L \geqslant POT(L)) $ | (30) |
| $ Y = \{ {y_1}, {y_2}, \cdots, {y_n}\} $ | (31) |
实验将模型PEAD与目前先进的多维时序数据异常检测模型作对比, 包括TranAD[13]、LSTM-NDT[10]、OmniAnomaly[11]和MERLIN[9]. 实验使用PyTorch 1.7.1版本.
所有模型统一使用AdamW优化器进行梯度下降, 初始学习率为0.01, 学习率更新因子为0.9 (每次下降10%), 滑动窗口大小都设置为10, 模型丢弃率设置为0.1, 损失函数使用均方误差.
PEAD的Transformer编码层和解码层的层数都为1, 前馈神经网络输入维度为2, 隐藏层维度为64. LSTM层数为2, 隐藏层维度为64. PSO粒子群个数为50, 迭代步数3000, 阈值1E–7, 粒子位置边界[0, 1], 粒子速度边界[−0.3, 0.3], 惯性权重、学习因子都设置为2. 对于POT参数, PEAD和TranAD保持一致[13], 系数为10E–4, MSL低分位数为0.001, 多头注意力机制的头数和时序数据的维度保持一致.
TranAD使用两个Transformer模型, 其中一个作为编码层, 层数为1, 另外一个作为解码层, 层数为1, 解码层的前馈神经网络单元为2, 编码层中的隐藏单元为64. TranAD使用GAN方式将编码层作为生成器, 解码层作为鉴别器, 第1阶段生成器生成的预测数据作为焦点得分和原始数据结合, 然后将带有焦点得分的数据输入到第2阶段生成预测数据, 预测数据再通过均方误差进行梯度下降, 迭代优化.
LSTM-NDT采用2层LSTM进行时序数据预测, 使用linear作为激活函数, 对预测数据构成的误差进行加权平均的平滑处理, 根据平滑后的数据计算阈值, 大于阈值的标记为异常, 和普通LSTM相比增加了非参数动态误差阈值.
OmniAnomaly采用2层GRU架构, 隐藏层单元为32, 激活函数采用ReLU和Sigmoid, 第1层GRU对时序数据进行编码后, 再对其使用VAE, VAE将编码后的数据映射到潜在空间z, 然后再用第2层GRU生成预测数据, 损失函数除了均方误差外还有KL散度.
MERLIN使用统计分布的办法进行异常检测, 算法整体分为两个阶段, 第1阶段目的是得到异常集合C, 对时间序列使用minL=60进行数据滑动得到不同的子序列, 再使用均方误差得到每两个子序列之间的误差, 误差大于阈值r的时间点加入异常集合C,
实验中使用的6个数据集如表1所示.
| 表 1 数据集 |
表1是实验使用公开数据集的详细信息[13], 包括训练集、测试集、维度和异常率, 异常率指的是测试集中数据点异常所占的百分比. 其中除了UCR是单维时序数据外其他数据集都是多维数据.
HexagonML数据集(UCR)是KDD 2021杯使用的数据集[22], 实验中仅使用InternalBleeding和EGG数据集. 火星科学实验室数据集(Mars science laboratory, MSL)来自火星车本身的传感器和制动器[10]. MIT-BIH室上性心律失常数据库(MIT-BIH supraventricular arrhythmia database, MBA)是4名患者的心电图集合, 包含了两种不同的心律失常的实例[23,24]. 多源分布式系统数据集(multi-source distributed system, MSDS)包含了分布式跟踪日志、应用程序日志和度量等多个维度[25]. 安全水处理数据集(secure water treatment, SWaT)来自真实水处理厂, 包括传感器值和制动器操作[26]. 服务器数据集(server machine dataset, SMD)包含了5周数据, 数据来自28台机器资源调度情况[11].
3.2 评估指标异常检测实验使用4个指标进行评估, 包括精确率(precision, P)、召回率(recall, R)、接受操作特征曲线下面积(area under the receiver operating characteristic curve, ROC/AUC)和F1值, 实验使用这4个指标评估所有模型性能.
| $ P = \frac{{TP}}{{TP + FP}} $ | (32) |
其中, TP表示正类预测为正类的个数, FP表示负类预测为正类的个数, P表示预测正确的个数在所有正类预测个数的比例.
| $ R = \frac{{TP}}{{TP + FN}} $ | (33) |
其中, FN表示正类预测为负类的个数, R表示正类被预测为正类的个数在所有标注数据上的占比.
| $ AUC = \frac{{\displaystyle\sum\nolimits_{i \in positive} {ran{k_i} - \frac{{M \times (M + 1)}}{2}} }}{{M \times N}} $ | (34) |
其中,
| $ F1 = \frac{{2 \times {\textit{P}} \times {\textit{R}}}}{{{\textit{P}} + {\textit{R}}}} $ | (35) |
其中, F1值表示精确率和召回率的调和平均数. P、R、AUC和F1值越大表示模型性能越好.
3.3 对比实验选取MERLIN、LSTM-NDT、OmniAnomaly和TranAD作为比较基准, 使用测试集对训练好的模型进行测试, 测试主要以AUC和F1的结果作为异常检测性能好坏的判断依据, 其中MERLIN、LSTM-NDT和OmniAnomaly的实验结果来自Tuli等人[13].
表2提供了对比模型在所有数据集上的得分, 粗体表示在所有对比模型中获得最高得分. PEAD模型在P、R、AUC和F1上的平均得分分别为0.9371、0.9275、0.9602、0.9259. 并且在MAB、SWaT、SMD和MSL这4个数据集上取得最高F1得分. 由于时序数据具有多种特性, 包括数据之间的时间关联、空间关联, 因此, 通过PSO分配权重给基模型Transformer和LSTM的预测数据, 使得预测数据各自占有最佳比例的权重, 然后通过加权求和生成最终预测数据, 最终预测数据带有模型的结构特点, Transformer由于多头注意力机制所以更注重全局特性, LSTM因为前一刻的输出作为下一刻的输入所以更关注时间特性, 相比单一的深度模型, 具备丰富时序特性的PEAD能够在大部分数据集上取得更好的得分.
PEAD模型在所有数据集的F1和AUC得分, 全部超过基于统计分布的传统算法MERLIN. 另外, 在多维数据集上, 所有深度模型F1和AUC得分普遍优于MERLIN. MERLIN属于统计分布的方法, 通过发现子序列不一致的情况判断该时序区间是否异常, 这种方法更适用于序列长且周期规律的时序数据, 面对分布不均的多维时序数据, MERLIN难以通过周期性进行异常检测, 而深度模型是通过预测的形式进行异常检测, 并不完全依赖周期规律, 所以深度模型在时序数据异常检测方面比传统方法更有优势.
PEAD模型与LSTM-NDT模型相比, 在单维数据集UCR上, 对比指标F1得分提高了36.8%, AUC得分提高了1.96%, 在其他多维数据集上, F1得分平均提高了13.8%, AUC得分平均提高了11.9%. PEAD模型与OminAnomaly模型相比, 在单维数据集UCR上, 对比指标F1得分下降了3.55%, 在其他多维数据集上, F1得分平均提高了5.35%, AUC得分平均提高了1.95%. PEAD模型与TranAD模型相比, 在单维数据集UCR上, 对比指标F1得分下降了9.48%, AUC得分下降了0.21%, 在其他多维数据集上, F1得分平均提高了1.11%, AUC得分平均提高了0.833%. 受限于基模型Transformer和LSTM的性能, PEAD模型的集成效果在UCR和MSD数据集上表现不如TranAD模型, 但在其余数据集上的AUC和F1得分都超过了TranAD模型. LSTM-NDT和OminAnomaly都是以RNN为主的深度模型, 模型的预测数据只与时序数据的时间特征相关联, TranAD是以Transformer为主的深度模型, 模型的预测数据只与时序数据的全局特征相关联, 这两类模型都只关注到单方面的时序特征, 预测数据的时序特征不够丰富, 包含信息量相对较少, 而PEAD通过PSO对预测数据分配权重, 使得最终预测数据同时关注到时序数据的时间特征(来自基模型LSTM)和全局特征(来自基模型Transformer), 预测数据包含的信息量大于其他深度模型, 因此在大部分数据集上表现良好.
| 表 2 PEAD模型和对比模型在所有数据集上的得分比较 (最佳F1得分和AUC得分用粗体表示) |
另外, 为了探究通过FFT生成的外部知识在PEAD模型中起的作用, 如图6所示, 上面的曲线是PEAD模型在MSL数据集第0维度上的预测曲线(虚线)和真实曲线(实线), 下面的曲线是OmniAnomaly模型在MSL数据集第0维度上的预测曲线和真实曲线. 从图6可以看出, PEAD模型的预测曲线在真实曲线突变点(值突然下降的点)可以较好地重构数据, 而没有外部知识引入的OminAnomaly模型, 它的预测曲线平缓, 对真实曲线突变点不敏感, 这是因为PEAD的基模型Transformer将高频预测数据和原始数据结合生成输入数据, 输入数据更加关注曲线陡峭的时间点, 从而有效地提高模型对时序数据局部趋势的建模能力, 最终提高模型的异常检测准确率.
3.4 消融实验为了进一步验证模型的效果, 表3显示了消融实验的结果. 包括PEAD模型、Transformer w/o FFT模型、LSTM模型和Transformer FFT模型在所有数据集上P、R、AUC和F1得分. Transformer w/o FFT模型作为单一模型进行测试, 不引入FFT生成的外部知识, LSTM模型和Transformer FFT模型也都作为单一模型进行测试, 但Transformer FFT模型引入FFT生成的外部知识.

|
图 6 PEAD (上)和OmniAnomaly (下) 在MSL数据集第0维度上的预测曲线和真实曲线 |
从所有模型在UCR、MBA、MSL、SWaT、SMD和MSDS数据集上的实验结果可以看出, PEAD对比Transformer w/o FFT模型、LSTM模型和Transformer FFT模型, F1得分平均提高了3%, AUC平均得分提高了1%. 虽然在MSDS数据集上PEAD模型的F1得分下降了0.112%, 但PEAD模型的F1得分十分接近Transform FFT模型. F1得分下降是因为MSDS数据集来自分布式系统, 包括指标、日志和跟踪数据, 这些维度的数据更加关注全局特征, 但加入了低F1得分的LSTM影响了PEAD的集成效果. 整体来看, PEAD模型集成效果大部分优于单个基模型, 这是因为生成的预测数据包含更丰富的时序特征, 所以集成模型PEAD更有助于提高模型性能.
为了再次验证FFT生成的外部知识对模型异常检测能力的影响, 如图7所示, 上面的曲线表示Transformer FFT模型在SWaT数据集第0维度上生成的预测曲线(虚线)和真实曲线(实线), 下面的曲线表示Transformer w/o FFT模型在SWaT数据集第0维度上生成的预测曲线和真实曲线, 从图7中可以看出, Transformer FFT模型的预测曲线更接近真实曲线的局部趋势, 说明模型引入FFT生成的外部知识可以有效关注到时序数据的局部趋势, 从而提高模型的异常检测能力.
| 表 3 PEAD、Transformer FFT、LSTM、Transformer w/o FFT在所有数据集上的得分 (最佳F1得分和AUC分数用粗体表示) |

|
图 7 Transformer FFT (上)和Transformer w/o FFT (下) 在SWaT数据集第0维度上的预测曲线和真实曲线 |
4 结论
本文提出了一种基于PSO和外部知识的异常检测模型PEAD, 并在UCR、MBA、MSL、SWaT、SMD和MSDS数据集上进行了异常检测实验, 实验结果表明, PEAD模型在大部分数据集上比只关注单一时序特征的MERLIN、LSTM-NDT、OmniAnomaly和TranAD模型的异常检测效果要好. 本实验得出如下结论.
(1) 使用PSO集成学习的方式可以使模型共同关注时序数据的全局特征和时间特征, 增强模型特征提取能力, 丰富时序特征, 从而提高模型异常检测能力.
(2) 基模型引入FFT生成的外部知识, 增强模型对时序数据局部趋势的建模能力, 从而提高模型整体异常检测能力.
本文提出的模型具有一定的实际意义: 与传统模型比较, 本文提出的模型提高了异常检测的准确率; 与深度模型比较, 本文提出的模型在提高准确率的同时保持模型架构的简洁, 丰富了PSO算法在集成学习方面的研究; 在不同维度的数据集上, 本文提出的模型表现良好, 具有一定的泛化能力, 可以迁移到其他领域进行更深入的研究. 虽然PEAD模型在大部分数据集上表现良好, 但在个别数据集上表现不佳, 除了受限于基模型的性能外, 另一方面是因为PSO算法有一定的概率会落入局部最优解, 模型通过局部最优解无法分配基模型的最佳权重. 后续将继续深入研究PSO算法和基模型之间的联系, 尝试解决算法陷入局部最优解的问题.
| [1] |
马浩轩, 杨笑千, 廖真, 等. 时序数据异常检测算法研究. 科学技术创新, 2022(6): 78-81. DOI:10.3969/j.issn.1673-1328.2022.06.020 |
| [2] |
Choi K, Yi JH, Park C, et al. Deep learning for anomaly detection in time-series data: Review, analysis, and guidelines. IEEE Access, 2021, 9: 120043-120065. DOI:10.1109/ACCESS.2021.3107975 |
| [3] |
徐天慧, 郭强, 张彩明. 基于全变分比分隔距离的时序数据异常检测. 计算机科学, 2022, 49(9): 101-110. |
| [4] |
吴星辰. 基于KNN算法的城市轨道车辆时序数据异常检测. 智能城市, 2021, 7(22): 20-21. DOI:10.19301/j.cnki.zncs.2021.22.007 |
| [5] |
闫媞锦, 夏元清, 张宏伟, 等. 一种非规则采样航空时序数据异常检测方法. 航空学报, 2021, 42(4): 525019. |
| [6] |
宋文燏, 周海波, 吴宗培, 等. 图记忆诱导的大气排污时序数据异常检测算法. 华东理工大学学报(自然科学版), 2023, 49(3): 341-350. DOI:10.14135/j.cnki.1006-3080.20221118001 |
| [7] |
刘明群, 何鑫, 覃日升, 等. 基于改进K-means聚类k值选择算法的配网电压数据异常检测. 电力科学与技术学报, 2022, 37(6): 91-99. DOI:10.19781/j.issn.1673-9140.2022.06.010 |
| [8] |
Yaacob AH, Tan IKT, Chien SF, et al. ARIMA based network anomaly detection. Proceedings of the 2nd International Conference on Communication Software and Networks. Singapore: IEEE, 2010. 205–209.
|
| [9] |
Nakamura T, Imamura M, Mercer R, et al. MERLIN: Parameter-free discovery of arbitrary length anomalies in massive time series archives. Proceedings of the 2020 IEEE International Conference on Data Mining (ICDM). Sorrento: IEEE, 2020. 1190–1195.
|
| [10] |
Hundman K, Constantinou V, Laporte C, et al. Detecting spacecraft anomalies using LSTMs and nonparametric dynamic thresholding. Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. London: ACM, 2018. 387–395.
|
| [11] |
Su Y, Zhao YJ, Niu CH, et al. Robust anomaly detection for multivariate time series through stochastic recurrent neural network. Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. Anchorage: ACM, 2019. 2828–2837.
|
| [12] |
Smagulova K, James AP. A survey on LSTM memristive neural network architectures and applications. The European Physical Journal Special Topics, 2019, 228(10): 2313-2324. DOI:10.1140/epjst/e2019-900046-x |
| [13] |
Tuli S, Casale G, Jennings NR. TranAD: Deep transformer networks for anomaly detection in multivariate time series data. Proceedings of the VLDB Endowment, 2022, 15(6): 1201-1214. DOI:10.14778/3514061.3514067 |
| [14] |
徐继伟, 杨云. 集成学习方法: 研究综述. 云南大学学报(自然科学版), 2018, 40(6): 1082–1092.
|
| [15] |
陈仲磊, 伊鹏, 陈祥, 等. 基于集成学习的系统调用实时异常检测框架. 计算机工程, 2023, 49(6): 162-169, 179. DOI:10.19678/j.issn.1000-3428.0065643 |
| [16] |
Li JB, Izakian H, Pedrycz W, et al. Clustering-based anomaly detection in multivariate time series data. Applied Soft Computing, 2021, 100: 106919. DOI:10.1016/j.asoc.2020.106919 |
| [17] |
Kennedy J, Eberhart R. Particle swarm optimization. Proceedings of the 1995 International Conference on Neural Networks. Perth: IEEE, 1995. 1942–1948.
|
| [18] |
吴颖超, 胡靖. 基于快速傅里叶变换和选择性卷积核网络的图像补全. 计算机系统应用, 2023, 32(11): 149-158. DOI:10.15888/j.cnki.csa.009298 |
| [19] |
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 6000–6010.
|
| [20] |
Siffer A, Fouque PA, Termier A, et al. Anomaly detection in streams with extreme value theory. Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Halifax: ACM, 2017. 1067–1075.
|
| [21] |
Boniol P, Palpanas T, Meftah M, et al. GraphAn: Graph-based subsequence anomaly detection. Proceedings of the VLDB Endowment, 2020, 13(12): 2941-2944. DOI:10.14778/3415478.3415514 |
| [22] |
Dau HA, Bagnall A, Kamgar K, et al. The UCR time series archive. IEEE/CAA Journal of Automatica Sinica, 2019, 6(6): 1293-1305. DOI:10.1109/JAS.2019.1911747 |
| [23] |
Goldberger AL, Amaral LAN, Glass L, et al. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation, 2000, 101(23): e215-e220. |
| [24] |
Moody GB, Mark RG. The impact of the MIT-BIH arrhythmia database. IEEE Engineering in Medicine and Biology Magazine, 2001, 20(3): 45-50. DOI:10.1109/51.932724 |
| [25] |
Nedelkoski S, Bogatinovski J, Mandapati AK, et al. Multi-source distributed system data for AI-powered analytics. Proceedings of the 8th Service-oriented and Cloud Computing: IFIP WG 2.14 European Conference. Heraklion: Springer, 2020. 161–176.
|
| [26] |
Mathur AP, Tippenhauer NO. SWaT: A water treatment testbed for research and training on ICS security. Proceedings of the 2016 International Workshop on Cyber-physical Systems for Smart Water Networks (CySWater). Vienna: IEEE, 2016. 31–36.
|
 2024, Vol. 33
2024, Vol. 33


