随着数字图像处理技术的不断发展和应用, 图片相似度算法在计算机视觉、图像检索等领域中扮演着重要的角色. 截至目前, 许多相关文献将一些图片相似度算法用于实际应用中, 例如人脸识别^[1]、签名比对^[2]、车牌比对^[3]、目标跟踪^[4]、行人重识别^[5]等, 然而对于传统图片相似度比对算法与基于深度学习的图片相似度比对算法的概括与总结, 很少有文献提及. 为此, 本文归纳与总结了一些传统图片相似度比对算法与基于深度学习的图片相似度比对算法, 并将这些算法用于药品图片相似度比对这一实际应用中. 表1列举了本文要对比的一些图片相似度比对算法.

表1中, 直方图法、余弦相似度法、全局哈希法、SIFT与ORB算法属于传统图像处理范畴, 孪生网络是基于深度学习的图像处理算法.

直方图法通过统计图像中不同像素点的个数, 得出像素点分布直方图, 进而使用几种相关性计算方法计算两张图片像素点分布直方图之间的相关性, 最后根据计算结果判断两张图片是否相似; 余弦相似度法常用于文本相似度或图片相似度的计算. 在应用余弦相似度比较两张图片是否相似之前, 需先将图片转换为向量形式, 之后, 通过计算两向量的余弦相似度来判断两张图片是否相似; 哈希法分为全局哈希法和局部哈希法. 其中, 全局哈希法包括均值哈希(AHash)、感知(PHash)和差值哈希(DHash)算法, 基本原理是将图像转换为一个固定长度的二进制编码, 通过计算两编码的距离判断两张图片是否相似; 局部哈希法包括SIFT (scale-invariant feature transform)、ORB (oriented FAST and rotated BRIEF)算法, 基本原理是找到并量化图像中的特征点, 通过计算两张图片量化特征点间的距离判断是否相似; 孪生网络是一种特殊的神经网络结构, 其中包含两个完全相同的子网络, 也被称为“孪生子网络”. 这两个子网络具有相同的结构和参数, 并且共享权重, 但是在训练过程中它们被独立地处理不同的输入数据. 其常被用于比较两个输入数据之间的相似度或距离, 在图像比对、文本匹配、人脸识别等领域被广泛应用. 表2列出了传统图像处理算法与深度学习图像处理方法的优缺点.

表2中, 传统图像处理方法经过长时间的发展和研究, 其算法和模型已经非常成熟, 具有相对较高的精度; 此外, 设计出的算法会利用专家的先验知识, 使算法的结果更加可解释, 并有利于深入研究算法的性能. 相较于深度学习方法, 传统方法的算法和模型规模较小, 需要的计算资源和时间较少. 然而, 对于数据量较大、复杂度高的任务, 传统方法的效率和精度会有所下降, 其泛化能力不足, 而且对于一些复杂的图像特征提取效果也不佳.

深度学习方法能够从原始数据中自动学习并提取出高阶特征, 从而处理更加复杂、抽象的问题, 减少了人工特征提取的繁琐过程. 同时, 其还具有良好的可扩展性和可伸缩性, 也可以实现模型的并行化和加速, 具有较强的泛化能力. 然而, 深度学习模型的结构和参数规模较大, 其内部的处理机制比较复杂, 导致其结果往往难以被解释和理解. 此外, 对于数据量较小的任务, 深度学习算法往往需要更多的数据才能达到较好的效果, 且存在过拟合的风险.

综上所述, 表1中的传统处理方法普遍存在计算速度偏高、复杂度与泛化能力偏低的特点, 基于深度学习的图像处理算法普遍存在计算速度偏低、复杂度与泛化能力偏高的情况. 然而, 在实际应用中, 通常利用GPU加速神经网络的训练和推理, 因此使用孪生网络进行推理的速度与传统方法进行推理的速度旗鼓相当.

本文主要贡献包括以下4个方面.

(1)我们首先比较了一系列图像相似度比对算法在药品图片相似度比对任务中的表现. 其次, 我们改进了效果最好的孪生网络算法, 进一步提升了其性能. 实验结果显示, 该算法的推理速度约为38次/s, 准确率达到了98.5%. 最终, 该算法成功应用于该任务.

(2)为解决药品图片特征点少所造成相似度匹配失效的情况, 本文在图片相似度比对前先判断图片中特征点数量是否达到比对标准. 我们设计了一套准则来制作标签, 使用ResNet分类网络, 最终在测试集上的分类准确率达95.51%.

(3)鉴于孪生网络需要成对的输入, 本文设计出一种标签制作方法, 在训练期间既能保证数据在GPU与CPU之间的传输速率, 又能保证正负样本均衡.

(4)鉴于样本图像受拍摄现场光照以及药盒颜色的影响, 本文设计了一系列数据增强策略来模拟现实情况, 增强孪生网络的泛化能力.

1 相关工作

直方图法的起源可以追溯到19世纪初, 当时英国的数学家皮尔逊提出了统计学中的频数分布表, 为后来直方图法的发展提供了基础. 在图像相似度比对领域, 直方图法也得到了广泛的应用. 王宁邦等人^[11]利用直方图匹配法, 使用巴氏系数(Bhattacharyya)判断两张资产图片的直方图是否相似, 进而实现资产图片的核对; 薛向阳等人^[12]提出了一种基于聚类的颜色直方图匹配法, 用于检索自然风格相近的图像; 芦俊等人^[13]使用直方图法并结合差分进化算法进行目标图片与模板图片的匹配; 邹承明等人^[14]使用直方图法与灰度共生矩阵法结合的方式进行图片匹配; 陈会鸽等人^[15]使用目标图片直方图与模板图片直方图作差的方式进行中央空调风管附尘度检测; 丁建平等人^[16]使用相关系数计算不同视频帧中目标图像灰度直方图的相关性, 从而进行铁路目标追踪.

在18世纪, 瑞士数学家欧拉在研究数学向量时首次提出了余弦相似度的概念. 后来余弦相似度法也被广泛应用于图像处理、文本处理等领域. 李阳齐等人^[17]将音乐属性转化为特征向量, 使用余弦相似度计算不同音乐间的相似性; 刘冰等人^[18]使用余弦相似度进行当前位置强度向量与定位服务器数据库中的位置强度向量比对, 从而定位当前位置; 魏玮等人^[19]利用余弦相似度更正SIFT算法误匹配的人脸特征, 进而提高人脸匹配的准确度.

哈希法起源于1992年, 当时NASA的天文学家发明了一种叫做“星形哈希 (star-hash)”算法^[20], 用于识别并匹配天文图像. 徐贤局等人^[21]使用AHash得到无疵点织物和有疵点织物的图片向量, 使用汉明距离计算差异, 定位疵点位置; 赵杰等人^[22]利用PHash得到不同图片区域的向量, 通过计算相邻图片块向量的相似性及位移矢量检测图像篡改区域; 郭玮^[23]利用分块图像的PHash进行不同区域类型遥感图像的匹配; 吴子岳等人^[24]使用拉普拉斯变换与DHash结合的方式得到不同视频帧目标区域的向量, 利用汉明距离计算其差异, 从而实现目标跟踪.

图像间的相似度比对可以间接转化为特征点间的相似度比对. 特征检测算法起源于20世纪六七十年代, 当时的研究主要是基于手工设计的滤波器和边缘检测算子, 例如Sobel算子^[25]、Laplacian算子^[26]等, 用于寻找图像中的边缘和角点等特征. 1996年, Lowe等人^[9]提出SIFT算法. 于明等人^[27]使用SIFT算法进行充电孔的识别与定位; 韩宇等人^[28]使用改进的SIFT算法实现无人机航拍图片的快速匹配; 任晶秋等人^[29]使用Harris与SIFT结合的方式进行图片的快速匹配.

ORB是另一种特征点检测与描述算法, 由Rublee等人^[10]于2011年提出. 其设计在保持速度优势的同时提高SIFT特征算法的精度, 以适应嵌入式设备等计算能力有限的场景. 杨金玲等人^[30]使用改进的ORB算法进行近红外和可见光图像的特征点检测与匹配; 姚三坤等人^[31]使用改进的ORB算法进行视频不同帧场景的匹配.

孪生网络最初应用于签名识别和文本相似度计算. 该模型是由Bromley等人^[2]在1993年提出, 它包含两个完全相同的子网络, 子网络间共享权重. 训练时并行处理两个输入序列, 对输出进行比较并计算损失. 2006年, Hadsell等人^[32]提出了一种计算孪生网络损失的方法: Contrastive Loss, 该方法利用欧氏距离来度量两个样本之间的相似度; 火善栋^[33]使用孪生网络进行人脸识别, 训练时使用Contrastive Loss; 吴正文^[34]使用U-Net类型的孪生网络, 并结合注意力机制进行遥感建筑物变化检测.

以上文献只是针对某个任务, 选取一种或两种图片相似度比对算法进行分析, 为此, 本文将使用上述提及的所有算法用于药品图片相似度比对, 并从中选取最佳算法用于实际工业生产中.

2 图片相似度算法对比研究 2.1 直方图法

直方图法统计图片的颜色和灰度分布情况. 计算直方图时, 将像素值范围划分成若干区间, 每个区间内像素点数量即为该区间的统计量.

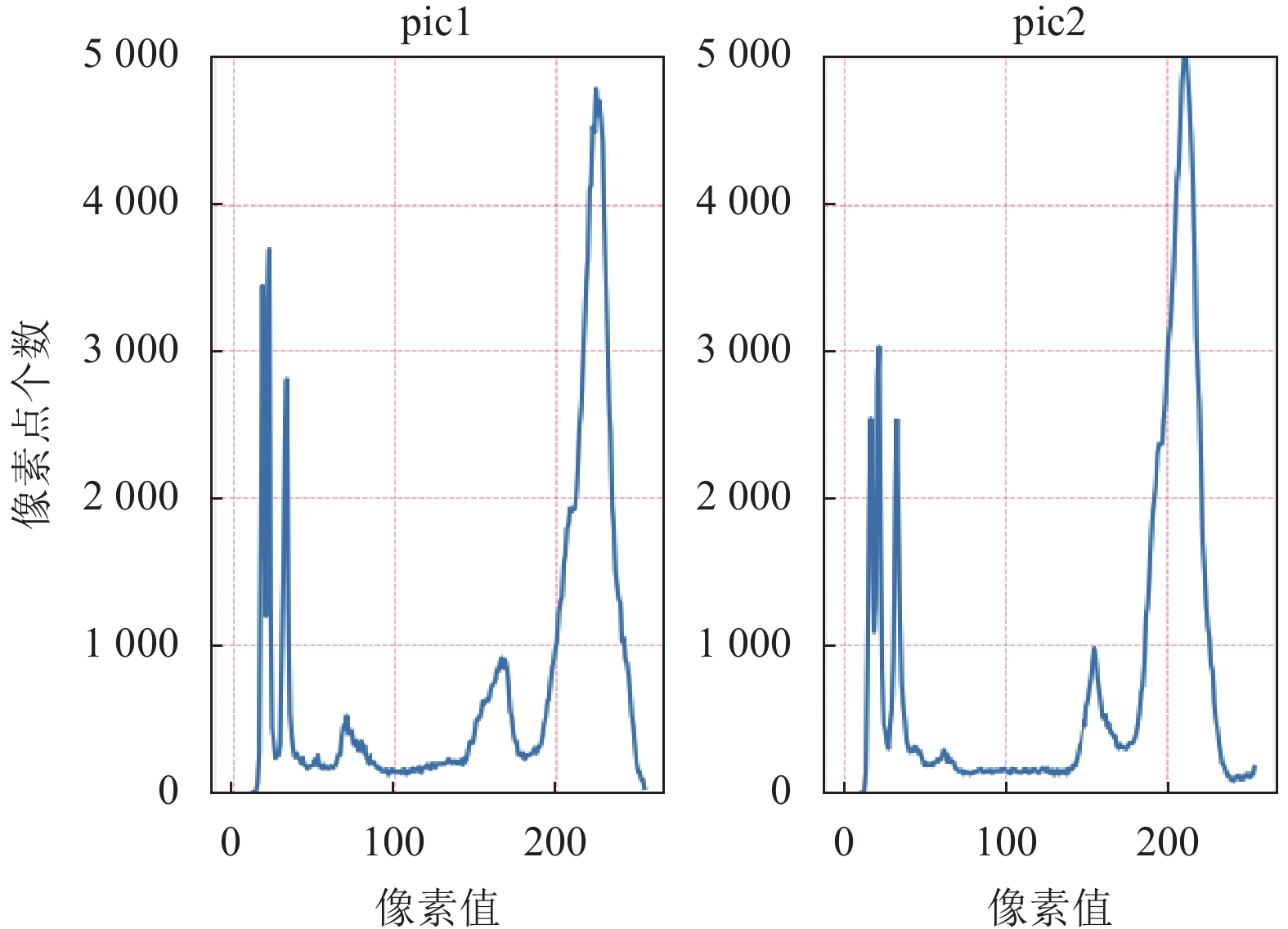
本文实验中, 区间范围为0–255, 每个像素值代表一个区间. 图1展示了两张样例图片, 图2展示了图1中两张图片的像素分布直方图.

计算像素分布直方图的相关性方法有Correlation、Chi-Square、Intersection、Bhattacharyya distance.

Correlation计算公式见式(1):

$ d\left( {{H_1}, {H_2}} \right) = \frac{{\displaystyle\mathop \sum \nolimits_I \left( {{H_1}\left( I \right) - \overline {{H_1}} } \right)\left( {{H_2}\left( I \right) - \overline {{H_2}} } \right)}}{{\sqrt {\displaystyle\mathop \sum \nolimits_I {{\left( {{H_1}\left( I \right) - \overline {{H_1}} } \right)}^2}\displaystyle\mathop \sum \nolimits_I {{\left( {{H_2}\left( I \right) - \overline {{H_2}} } \right)}^2}} }} $

(1)

其中, $ \overline {{H_k}} = \dfrac{1}{N}{\displaystyle\sum\nolimits_j H _k}(j) $, N为直方图中bin的个数(即组数). 计算结果最大值为1, 最小值为−1, 取绝对值后, 值越大, 相关度越高.

Chi-Square计算公式见式(2):

$ d\left( {{H_1}, {H_2}} \right) = \mathop \sum \limits_I \frac{{{{\left( {{H_1}\left( I \right) - {H_2}\left( I \right)} \right)}^2}}}{{{H_1}\left( I \right)}} $

(2)

计算结果越小, 相关度越高, 最小值为0, 最大值无上界.

Intersection计算公式见式(3):

$ d\left( {{H_1}, {H_2}} \right) = \mathop \sum \limits_I \min\left( {{H_1}\left( I \right), {H_2}\left( I \right)} \right) $

(3)

计算结果越大, 相关度越高, 最大值无上界, 最小值为0.

Bhattacharyya distance计算公式见式(4):

$ d\left( {{H_1}, {H_2}} \right) = \sqrt {1 - \frac{1}{{\sqrt {\overline {{H_1}} \overline {{H_2}} {N^2}} }}\mathop \sum \limits_I \sqrt {{H_1}\left( I \right) \cdot {H_2}\left( I \right)} } $

(4)

计算结果越小, 相关度越高, 最小值为0, 最大值为1. 表3列出了图1的相关性计算结果.

表3中, 4种度量计算结果与实际几乎相反, 且易受外界因素影响, 例如亮度、药盒颜色等, 因此不能作为图片相似度比对的最佳算法, 在实验部分会进一步说明.

2.2 余弦相似度法

余弦相似度是一种常用的图片相似度比对法. 在预处理阶段, 将两张图片调整为同样大小、灰度化图片. 此步的目的是获得相同规模的图片向量, 方便计算. 利用得到的两个图片向量A, B, 代入式(5)中, 得到结果.

$ cosine{\text{\_}}similarity = \frac{{\displaystyle\mathop \sum \nolimits_{i = 1}^n {A_i}{B_i}}}{{\sqrt {\displaystyle\mathop \sum \nolimits_{i = 1}^n A_i^2} \sqrt {\displaystyle\mathop \sum \nolimits_{i = 1}^n B_i^2} }} $

(5)

结果在[−1, 1]之间, 值接近1表示两个向量相似、接近−1表示两个向量不相似. 本文为余弦相似度设置一个合适的阈值, 例如 0.8, 表示当两张图片的余弦相似度大于等于 0.8 时, 判定两张图片相似. 以图1为例, 两张图片的余弦相似度为0.80183, 可以判定其相似.

2.3 全局哈希法

哈希法通过将图片转换为一系列数字表示, 从而快速比较两张图片的相似度. 全局哈希法将整张图片作为一个整体进行哈希处理, 得到一组唯一的哈希码. 全局哈希法包含: AHash、PHash、DHash.

AHash计算过程如下.

(1)缩小图片至8×8大小.

(2)灰度化缩小后的图片, 计算出所有像素的平均灰度值$ \hat{P} $.

(3)根据式(6)比较每个像素的灰度值P(i, j)与平均灰度值$\hat P$, 得到由0、1组成的64位哈希码.

$ P'\left( {i, j} \right) = \left\{ {\begin{array}{*{20}{c}} {0, \;\hat P \geqslant P\left( {i, j} \right)} \\ {1,\; \hat P < P\left( {i, j} \right)} \end{array}} \right. $

(6)

PHash在AHash的基础上增加DCT (discrete cosine transform), 进而获取图片低频信息, 计算过程如下.

(1)将图片缩小至32×32大小并进行灰度化处理.

(2)进行DCT变换, 取前8×8个DCT系数, 计算其平均值$\widehat {dct}$.

(3)根据式(7)比较每个DCT系数dct(i, j)与DCT系数的平均值$\widehat {dct}$, 得到由0、1组成的64位哈希码.

$ dc{t'}\left( {i, j} \right) = \left\{ {\begin{array}{*{20}{c}} {0,\; \widehat {dct} \geqslant dct\left( {i, j} \right)} \\ {1, \;\widehat {dct} < dct\left( {i, j} \right)} \end{array}} \right. $

(7)

DHash计算过程如下.

(1)将图片缩小到9×8并灰度化, 得到P(i, j).

(2)根据式(8)比较相邻像素之间的差异, 得到由0、1组成的64位哈希码.

$ P'\left( {i, j} \right) = \left\{ {\begin{array}{*{20}{c}} {1,\; P\left( {i, j - 1} \right) \geqslant P\left( {i, j} \right)} \\ {0, \;P\left( {i, j - 1} \right) < P\left( {i, j} \right)} \end{array}} \right. $

(8)

得到两张图片的哈希码后, 统计对应位置元素相同的个数并设定阈值, 如果相同的个数大于等于阈值, 则判定两张图片相似. 以图1为例, 表4展示了3种全局哈希法的计算结果.

表4中, 3种方法的计算结果约占哈希码总长度的一半, 后续的实验会说明这3种算法并不适用.

2.4 SIFT算法

SIFT算法是一种尺度不变的特征转换算法, 能够定位图像中的局部性特征, 在尺度空间中寻找极值点, 并提取出其位置、尺度、旋转不变量.

SIFT算法流程分为3步: 尺度空间检测和极值点定位、特征点方向赋值、特征点描述子生成.

(1)尺度空间检测和极值点定位

为使特征点具备尺度不变性, SIFT算法使用高斯核函数$G\left( {x, y, {\sigma}} \right)$对图像$I\left( {x, y} \right)$进行不同尺度的滤波(卷积运算), 得到一系列不同尺度的尺度空间$L\left( {x, y, {\sigma}} \right)$, 见式(9)、式(10).

$ L\left( {x, y, {\sigma}} \right) = G\left( {x, y, {\sigma}} \right)\times I\left( {x, y} \right) $

(9)

$ G\left( {x, y, {\sigma}} \right) = \frac{1}{{2{\text{π }}{{\sigma}^2}}}{\mathrm{exp}}\left( { - \left( {{x^2} + {y^2}} \right)/2{\sigma ^2}} \right) $

(10)

之后使用高斯差分对其中的尺度空间进行极值点定位. 高斯差分尺度空间的计算见式(11).

$ \begin{split} D\left( {x, y, {\sigma}} \right) &= \left( {G\left( {x, y, k{\sigma}} \right) - G\left( {x, y, {\sigma}} \right)} \right)\times I\left( {x, y} \right) \\ & = L\left( {x, y, k{\sigma}} \right) - L\left( {x, y, {\sigma}} \right) \end{split} $

(11)

图3展示了高斯差分过程, SIFT算法取4层差分空间的中间两层做极值点检测, 见图4. 每一个采样点与其相邻的26个点进行比较, 如果采样点的值是相邻点中的最大值或最小值, 则被视为极值点.

(2)特征点方向赋值

为使特征点具备旋转不变性, 需要为每一个特征点分配一个基准方向. 对于某尺度下的图像L(x, y), 用像素插值估计图像梯度幅值m(x, y)与方向θ(x, y), 见式(12). 之后统计以特征点$3{\sigma {'}} = 3 \times 1.5\sigma $为中心范围内的像素梯度幅值及方向.

$ \left\{ {\begin{array}{*{20}{l}} m\left( {x, y} \right) =\\ \sqrt {{{\left( {L\left( {x + 1, y} \right) - L\left( {x - 1, y} \right)} \right)}^2} + {{\left( {L\left( {x, y + 1} \right) - L\left( {x, y - 1} \right)} \right)}^2}} \\ {\theta \left( {x, y} \right) = {\mathrm{tan}}{^{ - 1}}\dfrac{{L\left( {x, y + 1} \right) - L\left( {x, y - 1} \right)}}{{L\left( {x + 1, y} \right) - L\left( {x - 1, y} \right)}}} \end{array}} \right. $

(12)

利用梯度直方图统计法, 将得到的梯度方向划分成36个区域(每区域10°), 取直方图峰值的方向定为主方向.

(3)特征点描述子生成

此时每一个特征点都包含位置、尺度与方向信息, 根据这些信息计算特征点的描述子. 式(13)划定以关键点为中心的距离范围, 默认d=4.

$ r = \frac{{3\sqrt 2 \sigma \left( {d + 1} \right)}}{2} $

(13)

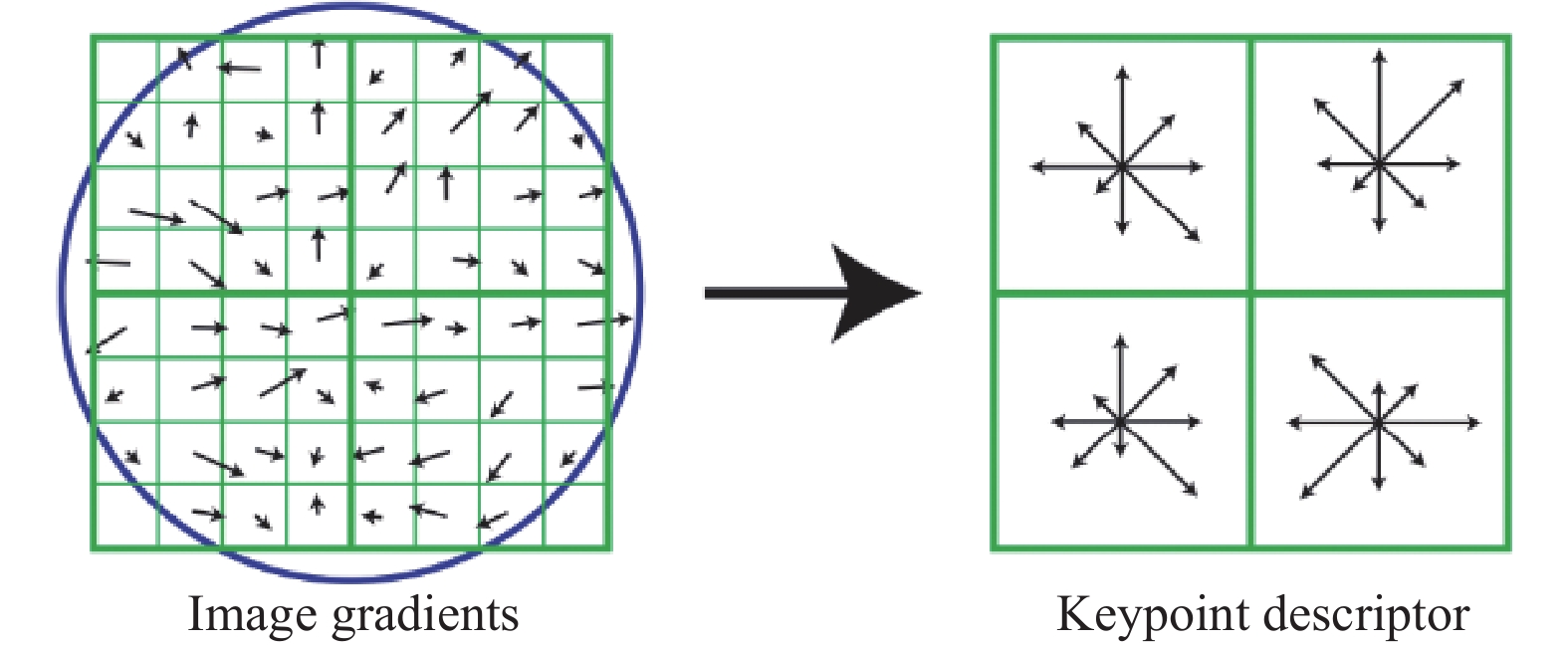
图5展示d=2时, 关键点梯度直方图统计结果, 每个区域45°, 一个关键点可由d×d×8位向量表示. 实际每个关键点会产生128位特征描述子.

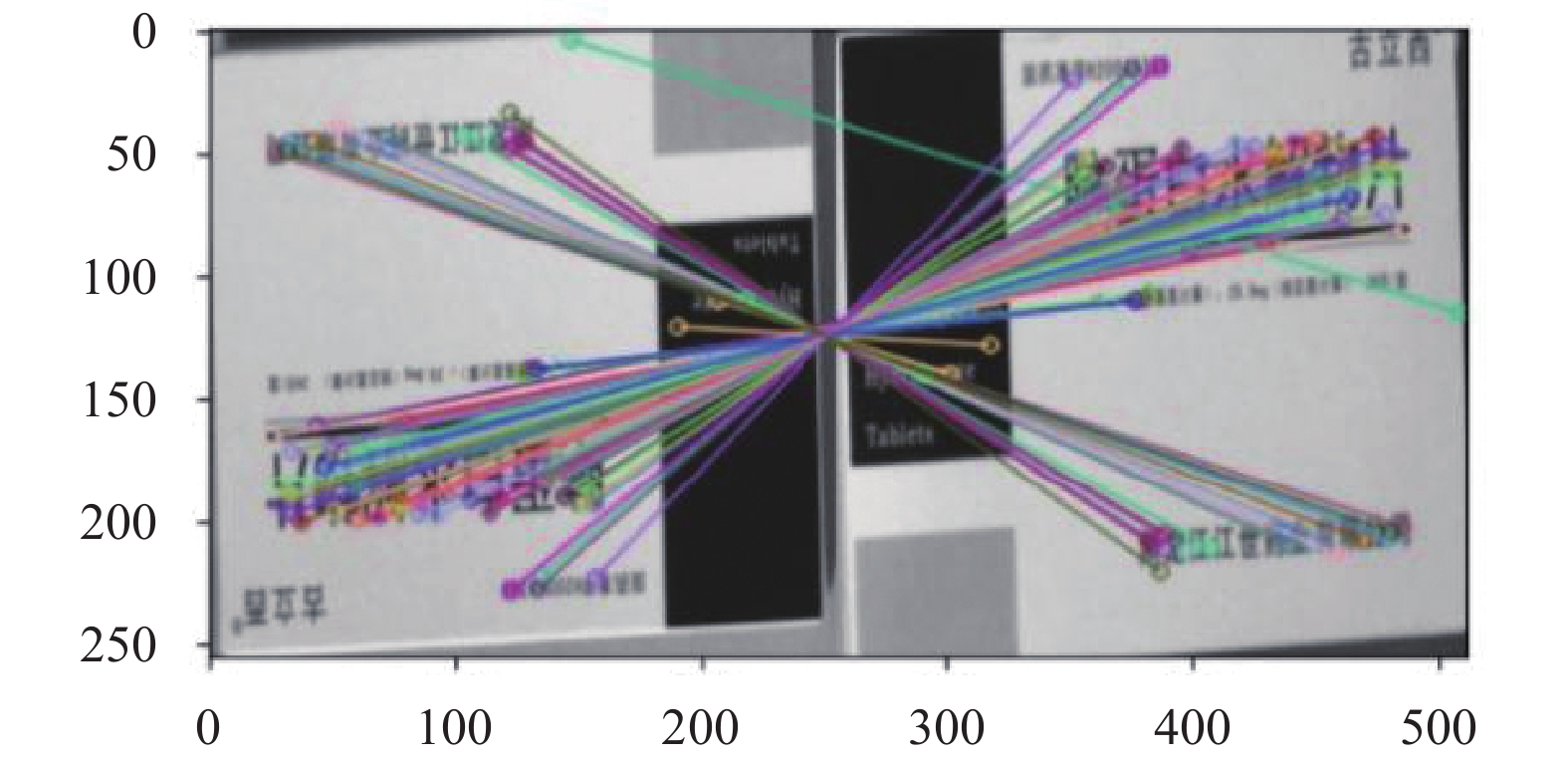
特征匹配时, 使用曼哈顿距离度量两张图片特征点描述子之间的距离, 并采用Brute-Force算法找到最接近的特征点. 设定阈值, 当成功匹配的特征点对数量超过阈值时, 认定两张图片相似. 在图6中, 使用SIFT算法对图1中的特征点进行匹配, 总共得到240对相似关键点(两张图片分别检测到391、368个关键点).

2.5 ORB算法

ORB算法是一种快速检测图像上的关键点并创建其特征向量的算法, 由oriented FAST特征检测^[35]与rotated BRIEF特征描述算法^[36]组成. 为满足缩放不变性, 首先构建图像金字塔, 见式(14). 之后对每一层图像进行关键点检测与描述.

$ \left\{ {\begin{array}{*{20}{l}} {{\sigma _s} = {\sigma^s _0}} \\ {{\textit{Size}} = \left( {H\times\dfrac{1}{{{\sigma _s}}}} \right) \times \left( {W\times\dfrac{1}{{{\sigma _s}}}} \right)} \end{array}} \right. $

(14)

其中, 第1行表示第s层的缩放尺度, 第2行表示第s层的图像尺寸, 默认${\sigma _0} = 1.2$.

(1) Oriented FAST特征检测算法步骤

1)对每一个像素点, 确定其周围R×R范围内的边缘像素点, 若其中有连续K个像素值与中心点像素值相差大于阈值T, 则该中心点视为关键点.

2)使用Harris角点^[37]响应函数解决特征点分布密集的情况: 计算每个特征点的响应值V, 选取前N个V值较大的关键点作为最终的关键点.

3)使用强度质心法(intensity centroid)^[38]计算特征点的方向, 强度质心法假设角的强度偏离其中心.

$ {m_{pq}} = \mathop \sum \limits_{x, y} {x^p}{y^q}I\left( {x, y} \right) $

(15)

$ C = \left( {\frac{{{m_{10}}}}{{{m_{00}}}}, \frac{{{m_{01}}}}{{{m_{00}}}}} \right) $

(16)

$ \theta = \arctan \left( {{m_{01}}, {m_{10}}} \right) $

(17)

式(15)计算特征点所在图像块的矩量, I(x, y)为图像灰度值, x, y∈[−r, r], r为以特征点为中心的图像块半径, 通过式(16)计算出灰度值质心, 通过式(17)计算特征点与灰度值质心之间的方向$\theta $, 并将其作为主方向.

(2) Rotated BRIEF特征描述算法

1)在原始BRIEF特征描述算法中, 以特征点为中心, S×S的范围内, 随机选取N组点对, 由式(18)、式(19)计算出关键点的二进制特征描述.

$ \tau \left(p;x, y\right)=\left\{\begin{array}{c}1:p\left(x\right)< p\left(y\right)\\ 0:p\left(x\right)\geqslant p\left(y\right)\end{array} \right.$

(18)

$ {f_n}\left( p \right) = \mathop \sum \limits_{1 \leqslant i \leqslant n} {2^{i - 1}}{\tau}\left( {p;{x_i}, {y_i}} \right) $

(19)

其中, p(x)表示图像区块p在点x的灰度值, ${f_n}(p)$表示特征点的n位向量表示. 由于原始BRIEF对噪声敏感, 在计算式(19)前需进行平滑处理: 在31×31的图像块上使用5×5的子窗口平滑图像.

2)鉴于图像平面旋转后造成匹配效果差的现象, 提出steered BRIEF: 根据特征点的旋转方向调整BRIEF的方向. 具体地, 在特征点S×S (默认S=31)范围内选取n对点集, 根据角度$\theta $与旋转矩阵${R_\theta }$, 得到旋转后的坐标, 见式(20), 之后利用式(21)得到旋转后的特征点描述, 最后使用贪婪搜索选取256个低相关性的像素块对, 作为最终的特征点描述子.

$ {D_\theta } = {R_\theta }D, D = \left( {\begin{array}{*{20}{c}} {{x_1}, {x_2}, \cdots , {x_n}} \\ {{y_1}, {y_2}, \cdots , {y_n}} \end{array}} \right) $

(20)

$ {g_n}\left( {p, \theta } \right) = {f_n}\left( p \right) $

(21)

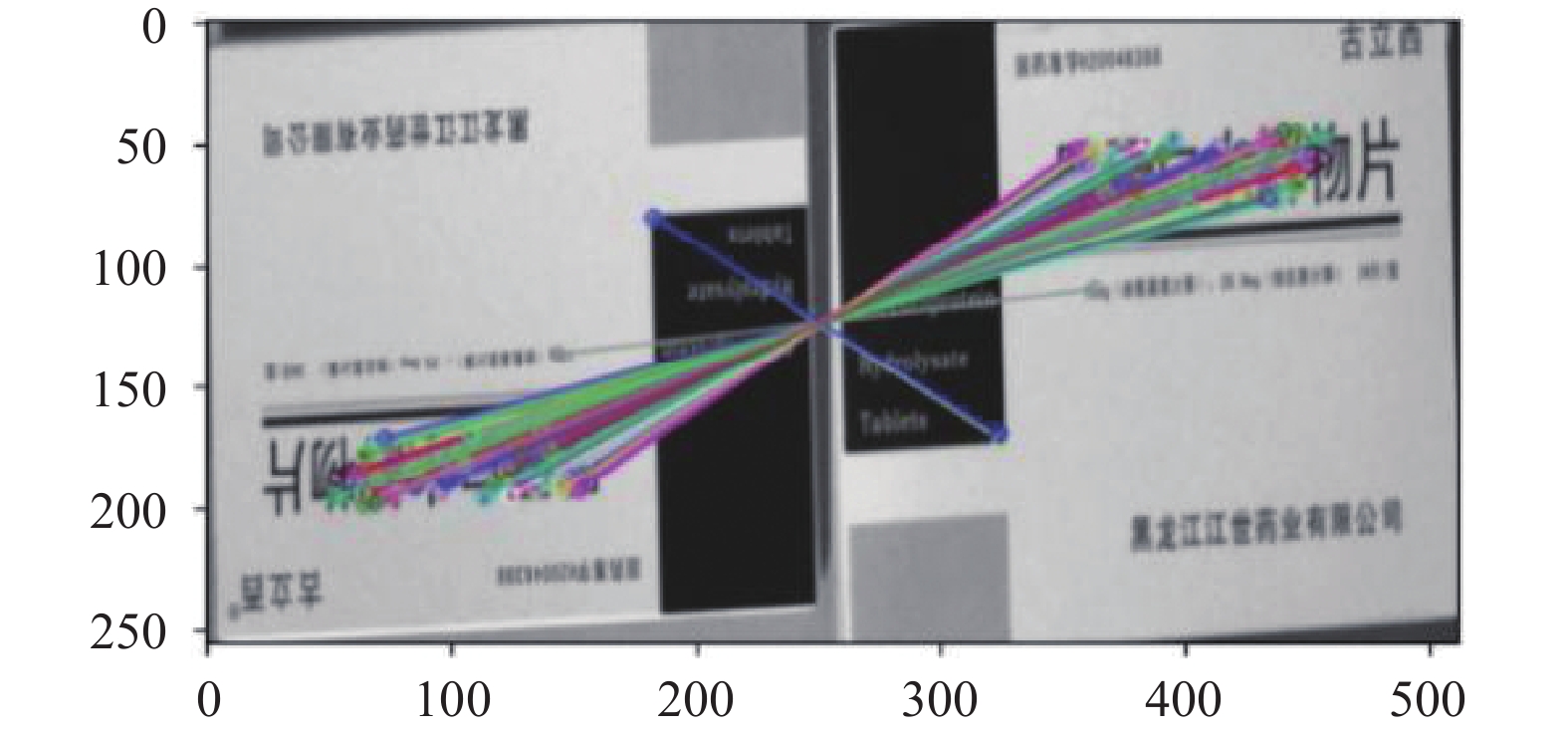
特征匹配时, 以两幅图片特征点描述子间的汉明距离为度量, 使用Brute-Force算法匹配距离两幅图最近的特征点. 设定阈值, 当成功匹配的特征点对数量超过阈值时, 认定两张图片相似. 在图7中, 使用ORB算法对图1中的特征点进行匹配, 总共得到277对相似关键点(两张图片分别检测到410、387个关键点).

2.6 孪生网络

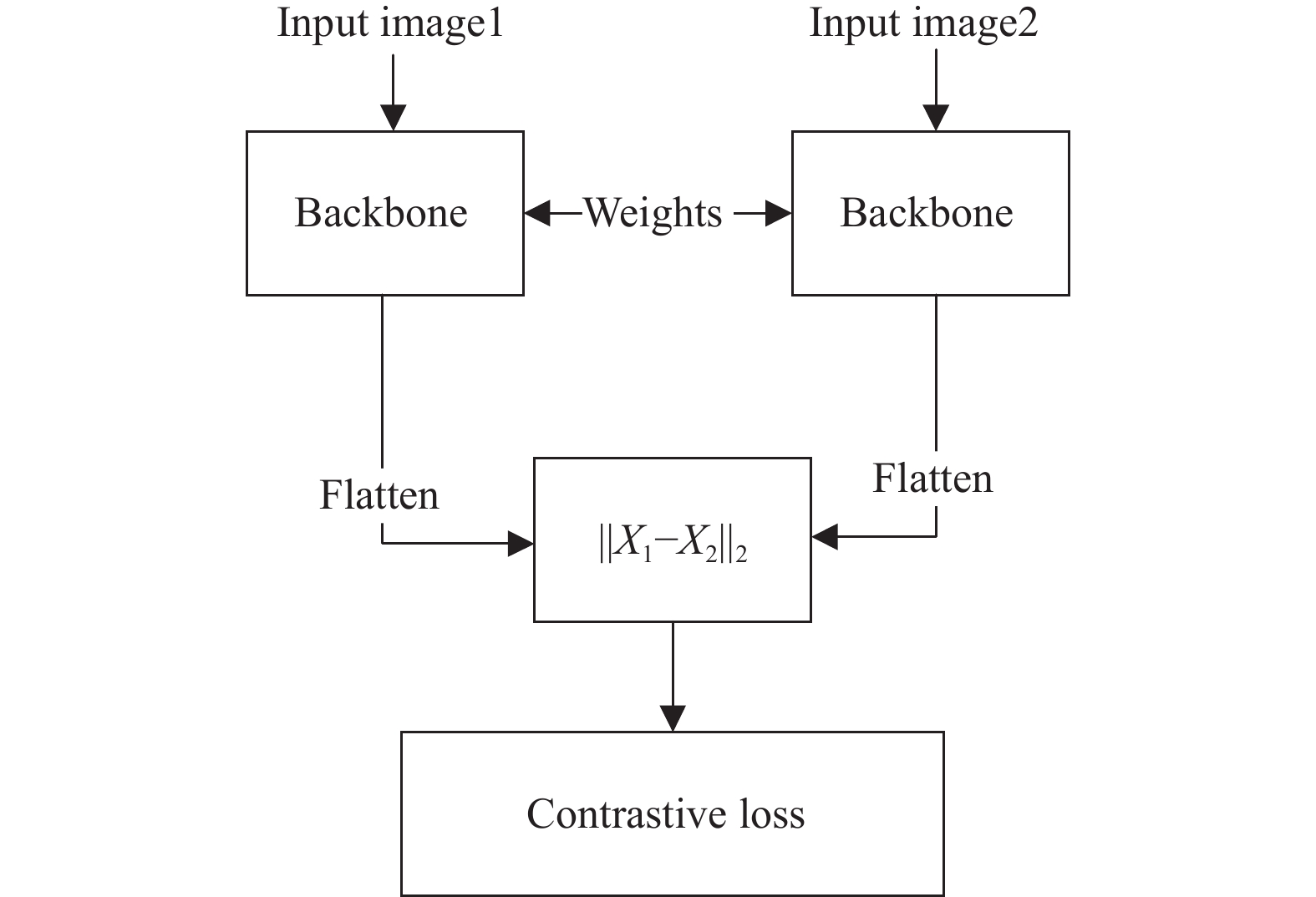
孪生网络是一种深度学习模型, 该模型结构由两个相同的子网络组成, 每个子网络都有相同的层次结构和参数. 这两个子网络并行地接受输入, 并通过共享权重来提取输入样本的特征表示. 这种共享权重的设计使得网络能够学习到一种通用的特征表示, 从而对输入样本进行比较和匹配. 经典孪生网络结构见图8.

图8中, 对于成对的输入图片, 孪生网络将每个样本通过共享权重的Backbone (子网络)进行前向传播, 提取得到对应的图片特征向量. 然后, 将两特征向量维度从多维变换成一维(Flatten操作), 在训练时使用对比损失(式(22)), 测试时根据计算得到的欧氏距离(式(23)), 设定阈值判定两张图片是否相似.

$ L = \frac{1}{2}\left( Y \right){D_w}^2 + \frac{1}{2}\left( {1 - Y} \right){\left\{ {\max \left( {0, m - {D_w}^2} \right)} \right\}^2} $

(22)

$ \begin{gathered} {D_w}\left( {{X_1}, {X_2}} \right) = |\left| {{X_1} - {X_2}} \right|{|_2} = \sqrt {\mathop \sum \nolimits_{i = 1}^P {{\left( {{X_1}^i - {X_2}^i} \right)}^2}} \end{gathered} $

(23)

式(22)中, 两样本相同则Y=1, 否则Y=0, 默认m=2. 表示如果两样本的距离达到临界值, 则断定两样本不同, 网络区分正确, 如果两样本相似, 则只考虑样本间的距离作为损失.

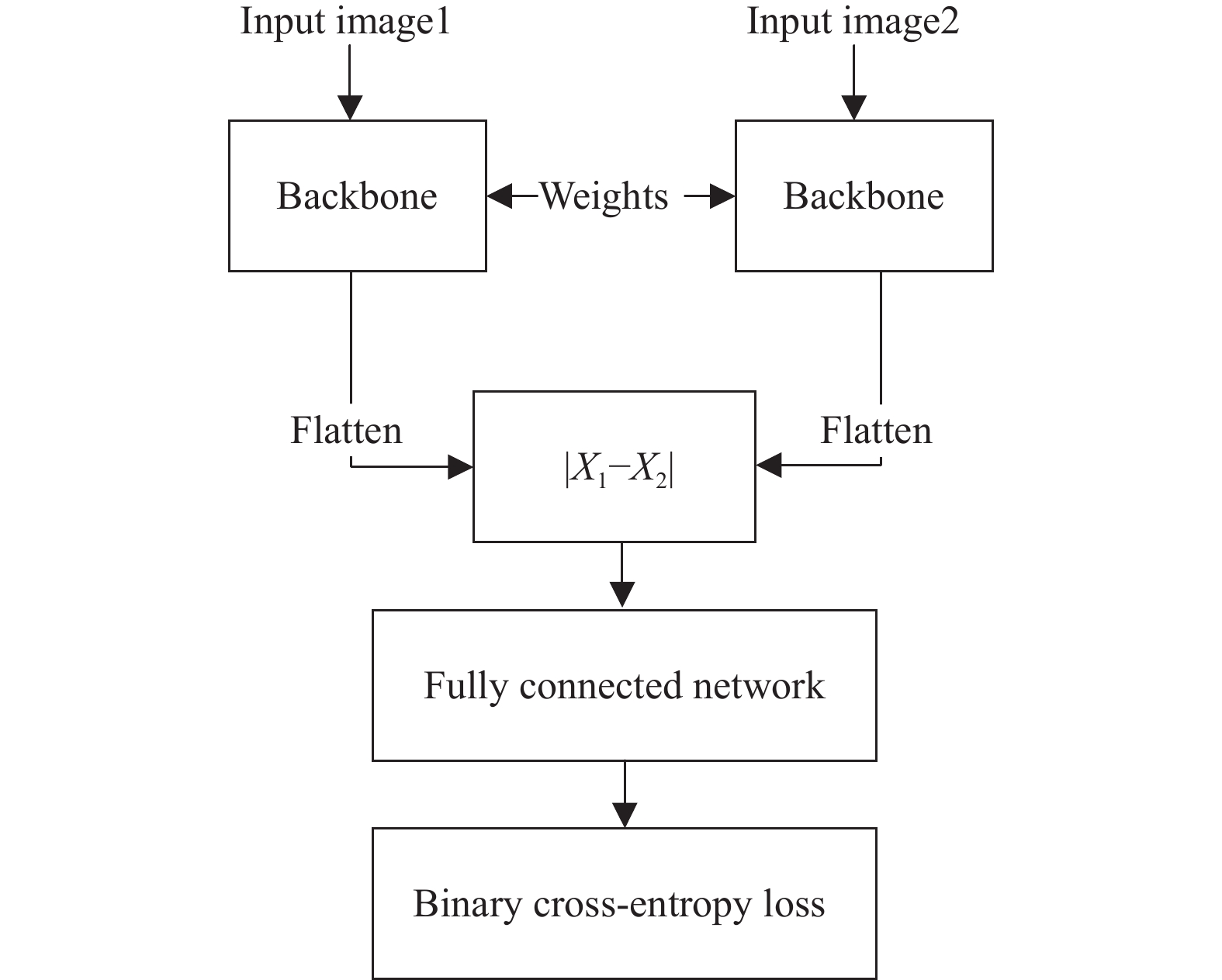
另外, 本文提出了一种改进的孪生网络结构(见图9), 用来进一步提升识别准确率.

类似地, 图片经过Backbone提取成对的特征向量后, 对成对向量作差并取绝对值, 然后使用全连接网络进一步学习差异向量, 训练时损失计算使用二分类交叉熵损失, 见式(24):

$ L = \frac{1}{N}\mathop \sum \limits_i - \left[ {{y_i}\log \left( {{p_i}} \right) + \left( {1 - {y_i}} \right)\log \left( {1 - {p_i}} \right)} \right] $

(24)

其中, N为样本数, ${y_i}$表示样本i的标签, ${p_i}$表示样本i预测为正类的概率. 测试时全连接网络的输出经过Sigmoid函数(将结果约束在[0, 1]范围内), 并设定阈值判定两张图片是否相似.

相比经典孪生网络结构, 改进的孪生网络具有以下优势.

(1)充分捕捉输入样本间的差异信息. 通过将向量作差(距离度量)得到差异向量, 其中每个维度表示对应特征的差异. 差异向量包含丰富的信息, 因为它们反映了输入样本在各个特征上的差异程度. 传入全连接层后, 网络可以通过学习适当的权重和偏差来进一步提取和组合这些差异特征, 从而计算出更具区分性的Loss. 然而传统方案中仅仅使用距离度量作为Loss计算, 无法充分利用向量中的细微差异, 从而限制了模型的表达能力.

(2)训练稳定性高. 在传统方案中, 对比损失在训练过程中易出现Loss=0的情况($Y = 0$, $m - D_w^2 \leqslant 0$). 在训练初期, 这会导致Loss值波动明显(时而为0, 时而很大). 相反, 改进的孪生网络结构使用交叉熵损失函数, 在计算Loss前先计算Softmax, 为模型的预测结果提供概率分布, 不会出现某类别概率完全为0的情况, 这表明Loss≠0, 也意味着在训练初期Loss波动幅度相对较小, 训练过程更稳定.

鉴于实时性的要求, Backbone选用轻量级的VGG16和ResNet18卷积网络. VGG16包含5个卷积模块, 1个全连接模块. 每个卷积模块由多层3×3卷积、ReLU激活函数、最大池化层组成, 全连接模块由3个全连接层组成; ResNet18包含5个卷积模块、1个均值池化层和1个全连接层. 第1个卷积模块由7×7卷积组成, 其余4个卷积模块由多层3×3卷积组成, 每个模块中包含残差连接.

3 特征面分类策略 3.1 存在问题

如图10, 数据集中存在药盒面是完全空白、大部分空白或因光照及药盒颜色导致图片模糊不清的情况, 这些情况会使特征检测与提取算法失效.

3.2 问题解决

为解决上述问题, 在进行特征提取前, 设计一个分类网络判断药盒面是否有较多的特征. 选用ResNet18作为二分类网络, 训练时采用二分类交叉熵损失(式(24)), 最终分类网络在测试集的准确率达95.51%, 推理速度达77.10张/s.

4 实验

由于传统的特征检测方法是根据图像本身固有属性进行的(例如像素值的比较、检测图像的角点), 不需要利用大量数据去学习、提取图像的特征, 所以对于传统方法的图片相似度比对只在测试集中展示其准确率.

4.1 数据集与标签

数据集含有153种药品, 每种药品拍摄多张药盒4–6个面的图片并放入对应类别的文件夹中, 每类药品图片数量从59–752张不等, 平均299张/类别, 数据集总共45826张图片. 表5展示了数据集所有药品中, 每个药盒面图片数量的最小值、最大值以及平均值.

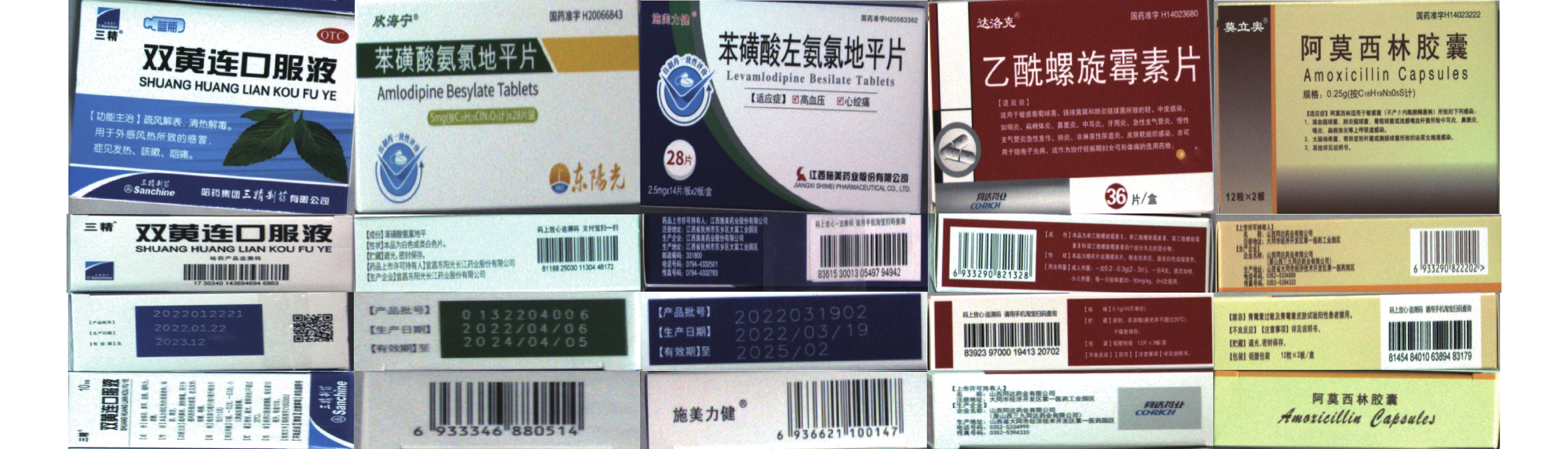
我们将1–133类中的图片划分为训练集, 总计42437张, 134–153类的图片划分为测试集, 总计3389张. 图11展示了从训练集中随机挑选的5种药品图片, 每种药品随机选取4个面.

4.1.1 特征面分类的标签制作

根据第3.2节提出的解决方案, 通过设置图片的名称来制作标签. 具体的, 将图片名称设置为“种类标识_图片序号_特征面种类(1表示满足特征匹配的图片)”格式, 写入到.txt文件内, 方便训练时读取.

4.1.2 图片对比标签的制作

我们提出了一种标签制作的方法, 能够在不影响CPU与GPU之间传输速度的情况下, 保持正负样本的平衡. 常规图片对的采集见算法1.

算法1. 常规训练数据采集算法

输入: 训练数据集ImageDataset.

输出: Img1、Img2、Label. //图片对、标签

1) Img1 = Select(ImageDataset); /*从训练数据集中随机抽取一张图片*/

2) T = Select(0, 1) //从集合{0, 1}中随机取一个数

3) If T == 1 //选取与Img1相同的图片//

4) 　While True

5) 　　　Img2 = Select(ImageDataset);

6) 　　　If Img1 == Img2: Break;

7) 　End While

8) End If

9) Else //选取与Img1不同的图片

10) 　While True

11)　　　 Img2 = Select(ImageDataset);

12)　　　 If Img1 != Img2: Break;

13) 　End While

14) End Else

15) Return Img1, Img2, Label

但算法1存在以下缺点.

(1)在训练的过程中, 随机的选择图片非常影响数据在CPU与GPU的传输速率.

(2)由于随机性, 最终只会产生4万多对训练数据, 而且仅考虑了类间非相似图片对, 没有考虑类内非相似图片对.

为解决上述问题, 本文设计了一种高效的方法, 在训练前生成图片名称对, 在训练的时候仅仅读取文本中的内容即可, 图片命名格式同第4.1.1节的命名格式. 见算法2.

算法2. 高效训练数据采集算法

输入: 训练数据集ImageDataset.

输出: Cls_Img_K、Cls_Img_K+1、Label1, Cls_Img_K、Img2、Label2.

1) For Each Cls_Imgs in ImageDataset: /*获取每一类药品所有图片的路径与名称*/

2) 　For Each Img_K in Cls_Imgs:

3) 　　For Each Img_K+1 in Cls_Imgs:

4) 　　If Cls_Img_K == Cls_Img_K+1:

5)　　　　　 T = Select(0, 1);

6)　　　　　 If T == 1: //从同类中选非同面当负样本

7) 　　　　　While True

8) 　　　　　　Img2=Select(Cls_Imgs);

9) 　　　　　　If Cls_Img_K != Img2: Break;

10) 　　　　 End While

11) 　　End If

12) 　　Else //从非同类中选某面当负样本

13) 　　　While True

14)　　　　　 Img2 = Select(ImageDataset);

15) 　　　　　If Cls_Img_K != Img2: Break;

16) 　　　End While

17) 　　End Else

18)　　　　　 Write(Cls_Img_K , Cls_Img_K+1, Label1) /*正样本对图片信息及标签写入文本*/

19) 　　　　　Write(Cls_Img_K, Img2, Label2) /*负样本对图片信息及标签写入文本*/

算法2中, 正样本的获取充分考虑每一张图片, 负样本的获取不仅考虑了类间非相似图片, 而且考虑类内非相似图片, 最后训练集总共获得约310万对图片, 测试集总共获得约12万对图片, 在训练与测试的时候仅读取.txt文件中的样本名称即可.

4.1.3 数据增强

在训练神经网络模型时, 为增强其泛化能力, 通常对训练数据进行数据增强. 针对药盒图片, 设置了图片上下翻转、水平翻转、旋转以及色彩变换. 其中上下翻转、水平翻转的概率设置为0.5; 旋转角度设置为0或180°; 为减轻光照及药盒颜色对模型的影响, 制定了色彩变换策略, 主要从亮度、对比度、饱和度以及色调4个方面进行调整. 由于数据集中存在很多忽明忽暗的图片, 所以在亮度方面调整力度较大, 参数范围在[0.5, 1.5]、对比度与饱和度参数范围在[0.9, 1.1], 色调参数范围在[−0.1, 0.1].

4.2 训练与测试细节

本文的实验配置环境如下: 对于特征面分类网络与孪生网络的训练, 在武汉大学超算平台上完成, 操作系统为CentOS 7.5 Linux, 显卡型号为Nvidia Tesla V100 16 GB, 采用PyTorch深度学习框架; 对于所有图片相似度对比算法的测试, 在本地运行, 操作系统为Windows 10, 显卡型号为Nvidia RTX 3050Ti, 采用PyTorch深度学习框架及OpenCV算法包.

4.2.1 特征面分类网络

在训练与测试前, 将图片调整到224×224大小. 训练时, 设置Epoch=30, Batchsize=64, 初始学习率Lr=0.001, 采用Adam优化器并设置学习率每隔7 epoch削减1/10.

4.2.2 孪生网络

在训练与测试前, 将图片调整到224×224大小. 训练时, 设置Epoch=5, Batchsize=64, 初始学习率Lr=0.0005, 采用Adam优化器并设置学习率每隔2 Epoch削减1/2, 根据经验, 图8的两种方案在训练与测试时设置阈值为0.8. 为增强孪生网络的泛化能力, 训练时不考虑特征面是否有效(见第3节).

4.3 结果与时间对比 4.3.1 特征面分类结果

训练完成后, 使用准确率最高的权重进行测试, 结果见表6.

模型在测试集上效果表现良好, 且推理速度快, 满足实时性的要求.

4.3.2 传统图像算法比对结果

由于传统图像算法不需要大量训练数据, 在计算准确率与推理速度时, 仅利用测试集中的数据.

对于直方图法、余弦相似度法、全局哈希法, 由于方法相较于ORB与SIFT更不稳定, 我们从测试集抽取1000对图片进行正负样本对输出值分析, 见表7.

表7中, 直方图法下标1、2、3、4分别代表Correlation、Chi-Square、Intersection、Bhattacharyya distance这4种度量方法. 对于直方图的4种距离计算方法, 正样本对的距离输出均值与负样本对的距离输出均值基本一致, 所以很难设置一个阈值将其准确区分; 对于余弦相似度比较法, 情况与直方图法类似, 而且由于其中涉及矩阵运算, 且没有GPU加速, 速度会略慢; 同理, 3种全局哈希法出现同样的情况; 对于SIFT与ORB算法, 正样本对的距离输出均值与负样本对的距离输出均值差别较大, 可以设定一个阈值进行准确判断: 取正样本输出均值与负样本输出均值的平均值, 计算得SIFT算法阈值约为160, ORB算法阈值约为200. 之后使用计算得到的阈值测试SIFT与ORB算法在完整测试集中的表现, 见表8.

由于ORB用到的算子运行速度快、准确率高, 所以ORB算法表现较好, 准确率达93.09%, 推理速度达31.88次/s.

4.3.3 孪生网络比对结果

根据训练结果, 选择使网络损失最低、准确率最高的权重文件进行测试, 训练与测试结果见表9.

表9中, 下标1代表使用改进的孪生网络结构, 下标2代表使用经典孪生网络结构. 可以看到使用改进的孪生网络准确率更高, 正是由于其使用表达能力强的全连接网络能够充分捕捉输入样本间的差异信息; 而经典的孪生网络结构, 对于两特征向量的关系学习较弱, 仅仅在计算损失的时候进行关系学习. 根据表8、表9, 选取准确率Top2的模型进行最终的测试.

4.3.4 总结果

本节将特征面分类网络与孪生网络结合, 采用以下策略进行测试: 对于测试过程中的某一对图片, 用特征面分类网络判断这两张图片是否有一张满足特征面匹配的条件, 如果是则进行图片比对, 否则跳过(不参与最终准确率的计算), 在测试集中的表现见表10.

根据表10, 最终选择ResNet18+ResNet18₁模型, 其准确率高达98.56%, 推理速度达约28次/s, 既满足了准确率的要求, 又满足了实时性的要求.

5 结论

本文首先阐述了一系列图片相似度比对算法及相关工作, 并着重改进孪生网络算法. 之后设置实验, 从中选取准确率最高、实时性较好算法用于实际应用中.

根据实验结果发现传统图像处理算法虽然在实时性方面表现优秀, 且不需要用大量数据去训练, 但其泛化能力较弱, 并不满足实际要求; 在深度学习图像处理算法上: 为提高神经网络的泛化性能, 设计一种高效的标签生成方法, 在保证正负样本平衡的情况下, 加速数据在CPU与GPU之间的传输速度, 使训练过程更高效; 在数据预处理方面, 考虑到实际场景中光照、药盒颜色等影响因素, 我们从亮度、对比度、饱和度与色调等方面按照一定概率进行数据增强; 在对数据集进行检查时, 发现并不是每个面都具有较强的特征, 所以进行图片相似度比对前, 先使用特征面分类网络过滤特征少的面; 在网络结构方面, 我们提出了一种改进的孪生网络, 在Backbone为ResNet18₁的情况下, 测试集上准确率最高达到98.50%, 比同类型经典孪生网络结构准确率高出2.99%; 将特征面分类网络与改进的孪生网络结合, 在测试集上最高准确率达98.56%, 推理速度达到约28次/s, 同时满足准确性和实时性要求.

目前工作仍存在不足之处: 在阈值的选择上仍有缺陷, 现在是根据正负样本对产生的相似度值取平均来设定阈值或根据数据的分布情况设定阈值, 但这种做法合理性较弱、主观性较强, 为此如何科学且有效地选择阈值是未来要研究的方面.