作为当前的热点研究方向, 基于传感器数据的人体动作分析技术广泛应用于医疗监测, 体育赛事分析, 自动驾驶和影视特效等领域. 传统的传感器设备往往只能对当前记录的数据进行分析判别, 而对历史数据的利用则较为粗糙, 且流行的神经网络模型往往做不到同时利用时间和空间结构信息对数据进行处理. 在时序数据的分类处理研究方面, 目前主流的研究方法包括循环神经网络(recurrent neural network, RNN)^[1], 及以其为基础扩展与演化的模型, 如长短时记忆模型(long short-term memory, LSTM)^[2], 门控单元模型(gate recurrent unit, GRU)^[3]等. 这些方法的共同优势在于能够充分利用时间序列的特征建模, 但却忽略了重要的空间结构信息. 此外, 在真实环境下数据类型可能会发生动态变化, 如生产环境中的新故障, 医疗场景中的疾病的新分类等, 而神经网络基于梯度对模型更新时, 则会因为新知识对旧知识的干扰甚至覆盖而出现灾难性的遗忘问题, 导致模型性能骤降, 如图1所示. 而将新旧任务数据合并, 利用全部数据对重新训练模型, 则会造成时间与计算资源的浪费.

针对以上两个问题, 本文提出了图注意力网络与生成式回放机制融合方法(generated memory replay graph attention network, GMR-GAT). 首先, 利用卷积神经网络(convolutional neural networks, CNN)^[4], 对传感器内局部时空信息进行特征提取, 之后利用图注意力网络(graph attention networks, GAT)^[5]对传感器间的空间及时间结构信息进行处理, 其中注意力机制可以使模型能够关注更重要的时间或空间节点, 进而提高模型的性能^[6]. 此外, 引入了基于条件变分自编码器(conditional variational autoencoders, CVAE)^[7]作为深度生成模型, 以在不存储原始数据的条件下, 针对样例数据分布进行记忆, 通过情景记忆回放辅助训练的方式缓解灾难性遗忘问题.

1 相关工作

目前, 图神经网络已广泛用于解决图形结构化数据的问题^[8]. Gori等^[9]使用了RNN以提取节点信息并学习图节点的标签, 图神经网络这一概念自此诞生. 之后文献[10]提出图卷积网络(graph convolutional network, GCN), 提出利用CNN对图结构的数据进行建模, 使得模型能够提取中心节点和邻居节点的特征和标签信息, 并将其输入到CNN中, 这令GCN具备了提取多尺度信息的能力, 从而实现对图结构信息和属性信息的有效利用^[11,12]. 注意力机制通过选择特定的输入, 使神经网络更关注那些与学习任务关联度更高的信息^[13]. 文献[5]首次提出将注意力机制应用到GNN, 二者结合后形成了图注意力网络(graph attention network, GAT). 但只利用常规图神经网络无法克服深度学习中出现的灾难性遗忘问题.

持续学习指的是模型在保留先前所学知识的同时, 不断学习新知识, 并避免对旧任务的遗忘与性能骤降. 使人工智能系统具备持续学习能力是当今智能学习领域面临的重要挑战^[14,15]. 目前主流的持续学习方法包括以可塑权重巩固(elastic weight consolidation, EWC)^[16], 突触智能(synaptic intellgence, SI)^[17], 无遗忘学习(learning without forgetting, LwF)^[18], 记忆感知突触(memory aware synapses, MAS)^[19]为代表的通过对模型实施正则化约束以避免遗忘的正则化方法和深度生成重放(deep generative replay, DGR)^[20], 经验回放(experience replay, ER)^[21], 梯度情景记忆(gradient episodic memory, GEM)^[22]及平均梯度情景记忆(averaged gradient episodic memory, A-GEM)^[23]为代表的重复学习以避免遗忘的情景记忆回放方法等. 然而, 正则化方法下, 模型的大小会随任务数量的增加而迅速增加, 正则化效果则会逐渐下降. 情景记忆回放方法在减轻灾难性遗忘方面具有巨大优势, 然而, 该方法需要长期保存真实样例, 不利于数据安全保护.

自编码器(autoencoder, AE)是由Rumelhart等^[24]提出的一种无监督学习算法, 该算法的目的之一是对输入其中的数据进行压缩, 并且能够复现输出. Kingma等^[25]提出的变分自编码器(variational autoencoder, VAE)是一类应用较广的自编码器, 也是一类重要的生成模型. 变分自编码器能够以特定分布的随机样本作为输入, 生成相应的仿真样例. 在此基础上, Sohn等^[7]改进并提出了条件变分自编码器, 使模型能够根据特定条件, 如分类标签等, 合成对应的数据^[26].

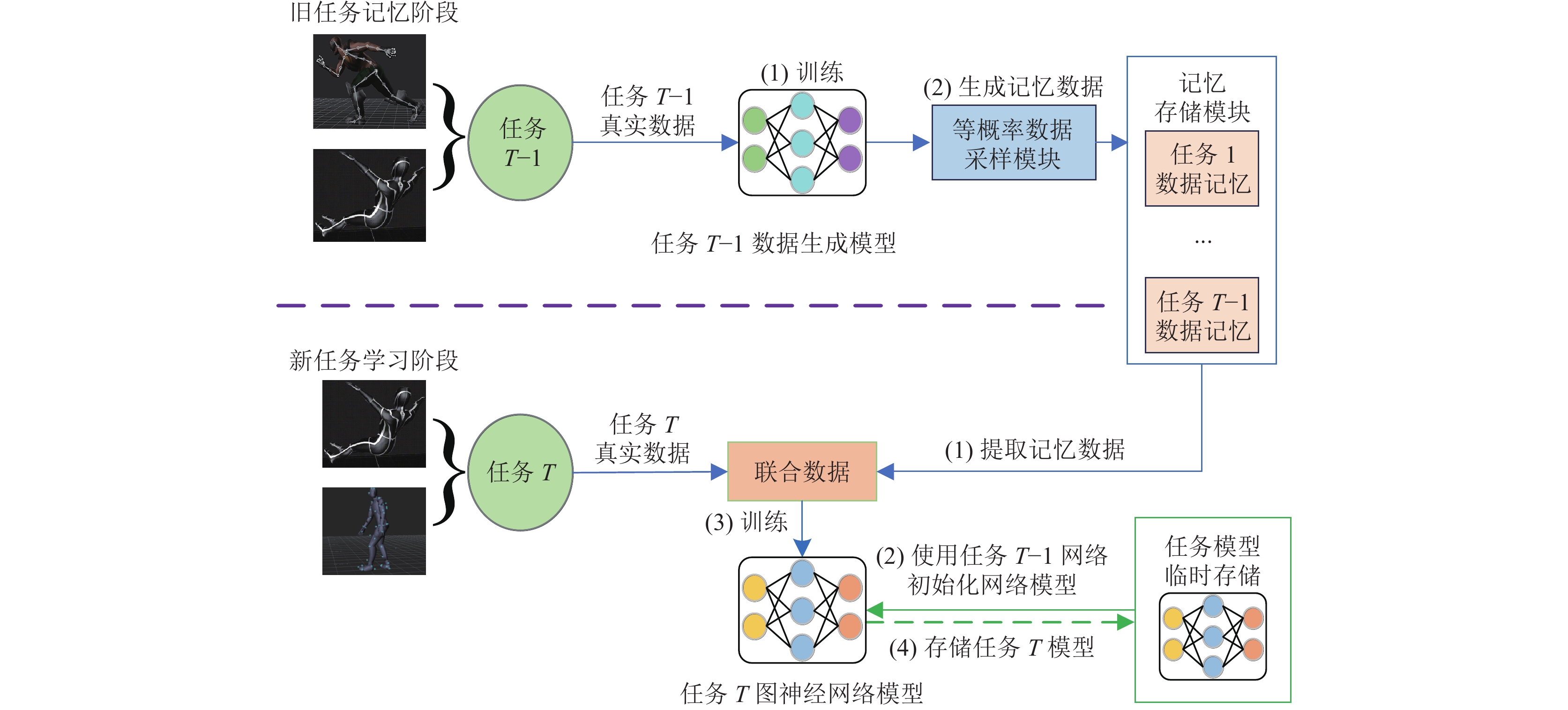
2 算法设计

为实现传感器时空结构数据的有效利用, 同时实现不存储原始数据条件下的持续学习功能, 本文提出了一种图注意力网络与生成式回放机制融合方法, 首次采用了条件变分自编码器作为深度生成重放中的深度生成模型, 结合了深度生成重放与经验回放两种记忆持续学习方法的优点, 避免了经验回放方法中, 训练方需要长期保留数据提供方提供的真实数据而可能造成的安全与隐私问题, 同时, 利用经验回放方法中的等概率记忆采样技巧, 稳定了生成数据类别的分布, 使最终用于回放的生成数据更贴近原始分布. 算法的输入为不同时段的任务, 不同任务包含不同类别的多维时序数据. 简化的算法流程如图2所示.

旧任务记忆阶段: 该阶段负责完成生成模型的训练和旧任务的记忆, 为新任务的学习做准备. 主要分为2个流程, 详细的流程描述如下.

(1) 训练网络模型: 使用T–1时刻任务的数据分别训练T–1时刻的网络模型和T–1时刻的数据生成模型.

(2) 生成记忆数据: 使用T–1时刻任务训练的数据生成网络进行仿真数据输出, 同时将生成数据通过等概率数据采样存入记忆存储模块.

新任务学习阶段: 该阶段主要完成任务T的图神经网络模型训练, 同时缓解对任务T–1的遗忘. 主要分为4个流程, 详细的流程描述如下.

(1) 提取记忆数据: 提取记忆存储模块中记录的记忆数据, 将记忆数据与新任务数据合并为联合数据.

(2) 初始化网络模型: 从任务模型存储模块中拉取旧任务的模型参数完成本次任务的网络初始化.

(3) 训练网络模型: 使用上一步初始化的网络和联合数据集进行本轮任务的训练.

(4) 存储模型: 将针对任务T训练后的模型入模型存储模块.

假设整个数据集被划分为T个任务, 重复执行以上两个阶段直到整个训练结束, 最后获得T任务结束后的网络模型, 使用该模型在测试集上进行测试.

本文所提出的改进后的图注意力网络, 在获取训练数据后, 首先按照传感器的时间与空间结构进行分割处理, 分割后的每一部分包含单个传感器内部一段时间的时序数据, 利用卷积神经网络对每个传感器的局部数据进行特征提取后, 形成多条传感器特征数据, 其数量与传感器数量, 分割时段数量有关. 将每条数据视为一个节点, 构建为全连接结构的图, 节点间的边代表传感器间的时空联系. 随后利用图注意力网络对形成的图结构数据进行处理, 并输出类别信息.

2.1 深度生成模型结构设计

由于将真实数据长期存放于训练方会存在安全隐私风险, 文献[20]提出可以利用深度模型记忆数据分布, 再利用生成的数据进行回放的思路. 受该理论的启发, 本文构造了数据生成回放模块, 提出了一种利用CVAE生成数据进行回放式记忆的处理框架.

变分自编码器由两部分组成: 将输入数据压缩为隐空间(latent space)中编码数据的编码器(encoder)和用于解压缩的解码器(decoder). 解码器应根据隐空间采样隐变量数据z, 输出准确表示原始数据分布的样本, 因此需要对未知概率分布函数进行建模. 从隐空间变量分布构建原始数据分布${p}\left(X\right)$的过程为:

$ {p}\left(X\right)=\sum _{Z}p\left(X\left|Z\right.\right)p\left(Z\right) $

(1)

其中, $ p\left(Z\right) $对应为事先指定的隐变量分布, 通常为标准正态分布. $ p\left(X\left|Z\right.\right) $对应于解码器所对应的由编码变量到解码变量的分布, 假设服从正态分布. 同样, $ p\left(Z\left|X\right.\right) $为编码器所对应的由原始变量到编码变量的分布, 且不难证明, $ p\left(Z\left|X\right.\right) $也满足正态分布.

根据贝叶斯公式, 可知:

$ p\left(Z\left|X\right.\right)=\frac{p\left(X\left|Z\right.\right)p\left(Z\right)}{p\left(X\right)}=\frac{p\left(Z\right)p\left(X\left|Z\right.\right)}{\int p\left(X|{\textit{z}}\right)p\left({\textit{z}}\right){\rm{d}}{\textit{z}}} $

(2)

然而, 在信息受限的情况下, 计算该公式的代价极大. 故采用变分贝叶斯方法, 借助另一个分布$ {q}\left(Z\left|X\right.\right) $来尽可能逼近$ p\left(Z\left|X\right.\right) $.

而CVAE的输入除样本数据x外, 还包括标签数据y. 根据上述理论, 构建CVAE模型如图3所示, 其运行流程如下.

(1)将数据$ {x}_{i} $, $ {y}_{i} $处理并拼接后输入编码器, 通过神经网络得到隐变量z服从的近似后验分布$ {{q}}_{{\phi }}\left({\textit{z}}\left|x\right. , y\right) $的参数, 对正态分布的参数$ {\sigma }^{2} $和$ \mathrm{\mu } $进行拟合.

(2)根据编码器得到的参数$ {\sigma }^{2} $和$ \mathrm{\mu } $, 从标准正态分布中采样得到$ \epsilon $, 令$ {{\textit{z}}}_{i}=\mu +\sigma \odot \epsilon $, 其中$ \odot $代表逐元素相乘, $ {{\textit{z}}}_{i} $服从$ {\sigma }^{2} $和$ \mathrm{\mu } $对应的正态分布.

(3)将$ {{\textit{z}}}_{i} $与指定的生成类别c (训练中为$ {y}_{i} $)拼接后输入解码器, 同样通过神经网络拟合$ p\left(x\left|{\textit{z}}\right.\right) $, 并根据该分布生成均值数据作为生成结果${x}'_{i}{{{}}}$并输出.

针对编码器的拟合过程, 利用KL散度损失函数, 衡量编码器拟合的分布与标准正态分布之间的差异. 针对解码器的拟合过程, 利用重构损失衡量输入样本与合成数据之间的差异, 本文中使用了MSE损失函数. 如式(3)所示:

$ {l}{o}{s}{s}={\textit{MSE}}\left({x}_{i}, {x}'_{i}{{{}}}\right)+KL\left({N}({\mu }, {\sigma }^{2}), {N}\left({0, 1}\right)\right) $

(3)

其中, 第2项的计算方式为:

$ {K}{L}\left({N}({\mu }, {\sigma }^{2}), {N}\left({0, 1}\right)\right)=\frac{{\mu }^{2}+{\sigma }^{2}-2{{\rm{log}}}\left(\sigma \right)-1}{2} $

(4)

2.2 等概率记忆采样

为保证数据集中的每个样本被记忆的概率相同, 本文采用了一种等概率样本选择方法.

设每个样本数据被保存在记忆中的概率为P, 记忆存储大小为M, 已处理的数据量为n, 则对不同条件下的样本有:

$ {P}=\left\{\begin{array}{l} 1, \qquad\qquad\quad\; n\leqslant M\\ M/n, \qquad\quad\;\;\;\; n > M且未被处理\\ \left(n-1\right)/n, \qquad n > M且已存储\end{array}\right. $

(5)

由上述公式, 可进行如下验证, 设${P}_{t, {t'}}$为任意t时刻未被处理的数据在其后的${t'}$时刻中存在于记忆中的概率, 可得:

$ {P}_{t, {t'}{{{}}}}=\frac{M}{{n}_{t}}\times \frac{{n}_{t}}{{n}_{t+1}}\times \dots \times \frac{{n}_{{t'}{{{}}}-2}}{{n}_{{t'}{{{}}}-1}}\times \frac{{n}_{{t'}{{{}}}-1}}{{n}_{{t'}{{{}}}}}=\frac{M}{{n}_{{t'}{{{}}}}} $

(6)

其中, $ {n}_{t} $代表t时刻处理的数据量. 式(6)可证明${P}_{t, {t'}{{{}}}}$只与存储大小以及当前时刻的数据量有关, 可以实现样本数据的等概率记忆采样.

2.3 图神经网络结构设计

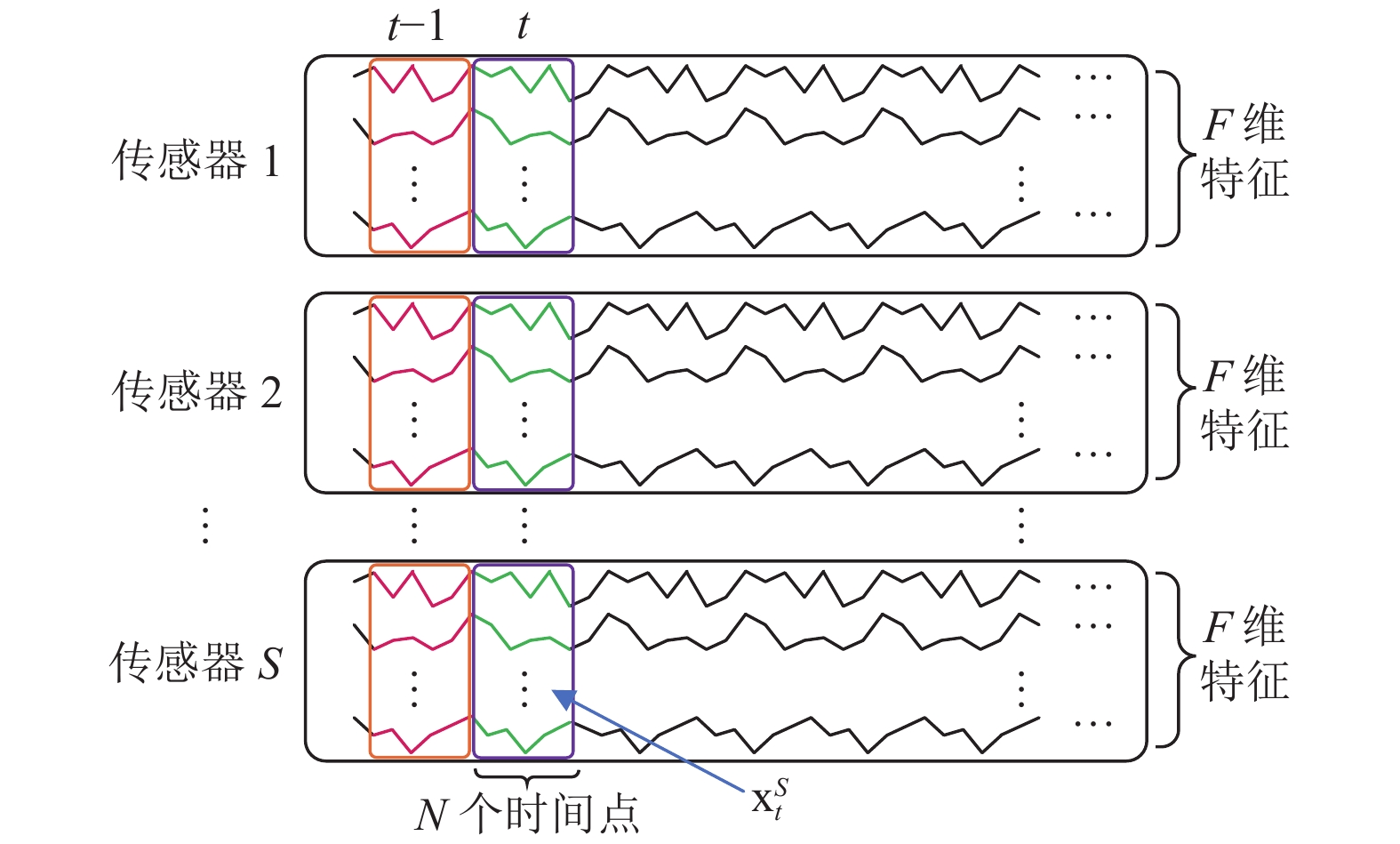
可穿戴式运动传感器, 能够采集并记录所佩戴部位运动时所产生的多维时序数据. 对于收集到的多维时序数据, 其特征维度以F表示, 传感器数量记为S. 并将来自单个传感器t时段内的N个连续数据点视为一个数据块进行, 在t时段内, 数据形式为$ {x}_{t}^{s}\in {\mathbb{R}}^{N\times F} $, 其中$s={1, 2}, \cdots , {S}$. 如图4所示. 而由于人体运动与时空结构密切相关, 可以假设$ {x}_{t-1}^{1} $, …, $ {x}_{t-1}^{s}, {x}_{t}^{1} $, …, $ {x}_{t}^{s} $之间存在潜在的关系, 并将其视为具有全连接关系的不同节点, 组成图结构数据. 此外, 从空间和时间的角度来看, 传感器之间联系的重要性也存在一定差异, 例如, 在跑步动作中, 当前时刻的左臂动作与上一时刻的右臂动作间的关联性可能与当前时刻的左臂动作, 上一时刻背部动作之间的关联性有所区别.

本文首先利用卷积神经网络对节点内局部数据进行特征提取, 将其转化为F维特征后, 将所有节点的特征组成全连接图, 作为图注意力网络的输入: $ h= \left\{{\overrightarrow{h}}_{1}, {\overrightarrow{h}}_{2}, \cdots , {\overrightarrow{h}}_{P\times S}\right\}, {\overrightarrow{h}}_{i}\in {\mathbb{R}}^{F} $, 其中P为参与计算的时段数量, 图注意力网络的输出为新的节点特征集合${{h'}}{{{}}}= \left\{{\overrightarrow{h'}}_{1}{{{}}}, {\overrightarrow{h'}}_{2}{{{}}}, \cdots , {\overrightarrow{h'}}_{P\times S}{{{}}}\right\}, {\overrightarrow{h'}}_{i}{{{}}}\in {\mathbb{R}}^{F}$. 计算方法如下式所示:

$ {\overrightarrow{h'}}_{i}{{{}}}=\sigma \left(\sum _{j\in {\mathrm{{\rm N}}}_{i}}{\alpha }_{ij}W{\overrightarrow{h}}_{j}\right) $

(7)

其中, $ \sigma $为ReLU激活函数, ${{{ N}}}_{i}$为与节点$ {\overrightarrow{h}}_{i} $在时间或空间上相邻的节点, $ W $为可学习参数, $ {\alpha }_{ij} $为注意力系数, 计算方法如式(8)所示:

$ {\alpha }_{ij}=\frac{{\rm{exp}}\left(LeakyReLU\left({\overrightarrow{a}}^{T}\left[W{\overrightarrow{h}}_{i}||W{\overrightarrow{h}}_{j}\right]\right)\right)}{\displaystyle\sum _{k\in {{{ N}}}_{i}}{\rm{exp}}\left(LeakyReLU\left({\overrightarrow{a}}^{T}\left[W{\overrightarrow{h}}_{i}||W{\overrightarrow{h}}_{k}\right]\right)\right)} $

(8)

其中, $ {\overrightarrow{a}}^{T} $的作用是将高维特征映射为一个实数, 通过单层前馈神经网络实现.

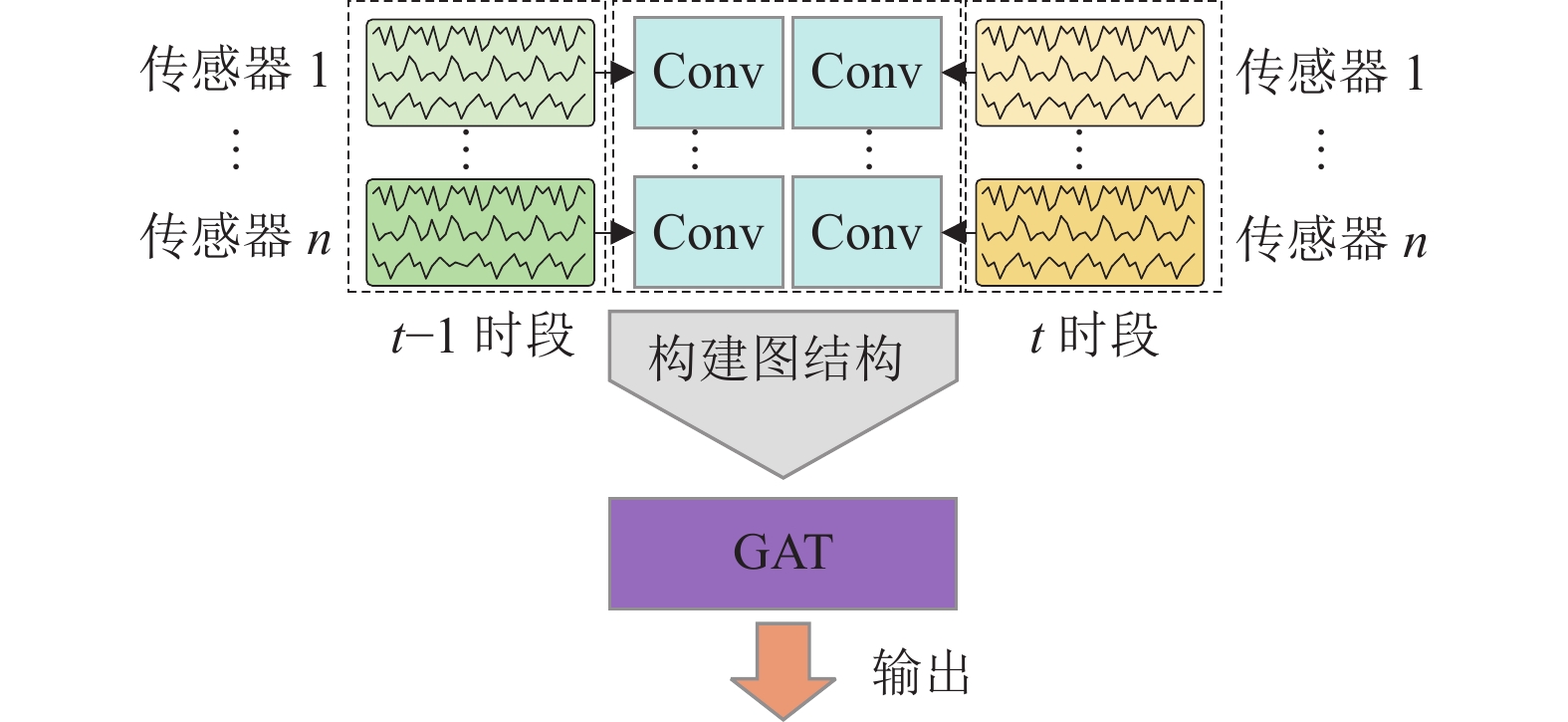
最后通过全连接层, 采用Softmax对提取到的特征进行分类输出. 其整体结构其如图5所示.

3 实验分析 3.1 实验环境

本文中进行的实验均基于Ubuntu 20.04操作系统; 硬件方面, 所采用GPU为Nvidia RTX 2080Ti, 显存大小为11 GB, CPU采用Intel(R) Core i9-9900K @ 3.60 GHz×8, 运行内存大小为32 GB; 软件方面, Python版本为3.8.10, PyTorch为1.12.0, CUDA版本为11.3.

3.1.1 数据集描述

如表1所示, 本文将所构建框架分别在3个不同的UCI公共数据集上进行训练和测试, 从各类别中采集1000条, 并按照7:3的比例划分测试集与训练集.

3个数据集包括日常和活动数据集(daily and sports activities data set, DSADS), 移动健康监测数据集(mobile health, MHEALTH), 现实传感器位移数据集(realistic sensor displacement, REALDISP).

DSADS数据集由45维, 19类不同活动的传感器时序数据组成. 其中传感器分布在身体的不同部位, 采集了包含各方向的加速度计, 陀螺仪, 磁强计等活动类型的数据, 活动类型包含上下楼梯, 跑步, 跳跃, 骑自行车等常见活动类型. MHEALTH数据集中包括了23维, 12类活动的时序数据. 23维中, 有21维是分布在身体的不同部位的运动传感器数据, 2维是心电信号数据, 活动类型包括弯腰, 屈膝, 躺下等. REALDISP数据集包含了来自不同部位传感器的117维, 33类活动的加速度计, 陀螺仪, 磁强计和四元数的时序数据, 活动类型包括跳绳, 前后跳跃, 旋转手臂等.

3.1.2 实验指标

为了更有效地评估持续学习的性能, 本文引入了该领域流行的两种指标: 平均准确率^[22], 定义为$ {A}_{q} $, 以及平均遗忘率^[27], 定义为$ {F}_{q} $. 其中, 平均准确率评估了当前模型在所有任务上的表现, 数值越大则表现越好. 平均遗忘率衡量了学习新任务而导致对旧任务的遗忘程度, 其数值越小代表遗忘程度越低.

平均准确率的计算公式为:

$ {A}_{q}=\frac{1}{q}\sum _{p=1}^{q}{a}_{q, p} $

(9)

其中, $ {a}_{q, p} $为模型学习完第q个任务后, 在第p个任务的测试集的准确率.

定义模型在完成任务q的训练之后, 对于第p个任务的遗忘程度的量化形式为遗忘率$ {f}_{p}^{q} $, 代表了任务p在持续学习过程中所取得的最好表现与在学习完q个任务后, 模型对任务p的表现的差异程度, 其计算公式为:

$ {f}_{p}^{q}=\underset{o\in \left\{1, \cdots , q-1\right\}}{\mathrm{max}}{a}_{o, p}-{a}_{q, p} $

(10)

通过模型对所有旧任务的遗忘率进行平均计算, 得到平均遗忘率的计算公式为:

$ {F}_{q}=\frac{1}{q-1}\sum _{p=1}^{q-1}{f}_{p}^{q} $

(11)

3.2 实验设计 3.2.1 特征提取实验

为了验证本文所提的特征提取方法的有效性, 首先将所提出的算法在总数据集上与多种基线算法进行了对比. 本实验方法采用的优化方式为随机梯度下降法(SGD), 学习率设置为0.01, 训练批次大小为10, 训练迭代次数为50. 基线算法包括图卷积网络(GCN)与长短期记忆神经网络(LSTM).

将上述建模方法与本文所提出的建模方法进行实验对比. 在全类别训练集的条件下, 采集不同时间长度作为历史信息的条件下进行实验, 以测试集准确率作为评价指标, 具体结果如表2所示.

表2中的GAT*代表不引入历史数据, 即只利用当前时刻的数据进行训练的表现. 通过表中的结果可以看出, 较不采用注意力机制的GCN, 忽略数据空间结构的LSTM和忽略数据的时间属性的情况GAT*, 采用本文所提的建模方法在不同数据集上均具有更好的表现, 验证了其有效性, 即能够更有效地处理包含空间结构的多维时序数据.

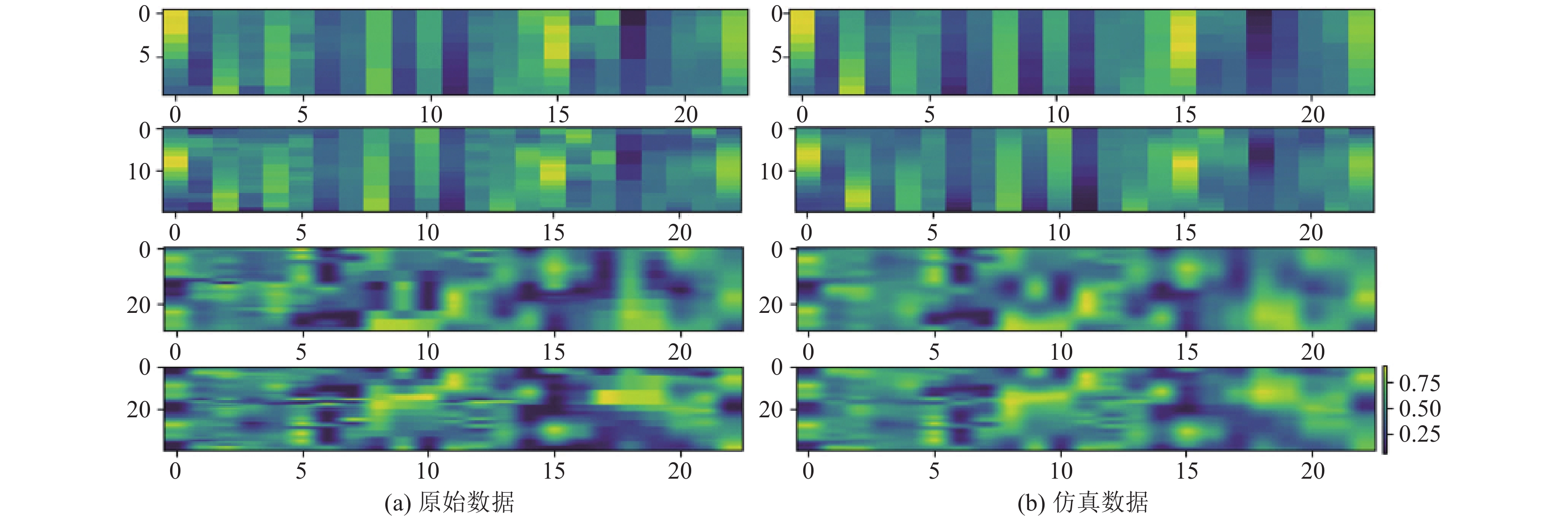
另外, 使用本文所提出的生成模块, 在不同时间采样长度下对所用数据集的部分生成结果进行了可视化, 如图6–图8所示, 左侧为原始数据, 右侧为仿真数据. 纵坐标代表采样长度, 横坐标代表数据维度, 颜色代表数据大小. 可以看出, 采用条件变分自编码器可以有效地实现对真实数据的仿真合成.

3.2.2 持续学习实验

本文将所提算法与多种持续学习方法进行了比较: (1) LwF^[18], 利用知识蒸馏策略缓解对旧任务知识的遗忘. (2) EWC^[16], 通过限制新旧任务之间模型参数的变化, 实现对旧任务知识的记忆. (3) GEM^[22], 利用记忆情景模型限制参数更新方向, 避免针对旧任务的损失上升. (4) MAS^[19], 通过寻找对旧任务重要的参数, 并降低其变化幅度, 防止与旧任务相关的重要知识被覆盖.

在本文设置的持续学习环境中, 训练数据被划分为任务队列, 由包含不同数据的任务组成. 为模拟数据的持续到来, 早期的任务只包含较少类别的数据, 且一个任务内最多容纳3类数据. 设c代表数据类别, k代表数据集的类别总数, 则有任务列表T的组成结构为$ \left\{\left[{c}_{1}\right], \left[{c}_{1}, {c}_{2}\right], \left[{c}_{1}, {c}_{2}{, c}_{3}\right], \cdots , \left[{c}_{k-2}, {c}_{k-1}, {c}_{k}\right]\right\} $.

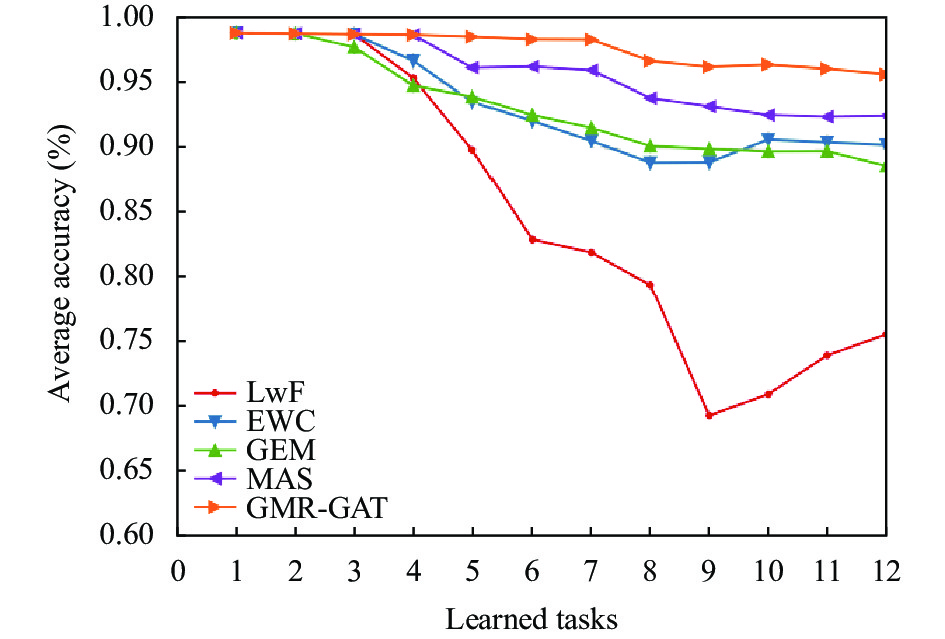
本文在DSADS, MHEALTH与REALDISP这3个数据集上进行了实验, 以平均准确率和平均遗忘率作为评价指标. 实验结果的平均准确率如表3所示, 平均遗忘率如表4所示, 此外, 图9–图11展示了持续学习过程中各方法下平均准确率的变化过程, 其中GMR-GAT是本文所提出的方法.

可以看出, 本文提出的方法在3个数据集上具有较高的平均准确率和较低的平均遗忘率. 灾难性遗忘的根本原因是在学习新任务时, 神经网络的权重会被不断动态调整以优先适应当前任务的数据. 而本实验的结果证明, 通过回放情景记忆, 可以使模型在适应当前任务的同时, 维持一部分有利于旧任务的神经网络参数, 通过这种方式所得到的模型能够在新任务与旧任务上均取得较好的表现, 实现了对灾难性遗忘的缓解. 而LwF在所有的数据集中的表现不如其他基线, 这表明LwF不能很好地适应前文所提的特征提取方法. 在训练新任务时限制重要模型参数变化的EWC和MAS方法, 在不同数据集上训练所得模型的表现较不稳定, 数据集的选取对测试结果存在较大影响. GEM在保持旧任务数据损失的同时, 限制模型参数的更新, 这使其在不同数据集上表现稳定, 且能取得较低的平均遗忘率, 但同时抑制了对新任务的学习, 导致其平均准确率的下降.

3.3 消融实验

为了验证情景记忆缓冲区大小对实验结果的影响, 本文使用了不同大小的记忆缓冲区的场景进行实验. 设缓冲区大小分别为平均每类20, 25, 30, 35, 40. 不同大小的记忆缓冲区下对平均准确率和平均遗忘率的影响分别如表5, 表6所示.

通过表中结果可以看出, 在记忆缓冲区较小时, 模型的持续学习效果较差, 持续学习效果随记忆缓冲区增大而变强, 但当缓冲区增大到一定程度时, 对持续学习效果的增强效果逐渐不明显.

为了验证等概率采样算法的有效性, 本文对采用不同方法构建缓冲区的情景记忆方式进行了实验测试, 其中, 当缓冲区满后, 随机采样策略1将缓冲区内的数据与当前数据合并后进行随机筛选丢弃, 最终缓冲区内中数据量满足限制要求, 随机采样策略2在数据到来前先对缓冲区内数据进行随机筛选丢弃, 数据到来后进入缓冲区, 也使缓冲区内中数据量满足限制要求. 不同策略下平均准确率表现如表7所示, 平均遗忘率表现如表8所示.

实验结果表明, 等概率记忆采样方法能够有效提高本算法的持续学习效果.

为了测试不同数据量环境下利用生成模块产生合成数据进行训练对模型效果的影响, 分别设置了利用40%, 70%和100%数据的训练环境, 并对比了去除生成器模块, 仅回放原始数据的策略. 实验结果的平均准确率对比表现如表9所示, 平均遗忘率对比表现如表10所示.

根据实验结果可以看出, 随着数据量的减少, 使用合成数据的方式的平均准确率下降速度及平均遗忘率上升速度低于不使用的情况, 总体上具有更好的效果, 能够在不影响模型效果的前提下, 通过不断回放合成数据, 缓解模型的灾难性遗忘问题, 同时实现对原始数据的保护.

4 总结

针对当前主流多维时序数据分析算法难以有效利用可穿戴式设备传感器数据的空间性与时间性结构特点的问题, 及多维时序数据分析结束后, 再对新类别数据进行训练出现的灾难性遗忘, 主流算法需要重新对整体数据进行训练的问题, 本文在图注意力网络的研究基础上, 改进了采样与处理方式, 提出了一种具有持续学习能力的算法框架.

首先利用卷积神经网络和对传感器数据中的局部时间和空间信息进行提取: 之后利用图注意力网络对各传感器之间的时间和空间信息进行处理, 通过注意力机制对不同的时空节点赋予不同权重以提升特征提取效果. 经过以上两个步骤, 能够同时提取到传感器的时间特征与空间特征, 并通过与基线算法进行对比实验和消融实验, 验证了本文所使用的特征提取模块的有效性. 此外, 设计了一种合成数据生成模块与对应的情景回放机制, 通过利用真实数据, 合成数据及情景记忆数据对模型进行训练, 缓解了模型的灾难性遗忘问题. 最后, 将该模型在3种不同的可穿戴式设备传感器数据集中进行验证, 结果表明, 与其他处理方式相比, 本文提出的算法框架不仅具有更高的准确率, 并且在持续学习方面的平均准确率与平均遗忘率这两种评价指标上均优于其他持续学习方法, 在训练时间受限等特殊环境中具有一定的实用价值. 由于目前采用的神经网络仍较为基础, 未来考虑将CNN替换为其他更先进的神经网络模型.