2. 中国民航大学 计算机科学与技术学院, 天津 300300
2. School of Computer Science and Technology, Civil Aviation University of China, Tianjin 300300, China
运动模糊是指在拍摄过程中由于相机与物体之间发生相对运动, 从而引起的一种非平稳的图像退化现象. 这种导致图像纹理细节和物体结构缺失的现象严重影响了图像的质量. 在图像去模糊研究中, 恢复出具有精确纹理细节和完整物体结构的清晰图像是一项具有挑战性的任务.
纹理细节是一种在图像中表现为颗粒状、斑点状、线条状等模式的全局特征. Huang等[1]在频率域中提出了一种基于小波的神经网络来获取人脸的纹理信息, 以此重建具有精确纹理细节的高分辨率人脸图像. 频率域可以提供图像中不同频率分量的信息, 而纹理是由不同频率分量的变化组成的. 因此, 频率域能够提供更丰富、更全面的纹理信息描述, 能够更准确地捕捉图像中的纹理细节. 相比之下, 在空间域中无法区分不同频率分量的变化, 只能通过像素点的强度值来表达图像信息.
结构信息是一种在图像中表现为物体几何形状和轮廓的具有一定方向性的特征. Pathak等[2]采用空间域图像中结构缺失区域周围像素信息的约束来修复物体结构, 但在纹理复杂的情况下会出现纹理细节扭曲甚至错误的现象. 空间域的每个像素都对应着实际图像中的一个点, 在进行图像处理时像素的空间位置和相邻像素之间的关系更有利于捕捉图像中的结构信息. 相比之下, 频率域无法直接反映出像素之间的空间关系, 只能表达不同频率分量的变化. 因此, 频率域更适合分析图像中的纹理细节, 空间域更适合分析图像的结构信息.
近年来, 大多数图像去模糊算法都只单独地在空间域或者频率域中提取特征重构清晰图像. Zou等[3]提出了一种利用频率域图像特征去模糊的方法, 该方法利用离散小波变换将扩展的卷积特征划分为4个频带的频率域特征, 进而对不同的频率信息细化. Xu等[4]提出了一种生成对抗网络(generative adversarial network, GAN), 能够利用空间域图像特征从一幅低分辨率的模糊图像中恢复出高分辨率的清晰图像.
为探究空间域和频率域在图像去模糊任务上的关联, 采用相同的网络结构对一张模糊图像分别在空间域和频率域上进行去模糊, 结果如图1所示. 图1中虚线框部分具有丰富的纹理细节, 实线框部分具有显著的物体结构. 计算峰值信噪比(PSNR)以及去模糊图像和真实清晰图像之间差异图的像素均值(Diff). PSNR越高, Diff越低表示去模糊效果越好.

|
图 1 图像去模糊算法DeblurGAN-v2在空间域和频率域恢复的图像对比 |
从图1的3组对比图可以看出, 对于具有丰富纹理细节的部分, 采用频率域去模糊方法恢复图像的PSNR为33.13 dB, 比空间域方法高1.27 dB. 同时, Diff相对较低, 为4.89. 说明频率域更关注纹理细节并且对于纹理部分的恢复效果更好. 对于具有显著物体结构的部分, 采用空间域去模糊方法恢复图像的PSNR为25.14 dB, 比频率域方法高1.09 dB; Diff更低, 为13.42. 说明空间域更关注结构信息并且对于物体结构部分的恢复质量更高.
由此得出: 空间域和频率域信息在去模糊任务中的关注点不同, 呈现出明显的互补性. 受此启发, 提出了一种端到端的融合空间域和频率域信息的图像去模糊框架. 该框架使用两个结构相同但独立的子网络, 分别从空间域和频率域学习模糊图像到清晰图像的映射关系. 随后使用一个融合网络, 融合并改善两个子网络学习到的去模糊结果. 3个网络链接在一起形成一个端到端的可学习的大网络, 不同网络之间相互影响, 建立一个最优的合作机制, 最终得到高质量清晰图像. 主要贡献如下.
(1) 根据空间域和频率域在去模糊任务中关注点不同所呈现的互补性, 提出了一种融合空间域和频率域信息的图像去模糊框架.
(2) 利用图像映射的循环一致性原理构造了基于生成对抗网络的循环对称结构, 增强了网络的去模糊性能.
(3) 在3个去模糊数据集上进行实验, 与9个现有的去模糊方法进行比较, 本文方法效果显著.
1 相关工作 1.1 空间域图像去模糊大多数图像去模糊方法是基于空间域信息展开的, 许多研究人员在空间域中进行分析从而提出图像去模糊算法. Tao等[5]提出一种多尺度循环神经网络, 该网络在不同尺度上对带有残差模块的编解码器训练并进行权重共享. Suin等[6]提出一种动态卷积模块进行图像中模糊的去除. Purohit等[7]提出一种具有自注意模块的编解码网络实现去模糊. Ye等[8]提出一种多尺度迭代网络, 该网络从图像的下采样尺度开始迭代, 每次迭代的输出都会放大, 直到恢复出全分辨率的去模糊图像. Zhang等[9]提出一种为每个位置的循环神经网络生成像素级权重从而增加感受野来进行去模糊的网络. 然而, 这些方法都会不可避免地导致计算损耗剧增和网络收敛缓慢的问题.
近几年由于GAN在建模能力上的优越性, 引起了众多计算机视觉领域研究者的关注, 并被应用在图像去模糊领域中. DeblurGAN[10]受CGAN启发提出了一种具有多分量损失函数的去模糊方法. DeblurGAN-v2[11]则是在DeblurGAN上进一步改进, 生成器部分采用特征金字塔结构进行特征提取, 判别器部分采用相对判别器对生成的去模糊图像和清晰图像进行区分. 虽然基于GAN的方法可以得到较为精确的恢复结果, 但是对于复杂的运动模糊, 去模糊图像仍然缺少许多纹理细节.
基于空间域的去模糊方法更关注图像结构信息, 对于纹理细节的恢复存在一定的限制, 导致空间域去模糊方法性能处于瓶颈.
1.2 频率域图像去模糊为了克服空间域中恢复图像纹理细节不精确的问题, 近年来出现了一些考虑图像频率域信息的去模糊方法. Chakrabarti[12]在频率域中进行模糊核估计, 该方法首先使用经过训练的神经网络对傅里叶系数进行预测, 然后将得到的预测结果与观察到的图像相关联, 进一步得到全局模糊核, 最终采用非盲反卷积得出清晰图像. Cho等[13]提出一种多输入多输出的去模糊网络, 同时使用基于傅里叶变换的频率域损失来指导网络训练. Min等[14]提出一种基于频率域中小波变换的去模糊方法, 其中小波变换用于分解和提取模糊图像的频率信息. Liu等[15]提出了一种利用小波变换对U-Net网络进行改进的多级小波卷积神经网络, 该网络可以更好地平衡感受野大小与计算效率, 减少特征图的规模并恢复出高分辨率图像.
空间域更关注图像结构, 频率域更关注纹理细节. 传统的图像去模糊方法往往只单独地聚焦空间域或者频率域, 没有考虑到两个域之间的互补性, 导致无法很好地恢复图像结构和纹理细节. 为了解决这个问题, 本文提出了一种融合空间域和频率域信息的图像去模糊模型, 综合利用空间域和频率域信息, 更全面地恢复图像结构和纹理细节.
2 本文方法给定模糊图像
| S=ϕ(B;W) | (1) |
其中,
与已有的单独在频率域[3]或者空间域[4]中建立映射函数
| SFu=ϕFu([ϕSp(B;WSp),ϕFe(B;WFe)];WFu) | (2) |
其中,
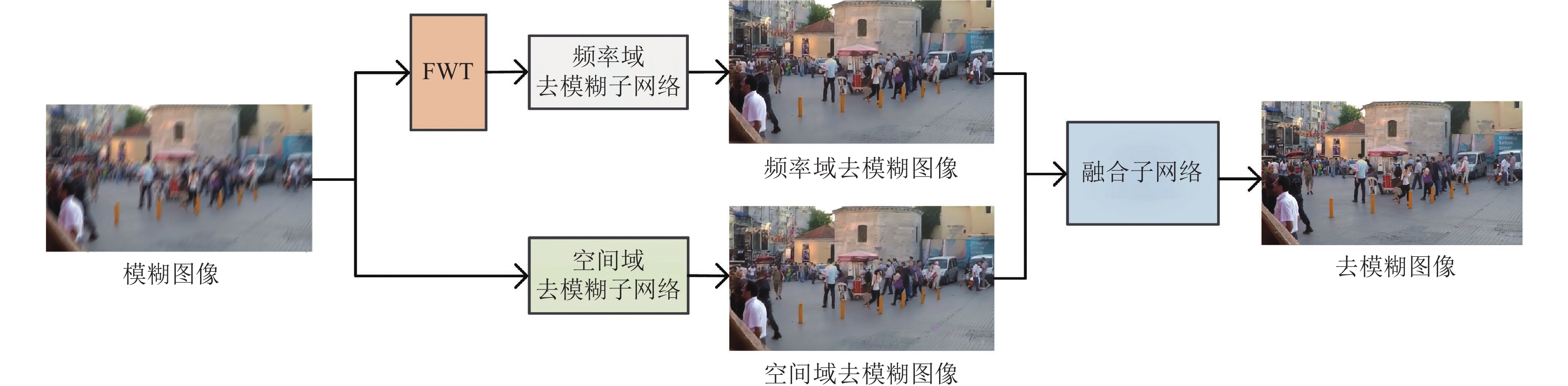
|
图 2 空间域频率域融合去模糊网络结构 |
2.1 空间域和频率域去模糊子网络
为了使空间域去模糊子网络和频率域去模糊子网络在特征提取能力上水平相同, 从而更好地发挥空间域和频率域在去模糊任务中的互补作用, 本文设计了两个结构相同的去模糊子网络. 并且在设计过程中, 特别注重其特征提取能力, 为后续融合子网络进行信息融合奠定基础.
在DeblurGAN-v2中, 生成器采用特征金字塔结构来提取不同尺度上的特征, 以捕获不同层次、不同大小的物体结构和纹理细节特征. 这种结构具有较强的特征提取能力, 但特征金字塔结构中进行多尺度变换的下采样和上采样操作会造成信息损失, 导致提取的特征不够准确, 影响模型性能.
根据循环一致性原理[16], 由模糊图像恢复得到的清晰图像可以反向转换还原回模糊图像, 而由清晰图像模糊后的图像也可以再次反向转换还原回清晰图像. 当生成图像经过反向转换后能够与原始图像保持一致时, 说明网络能够全面地捕捉到图像信息, 并以此重建图像. 陈涛等[17]采用循环一致性原理来解决图像信息丢失问题. 本文引入图像映射的循环一致性, 网络经过多次转换从不同的视角处理数据, 在这个过程中逐步学习提取更全面、更丰富特征的能力. 因此, 循环一致性原理能够克服特征金字塔的信息损失问题, 帮助网络全面提取有效特征.
本文在DeblurGAN-v2中特征金字塔结构的基础上结合循环一致性原理提出了增强特征提取能力的循环对称结构, 以提高网络的去模糊性能. 具体实现细节如图3所示,
| S∗1=G1(B),B∗1=G2(S∗1) | (3) |
| B∗2=G2(S),S∗2=G1(B∗2) | (4) |
生成器
融合子网络将从空间域中恢复的清晰图像
| SFu=ϕFu([S∗Sp,S∗Fe];WFu) | (5) |
为了体现以空间域和频率域互补性进行信息融合的优势, 融合策略既要有利于图像物体结构又要有利于纹理. 结构信息在图像中表现为物体的几何形状和轮廓, 是一种具有明确方向性的特征. 而条带池化在水平或者垂直方向上的操作能够捕捉不同方向上的结构信息, 符合结构信息的方向性.

|
图 3 循环对称结构 |
纹理细节在图像中表现为颗粒状、斑点状、线条状等模式, 体现了物体表面具有周期性变化的组织结构排列属性, 是一种全局性特征. 传统的池化操作对方形池化核区域内的像素值操作, 进行信息捕捉, 但是其方形的形状限制了信息捕获的距离. 由于窄核有利于捕捉局部信息, 长核有利于捕捉长程信息. 条带池化的长形狭窄带状核兼具长核和窄核的优势, 能够捕捉长程和局部上下文信息, 将局部特征整合到全局特征中, 符合纹理细节的全局性.
融合子网络的网络结构如图4所示, BAM是BANet[19]提出的去模糊感知模块(blur-aware attention module, BAM). BAM利用条带池化操作(strip pooling, SP)[20]的条带状长核提取特征, 在水平和垂直两个方向上对某一行或者某一列的特征取平均值, 然后以逐像素相加的方式融合两个方向上的条带状特征, 公式化表达如下:
| {yhi=1WW−1∑j=0xi,jyvj=1HH−1∑i=0xi,jy=yhi+yvj | (6) |
其中,
具体过程如下, 首先将
| {F1=CR([S∗Sp,S∗Fe])F2=CR(F1) | (7) |
其中, CR(
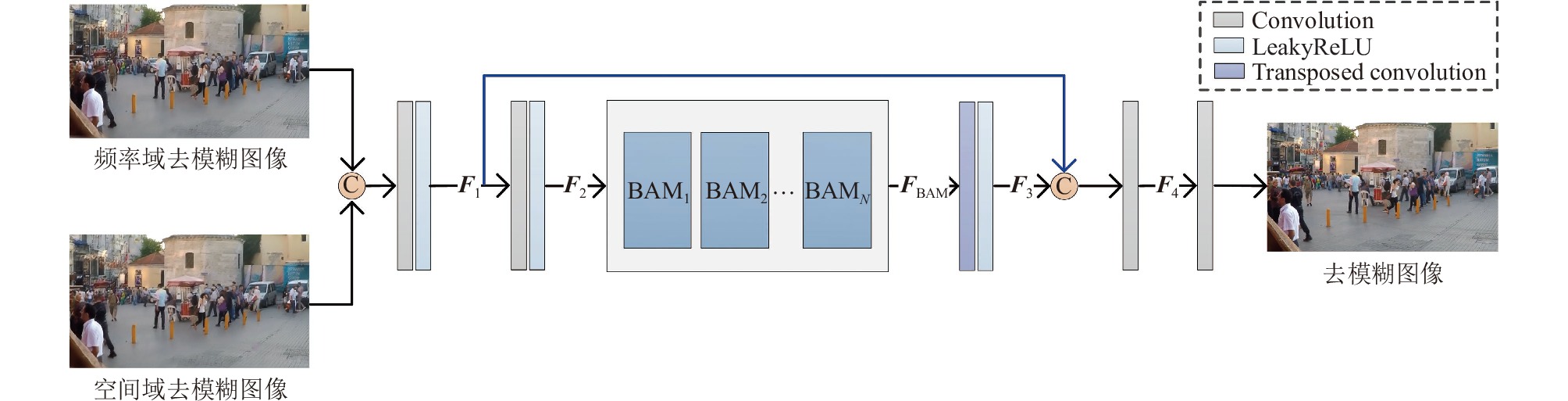
|
图 4 融合子网络结构 |
然后使用N个BAM模块进行信息融合, 每个BAM模块的输出特征作为下一个BAM模块的输入, 用
| {F3=TCR(FBAM)F4=C([F1,F3]) | (8) |
其中,
最终恢复的清晰图像
| SFu=C(F4) | (9) |
本文采用均方误差损失、循环一致性损失[16]、图像内容损失[11]和对抗损失[11]对空间域去模糊子网络和频率域去模糊子网络进行优化.
均方误差损失定义如下:
| Lmse=||S∗1−S||2 + ||S∗2−S||2 | (10) |
其中, ||·||2表示
循环一致性损失定义如下:
| Lcycle-consistency=||B∗1−B||1+||S∗2−S||1 | (11) |
其中, ||·||1表示
图像内容损失定义如下:
| Lcontent=||φ(S∗1)−φ(S)||2+||φ(S∗2)−φ(S)||2 | (12) |
其中,
对抗损失定义如下:
| Ladversarial=δ(S∗1,D1,S)+δ(S∗2,D1,S)+δ(B∗1,D2,B)+δ(B∗2,D2,B) | (13) |
其中,
| δ=Ex∼Pdata(x)[(D(x)−Ez∼Pz(z)D(G(z))−1)2]+Ez∼Pz(z)[(D(G(z))−Ex∼Pdata(x)D(x)+1)2] | (14) |
其中,
| L=λ1Lmse+λ2Lcycle-consistency+λ3Lcontent+λ4Ladversarial | (15) |
其中,
本文使用Charbonnier损失[21]和FFT损失[22]对融合子网络进行优化. Charbonnier损失定义如下:
| LCharbonnier=√||SFu−S||2+ε2 | (16) |
其中,
FFT损失定义如下:
| LFFT=||f(SFu)−f(S)||1 | (17) |
其中,
融合子网络的整体损失如下:
| LFu=Lcharbonnier+λ5LFFT | (18) |
其中,
为了实现端到端的运动图像去模糊, 将初始模糊图像作为空间域和频率域去模糊子网络的输入, 分别得到空间域和频率域的去模糊图像; 然后将得到的两个去模糊图像作为融合子网络的输入, 得到最终的清晰图像. 算法1为端到端的空间域频率域融合去模糊联合优化过程.
算法1. 端到端的空间域频率域融合去模糊联合优化过程
输入: 原始模糊图像和清晰图像对
输出: 空间域映射模型
1. 训练空间域映射模型
1.1. While not converged do:
1.2. 计算清晰图像
1.3. 计算清晰图像
1.4. 计算均方误差损失, 式(10);
1.5. 计算循环一致损失, 式(11);
1.6. 计算图像内容损失, 式(12);
1.7. 计算对抗损失, 式(13)和式(14);
1.8. 最小化目标函数L更新
1.9. 得到空间域映射模型
2. 训练频率域映射模型
2.1. While not converged do:
2.2. 利用快速小波变换, 得到频率信息
2.3. 计算清晰图像
2.4. 计算清晰图像
2.5. 计算均方误差损失, 式(10);
2.6. 计算循环一致损失, 式(11);
2.7. 计算图像内容损失, 式(12);
2.8. 计算对抗损失, 式(13)和式(14);
2.9. 最小化目标函数L更新
2.10. 得到频率域映射模型
3. 联合优化
3.1. While not converged do:
3.2. 将
3.3. 计算Charbonnier损失, 式(16);
3.4. 计算FFT损失, 式(17);
3.5. 最小化目标函数
3.6. 得到融合模型
数据集: 本文使用GoPro数据集[23], 其训练集有2103个图像对, 测试集有1111个图像对. 所有的对比方法都采用该数据集进行训练和测试. 除GoPro数据集外, 在Kohler数据集[24]上进行定性分析, 而Kohler数据集只包含4张清晰图像, 每张清晰图像有12张模糊图像与之对应. 该数据集图像数量较少, 并且它与GoPro数据集都是合成模糊数据集. 为了对本模型进行更加全面的测试和分析, 在真实世界的模糊图像数据集RWBI[25]上进行定性分析, 其包含22个不同场景, 共3112张现实世界模糊图像. 为评定恢复的去模糊图像的清晰度, 除采用主观性评价外, 还进行了定量分析.
量化指标: 本文采用峰值信噪比(peak signal to noise ratio, PSNR)、结构相似度(structure similarity index metric, SSIM)、平均绝对误差(mean absolute error, MAE)以及拉普拉斯梯度(Laplacian gradient, LAP)来评价不同图像去模糊方法的性能.
峰值信噪比的数值越大表示失真越小. 对于两张大小为
| PSNR=20×log101√MSE | (19) |
其中,
结构相似度的取值范围是[0, 1], 值越大表示去模糊图像与清晰图像越相似. 计算过程如下:
| SSIM=(2μxμy+c1)(2σxy+c2)(u2x+u2y+c1)(σ2x+σ2y+c2) | (20) |
其中,
平均绝对误差表示两张图像之间绝对误差的平均值, 其数值越小表示图像的恢复质量越好. 定义如下:
| MAE=1H×W∑0⩽ | (21) |
拉普拉斯梯度[26]用于进行无参考真实模糊图像的恢复质量评定. 它能够衡量图像的二阶导, 强调图像中快速变化的区域, 即边缘部分. 而清晰图像中边缘部分较多, 模糊图像则更加平滑, 边缘部分较少. 因此拉普拉斯梯度越大, 图像越清晰. 基于拉普拉斯梯度的图像清晰度是对图像灰度图采用拉普拉斯算子计算每个像素的拉普拉斯梯度, 并求其绝对值的方差. LAP定义如下:
| {\textit{LAP}} = {\sum\limits_{0 \leqslant {{i}} \lt {{H}}} {\sum\limits_{0 \leqslant {{j}} \lt {{W}}} {[|{{L}}({{i}}, {{j}})| - \overline {{L}} ]} } ^2} | (22) |
其中,
实施细节和训练设置: 空间域图像去模糊映射函数
为对比本文方法在图像去模糊任务上性能的优劣, 选取了常见的去模糊方法进行对比: DeblurGAN-v2[11]、BANet[19]、SRN[5]、DBRBGAN[25]、DeblurGAN[10]、DMPHN[28]、Liu等人[29]、DSD[30]和MTRNN[31], 结果如表1所示. 本文方法在峰值信噪比、结构相似度以及平均绝对误差这3个方面明显优于所有其他对比方法. 与BANet相比, 本文方法在PSNR上高出了0.24 dB, 在MAE上降低了1.25; 与DMPHN相比, 本文方法在PSNR上高出了1.69 dB, SSIM高出0.01, 在MAE上降低了3.09. 与DeblurGAN-v2相比, 本文方法在PSNR和SSIM上分别提高了4.82 dB和0.08, 在MAE上降低了12.82. 与同样使用了频率域信息的方法文献[29]相比, PSNR高出3.21 dB, SSIM高出0.02, MAE降低了10.18.
| 表 1 GoPro测试数据集上的测试结果比较 |
对于没有真值的现实世界真实模糊数据集RWBI, 使用拉普拉斯梯度对本文方法与其他去模糊方法进行客观评价. 结果如表2, 可以发现本文方法去模糊结果的拉普拉斯梯度最大, 为227.37. 与BANet、DMPHN、DeblurGAN-v2以及Liu等人[29]相比, 分别高出18.2、23.68、41.75和26.07. 说明在恢复真实模糊图像上, 本文方法与其他去模糊方法相比性能最好.
3.2.2 定性分析图5是在GoPro测试集上几种图像去模糊方法的视觉效果图. 除本文方法外, 其他对比方法无法很好地恢复出图5中第1行的地面纹理区域和第2行的文本区域, 其结果不仅仍然存在模糊, 还会得到错误的纹理细节甚至发生形状的改变; 对于最后一行的人脸区域, 其他方法无法得到清晰的五官和脸部轮廓, 本文方法可以得到轮廓分明的人脸, 并且眼睛以及所佩戴眼镜等细节都可以完整恢复.
| 表 2 RWBI测试数据集上的测试结果比较 |
图6是基于GoPro数据集训练后得到的权重在Kohler数据集上进行图像去模糊的视觉对比图. 从图中可以看出, 本文方法在恢复墙壁纹理和旗帜等具有复杂纹理细节以及座椅等具有较强结构的物体方面, 相较于其他去模糊方法更加精确. 结合图5和图6可以说明本文方法对于纹理细节和边缘结构都有更加精确的去模糊效果.
此外, 为了对去模糊算法进行更加全面的评价, 在现实世界的真实模糊图像数据集RWBI上与其他去模糊方法进行了主观视觉比较, 其去模糊权重是基于GoPro数据集训练后得到的. 如图7所示, 本文方法相比于其他方法恢复的现实世界中真实模糊图像质量更高, 去模糊效果更好.
3.3 消融实验为验证所提方法的有效性, 在GoPro数据集上进行了一系列消融实验. 由于训练设备的限制, 所有消融实验的迭代次数设置为300.
3.3.1 频率域信息转换为验证不同频率域信息转换方法对去模糊效果的影响进行了实验, 结果如表3所示, 基于哈尔小波的快速小波变换(fast wavelet transform, FWT)[27]去模糊效果最好, 与基于哈尔小波的离散小波变换(discrete wavelet transform, DWT)[32]以及离散余弦变换(discrete cosine transform, DCT)[33]相比, 在PSNR上分别高出0.08 dB和0.53 dB, 在MAE上降低了1.42和2.02. 这是因为在离散小波变换的处理过程中会对图像进行多次下采样而造成信息损失, 不利于图像纹理细节的恢复; 离散余弦变换适用于平稳信号的频谱分析, 对于非平稳信号处理能力较弱, 而模糊通常是非平稳的退化.
3.3.2 循环对称结构为了验证循环对称结构的有效性, 分别在空间域子网络和使用FWT的频率域去模糊子网络中进行实验, 比较了是否加入循环对称结构的效果. 实验结果如表4和表5所示, 当不添加循环对称结构时: 空间域的PSNR为29.02 dB, SSIM为0.84, MAE为107.97; 频率域的PSNR为29.65 dB, SSIM为0.86, MAE为105.88. 添加循环对称结构后: 空间域的PSNR和SSIM分别提升0.71 dB和0.03, MAE降低3.01; 频率域的PSNR和SSIM分别提升了0.09 dB和0.01, MAE降低1.26. 说明循环对称结构提取了更全面丰富的特征信息, 增强了频率域和空间域去模糊子网络的性能, 提高了去模糊图像的质量.
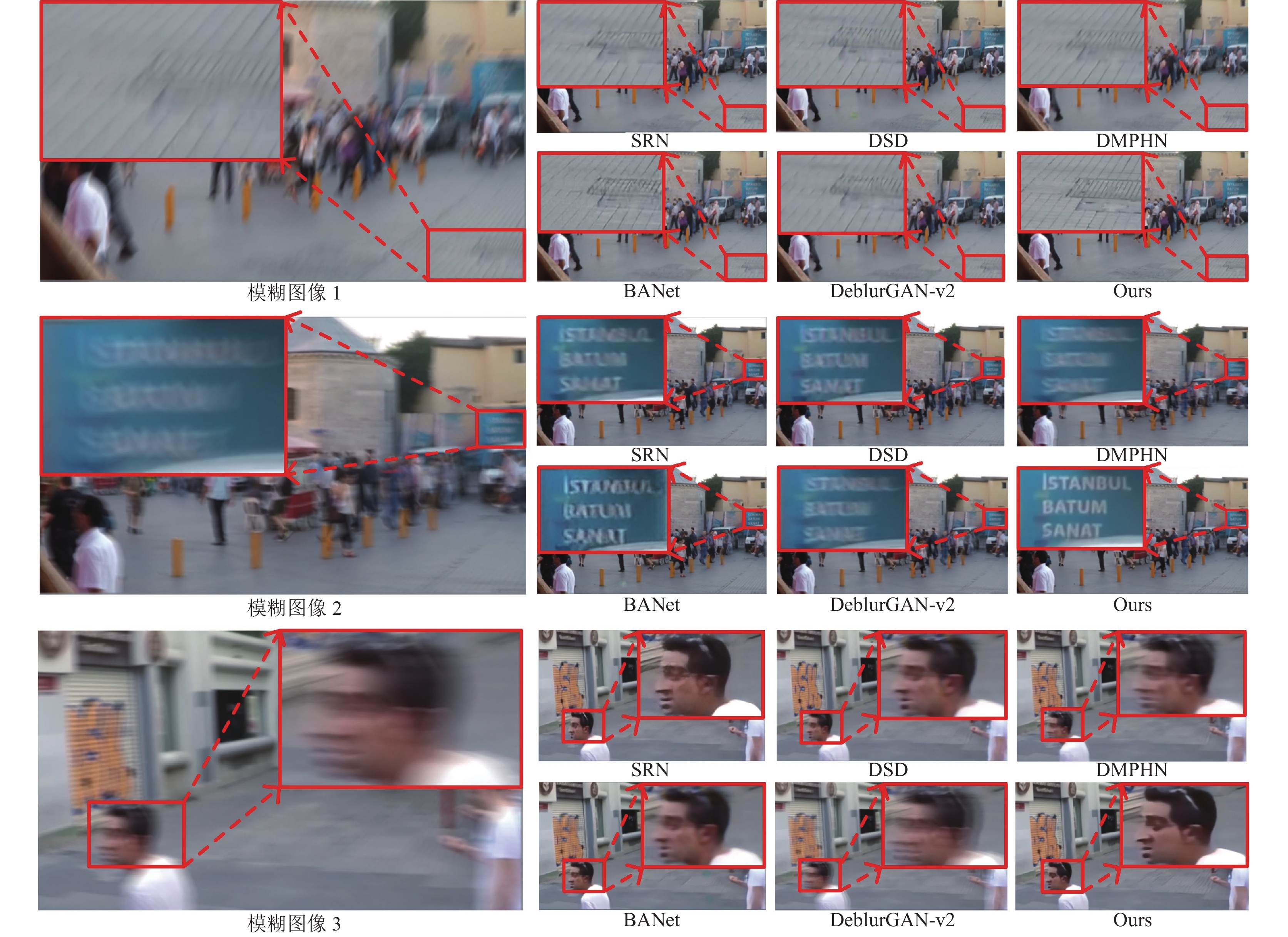
|
图 5 在GoPro测试数据集上的去模糊效果 |

|
图 6 在Kohler测试数据集上的去模糊效果 |

|
图 7 在RWBI测试数据集上的去模糊效果 |
| 表 3 不同频率域信息转换方式性能比较 |
| 表 4 空间域去模糊子网络是否加入循环对称结构性能比较 |
| 表 5 频率域去模糊子网络是否加入循环对称结构性能比较 |
3.3.3 融合子网络中空间域与频率域的融合方式
将空间域去模糊子网络与使用FWT的频率域去模糊子网络的结果作为融合子网络的输入, 进行信息融合. 对两种融合方式进行验证: 第1种方式是通过通道拼接进行信息融合; 第2种方式是通过逐像素相加进行信息融合. 不同融合方式结果如表6所示, 通道融合按顺序将多个通道连接起来形成一个更深的特征, 能够保留每个通道中的完整信息. 相比之下, 相加融合会导致不同通道特征的信息相互叠加, 造成某些特征的丢失或模糊.
| 表 6 不同融合方式的图像去模糊性能比较 |
3.3.4 融合子网络中条带池化
为验证条带池化在融合子网络中的有效性, 将其与平均池化和最大池化进行比较. 结果如表7所示, 条带池化的效果最好, 其PSNR为31.33 dB, SSIM为0.89; 最大池化和平均池化的PSNR分别为30.18 dB和30.19 dB, 均次于条带池化. 这是由于平均池化会将池化区域内的像素值取平均, 存在特征缺失; 而最大池化将池化区域内的最大值作为池化结果的像素值, 相比于平均池化只能提取图像中最为显著的特征, 存在更多的特征缺失.
3.3.5 融合子网络中特征F1的跳跃连接在经过一系列BAM模块处理后对是否要进行跳跃连接进行验证, 结果如表8所示. 进行跳跃连接的去模糊效果在PSNR上要比不进行跳跃连接高0.53 dB, MAE低5.69. 跳跃连接将低层信息传递到高层, 使网络能够同时利用不同层次的特征, 有助于弥补多个网络层导致的信息损失, 为图像去模糊提供了更全面的特征.
| 表 7 融合子网络不同池化方式的图像去模糊性能比较 |
| 表 8 是否进行跳跃连接的图像去模糊性能比较 |
3.3.6 融合子网络的作用
为探讨本模型中空间域去模糊子网络、频率域去模糊子网络以及融合子网络这3个部分对去模糊算法性能的影响进行了实验, 结果如表9所示. 空间域去模糊子网络效果最差, 而包含3个子网络的完整模型结构在所有指标上均达到最优. 融合空间域和频率域信息使得去模糊效果显著提升, 相比空间域去模糊子网络和频率域去模糊子网络, 在PSNR上分别提升了1.60 dB和1.55 dB; 在SSIM上分别提升了0.02和0.01; 在MAE上分别降低了6.92和6.07. 说明基于空间域与频率域的互补性进行的信息融合能够提升去模糊效果.
| 表 9 模型中各核心部分作用比较 |
4 结语
空间域信息与频率域信息在去模糊过程中关注点各有侧重且二者具有互补性. 基于此, 本文提出了一种有效的空间域频率域融合框架, 并设计了相应的网络结构负责空间域、频率域的图像去模糊, 然后使用一个简单的网络进行融合. 在合成模糊数据集GoPro、Kohler以及真实模糊数据集RWBI上的实验验证了该方法在图像去模糊任务上的有效性.
| [1] |
Huang HB, He R, Sun ZA, et al. Wavelet-SRNet: A wavelet-based CNN for multi-scale face super resolution. Proceedings of the 2017 IEEE International Conference on Computer Vision. Venice: IEEE, 2017. 1698–1706.
|
| [2] |
Pathak D, Krähenbühl P, Donahue J, et al. Context encoders: Feature learning by inpainting. Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 2536–2544.
|
| [3] |
Zou WB, Jiang MC, Zhang YC, et al. SDWNet: A straight dilated network with wavelet transformation for image deblurring. Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision Workshops. Montreal: IEEE, 2021. 1895–1904.
|
| [4] |
Xu XY, Sun DQ, Pan JS, et al. Learning to super-resolve blurry face and text images. Proceedings of the 2017 IEEE International Conference on Computer Vision. Venice: IEEE, 2017. 251–260.
|
| [5] |
Tao X, Gao HY, Shen XY, et al. Scale-recurrent network for deep image deblurring. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 8174–8182.
|
| [6] |
Suin M, Purohit K, Rajagopalan AN. Spatially-attentive patch-hierarchical network for adaptive motion deblurring. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020. 3603–3612.
|
| [7] |
Purohit K, Rajagopalan AN. Region-adaptive dense network for efficient motion deblurring. Proceedings of the 34th AAAI Conference on Artificial Intelligence. New York: AAAI, 2020. 11882–11889.
|
| [8] |
Ye MY, Lyu D, Chen GS. Scale-iterative upscaling network for image deblurring. IEEE Access, 2020, 8: 18316-18325. DOI:10.1109/ACCESS.2020.2967823 |
| [9] |
Zhang JW, Pan JS, Ren J, et al. Dynamic scene deblurring using spatially variant recurrent neural networks. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 2521–2529.
|
| [10] |
Kupyn O, Budzan V, Mykhailych M, et al. DeblurGAN: Blind motion deblurring using conditional adversarial networks. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 8183–8192.
|
| [11] |
Kupyn O, Martyniuk T, Wu JR, et al. DeblurGAN-v2: Deblurring (orders-of-magnitude) faster and better. Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019. 8877–8886.
|
| [12] |
Chakrabarti A. A neural approach to blind motion deblurring. Proceedings of the 14th European Conference on Computer Vision. Amsterdam: Springer, 2016. 221–235.
|
| [13] |
Cho SJ, Ji SW, Hong JP, et al. Rethinking coarse-to-fine approach in single image deblurring. Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021. 4621–4630.
|
| [14] |
Min C, Wen GQ, Li BR, et al. Blind deblurring via a novel recursive deep CNN improved by wavelet transform. IEEE Access, 2018, 6: 69242-69252. DOI:10.1109/ACCESS.2018.2880279 |
| [15] |
Liu PJ, Zhang HZ, Zhang K, et al. Multi-level wavelet-CNN for image restoration. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops. Salt Lake City: IEEE, 2018. 886–895.
|
| [16] |
Zhu JY, Park T, Isola P, et al. Unpaired image-to-image translation using cycle-consistent adversarial networks. Proceedings of the 2017 IEEE International Conference on Computer Vision. Venice: IEEE, 2017. 2242–2251.
|
| [17] |
陈涛, 魏为民, 申林帅. 一种CycleGAN结合膨胀卷积的指纹图像增强方法. 国外电子测量技术, 2022, 41(9): 47-53. DOI:10.19652/j.cnki.femt.2204009 |
| [18] |
Lin TY, Dollár P, Girshick R, et al. Feature pyramid networks for object detection. Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 936–944.
|
| [19] |
Tsai FJ, Peng YT, Tsai CC, et al. BANet: A blur-aware attention network for dynamic scene deblurring. IEEE Transactions on Image Processing. 2022, 31: 6789–6799.
|
| [20] |
Hou QB, Zhang L, Cheng MM, et al. Strip pooling: Rethinking spatial pooling for scene parsing. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020. 4002–4011.
|
| [21] |
Charbonnier P, Blanc-Feraud L, Aubert G, et al. Two deterministic half-quadratic regularization algorithms for computed imaging. Proceedings of the 1st International Conference on Image Processing. Austin: IEEE. 1994. 168–172.
|
| [22] |
Jiang LM, Dai B, Wu W, et al. Focal frequency loss for image reconstruction and synthesis. Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021. 13899–13909.
|
| [23] |
Nah S, Kim TH, Lee KM. Deep multi-scale convolutional neural network for dynamic scene deblurring. Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 257–265.
|
| [24] |
Köhler R, Hirsch M, Mohler B, et al. Recording and playback of camera shake: Benchmarking blind deconvolution with a real-world database. Proceedings of the 12th European Conference on Computer Vision. Florence: Springer, 2012. 27–40.
|
| [25] |
Zhang KH, Luo WH, Zhong YR, et al. Deblurring by realistic blurring. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020. 2734–2743.
|
| [26] |
Pech-Pacheco JL, Cristobal G, Chamorro-Martinez J, et al. Diatom autofocusing in brightfield microscopy: A comparative study. Proceedings of the 15th International Conference on Pattern Recognition. Barcelona: IEEE, 2000. 314–317.
|
| [27] |
Mallat SG. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1998, 11(7): 674-693. DOI:10.1109/34.192463 |
| [28] |
Zhang HG, Dai YC, Li HD, et al. Deep stacked hierarchical multi-patch network for image deblurring. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 5971–5979.
|
| [29] |
Liu Y, Fang FM, Wang TT, et al. Multi-scale grid network for image deblurring with high-frequency guidance. IEEE Transactions on Multimedia, 2021, 24: 2890-2901. DOI:10.1109/TMM.2021.3090206 |
| [30] |
Gao HY, Tao X, Shen XY, et al. Dynamic scene deblurring with parameter selective sharing and nested skip connections. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 3843–3851.
|
| [31] |
Park D, Kang DU, Kim J, et al. Multi-temporal recurrent neural networks for progressive non-uniform single image deblurring with incremental temporal training. Proceedings of the 16th European Conference on Computer Vision. Glasgow: Springer, 2020. 327–343.
|
| [32] |
Shensa MJ. The discrete wavelet transform: Wedding the a trous and mallat algorithms. IEEE Transactions on Signal Processing, 1992, 40(10): 2464-2482. DOI:10.1109/78.157290 |
| [33] |
Ahmed N, Natarajan T, Rao KR. Discrete cosine transform. IEEE Transactions on Computers, 1974, C-23(1): 90-93. DOI:10.1109/T-C.1974.223784 |
 2024, Vol. 33
2024, Vol. 33



