1 引言

医学图像配准的目标是通过寻找空间变化的算法, 将一幅图像中的区域识别并对齐另一幅图像中相似或者相同的解剖结构^[1], 使两幅图像在空间中相同的位置可以一一对应, 从而可以对不同的图像进行比较和融合. 医学图像配准可分为刚体配准和非刚体配准, 其中非刚体配准又称可变形图像配准^[2]. 刚体配准是指目标物体内部任意两点之间的距离在变换过程中保持不变, 刚体变换主要由平移和旋转操作组成. 由于刚体配准的参数有限, 无法适应于形态变量复杂的图像. 故目前应用的主流配准方法是可形变图像配准^[3].

可形变图像配准按照训练方式的不同, 分为基于传统算法的配准方法和基于深度学习的配准方法. 目前, 基于扩散模型的Demons算法^[4]及其变体是传统算法中的主流算法. Demons算法将图像配准视为一个扩散过程, 利用参考图像灰度梯度中产生的局部信息来驱动待配准图像向参考图像的扩散, 并对待配准图像进行迭代扭曲, 直到单次迭代中的形变位移足够小时完成迭代配准. 由于Demons算法在参考图像灰度梯度较小时迭代次数明显增加且效率较低, 因此Wang等人 ^[5]将每次迭代变形后的待配准图像与参考图像结合作为扩散过程中的驱动力. Zhang等人^[6]在每次迭代时观察两幅图像的相似度值变化, 当值达到最大时停止迭代优化. 然而, 这些迭代优化的配准算法非常耗时, 难以用于实时的医学图像配准应用. Jaderberg等人^[7]在反向传播算法的基础上提出空间转换网络(spatial Transformer network, STN), STN生成的形变场可以通过网络的反向传播进行优化并具有可微属性, 通过使用配准后图像之间的相似性损失函数, 可以避免复杂的损失函数设计. Balakrishnan等人^[8]通过融合STN结构提出了一种新的端到端的无监督图像配准模型(VoxelMorph), 此模型的自定义损失函数可以有效提升图像配准的速度. Zhao等人^[9]将级联网络运用到图像配准中, 并证明级联做法可以提升配准的准确率. 因此本文方法模型采用级联的设计对图像配准, 通过对图像块进行精细配准提升小区域的配准精度, 从而提高整体配准结果的稳定性.

计算机视觉领域中卷积神经网络(convolutional neural network, CNN)通常被用来提取局部特征, 但提取过程中是卷积层的感受野受到卷积核尺寸的限制, 这意味着只能捕捉到局部特征而难以学习到全局特征, 导致在处理复杂的医疗图像时出现配准误差, 并且随着卷积网络层数的加深, 图像中距离较远的像素点之间的依赖关系会急剧减小. 在处理复杂的医疗图像时, 这种依赖关系非常重要, 因为图像中不同区域间可能具有复杂的依赖关系. 为了解决这个问题, Liu等人^[10]提出了拥有移位窗口的层次化Transformer, 可以动态的调整网络对不同区域的关注度, 从而更好地学习全局特征. Chen等人^[11]首次将Transformer构造成编码器-解码器的结构应用到无监督配准中, 在实验结果中可以说明对比CNN网络的高效性和准确性. 但由于自注意力机制本身的计算特性, 导致纯Transformer构成的配准网络计算代价高昂, 并存在训练显存过大的问题. gConv网络是Rao等人^[12]总结了Transformer机制的成功之处, 并将其应用于普通CNN中, 以CNN的参数体量实现了接近Transformer网络的全局信息提取能力, gConv提出的方法借助门控卷积和递归运算, 可以高效地实现任意阶的空间交互, 然而gConv在医学图像配准中的应用仍处于起步阶段.

因此本文在以上观点的基础上提出一种基于多空间信息提取的级联多阶层配准模型, 该模型的主要特点是使用了多空间信息提取技术, 可以在不同尺度上提取图像的特征信息, 从而提高配准的准确度和鲁棒性. 同时, 该模型还采用了级联多阶层网络和分块模块, 可以降低计算复杂度和内存占用量, 适用于多种医学图像配准场景. 该模型包含: ① 构建由gConv网络组成的编码器, 构建Transformer、CNN组成的解码器, 并将二者组成U型基础配准网络. ② 构造分块融合模块, 对图像进行分块处理操作, 并按照一定规则进行拼接融合, 形成最终的形变场. ③ 将多个基础配准网络通过级联的方式连接起来, 并在每层网络对不同大小的图像进行优化, 从而解决图像中复杂局部区域的形变问题.

2 方法 2.1 总体架构

在计算机视觉领域中, 图像分块是一种常用的处理策略. 将图像分块后对每个图像块分别进行相应的处理, 并在处理完毕后再按照一定的规则进行拼接融合. 这种分块合并的方法可以更精确地处理图像的局部细小区域^[13], 提高配准的准确性和准确性. 同时, 由于医学图像分辨率高、数据尺寸大的特点, 通过将图像分块, 可以逐个读取和处理从而可以加快处理速度. 此模型由3层子网络和1个融合模块组成. 模型的整体架构如图1所示, 模型共有3层子网络和1个融合模块, 并在每层子网络中都包含分块模块和STN模块, 3个子网络的中的配准网络的结构是相同的, 可以实现参数共享, 从而提升配准的健壮性. 模型的整体架构按照由粗到精^[14]的配准原则, 自底向上的阶层顺序依次对图像进行配准, 每层子网络的输入为一对待配准的图像, 输出为对应的形变场块, 将此形变场块与输入的形变场块一起输入到分块模块和STN模块后, 输入到下一阶层子网络.

在融合模块中, 按照自顶向下的阶层顺序合并每层子网络产生的形变场块, 并且在合并过程中以上一层子网络产生的形变场块为参考, 以减少边缘效应.

2.2 基础配准网络

在计算机视觉领域, CNN网络的优点是局部感知性强, 可以有效地捕捉到局部空间的特征信息, 提高模型对局部特征的感知性. Transformer网络的优势是可以使用自注意力机制对全局空间特征信息进行提取, 可以有效捕捉到图像中的长期依赖关系, 而gConv网络结合了两种网络各自的优点.

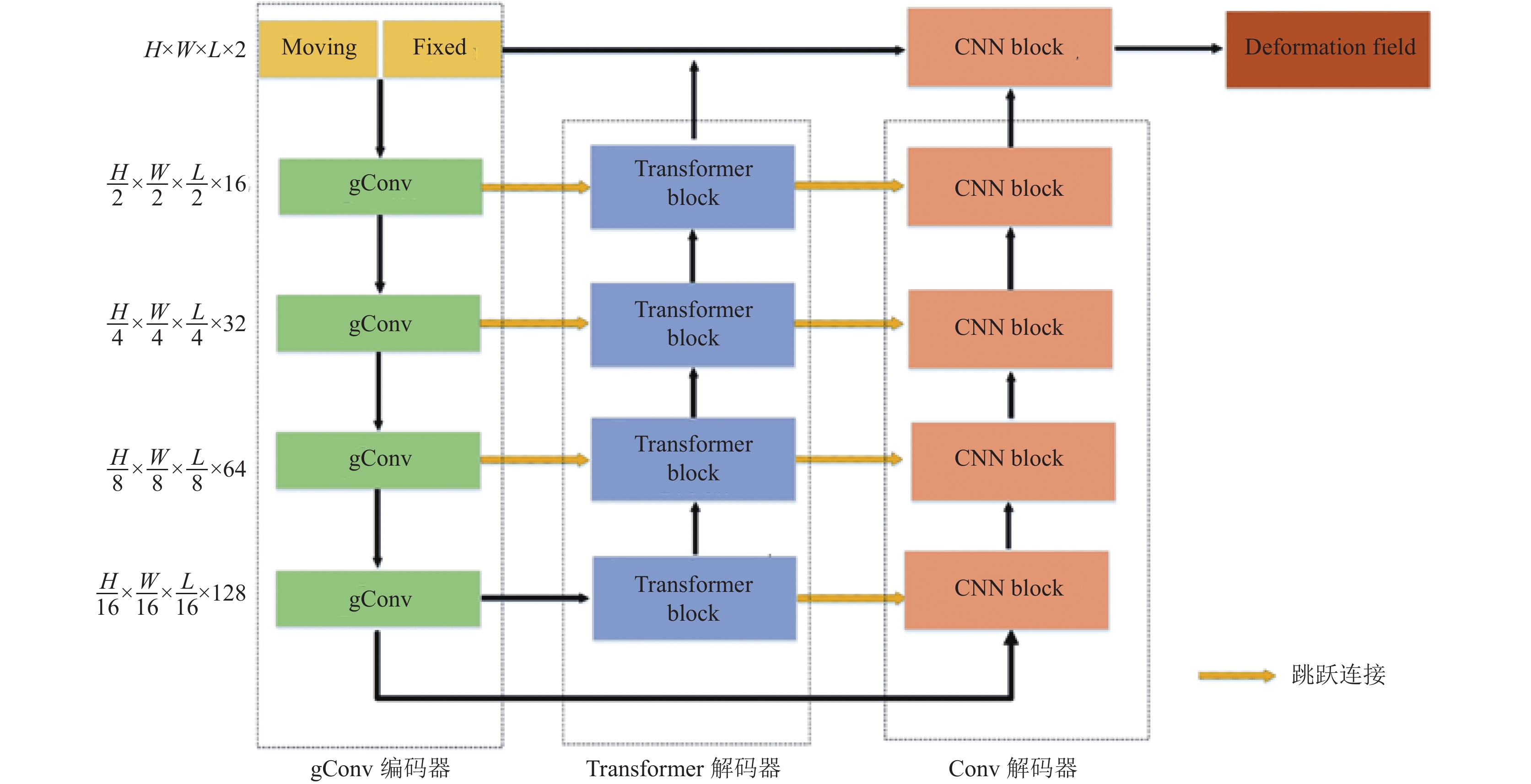
MainNet分为3个模块, gConv编码器、Transformer解码器和普通卷积解码器, 如图2所示. 基础配准网络使用gConv网络构成的编码器进行下采样的同时保留局部和全局空间信息, 使用Transformer和CNN构成的解码器应用于还原全局和局部空间信息, 并在形变场生成前, 将参考图像和Transformer和CNN的解码输出结合, 增强网络中特征图空间上的理解能力.

gConv编码器: 传统Transformer的成功因素包括动态权重、长距离建模和高阶的空间交互, gConv提取高阶的空间交互和局部特征, 可以获得更空间交互, 虽然通过使用卷积线性投影实现和element-wise乘法进行实现, 但具有和自注意力随的权重随输入变化而变化的功能. 通过使用3D卷积层的目标是在普通卷积的基础上实现长距离建模和局部特征, 可以获得更加精细的细节特征和提取图像的空间信息联系, 同时为了解决反向传播中的梯度消失问题, 每个gConv后都有一个(layer normalization, LN)模块.

Transformer解码器: 第2阶段由Transformer解码器建立一系列的序列信息还原图像的全局空间特征. 此解码器由4个Transformer blocks组成, 每个Transformer block由一个Transformer模块和上采样模块构成, 每个头都可以对输入的特征图进行注意力加权以提取到不同的特征, 再将输出进行拼接和线性变换, 从而学习到输入图像各部分的相关性.

CNN解码器: 第3阶段由CNN解码器还原图像的局部特征关系. CNN解码器由一系列的普通3D卷积构成, 作用是还原图像的局部特征信息, 通过将同级的Transformer block的输出进行跳跃连接弥补CNN对捕获全局空间信息的不足, 可以更好地学习到全局空间信息的相关性和共享性, 从而提高网络的性能和稳定性.

Transformer解码器和CNN解码器中上采样使用转置卷积层将低分辨率特征图的尺寸扩大为原尺寸的两倍, 相比于向上插值采样, 转置卷积学习能力更强, 可以学习到更复杂的特征信息, 并可以适应不同的数据集. 在最后阶段, 将网络最后一层的Transformer block和CNN block进行一次上采样操作还原到和原始输入图像相同的尺寸, 再将这三者经过一次卷积操作生成最终的形变场.

2.3 图像的分块与合并

医学图像配准的复杂程度体现在配准的结果上, 具体表现为不同区域之间的差异性, 在图像复杂区域的配准结果形变较大并且精度不高. 因此提高图像整体配准精度的一个有效方案是将图像分块并找到配准形变较大的区域进行精细配准.

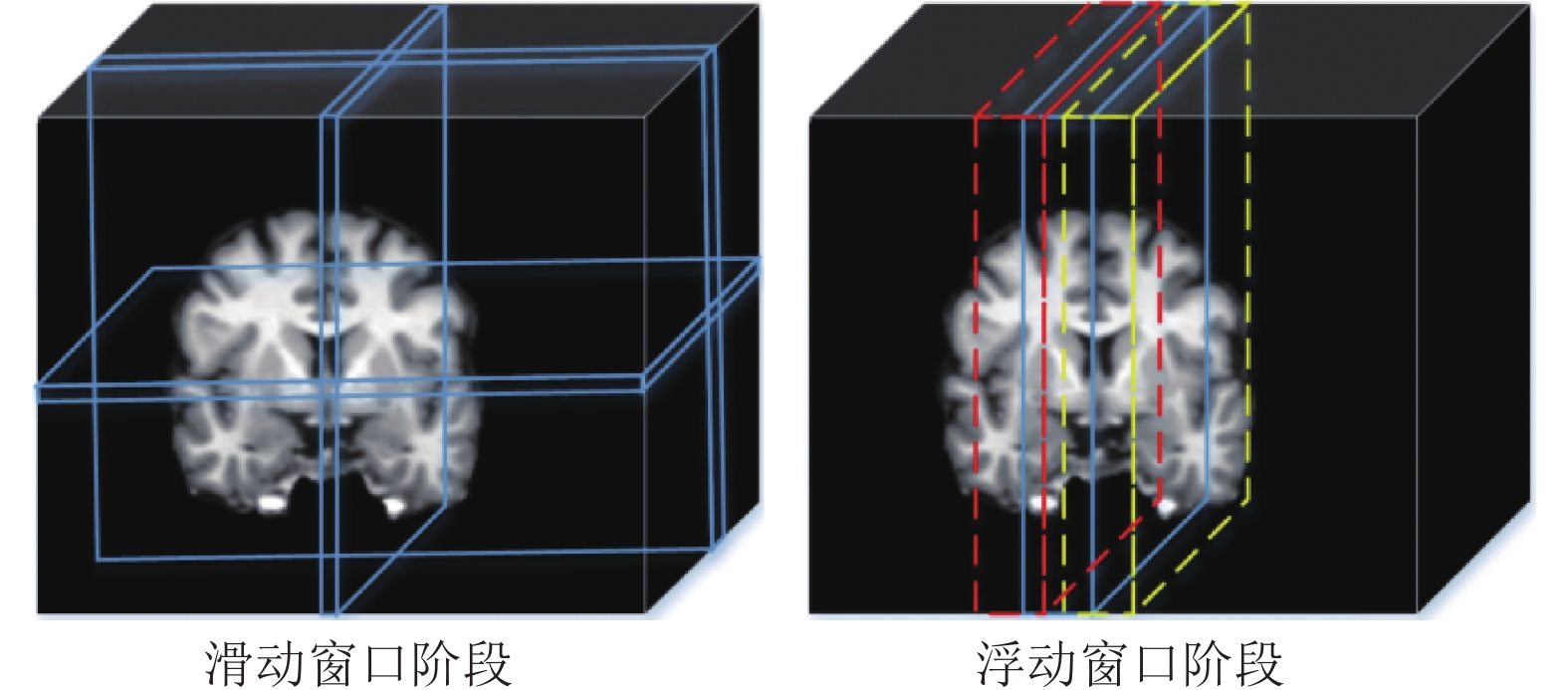
本模型在每一阶层的子网络中, 将产生的形变场和本层的输入图像进行形变扭曲生成配准后的图像, 将生成的图像和本层的输入图像在每个维度上同时使用滑动窗口计算两者相同位置差的平方值. 因为图像中越复杂的区域越难形变对齐, 所以选取差的平方值最小的位置为分割位置, 选取好分割位置后, 在选定的位置利用浮动窗口计算并得到最终的位置. 如图3所示, 在滑动窗口阶段, 通过滑动计算选定了各个维度的裁切位置, 在浮动窗口阶段在选定的位置进行浮动, 通过指定的浮动步长进行收缩或者扩张, 从而确定最后的裁切位置. 同时在图像进行裁切分块时, 需要在图像块的边缘预留一些重叠区域, 可以在后续的融合过程中可以平滑地处理边缘效应, 减少合并处理结果的误差.

具体在本模型第1阶层子网络中, 分块模块将完成初步配准的浮动图像和待配准图像在x和y轴上进行分块, 将图像分成4个图像块. 在第2阶层子网络中, 分块模块将完成二次配准的浮动图像和待配准图像在z轴上进行分块, 最终将图像分成8个子块 通过滑动窗口分块策略可以提高配准网络对复杂形变区域的关注度. 同时可以帮助避免一些块或子区域复杂区域过度密集或过于稀疏的问题^[15], 从而保持配准网络的均衡性和稳定性. 通过对比滑动窗口分块策略的配准结果和平均分块策略的配准结果, 可以发现滑动窗口分块策略在配准结果上最大提高了0.3%的准确率.

在每一层子网络中, 将图像分块成有重叠区域的子块并输入到相应的配准网络完成计算后, 参照上一层子网络输出的形变场, 将本层配准网络输出的形变场块的重叠区域进行合并融合操作, 来消除重叠区域并生成整体的形变场. 如图4所示, 若直接将生成的子块进行拼接, 会导致在拼接的边缘部分出现边缘效应并损失大量的边缘信息, 因此需要对重叠的边缘部分进行加权拼接处理.

形变场块的重叠区域如图5所示, Region A和Region B分别代表两块形变场块, 各有一块重叠区域, 将两块形变场的重叠区域的像素值按一定的权值相加合成以形成平滑的过度. 重叠边界区域经过融合后, 最终的权值分配结果如图6所示.

在两个形变场块的重叠区域使用一个滑动窗口计算合并加权值, 根据滑动窗口的大小将重叠区域分成N个子区域, 对于重叠区域S内任意一个子区域i来说, S最终确认为式(1)–式(5)所示:

${S_i} = {S_{iA}} \times {P_{iA}} + {S_{iB}} \times {P_{iB}}$

(1)

${{{P}}_{iA}} = \frac{{{D_{iA}}}}{{{D_{iA}} + {D_{iB}}}}$

(2)

${{{P}}_{iB}} = \frac{{{D_{iB}}}}{{{D_{iA}} + {D_{iB}}}}$

(3)

${{{D}}_{iA}} = {\textit{MSE}}\left( {{m_{if}} - {S_{iA}}\circ {O_{iA}}} \right)$

(4)

${{{D}}_{iB}} = {\textit{MSE}}\left( {{m_{if}} - {S_{iB}}\circ {O_{iB}}} \right)$

(5)

其中, ${S}_{iA}$是形变场块A中所包含的重叠区域中的子区域, ${S}_{iB}$是形变场块B所包含的重叠区域, ${{P}}_{iA}$表示为在最终的重叠区域${S}_{iA}$中形变场块A所占的比例, 其经过计算后, 其中${m}_{if}$为参考形变场对应的重叠区域, ${O}_{A}$为${S}_{A}$所对应的形变场, ${O}_{B}$为${{S}}_{{B}}$所对应的形变场.

2.4 损失函数

本模型为无监督学习的方法, 因此不需要在损失函数中计算预测值与真实标签的损失项, 只需在训练过程中最小化图像相似损失项即可. 模型总体损失函数如式(6)所示:

${{L}}\left( {F, M, \varphi } \right) = {{\lambda}_1}{L_{{\mathrm{sim}}}}\left( {F, M\circ \varphi } \right) + {{\lambda}_2}{R_{{\mathrm{diff}}}}\left( \varphi \right)$

(6)

其中, 在总体损失函数中分为两部分: 第1部分为衡量图像间相似度的损失函数${L}_{{\mathrm{sim}}}\left(F, M \circ \varphi \right)$, 其定义如式(7)所示, 其中F和M各自代表参考图像和待配准图像, $\varphi$为网络生成的形变场; 第2部分是保持形变场平滑度的扩散正则化项${R}_{{\mathrm{diff}}}\left(\varphi \right)$, 目的是为了防止在最小化${L}_{{\mathrm{sim}}}$时导致生成不平滑的形变场, 其定义如(8)所示, 其中$\Delta u\left(p\right)$是形变场中空间位移的前后差分, 其说明了各体素位置间的区别, $\Delta u\left(p\right)$的定义如式(9)所示. λ₁和λ₂为权重系数, 用来决定不同特征对模型输出结果的贡献大小. 该权重系数的最佳值为1和0.02, 因此将λ₁和λ₂大小各设置为1和0.02.

${L_{{\mathrm{sim}}}}\left( {F, M\circ \varphi } \right) = {\textit{MSE}}\left( {F, M\circ \varphi } \right)$

(7)

${R}_{{\mathrm{diff}}}\left(\varphi \right)={\displaystyle \sum }_{p\in\Omega }\parallel \Delta u\left(p\right){\parallel }^{2}$

(8)

$\Delta u\left(p\right)=u\left(p +1\right)-u\left(p\right)$

(9)

3 实验设置和评估标准 3.1 实验数据

为了测试此配准模型在不同器官的配准效果, 本文共使用3个数据集, 其中包括两个脑部数据集和一个膝盖软骨数据集: LPBA40数据集包括40个正常人的MRI扫描图像, 每个个体的图像数据包括T1加权和T2加权扫描图像. 此外, 该数据集还包括手动标注的脑部结构分割和3D形变场; OASIS-1数据集包含了416位参与者的MRI图像和临床信息. 每个参与者的MRI图像包括T1加权、T2加权和PD加权扫描图像, 以及手动标注的脑部结构分割和病变标注. OAI数据集包含了多种类型的膝盖软骨数据, 包括MRI图像、X光图像、病史信息、临床评估等, MRI图像包括膝盖、髋关节和手指等部位的图像.

数据集图像由于采集的时间、机器和其他原因导致数据间存在一定的差异, 不利于网络的训练和泛化能力^[16], 故对数据集进行对齐、归一化和裁剪等标准预处理操作, 将图像裁剪到160×192×160, 并将3个数据集通过随机配对的方式生成训练集、验证集和测试集, 分配比例为6:2:2, 并在训练过程中, 对训练图像进行5折训练.

3.2 实验配置

在验证实验中使用传统算法中准确率较高的几个算法: 对称归一化(symmetric normalization, SYN)^[17]、CycleMorph^[18]、VoxelMorph和TransMorph对本文方法进行对比. SYN是传统配准算法中性能最好的配准算法, 其主要思想是利用基于正态分布的模型来估计图像间的相似性度量^[19], 设置其最大迭代次数为160. CycleMorph是一种多尺度配准模型, 通过优化互信息的值来实现两幅图像之间的精确配准. VoxelMorph是目前在工业生产中常用的无监督配准方法, 本文使用其推荐的参数设置进行对比实验. TransMorph是将Transformer网络和无监督学习方法集合的配准网络, 使用其默认参数进行对比实验.

深度学习框架使用: PyTorch-GPU 1.7.2, 实验所使用的计算机配置如下: Nvidia Geforce RTX 3090, Intel Core i9-10900K CPU @ 3.70 GHz. 学习率初始化为1×10⁻⁴, 训练次数设为500, 训练时先随机初始化网络参数, 定义网络参数的初始值后进行训练.

3.3 实验评价指标

本方法使用的评估指标为戴斯相似系数(Dice similarity coefficient, DSC), DSC常用于测试医疗图像的相似度, 其取值在0和1之间, 表示两个样本集合的相似程度, DSC值越高, 说明图像相似度越高, 配准性能和准确性越好. DSC的具体定义如式(10)所示:

${\textit{DSC}}\left( {{S_F}, {S_M}} \right) = \frac{{\left| {{S_F} \cap {S_M}} \right|}}{{\left( {\left| {{S_F}} \right| + \left| {{S_M}} \right|} \right)/2}}$

(10)

其中, ${S}_{F}$和${S}_{M}$分别表示为参考图像的分割图和配准后图像的分割图, ${S}_{F}\cap {S}_{M}$为两个分割图的交集结果.

负雅可比行列式(negative Jacobian determinant, NJD)是用于描述一个变换对图像局部伸缩性影响的数学指标^[20], NJD可以用来评估图像变形程度, 特别是在非刚性变形(例如弯曲和扭曲)的情况下. 在医学图像配准中, 负雅可比行列式通常用于评估配准算法的效果. 雅可比行列式的值越小, 表示变形程度越大, 即图像发生了较大的缩小或扭曲. 在医学图像配准中, 通常会选择最小化负雅可比行列式的优化算法, 以最大程度地减小图像变形程度, 从而实现精确配准. NJD系数的定义如式(11)所示:

${\textit{NJD}}\left(\varphi \text{ }\left(p\right)\right)=-\left|\begin{array}{ccc} \dfrac{\partial i}{\partial x}& \dfrac{\partial j}{\partial x}& \dfrac{\partial k}{\partial x}\\ \dfrac{\partial i}{\partial y}& \dfrac{\partial j}{\partial y}& \dfrac{\partial k}{\partial y}\\ \dfrac{\partial i}{\partial {\textit{z}}}& \dfrac{\partial j}{\partial {\textit{z}}}& \dfrac{\partial k}{\partial {\textit{z}}}\end{array}\right|$

(11)

图像相似性评估系数是用来比较两幅图像之间相程度的指标, 常用的图像相似性评估系数有: 误差平方根(root mean square error, RMSE), RMSE是指两幅图像像素点之间差值的平方和的开方平均值, 通常用于评估图像的重建质量, 其定义如式(12)所示:

${\textit{RMSE}}\left( {{{F}}, {{M}}} \right) = \sqrt {{\textit{MSE}}\left( {F, M} \right)}$

(12)

结构相似性系数(structural similarity, SSIM), SSMI是指两幅图像之间亮度、对比度和结构的相似程度, 通常用于评估图像的质量和相似程度^[21], 其具体计算过程如式(13)–式(16)所示, 式中L(F, M)、C(F, M)、S(F, M)分别代表着参考图像F和待配准图像M两者的亮度、对比度和结构之间的比值差异. ${\mathrm{\mu }}_{F}$、${\sigma }_{F}$、${\mathrm{\mu }}_{M}$和${\sigma }_{M}$分别为参考图像和待配准图像的平均值和标准差, 同时为了避免分母过小造成误差在分母上加上非零常数${c}_{1}$、${c}_{2}$、${c}_{3}$, 并都设置为1.

${\textit{SSIM}}\left( {F, M} \right) = \left[ {L{{\left( {F, M} \right)}^a}} \right]\left[ {C{{\left( {F, M} \right)}^b}} \right]\left[ {S{{\left( {F, M} \right)}^c}} \right]$

(13)

$L\left( {F, M} \right) = \frac{{2{\mu _F}{\mu _M} + {c_1}}}{{\mu _F^2 + \mu _M^2 + {c_1}}}$

(14)

${{C}}\left( {{{F}}, {{M}}} \right) = \frac{{2{\sigma _{FM}} + {c_2}}}{{\sigma _F^2 + \sigma _M^2 + {c_2}}}$

(15)

$S\left( {F, M} \right) = \frac{{{\sigma _{FM}} + {c_3}}}{{{\sigma _F}{\sigma _M} + {c_3}}}$

(16)

互信息(mutual information, MI), MI是一种用于度量两幅图像之间相似性的指标, 它是指两幅图像之间像素值的相关程度. MI的定义如式(17) 所示, g(·, ·)为图像间的联合概率密度函数, g(F(p))和g(M(p))分别表示图像的边缘概率密度函数.

可通过这3个指标评判图像的相似性, 具体来说若两张图像间的RMSE高, 而MI和SSIM变低, 则表示两张图像相似性变差^[21].

${MI}\left({F}, {M}\right)={{\displaystyle \sum }}_{p\in\Omega }g\left(F\left(p\right), M\left(p\right)\right){\mathrm{log}}_{2}\frac{g\left(F\left(p\right), M\left(p\right)\right)}{g\left(F\left(p\right)\right)g\left(M\left(p\right)\right)}$

(17)

4 实验结果与定量分析

通过实验对本文方法和所有对比方法在脑部和膝关节的数据集上进行量化, 得到相关的量化结果对比如表1所示, 可以得知本文方法在两个脑部的数据集上的精准度均大于所有的对比方法, 并且NJD系数优于除SYN的算法.

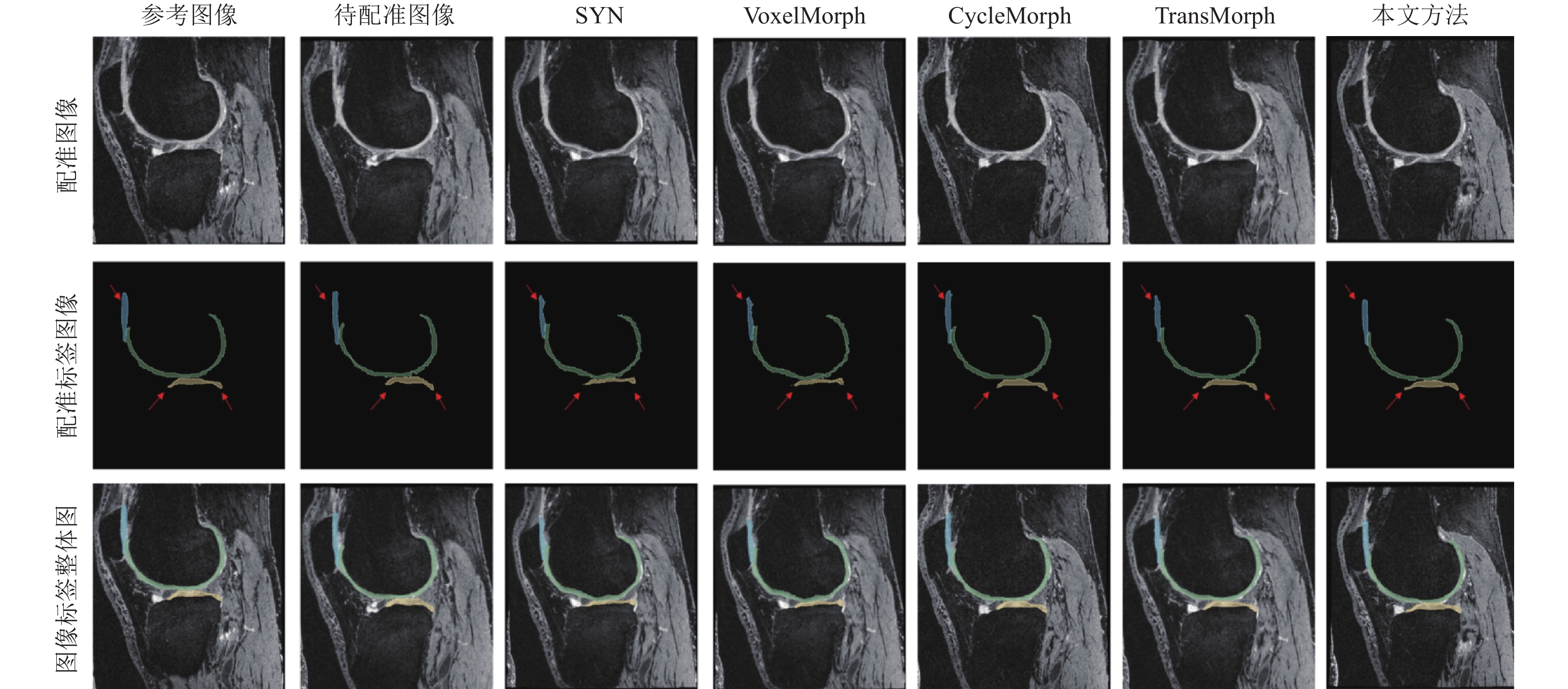
图7和图8是将方法作用在膝关节和脑部数据集上的对比图, 展示切面为矢状面, 图7中红色箭头指示的黄色区域所示可以观察出SYN和VoxelMorph方法对于胫骨外侧软骨的还原不完整, 并在软骨的中间位置还原的厚度比原图像单薄; 同时CycleMorph方法在软骨的边缘部位产生过度的扭曲, 导致生成的图像形态特征与参考图像相比有较大差距; TransMorph在软骨的两端较好地还原了形状, 但在软骨的中断位置产生过量的扭转偏移致使软骨的整体体积偏大, 而本文方法较好地还原了软骨的两端, 并在整体形态和大小方面也更符合固定图像. 图7中SYN和TransMorph没有将细节图中白质中圆形结构区域很好地还原为尖锐结构区域, VoxelMorph 在一定程度上还原了尖锐部分结构区域, 但是对于白质密集区域的还原能力较差, CycleMorph方法对于细节的处理最好, 但没有很好地对齐白质的长枝方向, 可以观察到本文方法生成的配准图像更加接近参考图像, 配准质量相比于其他配准方法精准度更高.

5 结论与展望

本文利用多空间信息提取的技术把多个子网络进行级联, 生成医学图像配准模型. 每层子网络都含有一个基于gConv-Transformer的基础配准网络, 此网络能够有效理解输入图像的空间信息, 并对局部和全局空间特征信息进行建模. 同时在模型中加入了分块融合模块, 对图像分块并依次进行精细配准, 在完成配准后依次将图像融合得到最后的形变场. 本文最后的对比实验结果表明, 与目前流行的无监督配准方法相比, 本文方法能够提高配准精度, 能够获得更准确的配准结果可以为医生提供更准确的图像数据支持, 有助于医生进行更准确的临床诊断, 从而帮助医生做出更准确的诊断和治疗决策.