优化是指对特定问题的解决方案进行调整和改进, 使其相关指标达到最优或近似最优的过程, 使用优化技术可以让人类更加合理有效地可持续使用资源. 传统的优化算法通常根据问题的情况使用特定的数学模型或求解方法进行寻优, 但这些算法通常存在一些局限性, 例如依赖于梯度信息、面对非线性复杂问题难以处理^[1]等, 为此, 启发式算法应运而生并被广泛应用于各领域. 启发式算法通过模拟自然界的演化^[2,3]、物理现象^[4–6]、人类的行为^[7,8]等, 来探索问题空间中的最优解决方案, 往往能够有效地在实际执行时间内解决传统算法无法解决的问题.

群体智能优化算法就是一种典型的启发式算法, 是一类受自然界中各种生物的群体行为启发而创造出的寻优方法. 种群个体在遵循相关规则进行交互的过程中实现对全局最优解的探索. 典型的群体智能优化算法有灰狼优化算法(grey wolf optimization, GWO)^[9]、鲸鱼优化算法(whale optimization algorithm, WOA)^[10]、哈里斯鹰优化算法(Harris hawks optimization, HHO)^[11]等. 根据没有免费午餐定理(no free lunch)^[12], 没有一种优化算法可以解决所有优化问题, 为此, 越来越多的优化算法被提出用于解决新的优化问题, 例如沙丘猫群优化算法(sand cat swarm optimization, SCSO)^[13]、海马优化算法(sea-horse optimization, SHO)^[14]等.

蜣螂优化算法 (dung beetle optimization, DBO)^[15]是Xue等人于2022年提出的一种新颖的优化算法. 该算法模拟了蜣螂推球、跳舞、觅食、偷窃以及繁殖等行为, 将蜣螂种群分为推球蜣螂、育雏球、小蜣螂以及小偷蜣螂4个角色, 分别按照不同的搜索策略对问题空间进行搜索. 蜣螂优化算法有着独特的结构, 其关注重点不再是种群的整体任务如觅食或躲避天敌等, 算法的主要思想是种群不同角色通过不同的生存行为及相互之间的经验交互获得有利于自身的位置信息, 蜣螂的位置越好表示其适应环境的生存能力越优秀, 每只蜣螂的位置代表问题的一个解, 最终, 最优蜣螂的位置即为所求问题最优解.

DBO独特的结构使其具有不错的寻优性能及实际应用潜力. 李晴^[16]将DBO用于水质COD预测模型优化; 董奕含等人^[17]引入Halton序列初始化DBO并用于瑞雷波频散曲线反演; 潘志远等人^[18]将DBO用于优化DV-Hop定位算法; Zhu等人^[19]引入量子计算等策略对DBO进行改进并将其用于多个实际工程约束优化问题的求解. 上述文献证明了DBO的实际应用价值, 相关改进也提升了DBO的寻优性能, 但是DBO在全局探索、寻优精度等方面仍有较大提升空间. 为此, 本文提出了一种多策略融合改进的蜣螂优化算法(multi-strategy fusion improved DBO, MSDBO), 首先, 使用社会学习策略引导推球蜣螂进行位置更新, 提升算法全局探索能力; 其次, 引入方向跟随策略, 增强算法局部开发能力, 提高了收敛精度; 最后, 引入环境感知概率控制方向跟随策略的调用频率, 平衡算法性能与运行时间消耗. 在12个基准测试函数与压力容器设计优化问题上的结果证明了改进算法的有效性与实用性.

1 蜣螂优化算法(DBO)

DBO根据蜣螂的不同社会分工, 将种群分为推球蜣螂、育雏球、小蜣螂及小偷蜣螂4个角色, 当种群数量$N = 30$时文献[15]将这4种蜣螂的数量分别设定为6, 6, 7, 11只. 蜣螂种群的位置表示为: $ X = \{ {X_{{i}}}{{|i}} = 1, 2, \cdots, {N_{{\text{all}}}} \} $. 为区分起见, 4种蜣螂子种群的位置使用不同符号表示为$ R=\left\{{R}_{{e}}\right|{e}=1, 2, \cdots, {N}_{\text{roll}}\} $、$ B=\left\{{B}_{{m}}\right|{m}= 1, 2, \cdots, {N}_{\text{ball}}\}、L=\{{L}_{{h}}|{h}=1, 2, \cdots, {N}_{\text{little}}\} $以及$T = \{ {T_{\textit{z}}}|{\textit{z}} = 1, 2, \cdots,{N_{{\text{thief}}}}\} $. 则有$ X = R{\text{ }} \cup B{\text{ }} \cup L{\text{ }} \cup T $且$ {N_{{\text{roll}}}} + {N_{{\text{ball}}}} + {N_{{\text{little}}}} + {N_{{\text{thief}}}} = {N_{{\text{all}}}} $. 若优化问题维度为$D$, 对应目标函数为${{f}}$, 则每只蜣螂的位置即问题的一个解表示为${X_{{i}}} = \{ {{{x}}_{{{i}}, 1}}, {{{x}}_{{{i}}, 2}}, \cdots, {{{x}}_{{{i}}, D}}\} $, 个体适应度值即最优值表示为${{f}}({X_{{i}}})$, $ {R}_{{e}}、{B}_{{m}}、{L}_{{h}}、{T}_{\textit{z}} $及对应适应度值的表示与${X_{{i}}}$类似. 算法按照不同策略更新不同角色蜣螂的位置, 根据适应度评估蜣螂的生存能力, 假设适应度值越小表示优化效果越好, 则适应度值越小表明蜣螂所处位置越佳, 其生存能力越优秀, 则最优及最差位置的数学表示如下:

$ \left\{\begin{array}{l}{{X}}^{{b}}=\left\{{X}_{{i}}\in X, {i}=1, 2, \cdots, N|\forall {{X}}_{{j}}, {{f(X}}_{{i}}{)}\leqslant {{f(X}}_{{j}}{)}\right\}\\ {{X}}^{{w}}=\left\{{X}_{{i}}\in X, {i}=1, 2, \cdots, N|\forall {X}_{{j}}, {f}({X}_{{j}})\leqslant {f}({X}_{{i}})\right\}\end{array}\right. $

最终得到的最优位置${X^{{b}}}$即为所求问题的最优解.

1.1 推球蜣螂位置更新

蜣螂会把动物粪便滚成球状并利用天体线索如太阳月亮等进行导航以实现有效的搬运. 当遇到障碍物时, 蜣螂通常会爬到粪球上跳舞决定新的移动方向.

为模拟推球行为, 蜣螂在整个搜索空间沿着给定方向移动, 推球蜣螂位置更新分为有障碍物与无障碍物两种情况, 当$\lambda < \gamma $时无障碍状态, 这里$\lambda $为随机数且$\lambda \in \left[ {0, 1} \right]$, $\gamma = 0.9$, 位置更新公式如下:

$ R_{{{{\mathrm{new}}, e}}}^{{{t}} + 1} = R_{{e}}^{{t}} + \alpha \times {{k}} \times R_{{e}}^{{{t}} - 1} + {{u}} \times \Delta {{x}} $

(1)

$ \Delta {{x}} = \left| {R_{{e}}^{{t}} - {X^{{w}}}} \right| $

(2)

其中, ${{t}}$表示当前迭代次数, $R_{{e}}^{{t}}$表示第${{e}}$只推球蜣螂在第${{t}}$次迭代后的位置. ${{k}}$为常数且$k \in \left( {0, 0.2} \right]$, 表示位置偏转系数. $\alpha $是一个自然系数用于模拟一些自然因素对于移动方向的影响, 当$\lambda < \eta $时$\alpha $为$1$否则$\alpha $为$ - 1$, 其中$\eta $为随机数且$\eta \in [0, 1]$, ${{u}}$为常数且${{u}} \in \left[ {0, 1} \right]$. $ {X^{{w}}} $代表全局最差位置, $\Delta {{x}}$用于模拟光照强度的变化, $\Delta {{x}}$值越高意味着光源越弱, 蜣螂的路线越弯曲. 当$\lambda \geqslant \gamma $时, 为有障碍物状态, 引入正切函数模拟蜣螂通过跳舞确定偏转角更改方向的行为, 位置更新如下:

$ R_{{{{\mathrm{new}}, e}}}^{{{t}} + 1} = R_{{e}}^{{t}} + \tan (\theta )\left| {R_{{e}}^{{t}} - R_{{e}}^{{{t}} - 1}} \right| $

(3)

其中, $\theta $为弧度表示的偏转角, $\theta $为随机数且$ \theta \in \left[ {0, {\text π} } \right] $, 若$ \theta $为$0, {\text π} /2, {\text π} $, 则不更新位置.

上述位置更新公式中$R_{{{{\mathrm{new}}, e}}}^{{{t}} + 1}$为个体第${{t}} + 1$次迭代时得到的候选位置, 最终将与历史最优位置对比, 择优保留, 即: 若${{f}}(R_{{{{\mathrm{new}}}}, {{e}}}^{{{t}} + 1}) > {{f}}(R_{{e}}^{{t}})$ 则$R_{{e}}^{{{t}} + 1} = R_{{e}}^{{t}}$, 否则$R_{{e}}^{{{t}} + 1} = R_{{{{\mathrm{new}}}}, {{e}}}^{{{t}} + 1}$. 其他蜣螂位置更新类似, 不再重复说明.

1.2 育雏球位置更新

蜣螂收集的粪球一部分作为食物, 另外一部分则推到安全的地方用于产卵, 作为育雏球繁育下一代, 育雏球所在的区域边界被严格限制如下:

$ \begin{gathered} L{{{b}}^*} = \max ({X^{{{b}}*}} \times (1 - Q), Lb) \\ U{b^*} = \min ({X^{{{b}}*}} \times (1 + Q), Ub) \\ \end{gathered} $

(4)

其中, $U{{{b}}^*}$与$L{{{b}}^*}$分别表示产卵区域的上下界. ${X^{{{b}}*}}$表示种群所有蜣螂当前的最优位置, $ Q = 1 - {{t}}/T $, $T$表示最大迭代次数, $U{{b}}$与$L{{b}}$表示优化问题的上下界.

将育雏球推到确定的产卵区域后, 雌性蜣螂就会在里面产卵, 每只雌性蜣螂在每次迭代过程中只产1颗卵, 育雏球的位置更新如下所示:

$ B_{{{{\mathrm{new}}, m}}}^{{{t}} + 1} = {X^{{{b}}*}} + {{{a}}_1} \times (B_{{m}}^{{t}} - L{{{b}}^*}) + {{{a}}_2} \times (B_{{m}}^{{t}} - U{{{b}}^*}) $

(5)

其中, $ B_{{m}}^{{t}} $表示第${{m}}$只育雏球在第${{t}}$次迭代后的位置, ${{{a}}_1}$和${{{a}}_2}$是两个大小为$1 \times D$的独立随机向量, $D$为优化问题解的维度.

1.3 小蜣螂位置更新

育雏球中的小蜣螂发育成熟后, 会钻出来寻找食物, 为此需要建立最优觅食区域引导他们觅食以达到对空间进行探索的目的. 最优觅食区域边界定义如下:

$ \begin{gathered} L{{{b}}'} = \max ({X^{{b}}} \times (1 - Q), L{{b}}) \\ U{{{b}}'} = \min ({X^{{b}}} \times (1 + Q), U{{b}}) \\ \end{gathered} $

(6)

其中, ${X^{{b}}}$表示全局最优位置, $U{{{b}}'}$和$L{{{b}}'}$分别表示最优觅食区域的上下界, $ Q、Lb $及${{Ub}}$的定义与式(4)中相同, 小蜣螂位置更新公式如下:

$ L_{{{{\mathrm{new}}, h}}}^{{{t}} + 1} = L_{{h}}^{{t}} + {C_1} \times (L_{{h}}^{{t}} - L{{{b}}'}) + {C_2} \times (L_{{h}}^{{t}} - U{{{b}}'}) $

(7)

其中, $ L_{{h}}^{{t}} $为第${{h}}$只小蜣螂在第${{t}}$次迭代后的位置, ${C_1}$是一个符合正态分布的随机数且${C_1} \in \left[ {0, 1} \right]$, ${C_2}$是各分量介于$0$到$1$之间的随机向量.

1.4 小偷蜣螂位置更新

并不是所有蜣螂都会努力地推球, 有些蜣螂会去偷窃推球蜣螂的粪球, 假设全局最优位置是最适合它们偷窃的位置, 那么小偷蜣螂的位置更新公式如下:

$ T_{{{{\mathrm{new}}, {\textit{z}}}}}^{{{t}} + 1} = {X^{{b}}} + S \times {{g}} \times \left(\left| {T_{\textit{z}}^{{t}} - {X^{{{b}}*}}} \right| + \left| {T_{\textit{z}}^{{t}} - {X^{{b}}}} \right|\right) $

(8)

其中, $ {X^b} $表示全局最优位置, ${X^{{{b}}*}}$的含义与式(4)中的描述相同. $ T_{\textit{z}}^{{t}} $表示第${\textit{z}}$只小偷蜣螂在第${{t}}$次迭代后的位置信息, $S$为常数且设置为$0.5$, ${{g}}$为各分量介于$0$到$1$之间的$D$维随机行向量.

1.5 标准DBO算法步骤

步骤1. 设置最大迭代次数为$T$, 种群大小为$N$, 随机初始化种群并计算个体对应的适应度值.

步骤2. 更新推球蜣螂位置, 若$\lambda < \gamma $, 为无障碍状态使用式(1)更新位置, 反之为有障碍状态按照式(3)更新, 其中$\lambda $为随机数且$\lambda \in \left[ {0, 1} \right]$, $\gamma = 0.9$.

步骤3. 根据式(5)更新育雏球位置并使用式(4)中的上下界对新位置进行边界约束.

步骤4. 由式(7)更新小蜣螂位置.

步骤5. 由式(8)更新小偷蜣螂位置.

步骤6. 更新全局最优位置${X^{{b}}}$及最差位置${X^{{w}}}$.

步骤7. 判断算法是否达到迭代次数, 若是则终止运行, 返回最优位置即问题最优解否则转步骤2.

2 多策略融合改进的蜣螂优化算法(MSDBO) 2.1 改进原因

虽然DBO有着不错的寻优性能, 但是仍然存在全局探索能力欠缺、易陷入局部最优的问题. 对问题解进行精确寻优要求算法同时具有良好的全局搜索能力与局部开发能力, 全局探索能力不足会让算法的寻优在局部最优区域停滞, 而局部开发能力不足则导致算法不能在全局最优区域取得更高的精度, MSDBO融合了社会学习策略、方向跟随策略以及环境感知概率对DBO进行改进, 兼顾算法的探索与开发, 提高了算法的寻优性能, 接下来具体介绍这3种策略.

2.2 社会学习策略

在进行位置更新时, 每只推球蜣螂个体主要依赖自身历史位置信息进行探索, 群体内部缺乏足够的信息交流, 导致对问题空间的探索过于随机、全局探索效率低, 受到哈里斯鹰优化算法^[11]中哈里斯鹰种群在探索阶段共享位置信息合作搜索猎物的策略启发, 提出了一种社会学习策略引导推球蜣螂进行位置更新, 以改善标准DBO全局搜索能力欠缺的问题.

与原算法不同, 在该策略中, 蜣螂遇到障碍物的概率被假设为$\gamma = 0.5$. 设$\lambda $为随机数且$\lambda \in [0, 1]$, 当$\lambda \leqslant \gamma $时, 生成一个随机数$\theta $且$\theta \in \left[ {0, {\text π} } \right]$, 当$ \theta =0, {\text π} /2, {\text π} $时不更新位置, 否则位置更新如下:

$ R_{{{{\mathrm{new}}, e}}}^{{{t}} + 1} = {R^{{b}}} - \bar R + \tan (\theta )\left| {R_{{e}}^{{t}} - R_{{e}}^{{{t}} - 1}} \right| $

(9)

其中, $ {R^b} $表示第$t$次迭代后最优推球蜣螂此时的候选位置, 定义如式(10)所示, $ \bar R $表示其他推球蜣螂此时的平均候选位置, 定义如式(11)所示, 式(9)用于替换式(3).

$ {R}^{{b}}=\{{R}_{\omega }\in {R}_{{{\mathrm{new}}}}, \omega =1, 2, \cdots, {N}_{{\rm{roll}}}|\forall \beta {, }{f}({R}_{\omega }^{{t}})\leqslant f({R}_{\beta }^{t})\} $

(10)

$ \bar R = \frac{1}{{{N_{{\rm{roll}}}} - 1}}\sum\limits_{\varepsilon = 1}^{{N_{{\rm{roll}}}}} {{R_{{{{\mathrm{new}}}}, \varepsilon }},\; \varepsilon \ne e} $

(11)

当随机数$\lambda > \gamma $时为无障碍状态, 位置更新如下:

$ R_{{{{\mathrm{new}}, e}}}^{{{t}} + 1} = {R^{{\mathrm{rand}}}} + {{u}} \times \Delta {{x}} + \alpha \times {{k}} \times R_{{e}}^{{{t}} - 1} $

(12)

$ \Delta {{x = Distanc}}{{{e}}_{{\text{chebychev}}}}(R_{{e}}^{{t}}, {R^w}) $

(13)

其中, $ {R^{{\mathrm{rand}}}} $表示随机选择的一只推球蜣螂此时的候选位置, $ {R^w} $表示第$t$次迭代后最差推球蜣螂此时的候选位置, 定义与上述${R^{{b}}}$类似, $\Delta {{x}}$表示第${{e}}$只推球蜣螂第${{t}}$次迭代后的位置$ R_{{e}}^{{t}} $与$ {R^w} $之间的切比雪夫距离, ${{u}}$为常数设置为2, 参数$\alpha , {{k}}$取值与标准DBO相同, 式(12)用于替换式(1).

引入上述策略改进后, 推球蜣螂内部具有了社会性质, 个体不仅可以利用自身信息, 还能充分利用其他推球蜣螂个体共享的信息进行位置迭代, 这不仅提高了全局探索效率, 还有助于算法跳出局部最优, 为其他类别的子种群在局部空间的精确寻优奠定基础.

2.3 方向跟随策略

标准DBO中, 虽提及了小偷蜣螂的偷窃行为, 但是并未直接建立其与推球蜣螂的交互, 两个群体各自的位置更新相对独立且缺乏必要的信息交流, 导致信息孤岛的形成并陷入局部最优. 本节将使用公式建立起小偷蜣螂与推球蜣螂之间的交互并作为改进方法避免算法陷入局部最优, 提高算法的寻优精度.

为提高算法的局部开发能力, 所有小偷蜣螂更新完位置之后采取方向跟随策略再次更新位置. 在偷窃前小偷蜣螂需要对推球蜣螂进行观察, 根据各自的观察随机选择一只推球蜣螂, 对其进行跟随以便于进行下一步的偷窃行为, 假设全局最优位置是最适合观察的位置, 使用方向跟随策略进行位置更新公式如下:

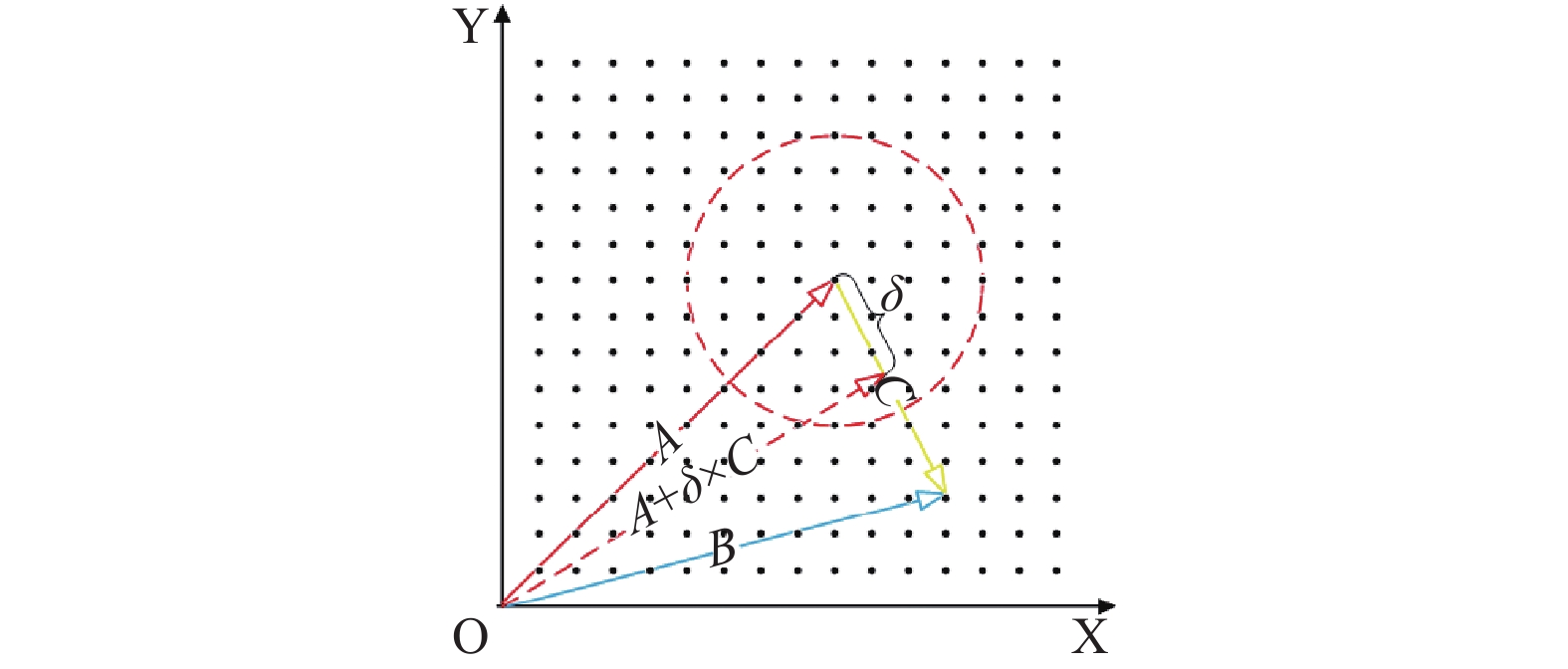
$ {{T}}_{{{{\mathrm{new}}, {\textit{z}}}}}^{{{t}} + 1} = {X^b} + Direction({R^{{{\rm{target}}}}} - {X^b}) \times \delta $

(14)

$ \delta = \frac{{{{({r_{21}} \times (1 - t/T))}^2}}}{t} \times \left(\left\| {{X^b} + {r_{22}} \times (Ub - Lb)} \right\|\right) $

(15)

其中, ${X^{{b}}}$为全局最优位置, $ {R^{{\text{t}}\arg {\text{et}}}} $为小偷蜣螂随机选择的目标推球蜣螂所在的位置, $Direction({R^{{\mathrm{target}}}} - {X^b})$表示从最优位置移动到随机选择的推球蜣螂所在位置的直线方向的单位向量, ${r_{21}}$与${r_{22}}$为随机数且$ {{r}}_{21}, {{r}}_{22}\in \left[0, 1\right] $, $\delta $是移动步长.

二维情况下所提出的方向跟随策略如图1所示. 其中, 实心点表示推球蜣螂可能的位置, $A$表示全局最优位置向量, $B$表示随机选择的一只推球蜣螂的位置向量, 将$B - A$记作$C$. 由运动的合成与分解可知, 设$\delta \geqslant 0$, 则$A + \delta \times C$表示从$A$沿着方向$C$移动了$\delta $个单位距离后一个新的位置向量. 由概率学理论可知, 推球蜣螂分布在最优位置周围各方向的概率相等, 因此, 小偷蜣螂群体采用该策略以一定步长从全局最优位置$A$处沿着方向$C$移动可以实现对最有希望找到最优解的区域(即图中虚线圆形区域)的充分开发, $A + \delta \times C$是采用方向跟随策略得到的新位置向量. 得到的新位置将与之前取得的位置对比, 择优保留.

2.4 环境感知概率

虽然上述提出的方向跟随策略可以提高算法的局部开发能力, 但是频繁地执行会消耗额外的运算时间, 且不一定会取得更好的结果, 应该考虑性能与时间消耗的平衡. 因此, 只有当小偷蜣螂采用原先的寻优策略陷入停滞的时候, 才会以一定的概率采用方向跟随策略建立与推球蜣螂之间的交互, 综上所述, 需要设定一个阈值去控制小偷蜣螂采用跟随策略的概率.

假定食物充足时, 小偷蜣螂不需要偷窃, 当食物不充足时, 小偷蜣螂对于环境缺乏食物的情况有所感知并转换搜索策略, 判定食物是否充足的依据是小偷蜣螂在新一轮迭代中是否取得了比上一轮迭代更好的解. 为此, 在小偷蜣螂更新位置前, 设定计数器$count$记录在新一轮迭代中未取得比上一轮更优解的小偷个体数量, 则环境感知概率计算公式如下:

$ prob = \sqrt {{{count}}/{N_{{\text{thief}}}}} $

(16)

其中, ${N_{{\rm{th}}{\text{ief}}}}$是小偷蜣螂数量, 得到环境感知概率后, 生成随机数$p \in \left[ {0, 1} \right]$, 当$p < prob$时, 小偷蜣螂采用方向跟随策略准备偷窃行为.

2.5 改进蜣螂优化算法的步骤及流程描述

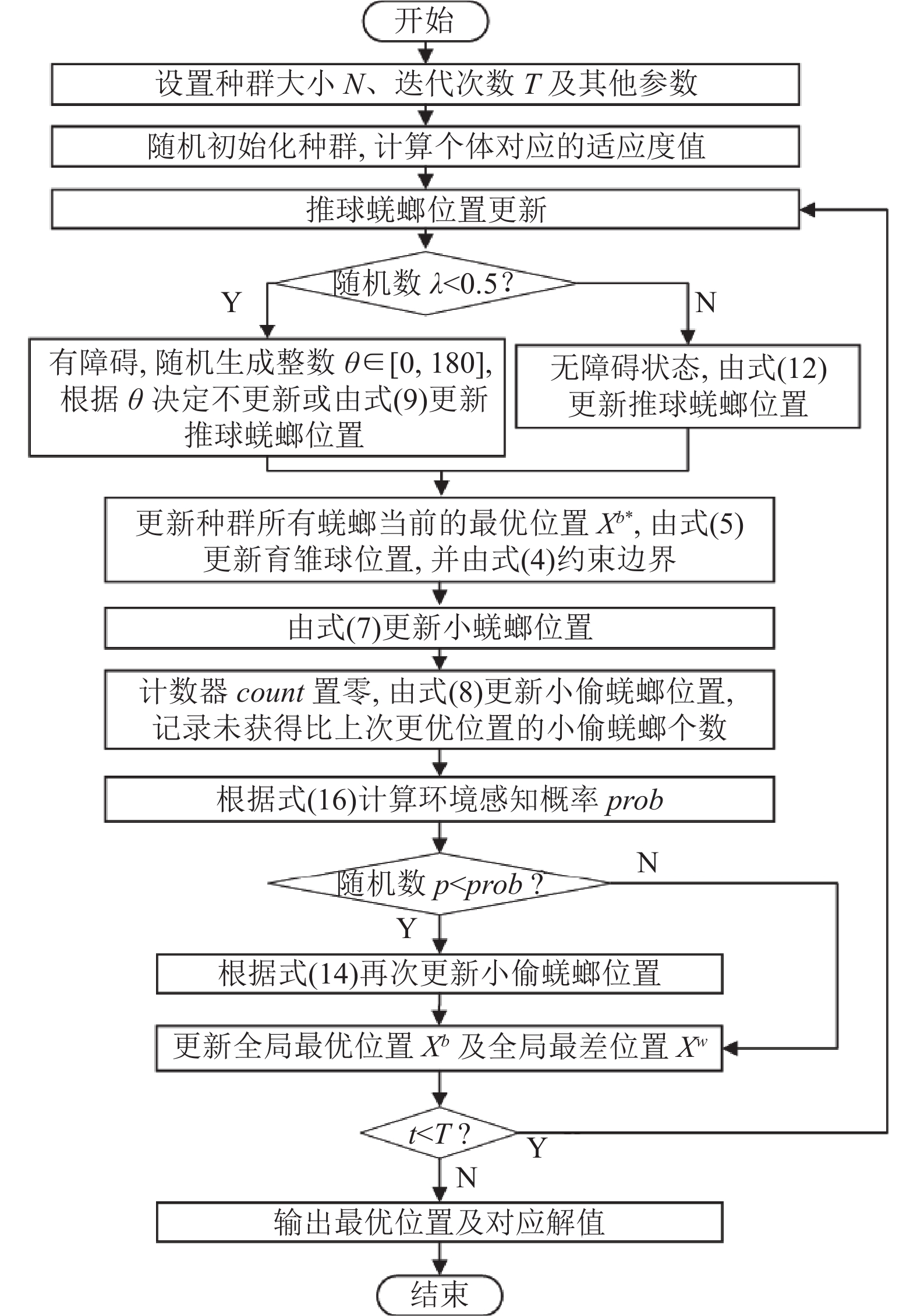
MSDBO的流程图如图2所示, 执行步骤如下.

步骤1. 设置最大迭代次数$ T $, 设置种群大小$N$, 随机初始化种群并计算个体对应的适应度值.

步骤2. 更新推球蜣螂位置, 若$\lambda < \gamma $, 为有障碍状态, 由式(9)更新位置, 反之为无障碍状态由式(12)更新, 其中$\lambda $为随机数且$\lambda \in [0, 1]$, $\gamma = 0.5$.

步骤3. 根据式(5)更新育雏球位置, 使用式(4)中的上下界对新位置进行边界约束.

步骤4. 由式(7)更新小蜣螂位置.

步骤5. 设置计数器$count$, 由式(8)更新小偷蜣螂位置, 记录未取得更优位置的小偷个体数.

步骤6. 根据式(16)计算环境感知概率$prob$, 生成随机数$p \in \left[ {0, 1} \right]$, 若$p < prob$, 小偷蜣螂子种群根据式(14)再次更新位置.

步骤7. 更新全局最优位置${X^{{b}}}$及最差位置$ {X^w} $.

步骤8. 判断算法是否达到迭代次数, 若是则终止运行, 返回最优信息, 否则跳转到步骤2.

2.6 时间复杂度分析

本文采用大$O$法分析算法的时间复杂度. 假设种群规模为$N$, 最大迭代次数为$T$, 问题规模为$D$, 种群初始化的时间复杂度为${\rm{O}}(N)$; 个体适应度计算及位置更新的时间复杂度为${\rm{O}}(N \times T + N \times T \times D)$. 则DBO的时间复杂度为:

$ {\rm{O}}(N + N \times (T + T \times D)) $

(17)

对于改进的DBO, 改进点1对于复杂度没有太大的影响, 假设改进点2的平均调用概率是$p$, 则改进点2的复杂度为${\rm{O}}(p \times {N_{{\rm{thief}}}} \times (T + T \times D))$, 所以, MSDBO的时间复杂度为:

$ {\rm{O}}(N + (N + p \times {N_{{\rm{thief}}}}) \times (T + T \times D)) $

(18)

综上所述, MSDBO与标准DBO相比, 时间复杂度是一个数量级的, 并没有增加太多时间复杂度.

3 仿真实验与结果分析 3.1 实验设计 3.1.1 实验环境

本文仿真实验操作系统为64位Windows 10, CPU为Intel(R) Core(TM) i7-7700HQ 2.80 GHz, 编程平台为Matlab R2022a.

3.1.2 测试函数

为有效验证本文所提出改进算法的寻优性能, 使用12个基准测试函数对算法进行测试. 其中, F₁–F₆为单峰测试函数, 用于评估算法的局部开发能力及求解精度, F₇–F₁₂为多峰测试函数, 具有多个局部最优解, 用于评估算法的全局探索能力与跳出局部最优的能力. 测试函数的信息如表1所示.

3.1.3 对比算法参数及实验设置

除了标准DBO以外, 本文选取3种被广泛应用的优化算法以及2种最近提出的优化算法作为对比, 分别是: GWO^[9]、WOA^[10]、HHO^[11]、SCSO^[13]、SHO^[14], 各算法参数均按对应原文设置, 如表2所示.

在实验设置上, 所有算法迭代次数均为500次, 种群规模均为30, 各独立运行30次. 采用平均值、标准差作为算法性能评价标准, 其中, 均值越小表示算法收敛精度越高, 标准差越小表示算法寻优越稳定. 为避免单次运行的偶然性, 采用30次独立运行的平均适应度变化曲线反映各算法的收敛速度与寻优性能.

3.2 实验分析

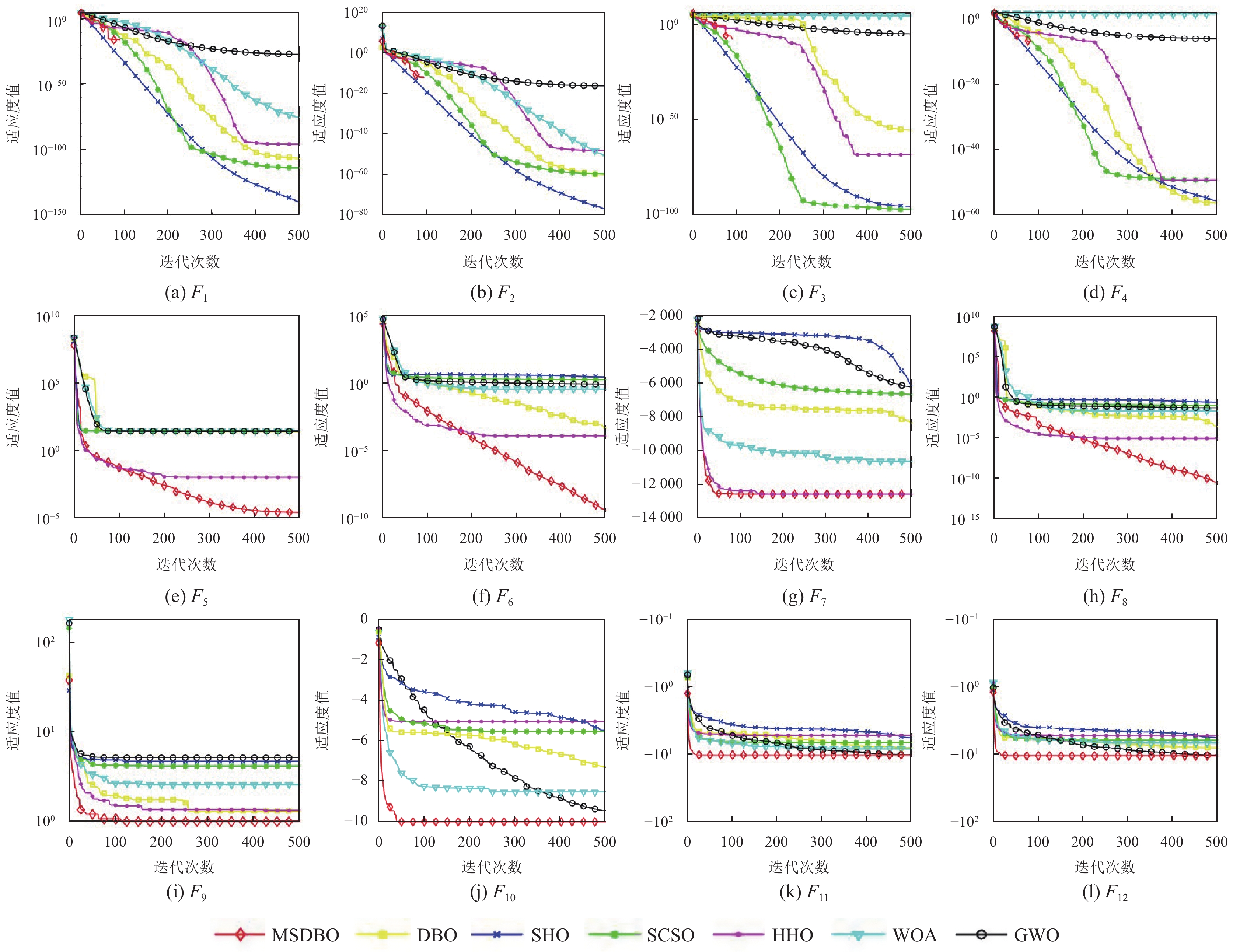
实验结果如表3所示, 平均适应度变化曲线如图3所示, 可以看出改进的蜣螂优化算法在12个选定的标准测试函数上的表现均优于其他对比算法.

对于单峰测试函数而言, 在F₁–F₄上, MSDBO可以稳定地寻找到最优值0, 从对应的迭代曲线上来看, MSDBO刚开始与其他算法性能相近, 当迭代进行到100次左右, MSDBO能迅速地收敛到最优值0, 而其他算法往往一直到迭代结束仍未收敛到最优值0, 这说明MSDBO不易陷入局部最优并且具备较强的局部开发能力, 而其他算法因为局部开发能力较弱从而在局部最优区域周围盲目开发陷入停滞; 在F₅与F₆上, MSDBO与其他算法相比, 取得了更高的精度, 从变化曲线上可以看出, 在F₅上, 绝大多数算法在进行到第100次迭代左右即陷入停滞, 而MSDBO在则迭代到第400次左右才陷入停滞, 在F₆上, 其他优化算法在迭代结束前或早或晚都陷入了停滞或者以缓慢的速度收敛, 而MSDBO直到500次迭代结束仍有较大的寻优提升空间.

对于多峰测试函数而言, 在F₇及F₉–F₁₂上, MSDBO都取得了更优结果, 从变化曲线可以看出, 其中, MSDBO在F₇及F₁₀–F₁₂上收敛较其他算法快且没有出现明显的停滞情况, 在F₉上, 虽然出现了多次停滞, 但在每次短暂的停滞之后总是能跳出局部最优, 并可以稳定地寻找到最优解, 在函数F₈上则取得了比其他算法更高的精度且仍有继续寻优的空间.

综上, MSDBO在上述不同类型的基准测试函数上的表现均优于对比算法.

3.3 压力容器设计问题

为了验证MSDBO对现实中工程设计问题的优化性能, 本文引入压力容器设计优化对算法进行测试, 各参数不变, 记录各算法独立运行30次所求得的最优解及最优解对应的解决方案进行对比, 如表4所示.

压力容器设计是一个经典的工程优化问题, 该问题的目标是在圆柱形容器壁厚度(${T_{{s}}}$)、封头厚度(${T_{{h}}}$)、容器内径($R$)、容器长度($L$)这4个变量在满足一定约束条件下总成本最小, 目标函数$f$、约束条件$g$及变量范围如下:

$ \left\{\begin{gathered} x = \left[ {{x_1}, {x_2}, {x_3}, {x_4}} \right] = [{T_s}, {T_h}, R, L] \\ f(x) = 1.7781{x_2}x_3^2 + 0.6224{x_1}{x_3}{x_4} \\ \qquad\quad +3.1661x_1^2{x_4} + 19.84x_1^2{x_3} \\ {g_1}(x) = 0.00954{x_3} \leqslant {x_2} \\ {g_2}(x) = 0.0193{x_3} \leqslant {x_1} \\ {g_3}(x) = {x_4} \leqslant 240 \\ {g_4}(x) = - 3{\text π} x_3^2{x_4} - 4{\text π} x_3^3 \leqslant - 3888000 \\ 0 \leqslant {x_1}, {x_2} \leqslant 99{\text{ 10}} \leqslant {x_3}, {x_4} \leqslant 200 \\ \end{gathered} \right.$

通过对上述的压力容器优化设计问题的测试, 可以看出本文算法在处理实际工程约束优化问题方面具有一定的应用潜力.

4 结论与展望

为克服标准DBO算法全局探索能力欠缺、收敛精度低等问题, 提出了一种多策略改进的蜣螂优化算法(MSDBO). 首先提出并使用了一种社会学习策略引导推球蜣螂进行位置更新, 提高了算法全局探索及跳出局部最优的能力; 其次, 提出方向跟随策略建立起小偷蜣螂与推球蜣螂之间的交互, 提高了算法的寻优精度. 最后, 提出环境感知概率引导小偷蜣螂个体合理采取方向跟随策略, 平衡了算法的性能与时间消耗. 通过对12个不同类型的基准测试函数的求解分析, 验证了改进算法具有良好的寻优性能, 在压力容器设计问题上的测试结果表明MSDBO在求解实际工程约束优化问题上也有着良好的应用潜力. 未来工作是研究MSDBO在聚类等问题中的应用.