1 概述

深度神经网络(DNN)在处理不同的计算机视觉任务中(如图像分类, 分割和目标检测)均表现了出色的性能, 适用于不同的应用邻域. 提高深度学习模型性能的因素之一是大规模数据集的使用, 如ImageNet. 然而, 大规模数据集的标注工作是昂贵且耗时的^[1], 研究人员有时采取更便宜的替代方案, 如网络搜索和众包^[2], 但这可能会产生带有错误或噪声标签的数据集. 不正确的标签也可能存在于小规模数据集中, 因其标注目标困难或标注者之间存在分歧, 例如医学图像的标注.

大多数基于DNN的工作都假设标签是由专家标注的, 或者是经过设计的, 因此会被认为是完美标注. 然而, 这个假设往往不符合现实, 标注的正确性会受到数据来源, 数据获取数据量以及人为因素等影响^[3]. McNicol ^[4]指出, 当涉及人类标注时, 噪声标签的产生可能无法避免. 因此, 使用噪声标签训练的DNN可能会降低准确性并需要更大的训练集. Zhang等人^[5]已经表明, 卷积神经网络(CNN)可以很容易地适应任何比率的噪声标签, 导致泛化性能变差. 然而, 研究表明, 模型会首先学习简单模式, 对应于具有干净标签的简单样本, 而更接近于噪声标签的困难模式则会在之后学习甚至“强行记忆”. 这就是神经网络的“记忆效应”.

基于这一特性, 用样本选择方法解决标签噪声问题无疑是简单直接的思路, 而这其中又多以小损失原则为干净样本假设. 这些工作试图从嘈杂的实例中选择干净的实例, 然后使用它们来更新网络. 直观地, 随着训练数据的标签噪声更少, 模型可以获得更好的性能. 其中, 代表性的方法是MentorNet和Decoupling. Jiang等人^[6]提出了MentorNet, 它预先训练一个额外的网络, 然后使用该网络来选择干净的实例来指导训练. 当没有干净的验证数据供使用时, MentorNet必须使用预定义的课程. 同时它也继承了样本选择偏差导致误差累积的劣势. Malach 等人^[7]提出了Decoupling同时训练两个网络, 然后仅使用来自这两个网络的具有不同预测的实例来更新模型. 尽管如此, 噪声标签均匀地分布在整个样本空间中. 因此, 不一致区域包括多个噪声标签, 而Decoupling不能显式地处理噪声标签. Han等人^[8]提出Co-teaching, 它不是训练单个深度神经网络, 而是同时训练两个深度神经网络, 并让它们在每一个mini-batch中相互教学, 根据其对等网络选择的数据更新自己. 由于两个网络具有不同的学习能力, 它们可以过滤由噪声标签引入的不同类型的错误. 然而, 随着训练时间的增加, 两个网络将趋于一致, Co-teaching在功能上将退化为为自我训练的MentorNet. Yu等人^[9]引入了“不一致更新”策略^[7]来保持Co-teaching网络的差异, 并将其方法命名为Co-teaching+. 一般来说, Co-teaching+包括不一致更新步骤和协同更新步骤. 在不一致更新步骤中, 两个网络首先对所有数据进行前馈和预测, 只保留预测不一致的数据. 这一步骤确保两个网络保持差异. 在协同更新步骤中沿用了Co-teaching的更新方法. Wei等人^[10]使用了与Co-teaching+相同的思想, 但它使用的是“联合一致策略”而非“不一致更新”策略, 并使用Co-regularization联合损失作计算.

可以总结这类方法的3个关键因素: (1)使用小损失技巧; (2) 两个网络的协同更新参数; (3)保持两个网络的差异.

除了基于小损失的样本选择方法外, 鲁棒损失^[11,12], 样本加权^[13,14], 元学习^[15,16], 组合方法^[17,18]也是常见的策略. 鲁棒损失即损失校正法, 通过添加正则项或修改网络概率, 从而对可能与噪声样本相关的低置信度预测减轻惩罚; 样本加权, 即通过不同样本的权重改变, 降低噪声样本的影响; 将元学习方法用来重加权或者过滤噪声样本; 组合方法则是结合各种方法的优点来获取更好的效果. 本文对样本选择方法展开深入研究.

目前提出的方法虽然性能有所提升, 但也付出了相应的代价. 一是方法越来越复杂, 各种方法的组合使网络模型变得庞大甚至臃肿, 训练成本也大大提升. 另一个方面, 各种方法为了提升性能也需要额外的信息, 包括需要为模型提供干净的训练子集, 需要假设噪声的比率, 甚至是模拟噪声的分布. 这些条件都让标签噪声问题变得复杂且特殊, 与噪声标签的普遍存在现实相背. 于是Feng等人^[19]考虑了一个新的问题设置, 学习未知标签噪声(LULN), 即模型学习时噪声的程度和类型是未知的. 为了追求简单性和鲁棒性, 他们提出了一种简单的LUNL方法, 即样本选择和重标签(SSR), 其中两个组件相互独立: 选择机制, 识别具有正确标签的干净样本, 以及重标签机制, 旨在恢复错误标记的噪声样本的正确标签. 这两个主要组成部分基于LULN的两个简单而必要的假设, 即具有与其邻域样本高度一致标注的样本通常是干净的, 并且高置信的模型预测通常是值得信赖的. 一旦以这种方式构建了良好标记的子集, 就可以使用最基本的监督训练方案, 并使用交叉熵损失作计算.

SSR方法简单高效, 既不需要结合半监督学习、自监督模型的预训练以及模型协同训练, 又不需要额外的干净子集辅助训练. 然而, SSR对特征空间的样本信息处理简单, 本文认为其仍具有进一步利用的空间, 在保有简洁高效特点的同时, 进一步提升对噪声样本的处理效果.

本文的主要工作如下.

(1)本文基于样本选择重标签方法, 提出了样本置信度特性假设, 即高置信度样本为干净样本概率大, 低置信度样本为干净样本概率小. 并提出了一种新的对标签噪声的图像分类方法, 即二阶段加权样本选择重标签方法(WSSR-2s).

(2)针对高低置信度样本, 设计了不同的样本选择优化策略. 从样本票权角度, 对于高置信度样本, 进行票权加权; 对于低置信度样本, 进行票权转移.

(3)本文进行了大量实验证明了本文方法的有效性.

2 相关工作

目前很多方法^[6,14,17]都受限于其模型的复杂程度或是额外的附加条件. SSR方法从简单适用的角度出发, 沿用了样本选择方法, 这也是最直观的解决标签噪声问题的思路. 但是其假设不同于MentorNet、Decoupling、Co-teaching等基于小损失方法, 而是基于邻域样本高度一致标注的样本通常是干净的这一假设. 即在特征表示层面上, 对样本作K近邻算法(KNN), 用余弦相似度度量, 以统计其邻域样本对样本各类别的票权. 当最多票权类别与标签相一致时, 认为该样本是干净样本, 进而选择其加入干净子集进行训练. 同时, SSR方法还提出样本重标签机制, 基于假设样本的高置信度预测认为是正确的. 即在预测层设定高阈值, 对预测高于该阈值的样本重标签. 可以看出, 该方法简洁清晰, 同时也表现了不错的性能. 同时, 样本的选择与重标签机制是相对独立的部分, 本文认为样本置信度的潜在价值未被完全利用. 基于此提出了高低置信度假设实现进一步改进.

算法1. SSR

输入: 数据集$\scriptstyle \left( {X, Y} \right) $, 样本选择阈值$\scriptstyle {\theta _s} $, 样本重标签阈值$\scriptstyle {\theta _r} $, 最大训练周期$\scriptstyle T $

1当$\scriptstyle 0 \leqslant i < T $时执行

2 　生成数据集$\scriptstyle \left( {X, {Y^r}} \right) $; // 根据样本重标签策略

3 　生成数据集$\scriptstyle \left( {{X_c}, Y_c^r} \right) $; // 根据样本选择策略

4 　训练模型;

5 结束

注意算法1中$ {Y^r} $表示原标签集$ Y $经过样本重标签策略新生成的标签集; $ \left( {{X_c}, Y_c^r} \right) $表示经过样本选择策略新生成的数据集. 训练模型指的是用选择出的干净数据集进行模型训练, 进而得到模型输出.

3 提出的WSSR-2s方法 3.1 问题定义

定义式(1):

$ X = \left\{ {{x_i}} \right\}_{i = 1}^N, {x_i} \in {R^d} $

(1)

为训练集($ d $表示数据映射维度), 其对应的独热向量标签为:

$ Y = \left\{ {{y_i}} \right\}_{i = 1}^N, {y_i} \in {\left\{ {0, 1} \right\}^M} $

(2)

其中, M是类别数量, N是样本数量. 方便起见, 定义对应于独热向量标签$ {y_i} $的每个样本$ {x_i} $的标签表示为:

$ {l_i} = {\arg _j}\left[ {{y_i}\left( j \right) = 1} \right] \in \left\{ {1, \cdots, M} \right\} $

(3)

其中, $ {\arg _j} $表示取满足条件的参数$ j $.

最后, 定义真实标签为:

$ {Y'} = \left\{ {y_i'} \right\}_{i = 1}^N $

(4)

显然, 对于开集噪声标签来说$ {y}_i' \ne {y_i}, \;{y}_i' \notin {\left\{ {0, 1} \right\}^M} $, 对于闭集噪声标签则$ {y}_i' \ne {y_i},\; {y}_i' \in {\left\{ {0, 1} \right\}^M} $.

本文将用于提取特征表示的分类网络视为编码器$ f $, 定义一个参数模型分类器$ \left( {{\mathrm{PMC}}} \right)\;{g_p} $用来处理分类问题, 同时定义一个基于编码器$ f $所提取特征表示的非参数K近邻分类器$ \left( {{\mathrm{NPK}}} \right)\;{g_q} $. 简单起见, 本文定义样本$ {x_i} $的特征表示为:

$ {f_i} \triangleq f\left( {{x_i}} \right) $

(5)

并将经PMC和NPK的预测向量分别定义为:

$ {p_i} \triangleq {g_p}\left( {{f_i}} \right) $

(6)

$ {q_i} \triangleq {g_p}\left( {{f_i}} \right) $

(7)

本文采取分阶段训练方案: (1)高置信度样本票权加权(训练初期), 以及(2)低置信度样本票权转移(训练中后期).

3.2 根据样本置信度改进样本票权

本文的样本置信度$ {\theta _h} $、$ {\theta _l} $于样本重标签方法的PMC分类器$ {g_p} $设置, 样本票权则是基于样本选择方法的特征邻域样本的标签$ y_i^r $设置. 根据高低置信度样本对特征邻域的样本票权改进, 以下是具体的方法.

(1)高置信度样本票权加权

首先, 高置信度样本基于PMC分类器$ {g_p} $, 通过设定高阈值$ {\theta _h} $得到. 具体地, 获取高置信度样本的索引集, 即用$ H $表示样本集$ X $中PMC分类器$ {g_p} $预测$ {p_i} $, 其最大元素超过阈值$ {\theta _h} $的所有样本$ {x_i} $的索引集. 其定义为:

$ H = \left\{ {i\Big|{{\arg }_i}\left[ {\mathop {\max }\limits_l {p_i}\left( l \right) > {\theta _h}} \right]} \right\} $

(8)

此集合表达式中$ {\arg _i} $表示取满足条件的$ i $, $ \max $表示对应下标参数$ l $使$ {p_i} $取得最大值.

接着, 根据得到的高置信度样本索引集$ H $, 将对应的高置信度样本的票权进行加权. 具体地, 对于包含在高置信度样本索引集中的样本索引$ i $, 其对应样本$ {x_i} $的样本票权$ y_i^r $乘权重系数$ w $以加权; 对于不包含在高置信度样本索引集中的样本索引$ i $, 其对应样本$ {x_i} $的样本票权$ y_i^r $保持不变. 形式上:

$ y_i^h = \left\{\begin{array}{l} {w \cdot y_i^r, \quad i \in H}\\ {y_i^r, \quad \quad \, i\; \notin \, H} \end{array}\right. $

(9)

这样, 加权过票权的高置信度样本票权可以修正NPK分类器$ {g_q} $的预测向量$ {q_i} $, 进一步帮助在模型训练初期更正确地选择出干净样本.

(2)低置信度样本票权转移

同样地, 低置信度样本基于PMC分类器$ {g_p} $, 通过设定低阈值$ {\theta _l} $得到. 具体地, 获取低置信度样本的索引集, 即用$ L $表示样本集$ X $中PMC分类器$ {g_p} $的预测$ {p_i} $, 其最大元素不及阈值$ {\theta _l} $的所有样本$ {x_i} $的索引集. 其定义为:

$ L = \left\{ {i\Big|{{\arg }_i}\left[ {\mathop {\max }\limits_l {p_i}\left( l \right) < {\theta _l}} \right]} \right\} $

(10)

此集合表达式中$ {\arg _i} $表示取满足条件的$ i $, $ \max $表示对应下标参数$ l $使$ {p_i} $取得最大值.

接着, 根据得到的低置信度样本索引集$ L $, 将对应的低置信度样本的票权进行转移. 具体地, 对于包含在低置信度样本索引集中的样本索引$ i $, 其对应样本$ {x_i} $的样本票权$ y_i^r $转移给在特征表示中与$ {x_i} $最相似的样本$ {x_s} $. 具体来说, 本文根据前文SSR方法, 用$ {s_{ij}}, \;i, j = 1, \cdots, N $表示任何两个样本$ {x_i} $和$ {x_j} $的特征表示$ {f_i} $和$ {f_j} $之间的相似性. 默认情况下, 本文使用余弦相似度, 即:

$ {s_{ij}} \triangleq \frac{{f_i^{\mathrm{T}}{f_j}}}{{||{f_i}|{|_2}||{f_j}|{|_2}}} $

(11)

同时基于所计算的相似性用$ Si $表示$ X $中的样本$ {x_i} $的最近邻样本的索引. 接着, 将原本的低置信度样本$ {x_i} $的票权权值置0, 其对应的样本$ {x_{Si}} $的票权权值加1; 对于不包含在低置信度样本索引集中的样本索引$ i $, 其对应的样本票权$ y_i^r $保持不变. 形式上:

$ y_i^l = \left\{\begin{array}{l} {y_{Si}^r, \quad \quad i \in L} \\ {y_i^r, \quad \;\;\;\;\;\; i\; \notin \, L} \end{array}\right. $

(12)

注意定义:

$ y_{Si}^r = \sum {y_i^r} \quad \quad i \in Si $

(13)

另需将被转移的票权置零, 这样, 转移过票权的低置信度样本票权可以修正NPK 分类器g_q的预测向量q_i, 进一步帮助模型训练在中后期更好地处理噪声样本.

至此算法WSSR-2s的流程总结如算法2.

算法2. WSSR-2s

输入: 数据集$\scriptstyle \left( {X, Y} \right) $, 高置信度样本阈值$\scriptstyle {\theta _h} $, 低置信度样本阈值$\scriptstyle {\theta _l} $, 最大训练周期$\scriptstyle T $, 训练转折期$\scriptstyle {T'} $

1当$\scriptstyle 0 \leqslant i < T $时执行

2 　根据SSR进行样本重标签和选择;

3 　当$\scriptstyle i < {T'} $时执行

4 　　根据式(9)得到高置信度样本票权$\scriptstyle y_i^h $; //高置信度样本票权加权

5 　当$\scriptstyle i \geqslant {T'} $时执行

6 　　根据式(12)得到低置信度样本票权$\scriptstyle y_i^l $; //低置信度样本票权转移

7 　根据干净样本训练模型;

8 结束

(3)对分阶段不同置信度票权改进的解释

本文将训练阶段分为初期和中后期. 在训练初期, 对高置信度样本票权加权; 在训练中后期, 对低置信度样本票权转移. 这里, 本文讨论这两种方法的有效性.

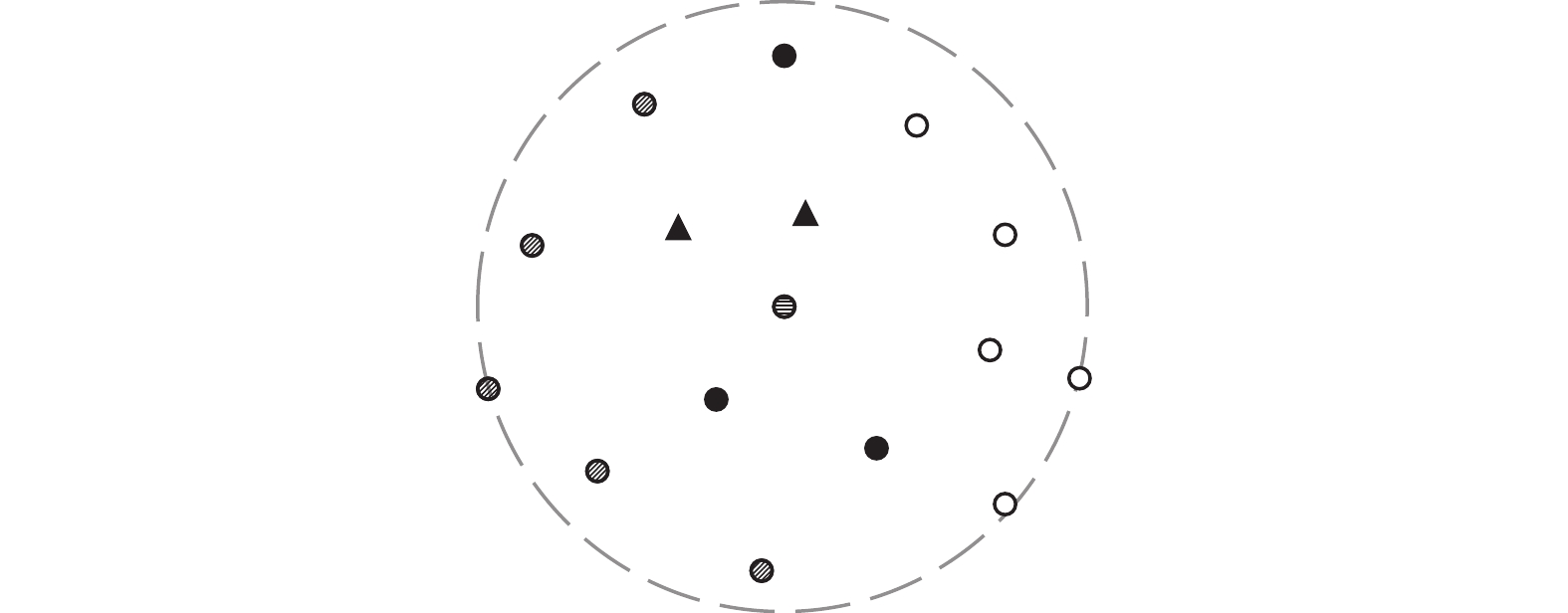
在训练初期, 大多数样本的置信度都处在较低水平. 对于那些能给出高置信度的样本, 本文假设其标签正确的概率大. 如图1所示, 竖线圆表示为当前样本, 虚线圈出的则是样本的特征邻域. 实心圆(或三角)、空心圆、斜线圆代表3种样本类别. 在不考虑高置信度样本的情况下, 特征邻域里3种类别样本数量相同, 对应的样本票权也相同. 这样, 样本无法由票权确定所属类别. 现在, 考虑高置信度样本, 对应于图1中的实心三角形样本. 当对这些样本票权进行加权后, 样本类别可以由票权确定, 并且因为高置信度特性, 所确定的样本类型大概率是正确的, 与之前的假设保持一致. 另一种形象的解释是, 在一场选举初期, 那些有想法有意见的人往往有更高的话语权. 需要说明的是, 此方法看起来和样本重标签方法有相似之处, 但是进一步利用了高置信度样本的价值. 将PMC分类器和NPK分类器通过高置信度样本联系起来, 利用高置信度样本的特性提升样本选择的正确率.

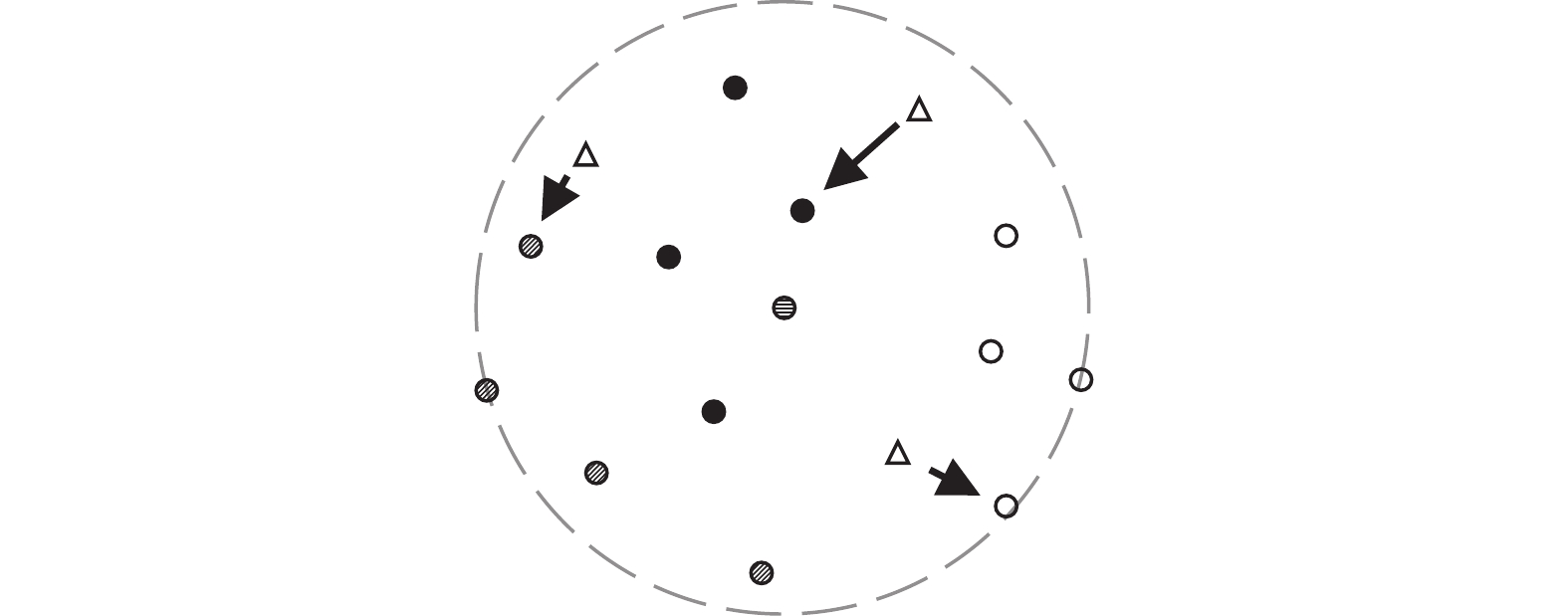
随着训练的进行, 越来越多的样本可以给出可靠的高置信度预测, 因此对高置信度样本票权加权的方法效果会退化. 所以, 在模型训练的中后期, 本文对低置信度样本作假设, 认为其标签正确概率小. 如图2所示, 空心三角形样本表示低置信度样本. 这些样本若符合假设, 其本身的标签意义就不大. 同时, 箭头指向的是与其特征表示最相似的样本. 将低置信度样本的票权转移给最相似的样本, 让这些样本代表原样本的票权, 可以在训练中后期降低噪声样本带来的干扰. 形象的解释是, 在选举的中后期, 中间派的意见往往是找最符合自身利益的派别. 需要说明的是, 该方法在高噪声多类别的情况下, 提升样本选择的正确率是更为有效的. 给特征相似的样本进行票权转移是符合假设的改进思路.

4 实验 4.1 概述

本文在基于合成噪声的标准数据集CIFAR-10和CIFAR-100以及两个真实世界噪声数据集ANIMAL-10N和WebVision进行了广泛实验. 简单起见, 本文为相应的噪声设置定义了缩写名称, 例如“Sym 50”表示50%对称噪声, “Asym 40”表示40%不对称噪声. 在第4.2节和第4.3节中, 本文将所提出的方法与合成噪声数据集和真实世界噪声数据集的最新技术进行了比较. 在第4.4节中, 本文进行了消融实验, 使所提出分阶段样本票权改进方法的有效性得到验证. 最后第4.5节为计算开销分析.

4.2 合成噪声数据集

遵循先前工作, 本文使用PresActResNet-18作为所有的CIFAR-10/CIFAR-100实验的主干. 与之前使用特定预热设置的CIFAR-10/CIFAR-100方法不同, 本文在所有实验中设定$ {\theta }_{s} $为1.0并从头开始训练模型. 同时对于较高的噪声比Sym 50、Sym 80和Sym 90设置 $ {\theta }_{r} $ 为0.8, 之外的所有CIFAR实验中的设置$ {\theta }_{r} $ 为0.9. 本文使用相同的SGD优化器并训练300个epoch, 动量设为0.9, 权重衰减为5E–4. 初始学习率为0.02, 并由余弦退火调度器控制. 批大小固定为128. 对于新参数设置$ {\theta }_{h}=0.85 $, $ {\theta }_{l}=0.1 $5, $ w=2 $, $ {T}' $设置为epoch的1/6为50.

本文将WSSR-2s与最近最具竞争力的工作进行比较. 表1、表2显示了CIFAR-10和CIFAR-100的结果. 再次说明, 本文方法没有使用模型协同训练或预训练. 很明显, 本文方法远远优于对比方法(例如在90%对称噪声的CIFAR-100上的准确度为63.6%), 不仅在对称噪声的情况下, 而且在更现实的非对称合成噪声设置中. 同时对于原方法, 在相同实验环境下, 本文方法实现了全方面改进.

表3显示出了本文的方法在更复杂的组合噪声场景中的性能(组合噪声指的是噪声由闭集噪声和开集噪声组合成的噪声, 例如NR=0.3、OR=0.5指的是总噪声率(noise ratio)为30%, 其中开集噪声(open ratio)占总噪声50%的噪声设置). 当开集噪声比从1降低到0.5时, 专门为开集噪声设计的先前方法迅速退化. 此外, 当开集噪声比增加时, 不考虑开集噪声的方法的像DivideMix的性能降低. EDM修改了DivideMix的方法来处理组合噪声, 然而, 报告的结果仍大大低于本文的结果. 相对于原方法, 本文的改进保持了稳定的提升.

4.3 真实噪声数据集

对于WebVision, 本文使用InceptionResNetv2. 具体地, 使用SGD优化器训练150个epoch, 动量为0.9, 权重衰减为1E–4. 初始学习率为0.01, 并且在50和100个时期之后降低10倍. 批大小固定为32. 对于ANIMAL-10N, 本文使用VGG-19, 并进行批归一化. 具体地, 使用SGD优化器训练150个epoch, 动量为0.9, 权重衰减为5E–4. 初始学习率为0.02, 并且在50和100个时期之后降低10倍. 批大小固定为128. 对于所有真实世界的噪声数据集, 本文设置$ {\theta }_{s} $为1从头开始训练模型, 而$ {\theta }_{r} $固定为0.95. 对于新参数设置$ {\theta }_{h}=0.9 $, $ {\theta }_{l}=0.2 $, $ w=2 $, $ {T}' $设置为epoch的1/6为25.

最后, 在表4、表5中, 本文分别显示了WebVision和ANIMAL-10N数据集的结果. 总而言之, 本文的方法在大规模网络爬取数据集和小规模人类标注的噪声数据集方面都取得了与当前最先进技术相比更好或具有竞争力的性能. 同时也都对原方法实现了一定的改进.

4.4 分阶段票权改进的有效性验证

本文也对所提出的分阶段票权改进方法的有效性做了消融实验来验证其有效性. 具体地, 分为原方法, 原方法加一阶段方法以及分阶段二进段改进方法在CIFAR-10、CIFAR-100上90%以及80%高噪声下(用90%N、80%N表示)作对比. 需要说明的是, 这里的一阶段指的是高置信度票权加权, 二阶段指的是低置信度票权转移.

由表6可以看出, 本文提出的两阶段方法都分步实现了性能提升. 值得注意的是, 在高类别高噪声的环境下, 阶段1高置信度样本票权加权的提升效果下降, 阶段2低置信度票权转移的提升效果上升. 这一现象验证了本文之前的观点, 即训练后期高置信样本数量增多, 加权效果减少, 反而是对低置信度样本的票权处理反而提升效果明显, 进一步说明本文正确地处理了标签噪声样本.

4.5 计算开销分析

在表7中, 我们记录了模型在我们实验的数据集上每个步骤的运行时间. 可以看出, 与梯度传播的时间相比, 样本选择和重新标记的时间几乎可以忽略不计. 同时, 我们的二阶段改进方法的时间开销同样可以忽略不计. 再次证明, 我们的方法不依托于任何固定的网络模型, 不需要复杂的机制组合, 不需要额外的附加信息, 不耗费大量额外的计算开销, 仅是作为一种训练策略, 就能对噪声标签的处理产生较好效果.

5 结论

本文基于样本选择重标签方法SSR, 提出了高低样本置信度假设, 并基于假设提出了分阶段的票权改进方法. 与以前的整合复杂机制以及额外信息的方法相比, 本文秉承了原方法简单和强大的特点. 同时进一步利用了样本置信度的信息, 将样本选择和重标签两个相对独立的部分联系起来. 经过广泛的实验和消融分析表明, 本文利用置信度信息进行的改进以及分阶段的策略是有效的, 效果超过了大部分先前的方法, 同时对原方法实现了可靠的改进. 后续将进一步分析样本空间中噪声样本特点, 提出合理假设以实现更好的效果.