前方障碍物的检测是移动机器人环境感知环节关键技术之一, 对系统的实时性和鲁棒性要求很高. 现在障碍物检测常用的传感器有: 激光雷达、视觉传感器、超声波传感器等, 根据工作原理分成主动式和被动式两种. 主动式传感器自身发射出测距信号, 在物体上反射后返回并被接收到, 分析返回信号的频率、时间、相位等信息, 获取障碍物的信息, 最为常见的则是TOF法, 在激光雷达、超声波传感器中应用最多. 而被动式传感器自身不发射测距信号, 通过外界的光线等信号来感知障碍物, 典型的就是视觉传感器. 激光雷达因为其精度高, 范围广等优点, 成为了障碍物检测技术中的主要应用传感器, 有众多学者研究了基于二维和三维激光雷达在室内或者室外环境下障碍物检测和跟踪技术^[1].

对于障碍物的检测, 有两个问题需要解决: 一是识别障碍物, 二是计算障碍物的位置. Nguyen等^[2]介绍了一种应用于无人驾驶的深度学习障碍物识别和跟踪方法, 采用一种新的深度学习方法, 利用多种模式对采集到的障碍物进行检测、识别和跟踪, 结果表明该方法有很高的检测识别能力, 但是对于硬件要求较高, 否则无法保证障碍物检测的实时性要求. Chen等^[3]提出了双检测方法, 采用RANSAC和最小二乘法对地面拟合, 基于地面平面检测是识别障碍物, 实验表明, 该方法的检测准确率得到了提升, 但是对数据处理量翻倍, 检测速率有所降低. 谢德胜等^[4]提出了一种基于三维激光的障碍物检测与跟踪方法, 将空间投影到二维栅格内处理, 提出了八邻域细胞聚类算法并采用改进的动态跟踪点模型, 和卡尔曼滤波算法对动态障碍物跟踪, 最终得到动态障碍物的运动轨迹, 缺点在于栅格的分辨率过大, 或者地图环境过大时, 栅格量几何式增长, 会增加计算量, 因此仅适用于小型的室内环境. 许艳伟^[5]开发了一套基于激光雷达的应用于无人驾驶的三维车辆检测系统, 将激光雷达和深度相机的融合, 通过深度学习方法和传统方法识别三维场景地图中物体的位置和种类, 该系统将先进的深度学习框架引入到了目标检测当中, 对于目标检测的准确率有了较大的提高, 存在的问题在于需要大量的经济和时间成本投入, 商业化应用难度大.

随着障碍物检测技术的深入研究, 许多研究人员已经不局限于对一帧障碍物的处理, 开始将研究重点转向了连续多帧的障碍物跟踪, 从而获取更多的障碍物信息. 对于障碍物跟踪的重点在于两帧障碍物的数据关联, 王涛等^[6]针对激光雷达在进行障碍物检测和跟踪时聚类适应性差、实时性低和跟踪准确度低等问题, 提出了一种自适应的密度聚类算法和多特征数据关联方法分别用于检测和跟踪, 实验表明能够对动态障碍物进行稳定的关联和跟踪, 但是对于复杂场景的障碍物跟踪存在跟踪准确度降低的情况; 何小英等^[7]提出了一种激光与视觉融合的目标跟踪系统, 将RGB信息融入到算法中去, 生成机器人运行位置环境地图, 有效地提高了机器人的跟踪效率, 但是由于数据量过于庞大存在数据冗余的情况, 系统的运行效率还有待提高; Ruoyu等^[8]获取了RGB图像数据, 增强了每个障碍物的特征, 使用YOLOV3深度学习神经网络用于实时目标跟踪, 得到了车辆的稳定且精确跟踪效果, 这种方法效果虽好, 但是需要较大的数据量作准备并且移植能力弱, 无法在商品性质的移动机器人中得到产品级别的应用; Fortin等^[9]提出了不经过目标检测直接跟踪原始点云数据的方法, 根据目标的几何不变特性及计算模拟方法完成对目标的跟踪, 该方法能够去除目标检测过程中的部分误差, 提高跟踪准确度, 但环境复杂时跟踪失败率较高.

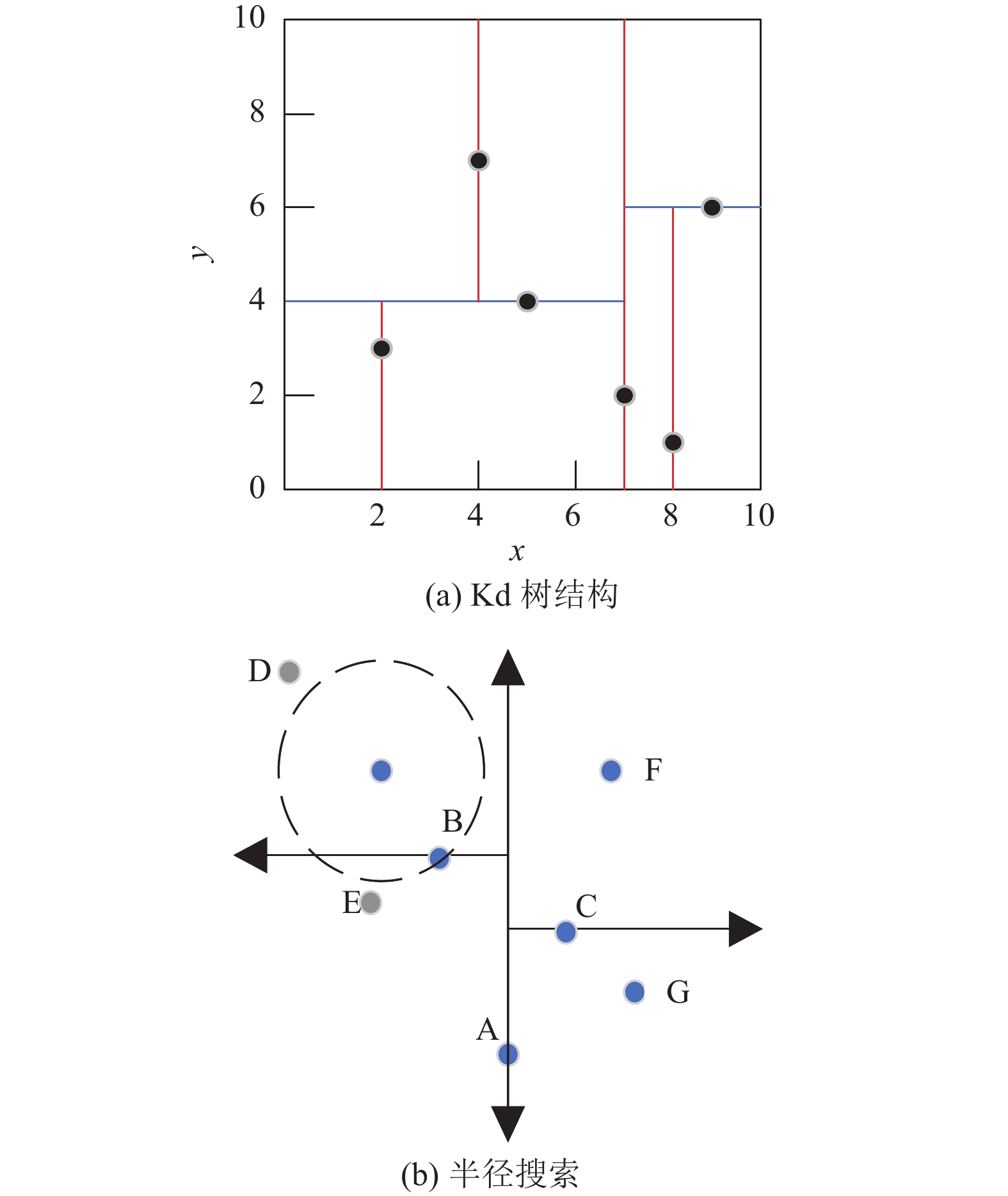
1 传统欧氏聚类

欧氏聚类算法^[10]原理如图1所示, 图1(a)为点云的分类保存形式. 将三维点云投影至XOY平面内并保存成Kd树模型. Kd树模型解决的是为K维数据的建立索引的问题, 如果按线性排列的索引方式采用线性搜索, 搜索复杂度为${\rm{O}}(n)$, 在数据量较大时存在搜索耗时过大的问题. Kd树的优点在于其特定的排序方式可以提高搜索速度, 搜索复杂度为${\rm{O}}(\lg (n))$, 通过空间换时间的方式减小时间复杂度.

图1(b)为欧氏聚类的搜索方法, 对于每个点云根据设定的距离阈值$ {r_{{\rm{th}}}} $, 寻找范围内的点云进行聚类, 再以这些满足要求的点云继续寻找, 经过多次迭代后即可将点云分割成若干个点云团, 并用相同数量的包围盒去包围每一个点云团, 并设定点云数量阈值, 当一个点云团的点云数量过少时, 则认为是干扰点而舍去, 拟合出的包围盒的几何中心视为障碍物的位置, 包围盒的长宽高视为障碍物的大小信息.

2 改进欧氏聚类

传统欧氏聚类的优点在于算法实时性好, 但容易出现过分割和欠分割的情况, 针对该问题, 本文对欧氏聚类做出以下改进.

对于深度相机的数据, 是从深度相机自身发射若干条红外光线, 检测距离靠TOF法来获得的, 这种方式获得的数据通常存在远处点云比较稀疏、近处点云比较密集的问题, 搜索半径固定时在远处易于出现过分割的情况. 本文提出一种根据点云的距离, 动态改变欧氏聚类半径搜索阈值的方法: 以移动机器人运动中心为圆心, 每隔一段距离就变化搜索半径的大小.

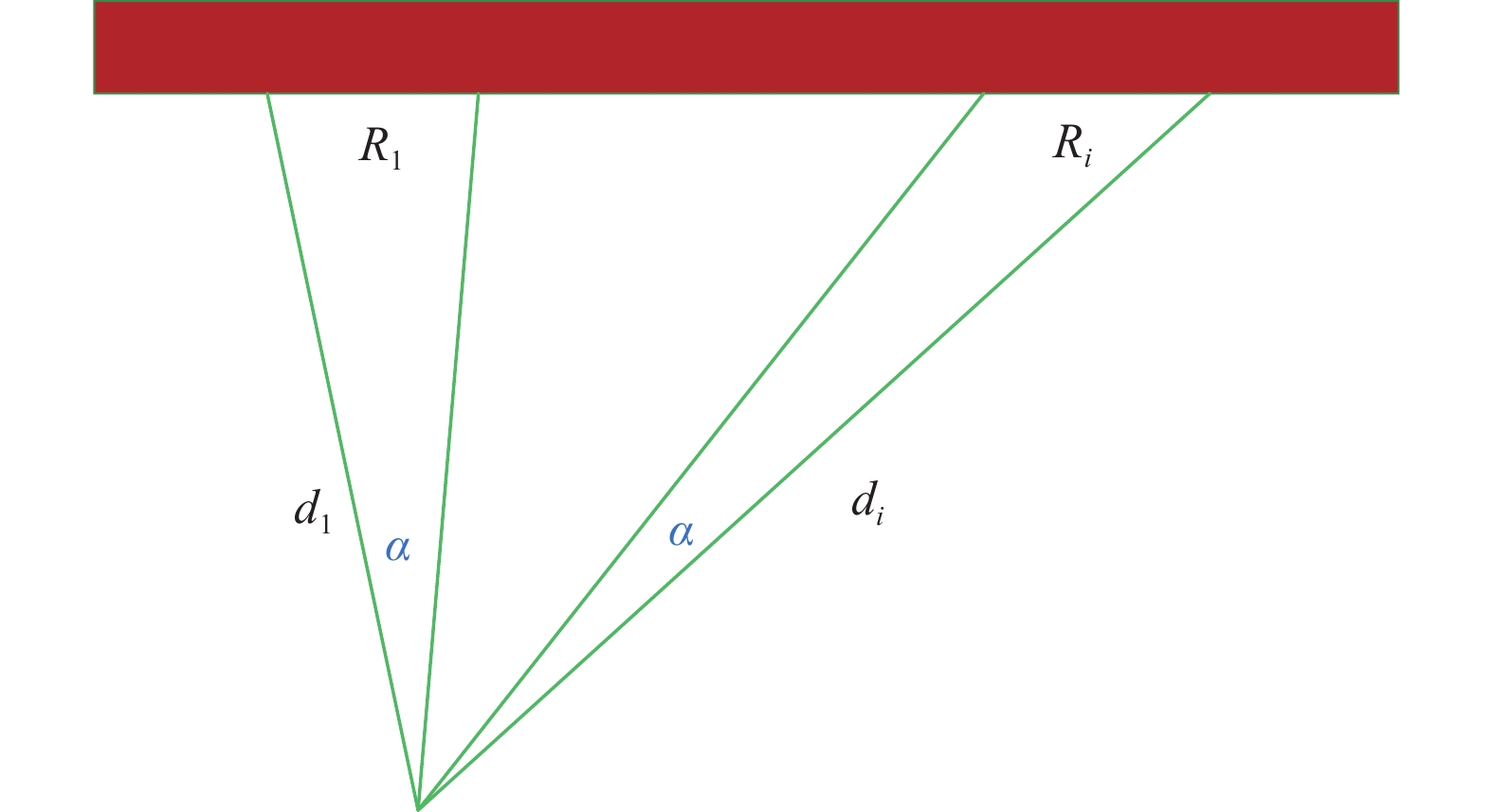
先配置好近距离时的搜索半径为$ {R_1} $, 由于深度TOF相机与激光雷达类似都有扫描分辨率, 即每隔一定的角度发射一道光线, 并且该值为定值. 本文设定扫描的角分辨率为α, 当光线扫到一个足够长的物体时, 可得到如图2所示的图像.

由于这个角分辨率足够小, 所以本文默认相邻的两条光线获取到的距离近似相等, 在远处时同样如此处理. 这样即可根据余弦定理, 得到扫描到该物体时, 相邻两点的距离为:

$ R_1^2 = 2d_1^2(1 - \cos \alpha ) $

(1)

$ R_i^2 = 2d_i^2(1 - \cos \alpha ) $

(2)

将式(2)和式(1)相除, 即可得到$ {R_1} $与$ {R_{{i}}} $的关系:

$ {R_i} = {R_1}\frac{{{d_i}}}{{{d_1}}} $

(3)

通过这种动态变化搜索半径的方式, 即可解决远处点云稀疏的问题.

对于深度相机的点云, 是从深度图像中转换得来的, 因此在图像坐标系下, X和Y的值都比较准确, 而深度Z方向的距离误差较大, 对于一般的TOF相机, 其深度距离靠的是红外摄像头射出的红外点阵, 检测距离以及检测精度相较于激光雷达有一定的差距, 因此在深度方向的点云波动较大, 易于出现过分割的问题. 为了解决上述问题, 在进行深度相机的点云欧氏聚类时, 需要扩大深度方向的搜索距离, 而成像平面XOY的搜索距离与激光雷达的大小相同, 如图3所示. 在传统的半径搜索中, 对于A点无法搜索到B点, 通过扩展Z搜索扩大距离, 呈现出椭圆形的搜索模型, 即可在X方向上不出现欠分割的前提下解决了Z方向的过分割的问题.

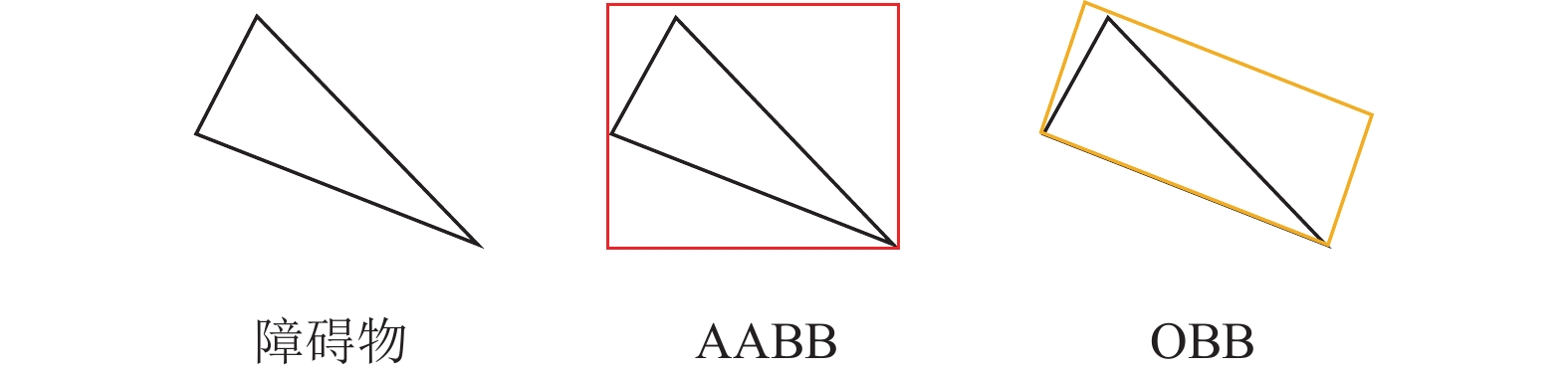
经过以上两点改进, 即可得到点云的准确聚类效果形成若干个点云团. 再对每个点云团求解重心位置得到障碍物位置信息X、Y、Z; 将每个点云团拟合成平行轴包围盒 (axis-aligned bounding box, AABB), 得到障碍物的大小信息Length、Width、Height. 为了之后两帧障碍物的准确匹配, 需要加入更多的可用信息, 因此改用定向包围盒算法 (oriented bounding box, OBB)来表示每个点云团, 其与平行轴包围盒算法的区别在于可得到点云团的六自由信息: X、Y、Z、Roll、Pitch、Yaw, 定向包围盒算法计算过程如下.

步骤1. 求解每个点云团的重心, 得到点云团位置X、Y、Z.

步骤2. 根据重心求解该点云团的协方差矩阵A:

$ A = \left[ {\begin{array}{*{20}{c}} {{{\rm{cov}}} (x, x)}&{{{\rm{cov}}} (x, y)}&{{{\rm{cov}}} (x, {\textit{z}})} \\ {{{\rm{cov}}} (x, y)}&{{{\rm{cov}}} (y, y)}&{{{\rm{cov}}} (y, {\textit{z}})} \\ {{{\rm{cov}}} (x, {\textit{z}})}&{{{\rm{cov}}} (y, {\textit{z}})}&{{{\rm{cov}}} ({\textit{z}}, {\textit{z}})} \end{array}} \right] $

(4)

其中, $ {{\rm{cov}}} ({X_i}, {X_i}) = E\left[ {({X_i} - {\mu _i})({X_i} - {\mu _i})} \right] $用于表示两个变量总体误差的期望, 协方差矩阵A可用来表示多维随机变量的概率密度.

步骤3. 由于$ {{\rm{cov}}} ({X_i}, {X_j}) = {{\rm{cov}}} ({X_j}, {X_i}) $的性质, 因此协方差矩阵A为实对称矩阵, A矩阵可对角化得到3个特征值$ {\lambda _1} $、$ {\lambda _2} $、$ {\lambda _3} $和对应的3个特征向量$ {\alpha _1} $、$ {\alpha _2} $、$ {\alpha _3} $.

步骤4. 将3个特征向量正交化, 得到$\; {\beta _1} $、$ {\beta _2} $、$ {\beta _3} $, 这3个向量便是包围盒的3个朝向, 与原坐标系求夹角即可得到Roll、Pitch、Yaw. 最终得到了定向包围盒如图4所示.

3 障碍物跟踪算法

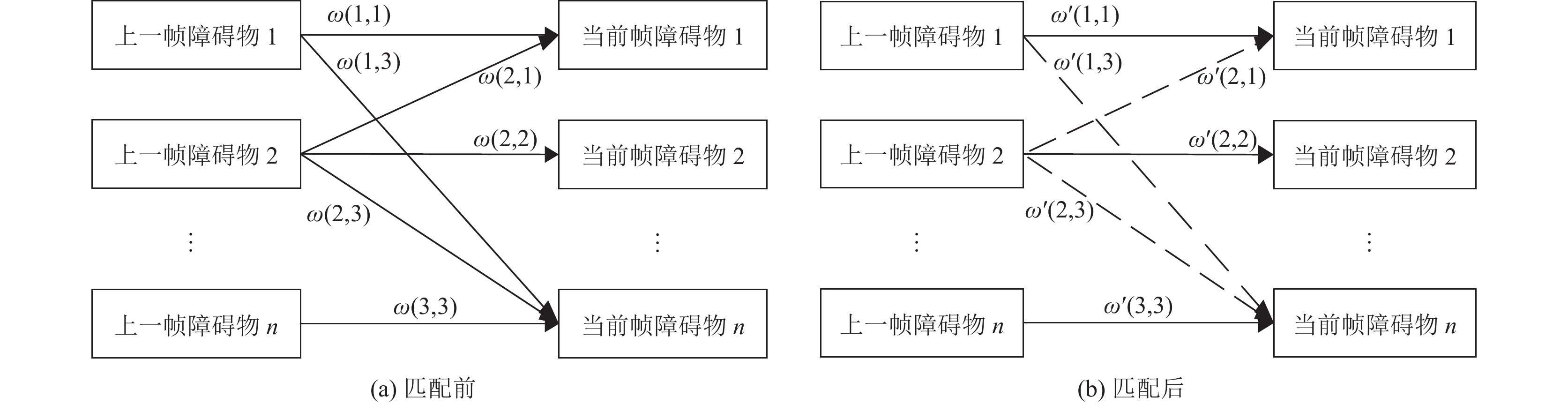
多帧匹配算法采用KM算法^[11], 该算法以匈牙利算法^[12]为基础, 改善后用于求解带权二分图的最佳匹配求解. 该算法复杂度较低、计算速度快, 适用于动态获取障碍物的运动速度和路径. KM算法的本质是二分图匹配, 在建立权重二分图之后, 找到匹配度最大的一组解, 初始时最大匹配为空, 不断寻找增广路线, 并不断扩大增广路线直到找不到增广路线位置.

首先建立初始权重二分图, 初始权值$ {\omega _1}(i, j) $由障碍物的位置关系d(i, j)和障碍物的大小关系s(i, j)所确定, 当两帧间障碍物较近, 并且大小类似时, 会得到更高的权值, 上一帧第i个障碍物和当前帧第j个障碍物的权值计算公式如下:

$ {\omega _1}(i, j) = \alpha \frac{1}{{d(i, j)}} + \beta \frac{1}{{s(i, j)}} + \gamma \frac{1}{{a(i, j)}} $

(5)

$ d(i, j) = \sqrt {{{({x_i} - {x_j})}^2} + {{({y_i} - {y_j})}^2}} $

(6)

$ s(i, j) = \left| {{w_i} - {w_j}} \right| + \left| {{l_i} - {l_j}} \right| + \left| {{h_i} - {h_j}} \right| $

(7)

$ a(i, j) = \left| {{R_i} - {R_j}} \right| + \left| {{P_i} - {P_j}} \right| + \left| {{Y_i} - {Y_j}} \right| $

(8)

其中, $ \alpha 、\beta 、\gamma $为可调系数, $ d(i, j) $通过上一帧第i个障碍物和当前帧第j个障碍物的欧氏距离得到, $ s(i, j) $通过计算两个障碍物长宽高的差值并求和得到, $ \alpha (i, j) $根据两障碍物的3个朝向角度偏差得到. 根据公式得到权值之后, 可以得到如图5(a)所示的权值二分图, 在匹配前, 有多种可能的匹配方式, 均用实线箭头表示.

求解最大匹配解的步骤如下.

步骤1. 首先选择顶点数较少的一侧为X部, 对X部的每一个顶点设置顶标, 顶标值为关联的最大权值, 另一边的Y顶标初始设置为0.

步骤2. 对于X部的每个顶点, 在相等子图中利用匈牙利算法找一条增广路径, 如果没有找到前往步骤3. 当每个点都找到增广路径时, 此时意味着每个点都在匹配中, 即找到了二分图的权值最大时的匹配, 即为二分图的最佳匹配.

步骤3. 修改顶标, 扩大相等子图, 左边的顶标减少1, 右边的顶标增加1, 并且满足两侧的顶标值之和始终不小于两者的权值, 得到新的匹配权值$ {\omega _2}(i, j) $, 返回步骤2.

经过KM算法求解后, 即可得到前后两帧障碍物的完美匹配, 如图5(b)所示, 当前帧的障碍物与上一帧最为相似的障碍物得到了匹配, 并舍弃其他匹配可能性, 留存的匹配组合用实线表示. 再根据采样时间差$ \Delta {{t}} $, 即可得到障碍物的运动速度和运动方向如式(9)和式(10)所示:

$ {v_{{\rm{ob}}}} = \frac{{\sqrt {{{({x_{{\rm{cur}}}} - {x_{{\rm{last}}}})}^2} + {{({y_{{\rm{cur}}}} - {y_{{\rm{last}}}})}^2}} }}{{\Delta t}} $

(9)

$ {\theta _{{\rm{ob}}}} = \arctan \left( {\frac{{{y_{{\rm{cur}}}} - {y_{{\rm{last}}}}}}{{{x_{{\rm{cur}}}} - {x_{{\rm{last}}}}}}} \right) $

(10)

4 算法对比实验与验证

为了记录实验中的障碍物的数据, 障碍物的所有信息都存于obstacles数组中. 为了体现数据的准确性, 主要有障碍物数量、位置、大小等因素, 因此本文设计的障碍物信息格式如表1所示. 由于移动机器人的运动模型一般为2自由度(X线速度, Z角速度), 或者3自由度(X线速度, Y线角度, Z角速度)两种, 因此对于障碍物的信息基本不考虑Z轴方向的运动, 只记录X和Y方向上的位置和运动属性.

4.1 算法改进效果对比实验

仿真实验在ROS平台下实现, 实验数据选择KITTI的开源数据, 发布数据在可视化界面Rviz中显示, 如图6所示.

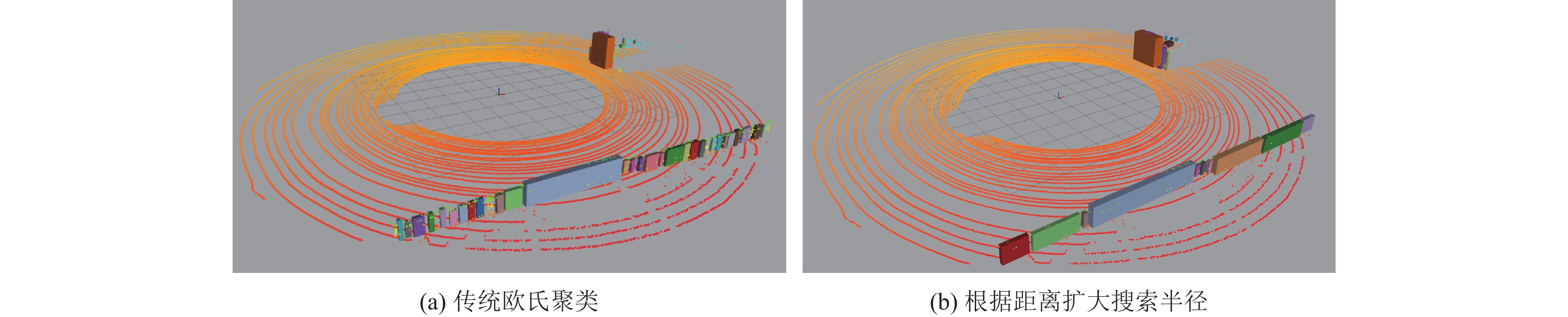
如图7所示, 对每一个聚类的点云团用平行轴包围盒来表示, 从图7(a)可以看出, 使用传统欧氏聚类, 能保证在一定距离内有较好的聚类效果, 但是远处的点云出现了明显的过分割的情况, 采用本文提到的改进方法, 对远处点云扩大搜索半径, 过分割情况得到明显改善.

本文认为每一个包围盒就是一个障碍物, 详细数据如表2所示, 从表2数据和图7效果不难看出, 传统欧氏聚类的过分割情况较为严重, 导致障碍物数量明显增加, 这将导致在之后进行多帧障碍物匹配时, 产生不必要的计算压力和运算耗时. 不仅如此, 在如此过分割的情况下, 也导致了远处的一些稀疏点云团因为点云量少, 没有被认为是障碍物, 这不仅将导致障碍物的大小存在误差, 甚至有可能漏检测一些重要的障碍物信息, 为之后的多帧障碍物匹配带来不必要的麻烦. 本文算法对以上的缺陷做出了优化, 为之后的多帧障碍物匹配提供了有效且稳定的数据.

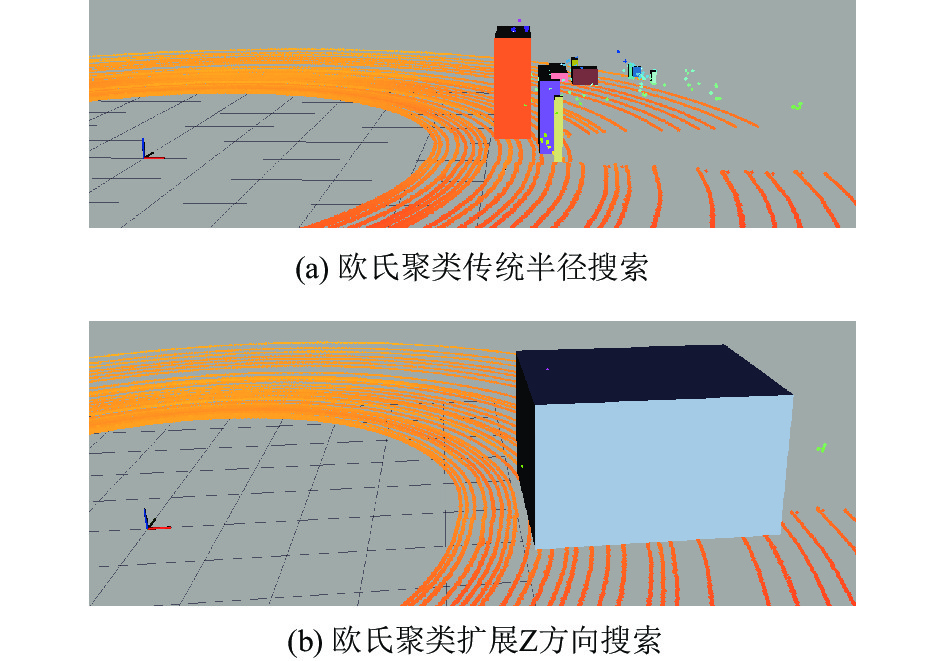
如图8(a)所示, 在深度方向上出现了明显的过分割情况, 而平面方向上聚类效果较好, 因此只需要扩大深度方向的搜索聚类, 得到了图8(b)所示的完整的聚类效果. 在得到每一帧数据的障碍物信息之后, 即可进行前后两帧数据的障碍物匹配, 得到障碍物运动速度和运动方向, 通过PoseArray数据格式在Rviz中显示.

4.2 算法改进性能对比实验

在设计障碍物检测与跟踪的性能对比实验时, 在车体前方1 m至2 m之间分别放置若干个10 cm、30 cm、50 cm、70 cm边长的立方体障碍物, 与检测的结果求偏差值, 将偏差最大的情况记录, 得到数据如表3所示. 从表中可以看出, 使用改进欧氏聚类后, 过分割和欠分割问题大大减少.

对以上4种不同障碍物的各项数据, 采用Bernardin 等^[13]提出的多目标跟踪评估指标: MOTA (多目标跟踪准确度)和MOTP (多目标跟踪精度), MOTA和MOTP的计算方法如式(11)和式(12)所示:

$ {\textit{MOTA}} = 1 - \frac{{\displaystyle\sum\nolimits_{{{t}} = 1}^N {({m_t} + f{p_t} + mm{e_t})} }}{{\displaystyle\sum\nolimits_{{{t}} = 0}^N {{g_t}} }} $

(11)

$ {\textit{MOTP}} = \frac{{\displaystyle\sum\nolimits_{t = 1}^N {{d_{i, t}}} }}{{\displaystyle\sum\nolimits_{{t}} {{c_t}} }} $

(12)

其中, $ {m_t} $, $ f{p_t} $, $ mm{e_t} $和$ {g_t} $依次为第t帧时目标漏检数、误检数、错误匹配目标数和总目标数. $ {d_{t, i}} $为第t帧目标i的质心和目标i匹配的预测质心之间的欧氏距离, $ {c_t} $为第t帧中的目标匹配数. 将本文数据代入式(11)与式(12), 以及算法耗时的对比, 将本文算法与文献[14]的进行对比, 得到数据如表4所示.

文献[14]与本文一样, 都是应用于大场景下的障碍物检测和跟踪算法, 该算法实验得到MOTA值略低, 但是MOTP值更高, 原因在于该算法采用了点云数据与RGB图像对齐的方法, 跟踪障碍物时的障碍物特征更加丰富, 因此跟踪效果较好, 但是也增大了算法计算压力. 本文算法最大的优势在于采用了高效的点云预处理算法和改进欧氏聚类算法, 极大地减少了障碍物漏检测和误检测的情况, 但是由于深度相机可获取的障碍物特征过于简单, 导致无法在多帧障碍物匹配阶段有更好的表现, 最终出现了部分的匹配错误的情况. 本文算法在运算耗时方面单帧处理时间最短, 可以满足了大部分的场景应用需求.

5 结论与展望

本文对障碍物点云数据进行检测与跟踪, 首先从深度相机的点云远处稀疏、深度方向检测不完全等问题入手, 对欧氏聚类进行针对性改进, 优化了欧氏聚类的过分割和欠分割的问题, 最后进行仿真实验对比证明了改进后的欧氏聚类比传统欧氏聚类有更好的检测表现. 在进行障碍物跟踪时采用了KM算法, 重点研究了传统欧氏聚类常用的AABB算法改进成OBB算法, 将障碍物的三自由度信息扩展到六自由度, 提高了障碍物的匹配准确率, 得到了动态障碍物准确的运动速度和运动轨迹. 最后实验证明, 本文提出的改进算法的障碍物检测准确率达到了95.2%, 多目标跟踪精度达到了13.2 mm, 在障碍物检测准确率方面有明显提升, 但是由于障碍物的特征获取方式限制, 多目标匹配存在一定的误差, 跟踪精度仍有提升的空间.