1 引言

随着油气开发持续推进, 常规油气藏逐渐减少, 非常规油气藏的开发日益重要. 在这种情况下, 传统的电缆测井技术已经不能完全满足油气开发的需求, 随钻测井技术逐步成为测井工程中一种重要方法^[1]. 随钻测井技术可以实时、准确地测量地层的电阻率特征^[2], 并且能够通过地质导向功能对钻进轨迹实时控制, 提高钻井效率和钻遇率^[3,4].

随钻电磁波电阻率测井技术是随钻测井技术的核心. 它可以在钻井的同时测得地层的视电阻率数据, 这些数据能够真实地反应地层的地质特征. 但是, 原始测量数据无法直接获得地层的电阻率以及仪器距离上下地层的距离^[5], 需要对原始数据进行反演处理才能得到这些信息. 准确、快速地反演随钻测井数据, 对于指导钻具在储层中准确移动, 并进一步提高油气采收率具有重要意义^[6,7].

常用的随钻测井资料反演方法为非线性迭代反演方法, 如高斯-牛顿法(Gauss-Newton)^[8]、阻尼最小二乘法(Levenberg-Marquarat)^[9,10]等. 杨震等^[11]使用拟牛顿法来进行随钻测井数据的研究, 并进行现场实验验证可行性; Wang等^[12]使用正则化的Levenberg-Marquarat最小化方法来进行随钻测井数据的反演. 迭代反演因需设置反演的初始模型与过多的迭代次数的原因, 会导致反演结果不稳定与计算效率低的问题^[13].

综合多种测井曲线进行解释是一个非线性问题, 而传统方法在处理多变量之间的非线性关系时存在一定的局限性. 深度学习在处理非线性数据问题上展示了其巨大的优势, 解决了传统方法依赖初始模型的弊端, 已经在地球物理反演和随钻测井数据反演方面得到了广泛的应用. 在地球物理反演方面: Moghadas^[14]提出一种基于卷积神经网络(CNN)的反演方法从电磁感应数据中估计地下电导率分层. Sun等^[15]开发了一种理论设计的递归神经网络(RNN)使用测量的地震数据进行地震全波形反演. Puzyrev^[16]提出了一种基于全卷积架构的深度神经网络反演方法, 使用全三维模拟的大型合成数据进行训练从而实现估计地下电阻率分布. 在随钻测井数据反演方面: Raj等^[17]将单层前馈神经网络应用在各向同性地层中的电阻率反演. Zhu等^[18]使用深度神经网络(DNN)进行各向异性的地层感应测井数据快速反演. Fan等^[19]使用双向长短期记忆神经网络进行随钻测井数据的三层参数反演. Shahriari等^[20,21]不仅使用DNN进行钻孔电阻率的反演, 还分析了神经网络中的误差控制和损失函数对于反演结果的影响.

随钻测井数据具有随井轨迹深度变化的趋势, 每个测量点数据之间存在前后关联, 具有序列数据的性质^[22], 能够采用深度学习方法中的循环神经网络(RNN)对其进行处理. 但传统RNN存在循环权矩阵的重复乘法操作, 会导致在训练过程中出现梯度消失和梯度爆炸问题. 为缓解这一现象, Hochreiter等^[23]和Chung等^[24]分别提出了长短期记忆神经网络(LSTM)与门控循环单元网络(GRU), 在一定程度上解决了梯度爆炸和梯度消失问题, 但是当此两种网络使用双曲正切函数(tanh)与Sigmoid函数时, 也会出现一定程度的梯度衰减. 为了应对上述现象, Li等^[25]提出了RNN的一种变体, 独立循环神经网络(independently recurrent neural network, IndRNN), 并且通过实验证明在各种任务上IndRNN均具有更好的性能. 但是, 对于不同的训练集和样本, IndRNN的各种参数, 如网络层数、隐藏层单元数以及批次大小会对预测性能产生很大影响.

针对随钻电阻率测井数据实时反演问题, 本文提出一种融合独立循环神经网络和粒子群优化算法(AP-IndRNN)的随钻测井数据实时反演方法. 首先对随钻测井数据进行最大最小值归一化操作, 并划分训练集与测试集; 然后构建IndRNN网络模型, 引入注意力机制关注对反演结果影响大的特征; 使用粒子群算法进行超参数优化, 不断更新粒子的速度与位置, 计算适应度值以更新粒子的个体最佳适应度与全局最佳适应度, 得出最佳超参数组合进行训练; 训练完成后使用测试集验证模型的准确率和可信性.

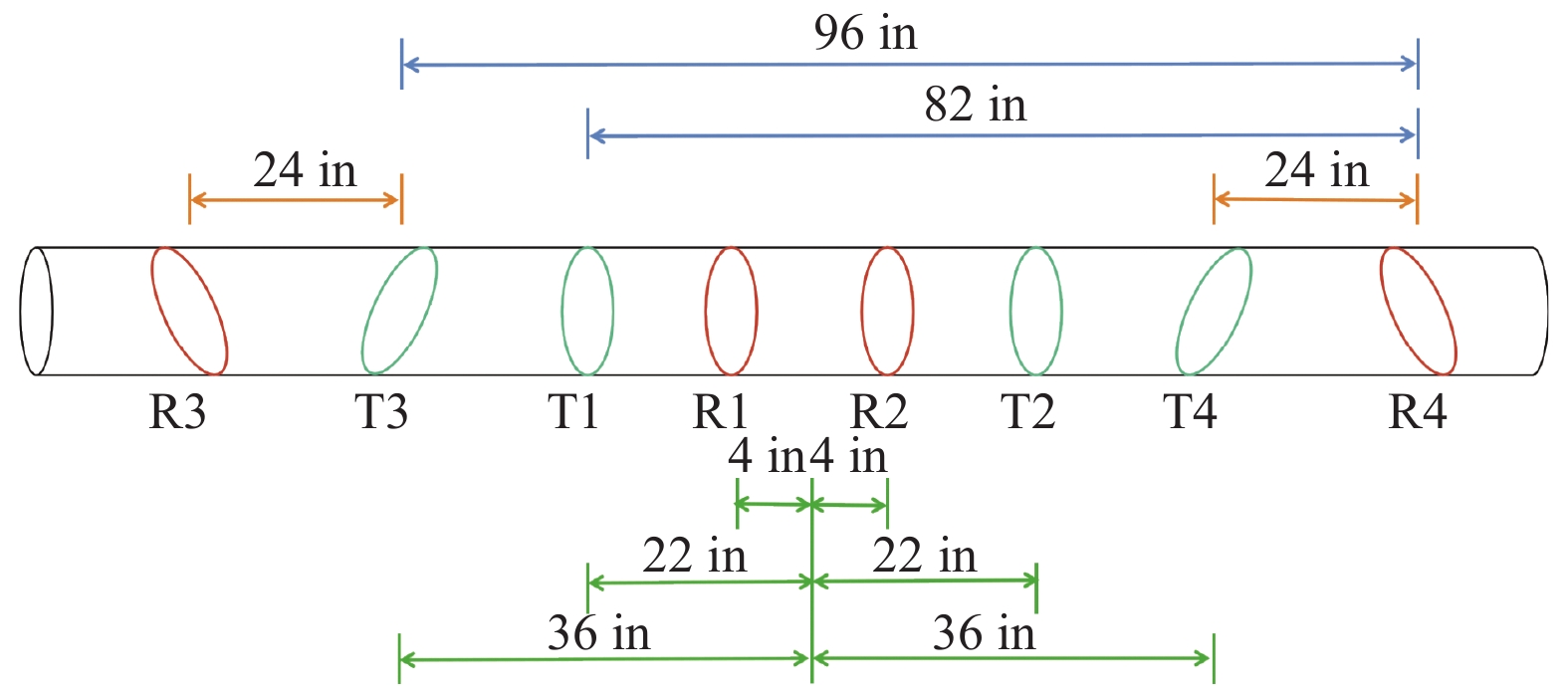
2 随钻电磁波电阻率测井仪器及其工作原理

新型随钻电磁波电阻率测井仪器(DWPR)^[26]采用倾斜发射—倾斜接受的双斜正交线圈系实现方位电磁信息测量, 仪器如图1所示. 图1中, T1–T4为发射线圈, R1–R4为接收线圈, 非法定计量单位1 in=2.54 cm.

DWPR测井仪器采用高(2 MHz)、中(400 kHz)、低频(100 kHz)这3种频率测量, 能同时对地层平均电阻率、方位电阻率、地质信号、各向异性信号以及成像测井信号进行测量. DWPR测井仪器可以提供9种不同探测深度(如22 in、36 in、60 in等)的相位差和幅度比电阻率、4种不同探测深度(如24 in、82 in等)的地质信号以及2种不同探测深度(24 in、96 in)的各向异性信号.

DWPR测井仪器工作原理为: 通过探头的发射线圈发射电磁波信号, 发射的信号在地下传播时, 地下岩石对发射的信号进行响应(反射与散射); 探头的接收线圈会接收地下岩石的相应信号, 根据接收到的信号的幅度比和相位差来计算地下岩层的电阻率; 然后对测得的电阻率数据进行滤波、降噪、解调和矫正等方式提取出地下岩石的准确电阻率信息; 结合地质背景和井孔岩心数据等信息, 进行地层解释和导向; 最后记录钻井过程中的电阻率数据和解释结果, 展示处理后的电阻率数据, 用于地质工作者的进一步研究和应用.

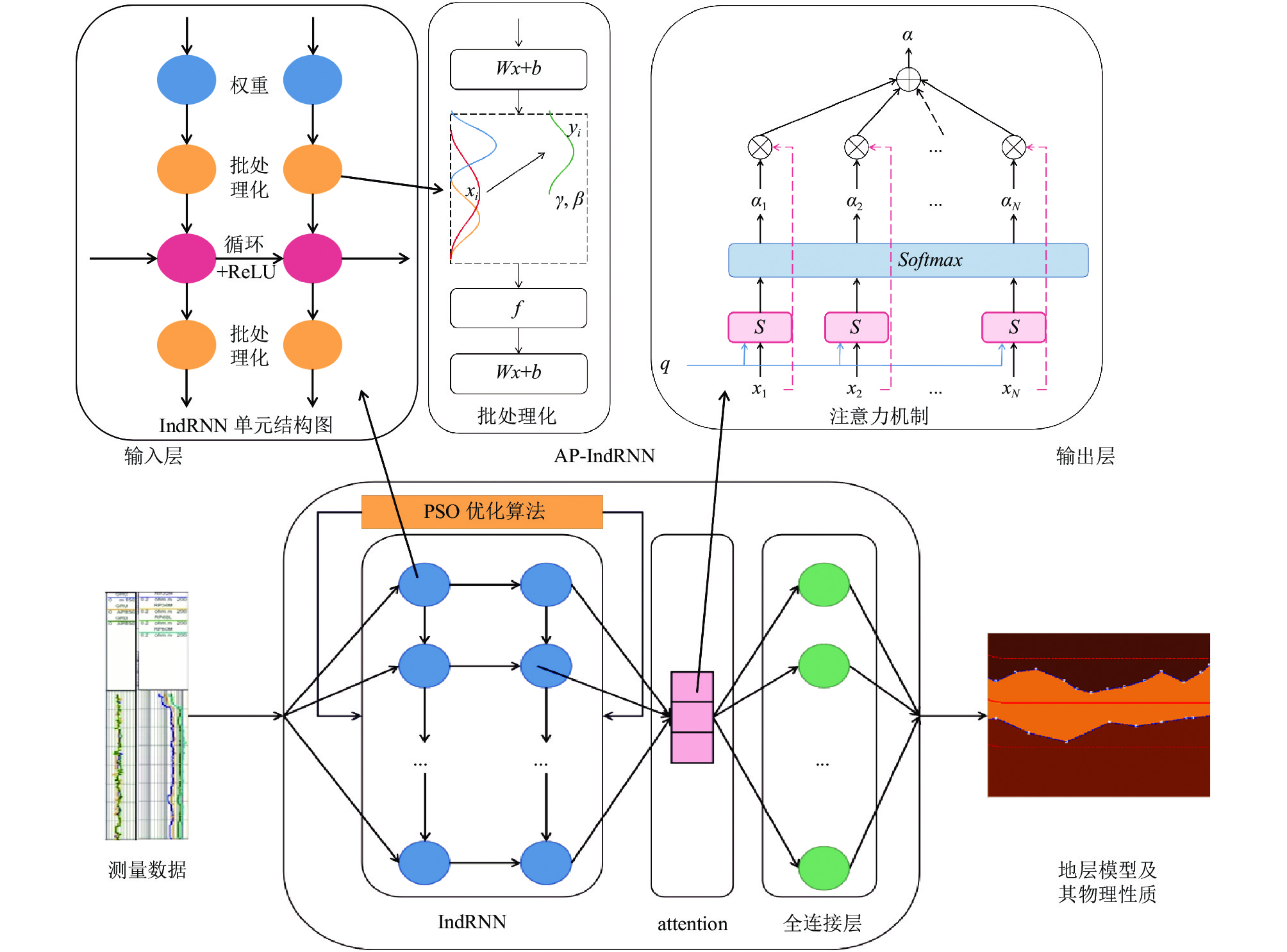
3 AP-IndRNN实时反演方法

在本节中, 介绍了AP-IndRNN反演DWPR测井数据的反演流程, 该流程如图2所示. 接着, 阐述了模型中各个方法的具体理论.

AP-IndRNN反演DWPR测井数据的具体流程如下: 将输入数据进行预处理(去掉异常值、最大最小值归一化操作等). 初始化PSO参数与IndRNN网络隐状态, 设定PSO需要优化的超参数、超参数搜索空间、适应度函数与随机权重更新公式. 通过搜索空间中的参数构建相应的IndRNN模型, PSO优化IndRNN超参数的流程图如图3所示. 将当前时间步的输入数据与前一个时间步的隐状态输入IndRNN, 更新当前时间步的隐状态, 通过当前时间步隐状态生成相应的输出, 重复数据传递、隐状态更新与生成输出的步骤, 直到处理完所有时间步. 将最后一个时间步的输出结果作为输入数据输入到注意力机制层, 将输入数据映射到适合注意力机制处理的特征空间, 进行得分函数的计算, 然后计算注意力权重, 最后进行加权平均并输出. 注意力机制层的输出数据作为全连接层的输入, 并与权重参数进行矩阵乘法运算, 使用非线性激活函数对运算后的结果进行处理, 经过处理后的结果作为全连接层的输出即为模型的输出. 计算粒子适应度, 更新粒子的速度与位置, 重复训练步骤, 达到PSO最大迭代次数后, PSO输出的组合即为IndRNN网络最优超参数组合. 根据最优超参数建立的IndRNN网络的输出结果最为模型的最终输出.

3.1 独立循环神经网络(IndRNN)

IndRNN采用哈达玛积代替了传统的矩阵乘法:

$ {h_t} = \sigma \left( {U \odot {h_{t - 1}} + W{x_t}} \right) $

(1)

其中, ${x_t}$为输入向量, ${h_t}$隐藏层向量, ${h_{t - 1}}$为上一时刻的隐藏层向量, $U$为输入层与隐藏层间的权重矩阵, $W$为隐藏层循环权重, $\sigma $表示激活函数, $ \odot $表示哈达玛积.

IndRNN中每一层的各个神经元之间是相互独立的, 神经元之间的连接可以通过堆叠2层或者多层IndRNN单元实现. 对于第n个神经元, 隐状态计算方式为:

$ {h_{n, t}} = \sigma ({U_n}{h_{n, t - 1}} + {W_n}{x_t}) $

(2)

其中, $ {W_n} $和${U_n}$分别表示第n个神经元的输入权重和隐藏权重.

在IndRNN中, 每一个神经元只接收此时输入的信息和自身上一时刻的隐藏信息, 独立地处理自身输出, 其结果不受上一时刻的其他神经元的影响, 可以构建更深的网络结构, 处理更长的序列. 采用ReLU非饱和函数进行训练, 网络具有更高的鲁棒性.

批处理化(batch normalization, BN)层能够缓解由于采用反向传播算法计算更新梯度而出现的梯度消失和梯度爆炸现象, 提升神经网络收敛速度, 提高稳定性, 解决了深层神经网络训练难的缺陷.

BN层首先对输入数据进行归一化处理:

$ \overset\frown{{x}_{{}_{i}}}=\frac{({x}_{i}-E(x))}{\sqrt{{\textit{Var}}(x)+\varepsilon }} $

(3)

其中, $E(x)$为某一批次的均值, ${\textit{Var}}(x)$为该批次的标准差, $\varepsilon $是极小的正数, 防止方差为0.

在深层神经网络中, BN层使得每一层网络的输出的每一维度特征均值为0, 标准差为$\varepsilon $, 降低了网络表达能力, 所以通过加入“比例及平移”操作来提高网络的表达能力, 即:

$ {y}_{i}=\gamma \overset\frown{{x}_{i}}+\beta $

(4)

其中, $\gamma $是用来调整数值分布的方差大小, $\;\beta $是用来调整数值均值的位置. 这两个参数通过网络训练过程学习得到, 可以使$ \overset\frown{{x}_{i}} $的分布向左或向右移动, 防止BN的“矫枉过正”. 特别地, 当$\gamma = \sqrt {\sigma _b^2 + \varepsilon } $ , $\;\beta = {u_b}$时, BN层的输出与原始输入相同.

3.2 注意力机制

注意力机制是一种模拟人类大脑注意力机制的模型, 借鉴了人类大脑在信息处理的过程中更加关注有用的信息, 忽略掉无关信息的原理. 在神经网络中, 当大量的输入信息输入到神经网络时, 不同的输入对输出值的影响是不同的. 为了提高神经网络的计算效率, 需要对重要的输入信息分配更多的计算能力.

注意力机制的计算主要包含以下步骤.

(1)计算注意力机制的得分函数:

$ s\left( {{x_i}, q} \right) = x_i^{\rm{T}}Wq $

(5)

其中, ${x_i}$为输入值, q为查询向量, s为注意力机制的得分函数, W为权重系数.

(2)使用Softmax函数进行归一化操作, 得到注意力分布${\alpha _i}$:

$ {\alpha _i} = \frac{{\exp (s({x_i}, q))}}{{\displaystyle\sum\limits_{i = 1}^n {\exp (s({x_i}, q))} }} $

(6)

(3) A为注意力分布式$\alpha_i$与输入值${x_i}$的加权平均:

$ A = \sum\limits_{i = 1}^n {{\alpha_i}{x_i}} $

(7)

3.3 粒子群优化算法(PSO)

粒子群优化算法(PSO)^[27]源于对鸟类捕食行为的研究, 通过模拟鸟类的觅食行为来实现信息共享, 从而在整个群体的觅食过程中获得群体合作的最佳结果. 它从随机解出发, 通过迭代寻找最优解, 期间由适应度函数评价解的品质, 通过追随当前搜索到的最优值来寻找全局最优.

在此算法中, 每个粒子由3个度量表征: 速度、位置和适应度值. 其中, 速度决定了粒子的下一次运动的方向和位移; 位置描述粒子的当前位置. 粒子群优化算法计算粒子适应度值, 并将其与粒子历史最佳适应度值p(i)和全局最佳适应度值g_best(i)进行比较. 在迭代过程中, 粒子的速度和位置不断更新, 以实现全局最优. 下为粒子的速度、位置更新与适应度函数公式:

$ v_{{i}}^{{{k + 1}}} = wv_i^k + {c_1}{r_1}(p_i^k - x_i^k) + {c_2}{r_2}(g_{{\rm{best}}}^k - x_i^k) $

(8)

$ x_i^{k + 1} = x_i^k + v_i^{k + 1} $

(9)

$ \varepsilon = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {{y_i} - {{\hat y}_i}} \right|} $

(10)

其中, $v_i^k$与$x_i^k$分别为粒子i在第k次迭代的速度与位置, ${c_1}$与${c_2}$为加速系数, ${r_1}$与${r_2}$为(0, 1)区间的两个随机数, $p_i^k$与$g_{{\rm{best}}}^k$分别为粒子i在迭代过程中所取得的个体最佳适应度值与全局最佳适应度值, ${y_i}$与${{{\hat y}}_i}$分别为样本的真实值与预测值, n表示样本的数量, w为惯性权重, 采用随机权重, 其更新公式为:

$ w = {u_{\min }} + ({u_{\max }} - {u_{\min }})rand(0, 1) + \sigma N(0, 1) $

(11)

其中, ${u_{\min }}$是随机惯性权重的最小值, $ {u_{\max }} $是随机惯性权重的最大值, rand()为[0, 1]均匀分布的随机数.

采用随机惯性权重可以解决迭代前期局部搜索能力差及迭代后期全局搜索能力不足的问题.

4 实验 4.1 数据集与评价指标 4.1.1 数据集

数据集包括正演模拟数据集与实际测井数据集.

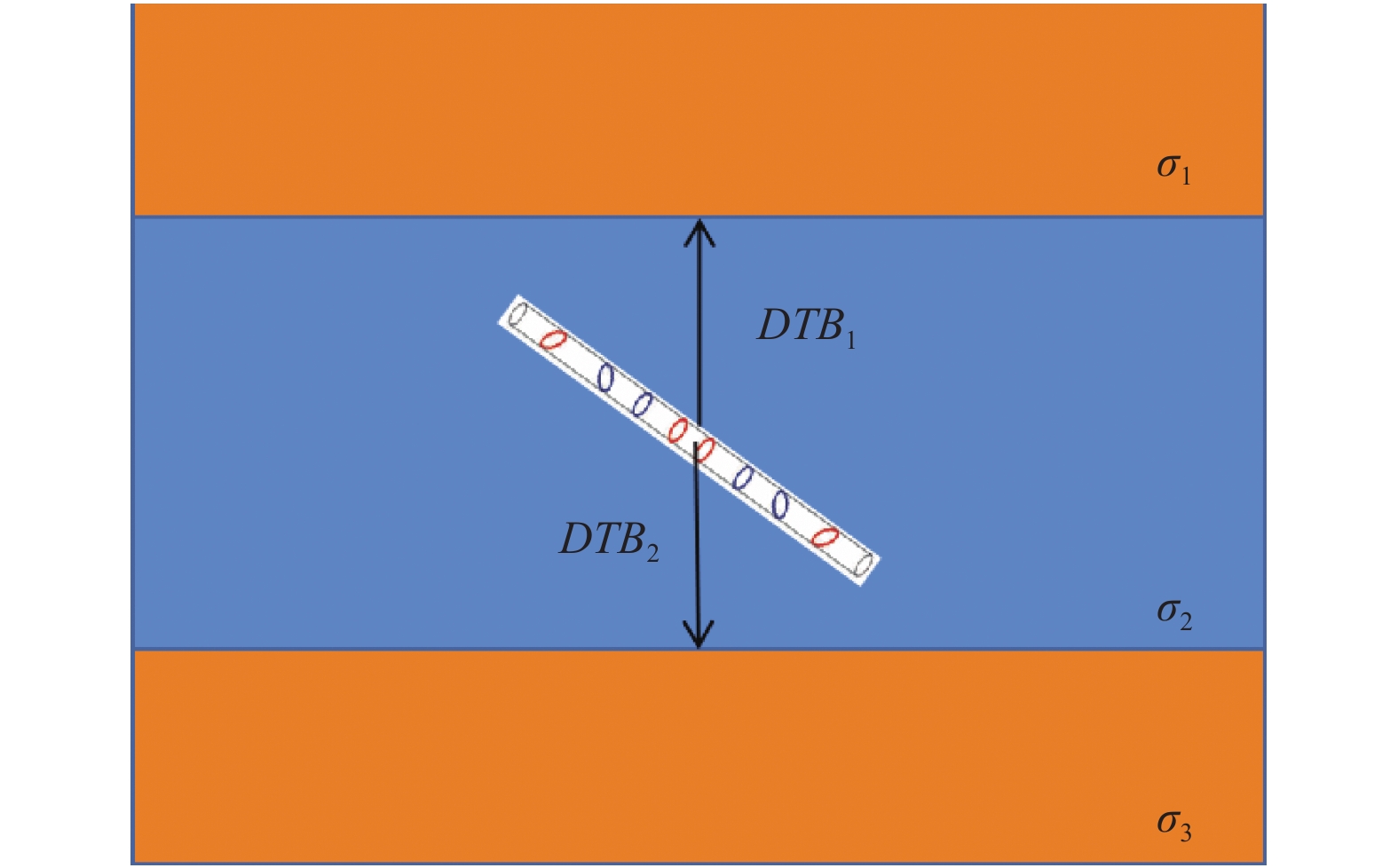
正演模拟数据是通过设定好的地层模型, 并根据DWPR测井仪器的特性, 采用正演模拟方式生成的. 为了获得正演模拟数据, 需要预先设置地层模型. 地层模型为如图4所示的3层地层模型, 图中${\sigma _1}$、$ {\sigma _2} $、${\sigma _3}$所代表的为地层上、中、下电阻率, ${{\textit{DTB}}_1}$、${{\textit{DTB}}_2}$为仪器距离上、下边界的距离. 地层模型是在一定范围内根据仪器性质确定的, 地层最大厚度为15 m, 间隔为0.1 m, 上下电阻率范围为1–5 Ω, 中层电阻率范围为0–50 Ω, 间隔为0.5 Ω.

按照地层模型的范围选择不同的地层厚度和电阻率组合成地层模型后, 通过正演模拟产生的含有不同源距与频率的电阻率和地质信号参数, 最终形成随钻电磁波电阻率测井正演模拟数据. 其中, 电阻率参数反映地层电性特征^[26], 地质信号参数反映地层边界位置与方位信息^[26]. 将此数据集按照7:3划分训练集与测试集.

实际测井数据集是利用DWPR测井仪器对某油田单井的1931–2132 m井段进行测量所得到的数据. 其中, 电阻率与地质信号数据均为实际测井工程中的测量数据, 地层最大厚度为12 m, 中层电阻率范围为14–34 Ω之间. 正演模拟数据集与实际测井数据集所含信息如表1所示.

4.1.2 评价指标

为了评估模型的预测精度, 选用均方根误差(RMSE), 拟合度(${r^2}$)对模型进行评价, 其计算公式如下:

$ {\textit{RMSE}} = \frac{{\sqrt {\displaystyle\sum\limits_{i = 1}^n {{{({X_i} - X'_i)}^2}} } }}{{\sqrt n }} $

(12)

$ {r^2} = \frac{{\displaystyle\sum\limits_{i = 1}^n {{{({X_i} - X'_i)}^2}} }}{{\displaystyle\sum\limits_{i = 1}^n {{{({X_i} - \bar X)}^2}} }} $

(13)

其中, ${X_i}$ 与$X'_i$ 分别表示第i个输出的真实值与模型预测值, $\bar X$ 表示真实值的平均值.

4.2 网络及实验参数设置

本实验程序使用Python编写, 基于TensorFlow框架来搭建模型, 使用“ReLU”函数作为激活函数, 优化算法为Adam算法. 然后使用粒子群算法对IndRNN网络的4个超参数进行寻优, 分别为: 隐藏层层数、隐藏层单元数、批次大小、学习率, IndRNN超参数的优化范围就是PSO的搜索空间, 如表2所示, PSO的参数设置如表3所示.

通过PSO算法计算得出IndRNN最佳超参数组合为{7, 128, 32, 0.001}, 即网络层数为7, 隐藏层单元数为128, 批次大小为32, 学习率为0.001.

4.3 实验结果分析 4.3.1 正演模拟数据消融实验与结果分析

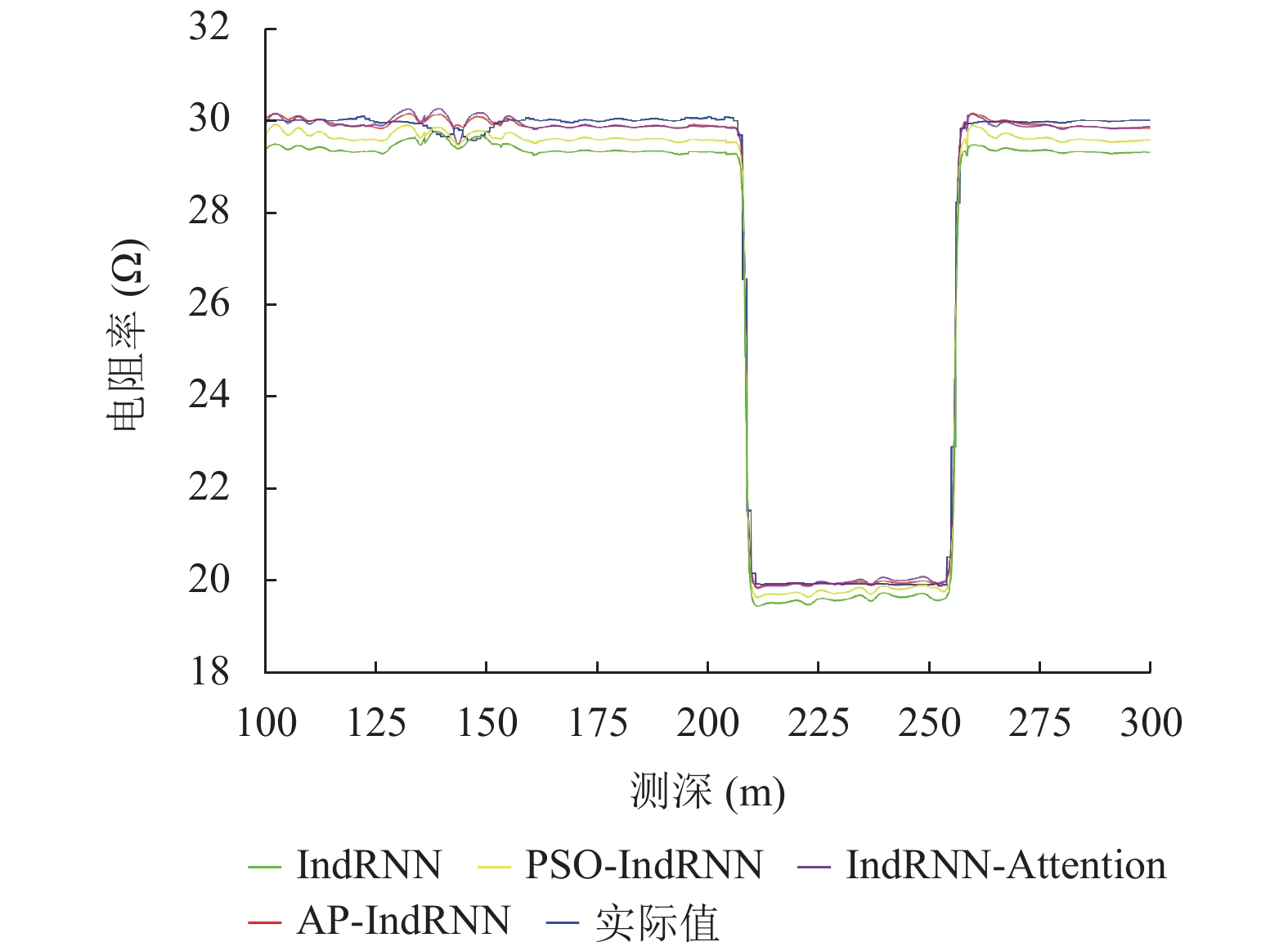
为了验证PSO与Attention的有效性, 使用正演模拟数据测试集进行消融实验, 实验结果如图5, 图6所示, 评价指标计算结果如表4所示.

通过图5、图6与表4的分析可得: 在随钻测井资料正演模拟数据反演方面. 在两种不同的指标下, 在仪器距离上下界面与目标地层电阻率反演方面, AP-IndRNN的RMSE最小, ${r^2}$最高, 预测性能最好. 与IndRNN、PSO-IndRNN以及IndRNN-Attention相比, 在仪器距离上界面的反演结果上, RMSE分别降低了0.366、0.187、0.105. 在仪器距离下界面的反演结果上, RMSE分别降低了0.254、0.16、0.064. 在目标地层电阻率的反演结果上, RMSE分别降低了0.363、0.15、0.017. 实验结果证明: PSO与Attention对于提高IndRNN网络的预测精度有积极作用.

4.3.2 正演模拟数据对比实验与结果分析

为了验证本文方法的有效性, 分别采用LSTM、BiLSTM、GRU、AP-IndRNN这4种反演方法对正演模拟数据测试集进行反演. 将不同方案得到的反演结果与实际值进行对比来评估预测结果的可靠性. 各个模型反演结果如图7, 图8所示, 评价指标计算结果如表5所示.

通过图7、图8与表5的分析可得: 在随钻测井资料正演模拟数据反演方面, AP-IndRNN相较于LSTM、BiLSTM、GRU模型在仪器距离上界面的反演结果上, RMSE分别降低了0.28、0.239、0.407. 在仪器距离下界面的反演结果上, RMSE分别降低了0.102、0.283、0.354. 在目标地层电阻率的反演结果上, RMSE分别降低了0.232、0.226、0.396. 实验结果证明, 与其他方法相比, 在模拟数据反演方面, AP-IndRNN展现出更高的稳定性与准确性, 能够提供更可靠和精确的随钻测井数据反演结果. 这意味着使用AP-IndRNN进行随钻测井数据的反演工作是可行的.

4.3.3 实际测井数据消融实验与结果分析

为了验证PSO与Attention在实际过程中的性能与泛化性, 选取某油田单井的1931–2132 m的测井数据进行消融实验, 实验结果如图9, 图10所示, 评价指标计算结果如表6所示.

通过图9、图10与表6的结果可得: 在随钻测井资料实际数据反演方面, 虽然实际数据的反演结果相较于正演模拟数据的结果均有所下降. 但AP-IndRNN的反演结果能够较好地预测出仪器距离上下界面距离与电阻率的整体趋势变化, 基本能够与地层情况符合, 整体误差最小. 实验结果证明, PSO与Attention可以提升IndRNN网络在实际数据反演中的性能. 这种改进验证了AP-IndRNN在处理实际数据时的鲁棒性.

4.3.4 实际测井数据对比实验与结果分析

为了检验本文模型在实际工程中的性能与泛化性选取某油田单井的1931–2132 m的测井数据进行实际应用, 反演结果如图11、图12所示, 评价指标计算结果如表7所示.

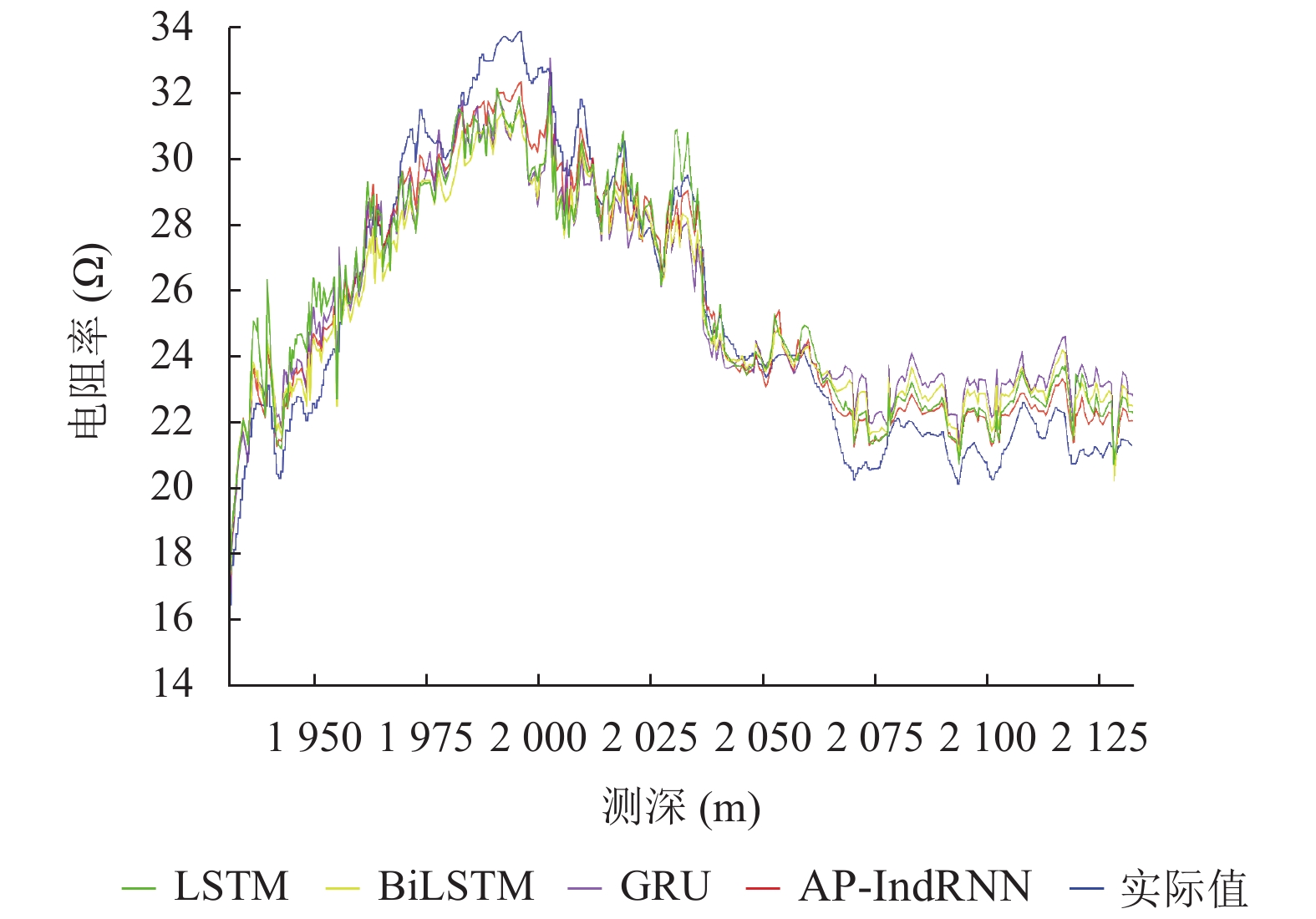
通过图11、图12与表7的结果可得: 在随钻测井资料实际数据反演方面, AP-IndRNN相较于LSTM、BiLSTM、GRU模型在仪器上界面距离反演结果上, RMSE分别降低了0.22、0.271、0.277, ${r^2}$分别上升了0.169、0.158、0.173. 在仪器下界面距离反演结果上, RMSE分别降低了0.141、0.237、0.257, ${r^2}$分别上升了0.101、0.152、0.158. 在目标地层电阻率反演结果上, RMSE分别降低了0.475、0.491、0.62, ${r^2}$分别上升了0.056、0.059、0.079. 实验结果证明, 尽管在实际数据上各个模型的预测准确性均有所下降, 但是与其他方法相比, AP-IndRNN仍表现出较低的误差和较高的准确性. 此外, AP-IndRNN的单点反演时间为0.04 s. 这意味着AP-IndRNN在实际测井数据反演工作中具有适用性与优越性, 使其成为可靠的选择用于随钻测井数据的反演工作.

5 结论

针对目前随钻电阻率测井资料反演问题, 本文提出一种融合独立循环神经网络和粒子群优化算法的随钻测井数据实时反演方法, 解决了迭代反演算法依赖初始模型导致其反演结果不确定与计算效率低的问题. IndRNN模型对于序列数据具有较强的建模和分析能力; 引入注意力机制对输出结果影响大的特征分配更大的权重, 来提高反演精度; 使用粒子群算法对IndRNN网络的隐藏层层数、隐藏层单元数、批次大小、学习率进行优化, 克服了人工确定IndRNN网络参数的缺点. 正演模拟数据与实际测井数据的消融实验与对比实验结果表明, PSO与Attention可以有效提高IndRNN网络的预测精度, 同时AP-IndRNN相较于LSTM、BiLSTM、GRU网络均有更好的性能, 能够满足随钻测井数据实时反演的需求.