在信息爆炸的数字经济时代, 推荐系统在缓解信息过载方面正发挥着越来越重要的作用^[1]. 其能够为用户呈现个性化信息, 帮助用户做出更有效的选择和决策, 从而提升用户体验. 大多数推荐方法假设用户信息及其长期历史交互可以获取^[2], 然而在许多实际场景中, 比如线上购物平台或流媒体平台在用户未登入的情况下是无法获取用户信息及其长期历史交互的, 而只能利用匿名用户的短期会话数据. 在此情形下, 这些推荐方法表现不是非常理想. 因此, 基于会话的推荐受到了研究者们的广泛关注, 其旨在研究如何根据匿名用户的短期会话数据预测用户下一次交互项目^[3].

基于会话的推荐早期使用马尔可夫链从会话数据中挖掘时序信息^[4]. 随着深度学习成为主流建模技术, 循环神经网络(recurrent neural network, RNN)被用于对序列数据模式进行建模并成为会话推荐的主流方法^[5]. 近期, 图神经网络(graph neural network, GNN)由于出色的建模复杂项目转换的能力而被引入会话推荐中, 并取得了比基于RNN的会话推荐模型更好的推荐性能^[6]. 虽然现有图神经网络模型取得了不错的推荐效果, 但仍然存在不足: ① 在聚合邻居节点嵌入用于更新中心节点嵌入的信息传播过程中, 这些模型给予所有邻居节点相同权重而没有区分它们对于中心节点的重要性, 从而给模型训练引入噪声. 例如, 假设中心节点Airpods有iPhone、iPad以及衣服3个邻居节点. 这些模型在更新Airpods嵌入的过程中, 给予3个邻居节点相同权重. 但实际上用户的偏好在于电子产品, iPhone、iPad与Airpods关联度较高, 应给予较大权重. 而衣服可能是用户误点击形成的噪声, 权重应该较小. ② 虽然这些模型都通过堆叠多层图神经网络获取高阶邻居信息, 但他们忽略了因此产生的过度平滑问题, 即随着网络层数的增加, 节点嵌入会趋向于类似变得难以区分.

为了解决上述问题, 文中提出结合跳跃连接的多层图注意力网络会话推荐模型(multi-layer graph attention network with skip connection for session-based recommendation, MGATSC). 首先利用图注意力网络(graph attention network, GAT)在信息传播过程中学习邻居节点对于中心节点的重要性以减少噪声引入, 并通过堆叠多层网络获取高阶邻居信息. 其次为了缓解过度平滑问题, 使用基于残差注意力机制的跳跃连接更新每层网络的节点嵌入以更好地保留节点的低阶与高阶信息, 并通过平均池化得到最终节点嵌入. 最后融合节点嵌入与反向位置嵌入, 经过预测层生成推荐列表.

本文的主要贡献如下.

(1) 利用图注意力网络为不同邻居节点分配不同权重以减少噪声对模型的影响.

(2) 通过基于残差注意力机制的跳跃连接更好地保留节点的低阶与高阶信息, 以缓解网络层数增加引起的过度平滑问题.

(3) 在Tmall、Diginetica与Retailrocket这3个公开数据集上进行实验, 结果表明所提模型优于所有基线模型, 验证了本模型的有效性和合理性.

1 研究进展 1.1 传统会话推荐

早期的会话推荐利用马尔可夫链从会话数据中获取时序信息. 马尔可夫链假设用户基于前一次交互做出下一次交互, 但这种假设可能会限制推荐的准确性^[7]. Zimdars等人^[8]研究了基于马尔可夫链的时序数据顺序, 并使用概率决策树建模项目间转换模式. Shani等人^[9]利用马尔科夫决策过程(Markov decision process, MDP)对项目之间的转换概率进行建模. Rendle等人^[10]提出FPMC模型, 通过基于矩阵分解和一阶马尔可夫链相结合的混合方法获取顺序模式和长期用户偏好以进行推荐. 虽然基于马尔可夫链的方法较为简单高效, 但其仅对两个相邻项目间的顺序转换进行建模, 模型推荐性能表现仍然欠足.

1.2 基于循环神经网络的会话推荐

随着深度学习的发展, 循环神经网络凭借其出色的建模序列数据的能力成为会话推荐的主流方法, 并在会话推荐场景中取得优异效果^[11]. 但当顺序转换不是影响用户偏好的唯一因素时, 基于RNN的会话推荐模型就不能有效捕捉用户偏好. Hidasi等人^[12]提出的GRU4Rec是第1个采用RNN对会话进行建模的模型. 该模型引入考虑项目顺序的排名损失函数以及同时考虑多个会话的并行小批量训练, 从而提升推荐准确性. Tan等人^[13]通过序列预处理以及嵌入丢弃策略实现数据增强, 从而防止过拟合并进一步提升基于RNN模型的性能. Li等人^[14]提出的NARM模型使用了一种基于注意力机制的混合编码器对用户的顺序行为进行建模以及捕捉当前会话中用户的主要偏好. 并且使用双线性匹配方案计算每个候选项目的推荐得分. Liu等人^[15]提出的STAMP模型利用注意力机制分别从当前会话的长期记忆和短期记忆中获取长期偏好和短期偏好. 然而与基于马尔可夫链的方法类似, 这些基于RNN的模型侧重于建模相邻项目间的顺序转换, 而不擅长捕捉复杂的项目转换模式.

1.3 基于图神经网络的会话推荐

最近, 图神经网络在建模复杂的项目转换模式方面展现出前所未有的高效性. 具体说, 图神经网络能够迭代聚合邻居节点的特征信息并在信息传播过程中将聚合信息与当前的中心节点嵌入相结合, 从而增强中心节点嵌入^[16]. 由于会话可以表示成图结构, 基于GNN的会话推荐模型不断涌现. Wu等人^[17]提出SR-GNN模型, 使用门控图神经网络(gated graph neural network, GGNN)传播会话图中的信息以学习项目嵌入. 然后根据每个项目和最后一个项目的相关性计算注意力权重, 并将每个学习到的项目嵌入与注意力权重相结合获得具有代表性的会话嵌入. 随着SR-GNN模型取得成功, 一些变体也被提出用于会话推荐, 例如GC-SAN^[18]模型. 其动态构建会话图, 并使用自注意力网络通过图信息聚合捕捉会话图中项目之间的依赖关系. Yu等人^[19]提出TA-GNN模型, 通过考虑给定目标项目的历史行为相关性自适应激活用户偏好, 从而进一步改善会话嵌入. 但这些模型在信息传播过程中并没有区分邻居的重要性, 而是给予它们相同权重. 同时也没有考虑堆叠多层网络所引起的过度平滑问题. Qiu等人^[20]提出FGNN模型, 采用多头注意力机制学习项目嵌入以捕捉项目转换模式的内在顺序, 并使用读取函数聚合学习到的项目嵌入生成最终的会话嵌入. Wang等人^[21]提出的GCE-GNN模型利用了来自其他会话的信息, 通过构建会话图和全局图以分别获取项目的会话级和全局级嵌入, 并使用软注意力机制聚合这两种级别的项目嵌入. 虽然它们取得了不错的推荐性能, 但过度平滑问题对模型产生了负面影响, 模型性能还有待改进提升.

2 结合跳跃连接的多层图注意力网络会话推荐模型

先前的图神经网络会话推荐模型大多在信息传播过程中赋予邻居节点相同权重而没有区分它们的重要性, 此外在网络层数增加所引发的过度平滑问题方面有待改进提升. 为了缓解这两个问题, 文中提出MGATSC模型. 其框架如图1所示. 该模型利用图注意力网络区分邻居节点的贡献, 并使用基于残差注意力机制的跳跃连接缓解多层网络堆叠引发的过度平滑问题, 从而提升模型性能. MGATSC模型主要分为会话图构建、项目嵌入学习、会话嵌入学习以及预测层4个部分. 本节首先对会话推荐任务以及相关符号进行定义, 然后再分别介绍模型的4个部分.

2.1 任务描述

令$ V = \{ {v_1}, {v_2}, \cdots, {v_n}\} $代表所有会话中不重复项目的集合, $ n $代表项目数量. 每个会话表示成序列$ s = \{ {v_1}, {v_2}, {v_3}, \cdots, {v_m}\} $, 由按交互时间排序的一系列项目组成. ${v_k} \in V \; (1 \leqslant k \leqslant m)$代表会话$s$中匿名用户的第$k$个交互项目, $m$代表会话长度. 将项目${v_i} \in V$嵌入到$d$维向量空间中并用$ {\boldsymbol{h}}_i^{(l)} \in {\mathbb{R}^d} $代表${v_i}$在第$l$层网络的嵌入, 其中${\boldsymbol{h}}_i^{(0)}$代表项目${v_i}$的随机初始化嵌入. 会话推荐的任务是根据会话$s$预测匿名用户下一次交互项目${v_{m + 1}}$. 会话序列$s$作为模型的输入, 输出为一个概率列表$\hat{y} = [{\hat{y} _1}, {\hat{y} _2}, {\hat{y} _3}, \cdots, {\hat{y} _n}]$. ${\hat{y} _i} \; (1 \leqslant i \leqslant n)$表示用户下一次与项目${v_i}$交互的概率. 模型最终选取交互概率最高的$K \; (1 \leqslant K \leqslant n)$个项目推荐给用户.

2.2 会话图构建

将会话序列构建成会话图的目的是通过图神经网络处理会话, 从而对会话中包含的复杂项目转换模式进行建模. 参照文献[21], 本文将会话序列$s$构建成有向图$ {G_s} = ({V_s}, {E_s}) $, ${V_s} \subseteq V$表示会话$s$中不重复交互项目的集合, ${E_s}$代表会话图中边的集合, 边$({v_i}, {v_j}) \in {E_s}$表示用户先后与项目$ {v_i}, {v_j} $进行交互. 在实际场景中由于匿名用户可能多次点击同一个项目, 所以会话图中的节点均添加了自循环边.

会话图中存在4种类型的边, 分别对应于项目${v_i}$与${v_j}$的4种不同的连接关系, 即${r_{{\rm{in}}}}$, ${r_{{\rm{out}}}}$, ${r_{{\text{in-out}}}}$以及${r_{{\rm{self}}}}$. 对于边$ ({v_i}, {v_j}) $, ${r_{{\rm{in}}}}$为${v_j}$指向${v_i}$的有向边, ${r_{{\rm{out}}}}$为${v_i}$指向${v_j}$的有向边, ${r_{{\text{in-out}}}}$为${v_i}$与${v_j}$的双向边, ${r_{{\rm{self}}}}$为自循环边. 以会话$s = [{v_1}, {v_4}, {v_3}, {v_4}, {v_2}]$为例, 会话图如图2所示.

2.3 项目嵌入学习 2.3.1 多层图注意力网络

由于邻居节点具有不同的重要性, 因此在构建会话图之后, 文中利用图注意力网络学习会话图中的节点嵌入. 图注意力网络假设邻居节点对于中心节点的重要性既不相同, 也不由图结构预先确定^[22]. 因此将注意力机制引入图神经网络中以区分邻居节点的贡献, 并通过聚合邻居信息更新中心节点嵌入从而实现节点间的信息传播. 图3展示了一个双层图注意力网络如何通过信息传播计算图2中节点${v_2}$的最终嵌入${\boldsymbol{h}}_2^{(2)}$. 嵌入${\boldsymbol{h}}_2^{(2)}$的计算基于节点${v_2}$的所有一阶与二阶邻居. 节点${v_2}$的一阶邻居为${v_4}$及其${v_2}$本身, 二阶邻居为${v_4}$的一阶邻居$({v_1}, {v_2}, {v_3}, {v_4})$与${v_2}$的一阶邻居$ ({v_2}, {v_4}) $.

对于信息传播的实现过程, 首先利用注意力机制计算当前会话$s$中每个项目${v_i}$的邻居的重要性:

$ {e_{ij}} = LeakyReLU\left( {{\boldsymbol{a}}_{{r_{ij}}}^{\rm{T}}\left( {{\boldsymbol{h}}_i^{(l - 1)} \odot {\boldsymbol{h}}_j^{(l - 1)}} \right)} \right) $

(1)

其中, ${e_{ij}}$表示邻居项目${v_j}$对于中心节点${v_i}$的重要性并选择$LeakyReLU$作为激活函数, ${\boldsymbol{h}}_i^{(l - 1)}$为项目${v_i}$在第$l - 1$层网络的嵌入, ${r_{ij}}$表示${v_i}$与${v_j}$的连接关系. ${{\boldsymbol{a}}_*} \in {\mathbb{R}^d}$为可学习的权重向量. 针对4种不同的连接关系, 训练4种不同的权重向量, 即${{\boldsymbol{a}}_{{\rm{in}}}}, {{\boldsymbol{a}}_{{\rm{out}}}}, {{\boldsymbol{a}}_{{\text{in-out}}}}, {{\boldsymbol{a}}_{{\rm{self}}}}$. 接着, 为便于对比不同项目间的注意力权重, 使用${\textit{Softmax}}$函数对${e_{ij}}$做归一化处理:

$ {\alpha _{ij}} = \frac{{{\rm{exp}}\left(LeakyReLU\left({\boldsymbol{a}}_{{r_{ij}}}^{\rm{T}}\left({\boldsymbol{h}}_i^{(l - 1)} \odot {\boldsymbol{h}}_j^{(l - 1)}\right)\right)\right)}}{{\displaystyle\sum\nolimits_{{v_k} \in {N_{{v_i}}}} {{\rm{exp}}\left(LeakyReLU\left({\boldsymbol{a}}_{{r_{ik}}}^{\rm{T}}\left({\boldsymbol{h}}_i^{(l - 1)} \odot {\boldsymbol{h}}_k^{(l - 1)}\right)\right)\right)} }} $

(2)

其中, 注意力系数${\alpha _{ij}}$是不对称的, 因为项目${v_i}$与${v_j}$具有不同的邻居, 所以它们对彼此的贡献是不同的. ${N_{{v_i}}}$表示项目${v_i}$的一阶邻居(因为节点有自循环边, 所以一阶邻居包含${v_i}$自身). 最后, 通过加权聚合${v_i}$本身及其所有一阶邻居${v_j} \in {N_{{v_i}}}$的嵌入得到项目${v_i}$在第$l$层网络的嵌入${\boldsymbol{h}}_i^{(l)}$, 其包含自身及其邻居项目的特征信息:

$ {\boldsymbol{h}}_i^{(l)} = \sum\limits_{{v_j} \in {N_{{v_i}}}} {{\alpha _{ij}}{\boldsymbol{h}}_{_j}^{(l - 1)}} $

(3)

上述方法自适应地为邻居项目分配合适的权重, 能够在信息传播过程中减少噪声的引入. 同时通过堆叠多层网络, 帮助每个节点获取到更高阶邻居的信息而不是像传统方法那样只能获取一阶邻居的信息, 使得模型能够更高效地对会话图中复杂的项目转换模式进行建模.

2.3.2 跳跃连接

通过堆叠多层网络, 每个节点都能获取到高阶邻居信息, 帮助模型更好地建模高阶图结构. 然而堆叠层数太多会使节点嵌入变得过度平滑, 不同节点会具有相似的嵌入, 导致性能下降. 为了缓解这个问题, 模型利用基于残差注意力机制的跳跃连接将$l$层与上一层的节点嵌入进行加权聚合以更新$l$层的节点嵌入. 由此, 节点可以更好地保留低阶与高阶信息. 对于会话$s$中的任意项目${v_i}$, 其$l$层嵌入${\boldsymbol{h}}_i^{(l)}$的更新过程如下:

$ {\beta _i} = {{\boldsymbol{W}}_1}(\sigma ({{\boldsymbol{W}}_2}{\boldsymbol{h}}_i^{(l - 1)} + {{\boldsymbol{W}}_3}{\boldsymbol{h}}_i^{(l)})) $

(4)

$ {\boldsymbol{h}}_i^{(l)} = {\beta _i}{\boldsymbol{h}}_i^{(l - 1)} + (1 - {\beta _i}){\boldsymbol{h}}_i^{(l)} $

(5)

其中, $ {{\boldsymbol{W}}}_{1}\in {\mathbb{R}}^{d}、{{\boldsymbol{W}}}_{2}, {{\boldsymbol{W}}}_{3}\in {\mathbb{R}}^{d\times d} $为可训练参数, $\sigma $为Sigmoid激活函数. 最后, 通过对项目${v_i}$在每一层网络的嵌入进行平均池化得到${v_i}$的最终嵌入${{\boldsymbol{h}}_i}$:

$ {{\boldsymbol{h}}_i} = \frac{1}{{L + 1}}\sum\nolimits_{l = 0}^L {{\boldsymbol{h}}_i^{(l)}} $

(6)

其中, $L$为图神经网络的堆叠层数.

2.4 会话嵌入学习

基于学习到的项目嵌入, 接下去介绍如何获得会话$s$的嵌入. 对于会话$s$, 不同位置的项目对下一次预测的贡献是不同的. 一般而言, 会话中位置越靠后的项目越能代表用户当前偏好, 即它们对于推荐的重要性更大. 虽然多层神经网络使模型能够获取会话图的高阶结构信息, 但无法对项目的位置信息进行编码. 位置嵌入是Transformer^[23]中引入的一项有效技术, 能够记忆项目位置信息. 因此, 通过可学习的位置矩阵${\boldsymbol{P}} = [{{\boldsymbol{p}}_1}, {{\boldsymbol{p}}_2}, {{\boldsymbol{p}}_3}, \cdots , {{\boldsymbol{p}}_m}]$将反向位置嵌入与学习到的项目嵌入相结合:

$ {{\textit{z}}_i} = {{\boldsymbol{h}}_i} + {{\boldsymbol{p}}_{m - i + 1}} $

(7)

其中, ${{\textit{z}}_i} \in {\mathbb{R}^d}$为融合了位置信息的项目${v_i}$的嵌入, ${{\boldsymbol{p}}_i} \in {\mathbb{R}^d}$代表位置$i$的嵌入, $m$代表当前会话$s$的长度.

会话嵌入通过聚合会话$s$中所有项目的嵌入获得. 由于不同项目具有不同优先级, 因此使用软注意力机制计算会话$s$的嵌入, 并应用dropout技术^[24]防止模型过拟合:

$ {\mu _i} = {{\boldsymbol{q}}^{\rm{T}}}\sigma ({{\boldsymbol{W}}_4}{{\textit{z}}_i} + {{\boldsymbol{W}}_5}{{\boldsymbol{h}}_s} + {\boldsymbol{b}}) $

(8)

$ {\boldsymbol{S}} = \sum\limits_{i = 1}^m {{\mu _i}{{\textit{z}}_i}} $

(9)

$ {\boldsymbol{S}} = {\textit{dropout}}({\boldsymbol{S}})$

(10)

其中, $ {\boldsymbol{q}}, {\boldsymbol{b}}\in {\mathbb{R}}^{d}、{{\boldsymbol{W}}}_{4}, {{\boldsymbol{W}}}_{5}\in {\mathbb{R}}^{d\times d} $用于学习项目权重$ {\mu _i} $的可训练参数. $ {{\boldsymbol{h}}_s} \in {\mathbb{R}^d} $通过平均会话$s$中所有项目的嵌入得到, 即:

$ {{\boldsymbol{h}}_s} = \frac{1}{m}\sum\limits_{i = 1}^m {{{\boldsymbol{h}}_i}} $

(11)

会话嵌入${\boldsymbol{S}}$由当前会话$s$中的所有项目构建而成, 其中每个项目的贡献不仅取决于会话图中的信息, 而且还由其在会话中的位置确定.

2.5 预测层

在获得会话嵌入${\boldsymbol{S}}$后, 将其与候选项目${v_i} \in V$的初始嵌入${\boldsymbol{h}}_i^{(0)}$做点积, 得到${v_i}$的推荐分数, 并对其应用${\textit{Softmax}}$函数:

$ {\hat y_i} = {\textit{Softmax}}({{\boldsymbol{S}}^{\rm{T}}}{\boldsymbol{h}}_i^{(0)}) $

(12)

其中, ${\hat{y} _i}$表示用户下一次交互的项目是${v_i}$的概率. 损失函数定义为预测值与真实值的交叉熵函数:

$ L = - \sum\limits_{i = 1}^n {{y_i}\log \left( {{{\hat y}_i}} \right) + \left( {1 - {y_i}} \right)\log \left( {1 - {{\hat y}_i}} \right)} $

(13)

图4展示了MGATSC模型分别在Tmall、Diginetica和Retailrocket这3个数据集上进行训练时的损失收敛曲线. 其中loss值的含义为每个训练轮次的平均批处理损失.

3 实验与分析 3.1 数据集与预处理

本文在Tmall、Diginetica以及Retailrocket这3个公开数据集上对所提模型MGATSC进行验证. Tmall数据集包含匿名用户在天猫线上购物平台上的消费日志, 来源于IJCAI-15竞赛. Diginetica数据由一系列的交易数据组成, 来源于CIKM Cup 2016. Retailrocket为一家电子商务公司发布的 Kaggle 竞赛数据集, 其中包含用户在6个月内的浏览活动.

实验参照文献[17, 18]对3个数据集进行预处理. 具体而言, 将3个数据集中长度为1的会话以及出现次数小于5次的项目过滤. 最新的数据(比如上周的数据)作为测试集, 其余数据则作为训练集. 此外, 通过对会话序列$ s = \{ {v_1}, {v_2}, {v_3}, \cdots, {v_m}\} $进行分割, 生成多个具有相应标签的子序列$([{v_1}], {v_2}), ([{v_1}, {v_2}], {v_3}), \cdots, ([{v_1}, {v_2}, {v_{m - 1}}], {v_m})$. 经过预处理后, 3个数据集的相关信息如表1所示.

3.2 评价指标

参照文献[15,17], 实验选取P@K (precision)与MRR@K (mean reciprocal rank)两种指标评估模型有效性. P@K用于度量预测精准度, 表示交互概率最高的前K个推荐项目中正确推荐的项目所占比例. P@K不考虑项目的实际排名, 而只关注项目是否在前K个推荐项目中; 而MRR@K考虑了项目排名, 表示正确推荐项目的倒数排名的平均值. MRR值越大表示项目排名越靠前, 推荐效果越好. 如果排名大于K, 则倒数排名设置为0. 本实验K取10和20.

3.3 基线模型

为了评估MGATSC模型的推荐性能, 将其与以下基线模型作对比.

(1) FPMC^[10]: 一种基于矩阵分解与马尔可夫链的序列方法, 其根据顺序行为预测下一次交互项目. 为了使其适用于会话推荐, 模型在计算推荐分数时不考虑用户的潜在嵌入.

(2) GRU4Rec^[12]: 一种基于循环神经网络的模型, 其采用门控循环单元对匿名用户的会话序列进行建模.

(3) NARM^[14]: 一种基于RNN的模型, 其通过注意力机制获取用户主要意图, 并结合顺序行为特征生成推荐.

(4) STAMP^[15]: 使用注意力层代替RNN编码器, 并利用自注意力机制提升会话推荐的性能.

(5) SR-GNN^[17]: 利用门控图神经网络获得项目嵌入, 并采用软注意力机制计算会话嵌入.

(6) GCE-GNN^[21]: 首个利用当前会话之外的其他会话信息生成全局级项目嵌入, 以提升模型性能.

(7) S²-DHCN^[25]: 通过构建两种不同类型的超图学习会话内与会话之间的信息, 并利用自监督学习缓解会话数据稀疏性, 提升模型性能.

3.4 参数设置

嵌入维度设置为100, 批处理大小从$\{ 64, 128, 256, 512\} $中选取, 图注意力网络的堆叠层数从$\{ 1, 2, 3, 4, 5, 6\} $中选择, dropout率从$\{ 0, 0.1, 0.2,\cdots, 0.8\} $中选取. 使用初始学习率为0.001的Adam优化器优化模型参数, 每迭代3次学习率衰减0.1. 正则化系数L2设为10⁻⁵. 所有参数使用均值为0、标准差为0.1的高斯分布进行初始化. 并从训练集中随机抽取10%作为验证集.

3.5 实验结果与分析

表2记录了所提模型与所有基线模型在3个公开数据集上的实验结果. 每一列的最优结果用粗体标注, 次优结果用下划线标注. 提升率是通过计算MGATSC模型与最优基线模型的性能差值除以后者性能得到的. 对于各种指标, MGATSC模型在3个数据集上均取得了最好的表现, 这证明了所提模型的有效性. 观察表2可以得出如下结果.

(1) 传统会话推荐模型(FPMC)的性能在所有基线模型当中竞争力不足, 这是因为其仅考虑相邻项目间的顺序转换而忽略了会话中包含的时序信息. 而所有基于神经网络的模型(除FPMC之外)的性能均优于传统模型, 这表明深度学习在会话推荐领域的优越性.

(2) 与不考虑时序信息的传统会话推荐模型相比, 考虑时序信息的深度学习模型(GRU4Rec、NARM、STAMP)推荐性能表现较为优秀, 说明在会话推荐中捕获项目间顺序依赖的重要性. 此外, 在基于RNN的模型中, NARM与STAMP的性能优于GRU4Rec. 这是因为NARM与STAMP不仅使用RNN建模顺序行为, 而且在学习会话嵌入时利用注意力机制学习每个项目的重要性, 从而提升了推荐效果. 然而仅使用门控循环单元(gated recurrent unit, GRU)的GRU4Rec只考虑了顺序行为, 难以处理用户偏好的变化. 这说明仅使用RNN学习会话嵌入可能会导致推荐偏差, 也证明区分当前会话中不同项目的重要性有助于更准确地获取用户偏好.

(3) 表2中所有基于GNN的模型(SR-GNN, S²-DHCN, GCE-GNN)的性能要优于基于RNN的模型, 表明GNN能更有效地对会话数据进行建模, 捕获更复杂的项目转换关系. 其中, GCE-GNN与S²-DHCN的表现优于SR-GNN模型. GCE-GNN通过构建局部会话图和全局会话图以分别获取会话级和全局级信息. S²-DHCN通过构建两种类型的超图以学习会话内与会话之间的信息. 然而SR-GNN仅基于当前会话进行建模. 这说明利用其他会话捕获不同层级的信息有助于更精确的学习用户意图与偏好. 与GCE-GNN相比, S²-DHCN在Tmall和Diginetica数据集上的表现较差, 说明自监督学习在提升会话推荐效果方面存在着局限性, 而融合来自其他会话的信息则更为有效. 虽然GCE-GNN取得了不错的性能, 但由于其复杂的模型结构, 在运行Retailrocket数据集时出现内存不足的问题.

(4) 所提模型MGATSC利用图注意力网络在信息传播过程中自适应学习每个邻居的重要性从而减少模型训练过程中噪声的引入, 并通过堆叠多层网络获取会话图的高阶结构信息. 同时采用基于残差注意力机制的跳跃连接缓解过度平滑问题, 进而提升推荐效果. 与最优基线模型相比, MGATSC在Tmall数据集上P@20与MRR@20分别提升10.05%和9.21%; 在Diginetica数据集上, P@20与MRR@20分别提升0.76%与1.10%. 在Retailrocket数据集上, P@20与MRR@20分别提升1.75%和5.93%. 可以看出, MGATSC模型性能在3个数据集上优于所有基线模型. 尤其是在Tmall数据集上, 其表现优势较为明显, 验证了MGATSC模型的有效性和合理性.

3.6 消融实验

在本节, 为了探究模型中各个组件的贡献, 本文设计了MGATSC模型的4种变体与其自身进行对比实验.

(1) MGATSC-GGNN: 用门控图神经网络代替图注意力网络学习会话中的项目嵌入, 在信息传播过程中不对邻居的重要性进行区分.

(2) MGATSC-NSC: 移除基于残差注意力机制的跳跃连接, 忽略过度平滑问题.

(3) MGATSC-NP: 移除反向位置嵌入, 不考虑位置信息.

(4) MGATSC-NA: 移除软注意力机制并将会话中所有项目的平均嵌入作为会话嵌入.

对比实验的结果如表3所示. 从中可以看出: (1) MGATSC-GGNN的效果差于MGATSC, 这是因为GGNN在信息传播过程中平等对待邻居节点, 从而引入噪声误导模型, 使得模型不能有效学习项目嵌入. 而图注意力网络能够为邻居节点自适应分配合适的权重, 这表明在信息传播过程中区分邻居节点的重要性是很有必要的. (2)在移除跳跃连接后模型性能出现了下降, 说明跳跃连接能够缓解堆叠多层图注意力网络所引发的节点嵌入过度平滑问题, 从而提升模型性能. (3)当项目嵌入不与反向位置嵌入融合时模型性能出现了下滑, 说明反向位置嵌入能够为模型提供有效的位置信息, 从而提升推荐效果. (4)将平均项目嵌入作为会话嵌入时, 模型性能出现了极大下降, 这表明在生成会话嵌入时利用注意力机制区分不同项目优先级的必要性.

3.7 聚合操作的影响

为了探究项目嵌入${{\boldsymbol{h}}_i}$与反向位置嵌入${{\boldsymbol{p}}_{m - i + 1}}$的不同聚合操作对模型性能的影响, 本文选择了5种不同的聚合操作在3个数据集上进行实验. (1)求和池化, 即式(7). (2)均值池化是求和池化的特殊表现形式, 其在求和的基础上进行平均. (3)最大池化, 在每个维度上取两种嵌入的最大值. (4)拼接, 对${{\boldsymbol{h}}_i}$与${{\boldsymbol{p}}_{m - i + 1}}$进行拼接, 即:

$ {{\textit{z}}_i} = {\boldsymbol{M}}({{\boldsymbol{h}}_i}||{{\boldsymbol{p}}_{m - i + 1}}) $

(14)

其中, ${\boldsymbol{M}} \in {\mathbb{R}^{d \times 2d}}$为可训练参数. (5)门控融合, 对${{\boldsymbol{h}}_i}$与${{\boldsymbol{p}}_{m - i + 1}}$使用线性插值, 即:

$ {c_i} = \sigma ({{\boldsymbol{W}}_h}{{\boldsymbol{h}}_i} + {{\boldsymbol{W}}_p}{{\boldsymbol{p}}_{m - i + 1}}) $

(15)

$ {{\textit{z}}_i} = {c_i}{{\boldsymbol{h}}_i} + (1 - {c_i}){{\boldsymbol{p}}_{m - i + 1}} $

(16)

其中, ${{\boldsymbol{W}}_h}, {{\boldsymbol{W}}_p} \in {\mathbb{R}^{d \times d}}$为可训练参数, ${c_i}$用于平衡两个嵌入的重要性.

实验结果如表4所示. 从中可以看出, 求和池化和均值池化的性能优于其他聚合操作. 最大池化也展现出不错的效果, 这源于其相对较高的计算效率以及能较为有效地捕获最重要的信息. 门控融合通过注意力机制为项目嵌入和位置嵌入分配合适的权重, 也有不错的表现. 但可能由于参数较多导致过拟合, 其性能差于求和池化. 拼接的性能是最差的, 可能是由于简单的整体平滑无法对两种嵌入进行有效融合.

3.8 网络层数的影响

为了研究图注意力网络堆叠层数对模型性能的影响, 实验将网络层数设置为$\{ 1, 2, 3, 4, 5, 6\} $. 从图5可以看出, 对于Tmall数据集, 随着层数的增加模型性能存在较大波动, 当层数为6时模型取得最好性能; 而对于Diginetica数据集, 模型性能则较为稳定, 层数为2时性能达到最佳. 当层数大于2时性能逐渐下降, 这是因为随着堆叠层数的增加, 过度平滑问题随之产生.

3.9 dropout比例的影响

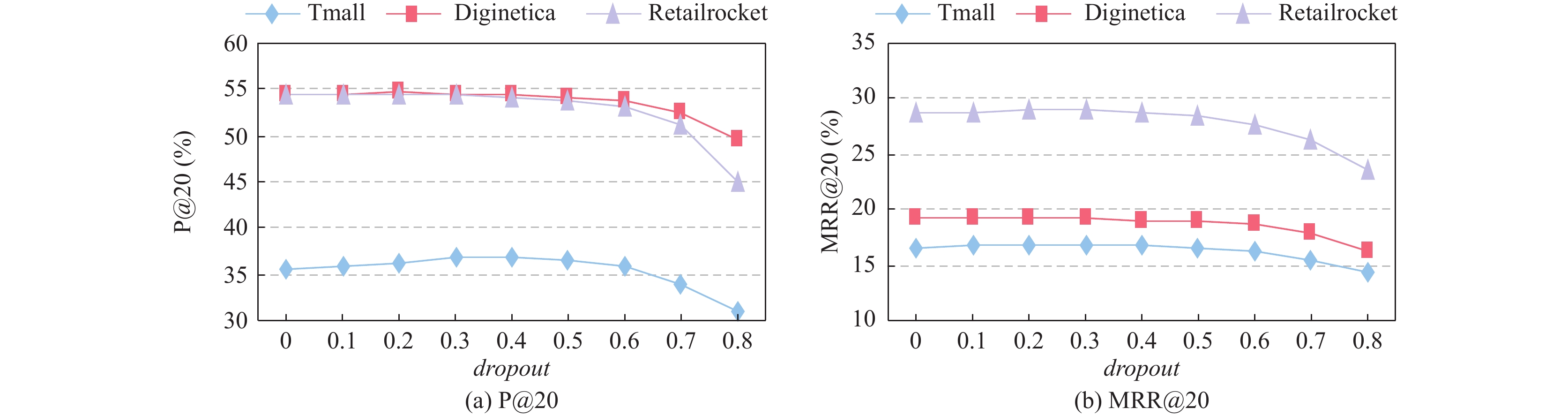
为了防止模型过拟合, 文中采用了dropout正则化技术. 该技术已被证明在包括图神经网络在内的各种神经网络架构中有效^[26,27]. dropout的核心思想是在训练过程中以概率$p$随机丢弃神经元, 而在测试时则使用所有神经元. 本文将$p$设置为$\{ 0, 0.1, 0.2, \cdots, 0.8\} $并在3个数据集上进行实验. 实验结果如图6所示, 当dropout率较小时, 模型在3个数据集上均表现不佳, 因为容易出现过拟合的情况. 当dropout率在Diginetica、Retailrocket、Tmall上分别设置为0.2, 0.2和0.3时, 模型效果最好. 然而随着dropout率继续增加模型性能开始衰退, 这是因为模型很难通过有限的神经元从数据中学习.

3.10 模型复杂度分析

为了探究模型的复杂度, 本节从时间和空间两个方面对模型进行分析. 模型MGATSC的时间复杂度主要集中在多层图注意力网络、跳跃连接以及注意力机制3个部分. 设会话长度为$m$, 嵌入维度为$d$, 图注意力网络层数为$L$. 则多层图注意力网络部分的时间开销为${\rm{O}}(L{m^2}d)$, 跳跃连接部分的时间开销为${\rm{O}}(m{d^2})$, 注意力机制部分的时间开销为${\rm{O}}(md)$. 因此, 模型的时间复杂度为${\rm{O}}(L{m^2}d + md(d + 1)) = {\rm{O}}(L{m^2}d + m{d^2})$. 可以看出模型的时间复杂度主要与会话长度、嵌入维度以及网络层数有关. 表5展示了MGATSC模型与基线模型在Tmall和Diginetica两个数据集上的平均每轮次训练时间. 从表5可以看出, MGATSC模型的平均每轮次训练时间基本短于所有基线模型, 训练效率更高. 同时, GCE-GNN和S²-DHCN的平均训练时间比MGATSC长得多, 原因是GCE-GNN和S²-DHCN均依赖于由全部会话序列构成的完整图结构, 模型计算量较大. 而MGATSC模型仅通过当前会话序列形成的会话图进行学习, 计算量较小.

同时为了探究模型的空间复杂度, 本文从模型的参数量以及大小两个维度进行分析. 从表5可以看出, MGATSC模型的参数量、大小与基线模型几近相当. 这说明MGATSC模型在提升推荐性能的同时, 并没有产生较多的额外开销.

综合来看, MGATSC模型较为轻便高效, 适用于用户偏好更多地取决于短期交互数据而非长期历史交互数据的场景. 比如某用户近期需要购买苹果手机及相关配件. 同时该用户是一名经常在电商平台上购买各类服饰的穿搭爱好者. 在这种情况下, 该用户过往的交互数据并不能产生合适的推荐, 而只能依靠用户浏览苹果手机及相关配件的短期交互数据进行推荐.

4 结语

先前的图神经网络会话推荐模型大多在信息传播过程中赋予邻居节点相同权重而没有区分它们的重要性, 此外在网络层数增加所引发的过度平滑问题方面有待改进提升. 针对这两个问题, 文中提出结合跳跃连接的多层图注意力网络会话推荐模型MGATSC. 该模型通过图注意力网络自适应学习邻居节点的重要性, 减少噪声引入. 并利用基于残差注意力机制的跳跃连接更有效地保留节点的低阶与高阶信息, 从而缓解过度平滑问题. 文中通过消融实验验证了图注意力网络在区分邻居节点贡献时发挥了重要作用, 且跳跃连接能够较为有效地缓解过渡平滑问题. 通过对比实验表明MGATSC模型的性能优于S²-DHCN, GCE-GNN等主流基线模型, 验证了模型的有效性与合理性.