2. 南京邮电大学 物联网学院, 南京 210003
2. School of Internet of Things, Nanjing University of Posts and Telecommunications, Nanjing 210003, China
高光谱图像(hyperspectral image, HSI)是一种具有数百个连续光谱波段的高维图像, 既包含空间信息, 又包含丰富的光谱信息. HSI具有识别弱信息和定量检测的优点. 随着高分辨率成像技术的不断发展, 高光谱遥感已成为21世纪遥感领域的重要研究方向之一. 目前, 高光谱遥感已应用于环境与灾害探测、精准农业、地质勘探、地球资源调查[1]等领域.
近年来, 深度学习在各个领域取得了显著的成绩, 由于其能够提取高级语义特征, 因此成为高光谱图像分析的新趋势[2]. 实践证明, 深度模型能够在计算机视觉和自然语言处理任务中有效地提取不变量和判别特征. 在这些蓬勃发展的技术的启发下, 人们设计了深度模型来对高光谱图像进行分类. Chen等人[3]首次提出了一种基于深度学习的HSI分类方法, 并采用了一种堆叠自编码器(SAE)作为分类器. 文献[4]中引入了深度置信网络(DBN)进行光谱空间信息探测. Pan等人[5]提出了一种考虑HSI物理特性的顶点成分分析网络(VCANet). 当训练样本有限时, VCANet能够利用鉴别特征.
近年来, 卷积神经网络(CNN)广泛应用于图像处理和模式识别等方面. 卷积神经网络在HSI分类中得到了广泛的应用. CNN利用区域连接提取上下文特征, 并表现出了出色的分类性能. 在文献[6]中, Zhang等人通过一维CNN提取光谱特征, 通过二维CNN挖掘空间特征. 然后结合光谱特征和空间特征进行分类. 肖志云等人[7]通过改进传统的高光谱3D卷积方式, 获得“空谱”结合的特征, 并结合树形Parzen估计算法实现更高精度的分类. 在文献[8]中, Gabor滤波器与卷积滤波器相结合, 缓解了CNN训练中的过拟合问题. 受inception模块[9]的启发, Gong等人[10]提出了一种具有多尺度卷积的CNN. 多尺度滤波器组丰富了深度模型的表示能力. 王雷全等人[11]利用DenseNet结合3DCNN有效地提取图像的光谱特征和空间特征. 针对传统分类模型存在空间光谱特征提取不充分、计算量大的问题, 巩传江等人[12]提出了基于小波卷积网络的高光谱图像分类方法. 吴鸿昊等人[13]通过基于不同尺度的双通道3维卷积实现更高精度的分类.
基于CNN的HSI分类方法已经取得了巨大的进展. 然而, 这些分类方法的性能在很大程度上取决于训练样本的数量. 通常, 从HSI中收集大量的训练样本是一项具有挑战性的任务. 这个问题可以通过数据增强来缓解. 裁剪、水平翻转、生成模型是典型的数据增强技术. 近年来, 生成模型受到了广泛的关注, 因为它能够生成高质量的样本来缓解过拟合问题. Goodfellow等人[14]设计了生成对抗网络(GAN), 它由一个生成器和一个判别器组成. 生成器捕获数据分布, 而判别器判断样本是来自生成器还是来自训练数据. 生成器可以被认为是一种正则化方法, 可以在很大程度上有效地缓解过拟合问题.
研究人员努力设计基于GAN的模型, 以缓解高质量样本有限的问题. Zhan等人[15]提出了一种基于1D-GAN的半监督框架. 之后, Zhu等人[16]提出了一种3D-GAN用于HSI分类. 在考虑空间信息的基础上, 在判别器中采用了Softmax分类器进行辅助分类. Feng等人[17]提出了一种用于HSI分类的多类别GAN. 在多类别GAN中设计了两个生成器来生成高光谱图像补丁, 并设计了一个判别器来输出多类别概率. Zhong等人[18]将GAN和条件随机场(CRF)集成在一起, 其中密集的CRF对GAN的判别器施加图约束, 以细化分类结果.
尽管这些基于GAN的模型取得了令人满意的效果, 但是, 高光谱图像分类仍然存在两个急需解决的缺陷.
第1个挑战是训练数据的不平衡. 当可用的训练样本在不同类别之间分布不均匀时, 分类的准确性可能会下降. 然而, 不平衡的训练数据问题是HSI的基本问题, 因为在特定场景中存在不同大小的对象[19]. 在Zhu等人[16]的工作中, 使用辅助分类器GAN (ACGAN)[20]进行HSI分类. 在ACGAN中, 判别器有两个输出: 一个是区分真假样本, 另一个是对样本进行分类. ACGAN能够产生特定类别的样本. 在实际应用中, 在生成少数类样本时, 可以观察到判别器的两个损失函数存在缺陷. 出现这种现象的原因是, 当少数类样本被传递给判别器时, 它们很可能被分配到假标签. 因此, 判别器试图将假标签与少数类样本相关联. 此时, 生成器生成看起来真实但不代表少数类的样本. 生成的样本质量变差, 从而影响分类性能.
另一个关键问题是模式崩溃. 生成器通过只产生来自相同数据模式的数据来欺骗判别器[21]. 它导致产生了一个只能在数据空间的狭窄范围内生成样本的生成器, 因此, 生成的样本过于相似, 模型无法学习到真实的数据分布, 模型很难学习到完整的数据分布. 模型崩溃可以被认为是对判别器反馈的过拟合的结果.
本文针对以上问题做了相关研究, 主要工作如下.
(1)提出了一种改进的基于GAN网络的HSI图像分类方法, 该方法将Wasserstein距离引入ADGAN网络, 用以缓解训练数据的不平衡以及模型崩溃的问题.
(2)运用SPCA方法对高光谱数据进行降维, 进而提高对高光谱图像的分类精度.
(3)本文GAN网络中设计了独立的分类器用于提升分类性能, 并通过大量实验证明了本文方法的有效性.
1 相关工作在原始GAN网络中, 判别器只判断输入样本的真假, 不适合多类图像分类. Wang等人[22]提出了ADGAN (adaptive drop block enhanced GANs). 在ADGAN中, 判别器D是一个Softmax分类器, 可以输出多种类别的标签概率.
ADGAN框架如图1所示. 通过PCA[23]将输入HSI的光谱波段数减少到3个分量, 这可以极大地降低计算复杂度, 有助于训练一个健壮的生成器G. 生成器G的输入包括噪声z和类别标签c, 输出匹配所需类标签的图像块; 判别器D接收到来自真实数据中图像块Xreal和生成器生成的假图像块Xfake=G(z). 与ACGAN不同, 判别器D只有一个单一的输出, 即返回特定的类别c或假标签. 为此, 训练判别器D以使以下的对数似然值最大化, 如下所示:
| LD=E[logP(C=c|Xreal)]+E[logP(C=fake|Xfake)] | (1) |
其中, C表示判别器D的输出, Xreal和Xfake分别代表来自真实数据的图像与生成的图像.

|
图 1 ADGAN结构图[22] |
对生成器G进行训练, 使以下的对数似然值最大化, 如下所示:
| LG=E[logP(C=c|Xfake)] | (2) |
如何利用有限数据样本的丰富特征来提高分类精度是HSI分类研究的一个热点. 为了更好地利用HSI的丰富特征, 同时利用Wasserstein距离来缓解GAN网络中存在的模式崩溃问题, 本文在ADGAN方法的基础上进行了改进, 提出了新的SPCA-AD-WGAN方法用于HSI分类, 框架如图2所示.
由于高光谱图像包含数百个波段, 波段之间存在大量冗余, 生成器难以模拟真实数据, 无法获得具有鲁棒性的生成器. 因此, 本文首先通过SPCA方法对输入的HSI图像进行降维, 降低计算复杂度, 提取更多的低维有效数据来训练网络. 同时, 本文将ADGAN网络中, 判别器判断图像真假与为图像分类标签的任务分开进行. 判别器D只负责判断图像的真假; 使用单独的辅助分类器C, 用于分辨图像的类别. 这样, 判别器与分类器分别完成两个不同的任务. 生成器G与判别器D之间通过基于Wasserstein距离的GAN网络进行训练. 网络通过引入Wasserstein距离来缓解模式崩溃问题; 同时判别器的训练结果也会作用于分类器的训练过程, 帮助分类器提高分类精度. 判别器与分类器将结果反馈给生成器. 生成器继续生成图像, 直到判别器不能再区分它为止; 同时, 分类器对图像类别的判断精度也在不断提高. 然后, 通过循环训练网络, 就可以获得理想的HSI分类精度.
2.2 AD-WGAN框架在ADGAN网络中, 判别器D用来给输入的图像块分配标签. 当图像是来源于训练集的真实图像时, 判别器希望输出符合原标签的类别信息; 当图像是生成器G生成的假图像时, 判别器希望将假图像的标签信息与单独添加的类别——“fake”类别联系在一起. 对于GAN网络可能产生的模式崩溃现象, ADGAN网络使用了自适应的DropBlock方法来缓解这一问题. 然而DropBlock方法本身存在一定的不足: DropBlock方法会丢弃特征图中连续区域的单元, 从而可能会丢失一些重要的特征信息. 因此, 虽然DropBlock方法可以在一定程度上缓解模式崩溃问题, 但是某些特征信息的丢失也会可能影响网络对高光谱图像的分类精度. 本文希望从网络结构的角度上缓解模式崩溃问题: 将Wasserstein GAN对于原始GAN网络损失函数的更新引入ADGAN网络, 并且设立单独的判别器用以改善原始网络训练不稳定以及模式崩溃的问题, 进而提高对高光谱图像的分类精度.

|
图 2 SPCA-AD-WGAN结构图 |
在原始的GAN网络中, 当判别器被训练到最优时, 其表达式如下:
| D∗(x)=Pr(x)Pr(x)+Pg(x) | (3) |
其中, Pr(x)代表真实数据的分布, Pg(x)代表生成的数据的分布. 将式(3)代入GAN网络的目标函数, 并结合JS散度的表达式, 即可得到最优判别器下的GAN网络目标函数:
| 2JS(Pr||Pg)−log2 | (4) |
即当判别器训练到最优时, 原始GAN网络定义的生成器loss等价变换为最小化真实分布Pr 与生成分布Pg之间的JS散度. 然而当生成器产生的样本分布与真实样本分布有重叠部分较小或二者没有重叠部分时, JS散度会等于一个恒定值. 在这种情况下判别器会出现饱和状态, 即所有生成的样本都被判别为假样本. 在这种情况下, 生成器无法得到有效的反馈信号, 导致生成器无法学习到真实分布的信息, 从而陷入模式崩溃的状态. Wasserstein GAN网络通过将Wasserstein距离代替JS散度, 在样本分布与真实样本分布有重叠部分较小或二者没有重叠部分时仍然可以判断两个分布之间的差异. 本文通过使用Wasserstein距离的方式来缓解模式崩溃问题. 在得到近似最优判别器D的前提下, 优化生成器G减小Wasserstein距离, 可以有效缩短生成图像的分布与真实图像分布之间的距离. 改进之后的目标函数如式(5):
| minGmaxDEx∼Pr[D(x)]+E˜x∼Pg[D(˜x)] | (5) |
其中, x表示符合真实分布的样本;
判别器D的输入由真实图像的patch块 、带有类别标签的生成的假样本Xfake组成, D的输出是一个概率分布D(x). 判别器的作用是判断样品的真假. 设计D和C的目的是为AD-WGAN的每个部分分配一个特定的任务.
2.2.1 生成器结构生成器G接受随机高斯噪声z作为输入. 在谱域中用3个波段将噪声 变换为与真实输入数据相同的大小. 本文使用的生成器的结构如图3所示. 生成器使用5层上采样的2D转置卷积, 将100×1×1的噪声向量与类别标签c作为输入, 输出3×64×64的图像块. 然后这些带有标签的图像块将会和真实图像一起送入判别器与分类器进行训练.

|
图 3 生成器结构图 |
生成器的目标函数由两部分组成. 一部分来自于判别器D, 它保证了判别器不会识别由生成器产生的样本. 另一部分来自分类器C, 它保证了生成器生成的样本最大程度地属于相应的类别. 第2部分强化了类别信息和生成样本之间的联系. 因此, 这两部分之和构成了生成器G的目标函数:
| LG=E˜x∼Pg[D(˜x)]+E[logP(C=c|Xfake)] | (6) |
判别器D的结构如图4所示. 判别器D接受来自训练集中的图像块或生成的图像块作为输入, 输出这些图像块为真的概率分布. 输入图像进入判别器D后, 经过5层下采样卷积, 将3×64×64输入样本转换为128×1×1的数据, 最后经过全连接层, 输出图像为真的概率.
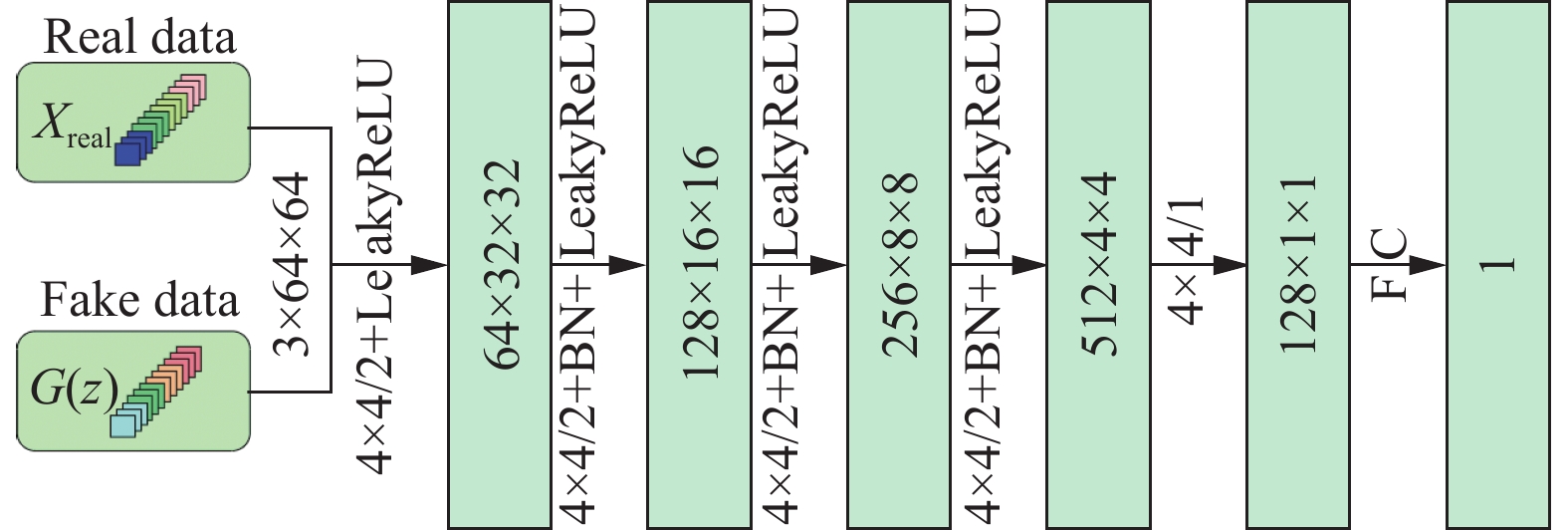
|
图 4 判别器结构图 |
判别器D的作用是判断图像的真假, 再结合Wasser-stein距离对网络损失的更新, 判别器D的目标函数为:
| LD=Ex∼Pr[D(x)]−E˜x∼Pg[D(˜x)] | (7) |
分类器C的结构如图5所示. 其中, N表示数据集中的类别数量. 分类器C与判别器拥有相同的输入. 对判别器判断为真实的图像, 分类器输出图像的类别标签; 对判别器鉴定为假的图像, 分类器则将图像与假标签相关联. 输入分类器的图像首先经过5层下采样的2D卷积层, 然后经过全连接层, 输出每个图像的类别.

|
图 5 分类器结构图 |
分类器C的作用是输出每个图像的类别标签, 其目标函数如下:
| LC=Ex∼Pr[logP(C=c|D=real)]+Ex∼Pg[log(C=fake|D=fake)] | (8) |
HSI数据的高维特性带来了维数灾难和数据传输存储的负担. 因此, HSI预处理步骤中广泛采用降维技术来缓解这些问题, 同时将重要的信息保存在低维空间中. 在文献[24]中, Jiang等人开发了一种基于多尺度分割的SuperPCA模型, 用于高光谱图像分类. 本文使用基于超像素的图像分割将观察到的图像分割成许多不同的区域, 并且认为其中每个区域中的光谱特征是相似的. 对分割后的区域单独进行PCA降维, 然后再把这些区域拼接起来, 组合成降维后的图像. SPCA的结构如图6所示. 首先通过超像素分割将一个L×M×N的原始高光谱图像划分为许多个区域. 将这些区域用矩阵表示, 矩阵的列是像素的光谱向量. 分别对这些高维矩阵进行PCA降维, 得到降维矩阵. 降维后矩阵的列d<L. 最后, 对这些低维矩阵进行重新排列和组合, 形成降维后的高光谱图像.
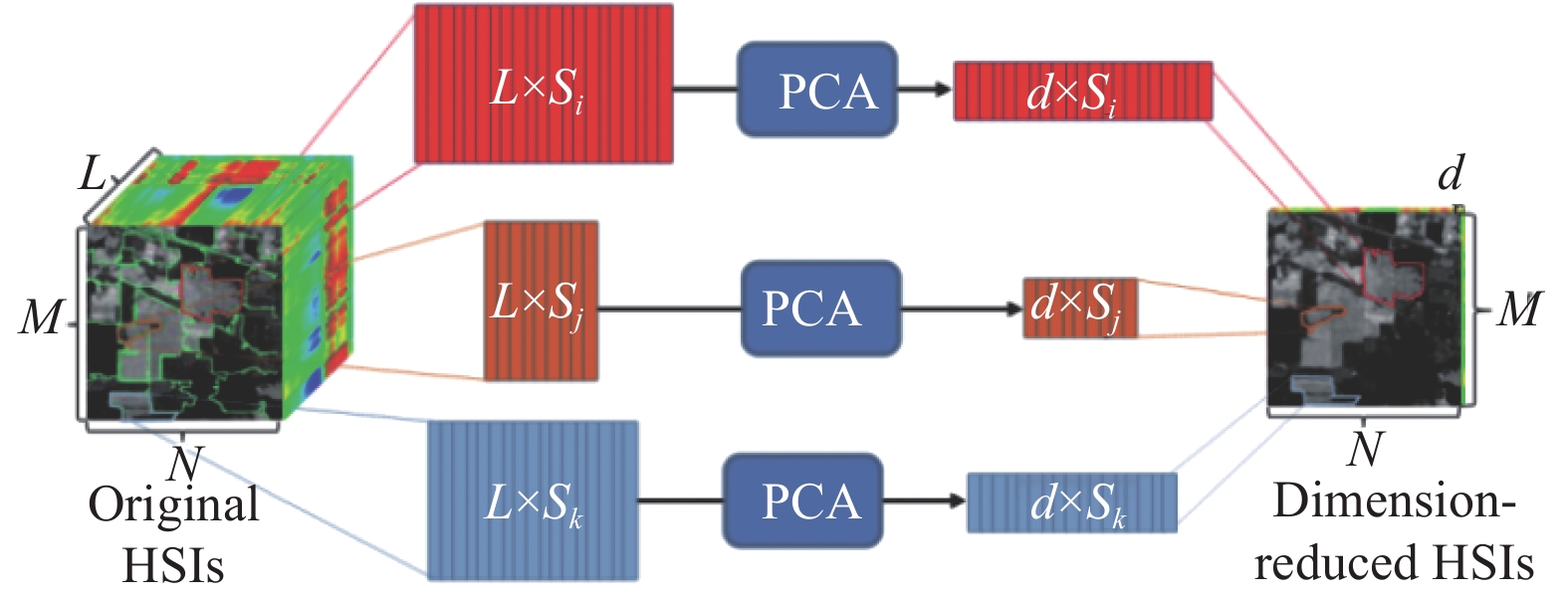
|
图 6 基于SuperPCA的HIS降维[24] |
3 实验分析 3.1 实验数据集
本文使用两个具有代表性的高光谱遥感图像数据集: Indian Pines数据集、Pavia University数据集分别作为实验数据进行实验.
3.1.1 Indian Pines数据集Indian Pines数据集包括1992年美国印第安纳州西北部的农业和森林地区的高光谱图像, 该数据集由利用机载可见/红外成像光谱仪(AVIRIS)的遥感设备收集. 数据集中的图像为145×145像素, 其空间分辨率为20 m/像素. Indian Pines数据集包含220个光谱波段, 其中去除了20个严重吸水波段, 本文对剩下的200个光谱波段进行了实验. 伪彩色合成图像和ground truth图像如图7所示.

|
图 7 Indian Pines伪彩色合成图与真值图 |
3.1.2 Pavia University数据集
Pavia University数据集由反射光学系统成像光谱仪(ROSIS)传感器在意大利帕维亚大学收集. 该图像大小为610×340像素, 包含430–860 nm波长范围内的103个光谱带. 假彩色图像和地面真值如图8所示, 其中包含9个具有代表性的城市类别.
3.2 实验设置为了验证所提出的SPCA-AD-WGAN的性能, 本文将其与2DCNN[25]、3DCNN[26]、3DGAN[16]、ADGAN[22]、patch-wise SpectralFormer (SpectralFormer)[27]进行了比较. 为了保证实验结果的公正性, 所有方法使用相同的训练集. 所有的实验结果都是通过随机分割训练集和测试集得到的. 在Indian Pines数据集中随机选择307个训练样本; 在Pavia University数据集中随机选择1000个训练样本, 拥有很小比例的训练集被用于模拟带有少量标记样本的场景. 对于只有一个样本的类别, 进行重采样等数据增强操作, 方法与文献[17]相同. 结果独立运行超过15次. 所有方法按照默认最优参数, 使用PCA的前3个主成分作为输入.
所有测试样本都有3个评价标准, 包括总体准确率(OA)、平均准确率(AA)和Kappa系数.

|
图 8 Pavia University伪彩色合成图与真值图 |
总体准确率表示被正确分类的测试样本数在所有测试样本数中的比率; 平均准确率表示所有类别分类精度的平均值; Kappa系数表示测试样本的分类预测类别与实际类别的一致性检测指标系数. 具体计算公式如下:
| OA=K∑i=1P(i,i)N | (9) |
| AA=K∑i=1OA(i)K | (10) |
| Kappa=NK∑i=1P(i,i)−K∑i=1P(i,)P(,i)N2−K∑i=1P(i,)P(,i) | (11) |
其中, K表示类别数; N表示测试样本总个数; P(i, i)表示第i类被正确分类; OA(i)表示第i类的总分类精度; P(i, )和P(, i)分别表示第i行和第i列的总测试样本数.
对于ADGAN和SpectralFormer, 使用提供的源代码, 默认最优参数参见文献[22,27]. 对于3DGAN, 使用大小为64×64的邻域, 将输入图像归一化到[−0.5, 0.5]的范围内. 其他比较方法的实验设置都是在文献[25]的基础上, 按主成分分析法个数进行设置. 对于本文提出的SPCA-AD-WGAN, 判别器D与生成器C的模型参数使用RMSprop优化器进行优化; 分类器C使用Adam优化器进行优化. 对于两个数据集, epoch个数设置为500个, 学习率设置为0.0002, 图像块的大小设置为64×64.
3.3 实验结果本文在Indian Pines数据集中随机选择307个训练样本(具体见表1), 在Pavia University数据集中随机选择1000个训练样本(具体见表2). 表3、表4分别记录了比较算法和本文提出的SPCA-AD-WGAN方法在两个数据集上的平均分类精度和相应的标准差. 表格的前几行表示每个类别的结果, 后3行分别是OA、AA和Kappa系数的结果.
3.3.1 Indian Pines数据集实验结果Indian Pines数据集的训练和测试样本数量见表1. 表3显示了Indian Pines数据集的分类结果. 图9显示了各类方法在Indian Pines数据集上的分类效果. 本文提出的方法OA达到了 91.74%, AA达到了83.77%, Kappa系数为90.79%. 相比较于总体分类精度较好的ADGAN网络, 本文提出的方法在AA、OA、Kappa系数3个方面分别高出1.52%、4.61%、0.66%. 本文提出的SPCA-AD-WGAN在16个类别中有10个类别的准确率最高. 这说明本文提出的方法在总体分类精度方面取得了最好的效果.
| 表 1 Indian Pines数据集中的训练和测试像素的个数 |
| 表 2 Pavia University数据集中的训练和测试像素的个数 |
| 表 3 Indian Pines数据集分类精度(%) |
在训练样本较少的类别如Alfalfa、Corn、Grass pasture mowed 和Oats, 本文提出的方法取得了最好分类精度, 分别达到了53.33%、86.76%、60.87%、57.89%. 比较于其他的分类方法, 分别提高了3.68%、1.88%、9.35%、7.65%; 相比较于ADGAN网络, 在样本较少的类别上的分类精度都有较大幅度的提升. 这表明, 在样本数量较少的类别, 生成器依然可以生成多样化的样本, 而不是只生成数量较多类别的样本. 这说明本方法可以学习到这些样本的本质特征, 在训练样本较少的类别中也能生成高质量的HSI样本. 这说明模式崩溃问题得到了缓解.
3.3.2 Pavia University数据集实验结果Pavia University数据集的训练和测试样本数量见表2. 表4显示了Pavia University数据集的分类结果. 图10显示了各类方法在Pavia University数据集上的分类效果. 本文提出的方法OA达到了 96.89%, AA达到了95.76%, Kappa系数为96.34%. 相比较于总体分类精度较好的ADGAN网络, 本文提出的方法在AA、OA、Kappa系数3个方面分别高出1.51%、1.05%、1.13%. 总体而言, 本文提出的方法取得了较好的分类精度.
在训练样本较少的类别(如Bitumen), 除了3DGAN网络, 其他的方法都低于89%; 而本文提出的方法取得了最高的分类精度. 相比较于ADGAN网络, 在样本较少的类别上的分类精度都有比较明显的提升. 这表明, 对于Pavia University数据集中样本数量较少的类别, 生成器依然可以生成多样化的样本, 而不是只生成数量较多类别的样本. 结合两个数据集上本文提出的方法在训练样本较少的类上的表现, 说明提出的方法可以学习到这些样本的本质特征, 即使在训练样本较少的类别中也能生成高质量的HSI样本, 有效缓解了模式崩溃的问题.
| 表 4 Pavia University数据集分类精度(%) |
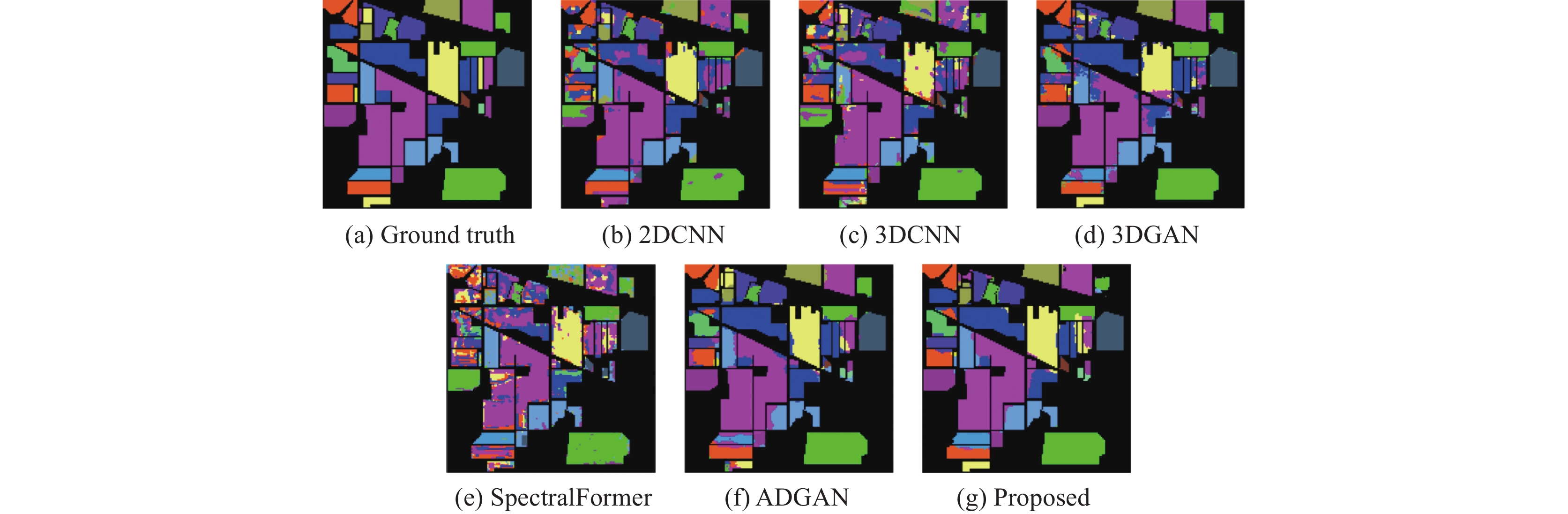
|
图 9 Indian Pines数据集分类效果图 |
3.4 消融实验
在消融实验部分, 本文将分别验证模型中的提出方法的有效性. 实验将本文模型与3个模型进行比较, 分别是: 1) ADGAN; 2) AD-WGAN, 在ADGAN的基础上引入Wasserstein距离; 3) SPCA-ADGAN, 是指在ADGAN的基础上运用SPCA方法对数据进行降维; 4) SPCA-AD-WGAN. 本次所有的消融实验均在Indian Pines与Pavia University两个数据集上进行, 参数设置与实验过程保持一致.
表5、表6分别是不同的方法在两个数据集上的分类效果对比. 通过实验结果可以发现, 在Pavia University数据集上AD-WGAN在OA、AA、Kappa系数3个方面对比原方法分别提升了0.65%、0.59%、0.70%; SPCA-ADGAN在OA、AA、Kappa系数3个方面对比原方法分别提升了0.46%、0.22%、0.11%; 在Indian Pines数据集上AD-WGAN在OA、AA、Kappa系数3个方面对比原方法分别提升了0.98%、2.21%、0.54%; SPCA-ADGAN在OA、AA、Kappa系数3个方面对比原方法分别提升了0.33%、0.90%、0.18%. 这说明了本文提出的方法的有效性. 同时, 通过SPCA-ADGAN与AD-WGAN的比较, 可以发现引入Wasserstein距离对分类结果的提升效果更加显著.

|
图 10 Pavia University数据集分类效果图 |
| 表 5 Indian Pines数据集消融实验对比(%) |
| 表 6 Indian Pines数据集消融实验对比(%) |
4 结论
本文提出了一种用于HSI分类的SPCA-AD-WGAN模型方法. 该方法使用SPCA方法将高光谱数据集进行降维; 在ADGAN网络的基础上, 引入了单独的分类器, 用于样本的分类任务; 同时, 将Wasserstein距离引入模型, 更新判别器与生成器的损失, 缓解GAN网络存在的模式崩塌问题, 进而提高对高光谱图像的分类精度. 在Indian Pines、Pavia University两个高光谱数据集上进行了实验. 结果表明, 本文提出的方法与2DCNN, 3DCNN, 3DGAN、SpectralFormer、ADGAN相比, 提出的方法总体获得了更高的分类精度, 在样本数量较少的类别也取得了较好的结果, 证明了本文提出方法的有效性.
| [1] |
Audebert N, Le Saux B, Lefèvre S. Deep learning for classification of hyperspectral data: A comparative review. IEEE Geoscience and Remote Sensing Magazine, 2019, 7(2): 159-173. DOI:10.1109/MGRS.2019.2912563 |
| [2] |
覃寓媛, 佃松宜. 多尺度3D胶囊网络高光谱图像分类. 计算机系统应用, 2022, 31(12): 220-226. DOI:10.15888/j.cnki.csa.008837 |
| [3] |
Chen YS, Lin ZH, Zhao X, et al. Deep learning-based classification of hyperspectral data. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(6): 2094-2107. DOI:10.1109/JSTARS.2014.2329330 |
| [4] |
Chen YS, Zhao X, Jia XP. Spectral–spatial classification of hyperspectral data based on deep belief network. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(6): 2381-2392. DOI:10.1109/JSTARS.2015.2388577 |
| [5] |
Pan B, Shi ZW, Xu X. R-VCANet: A new deep-learning-based hyperspectral image classification method. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(5): 1975-1986. DOI:10.1109/JSTARS.2017.2655516 |
| [6] |
Zhang HK, Li Y, Zhang YZ, et al. Spectral-spatial classification of hyperspectral imagery using a dual-channel convolutional neural network. Remote Sensing Letters, 2017, 8(5): 438-447. DOI:10.1080/2150704X.2017.1280200 |
| [7] |
肖志云, 蒋家旭, 倪晨. 自适应深层残差3D-CNN高光谱图像快速分类算法. 计算机辅助设计与图形学学报, 2019, 31(11): 2017-2029. DOI:10.3724/SP.J.1089.2019.17552 |
| [8] |
Chen YS, Zhu L, Ghamisi P, et al. Hyperspectral images classification with Gabor filtering and convolutional neural network. IEEE Geoscience and Remote Sensing Letters, 2017, 14(12): 2355-2359. DOI:10.1109/LGRS.2017.2764915 |
| [9] |
Szegedy C, Liu W, Jia YQ, et al. Going deeper with convolutions. Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston: IEEE, 2015. 1–9.
|
| [10] |
Gong ZQ, Zhong P, Yu Y, et al. A CNN with multiscale convolution and diversified metric for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(6): 3599-3618. DOI:10.1109/TGRS.2018.2886022 |
| [11] |
王雷全, 周家梁, 林瑶. 基于全局注意力信息交互的高光谱图像分类. 计算机系统应用, 2023, 32(5): 28-35. DOI:10.15888/j.cnki.csa.009120 |
| [12] |
巩传江, 臧德厚, 郭金, 等. 基于小波卷积网络的高光谱图像分类. 计算机系统应用, 2023, 32(7): 23-34. DOI:10.15888/j.cnki.csa.009186 |
| [13] |
吴鸿昊, 王立国, 石瑶. 高光谱图像小样本分类的卷积神经网络方法. 中国图象图形学报, 2021, 26(8): 2009-2020. DOI:10.11834/jig.210103 |
| [14] |
Goodfellow I, Pouget-Abadie J, Mirza M, et al. Generative adversarial networks. Communications of the ACM, 2020, 63(11): 139-144. DOI:10.1145/3422622 |
| [15] |
Zhan Y, Hu D, Wang YT, et al. Semisupervised hyperspectral image classification based on generative adversarial networks. IEEE Geoscience and Remote Sensing Letters, 2018, 15(2): 212-216. DOI:10.1109/LGRS.2017.2780890 |
| [16] |
Zhu L, Chen YS, Ghamisi P, et al. Generative adversarial networks for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(9): 5046-5063. DOI:10.1109/TGRS.2018.2805286 |
| [17] |
Feng J, Yu HP, Wang L, et al. Classification of hyperspectral images based on multiclass spatial-spectral generative adversarial networks. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(8): 5329-5343. DOI:10.1109/TGRS.2019.2899057 |
| [18] |
Zhong ZL, Li J, Clausi DA, et al. Generative adversarial networks and conditional random fields for hyperspectral image classification. IEEE Transactions on Cybernetics, 2020, 50(7): 3318-3329. DOI:10.1109/TCYB.2019.2915094 |
| [19] |
Li JJ, Du Q, Li YS, et al. Hyperspectral image classification with imbalanced data based on orthogonal complement subspace projection. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(7): 3838-3851. DOI:10.1109/TGRS.2018.2813366 |
| [20] |
Odena A, Olah C, Shlens J. Conditional image synthesis with auxiliary classifier GANs. Proceedings of the 34th International Conference on Machine Learning. Sydney: JMLR.org, 2017. 2642–2651.
|
| [21] |
Chavdarova T, Fleuret F. SGAN: An alternative training of generative adversarial networks. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake: IEEE, 2018. 9407–9415.
|
| [22] |
Wang JJ, Gao F, Dong JY, et al. Adaptive DropBlock-enhanced generative adversarial networks for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(6): 5040-5053. DOI:10.1109/TGRS.2020.3015843 |
| [23] |
Licciardi G, Marpu PR, Chanussot J, et al. Linear versus nonlinear PCA for the classification of hyperspectral data based on the extended morphological profiles. IEEE Geoscience and Remote Sensing Letters, 2012, 9(3): 447-451. DOI:10.1109/LGRS.2011.2172185 |
| [24] |
Jiang JJ, Ma JY, Chen C, et al. SuperPCA: A superpixelwise PCA approach for unsupervised feature extraction of hyperspectral imagery. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(8): 4581-4593. DOI:10.1109/TGRS.2018.2828029 |
| [25] |
Paoletti ME, Haut JM, Plaza J, et al. Deep learning classifiers for hyperspectral imaging: A review. ISPRS Journal of Photogrammetry and Remote Sensing, 2019, 158: 279-317. DOI:10.1016/j.isprsjprs.2019.09.006 |
| [26] |
Hamida AB, Benoit A, Lambert P, et al. 3-D deep learning approach for remote sensing image classification. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(8): 4420-4434. DOI:10.1109/TGRS.2018.2818945 |
| [27] |
Hong DF, Han Z, Yao J, et al. SpectralFormer: Rethinking hyperspectral image classification with transformers. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5518615. |
 2024, Vol. 33
2024, Vol. 33



