2. 北京工业大学 信息学部, 北京 100124
2. Faculty of Information Technology, Beijing University of Technology, Beijing 100124, China
污水处理是实现水资源循环利用的重要举措[1]. 作为污水处理系统的核心设备, 鼓风机具有输送, 增压和曝气等重要作用[2]. 然而, 由于鼓风机长期不间断运行, 轴承的磨损与故障不可避免, 这将对系统正常运行造成严重影响[3–5]. 因此, 准确预测轴承温度并及时进行维护保养对保证鼓风机正常运行至关重要[6].
传统的鼓风机轴温监测方法多采用温度传感器进行实时监测, 例如热电偶温度计[7], 霍尔效应传感器[8], 微机电系统温度传感器[9], 电感-电容温度传感器[10], 基于纳米颗粒的测温技术[11]. 然而, 这类方法无法预知轴温的变化趋势, 只能进行现场监控和发生异常后报警处理, 不能提前采取预防措施[12].
近年来, 利用物联网技术和传感器网络, 通过对鼓风机系统进行全面监测和数据采集, 可以获取海量的数据资源[13]. 然后, 借助智能技术[14], 从数据中提取运行规律和趋势, 预测鼓风机轴温未来的变化趋势, 为鼓风机轴承温度监控提供新的解决方案[15]. 例如, 王新[16]利用回归参数算法建立系统模型, 捕捉相关变量与轴温的关系, 实现轴承超温的提前预警. 卢艳霞[17]引入支持向量机作为预测模型, 从历史监测数据中挖掘变量间的关联性, 实现轴承温度的预测. 然而, 由于轴承温度变化具有季节特性[18], 上述统计方法中静态模型难以模拟鼓风机动态运行规律, 导致预测精度降低[19].
为了实现轴承温度的动态预测, 马明骏等[20]利用威布尔比例风险-长短期记忆神经网络模型建立轴承温度与外界环境和风机运行特性的映射关系, 实现鼓风机在不同运行状态下轴承温度的趋势预测. Li等[21]利用径向基神经网络建立鼓风机系统的仿真模型. 该模型结合历史数据和实时数据, 利用最小二乘算法对参数进行实时调整并预测轴承的工作温度. 动态智能方法分析了数据的动态规律, 并挖掘出轴承温度随时间变化的季节特征[22]. 然而, 由于鼓风机系统复杂的运行机理, 上述模型需要大量参数进行模拟, 容易导致过拟合问题[23].
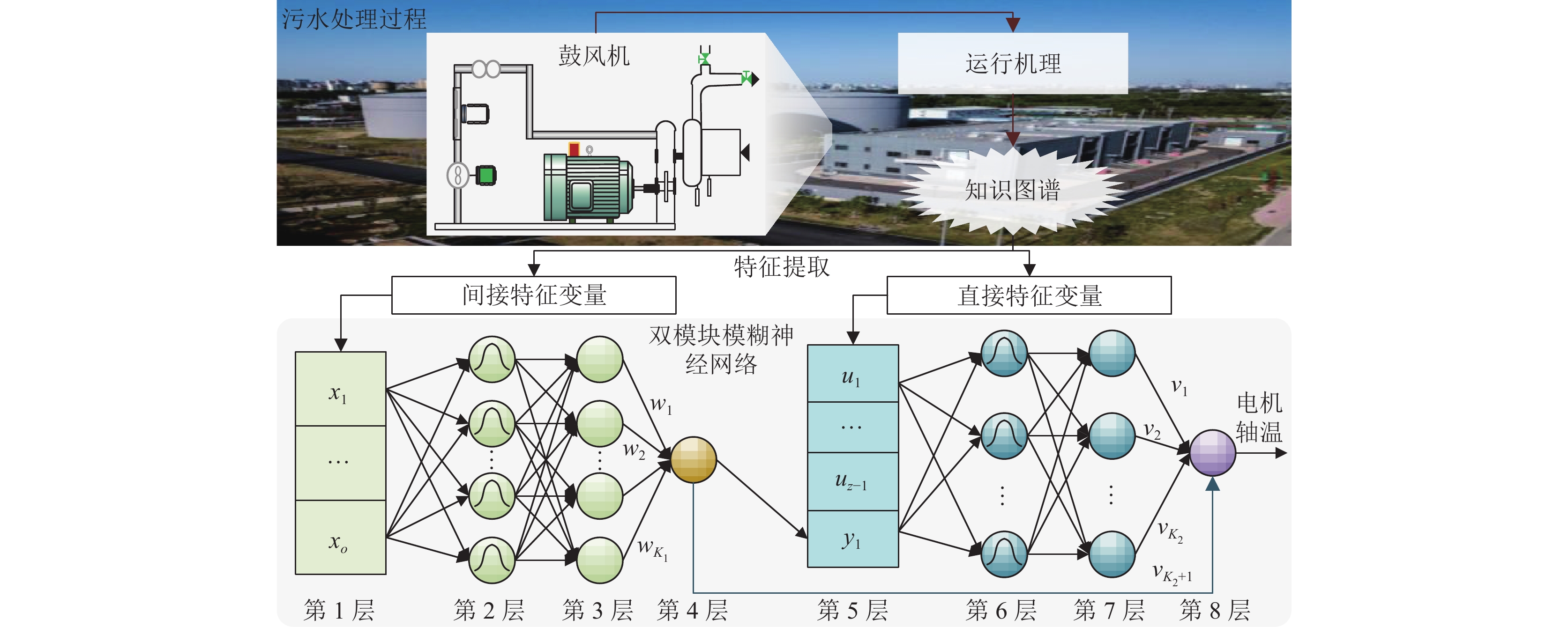
为此, 本文提出一种基于知识图谱的鼓风机轴承温度智能预测方法, 实现鼓风机轴温的实时监测. 这有助于提前发现和解决潜在问题, 提高鼓风机设备的稳定性. 本文提出的方法具有以下优势: 1)采集与鼓风机运行相关的数据和信息, 包括环境因素, 运行状态等, 从而实现鼓风机系统的全面, 准确描述; 利用统计方法分析运行特点, 获取与轴承温度相关的影响因素; 2)采用知识图谱系统地描述鼓风机运行系统和相关因素之间的关系, 辨识直接相关特征和间接相关特征; 3)设计一种双模块模糊神经网络(dual modular fuzzy neural network, DMFNN), 通过对DMFNN进行推理, 综合考虑各种因素对轴温的影响, 实现轴承温度的高精度, 实时预测.
1 相关知识 1.1 污水处理过程鼓风机运行概况污水处理过程中, 一级处理过程主要用于去除水体中的悬浮物, 沉淀物等. 这些物质会堵塞鼓风机和其他处理设备. 二级处理过程是全流程的核心环节, 利用生化反应去除水体中的有害物质, 如磷和氮等物质. 这个过程需要鼓风机为生化反应提供充足的氧气, 它们通过向反应池中注入空气来促进微生物的新陈代谢和分解过程. 三级处理过程可以深度去除水体中的悬浮物, 有机污染物等.
鼓风机稳定运行对污水处理过程的稳定性和经济性至关重要. 设备温度是影响鼓风机稳定运行的关键因素. 通过温度监控, 可以及时发现和解决设备过热, 故障预防, 优化运行效率. 图1为鼓风机运行原理图.
1.2 知识图谱知识图谱是描述研究对象中实体(节点)及其关系(边)的一种具有有向关系的知识网, 由多个<实体, 关系, 实体>的三元组构成. 其中, 知识图谱被形式化定义为G={G1, G2, …, Gd, …, GD}, Gd=(Ei, Rij, Ej)为第d个三元组, Ei是第i个实体, Ej是第j个实体, Rij是第i个和第j个实体的有向关系, D是知识图谱中三元组的数量.
知识图谱将实体和关系组织成知识网, 以便清晰, 完整地展示实体之间的各种关联关系, 具有强大的语义表达能力, 使机器能够理解和处理知识.
2 基于知识图谱的鼓风机轴温智能预测方法 2.1 鼓风机轴温相关因素电机轴承温度过高易导致鼓风机发生故障. 对电机轴承温度进行监测和控制可以降低其他故障的发生概率, 保证鼓风机的使用寿命. 因此, 通过对鼓风机轴温进行监测, 保证其在正常范围内对于保障污水处理系统的稳定运行至关重要.
根据鼓风机运行机理, 电机的轴温受多种相关因素影响, 主要包括以下方面.
进气状态: 相关变量有进口空气温度, 压力, 流量. 进气状态会影响到鼓风机的进气阻力和进气流量, 容易导致电机轴承温度过高, 甚至引起安全事故.
轴承状态: 主要指轴承磨损度和润滑度. 轴承磨损或润滑不足均造成轴温超过正常限值.

|
图 1 鼓风机运行原理图 |
电机状态: 电机电流, 电机绕组温度, 电机振动情况等过高会导致电机散热不良, 使电机的轴承温度急速升高.
其他因素: 过大的电机负载, 过高的电机转速或者过长的电机运行时间均使轴承温度升高. 此外, 鼓风机的出口压力直接影响电机的输出功率和流量, 从而影响到其运行效率和能耗. 出口压力过大会造成电机轴温过高.
2.2 基于知识图谱的特征提取(1) 基于运行机理的知识图谱建立
为了构建知识图谱, 利用鼓风机机理知识获取描述鼓风机系统中的实体(节点)及其关系(边). 基于鼓风机轴温相关因素分析, 鼓风机系统中具体实体见表1.
鼓风机系统中实体间的关系包括: 线性相关(正相关, 负相关), 非线性相关和不相关. 例如, 过高的负荷导致轴承温度升高, 具有正相关关系; 高轴承润滑度可以减少轴承摩擦损失和轴承温度, 其呈现负相关关系; 某些因素可能会在一定范围内对轴承温度产生正相关影响, 超过一定范围则产生负相关影响, 呈现非线性相关; 进口空气温度与出口空气压力不相关. 图2为构建的知识图谱.
从知识图谱可以看出, 鼓风机系统主要由电机和风机两部分组成, 两部分之间通过联轴器连接. 主电机电流受到设备在工作时产生, 消耗的功率的影响, 即主电机负荷的影响; 流量, 入口温度影响主电机负荷. 主电机负荷与三相绕组温度呈正相关. 影响电机运行的关键因素为主电机电流, 轴承温度和三相绕组温度. 其中, 影响电机轴承温度的因素有鼓风机罩内的环境温度, 轴承润滑度和电机振动值. 影响风机运行的关键因素为风机低速轴轴承温度, 高速轴轴承温度, 进气温度, 高速轴振动值和出口空气压力. 影响风机高速轴温度的因素有导叶开度和轴承润滑度.
| 表 1 鼓风机系统中的实体 |

|
图 2 鼓风机运行关系知识图谱 |
(2) 特征提取
为了提取预测鼓风机电机轴温的相关变量, 利用知识图谱从上述变量中提取特征变量. 核心思想为: 1) 提取间接特征变量: 该类特征变量可以直接预测风机轴承温度, 再通过风机轴承温度的变化来间接地预测电机轴承温度; 2) 提取直接特征变量: 该类变量与电机轴温直接相关, 实现电机轴承温度的直接预测. 表2为实体中的间接特征变量和直接特征变量.
2.3 基于双模块模糊神经网络的轴温预测针对鼓风机运行系统中提取的直接特征变量与电机轴温的关系简单且存在较强的关联性, 可以利用简单的模型进行表达; 间接特征变量与电机轴温的关系复杂且相关关系被弱化, 需要复杂的模型捕获相关关系. 由于直接特征变量与间接特征变量提供的信息不同, 需要不同的特征处理方式, 单一建模方法难以同时处理两种特征变量, 导致检测效果差. 因此, 设计了双模块模糊神经网络预测轴温, 如图3所示.
| 表 2 间接/直接特征变量总结 |
|
图 3 基于双模块模糊神经网络的轴温预测模型 |
(1) 预测模型
结合知识图谱和双模块模糊神经网络(knowledge graph-based DMFNN, KG-DMFNN)的轴温预测模型由两个模块组成, 共8层, 各层具体表达式如下.
模块1输入层(第1层): 该层神经元将间接特征变量输入到预测模型. 该层神经元的输出为x(t)=[x1(t), x2(t), …, xo(t)], xi(t)为t时刻第i个间接特征变量, i=1, 2, …, o, o是间接特征变量的数量.
模块1径向基函数层(第2层): 该层共有K1个神经元. 该层利用高斯函数作为隶属函数, 用于模拟间接特征变量与轴温的关系. 该层t时刻第j个神经元的输出为高斯隶属函数的乘积, 计算公式为:
| $ {\mu _j}(t) = \prod\limits_{i = 1}^o {{{\rm{e}}^{ - \frac{{{{\left( {{x_i}(t) - {c_{ij}}(t)} \right)}^2}}}{{2{{\left( {{\sigma _{ij}}(t)} \right)}^2}}}}}} $ | (1) |
其中, 第1层神经元的输出xi(t)作为第2层神经元的输入, μj(t)为第j个神经元的输出值, j=1, 2, …, K1, K1为该层神经元的数量, e为自然对数的底数, cij(t)和σij(t)分别为t时刻第1个模块中第j个神经元第i个输入对应的中心和宽度.
模块1归一化层(第3层): 该层由K1个神经元组成. 第2层神经元的输出μj(t)作为该层神经元的输入. 该层t时刻第j个神经元的输出
| $ {\varphi _j}(t) = \frac{{{\mu _j}(t)}}{{\displaystyle\sum\limits_{j = 1}^{{K_1}} {{\mu _j}(t)} }} $ | (2) |
模块1输出层(第4层): 该层具有一个神经元, t时刻输出y1(t)计算为:
| $ {y_1}(t) = \sum\limits_{j = 1}^{{K_1}} {{w_j}(t){\varphi _j}(t)} $ | (3) |
其中, 第3层神经元的输出
模块2输入层(第5层): 该层神经元用于将从鼓风机中提取的直接特征变量输入到预测模型. 该层神经元的输出为u(t)=[u1(t), u2(t), …, uz(t)], 其中, u1(t), …, uz–1(t)为t时刻直接特征变量, z–1是直接特征变量的数量, uz(t)为第4层神经元的输出值y1(t).
模块2径向基函数层(第6层): 该层包括K2个神经元. 神经元利用高斯隶属函数模拟直接特征变量与轴温的关系. 该层第n个神经元的输出ηn(t)为:
| $ {\eta _n}(t) = \prod\limits_{m = 1}^{\textit{z}} {{{\rm{e}}^{ - \frac{{{{\left( {{u_m}(t) - {\alpha _{mn}}(t)} \right)}^2}}}{{2{{\left( {{\beta _{mn}}(t)} \right)}^2}}}}}} $ | (4) |
其中, um(t)为该层神经元的输入, m=1, 2, …, z, z是第5层神经元的数量, n=1, 2, …, K2, K2为该层神经元的数量, αmn(t)和βmn(t)分别为t时刻第2个模块中第n个神经元第m个输入对应的中心和宽度.
模块2归一化层(第7层): 该层的神经元数量为K2. t时刻第n个神经元的输出为:
| $ {\phi _n}(t) = \frac{{{\eta _n}(t)}}{{\displaystyle\sum\limits_{n = 1}^{{K_2}} {{\eta _n}(t)} }} $ | (5) |
其中, 第6层神经元的输出值ηn(t)为该层神经元的输入, ϕn(t)为第2个模块中第n个神经元输出.
集成输出层(第8层): 该层具有一个神经元, 该层神经元的输入向量为[ϕ1(t), …, ϕK2(t), y1(t)], 该层神经元输出计算为:
| $ y(t) = \left( {\sum\limits_{n = 1}^{{K_2}} {{v_n}(t){\phi _n}(t)} } \right) + {v_{{K_2} + 1}}(t){y_1}(t) $ | (6) |
其中, vn(t)为第2个模块中归一化层和集成输出层之间的第n个权值,
(2) 学习目标函数
KG-DMFNN学习的目标是模拟鼓风机运行系统中特征变量与轴承温度的非线性映射关系. 学习目标函数的设置可以明确训练目标, 通过最小化目标函数值, 使神经网络在训练过程中逐步学习到期望的结果. 在本文中, 将误差平方和作为目标函数, 公式如下:
| $ E(t) = \frac{1}{2}\sum\limits_{t = 1}^D {\left( {y(t) - {y_d}(t)} \right)} $ | (7) |
其中, D为样本数, E(t)为目标函数的输出值, yd(t)为轴承温度的真实值. 通过最小化式(7), 即最小化预测结果与实际结果之间的差异, 实现KG-DMFNN对鼓风机运行系统的模拟仿真.
(3) 学习算法
为了提高模型预测精度, 根据式(7), 利用梯度下降算法对KG-DMFNN的参数同时进行更新. 参数更新公式为:
| $ \left\{\begin{gathered} C(t + 1) = C(t) - \lambda \Delta C(t) \\ \varTheta (t + 1) = \varTheta (t) - \lambda \Delta \varTheta (t) \\ W(t + 1) = w(t) - \lambda \Delta w(t) \\ \varPhi (t + 1) = \varPhi (t) - \lambda \Delta \varPhi (t) \\ \varLambda (t + 1) = \varLambda (t) - \lambda \Delta \varLambda (t) \\ V(t + 1) = v(t) - \lambda \Delta v(t) \\ \end{gathered}\right. $ | (8) |
其中, λ为学习因子, C(t)=[c1(t), c2(t), …, cK1(t)],cj(t)=[c1j(t), c2j(t), …, coj(t)], Θ(t)=[σ1(t), σ2(t), …, σK1(t)],σj(t)=[σ1j(t), σ2j(t), …, σoj(t)], W(t)=[w1(t), w2(t), …,wK1(t)], Φ(t)=[α1(t), α2(t), …, αK2(t)], αj(t)=[α1j(t), α2j(t),…, αzj(t)], Λ(t)=[β1(t), β2(t), …, βK2(t)], βj(t)=[β1j(t), β2j(t),…, βzj(t)], V(t)=[v1(t), v2(t), …, vK2+1(t)], ∆C(t), ∆Θ(t), ∆w(t), ∆Φ(t), ∆Λ(t), ∆v(t)为模型参数的梯度, 可以指示模型参数的更新方向, 指导网络向更优的方向调整.
由于模块1的输出既作为模块2的输入也是集成输出层的输入, 模块2和集成输出层的误差均反馈到模块1. 因此, 模块1的中心∆C(t), 宽度∆Θ(t), 权值∆w(t)对应的梯度同时受到模块2和集成输出层的影响. 模块2的输出仅作用于集成输出层, 因此, 模块2的中心∆Φ(t), 宽度∆Λ(t), 权值∆v(t)对应的梯度仅依赖于集成输出层.
(4) 鼓风机轴温预测流程
结合上述内容, 为了准确预测鼓风机轴温, 首先, 根据知识图谱确定直接特征变量和间接特征变量; 其次, 利用梯度下降算法同时更新KG-DMFNN的参数C(t), Θ(t), W(t), Φ(t), Λ(t), V(t), 具体流程如下.
步骤1: 初始化最大迭代次数, 滑窗数P, 双模块模糊神经网络隐含层节点数K1和K2, 参数C(1), Θ(1), W(1), Φ(1), Λ(1), V(1), 初始时刻t=1.
步骤2: 获取当前t时刻样本, 利用知识图谱确定模型的直接特征变量值和间接特征变量值.
步骤3: 若时刻t<P, 对1: t组输入和输出变量分别归一化处理, 根据式(1)–式(3)计算模块1输出y1(1), …, y1(t); 根据式(4)–式(6)计算模块2输出y(1), …, y(t)并得到误差e(1), …, e(t); 利用梯度下降算法完成网络参数梯度求解. 若t≥P, 对t–P+1: t组输入和输出变量分别归一化处理, 根据式(1)–式(3)计算模块1输出y1(t–P+1), …, y1(t); 根据式(4)–式(6)计算模块2输出y(t–P+1), …, y(t)并得到误差e(t–P+1), …, e(t); 利用梯度下降算法完成网络参数梯度求解.
步骤4: 根据式(8)获得C(t+1), Θ(t+1), W(t+1), Φ(t+1), αj(t+1), Λ(t+1), β(t+1), V(t+1).
步骤5: 根据式(1)–式(6)预测下一时刻轴温并存储数据.
步骤6: 判断是否可以获取新数据, 若可以获取, 则t=t+1并返回步骤2; 否则, 停止计算.
3 实验结果与分析 3.1 实验设计为了验证KG-DMFNN的有效性, 本文利用来自某实际污水处理厂鼓风机系统运行的真实数据为实验样本进行仿真实验, 并分析相应实验结果. 算法运行环境为英特尔酷睿i7-11700, 内存16 GB和Windows 10操作系统. 选取均方根误差(root mean square error, RMSE), 平均绝对百分比误差(mean absolute percent error, MAPE)和决定系数(R-square, R2)作为评价指标, 评估所提出方法的轴温预测精度. 上述指标的具体计算公式为:
| $ \left\{\begin{gathered} {\textit{RMSE}} = \sqrt {{{\displaystyle\sum\limits_{t = 1}^T {{{\left( {y(t) - \hat y(t)} \right)}^2}} } / T}} \\ {\textit{MAPE}} = \frac{1}{T}\displaystyle\sum\limits_{t = 1}^T {\frac{{\left| {y(t) - \hat y(t)} \right|}}{{\hat y(t)}}} \\ {R^2} = {\text{1}} - \frac{{\displaystyle\sum\nolimits_{t = 1}^T {{{\left( {\hat y(t) - y(t)} \right)}^2}} }}{{\displaystyle\sum\nolimits_{t = 1}^T {{{\left( {\hat y(t) - \bar y(t)} \right)}^2}} }} \\ \end{gathered}\right. $ | (9) |
其中, y(t)是模型输出, ŷ(t)为实际轴承温度值, ȳ(t)为实际轴承温度的平均值, T为样本总数.
本文采用鼓风机系统2022.7.1–2022.12.31中的运行数据, 采样间接为4 h. 可采集到的变量包括: 出口空气压力(KPa), 高速轴驱动端轴承温度(°F), 高速轴振动值(mm/s), 进口空气温度(°F), 主电机电流(A), 主电机轴承温度(°F). KG-DMFNN中模块1和2中的中心, 宽度和权值从(0, 1)被随机选取, 模块1的径向基函数层和归一化层神经元数均为4, 模块2的径向基函数层和归一化层神经元数均3, 学习率为0.005, 最大迭代次数为50, 滑窗数为18. 由于鼓风机系统的过程变量对鼓风机电机轴承温度具有季节性的影响, 因此, 本方法基于滑动窗口进行在线实时预测. 具体过程如下: 在训练阶段使用t–18, t–17, …, t–1时刻的样本训练本文提出模型, 然后使用该模型来预测时间t的输出. 该模型的训练和测试过程交替进行.
3.2 实验结果与分析本节通过对轴温进行实时预测和超前预测以验证本文提出的模型. 首先, 对现场采集的数据进行预处理(异常处理和归一化处理). 其次, 根据基于知识图谱的特征提取方法确定出口空气压力, 高速轴驱动端轴承温度和高速轴振动值为鼓风机预测模型的间接特征变量; 进口空气温度, 主电机电流和历史主电机轴承温度为鼓风机预测模型的间接特征变量.
(1) 鼓风机轴温实时预测结果
为了证明所提出的方法, 分别与基于间接特征变量的FNN (I-FNN), 基于直接特征变量的FNN (D-FNN)和基于两类特征变量的FNN (ID-FNN)进行比较. I-FNN, D-FNN和ID-FNN的结构分别为3-4-4-1, 3-3-3-1和6-7-7-1. 其中, S1-S2-S3-S4的物理意义为输入神经元数-径向基函数层神经元数-归一化层神经元数-输出层神经元数; I-FNN, D-FNN和ID-FNN的中心, 宽度和权值均从(0, 1)被随机选取, 其他参数与训练过程与KG-DMFNN一致.
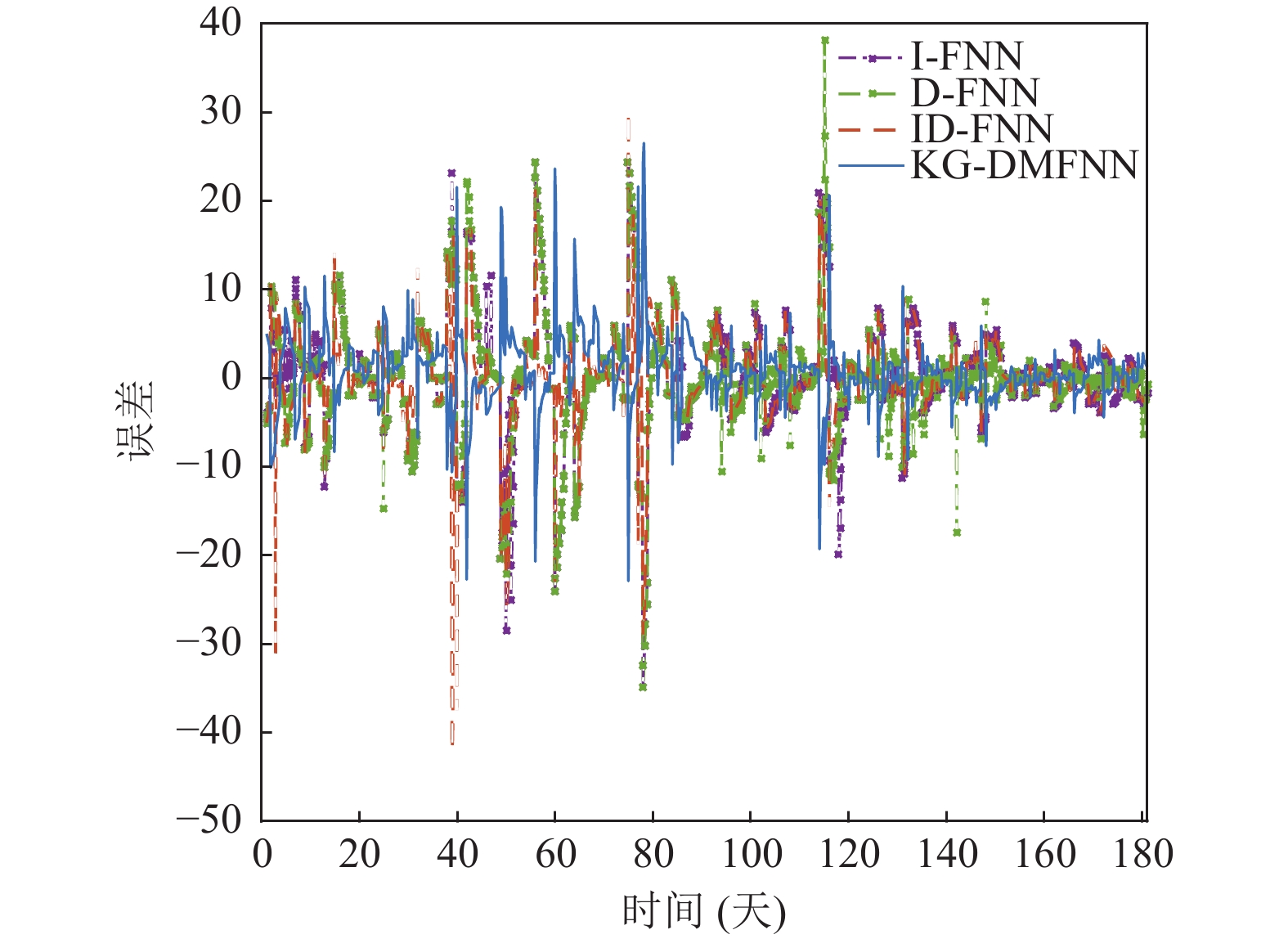
电机轴温的实验结果如图4–图6所示. 图4为4种方法的训练RMSE结果. 从图4中可以看出, I-FNN, D-FNN和ID-FNN的训练RMSE呈现锯齿状, 在多个训练过程难以收敛到较好的RMSE. 相比于I-FNN, D-FNN和ID-FNN, KG-DMFNN在训练过程较为稳定, 具有最好的训练效果. 图5和图6展示了方法预测输出和预测误差. 由于I-FNN, D-FNN和ID-FNN具有多个过大的训练RMSE值, 这说明其无法对鼓风机系统进行高精度建模, 导致预测效果差. 从图6中可以看出, 除了第38天和42天的预测点, KG-DMFNN的预测误差均小于其他对比方法, 具有良好的预测效果.
此外, 表3提供了KG-DMFNN, I-FNN, D-FNN, ID-FNN, 反向传播神经网络(back propagation neural network, BPNN)[24], 长短时记忆神经网络(long short term memory neural network, LSTM)和基于FNN的自回归模型(autoregressive model with FNN, FNN-AR)的测试RMSE, 测试MAPE和测试R2. 指标结果的平均值(mean)根据20次实验独立运行获得. I-FNN和D-FNN的输入变量仅包括部分变量, 由于提供的特征信息不足, 导致模型训练和预测效果差. 相比于ID-FNN, KG-DMFNN引入知识图谱将特征变量分为间接特征变量和直接特征变量, 同时利用两个模块提供合适的特征处理方式以期望提高建模精度. FNN-AR利用轴承温度的历史数据, 而没有考虑到特征变量对输出的影响. 由于特征变量包含大量当前的运行信息, KG-DMFNN可以提取特征变量与轴承温度的非线性关系, 具有比FNN-AR更好的运行效果. 相比于LSTM和BPNN, KG-DMFNN引入高斯隶属函数降低的数据噪声对建模效果的影响. 测试RMSE指标比测试MAPE指标对较大误差值更加敏感. 虽然KG-DMFNN的测试MAPE (0.0499)比BPNN的测试MAPE大, 但是KG-DMFNN的测试RMSE (3.5648) 比BPNN的测试MAPE小. 这说明BPNN存在非常显著的误差, 而KG-DMFNN的预测误差相对较小. 根据表3结果可以看出, KG-DMFNN对测试样本具有最小的测试RMSE (3.5648)和最大的测试R2 (0.9001), 这证明了本文提出方法的有效性.

|
图 4 训练过程的RMSE |

|
图 5 测试过程的预测输出值 |

|
图 6 测试过程的预测误差值 |
| 表 3 不同算法的性能比较 |
(2) 鼓风机轴温超前预测结果
为了进一步评估KG-DMFNN的有效性, 将待建模的鼓风机系统设计为:
| $ h(t) = g(\varGamma (t - 6)) $ | (10) |
其中, h(t)为t时刻的轴温, Γ(t–6)为t–6时刻特征变量, g(·)为特征变量与轴温的映射关系. 因此, KG-DMFNN利用当前时刻特征变量Γ(t)预测t+6时刻轴温h(t+6).
为验证方法性能, KG-DMFNN与I-FNN, D-FNN和ID-FNN进行比较. 本节对比实验与第3.2节第(1)部分参数设置一致. 轴温超前预测结果如图7–图9所示. 其中, 图7为4种方法的训练RMSE结果. 从图7中可以看出, 本文提出的方法在训练全程均具有较小的训练RMSE, 可以获得具有高训练精度的模型. 图8, 图9为测试样本的预测输出和预测误差. 相比于图5, 图6, 由于轴温超前预测任务复杂, 该种情况下的预测效果变差. 与I-FNN, D-FNN和ID-FNN相比, KG-DMFNN预测结果与真实轴温曲线最接近. 该方法提高了模型的总体性能.
此外, 从表4可以看出, 由于I-FNN和D-FNN中少量的特征变量提供的信息不足, 其具有较差的预测效果. ID-FNN将特征变量同时输入到模型, 无法适应不同特征信息的提取需求, 导致检测效果差. 由于FNN-AR忽略了特征变量与轴承温度的相关关系, FNN-AR的预测表现不佳. 在超前预测需求下, LSTM侧重于捕捉长期依赖关系, 从而可以较好地处理复杂的超前预测任务. 根据表4的实验结果, LSTM的预测性能仅次于KG-DMFNN. BPNN难以克服数据噪声对预测效果的影响, 会存在非常显著的误差值. 根据表4的结果可以看出, KG-DMFNN对测试样本具有最小的测试RMSE (4.7374), 最小的测试RMSE (0.0709)(除了BPNN和LSTM)和最大的测试R2(0.8191). 相较于其他方法, KG-DMFNN总体预测性能较好, 可以更好地满足轴温预测要求, 保证预测准确性和实时性.

|
图 7 训练过程的RMSE值 |

|
图 8 测试过程的预测输出值 |
4 结论与展望
本文提出一种基于知识图谱的鼓风机轴温智能预测方法, 通过实验验证了方法性能, 得出以下结论.
|
图 9 测试过程的预测误差值 |
| 表 4 不同算法的性能比较 |
(1)在特征选取方面, 利用知识图谱分析鼓风机运行系统中变量的相关关系, 直观地展示了与主电机轴承温度相关的直接特征变量和间接特征变量, 提高了特征选取的可解释性. 同时, 通过对比实验, 验证了KG-DMFNN相较于ID-FNN在预测轴温时的优势.
(2)在模型设计方面, 应用双模块模糊神经网络分别模拟直接和间接特征变量与主电机轴温间的映射关系, 通过提供适当的隐含层神经元数量, 保证模型简洁性的基础上提高模型的预测精度. 通过两组对比实验, 验证了模型相较于其他方法的在预测结果上具有优势.
(3)针对污水处理过程鼓风机中主电机轴温预测问题, 实验部分展示KG-DMFNN在轴温实时预测和超前预测两种情况下的仿真结果. 可以看出, KG-DMFNN可以较好地满足轴温预测要求, 保证预测的准确性.
由于鼓风机系统中各种变量的采集频率难以同步, 未来工作将着重研究在多时间尺度数据下的轴承预测问题.
| [1] |
Han HG, Sun CX, Wu XL, et al. Dynamic-static model for monitoring wastewater treatment processes. Control Engineering Practice, 2023, 132: 105424. DOI:10.1016/j.conengprac.2022.105424 |
| [2] |
周月侠. 污水处理中鼓风机智能控制方案的研究. 现代制造技术与装备, 2021, 57(4): 131-132. DOI:10.3969/j.issn.1673-5587.2021.04.046 |
| [3] |
Sun YL, Zhang C, Zhao X, et al. Transient thermal analysis model of damaged bearing considering thermo-solid coupling effect. Sensors, 2022, 22(21): 8171. DOI:10.3390/s22218171 |
| [4] |
Dindar A, Hong I, Garg A, et al. A methodology to measure power losses of rolling element bearings under combined radial and axial loading conditions. Tribology Transactions, 2022, 65(1): 137-152. DOI:10.1080/10402004.2021.1937760 |
| [5] |
Huang HB, Yi TH, Li HN, et al. Sparse Bayesian identification of temperature-displacement model for performance assessment and early warning of bridge bearings. Journal of Structural Engineering, 2022, 148(6): 04022052. DOI:10.1061/(ASCE)ST.1943-541X.0003354 |
| [6] |
Wang BS, Liu YQ, Zhang B, et al. Analysis of the temperature characteristics of high-speed train bearings based on a dynamics model and thermal network method. Chinese Journal of Mechanical Engineering, 2022, 35(1): 104. DOI:10.1186/s10033-022-00789-y |
| [7] |
Li N, Yun XH, Han QK, et al. Characterization method of rolling bearing operation state based on feature information fusion. Journal of Mechanical Science and Technology, 2023, 37(3): 1197-1205. DOI:10.1007/s12206-023-0207-1 |
| [8] |
Kumar D, Suman KG. Noninvasive temperature measuring and early fault detecting system for manufacturing industry. MAPAN-Journal of Metrology Society of India, 2019, 34(4): 541-550. |
| [9] |
Scott S, Sadeghi F, Peroulis D. Highly reliable mems temperature sensors for 275 °C applications-part 1: Design and technology. Journal of Microelectromechanical Systems, 2013, 22(1): 225-235. DOI:10.1109/JMEMS.2012.2227947 |
| [10] |
Li C, Feng QY, Hong YP, et al. Wireless LC conformal temperature sensor based on Ag film (9912-K FL) for bearing temperature measurement. Nanomaterials, 2022, 12(17): 2899. DOI:10.3390/nano12172899 |
| [11] |
Zhang P, Pan AZ, Yan K, et al. High stability temperature sensors by CdTe quantum dots encapsulated in SiO2/PVA hybrids for bearing rotating elements. Materials Today Communications, 2023, 34: 105456. DOI:10.1016/j.mtcomm.2023.105456 |
| [12] |
Nikolic N, Antonic Z, Doric J, et al. An analytical method for the determination of temperature distribution in short journal bearing oil film. Symmetry, 2020, 12(4): 539. DOI:10.3390/sym12040539 |
| [13] |
Wu XL, Han HG, Qiao JF. Data-driven intelligent warning method for membrane fouling. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(8): 3318-3329. DOI:10.1109/TNNLS.2020.3041293 |
| [14] |
Lv MZ, Liu SX, Su XM, et al. General log-linear Weibull model combining vibration and temperature characteristics for remaining useful life prediction of rolling element bearings. Shock and Vibration, 2020, 2020: 8829823. |
| [15] |
Cheng Y, Wang ZW, Zhang WH. A novel condition-monitoring method for axle-box bearings of high-speed trains using temperature sensor signals. IEEE Sensors Journal, 2019, 19(1): 205-213. DOI:10.1109/JSEN.2018.2875072 |
| [16] |
王新. 基于回归参数算法的风机轴承超温故障预警. 数字技术与应用, 2020, 38(2): 98, 180. |
| [17] |
卢艳霞. 基于机器学习算法在风机故障预测中的分析与应用[硕士学位论文]. 北京: 华北电力大学(北京), 2018.
|
| [18] |
Ai SY, Wang WZ, Wang YL, et al. Temperature rise of double-row tapered roller bearings analyzed with the thermal network method. Tribology International, 2015, 87: 11-22. DOI:10.1016/j.triboint.2015.02.011 |
| [19] |
Hu YG, Li H, Shi PP, et al. A prediction method for the real-time remaining useful life of wind turbine bearings based on the wiener process. Renewable Energy, 2018, 127: 452-460. DOI:10.1016/j.renene.2018.04.033 |
| [20] |
马明骏, 赵海心, 姜孝谟, 等. 基于LSTM-WPHM模型的风机轴承故障报警与寿命预测方法. 风机技术, 2022, 64(3): 63-71. DOI:10.16492/j.fjjs.2022.03.0010 |
| [21] |
Li J, Xiao JW, Hu YL, et al. Temperature prediction of multi-Factor rolling bearings based on RBF neural network. Proceedings of the 2017 Chinese Automation Congress. Jinan: IEEE, 2017. 425–429.
|
| [22] |
Laubichler C, Kiesling C, da Silva M M, et al. Data-driven sliding bearing temperature model for condition monitoring in internal combustion engines. Lubricants, 2022, 10(5): 103. DOI:10.3390/lubricants10050103 |
| [23] |
Xiao XC, Liu JX, Liu DS, et al. SSAE-MLP: Stacked sparse autoencoders-based multi-layer perceptron for main bearing temperature prediction of large-scale wind turbines. Concurrency and Computation: Practice and Experience, 2021, 33(17): e6315. DOI:10.1002/cpe.6315 |
| [24] |
Mokhtari HA, Mirbagheri SA. Investigation and modeling of a hybrid activated sludge system for municipal wastewater treatment using multi-layer perceptron neural networks. Desalination and Water Treatment, 2021, 210: 123-133. DOI:10.5004/dwt.2021.26599 |
 2024, Vol. 33
2024, Vol. 33


