在业务流程挖掘研究中, 预测型业务流程监控尤为关键. 通过分析日志数据预测流程的未来特征, 如下一步活动、实例总时间以及剩余时间等, 可以实现业务流程的优化, 提升企业效率. 特别是利用日志数据预测流程实例的剩余执行时间, 被认为是业务流程监控的重要研究任务. 通过预测实例的剩余时间, 有助于发现流程中的瓶颈和低效环节, 为流程优化和改进提供依据. 近年来, 利用深度学习预测流程实例剩余时间的效果日趋显著. 它已在多个实际案例中证明了可行性与有效性. 这表明, 深度学习在业务流程挖掘与优化方面具有广阔的应用前景.

但现阶段的基于深度学习的剩余时间预测还存在着以下一些问题.

当前, 剩余时间预测中的轨迹前缀相关研究多集中于轨迹前缀序列本身的分析, 较少考虑事件的时间特征. 仅依据事件序列信息进行预测, 忽视了时间对流程执行的重要影响. 不同事件发生的时间间隔会对流程执行产生显著影响, 如果忽略时间特征, 很难准确捕捉流程的动态变化.

尽管当前一些方法已经采用了较为先进的Transformer模型, 在流程实例剩余时间预测效果上相较于以前的模型取得了显著提升, 但这些方法的预测精度仍未达到令人满意的水平.

从模型结构来看, Transformer模型通过自注意力机制来学习轨迹前缀数据中的长距离依赖关系, 对轨迹前缀序列的全局模式建模效果较好. 但是, Transformer对轨迹前缀序列数据的局部依赖关系学习能力较为薄弱. 自注意力机制过于关注全局的依赖关系, 而较少建模轨迹前缀序列的局部依赖关系. 这主要源于Transformer模型的编码器部分只包含自注意力层. 尽管自注意力能够较好地建模全局依赖关系, 但也稀释了局部邻近位置的关联. 这一缺陷限制了Transformer在剩余时间预测上的效果, 也为进一步优化该模型提供了方向.

为提高剩余时间预测的精度, 本研究对Transformer模型进行了优化. 首先, 在模型中加入时间特征, 以增强对事件间的时间依赖关系的建模. 过去更多依赖事件的顺序特征, 而忽略了时间相关性, 这降低了预测的准确性和可靠性. 其次, 改进了Transformer模型的结构, 在Transformer编码器输出后加入了局部依赖增强模块. 局部依赖增强模块通过卷积层通过卷积核提取局部特征, 最大池化层进行下采样. 卷积操作能够学习特征之间的局部相关性, 而池化通过聚合邻近特征实现信息整合. 局部依赖增强模块的加入增强了模型对轨迹前缀的局部模式的建模能力. 卷积层的多层堆叠结构使得模块可以学习复杂的局部依赖关系. 与自注意力机制不同, 卷积专注于局部相邻特征, 可以提供互补的局部依赖建模.

通过引入时间特征和局部依赖捕捉模块, 改进后的模型兼具自注意力的全局建模能力和卷积的局部建模能力. 全局信息和局部特征的融合提升了模型对轨迹前缀的表示能力, 增强了流程实例剩余时间预测的准确性.

1 研究现状

剩余时间预测按照其发展的不同阶段, 主要可以分为3个不同的研究方向, 分别为: 基于统计学的剩余时间预测方法、基于机器学习的剩余时间预测方法、基于深度学习的剩余时间预测方法.

早期的剩余时间预测方法主要为基于统计学的剩余时间预测方法, 主要通过运用统计学方法对收集到的事件日志数据进行整理、统计和分析, 从而确定每项活动的平均执行时间和概率分布, 以此来实现对剩余时间的预测. van der Aalst等^[1]从业务流程的日志当中挖掘出标注的变迁系统进行预测, Folino等^[2]在van der Aalst等^[1]的研究基础上提出了分布式变迁随机Petri网进行预测, 基于当前执行状态, 生成n个可能的剩余时间, 对这n个结果求平均值来预测剩余处理时间. 高俊涛等^[3]在传统的变迁系统的基础上提出了在线预测模型的构建及剩余时间预测方法, 设计出了能够及时反映系统运行规律的增量式模型构建计算算法, 降低了传统方法的预测波动性, 提高了预测模型的可信度. 基于统计学的剩余时间预测方法虽然对流程有结构化的理解, 便于分析和解释. 但是其预测精度较低, 并且其在大规模的事件日志当中的预测表现并不理想.

基于机器学习的剩余时间预测方法主要是通过一些机器学习方法辅助预测剩余时间. Polato等^[4]将朴素贝叶斯和支持向量机应用到基于变迁的预测系统当中, 以辅助预测的方式参与到了剩余时间预测当中. Pandey等^[5]将隐马尔可夫模型应用于标注的变迁系统. 尽管机器学习在处理复杂数据集、发现潜在模式和关系方面更为强大, 但是机器学习的算法在处理非线性、复杂的关系时可能会受限.

近几年深度学习的火爆带动了研究者利用深度学习技术进行剩余时间预测. Navarin等^[6]提出了一种LSTM结构来预测轨迹的完成时间. Tax等^[7]首先利用onehot编码技术将事件数据转化为特征向量输入LSTM模型进行预测. Taymouri等^[8]首次将生成式对抗网络应用到业务过程领域中用于剩余事件预测. 随着深度学习的不断发展, 一些新兴出现的神经网络模型和神经网络机制也得到了应用. 倪维健等^[9]通过引入双向循环神经网络^[10], 并且对不同轨迹长度的分别训练剩余时间预测模型, 提高了业务流程剩余时间预测的准确度. Bukhsh等^[11]通过结合了长程记忆, 以及自注意力机制, 建立了大量的事件序列和相应的输出之间的依赖关系, 并且使用Transformer模型^[12]实现了对业务流程的剩余时间的准确预测. 徐兴荣等^[13]将Word2Vec^[14]应用于事件的表示, 为预测模型提供了高质量的输入事件向量. 并且提出了带有注意力机制的双向准循环神经网络, 以及迁移学习的方法对数据量较少的长轨迹前缀进行训练并获得了较好的预测结果. 郭娜等^[15]提出了一种可解释特征分层的方法, 通过LightGBM^[16]对事件日志进行特征组合选择, 在保证了准确率的前提下减少了特征选取的数量, 提升了预测的效果.

2 预备知识

本节将对业务流程剩余时间预测任务的相关知识进行详细介绍, 并给出相关定义.

定义1. 轨迹. 轨迹是一种有序的事件序列, 表示为$\sigma = \left\langle {{e_1}, {e_2}, {e_3}, \cdots , {e_n}} \right\rangle $. ${e_i}$代表第${{i}}$个执行的事件.

定义2. 事件. 事件是业务系统中某个活动被实际执行的具体实例, 也是业务流程的构成的基本元素. 表示为元组$e = \left\{ {CaseID, activity, time} \right\}$, $CaseID$为当前事件所属的流程的实例的$ID$, $activity$为当前事件的活动名称, $time$为事件的发生时间. 定义2阐述了进行流程挖掘所必需的基础事件属性模型. 虽然实际的事件日志可能包含更丰富的信息, 如资源、经办人或资源使用量等, 为了研究的普遍适用性, 本研究将使用基本属性来探讨剩余时间预测的方法.

定义3. 轨迹前缀. 轨迹前缀是通过截取轨迹$\sigma $的前$k$个事件得到的, 其中轨迹${\sigma _k}$代表截取了前$k$个事件, 记作${\sigma _k} = \left\langle {{e_1}, \cdots , {e_k}} \right\rangle $. 轨迹前缀的剩余时间可以表示为:

$ RT(\sigma , k) = {e_{\left| \sigma \right|.}}Tim{e_{{\mathrm{end}}}} - {e_{k.}}Tim{e_{{\mathrm{end}}}} $

(1)

定义4. 流程实例. 流程实例是一个流程从开始到结束的完整执行, 表示为$ {\textit{z}} = \left\{ {Caseid, \sigma , {P_{\{ 1, 2, \cdots , n\} }}} \right\} $, $CaseID$为流程实例的$ID$, $\sigma $为流程实例中的轨迹, $ {P_{\{ 1, 2, \cdots , n\} }} $为该流程的其他属性.

定义5. 事件日志. 事件日志是流程实例的集合, 是业务系统具体的执行情况记录, 表示为$L = \{ {{\textit{z}}_1}, {{\textit{z}}_2}, \cdots , {{\textit{z}}_{\left| l \right|}} \}$.

3 剩余时间预测方法

本节将详细介绍本研究中提出的剩余时间预测方法, 本研究通过Transformer编码器、局部依赖增强模块和时间特征的融合, 实现了对轨迹前缀序列的全局和局部特征的学习和挖掘, 以精确预测流程实例的剩余时间.

3.1 事件日志数据处理 3.1.1 前缀序列处理

轨迹前缀序列获取的主要处理步骤为: 初始化一个字典来存储每条轨迹的前缀序列, 初始化一个集合来存储所有不同的前缀. 遍历轨迹日志中的每一条轨迹, 对于每条轨迹, 逐步生成从长度为1到全长的所有前缀子序列. 在生成每个前缀时, 需要判断它是否已经存在于前缀集合中, 如不存在, 就将其添加到集合中, 同时也添加到该条轨迹的前缀序列中. 最终, 返回存储每条轨迹前缀序列的字典以及包含所有前缀的集合. 具体见算法1.

算法1. 获取轨迹前缀序列

输入: 轨迹日志traces.

输出: 前缀轨迹序列 prefix_seqs, 前缀轨迹集合 prefixes.

算法过程:

prefix_seqs = {} # 存储每个trace的前缀序列

prefixes = set() # 前缀集合, 使用set避免重复

for trace in traces:

　prefix_seq = [] # 当前trace的前缀序列

　for i in range(len(trace)):

　　prefix = trace[1:i+1] # 生成前缀轨迹

　　if prefix not in prefixes:

　　　prefixes.add(prefix) # 如果前缀轨迹不在集合中, 添加

　　prefix_seq.append(prefix) # 将前缀添加到当前trace的前缀序列中

　prefix_seqs[trace] = prefix_seq # 将当前trace的前缀序列存储到字典中

return prefix_seqs, prefixes

基于上述算法获得了轨迹前缀向量. 这为后续的时间特征融合和模型训练提供了高质量的输入数据, 有助于提高模型的预测准确性和泛化能力.

3.1.2 时间-轨迹前缀序列处理

在处理轨迹前缀序列的基础上, 对每个序列的时间进行处理, 以便将时间转化为特征输入模型中.

在获取轨迹的前缀序列后, 需要进一步处理时间特征, 以便将其转换为模型的输入. 具体步骤如下: 从日志数据中提取时间相关字段, 将提取的时间日期转换为datetime格式, 从中分别提取年、月、日作为新的特征. 对前缀序列进行填充(padding), 使其达到统一长度. 最后, 将年、月、日特征拼接到前缀序列的前部. 最终, 包含时间特征的前缀序列将作为模型的输入.

算法2. 时间-轨迹前缀序列处理

输入: 经过算法1处理的轨迹数据 trace_data.

输出: 融合时间特征的轨迹编码序列 encoded_data.

算法过程:

time_features = {} # 存储时间特征的字典

encoded_sequences = [] # 存储编码后的轨迹序列列表

max_length = 0 # 最大序列长度

# 步骤1: 提取时间相关特征

for data_point in trace_data:

　datetime_feature = extract_datetime_features(data_point['datetime'])

　if datetime_feature not in time_features:

　　time_features[data_point['datetime']] = datetime_feature

# 步骤2: 对轨迹序列进行编码

for trajectory in trace_data:

　encoded_trajectory = []

　for data_point in trajectory:

　　transformed_point = transform_time_feature(time_features[data_point['datetime']])

　　encoded_trajectory. append(transformed_point)

　encoded_sequences. append(encoded_trajectory)

　if len(encoded_trajectory) > max_length:

　　max_length = len(encoded_trajectory)

# 步骤3: 序列等长padding和特征融合

for i, sequence in enumerate(encoded_sequences):

　while len(sequence) < max_length:

　　sequence. append(padding_element) # padding_element是预定义的填充元素

　encoded_sequences[i] = concatenate_features(sequence, trajectory_features[i])

# 输出处理后的数据

encoded_data = encoded_sequences

return encoded_data

将时间特征和轨迹前缀序列进行了编码和融合之后, 确保了每个轨迹都被等长表示, 同时含有丰富的时间信息. 这样的处理标准化了输入数据格式, 使其适合于大多数监督学习算法.

3.2 时间特征融合

在流程实例的剩余时间预测任务中, 充分利用事件过程中的时间信息至关重要, 因为时间特征对于准确预测剩余执行时间起着关键作用. 事件日志数据中往往蕴含着许多复杂的时间模式, 如周期性、趋势性等, 这些对于准确预测剩余时间至关重要. 但如果方法无法有效利用时间信息, 就难以从数据中学习到这些有价值的时间模式知识, 从而导致预测性能的下降. 当前的剩余时间预测方法中一般只会考虑相对时间特征, 相对时间信息只反映了事件之间的先后顺序和时间间隔, 但无法体现事件发生的绝对时间信息. 然而, 不同的时间可能对应着完全不同的时间环境, 如工作日/节假日, 这些时间环境的动态变化会极大影响流程的执行效率和剩余时间. 缺乏绝对时间信息, 模型将难以适应这种时间环境的动态变化. 绝对时间信息可以帮助发现流程事件发生的时间规律, 如工作日/节假日的周期性规律、特定时间段的高峰/低峰等. 同时也有助于发现异常事件, 如在非工作时间突然发生的事件. 缺少绝对时间信息, 模型将无法高效发现和利用这些规律性和异常情况.

为获取语义合理且富有区分度的时间表示, 本研究构建了一个可学习的时间编码模块来捕捉时间戳的内在时间信息, 通过融合相对时间和绝对时间这两类特征, 来提高模型对时间特征的利用.

3.2.1 绝对时间信息的嵌入表示

具体而言, 将原始时间戳拆解为“年-月-日”的粒度, 并为每个粒度定义可学习的嵌入映射, 以学习时间点的语义表示:

$ {E_{{\mathrm{year}}}}, {E_{{\mathrm{month}}}}, {E_{{\text{day}}}} = Embedding(y, m, d) $

(2)

其中, ${E_{{\mathrm{year}}}}, {E_{{\mathrm{month}}}}, {E_{{\mathrm{day}}}}$分别表示对年、月、日进行嵌入映射学习所得到的嵌入表示.

随后采用特征级拼接, 在特征维度上堆叠各时间粒度的Embedding向量, 以获得一个固定长度的时间特征表达:

$ {E_{{\mathrm{absolute}}}} = [{E_{{\mathrm{year}}}};{E_{{\mathrm{month}}}};{E_{{\mathrm{day}}}}] $

(3)

其中, $[;]$表示特征拼接操作.

3.2.2 相对时间信息的嵌入表示

相对时间信息能有效捕捉轨迹前缀序列中时间的动态变化. 本研究主要考虑以下两种相对时间差值.

(1) 流程首事件的时间戳差值

这个时间差值表示当前事件与整个流程第1个事件之间的时间间隔, 反映了事件发生的相对时间位置. 用公式表示为:

$ \Delta {t_{{\mathrm{start}}}} = {t_{{\mathrm{current}}}} - {t_{{\mathrm{start}}}} $

(4)

其中, $ {t_{{\mathrm{current}}}} $是当前事件的时间戳, $ {t_{{\mathrm{start}}}} $是当前实例下第1个事件的时间戳.

(2) 与相邻事件的时间戳差值

这个时间差值表示当前事件与前一个事件之间的时间间隔, 捕捉了事件之间的局部时间关系. 用公式表示为:

$ \Delta {t_{{\mathrm{prev}}}} = {t_{{\mathrm{current}}}} - {t_{{\mathrm{prev}}}} $

(5)

其中, $ {t_{{\mathrm{prev}}}} $是相邻事件的时间戳.

将得到的时间差特征进行嵌入表示:

$ {E_{{\mathrm{start}}}} = Embedding(\Delta {t_{{\mathrm{start}}}}) $

(6)

$ {E_{{\mathrm{prev}}}} = Embedding(\Delta {t_{{\mathrm{prev}}}}) $

(7)

最后, 将这两个嵌入表示在特征维度上进行拼接, 得到最终的相对时间嵌入表示.

$ {E_{{\mathrm{relative}}}} = [{E_{{\mathrm{start}}}};{E_{{\mathrm{prev}}}}] $

(8)

为了将绝对时间信息和相对时间信息融合, 首先将绝对时间嵌入表示和相对时间嵌入表示在特征维度上拼接:

$ {E_{{\mathrm{combined}}}} = [{E_{{\mathrm{absolute}}}};{E_{{\mathrm{relative}}}}] $

(9)

为使该时间表示适配后续模块, 将一个线性层将拼接后的时间Embedding投影到与位置编码相同的嵌入空间:

$ {E_{{\mathrm{proj}}}} = {W_f}({E_{{\mathrm{combined}}}}) + {b_f} $

(10)

其中, $ {E_{{\mathrm{proj}}}} $投影后的时间嵌入表示. $ {W_f} $和${b_f}$分别为线性层的权重和偏置参数.

这种基于时间粒度拆解与重构的时间建模方式综合了下述优点.

(1) 借助Embedding学习各时间粒度的语义信息, 增强时间表示的语义性.

(2) 拼接不同粒度的表示并映射到固定长度, 保证时间表达的判别性与可融合性.

通过增强对时间特征的建模, 该时间编码机制提供了绝对时间和相对时间信息的多粒度融合, 增强了模型学习时间依赖的能力. 这为预测业务流程的剩余时间提供了支持.

3.3 基于局部依赖增强的Transformer剩余时间预测模型

处理剩余时间预测的问题上, 当前深度学习模型已取得长足进展. 许多研究采用循环神经网络或注意力机制来挖掘轨迹前缀序列的内在依赖关系. 例如, Transformer模型通过multi-head attention机制捕捉轨迹前缀中的全局信息. 然而, 仅依赖全局上下文的方法在学习局部特征时存在弱点. 而卷积神经网络具有直接对局部特征进行建模的优势.

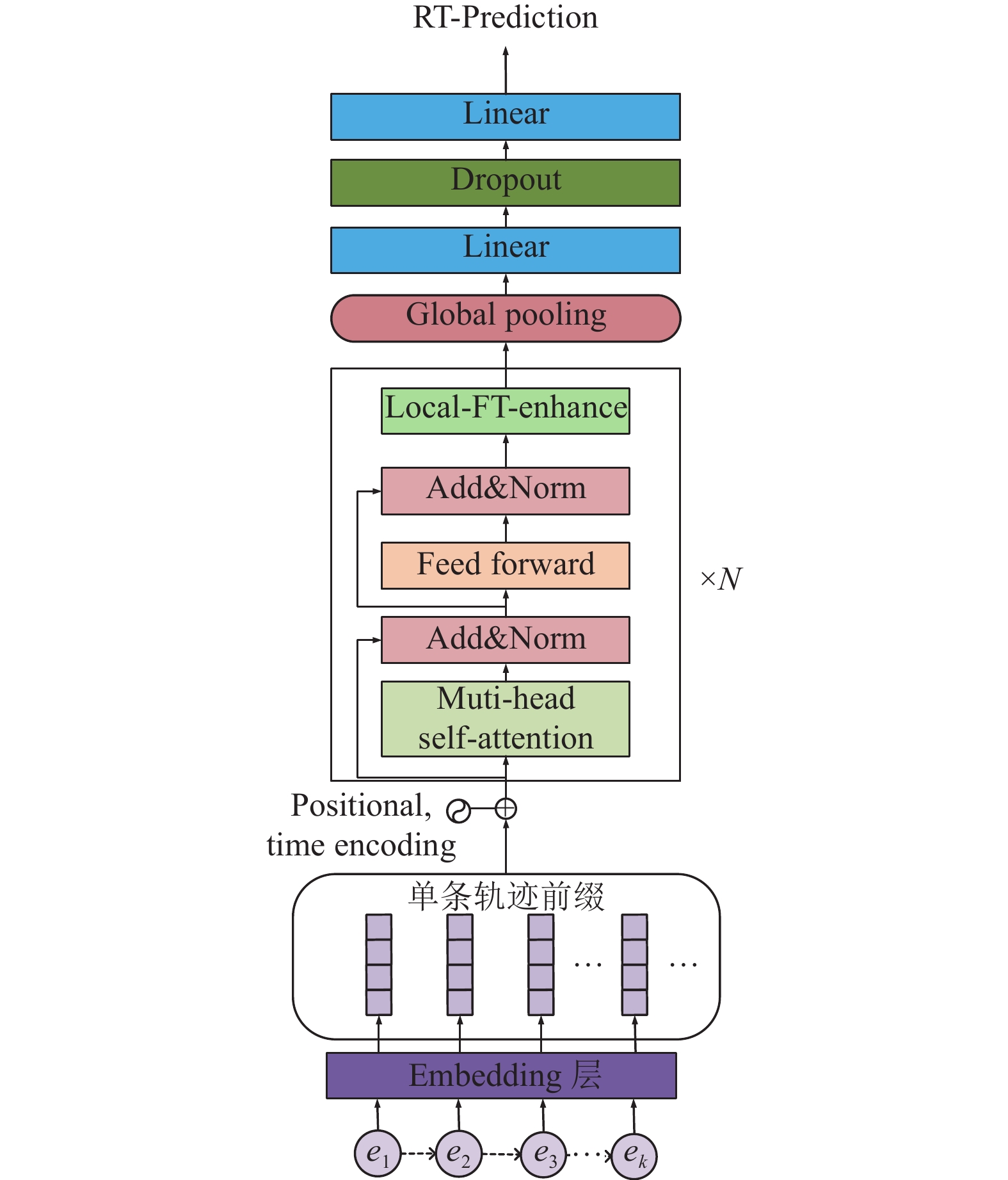
本节基于 Transformer模型, 结合局部依赖增强, 提出了一种剩余时间预测模型, 命名为 LEN-Transformer模型. 该模型在 Transformer编码器的基础上, 通过引入局部依赖增强层, 增强了模型对局部特征的提取能力, 同时保留了 Transformer的全局信息捕捉能力. LEN-Transformer模型的整体结构如图1 所示. 模型主要由嵌入层(Embedding)、位置编码(positional encoding)、时间编码(time encoding)、Transformer编码器模块(Transformer block)、局部依赖增强模块以及全连接层组成.

具体如下, 模型输入为业务流程前缀轨迹特征. 嵌入层将其映射为固定维度的嵌入向量, 位置编码捕捉前缀轨迹中的位置信息, 时间编码捕捉时间信息. 嵌入向量通过 Transformer 编码器处理, 自注意力机制学习前缀轨迹中的全局依赖关系. Transformer 的输出经过局部依赖增强, 学习轨迹前缀中的局部依赖关系. 最后, 通过线性层预测业务流程的剩余时间.

3.3.1 局部依赖增强

尽管自注意力机制能够有效建模长期依赖, 但由于自注意力计算基于整个序列, 因此难以捕捉局部依赖关系, 影响了剩余时间预测的准确性. 为解决这一问题, 设计了局部增强网络 (local enhancement network, LEN). LEN是基于卷积神经网络(CNN)设计的模块, 通过卷积滤波器对输入序列进行卷积操作, 从而增强局部依赖关系的捕捉能力.

首先将输入数据X传递给卷积层(Conv1d), 它对特征进行加权求和, 并添加偏置.

$ C = {{Conv1d}}(X;{W_{{\mathrm{conv}}}}, {b_{{\mathrm{conv}}}}) $

(11)

其中, ${W_{{\mathrm{conv}}}}$代表卷积层的权重, ${b_{{\mathrm{conv}}}}$而是相应的偏置. 这一步的作用是提取局部特征, 以补充Transformer编码器输出的全局信息.

为了加强模型的泛化能力, 在卷积操作之后应用批量归一化(BatchNorm1d). 加速训练过程, 减少模型对初始权重的依赖.

$ C' = {{BatchNorm1d}}(C) $

(12)

使用ELU (指数线性单元)作为非线性激活函数, ELU能够提供平滑的非线性变换, 有助于缓解梯度消失问题, 并能捕捉到更加复杂的数据特征.

$ E = {{ELU}}(C' ) $

(13)

最后, 在卷积激活后引入最大池化层(MaxPool1d), 以实现特征的下采样.

$ M = {{MaxPool1d}}(E) $

(14)

池化层通过汇总邻近数据点的信息, 提取出代表局部区域的重要特征, 同时显著减少数据维度, 降低了模型的计算复杂度. 这一操作不仅减轻了模型对局部位置的敏感性, 而且加强了特征的平移不变性, 这对于剩余时间预测具有重要意义.

通过该模块有效地从Transformer编码器输出中提取出局部和全局信息, 为剩余时间预测提供了更加丰富和精细化的特征表示.

3.3.2 Transformer编码器

Transformer编码器是LEN-Transformer模型的核心组件, 负责捕捉业务流程前缀轨迹中的全局依赖关系. Transformer编码器由多个相同的层堆叠而成, 每一层包括两个子层: 多头自注意力机制(multi-head attention)和前馈神经网络(feed forward network).

多头自注意力机制(multi-head attention)允许模型在不同的表示子空间中并行地学习注意力权重. 给定输入矩阵 , multi-head attention的计算过程如下:

通过线性变换得到Query矩阵、Key矩阵和Value矩阵:

$ Q = X{W^Q}, K = X{W^K}, V = X{W^V} $

(15)

其中, Q、K、V是查询(Query)矩阵、键(Key)矩阵和值(Value)矩阵. $ X $是输入矩阵, $ {W^Q}、{W^K}、{W^V} $是对应的权重矩阵.

将$ Q, K, V $划分为h个头, 每个头的维度为${d_{{k}}}$, 再对每个头并行计算注意力:

$ \begin{array}{*{20}{c}} {Attention\left( {{Q_i}, {K_i}, {V_i}} \right) = {\textit{Softmax}}\left( {\dfrac{{{Q_i}K_i^{\text{T}}}}{{\sqrt {{d_{{k}}}} }}} \right)} \end{array} \cdot {V_i} $

(16)

其中, ${d_{{k}}}$为缩放因子.

最后将所有头的输出拼接起来, 经过另一个线性变换得到最终的多头注意力输出:

$ MultiHead(Q, K, V) = Concat({h_{1}}, \cdots, {h_h}){W^O} $

(17)

其中, $ {W^O} $为另一个可学习的权重矩阵.

多头自注意力的输出经过残差连接和层归一化后, 再输入到前馈神经网络中. 前馈神经网络包含两个线性变换, 中间用ReLU激活函数:

$ {\textit{FFN}}(x) = ReLU(x \cdot {W_1} + {b_1}) \cdot {W_2} + {b_2} $

(18)

其中, ${W_1}$、${W_2}$为可学习的权重矩阵, 为偏置向量.

前馈神经网络的输出同样经过残差连接和层归一化, 作为当前Transformer编码器层的最终输出. 通过堆叠多个这样的编码器层, 模型能够学习到输入序列中的深层次全局依赖关系.

Transformer编码器通过自注意力机制有效地捕捉了业务流程前缀轨迹的长期依赖, 但对局部依赖的建模能力有限. 因此, 本文引入了局部增强模块来增强模型对局部依赖的提取能力, 与Transformer编码器形成互补, 共同构建了LEN-Transformer模型用于业务流程剩余时间预测任务.

4 实验结果与分析

本节将根据提出的基于Transformer和局部依赖增强模块以及时间特征的剩余时间预测方法, 进行实验和研究.

4.1 实验数据

本研究使用了来自4TU Center for Research平台公开的7个事件日志数据集, 分别为Production、BPIC_2015_1、BPIC_2015_2、BPIC_2015_3、BPIC_2015_4、BPIC_2015_5、Helpdesk. 其中, Helpdesk事件日志记录了某公司技术支持系统的问题处理流程. Production事件日志包含了某生产车间2012年1–3月部分产品的生产流程数据. BPIC2015事件日志来自2015年BPI挑战赛, 共包含以上5个事件日志, 事件日志数据集的详细统计信息如表1所示.

4.2 实验评价标准

本研究选用平均绝对误差MAE (mean absolute error)作为评价模型预测精度的指标. MAE是一种广泛使用的统计误差度量方法, 通过计算预测结果与真实值之间差异的平均绝对值, 来反映模型的预测准确程度. 相比之下, 平均平方误差(MSE)由于计算误差的平方, 容易受到个别大误差的影响. 而MAE则能够更好地反映平均误差的整体情况. $MAE$的定义如下:

$ MAE = \frac{1}{{|D|}}\sum\limits_{{\sigma _{{k}}} \in D} {} |f({\sigma _k}) - RT({\sigma _k})| $

(19)

其中, 函数$ f({\sigma _k}) $表示轨迹前缀$ {\sigma _{{k}}} $的剩余时间的预测值, $ RT({\sigma _k}) $表示相应的真实剩余时间. $D$代表测试数据集中的轨迹前缀集合, $ {\sigma _{{k}}} $表示截取自完整轨迹$\sigma $的前${{k}}$个事件的子序列. $MAE$的值越低, 说明预测的效果越好.

4.3 实验结果 4.3.1 不同方法对比实验

本研究在7个事件日志数据集上, 与LSTM、ProcessTransformer、Auto-encoded、EFH等方法进行了对比实验. 表2展示了不同方法在各数据集上的平均绝对误差(MAE)结果.

本研究提出的方法与LSTM、ProcessTransformer、Auto-encoded和EFH方法在7个公开数据集上的对比结果表明, 本方法总体上优于其他方法, 能够达到更高的预测精度.

具体来看, 在BPIC2015系列的5个数据集上, 本方法的平均绝对误差(MAE)在11.91–29.99之间, 而其他方法的MAE普遍在17.544–151.565之间, 本方法较之降低了约10%–80%. 结果表明本研究方法可以更好地建模这类较大规模的日志数据.

在Production生产流程数据集上, 本方法MAE仅为4.23, 比其他方法减小了约40%, 展现了显著的优势.

Helpdesk技术支持日志上, 本方法MAE虽高于EFH方法, 但仍低于LSTM等其他方法. 由于Transformer擅长捕捉长距离依赖, 而LSTM更擅长处理短期依赖. Helpdesk的平均轨迹长度仅为4.66, 极短的平均轨迹长度意味着模型在预测时可参考的历史信息极为有限, 不足以发挥Transformer的优势.

本方法集全局依赖和局部依赖关系于一体的技术设计, 使其可以适应规模不同、复杂度不同的业务流程日志, 在多个公开数据集上展现出较强的泛化性能, 这也验证了方法的有效性.

4.3.2 模块验证实验

为验证所提出方法中时间特征模块和局部依赖增强模块的有效性, 设计了消融实验对模型进行模块析构, 分析每个组件的贡献.

具体实验设计如下.

以Transformer为基础模型, 分别将带有时间特征的轨迹前缀特征的局部依赖增强模块的Transformer编码器(命名为TF-LEN-Transformer), 带有局部依赖增强模块的Transformer原编码器(命名为LEN-Transformer), 以及不带有时间特征的轨迹前缀特征的原编码器(命名为EN-Transformer), 在中长轨迹前缀上的数据集上对比实验, 以验证时间特征对剩余时间预测的影响, 以及改进后的局部依赖增强机制能否提升预测的实际效果. 具体的实验结果如表3所示.

从表3中可以看出, 相比EN-Transformer, 无论是引入局部依赖增强模块的LEN-Transformer模型, 还是在此基础上进一步加入时间特征的TF-LEN-Transformer, 在所有数据集上的预测误差都有明显的降低. 这验证了本研究提出的两个改进模块的有效性.

具体来看, LEN-Transformer相比EN-Transformer减小了50%以上的误差, 如在BPIC_2015_1数据集的误差由39.472降至18.38. 这显示出局部依赖增强模块的引入增强了模型对轨迹前缀序列的局部特征的建模和利用能力. 卷积操作可以捕捉局部元素之间的依赖关系. 这种局部特征学习减小了预测误差.

而TF-LEN-Transformer在LEN-Transformer的基础上加入时间特征后, 进一步减小了预测误差. 如在Production数据集上, 误差由7.07降至4.287. 这显示时间特征的加入增强了模型对时间相关性的建模. 绝对时间编码和相对时间编码提供了多粒度的时间信息, 使模型更准确地把握轨迹前缀序列中的时间依赖关系, 提升了预测性能.

本研究提出的LEN-Transformer和TF-LEN-Transformer作为通用的剩余时间预测建模框架, 在多个公开业务流程挖掘的数据集上都取得了较好的提升. 这充分验证了局部依赖增强模块和时间特征对剩余时间预测具有一定的优化效果. 未来工作将在此基础上继续优化模块设计和特征提取, 以获得对时间相关性和局部特征建模更优的模型, 从而提高复杂业务流程的剩余时间预测的准确性.

5 结论与展望

本研究通过建立带时间特征的Transformer模型和局部依赖增强模块, 来预测业务流程的剩余时间. 该方法在Transformer模块中加入时间特征, 增强对事件时间依赖关系的建模. 另外, 方法在Transformer编码器后接入了局部增强模块, 用于学习轨迹前缀序列的局部依赖, 与Transformer的全局模式建模能力形成互补. 实验结果显示, 在多个公开日志数据上, 本研究方法相比LSTM等算法提高了10%–80%的预测精度, 这验证了模型的融合有效提升了预测能力.

虽然本研究所提的方法提高了预测的效果, 但是如何在轨迹流程相对较短的数据集中提高预测精度还需要进一步的研究. 未来可继续改进卷积模块的结构, 以获得更好的短轨迹流程的剩余时间预测模型. 这也是未来进一步研究的方向.