在当前社会, 随着共享经济、电子商务和互联网技术的蓬勃发展, 线上外卖和快递业务已经渗透到人们日常生活的方方面面. 社会生活节奏的加快, 使得用户对服务质量的需求持续攀升. 与此同时, 由于线上业务规模的扩大, 小批量、小质量、多频次的配送需求呈爆发式增长, 传统专业配送在配送价格、服务质量、时效性等方面面临着前所未有的考验[1]. 为了降低物流企业的配送成本, 同时满足特定时段激增的订单量, 一种基于共享经济理念的众包配送模式被提出并得到了应用[2].
基于众包的配送模式通常指的是众包配送平台将配送任务合理地分配给社会中的闲置劳动力, 在降低物流企业成本, 减少资源浪费的同时也缓解高峰期的配送压力. 常见的众包配送模式可分为平台派单模式和骑手抢单模式. 在抢单模式下, 众包平台在接收到订单后将这一时刻产生的所有订单放入抢单池中, 众包骑手根据自身的能力、喜好自主进行抢单; 在派单模式下, 众包平台直接分配订单给众包骑手并规划路线. 目前众包平台更倾向于发展派单模式并逐渐将抢单模式转变为派单模式.
在当前众包配送领域的研究中, 大多研究集中于单一类型的骑手参与配送活动, 具体而言, 即外卖骑手仅负责外卖订单的配送, 快递骑手仅处理快递订单. 然而, 当多个不同类型的订单在地理位置相近的地方出现时, 通常会导致对更多骑手的需求, 从而造成人力资源的过度投入与浪费; 与此同时, 众包配送过程中参与的主体有平台、商家、顾客和骑手, 各方利益密切相关且相互影响, 现有研究聚焦于平台、顾客和骑手对于服务质量和配送效率的提升, 缺少对于商家满意度的考虑. 因此设计考虑骑手异质性, 满足高配送效率、高商家和顾客满意度的众包订单分配与路径规划方案, 是本文要解决的问题.
1 相关研究众包配送问题可以看作是订单分配与路径规划的组合优化问题[3].
对于订单分配问题, 许多学者进行了研究, Arslan等[4]研究如何使用剩余的社会资源, 来构建包裹配送和临时众包配送匹配的服务平台, 在此基础上设计一种基于滚动视图的建模方法以解决实时分配的动态拾取和交付问题. 王爽等[5]提出一种众包车辆和物流企业合作的新模式, 在此基础上制定“众包司机-订单”匹配策略, 设计众包司机配送方案. 邓娜等[6]从订单分配中的任务分配环节出发, 提出了一种结合聚类分析和最小距离匹配原则的订单集指派模式. 戴韬等[7]从订单选择及订单执行路径出发, 设计双层算法来比较接受不同订单所带来的收益, 从而进行订单分配. 冯爱兰等[8]考虑在抢派结合的模式下, 设计离散选择模型模拟骑手抢单决策, 提高骑手对于订单的自主选择性. 刘春玲等[9]基于众包配送时效性问题, 通过动态筛选订单配送方, 结合冷链配送任务设计模糊机会策略进行订单分配.
对于路径规划问题, 车辆路径问题作为物流配送中的关键环节, 是当前相关研究中的热点[10]. 众包配送问题具有多骑手、时间窗约束、先取后送和开环等特征, 可以看作是带时间窗的取送货车辆路径问题. 许多学者对此类问题进行了研究, 陈星光等[11]从配送员的角度出发, 以配送员总收益最大化、配送总时长最小化为目标建立车辆路径模型, 考虑外卖配送员依据偏好选取订单的决策行为, 在此基础上设置配送系统优化策略. Ren等[12]通过将商家和顾客的满意度转化为惩罚函数来构建外卖配送的取送货车辆路径模型, 旨在将总配送成本降至最低. 孙云霄等[13]考虑到配送员由于等级不同带来的载重能力和运营成本的不同, 将众包配送员等级与最大承单量、额外成本相结合, 求解取送货交叉的路径优化问题. 刘烁佳等[14]通过引入时间窗参数, 研究如何调整客户的优先级来减少车辆的等待时间, 建立了带时间窗的车辆路径优化模型. 赵佳欣等[15]从客户角度出发, 考虑了不同载重、不同速度的多车型, 建立了时变网络下同时取送货车辆的车辆路径优化模型.
在特定的情况下, 通过对多个目标进行集成优化, 可以对问题进行更全面的思考, 并取得比较好的结果. 因此, 学者们将取送货问题的研究推广至多目标优化领域. 张力娅等[16]考虑到众包配送的实际流程, 提出了顾客的优先等级, 基于顾客满意度最大化和平台成本最小化为优化目标建立了众包配送车辆路径问题模型. 熊浩等[17]从平台、骑手和顾客3个角度出发, 建立多目标外卖配送路径优化模型, 解决动态场景下多目标的外卖配送问题. 陈高华等[18]针对配送过程中产生的配送成本和碳排放量, 考虑车辆的不同速度和载重负荷, 提出了同时考虑碳排放量和配送总成本的多目标车辆路径优化模型, 旨在解决带时间窗和容量约束的车辆路径问题.
在求解算法方面: Ibrahim等[19]在交叉和变异操作中考虑基因序列之间的距离, 设计了一种改进的遗传算法, 旨在找到一种解决VRPTW问题的最佳方案. 田亮等[20]对送达时间不在时间窗口内的车辆采取一定的时间惩罚措施, 将带软时间窗的节约算法与时间惩罚成本进行结合, 设计改进的节约算法来解决配送路线中的车辆安排问题. 闫军等[21]根据配送服务的特性, 设计一种将聚类处理与蚁群算法相结合的混合算法来解决两指标的PDPTW问题. 陈凯等[22]通过引入移除-修复算子, 设立带评分的领域搜索策略, 在保留算法核心搜索机制的基础上, 设计了一种改进的离散灰狼优化算法, 旨在解决带时间窗约束的同时取送货车辆路径问题. 刘建胜等[23]对头脑风暴算法进行改进, 提出自适应头脑风暴算法, 用于求解车辆使用成本和车辆行驶距离成本最少的路径优化模型.
综合相关研究来看, 国内外学者对于众包订单分配与路径规划问题, 提出的相关模型和算法基本成熟, 但实际众包配送服务中, 现有研究仍存在一些尚未解决的弊端. 首先, 现有研究主要集中分析不同车辆的载重、速度、成本等方面的差异, 以及单一服务类型配送员的不同等级、配送能力等方面的差异, 鲜少考虑在实际众包配送过程中, 不同服务类型的骑手对于配送同类或者不同类型订单在许多方面具有显著差异. 其次现有研究主要从平台、顾客或者骑手的角度出发, 考虑最小化配送平台的总成本、最大化顾客的满意度或者最大化骑手收益等目标, 而将商家和顾客的满意度同时考虑在内的较少. 因此, 与以往的研究不同, 本文研究的是具有多服务类型骑手的众包取送货车辆路径问题, 从众包平台角度出发, 兼顾商家和顾客的满意度, 旨在提升众包平台的配送效率以及降低平台的配送成本.
2 问题分析及模型 2.1 问题描述本文研究的是众包平台派单模式下订单分配与路径优化的实际场景, 即对于某一时刻产生的订单, 众包平台如何把这些不同类型的订单分配给不同服务类型的骑手, 并进行合理的配送路线规划, 以最小化平台总配送成本.
文章构建的具体场景为: 在某一区域内某众包平台拥有多个外卖、快递订单和多个可供分配的众包骑手, 骑手分为单一型骑手(单一外卖型、单一快递型)和全能型两种服务类型的骑手. 顾客在手机APP上提交外卖或者快递订单, 对于某一时刻的所有订单, 众包平台会将订单信息放入订单池, 通过算法处理完成对骑手的订单分配与路径规划工作, 将优化后的订单配送路径信息派发给骑手. 骑手分散在各个不同的地点, 具有不同的配送起点位置, 且骑手在完成订单任务后不用返回起点.
2.2 基本假设及参数说明 2.2.1 基本假设1) 各个骑手的位置, 各个顾客与商家的位置、时间窗、最大容忍时间、费用系数均已知.
2) 同服务类型的骑手, 各项参数均相同.
3) 平台内众包骑手的数目远远满足平台的配送需求.
4) 骑手的实际配送时间仅考虑在配送路途中的行驶时间, 在取送货点的等待与服务时间均不计入骑手的配送时间.
2.2.2 符号说明1) 集合
| N:N=P∪D={1,2,⋯,n,n+1,⋯,2n}. |
2) 参数
3) 决策变量
本文考虑的是商家和顾客对于骑手到达取货点和送货点的时间满意度的刻画. 现有研究大多使用软时间窗下的连续线性时间满意度函数来衡量客户的满意度变化情况[24].
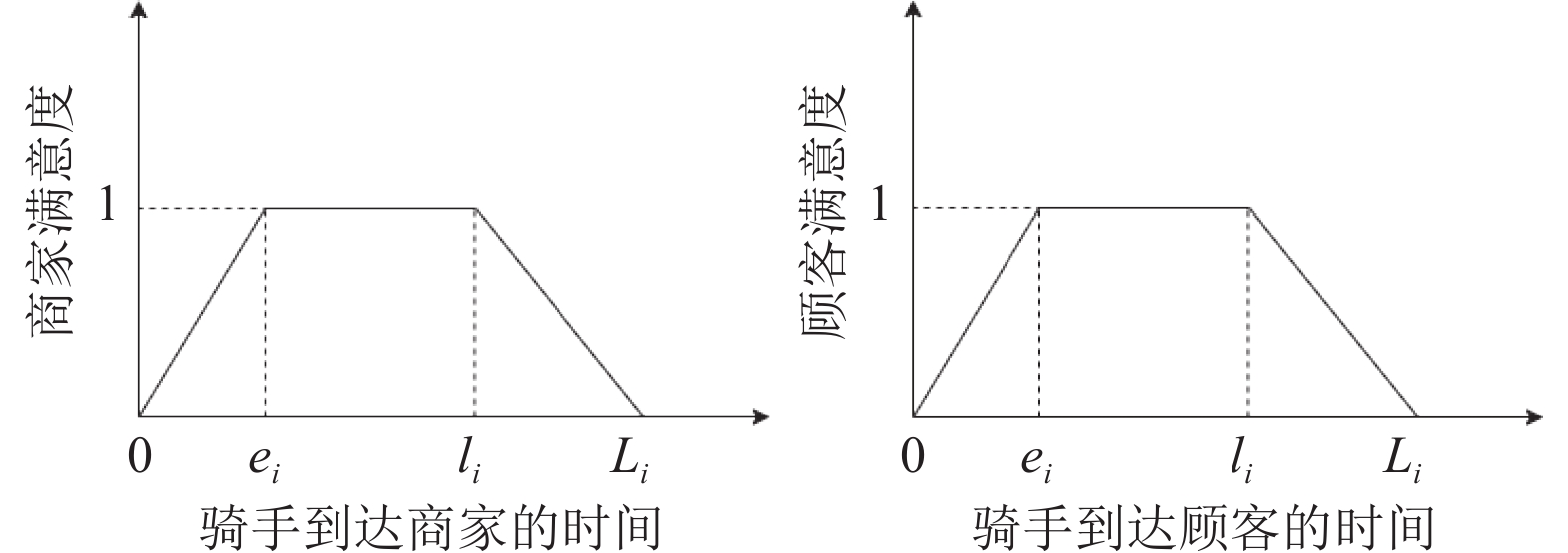
对于商家来说, 如果骑手到达的时间早于其期望的左时间窗, 这时候商家可能未准备好货, 那么商家的满意度随着骑手的到达时间线性上升; 如果骑手到达时间晚于其期望的右时间窗, 这个时候货物早已备好, 一些货物比如水果生鲜的质量会下降, 此时商家的满意度也会随着骑手的到达时间线性下降; 如果骑手到达商家的时间在其期望的时间窗内, 则商家的满意度为1.
同理, 对于顾客来说, 当骑手到达的时间在其期望的时间窗之外, 那么顾客的满意度随着骑手到达时间与期望时间差值的增大呈线性变化, 如果骑手到达顾客点的时间在其期望的时间窗内, 则顾客的满意度为1. 因此商家和顾客对于取送货时间的满意度, 可以看作同一个函数, 满意度成本函数和图像分别如式(1)和图1所示.
| Aki={Tiei,0<Ti<ei1,ei⩽Ti⩽liLi−TiLi−li,li<Ti<Li0,Ti⩾Li | (1) |
|
图 1 考虑模糊时间窗的商家和顾客满意度 |
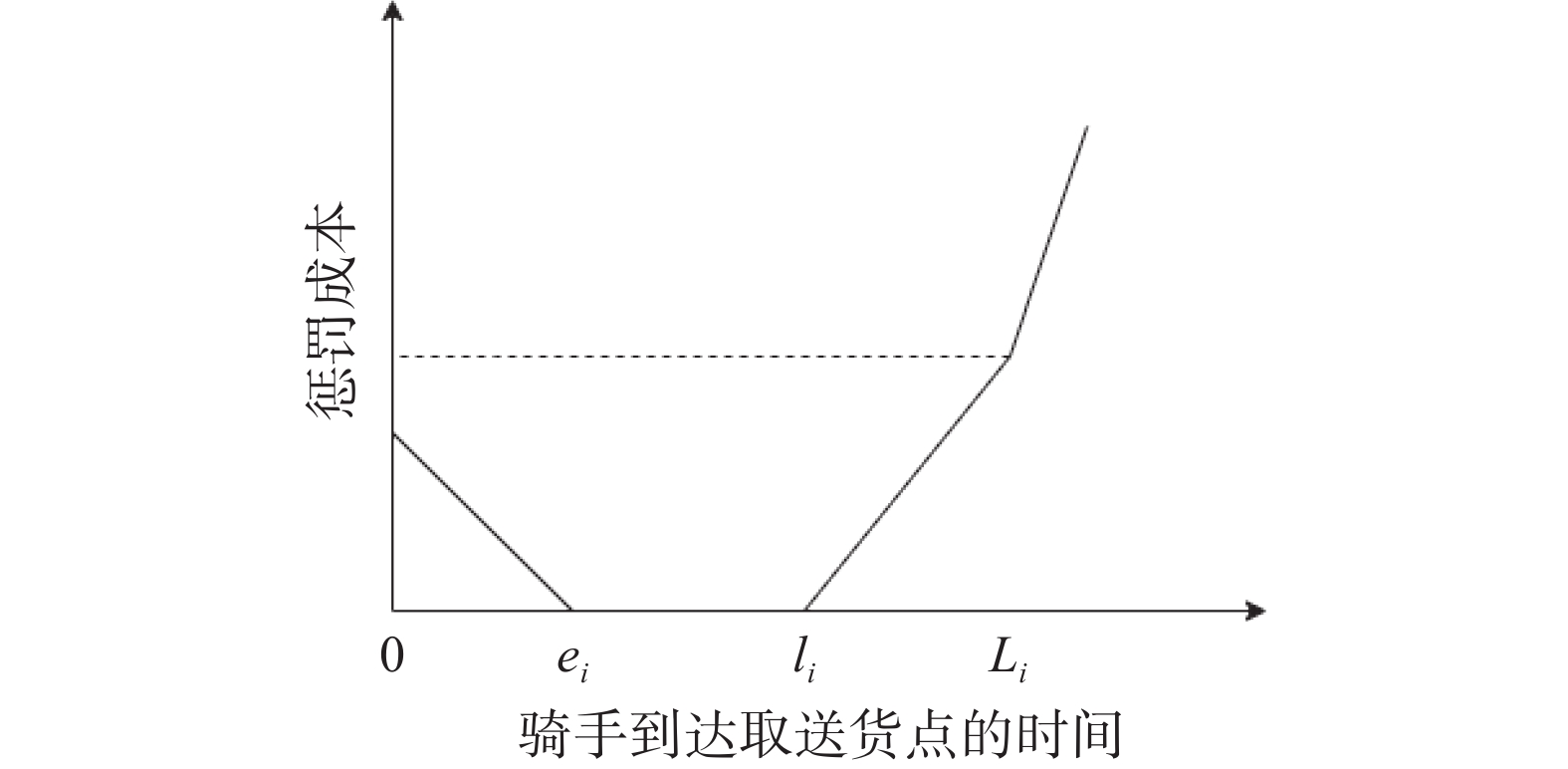
客户满意度和交付成本是不同维度的, 因此需要规范, 将客户满意度函数转化为惩罚函数. 商家和顾客满意度最大可以转换成时间惩罚成本最小[24], 转化后时间惩罚成本的函数图像如图2所示.
|
图 2 客户满意度转化为惩罚成本 |
对应的惩罚函数表示如下:
| Pki={c1(ei−Ti),0<Ti<ei0, ei⩽Ti⩽lic2(Ti−li), li<Ti<Lic2(Li−li)+c3(Ti−Li), Ti⩾Li | (2) |
在商家和顾客所期望的时间段
惩罚成本数学表达式为:
| ∑i∈N∑k∈R{c1max | (3) |
其中,
配送路径成本指的是骑手完成所有节点取送货任务的配送成本, 包括骑手从当前位置到路线中第1个节点的距离成本以及骑手配送路线中各个节点之间的距离成本.
数学表达式为:
| {\displaystyle \sum }_{i\in N}{\displaystyle \sum }_{j\in N}{\displaystyle \sum }_{k\in R}{c}_{4}\left({x}_{{k}^{0}, i}^{k}{d}_{{k}^{0}, i}^{k}+{x}_{i, j}^{k}{d}_{i, j}^{k}\right) | (4) |
其中,
人员运营成本指的是在骑手完成所有节点取送货任务后, 众包平台会给予相应的津贴, 从而有效吸引和激励众包骑手, 长远发展运营平台. 众包平台对于每个类型的骑手完成一次配送任务的运营成本是一样的.
数学表达式为:
| \sum_{j \in N} \sum_{k \in R} c_5 x_{k^0, j}^k | (5) |
其中,
数学模型的目标函数如下所示:
| \begin{split} {\min}Z=&\displaystyle \sum _{i\in N}\displaystyle \sum _{k\in R}\left\{{c}_{1}\max\left({{e}}_{i}-{T}_{i}^{k}, 0\right)\right.\\ & \left.+{c}_{2}\max\left({T}_{i}^{k}-{l}_{i}, 0\right)+{c}_{3}\max\left({T}_{i}^{k}-{l}_{i}-{L}_{i}, 0\right)\right\}\\ & +\displaystyle \sum _{i\in N}\displaystyle \sum _{j\in N}\displaystyle \sum _{k\in R}{c}_{4}\left({x}_{{k}^{0}, i}^{k}{d}_{{k}^{0}, i}^{k}+{x}_{i, j}^{k}{d}_{i, j}^{k}\right) +\displaystyle \sum _{j\in N}\displaystyle \sum _{k\in R}{c}_{5}{x}_{{k}^{0}, j}^{k}\end{split} | (6) |
其中, 目标函数为最小化平台总配送成本, 包含3个部分: 完成所有订单的时间惩罚成本、路径行驶成本以及人员运营成本.
2.6 约束条件数学模型的约束条件如下所示:
| \sum\limits_{i \in P} {\sum\limits_{j \in D} {\mathop x\nolimits_{i, j}^k } } = 1, \;\forall k \in R | (7) |
| \sum\limits_{j \in N} {\sum\limits_{k \in R} {x_{{k^0}, j}^k} } \leqslant R | (8) |
| \sum_{i \in N \cup\left\{k^-\right\}} x_{k^0, i}^k=1, \;\forall k \in R | (9) |
| \displaystyle \sum _{i\in N\cup \left\{{k}^{0}\right\}}{x}_{i, {k}^-}^{k}=1,\; \forall k\in R | (10) |
| \sum_{i \in N} x_{k^0, i}^k \leqslant 1,\; \forall k \in R | (11) |
| \sum_{j \in N \cup\left\{k^0\right\}} x_{j, i}^k-\sum_{j \in N \cup\left\{k^-\right\}} x_{i, j}^k=0,\; \forall i \in N, \forall k \in R | (12) |
| \sum_{j \in N} x_{i, j}^k-\sum_{j \in N} x_{j, i+n}^k=0,\; \forall i \in P, \forall k \in R | (13) |
| T_{{k^0}}^k = 0,\; \forall k \in R | (14) |
| T_j^k=T_i^k+\frac{d_{i j}}{v},\; \forall k \in R \text {, 且 } x_{i, j}^k=1, \forall i \in P, \forall j \in D | (15) |
| T_i^k < T_{i + n}^k, \;\forall i \in P, \forall k \in R | (16) |
其中, 式(7)–式(13)表示配送路径选择相关约束, 式(7)表示每个订单仅能由一名众包骑手进行配送; 式(8)表示进行配送的众包骑手不能超过骑手总数; 式(9)、式(10)表示每个骑手在配送路径上存在起点和终点, 也就是每个骑手从其起始点开始配送, 一直到终点结束配送任务, 这里的终点是虚拟终点, 从最后一个节点到它的距离不计入骑手的配送路径; 式(11)表示不一定每个众包骑手都被分配到订单; 式(12)表示所有骑手在抵达一个节点之后, 必定会从那个点离开; 式(13)表示订单一定是成对的; 式(14)–式(16)表示配送时间相关约束, 式(14)表示众包骑手从自己起始位置出发的时刻设置为0; 式(15)表示众包骑手从
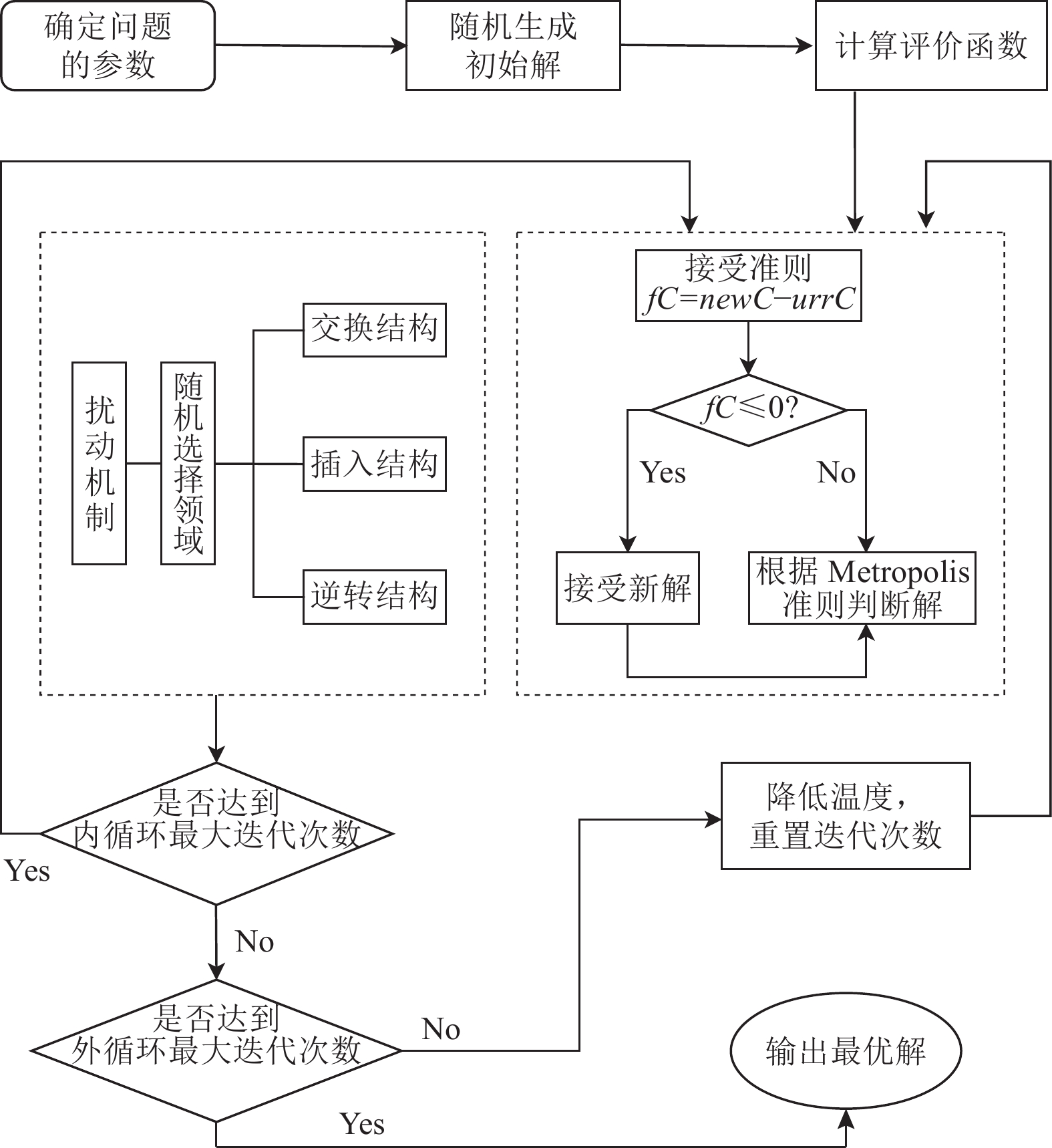
模拟退火算法流程图见图3, 具体步骤如下.
|
图 3 模拟退火算法流程图 |
步骤1. 设计初始温度
步骤2. 对当前解
步骤3. 接受准则基于新解与当前解的目标函数值差异以及当前温度来决定是否接受新解. 在当前温度
概率
| P = \exp \left( { - \frac{{delta}}{T}} \right) = \exp \left( { - \frac{{{{new}}S - {{curr}}S}}{{{{curr}}S \times T}}} \right) | (17) |
其中,
步骤4. 比较当前内循环次数
步骤5. 内层循环完成后, 更新当前温度, 比较当前外层循环次数
遗传算法具体步骤如下.
步骤1. 由于众包订单配送在路线的规划中, 必须兼顾订单的配对和配送优先性, 所以本文采用整数编码方式进行染色体编码. 考虑到订单类型的多样性(外卖订单、快递订单)以及骑手的不同服务类别(单一外卖型、单一快递型和全能型), 将初始种群的生成分为如下几步: 首先生成局部的初始种群, 包括单一外卖型初始编码序列
步骤2. 解码需要先提取染色体中每个骑手的订单配送路径信息, 来识别所有分割点的位置. 第1个节点0以前的所有节点都表示编号为1的骑手的配送任务路径; 第
步骤3. 根据平台的总配送成本计算适应度函数.
步骤4. 采用精英选择策略将预先设定的一定数量的较优个体从种群中选出, 直接进入到下一代, 对于剩余个体采用随机遍历抽样策略挑选出合适个体填充子代种群.
步骤5. 考虑到订单与骑手的类型是否匹配, 本文采用顺序交叉方式, 以一定的交叉概率对选择的染色体进行交叉操作进行交叉操作. 随机选取两对父代染色体, 从中提取第1个骑手的基因片段, 将其交叉放在父代染色体的最前端, 并删除染色体中的重复节点.
步骤6. 考虑到订单与骑手的类型是否匹配, 采用随机两点变异进行变异操作. 从父代染色体中提取全能型骑手的基因片段, 在全能型基因片段上随机选择两个不同的取送货节点对基因进行置换.
3.3 混合算法设计作为启发式算法, 遗传算法、模拟退火算法都存在收敛速度较慢、搜索能力不强、运行时间较长等缺点[3], 因此本文采取遗传算法与大领域搜索算法相结合的方式, 先采用遗传算法进行全局搜索, 然后再用大领域搜索算法进行局部搜索, 来求解众包配送过程中订单分配和路线规划组合优化问题. 局部搜索操作的具体步骤如下.
3.3.1 移除操作在ALNS中,
首先, 从所有取送货节点的集合
相关性
| {R_{ij}} = 1\Big/\left( {{V_{ij}} + {D_{ij}} + {T_{ij}} + {O_{ij}} + {K_{ij}}} \right), \forall i \in removed, \forall j \in in | (18) |
| {V_{ij}} = \mathop \sum \limits_{m \in N} x_{im}^k\mathop \sum \limits_{m \in N} x_{mj}^k, \forall i \in removed, \forall j \in in, k \in R | (19) |
| {D_{ij}} = {d_{ij}}/\max\left\{ {{d_{ij}}} \right\}, \forall i \in removed, \forall j \in in | (20) |
| {T_{ij}} = \left| {{e_i} - {e_j}} \right|/\max\left\{ {\left| {{e_i} - {e_j}} \right|} \right\}, \forall i \in removed, \forall j \in in | (21) |
| {O}_{ij}=\left\{\begin{array}{l}0.1,\; 如果i与j订单类型相同\\ 0.7,\; 如果i与j订单类型不相同\end{array}\right. | (22) |
其中,
修复操作是将被移除的取送货节点对重新插回到解中.
首先, 从
由于变异概率较低以及算法的迭代更新, 新生成的个体与其附带个体之间存在的差异可能非常小, 容易产生重复个体. 设计有效的机制, 去除重复个体, 维持种群多样性, 增强算法的全局搜索能力.
3.4.2 补足染色体种群删除重复的染色体后, 种群数量会相对变少, 为了维持种群的多样性, 提升算法的求解速度与收敛性, 随机生成新的个体来补足种群规模.
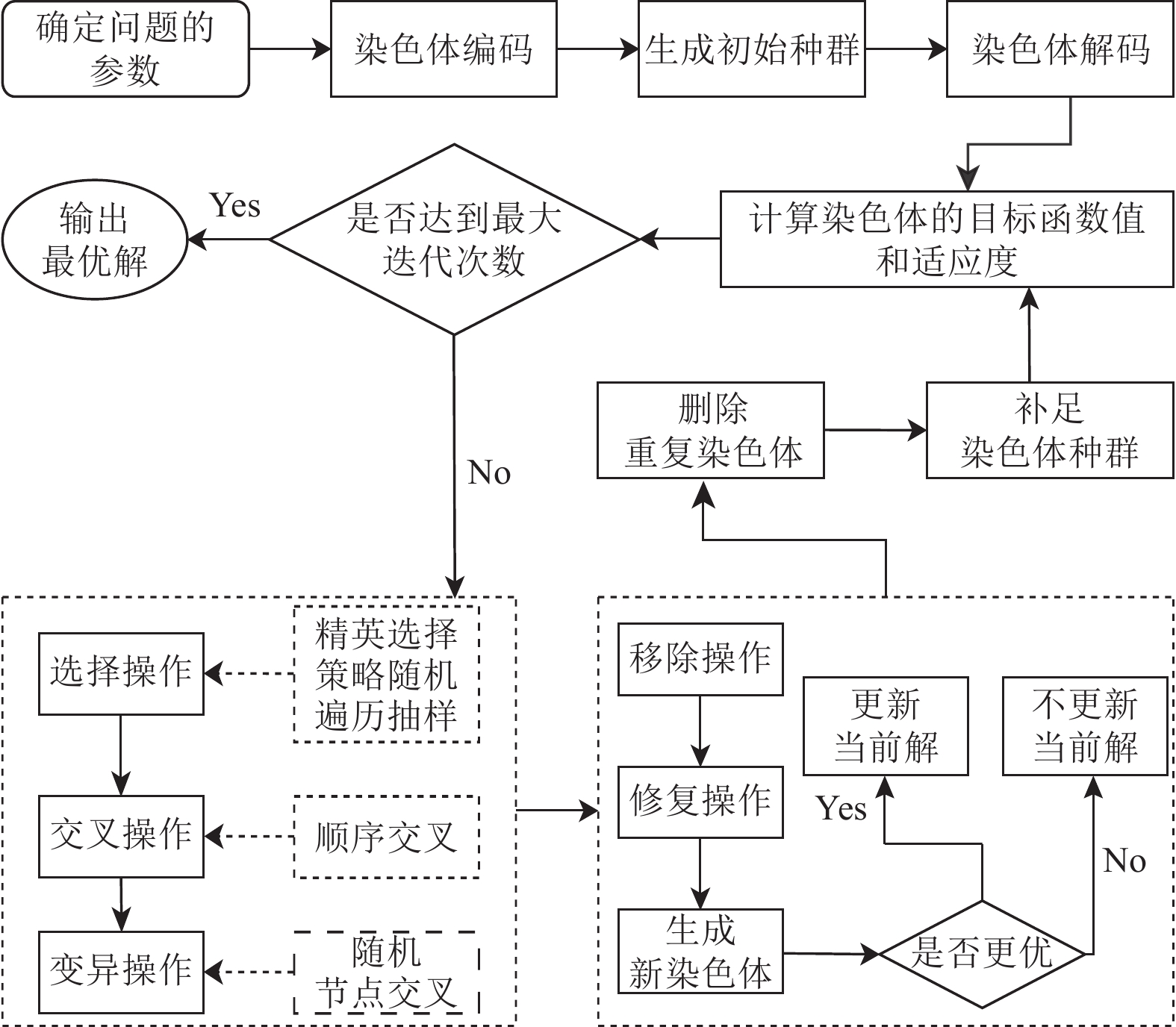
3.4.3 算法终止条件及流程图当算法达到预先设定迭代次数时, 就停止运行算法. 混合算法的流程图如图4所示.
|
图 4 混合算法流程图 |
4 仿真实验与结果分析
本文利用Matlab R2020b进行编程求解, 所有数据均在11th Gen Intel(R) Core(TM) i7-1195G7 @ 2.90 GHz配置的计算机上进行仿真实验. 具体如下.
4.1 算例选取选取某众包平台在某一时刻生成的30个订单数据, 随机将数据中的节点设定为外卖节点(标记为0)和快递节点(标记为1), 将数据转换成本文所需的订单算例. 为了确保众包骑手的数量能够满足该地区的订单配送任务, 假设众包平台可以参加配送任务的骑手有15人, 在该平台设定的配送区域内随机生成15个众包骑手的位置点信息, 并在此基础上生成15个骑手的各个订单类型(单一外卖型骑手标记为0, 单一快递型骑手标记为1, 全能型骑手标记为2). 算例数据如表1和表2所示.
4.2 参数有关参数设置如表3所示.
4.3 模拟退火算法求解结果如图5, 通过模拟退火算法可以求解得出, 该模型的目标函数值为220.12元, 配送路线总长为51.89 km, 超时时间总计为46.71 min, 使用的骑手数为9个, 具体配送路线如表4所示.
| 表 1 骑手算例数据 |
| 表 2 订单算例数据 |
4.4 遗传算法求解结果
如图6, 通过遗传算法可以求解得出, 该模型的目标函数值为215.402元, 配送路线总长为47.35 km, 超时时间总计为38.25 min, 使用的骑手数为10个, 具体配送路线如表4所示.
4.5 混合算法求解结果如图7, 通过混合算法可以求解得出, 该模型的目标函数值是181.42元, 配送路线总长为49.23 km, 超时时间总计为6.31 min, 使用的骑手数为8个, 配送路线如表4所示.
| 表 3 参数设置 |
4.6 结果对比分析
从图5–图7的结果对比可以得出, 在基于算例的求解过程中, 混合算法展现出了较优的求解性能, 更适用于解决具有异质性的众包配送路径规划问题. 具体来看, 模拟退火算法和遗传算法分别在第320代、第221代收敛, 而混合算法在第24代收敛. 在算法的中期阶段, GA和SA就已陷入局部最优, 而混合搜索算法具有一定的局部搜索能力, 在逐渐接近问题的最优解.
通过分析进一步表明, 局部搜索操作的加入, 使得每次遗传迭代后的染色体经过移除与修复操作, 进一步得到了优化. 移除操作有选择地从当前解中删除一些元素, 使得算法能够离开当前解所在的局部最优区域, 探索新的可能性空间, 有效避免GA、SA在迭代过程中出现早熟收敛以及依赖初始解的情况. 修复操作在遵循一系列约束条件的情况下, 将受损的染色体进行修复, 生成改良后的新染色体, 维持了种群的多样性. 这种新产生的染色体显著提高了质量, 从而有效增强了算法的收敛速度, 以及全局搜索和局部搜索的效率.
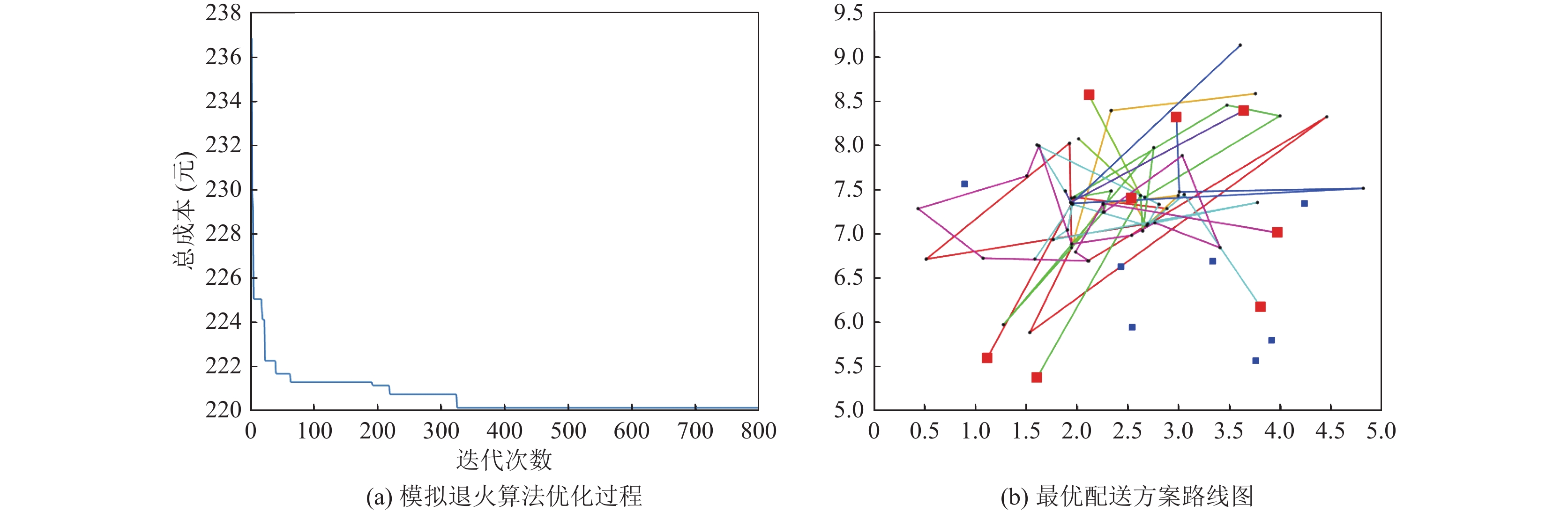
|
图 5 模拟退火算法迭代次数与配送路径图 |
| 表 4 最优路径方案(骑手编号: 配送路径) |
由表5中算法优化结果对比可知, 本文的混合算法主要有以下优点.
(1)模拟退火算法、遗传算法与混合算法的目标函数值分别为220.12元、215.40元、181.42元, 混合算法的目标函数相比于模拟退火算法和遗传算法分别下降了38.7元、33.98元, 目标函数值质量分别提升了17.59%、15.78%.
(2)在时间惩罚成本方面, 模拟退火算法、遗传算法与混合算法中骑手提前到达商家或者顾客的总时间分别为1.42 min、0.54 min、0, 到达商家和顾客的时间超过其期望的右时间窗但低于最大容忍时间的总超时时间分别为41.89 min、34.45 min、4.42 min, 到达商家和顾客的时间超过其最大容忍时间分为4.82 min、3.27 min、1.89 min; 模拟退火算法、遗传算法与混合算法的骑手总时间惩罚成本分别为26.33元、20.70元、2.97元, 混合算法相比较模拟退火算法与遗传算法分别下降了88.72%、85.65%, 这同时也代表着商家和顾客的时间满意度在增加.
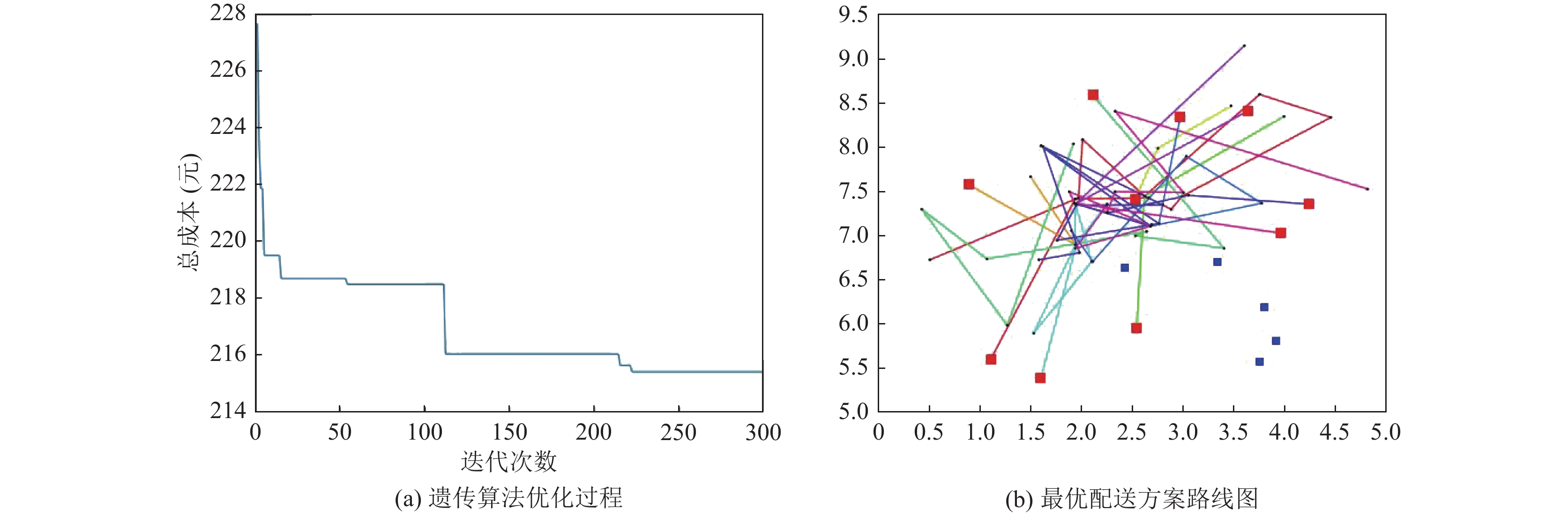
|
图 6 遗传算法迭代次数与配送路径图 |
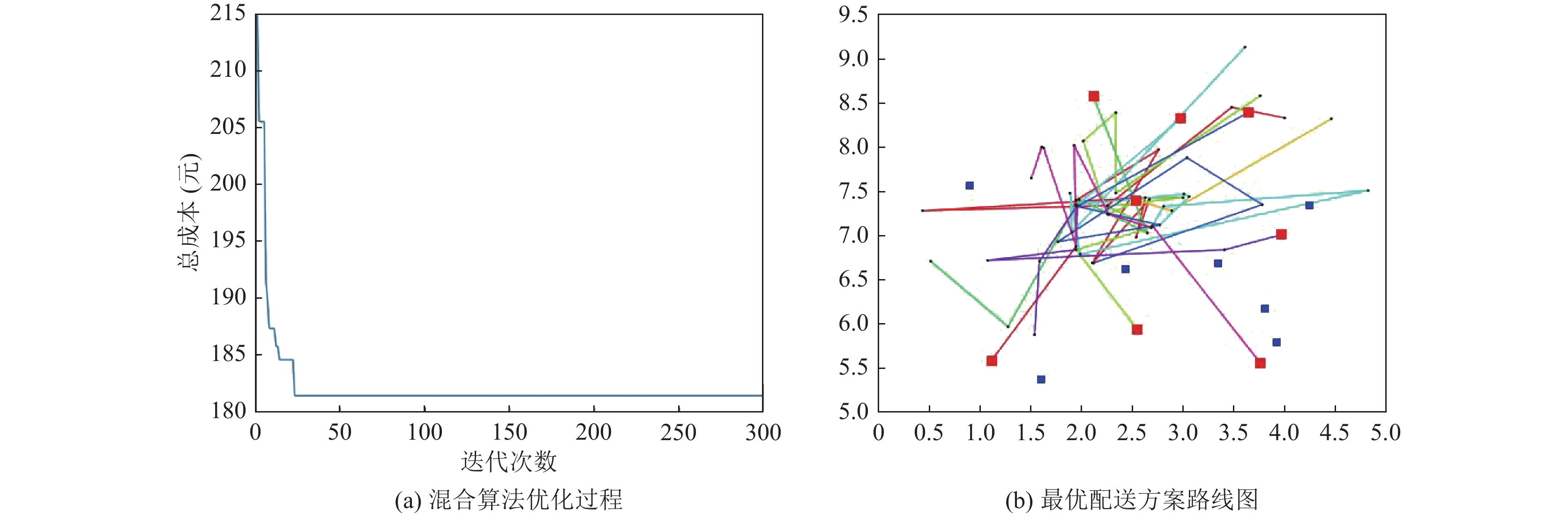
|
图 7 混合算法迭代次数与配送路径图 |
| 表 5 算法优化结果对比 |
(3)在路径行驶成本方面, 模拟退火算法和混合算法的总行驶距离分别为51.89 km、49.23 km, 总路径行驶成本分别为103.79元、98.45元, 相比较下混合算法总路径行驶成本下降了5.14%.
(4)在人员运营成本方面, 模拟退火算法所需骑手数为9个, 其中单一外卖型骑手有4个, 单一快递型骑手有3个, 全能型骑手有2个; 遗传算法所需骑手数为10个, 其中单一外卖型骑手有6个, 单一快递型骑手有3个, 全能型骑手有1个; 混合算法所需骑手数为8个, 其中单一外卖型骑手有4个, 单一快递型骑手有2个, 全能型骑手有2个. 模拟退火算法、遗传算法与混合算法骑手总运营成本分别为90元、100元、80元, 相比较下混合算法骑手总运营成本分别下降了10%、20%.
因此, 本文设计的混合算法可以有效减少骑手的总行路径驶距离, 以及降低骑手提前到达时间和超时时间, 也就是能有效提高顾客和商家的满意度. 在保持较低路径行驶成本和较低惩罚时间成本(也就是较高商家和顾客满意度)的同时, 还可以减少众包骑手的使用数目, 提高众包平台人员利用率, 从而提高众包平台配送效率, 减少众包平台总配送成本.
5 结论针对当前众包平台面临的订单类型多样性和配送骑手的单一型, 即外卖骑手仅负责外卖订单的配送, 快递骑手仅处理快递订单. 本文考虑了多服务类型骑手的众包配送策略问题, 同时考虑到当前研究中较少同时关注商家和顾客满意度的情况, 构建基于模糊时间窗的商家和顾客对于骑手到达取送货点时间的满意度成本函数, 将商家和顾客的满意度转化为时间惩罚函数, 建立了以时间惩罚成本、路径行驶成本、人员运营成本最小化为目标的模型; 在算法求解方面, 考虑到传统启发式算法(如遗传算法、模拟退火算法)存在的不足以及待求解问题的复杂性, 设计了一种遗传算法与局部搜索算法相结合的混合算法进行求解, 运用算例, 采用不同算法进行仿真实验以及求解结果对比, 验证了本文构建的模型以及设计的求解算法的可行性和有效性. 虽然本文建立的众包配送模型有一定的实践价值, 但是在建模过程中没有考虑到一些现实因素, 存在以下几点不足, 可作为下一步研究方向.
(1)对于商家和顾客的满意度, 本文只考虑了骑手到达取送货点的时间对商家和顾客满意度的影响, 在现实生活中, 商家和顾客的满意度还会受到诸多因素的影响, 例如订单的配送费用、订单的处理速度、骑手的服务态度、货物的配送质量、平台的使用情况等, 需要多维度考虑.
(2)本文考虑的是静态场景下的众包配送问题, 而在实际生活中, 外卖订单和快递订单具有动态性和高频性, 需要考虑订单动态产生的情况.
| [1] |
赵建有, 李玥, 田浩, 等. 众包配送研究综述. 交通运输工程学报, 2023, 23(5): 62-84. DOI:10.19818/j.cnki.1671-1637.2023.05.004 |
| [2] |
杜子超, 卢福强, 王素欣, 等. 众包物流配送车辆调度模型及优化. 东北大学学报(自然科学版), 2021, 42(8): 1210-1216. DOI:10.12068/j.issn.1005-3026.2021.08.021 |
| [3] |
李雪妍. 派单模式下考虑“取餐+送餐”的众包外卖配送优化研究 [硕士学位论文]. 北京: 北京交通大学, 2019. [doi: 10.26944/d.cnki.gbfju.2019.001020]
|
| [4] |
Arslan AM, Agatz N, Kroon L, et al. Crowdsourced delivery—A dynamic pickup and delivery problem with Ad Hoc drivers. Transportation Science, 2019, 53(1): 222-235. DOI:10.1287/trsc.2017.0803 |
| [5] |
王爽, 陈淮莉. 众包模式参与下“最后一公里”协同配送研究. 计算机应用与软件, 2022, 39(10): 315-321. DOI:10.3969/j.issn.1000-386x.2022.10.046 |
| [6] |
邓娜, 张建军. O2O外卖订单配送任务分配模式研究. 上海管理科学, 2018, 40(1): 63-66. DOI:10.3969/j.issn.1005-9679.2018.01.012 |
| [7] |
戴韬, 沈静. 基于众包的外卖配送订单选择研究. 工业工程, 2021, 24(2): 125-133. DOI:10.3969/j.issn.1007-7375.2021.02.016 |
| [8] |
冯爱兰, 周映雪, 龚艳茹, 等. 抢派结合模式下外卖配送问题研究. 控制与决策, 1–8. https://doi.org/10.13195/j.kzyjc.2022.1420. (2023-10-08)[2024-03-06].
|
| [9] |
刘春玲, 王俊峰, 黎继子, 等. 众包模式下冷链物流配送模型的仿真和优化分析. 计算机集成制造系统, 2019, 25(10): 2666-2675. DOI:10.13196/j.cims.2019.10.025 |
| [10] |
罗明亮, 袁鹏程. 考虑客户满意度的车辆路径优化及其算法研究. 河南师范大学学报(自然科学版), 2024, 52(2): 51-61. DOI:10.16366/j.cnki.1000-2367.2022.10.01.0002 |
| [11] |
陈星光, 李心宇, 程鲁强. 考虑订单偏好的外卖众包配送优化策略研究. 中国管理科学, 2024, 32(6): 86-97. DOI:10.16381/j.cnki.issn1003-207x.2021.1262 |
| [12] |
Ren T, Xu HB, Jin KN, et al. Optimisation of takeaway delivery routes considering the mutual satisfactions of merchants and customers. Computers & Industrial Engineering, 2021, 162: 107728. DOI:10.1016/j.cie.2021.107728 |
| [13] |
孙云霄, 马继东. 基于配送员等级的多目标众包配送路径优化研究. 中国新技术新产品, 2023(10): 134-136. DOI:10.13612/j.cnki.cntp.2023.10.012 |
| [14] |
刘烁佳, 李学强. 基于启发式带时间窗的车辆路径规划问题求解. 计算机系统应用, 2022, 31(11): 275-281. DOI:10.15888/j.cnki.csa.008818 |
| [15] |
赵佳欣, 雷斌, 王菀莹. 时变网络下多车型同时取送货车辆路径优化. 计算机工程与设计, 2023, 44(10): 3096-3102. DOI:10.16208/j.issn1000-7024.2023.10.028 |
| [16] |
张力娅, 张锦, 肖斌. 考虑顾客优先级的多目标O2O外卖即时配送路径优化研究. 工业工程与管理, 2021, 26(2): 196-204. DOI:10.19495/j.cnki.1007-5429.2021.02.024 |
| [17] |
熊浩, 郭昊颖, 鄢慧丽, 等. 外卖配送路径多目标实时优化研究. 工业工程, 2023, 26(1): 98-107. DOI:10.3969/j.issn.1007-7375.2023.01.011 |
| [18] |
陈高华, 郗传松. 求解多目标车辆路径优化的改进蚁群算法研究. 机械设计与制造, 2023(9): 231-236. DOI:10.19356/j.cnki.1001-3997.20230322.004 |
| [19] |
Ibrahim MF, Nurhakiki FR, Utama DM, et al. Optimised genetic algorithm crossover and mutation stage for vehicle routing problem pick-up and delivery with time windows. IOP Conference Series Materials Science and Engineering, 2021, 1071: 012025. DOI:10.1088/1757-899X/1071/1/012025 |
| [20] |
田亮, 李亚东. 考虑时间惩罚成本的配送路线优化. 物流工程与管理, 2020, 42(4): 105-109. DOI:10.3969/j.issn.1674-4993.2020.04.034 |
| [21] |
闫军, 常乐, 王璐璐, 等. 带时间窗的同时取送货车辆路径问题求解算法. 工业工程, 2021, 24(5): 72-76. DOI:10.3969/j.issn.1007-7375.2021.05.009 |
| [22] |
陈凯, 邓志良, 龚毅光. 离散灰狼优化算法求解VRPSPDTW问题. 计算机系统应用, 2023, 32(11): 83-94. DOI:10.15888/j.cnki.csa.009305 |
| [23] |
刘建胜, 蔡祥, 黄纪绘, 等. 考虑同时取送和时间窗的车辆路径及求解算法. 计算机工程与应用, 2023, 59(16): 295-304. DOI:10.3778/j.issn.1002-8331.2205-0405 |
| [24] |
任腾, 陈玥, 向迎春, 等. 考虑客户满意度的低碳冷链车辆路径优化. 计算机集成制造系统, 2020, 26(4): 1108-1117. DOI:10.13196/j.cims.2020.04.024 |
 2024, Vol. 33
2024, Vol. 33



