近年来, 随着人工智能科技的快速发展, 深度神经网络已成熟应用于各类计算机视觉任务中, 且都具有较高的预测精度. 由于深度学习模型通常含大量占用存储空间的参数, 在推理阶段也需要大量得计算资源, 从而难以部署在一些资源受限的嵌入式设备或者边缘端设备上. 因此, 研究人员针对深度卷积神经网络模型的压缩与加速方法展开了大量研究, 现有的一些模型压缩方法有: 网络剪枝, 模型量化, 知识蒸馏以及低秩分解等. 模型量化由于近年来新兴硬件加速支持低精度快速推理而引起研究人员的兴趣. 模型量化技术通常是将全精度模型(FP32)参数通过某种量化方法将其量化为整型低位(INT8、INT4、INT2等), 量化后的模型可以大幅减少模型的计算量和存储需求, 提升模型整体推理速度等. 通过模型量化技术, 可以满足边缘计算需求并优化能效, 将复杂的深度学习模型高效的部署在一些移动设备和物联网设备如智能手机手表、平板电脑、智能家居、传感器等.
模型量化技术在学术界和工业界的研究与应用已取得了不错的进展, 如Google等公司推出的量化白皮书[1], 系统阐述了模型量化过程和原理, 并通过大量实验和研究表明, 模型量化在模型训练和推理加速方面都取得了巨大成功. 还有Qualcomm公司推出的AIMET (AI model efficiency toolkit)[2]和NVIDIA公司推出的TensorRT[3]等模型量化部署框架, 可以将量化后模型更加快速稳定的应用在自动驾驶和智能交通等行业.
最近的一些量化方法大多是贴近工业应用的训练后量化, AdaRound[4]中利用泰勒展开方法分析量化带来的损失变化, 提出一种可学习的舍入取整来重建预训练模型特征的方法; 而文献[5]则认为AdaRound方法权值扰动较大, 因此使用Gauss-Newton矩阵分析二阶Hessian矩阵误差, 采用块重建的方式提出了BRECQ量化方法, 进一步提升训练后量化模型的精度; 在PD-Quant[6]中发现现有的量化方法在确定量化参数时只考虑了局部信息, 并不能调解最佳量化参数, 从而提出一种使用量化前后的网络预测差异信息来确定量化参数的方法, 调整了PTQ中激活的分析, 缓解了过拟合问题. 然而, 对于训练后量化这种由人为或者简单的利用一些先验知识分配量化的比特位宽, 这可能是次优的且有偏差性, 会对模型的整体性能造成一定的损失.
由于神经网络模型中每一层网络具有不同的参数量和权值分布, 因此具有不同的量化敏感度, 通过优化网络模型中每一层的比特分布空间, 以此对网络每一层分配不同的量化位宽可能是更优的选择, 尤其是在低位量化的情况下. 所以, 在训练后量化过程中引入混合精度量化方法可以进一步提升网络模型性能. 在现有的训练后混合精度量化方法中, ZeroQ[7]算法使用知识蒸馏的思想来衡量网络模型每层的量化敏感度, 然后选择在模型特定约束条件下的总体量化敏感度最小的混合精度配置, 然而, 该方法是建立在假设其他层比特位宽选择不影响不同层的量化敏感度. AdaQuant[8]算法则是通过分析整数规划公式来分配每一层的量化比特位宽, 但在混合精度量化分配位宽过程中也没有考虑网络模型每一层之间的潜在影响. 因此, 在深度神经网络中更深层次的网络层必然会受到其他层的影响, 在训练后混合精度量化过程中, 我们要考虑网络每一层之间的关系并选择合适的度量标准来以此决定不同层的量化位宽.
在本文中, 我们提出一种基于金字塔池化权值印记的训练后混合精度搜索量化算法—MSQ (mixed-precision search quantization), 该算法从任务精度的角度来确定网络层的比特位宽, 具有更好的解释性. MSQ通过在网络模型每一层后面加入一个改进的任务预测器模块来估计当前层的精度收益, 对低精度收益的网络层会降低量化比特并重新进行量化校准过程.
如图1所示, 改进的任务预测器模块结合了任务预测器模块、金字塔池化模块以及权值印记技术. 由于原始任务预测器模块只能单一的捕获网络每一层的参数信息, 在训练过程中无法衡量网络每一层的精度增益, 因此将金字塔池化模块[9]融入任务预测器模块中, 用于提取网络模型中全局特征信息和局部细节信息进行分析, 并引入权值印记(weight imprinting)技术[10]来近似任务预测器模块中全连接层的权值, 其中, 印记就是用样本的特征来当作分类器对应类别的权值, 以解决在训练后量化过程中没有足够的训练数据和大量的计算资源, 从而无法准确获取网络模型每层网络的精度增益问题.
综上所述, 本文的主要贡献如下.
(1)本文提出一种融合金字塔池化模块和权值印记技术的混合精度搜索量化方法MSQ, 利用精度估计的思想对网络层进行评估, 以混合精度的优势来实现训练后量化最终对模网络型的压缩效果. 相比一些现有的混合精度方法, MSQ方法能够更好地度量网络每一层的比特位宽分配.
(2)本文对现有的一些网络架构在ImageNet和CIFAR-10数据集上进行量化实验, 并在边缘硬件设备上进行测试, 在相似的实验约束下, 与一些SOTA量化方法进行对比, 经过MSQ量化后的网络模型整体性能更好. 此外, 在对一些网络模型混合精度量化与固定量化方法进行对比分析, 发现MSQ在整体量化过程中效果更佳.
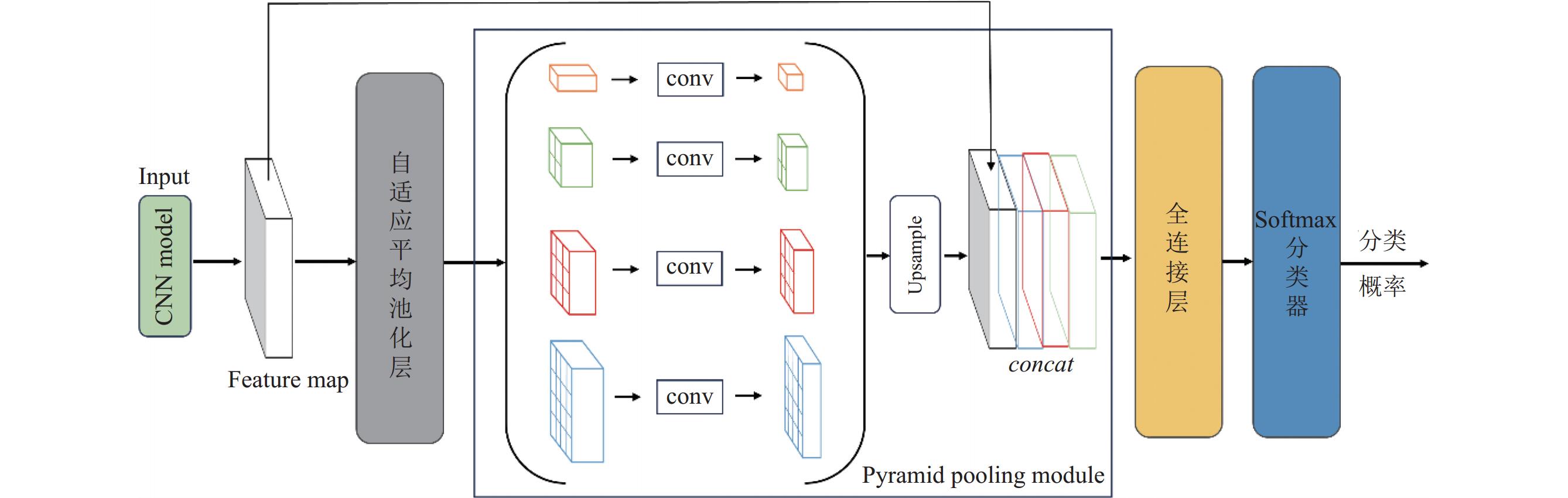
|
图 1 改进任务预测器模块 |
2 相关工作
模型量化技术一般可以分为量化感知训练和训练后量化两种类型. 量化感知训练一般是解决在量化过程中对神经网络模型的权值和激活值所造成的误差, 通过梯度下降等优化方法对量化模型进行重新训练, 从而使量化模型在优化过程中收敛到一个局部最优点. 目前一些较优的量化感知训练方法有: Esser等人研究出可学习步长量化LSQ[11], Bhalgat等人提出LSQ的改进方法LSQ+[12], 给出了数值在截断范围内外通过直通估计器的梯度. Liu等人[13]提出使用自适应的直通估计器来进行梯度估计, 使其在训练过程中能够更准确地估计有利于量化神经网络优化的反向传播的梯度, 在低位宽量化达到了接近全精度网络模型的效果.
量化感知训练方法在训练过程中需要消耗大量计算、时间成本, 以及对数据集的高度依赖性, 使得网络模型难以快速部署到硬件边缘设备上, 因此, 人们对不需要对神经网络模型进行重新训练的训练后量化方法研究更多. 近年来, 基于重建的训练后量化方法不断突破低位量化的极限, 已成为目前训练后量化的主流方法之一.
AdaRound[4]使用泰勒展开式对全局损失进行二阶近似, 将全局损失转化为海森矩阵形式, 最终将对全局损失的优化问题转化为对每个参数层输出的均方误差的优化问题. 至此之后, 以自适应舍入的方式来优化量化效果的研究方法不断涌现. AdaQuant[8]方法将自适应舍入的范围扩大到了整个量化电平内; AQuant[14]为解决激活舍入的动态性问题, 在推理阶段通过一个简单的函数自适应的调整舍入边界, 以此来生成舍入方案; AttentionRound[15]基于高斯分布来确定舍入的取值在量化电平内的分布; 块级重建量化BRECQ在AdaRound的基础上, 提出将输出重建的优化粒度扩大到块级, 并引入了Fisher信息矩阵来提供更多权值参数之间的相关信息. QDrop[16]在输出重建的优化过程中同时进行对激活值量化, 使极低位宽下的优化损失平面变得平滑, 更有利于模型收敛. 此外, RAPQ[17]将BRECQ方法扩展到全整形量化来弥补精度损失; Mr. BiQ[18]则将BRECQ方法扩展到了非均匀量化, 以及NWQ[19]通过激活正则化技术缓解了过拟合问题, 该技术更好地控制了激活分布.
在上述量化方法中, 采用固定位宽分配策略往往不能达到网络模型的最佳性能, 原因是不同的网络层对整个网络模型的推理时间和任务性能有不同的影响. 因此, 选择混合精度量化能够达到更优的量化效果. HAQ[20]提出了一种硬件感知的量化算法, 将硬件模拟器评估的推理速度信息反馈到训练周期中, 并主要通过深度强化学习来逐层分配位宽. HAWQ[21]提出一种基于海森矩阵特征值来计算每个网络层量化敏感度的方法, 以此决定不同网络层的量化位宽; TRQ[22]将权值主体和残差部分进行二值化, 实现权值主体的重建, 提高量化模型任务性能; BSQ[23]将每一位量化权重视为独立的训练变量, 引入可微位稀疏正则化, 从诱导位级稀疏性的角度处理混合精度量化; FBM[24]通过模拟特定设备测量每层网络来找到最佳位宽分配; SAQ[25]提出锐度感知量化, 通过同时最小化损失值和损失曲率来提高模型的泛化性能; 以及随机可微量化SDQ[26]在更加灵活和全局优化的空间中自动学习混合精度量化略, 在SDQ中将混合精度量化分为3类; 基于搜索的方法、基于度量的方法和基于优化的方法, 并指出SDQ属于量化感知训练和基于优化的混合精度方法, 根据SDQ对量化方法的分类, 本文的MSQ属于训练后量化和基于度量的混合精度方法.
3 方法 3.1 先验知识在本节中, 首先根据文献[1]中的量化基本公式(假设采用8位的非对称量化)介绍模型量化的基本原理.
| r=S(q−z) | (1) |
| q=clip(Round(rS+Z),0,255) | (2) |
其中,
| S = \frac{{{r_{\max }} - {r_{\min }}}}{{{q_{\max }} - {q_{\min }}}} | (3) |
| \;Z = clip\left(Round\left({q_{\max }} - \frac{{{r_{\max }}}}{S}\right), 0, 255\right) | (4) |
量化方法确定后,
在训练后量化的过程中, 需要采用合适的量化策略来寻找量化参数, 以搜索最佳
假设量化前的浮点权值参数为
| \overline r = S\times(q - Z) = S\times \left(clip\left(Round\left(\frac{r}{S} + Z\right), 0, 255\right) - Z\right) | (5) |
接下来度量量化信息损失, 以EasyQuant[27]中的余弦相似性方法进行度量, 假设校正数据集共有
| \frac{1}{N}\sum\nolimits_i^N {\cos ({r_i}, \overline {{r}}_i ) = } \frac{1}{N}\sum\nolimits_i^N {\frac{{{r_i}\overline {{r}}_i }}{{||{r_i}||||\overline {{r}}_i ||}}} | (6) |
那么所要求解的就是使得相似性最大的
| \mathop {\max }\limits_{S, Z} \frac{1}{N}\sum\nolimits_i^N {\frac{{{r_i}\overline {{r}}_i }}{{||{r_i}||||\overline {{r}}_i ||}}} | (7) |
在本文中, 首先通过上述训练后量化过程对一些网络模型进行量化, 再使用本文提出的混合精度搜索策略(见第3.2节)分配量化比特位宽, 从而得到最终量化结果. 此外, 我们还采用AdaRound和PD-Quant方法为本文训练后量化方法. AdaRound量化方法大大降低了过拟合敏感度, 可以在非常小的校准集上使用, 并且在ResNet50上实现了所有层权重和激活4-bit量化, 精度下降不到1%. 因此AdaRound量化后的网络模型更加适配本文所提出的混合精度搜索策略, 且在量化后精度对比方面可以更加体现出MSQ的优越性. 而PD-Quant是在低比特设置下仍有较高预测精度的量化方法, 以此作为本文训练后量化可以验证MSQ在低比特位时的有效性.
3.2 混合精度搜索策略在网络模型每层后面插入一个任务预测器模块可以准确测量每一层网络的参数冗余度. 该模块由自适应平均池化层、一个或多个全连接层以及Softmax分类器组成. 在训练过程中, 该模块的参数会根据新任务的数据进行更新, 并学习新任务的特定特征. 通过在原始训练集上对其参数进行训练更新, 由训练完成后所得到的精度增益来对网络中的所有层进行排序.在训练后量化的过程中, 由于训练数据有限且计算资源不够充分没导致无法完成上述过程. 为了在训练后量化过程中准确地获取网络模型中每层网络的精度增益, 我们引入权值印记技术来近似任务预测器模块中全连接层的权值, 该过程无需对网络进行端到端的训练.
权值印记技术[10]是一种在小样本学习领域将CNN分类器和嵌入方法结合起来, 通过直接将样本的高维嵌入特征设置为分类器的权值, 使得网络模型可以识别一些新的样本类别.
从本质上讲, 权值印记技术就是通过在卷积神经网络中的激活特征值在小样本数据上做一些合适的缩放操作, 那么就可以直接为新类别设置合适的分类权值. 其实也就是利用了全连接层中归一化输入和权值之间的对称性, 将新样本的嵌入特征复制到一组新的网络权值中. 此外, 将每一个任务预测器模块中的全连接层权值矩阵看作是对应类别的模板, 在网络的前向推理过程中, 首先得到输入待预测样本图片在网络中的高维嵌入特征
| \stackrel{}{y}=\arg\underset{\text{ }c\in C}{\max}{W}_{c}^{\rm T}\varphi (\text{x})=\arg\underset{\text{ }c\in C}{\min}Dist\left(\varphi ({x}), {W}_{c}\right) | (8) |
其中,
在一般情况下, 上述权值印记过程需要足够多的训练样本数据才能达到不错的效果, 而在一些现实场景中并不是所有训练数据都可以使用. 因此, 本文提出一种金字塔池化权值印记方法, 该方法通过将金字塔池化模块引入到任务预测器模块中, 使得不同网络层在做权值印记时的嵌入特征保持一致, 并且能够更加充分地利用有限的训练数据, 从而更加准确的度量网络中每一层的精度增益.
金字塔池化[9]是一种可以聚合不同区域的上下文信息, 以提高网络获取全局信息能力的模块. 其具体做法是在原始特征图上采用不同尺度的池化, 得到多个不同尺寸的特征图, 再在通道维度上拼接这些特征图, 最终输出一个融合了多种尺度的复杂特征图, 从而达到兼顾全局信息与局部细节信息的目的.
基于结合金字塔池化模块与权值印记技术的任务预测器, 如图1所示, 通过以下过程来度量网络层的精度增益.
首先, 对由卷积层所提取到的feature map进行
| e_i^d = AdaptiveAvgpool({F_i}, d) | (9) |
其中,
为了便于计算在任务预测分类器模块中全连接层的权值矩阵, 对统计到的高维特征进行维度变化, 将其转变为一维向量, 然后用来计算全连接层中的权值矩阵
| W_i^d[:, C] = \frac{{\displaystyle\sum\nolimits_{j = 1}^{Nu{m_c}} {Conf({x^{(j)}})e_{i, j}^d} }}{{\displaystyle\sum\nolimits_{j = 1}^{Nu{m_c}} {Conf({x^{(j)}})} }} | (10) |
其中,
利用校准数据集对目标网络进行前向计算得到任务预测器模块中全连接层的权值矩阵
| {e}_{i}^{\rm fuse}=concat({e}_{i}^{1}, {e}_{i}^{2}, \cdots \text{, }{e}_{i}^{n}) | (11) |
使用融合后的特征信息对权值矩阵
| S_{i, j}^d = W_i^de_{i, j}^{\rm fuse}\;\;(d = 1, 2, \cdots , n) | (12) |
对查询结果值利用Softmax操作将其转换为对应物体类别的概率向量:
| P_{i, j}^d[k] = \frac{{\exp (S_{i, j}^d[k])}}{{\displaystyle\sum\nolimits_{k = 1}^{nclass} {\exp (S_{i, j}^d[k])} }} | (13) |
其中,
| H_{i, j}^d = - \sum\limits_{k = 1}^{nclass} {p_{i, j}^d} [k]\log (p_{i, j}^d[k]) | (14) |
熵值越大, 确定性和信息量就越大, 反之同理. 因此我们对最后查询结果值
| {S_{i, j}} = \frac{{H_{i, j}^1S_{i, j}^1 + H_{i, j}^2S_{i, j}^2 + \cdots + H_{i, j}^nS_{i, j}^n}}{{H_{i, j}^1 + H_{i, j}^2 + \cdots + H_{i, j}^n}} | (15) |
以
基于上述所提出的训练后量化策略和混合精度搜索策略, 本文提出一种用于调整训练后量化比特位宽的混合精度搜索算法(MSQ), 通过引入精度估计的思想, 使用金字塔池化权值印记度量策略来获取量化网络每一层的精度增益, 并对其全局进行排序, 从而确定量化网络中每一层的量化比特位宽. 在训练后混合精度比特搜索过程中, 对每一次迭代更新后所得的混合精度配置
算法1. MSQ算法
输入: 校准数据集
初始化: 设置所有网络层权值和激活值比特位宽为
While 混合精度配置
do
1) 在网络当前混合精度配置
2) 采用金字塔池化权值印记混合精度搜索策略在验证数据集
3) 计算量化网络模型每一层的精度增益
4) 查询Diff最小值对应下标
5) 更新第
6) 保存当前网络的混合精度配置
输出: 目标网络在不同参数量下混合精度配置集合
与ZeroQ算法中使用的量化敏感度指标和AdaQuant算法中使用的整数线性规划方法相比, MSQ算法的准确率感知标准可以更加准确地获得不同网络层的比特位宽, 并从任务精度的角度来度量网络层的重要性, 因而具有更好的解释性.
4 实验设置与结果本文使用 ResNet18/20/50[28] 和MobileNet-V2 [29]等模型作为量化架构, 并在不同压缩率下进行了验证实验, 其中所有全精度预训练模型均来自文献 [4,5], 量化数据集包括 ImageNet、CIFAR-10 等. 用于实验的服务器配备了 NVIDIA GeForce RTX 3080 Ti GPU、11 GB 显存和256 GB 内存.
在训练后量化过程中, 从原始数据集的所有类别中选取适当数量的图像样本作为校准数据集, 并保持与文献 [1,4,6] 所用方法相同的量化设置. 在训练后的混合精度搜索中, 对校准数据集中的样本进行随机裁剪和水平翻转等数据扩增, 然后再执行金字塔池化权重印记度量. 通过与现有的 SOTA 方法进行比较, 验证了 MSQ 的优越性.
4.1 MSQ在CIFAR-10数据集上实验如第3.1节所述, 首先以EasyQuant[23]中余弦相似性作为训练后量化方法, 在训练后量化过程中使用MSQ进行混合精度搜索分配比特位宽, 表1展示了MSQ在CIFAR-10数据集上使用ResNet20网络与现有的一些量化方法进行比较.
| 表 1 CIFAR-10上MSQ 与一些混合精度量化方法的比较 |
表1中, Bit-width (W/A)表示权重和激活值量化的比特位宽, Mixed表示是否为混合精度量化, FP Top-1 Acc表示全精度模型精确度. 将权重同样量化到2位以下以此来验证MSQ, 可以看出MSQ方法相较于一些固定量化方法和混合精度量化方法在压缩比更高的情况下精确度也更高.
4.2 MSQ在ImageNet数据集上实验表2是在ImageNet数据集中MSQ方法与一些现有的SOTA量化方法实验比较结果. 其中, MP表示混合精度量化, MSQ[Ada]和MSQ[PD]分别表示使用第3.1节所述的AdaRound和PD-Quant训练后量化方法, 在量化过程中再使用MSQ进行混合精度搜索分配比特位宽, 以此来验证本文所提出的训练后混合精度量化方法的有效性.
从表2中可以看出, 将各类网络模型的激活值和权值进行4-bit量化时, MSQ相比原训练后量化方法在实现更高压缩比情况下, 精度也都有所提升, 尤其是在轻量级神经网络模型MobileNet-V2中, 经过MSQ混合精度搜索后的PD-Quant精度提升0.92%. 在权值和激活值的平均比特大约为3-bit低比特位量化中, MSQ对ResNet18和ResNet50网络实现了10.87倍和10.96倍更高压缩比, 且与 AdaRound原始量化方法相比, 模型精度均提升了近2%左右, 在MSQ对PD-Quant量化方法进行混合精度搜索后, ResNet50达到70.25%的Top-1精度, 而轻量化神经网络MobileNet-V2也取得了60.04%的精度以及11.23倍的高压缩比. 在更低位的2-bit量化中, MSQ算法也展现出其强大的性能, 虽然压缩比有所减小, 但所有模型的Top-1精度均有所提升. 可见, 无论是与低位或是更低位的量化方法相比, MSQ始终具有不错的性能效果.
为了进一步验证混合精度量化之后对网络模型带来的性能提升, 在图2中比较了MSQ混合精度量化和固定精度量化(Base)的差异, 并采用了MSQ[Ada]对ResNet50网络模型在不同大小下进行混合精度搜索配置.
| 表 2 MSQ 与其他量化方法在 ImageNet 数据集上的性能比较 |
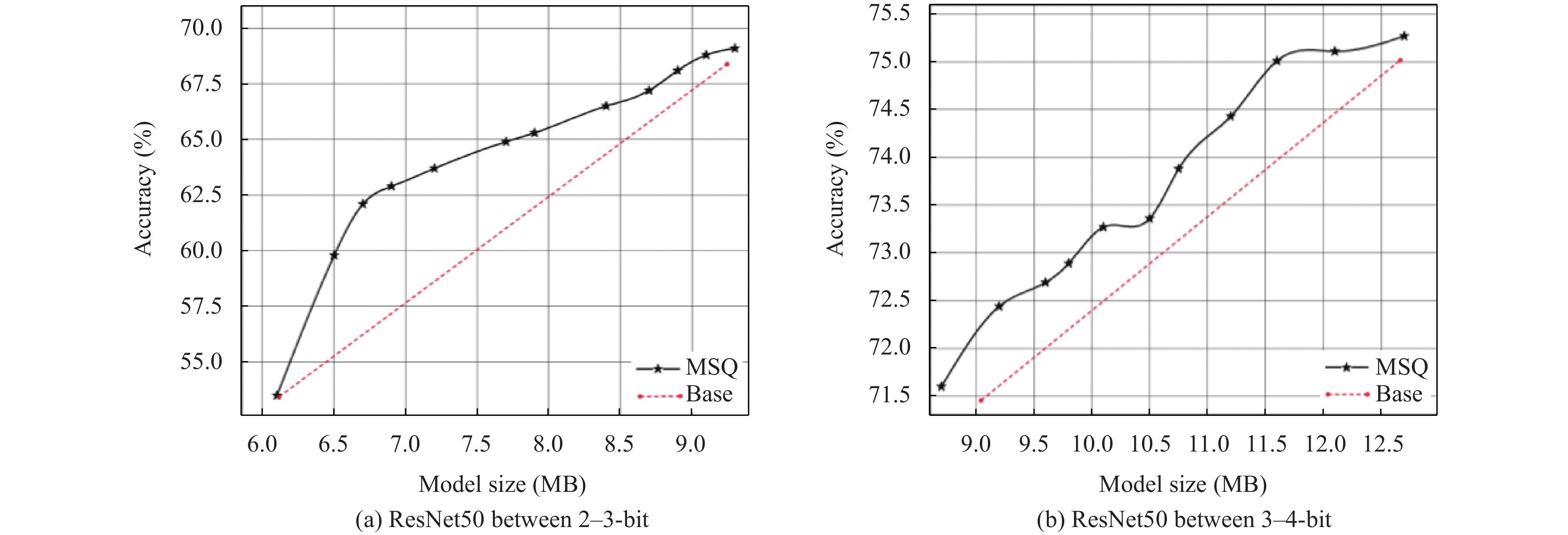
|
图 2 ResNet50在ImageNet上混合精度和固定精度量化比较 |
从图2中可以看出, 无论是在低位或更低位量化过程中, 混合精度量化网络模型始终整体优于固定量化网络模型, 因此, 混合精度量化由于其可以拥有不同模型大小的比特配置, 可以更加灵活高效的适用于不同的边缘设备端.
4.3 在硬件设备上评估结果本文将量化后的ResNet50网络模型部署在边缘硬件设备上评估其性能, 所使用硬件设备是 NIVIDIA 公司的边缘硬件设备 Jetson Nano 作为验证实验平台, 操作系统为以 Linux 为内核的 Ubuntu 系统, GPU 采用 Maxwell 架构, 浮点计算速度为 0.5 TFLOPs, CPU 为 Cortex-A57 MPCore 处理器, eMMC5.1-16 GB 内存. 主要测试ResNet50网络模型在使用混合精度量化后部署在硬件设备边缘设备端的时延对比.
表3中使用了MSQ混合精度量化方法以及AdaRound和PD-Quant训练后量化方法对ResNet50进行量化部署, 通过对比可以发现, MSQ在实现更高量化压缩比的情况下, 时延得到大幅提升. 近年来, 资源受限的边缘硬件设备在我们的生活中越来越多, 设计更加高效的模型量化方法, 可以更好地满足我们的生活所需. MSQ在边缘硬件设备端的表现, 更加体现出混合精度量化的优越性与高效性, 在后续的工作中, 我们会验证MSQ量化方法到更多的主流网络模型中, 并在更多的硬件设备中测试效果.
| 表 3 MSQ在边缘硬件设备端上的性能分析 |
5 总结
本文通过分析现有的训练后混合精度量化方法中忽略对网络模型层与层之间存在潜在影响, 从而导致网络层比特位宽分配存在分配不当等问题, 提出一种基于金字塔池化权值印记技术的训练后混合精度量化算法(MSQ), 以精度估计的思想更好的度量网络每一层的精度增益, 从而提供了一个可以评判网络模型每一层量化敏感度的标准, 以该标准搜索网络层的比特位宽并进行分配, 可以提升训练后量化模型的整体性能. 通过在CIFAR-10和ImageNet数据集上对不同网络模型架构进行实验验证, 证明了MSQ混合精度搜索算法的高效性, 且经过MSQ量化后的网络模型由于可以有不同的比特位宽, 在部署到一些硬件或者边缘端设备上时更具鲁棒性.
| [1] |
Krishnamoorthi R. Quantizing deep convolutional networks for efficient inference: A whitepaper. arXiv:1806.08342, 2018.
|
| [2] |
Siddegowda S, Fournarakis M, Nagel M, et al. Neural network quantization with AI model efficiency toolkit (AIMET). arXiv:2201.08442, 2022.
|
| [3] |
Reed JK, DeVito Z, He H, et al. torch.fx: Practical program capture and transformation for deep learning in Python. Proceedings of the 5th Machine Learning and Systems. Santa Clara: mlsys.org, 2022. 638–651.
|
| [4] |
Nagel M, Amjad RA, van Baalen M, et al. Up or down? adaptive rounding for post-training quantization. Proceedings of the 37th International Conference on Machine Learning. JMLR.org, 2020. 667.
|
| [5] |
Li YH, Gong RH, Tan X, et al. BRECQ: Pushing the limit of post-training quantization by block reconstruction. Proceedings of the 9th International Conference on Learning Representations. OpenReview.net, 2021.
|
| [6] |
Liu JW, Niu L, Yuan ZH, et al. PD-Quant: Post-training quantization based on prediction difference metric. Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Vancouver: IEEE, 2023. 24427–24437.
|
| [7] |
Cai YH, Yao ZW, Dong Z, et al. ZeroQ: A novel zero shot quantization framework. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020. 13166–13175.
|
| [8] |
Hubara I, Nahshan Y, Hanani Y, et al. Improving post training neural quantization: Layer-wise calibration and integer programming. arXiv:2006.10518, 2020.
|
| [9] |
Zhao HS, Shi JP, Qi XJ, et al. Pyramid scene parsing network. Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 6230–6239.
|
| [10] |
Qi H, Brown M, Lowe DG. Low-shot learning with imprinted weights. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Lake City: IEEE, 2018. 5822–5830.
|
| [11] |
Esser SK, McKinstry JL, Bablani D, et al. Learned step size quantization. Proceedings of the 8th International Conference on Learning Representations. Addis Ababa: OpenReview.net, 2020.
|
| [12] |
Bhalgat Y, Lee J, Nagel M, et al. LSQ+: Improving low-bit quantization through learnable offsets and better initialization. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops. Seattle: IEEE, 2020. 2978–2985.
|
| [13] |
Liu ZG, Mattina M. Learning low-precision neural networks without straight-through estimator (STE). Proceedings of the 28th International Joint Conference on Artificial Intelligence. Macao: ijcai.org, 2019. 3066–3072.
|
| [14] |
Li ZY, Guo C, Zhu ZD, et al. Efficient adaptive activation rounding for post-training quantization. arXiv:2208.11945, 2022.
|
| [15] |
Diao HB, Li GY, Xu SY, et al. Attention Round for post-training quantization. Neurocomputing, 2024, 565: 127012. DOI:10.1016/j.neucom.2023.127012 |
| [16] |
Wei XY, Gong RH, Li YH, et al. QDrop: Randomly dropping quantization for extremely low-bit post-training quantization. Proceedings of the 10th International Conference on Learning Representations. OpenReview.net, 2022.
|
| [17] |
Yao HY, Li P, Cao J, et al. RAPQ: Rescuing accuracy for power-of-two low-bit post-training quantization. Proceedings of the 31st International Joint Conference on Artificial Intelligence. ijcai.org, 2022. 1573–1579.
|
| [18] |
Jeon Y, Lee C, Cho E, et al. Mr. BiQ: Post-training non-uniform quantization based on minimizing the reconstruction error. Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New Orleans: IEEE, 2022. 12319–12328.
|
| [19] |
Wang CB, Zheng DD, Liu YL, et al. Leveraging inter-layer dependency for post-training quantization. Proceedings of the 36th International Conference on Neural Information Processing Systems. New Orleans: Curran Associates Inc., 2022. 483.
|
| [20] |
Wang K, Liu ZJ, Lin YJ, et al. HAQ: Hardware-aware automated quantization with mixed precision. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 8604–8612.
|
| [21] |
Dong Z, Yao ZW, Gholami A, et al. HAWQ: Hessian aware quantization of neural networks with mixed-precision. Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019. 293–302.
|
| [22] |
Li Y, Ding WR, Liu CL, et al. TRQ: Ternary neural networks with residual quantization. Proceedings of the 35th AAAI Conference on Artificial Intelligence. AAAI, 2021. 8538–8546.
|
| [23] |
Yang HR, Duan L, Chen YR, et al. BSQ: Exploring bit-level sparsity for mixed-precision neural network quantization. Proceedings of the 9th International Conference on Learning Representations. OpenReview.net, 2021.
|
| [24] |
Kimhi M, Rozen T, Kopetz T, et al. FBM: Fast-bit allocation for mixed-precision quantization. arXiv:2205.15437, 2022.
|
| [25] |
Liu J, Cai JF, Zhuang BH. Sharpness-aware quantization for deep neural networks. arXiv:2111.12273, 2021.
|
| [26] |
Huang XJ, Shen ZQ, Li SC, et al. SDQ: Stochastic differentiable quantization with mixed precision. Proceedings of the 39th International Conference on Machine Learning. Baltimore: PMLR, 2022. 9295–9309.
|
| [27] |
Wu D, Tang Q, Zhao YL, et al. EasyQuant: Post-training quantization via scale optimization. arXiv:2006.16669, 2020.
|
| [28] |
He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 770–778.
|
| [29] |
Sandler M, Howard A, Zhu ML, et al. MobileNet-V2: Inverted residuals and linear bottlenecks. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 4510–4520.
|
 2024, Vol. 33
2024, Vol. 33



