随着民航事业的飞速发展, 空域资源紧张问题也越来越突出. 航路网络对于各种突发情况的“抵抗力” 也越来越弱, 由此造成的各类问题也越来越严重. 航路网络是航空客货运的载体, 是实现空中交通的物理空间, 其结构是影响空中交通流稳定的重要因素. 航路点是航路网络的重要组成部分, 小部分航路点分担了航路网络中的大部分流量, 因此识别关键节点对消除航路瓶颈, 提高空域容量合理分配航线有重要意义.
在航路网络关键节点和连边识别过程中, 通常包括空域建模和识别两个部分. 空域建模是将其简化为复杂网络, 将描述对象的个体抽象为节点, 个体之间的关系抽象为连边, 在此基础上生成图. 网络中边重要性的评估方法主要为基于网络拓扑结构的方法和基于传播识别关键边. 基于边的两端节点共同邻居越少, 边的重要程度越高理论提出了Jaccard系数, 打开了关键连别识别的大门. 2002年, Holme等人[1]提出度积(degree product, DP)为两端点度的乘积以此量化边的重要程度. 2020年, Sun等人[2]提出link shell评价方法, 顾名思义根据两个端点在k核分解出来的shell值表征边的重要程度. 基于网络拓扑结构的关键边识别方法还包括连边删除评估法、边介数排序法和最短路径排序法等. 2018年, 李佳威等人[3]提出一种基于最小连通支配集的复杂网络边识别方法, 采用度中心性、接近中心性、介数中心性与PageRank, 对所有节点进行重要度评估. 2022年, 朱新建等人[4]采用删除节点导致网络效率的减少程度大小表征连边的重要程度. 除此之外, 基于传播识别关键边中, 2015年, Liu等人[5]认为连边在信息传播过程中传播的越多, 则重要性越高.
节点识别主要焦距在网络拓扑结构方面和航段流量两个方面. 基于网络拓扑结构的重要节点识别方法可分为两类: 第1类方法一般通过节点在网络拓扑中的中心性程度进行评估, 第2类方法为去除节点之后分析网络的性能毁坏程度. 2008年, 邓贵仕等人[6]基于复杂网络基础知识将度分布、聚集系数、网络效率等指标应用于航路网络, 除此之外, 诸多学者对评价指标进行了优化, 2012年, 周璇等人[7]采用节点效率、节点度值和节点重要的贡献修补了节删除法、节点收缩法和介数法的不足, 并且提出了一种利用重要度评价矩阵来确定复杂网络关键节点的方法. 2017年, 程光权等人[8]考虑到了实际网络中存在的物质流动给网络带来的影响, 并且利用节点的重要度表征节点由于过载对近邻节点负载的震荡程度, 以此来识别关键节点. 2018年, 蔡若男[9]在高速铁路光传送网络的节点重要度评估时, 考虑了静态网络指标和动态网络指标, 并结合二维评估法TDEA共同评估节点重要程度. 2022年, 贾俊杰[10]就基于邻居节点的重要性、基于全局信息的重要性、基于特征向量的重要性和基于结构洞的重要性4个方面提出了评价指标评价节点的重要程度. 2022年, 田文等人[11]结合中心性、破坏性两个方面以及节点实际情况建立了航路网络关键节点评价指标体系, 采用相对熵改进逼近理想值排序法结合灰色关联分析法综合评价航路点的重要程度, 最后结合聚类算法划分航路点重要程度等级, 在此基础上, 2023年, 徐凤等人[12]引入了熵权法为指标分配权重, 提升关键节点识别的全面性和准确性. 2023年, 马小琦[13]采用信息贡献率和相关度分析去除关键节点评价指标中影响较弱和较强的指标, 剩余指标组成了关键节点评价指标体系. 同年, 宇文翀[14]在联合交通下公路网络的交通需求预测和布局方法研究的过程中, 采用邓氏关联度探究了公路、铁路和航空等不同交通运输方式客货运量与其影响因素之间的关联度, 为后续各个产业在货运量预测中赋予较低权重.
从总体来看, 国内外针对关键连边识别的研究较少, 且在关键节点和关键连边识别相关研究中只分析了在静态拓扑结构下的节点和连边的重要程度, 忽略了流量和由于节点或连边失效, 流量分散导致的级联失效情况. 本文将结合网络实际运行情况, 将航路点简化为节点, 将航班计划中给出的航段简化为连边, 构成无向网络, 同时借鉴相对成熟的路网交通指标和复杂网络指标, 将其映射到关键连边的识别过程中, 采用TOPSIS-EWM方法识别关键节点和连边, 最后计算各个指标与节点或连边得分的关联程度, 为航路网络规划提供建议.
1 关键节点识别指标关键节点识别指标从静态指标和动态指标出发. 将航路网络拓扑结构和航段流量信息采用图论的方式进行描述, 将其定义为无向图
| $ {e}_{ij}=\left\{\begin{array}{*{20}{l}} \sqrt{{({x}_{i}-{x}_{j})}^{2}+{({y}_{i}-{y}_{j})}^{2}}{ },&{v}_{i}, {v}_{j}\text{ }存在直连\\ 0,&{v}_{i}\text{, }{v}_{j}\text{ }没有直连\end{array} \right. $ | (1) |
在复杂网络中, 节点间的联系通过邻接矩阵
静态指标为拓扑结构指标, 主要包括节点度、节点介数、聚集系数和度与相邻节点度的乘积.
1.1.1 节点的度在图论中, 节点的度是指与该节点相连的边的数量, 通常与航路网络节点的重要程度成正比, 其度量了节点的连接性或相邻关系. 计算方法如下:
| $ {k_i} = \sum\limits_j^N {{a_{ij}}} $ | (2) |
其中, 若节点
节点介数是一种用于衡量网络中节点在不同节点间通信或传递信息时的重要性的指标. 节点介数越高, 意味着该节点在网络中的地位越重要, 因为它位于不同节点之间的最短路径上, 起到了连接节点的作用. 是一个节点在图中所有最短路径中出现的频率的累加值, 即一个节点通过其存在于最短路径上的次数来衡量其在网络中的中介地位, 介数高的节点通常在网络中充当信息传递的枢纽. 计算方法如下:
| $ {C_B}\left( v \right) = \sum\limits_{i \ne v \ne j} {\frac{{{\sigma _{ij}}\left( v \right)}}{{{\sigma _{ij}}}}} $ | (3) |
其中,
节点聚集系数用于衡量图中节点的邻居之间形成紧密联系的程度. 这一指标度量了一个节点的邻居之间相互连接的程度, 反映了图中局部的连通性. 节点聚集系数是一个介于 0–1 之间的值, 其中 0 表示邻居节点之间没有连接, 而 1 表示邻居节点之间全部相互连接. 计算方法如下:
| $ X\left( i \right) = \frac{{2{E_i}}}{{{k_i}({k_i} - 1)}} $ | (4) |
其中,
度与相邻节点度的乘积通常用于衡量网络中节点的结构特征, 尤其是节点的邻居节点的连接性. 这个指标可以反映节点在网络中的影响力或重要性. 计算方法如下:
| $ {P}_{i}={k}_{i}\cdot{\displaystyle \prod _{u\in N(i)}{k}_{u}} $ | (5) |
其中,
动态指标包括典型日流量和网络效率变化率.
1.2.1 典型日流量“典型日”指的是在某个特定时间范围内具有代表性、典型性质的一天. 典型日流量的分析对于航路网络关键节点识别方面具有重要意义. 从历史数据中可得计算结果.
1.2.2 网络效率变化率航路网络的网络效率涉及交通流的顺畅程度、拥堵情况以及整个航路网络的运行效率. 需要先明确节点的极限容量, 计算节点失效时, 由于流量分散而导致的网络级联失效程度. 计算步骤如下:
| $ Q = \frac{1}{T} $ | (6) |
| $ {R_i} = \frac{{{D_0} - {D_i}}}{{{D_0}}} \times 100{\text{%}} $ | (7) |
其中,
| $ \begin{gathered} \qquad\qquad\qquad\begin{array}{*{20}{c}} \;{{v_1}}&\;\;{v_2}&\;\;{v_3}&\;\; \cdots &\;\;{{v_n}} \end{array} \\ G(V, E) = \begin{array}{*{20}{c}} \begin{gathered} {v_1} \\ {v_2} \\ \end{gathered} \\ {{v_3}} \\ \vdots \\ {{v_n}} \end{array}\left[ {\begin{array}{*{20}{c}} {{e_{11}}}&{{e_{12}}}&{{e_{13}}}& \cdots &{{e_{1n}}} \\ {{e_{21}}}&{{e_{22}}}&{{e_{23}}}& \cdots &{{e_{2n}}} \\ {{e_{31}}}&{{e_{32}}}&{{e_{33}}}& \cdots &{{e_{3n}}} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {{e_{n1}}}&{{e_{n2}}}&{{e_{n3}}}& \cdots &{{e_{nn}}} \end{array}} \right] \\ \end{gathered} $ | (8) |
静态指标为拓扑结构指标, 主要包括连边介数、节点对之间的平均最短路径长度、Jaccard系数、度积.
2.1.1 连边介数在图论中, 用来衡量网络中节点在不同节点之间的最短路径中起到的中介作用程度的指标. 一个节点的介数越高, 意味着它在网络中连接其他节点的最短路径上起到的中介作用越大. 计算方法如下:
| $ {C_i} = \sum\limits_{s \ne i \ne t} {\frac{{{\sigma _i}\left( {st} \right)}}{{\sigma (st)}}} $ | (9) |
对于网络中的节点
节点对之间的平均最短路径长度是用来衡量网络中节点对之间相互连接的距离的指标. 它表示在网络中选择所有可能的节点对, 然后计算每一对节点之间的最短路径长度, 最后取平均值. 计算方法如下:
| $ L = \frac{1}{{N(N - 1)}}\sum\limits_{i \ne j} {{d_{ij}}} $ | (10) |
其中,
Jaccard系数是一种用于衡量两个节点的邻居集合之间相似度的指标. 它定义为两个节点共同邻居节点数目除以它们的邻居节点的并集数目. 如果两个节点的邻居节点集合有很大的重叠, 那么它们的Jaccard系数就会接近1, 表示它们在邻居节点方面有很高的相似度; 反之, 如果它们的邻居节点集合几乎没有重叠, Jaccard系数就会接近0, 表示它们在邻居节点方面相似度较低. 计算方法如下:
| $ {J_{ij}} = {\frac{\left|{{N_i} \cap {N_j}}\right|}{\left|{{N_i} \cup {N_j}}\right|}} $ | (11) |
其中,
连边的度积是一种用于衡量网络中节点对之间边的连接强度的度量. 是指两个节点之间边的度的乘积. 度积的概念可以用于研究节点对之间的连接关系, 并在网络分析中提供关于节点对连接强度的信息. 计算方法如下:
| $ {k}_{ij}={k}_{i}\cdot{k}_{j} $ | (12) |
其中,
关键连边识别动态指标与第1.2节相似.
2.2.1 典型日流量参考第1.2.1节, 此处为典型日实际统计的经过各个连边的流量.
2.2.2 网络效率变化率参考第1.2.2节, 此处为连边失效后, 航路网络效率的变化差值数.
3 评价模型 3.1 熵权法(1)指标的归一化处理
当
| $ {X_{ij}} = \frac{{{x_{ij}} - \min \{ {x_{ij}}, \cdots , {x_{nj}}\} }}{{\max \{ {x_{1j}}, \cdots , {x_{nj}}\} - \min \{ {x_{1j}}, \cdots , {x_{nj}}\} }} $ | (13) |
当
| $ {X_{ij}} = \frac{{\max \{ {x_{ij}}, \cdots , {x_{nj}}\} - {x_{ij}}}}{{\max \{ {x_{1j}}, \cdots , {x_{nj}}\} - \min \{ {x_{1j}}, \cdots , {x_{nj}}\} }} $ | (14) |
(2)计算第
| $ {p_{ij}} = \frac{{{X_{ij}}}}{{\displaystyle\sum\limits_{j = 1}^n {{X_{ij}}} }},\;i = 1, \cdots , n;j = 1, \cdots , m $ | (15) |
(3)计算第
| $ {w_i} = \frac{{1 + \dfrac{1}{{\ln (m)}}\displaystyle\sum\limits_{j = 1}^m {{p_{ij}}\ln ({p_{ij}})} }}{{\displaystyle\sum\limits_i^n {1 + \dfrac{1}{{\ln (m)}}\displaystyle\sum\limits_{j = 1}^m {{p_{ij}}\ln ({p_{ij}})} } }} $ | (16) |
本文使用带权重的优劣解距离法, 采用上文熵权法的计算结果代入评价计算过程中. 最大值、最小值分别表示为:
| $ \left\{\begin{gathered} {X_{i\max }} = \max \left\{ {{x_{i1}}, \cdots , {x_{im}}} \right\},\;i = 1, \cdots , n;j = 1, \cdots , m \\ {X_{i\min }} = \min \left\{ {{x_{i1}}, \cdots , {x_{im}}} \right\},\;i = 1, \cdots , n;j = 1, \cdots , m \\ \end{gathered}\right. $ | (17) |
其中, 最优解和最劣解的距离分别记为:
| $ \left\{\begin{gathered} {D^ + } = \sqrt {{w_i}{{({X_{i\max }} - {X_{ij}})}^2} + \cdots + {w_n}{{({X_{n\max }} - {X_{nj}})}^2}} ,\\ i = 1, \cdots , n;j = 1, \cdots , m \\ {D^ - } = \sqrt {{w_i}{{({X_{i\min }} - {X_{ij}})}^2} + \cdots + {w_n}{{({X_{n\min }} - {X_{nj}})}^2}} ,\\ i = 1, \cdots , n;j = 1, \cdots , m \\ \end{gathered}\right. $ | (18) |
本文将采用Pearson相关系数计算各个指标计算结果和节点得分之间的关联程度, 确定指标结果与得分之间的相互作用. 若结果为1则表示两者之间完全正相关, −1表示两者之间完全负相关, 0表示没有线性关系. 计算方法如下.
(1)计算协方差
| $ Cov({X_i}, Y) = \frac{{\displaystyle\sum\limits_{j = 1}^m {\left({X_{ij}} - \dfrac{{\displaystyle\sum\limits_{j = m}^m {{x_{ij}}} }}{m}\right)\left({Y_j} - \dfrac{{\displaystyle\sum\limits_{j = m}^m {{y_j}} }}{m}\right)} }}{{m - 1}} $ | (19) |
(2)计算Pearson相关系数
| $ \begin{split} T&=\frac{\frac{{\displaystyle \sum _{j=1}^{m}\left({X}_{ij}-\dfrac{{\displaystyle \sum _{j=m}^{m}{x}_{ij}}}{m}\right)\left({Y}_{j}-\dfrac{{\displaystyle \sum _{j=m}^{m}{y}_{j}}}{m}\right)}}{m-1}}{\sqrt{\dfrac{{\displaystyle \sum _{j=1}^{m}({X}_{ij}-\overline{{X}_{i}})}}{m-1}}\cdot\sqrt{\dfrac{{\displaystyle \sum _{j=1}^{m}({Y}_{j}-\overline{Y})}}{m-1}}}\\ &=\frac{Cov({X}_{i}, Y)}{{\textit{SD}}({X}_{i})\cdot {{\textit{SD}}(Y)}},\;i=1, \cdots , n \end{split} $ | (20) |
若结果为1则表示两者之间完全正相关, −1表示两者之间完全负相关, 0表示没有线性关系. 全文流程图如图1所示.
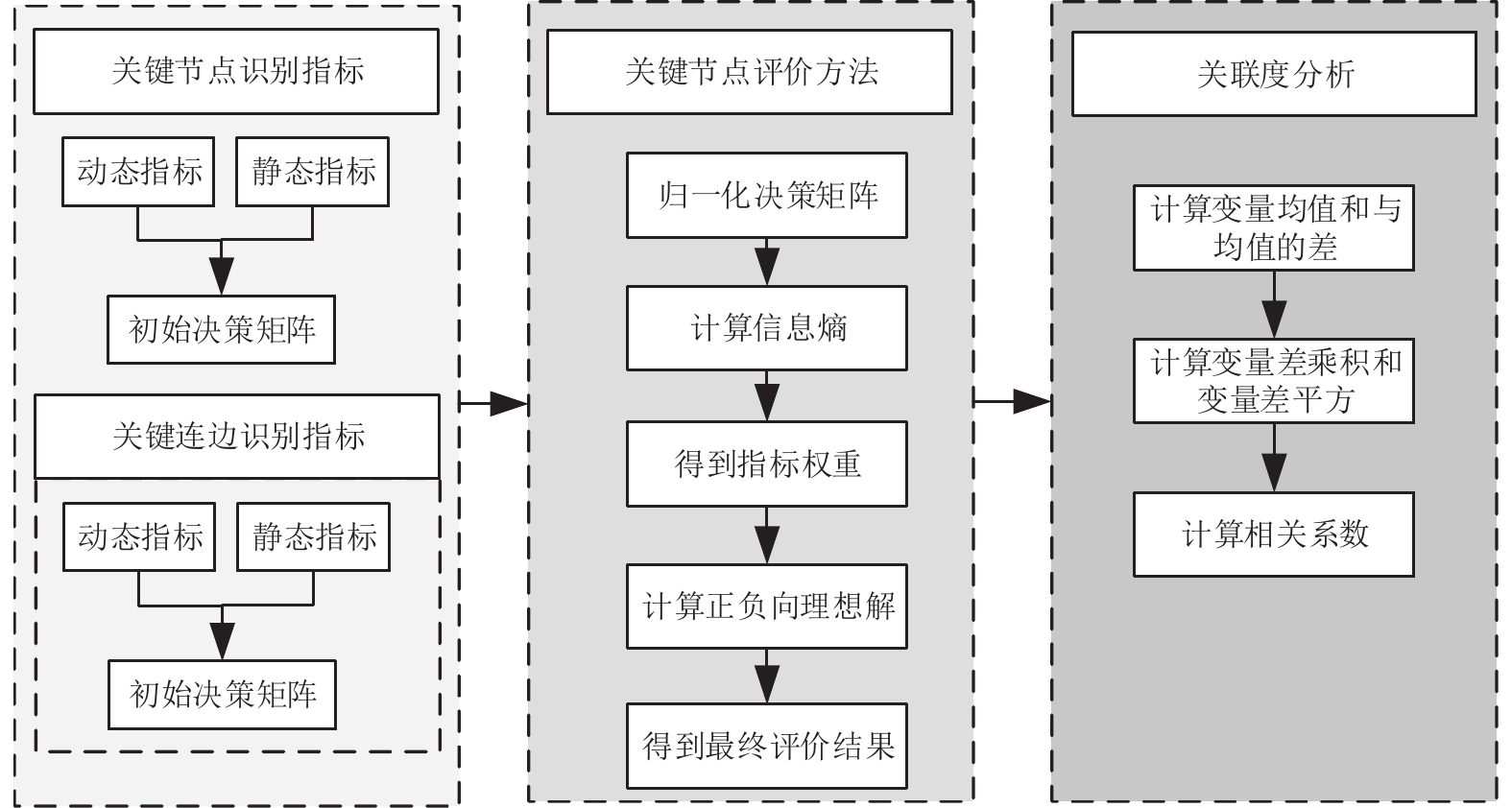
|
图 1 技术路线图 |
5 实例验证
采用民航中南地区航路网络2023年5月的实际运行数据, 该地区包括湖南省、湖北省、广东省、广西壮族自治区、海南省和江西省. 图2为2023年中南地区航路网络结构图.
5.1 关键节点识别结果根据第1节所选取的指标, 结合实际运行情况计算中南地区航路点的指标值, 形成原始决策矩阵. 通过指标分析发现, 所选指标数值越大, 航路点越重要, 均为正向指标. 通过熵权法计算各个指标权重, 如图3所示, 可以看出节点介数、聚集系数和度和相邻节点度数乘积权重值相差不大, 其中影响程度最高的是流量和网络效率变化率, 这表明了动态指标对于航路网络关键节点识别的重要程度, 其与实际运行情况一致, 即熵权法计算结果是合理的.
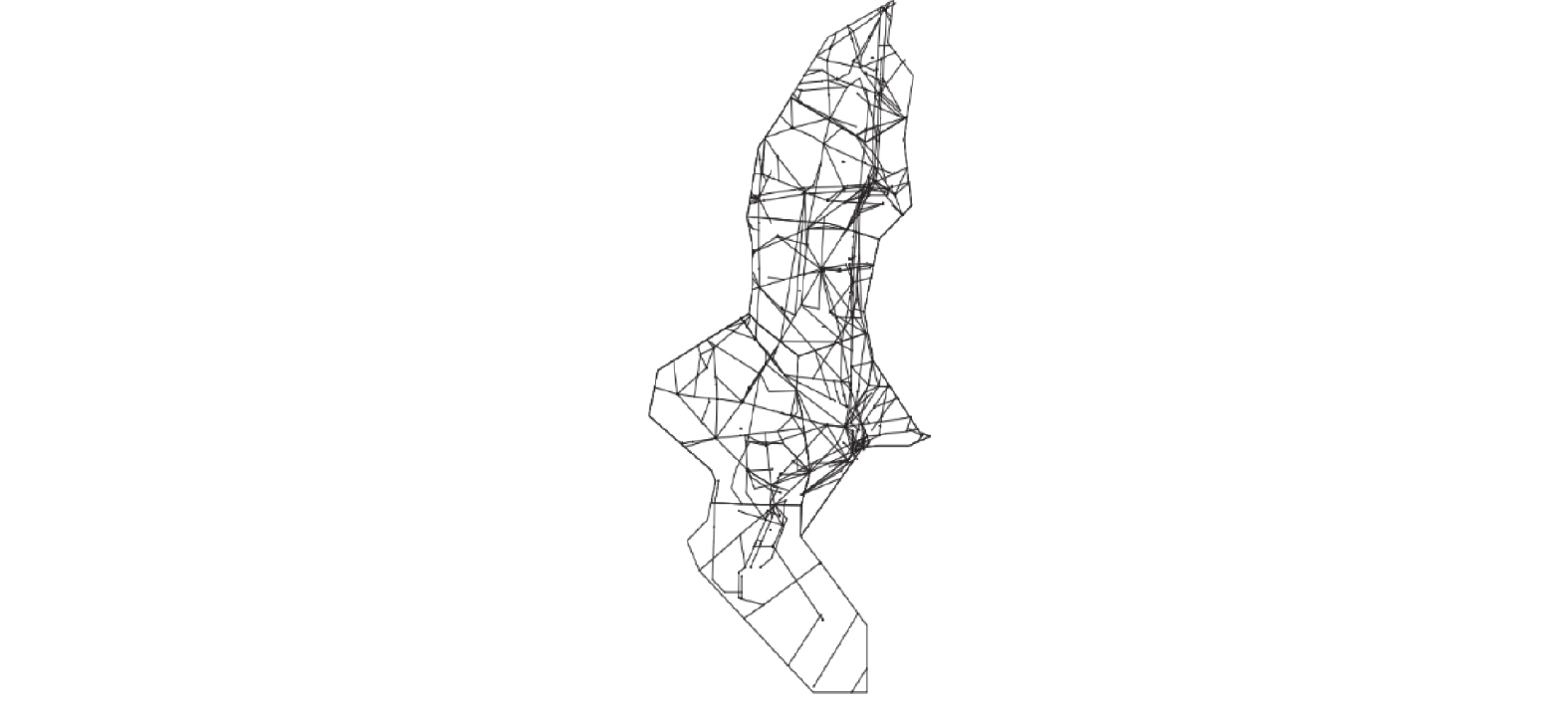
|
图 2 中南地区结构图 |
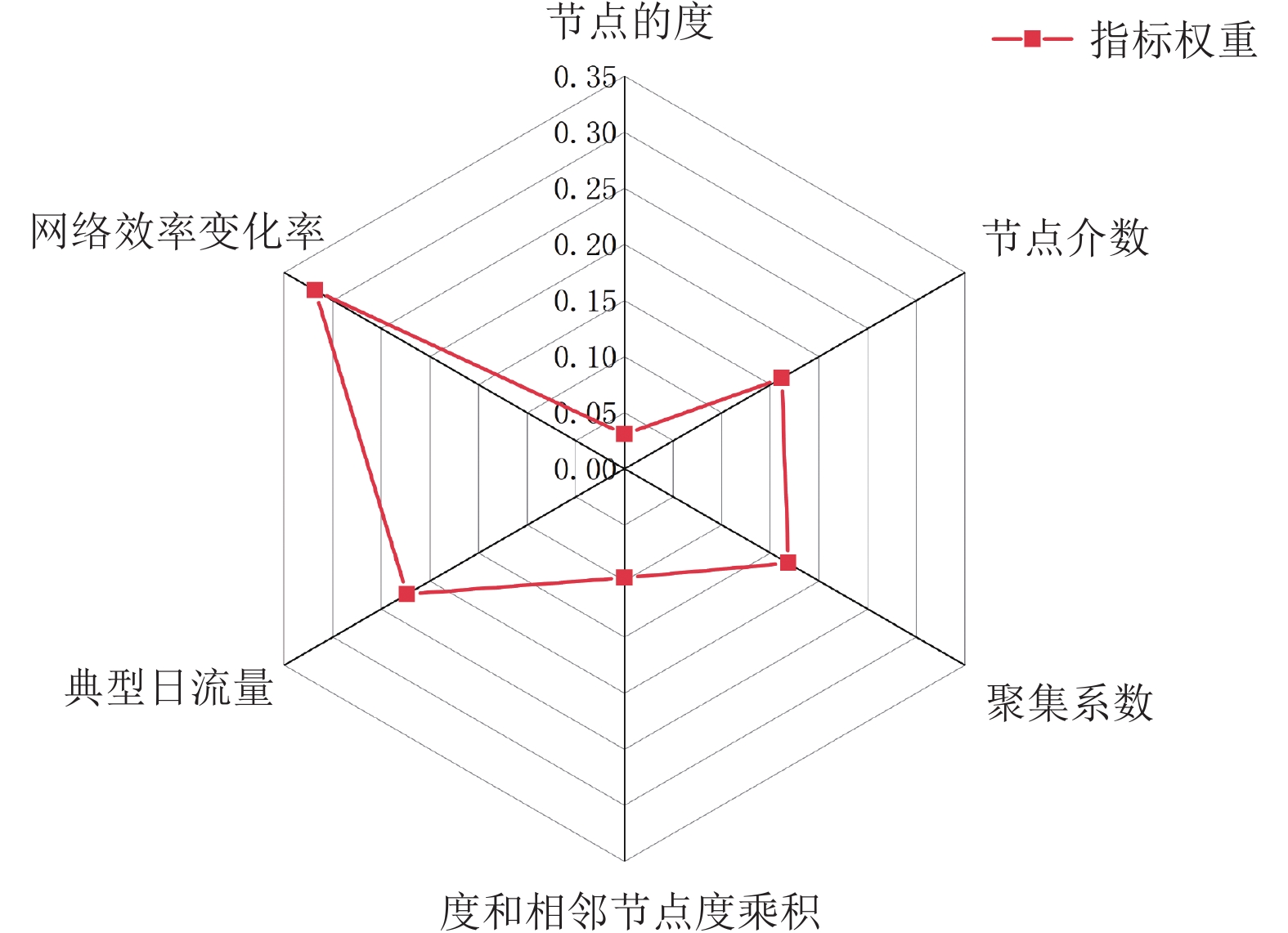
|
图 3 关键节点识别指标权重计算结果 |
紧接着采用TOPSIS法计算正负解, 得到节点得分, 对中南地区关键航路点进行识别, 结果分布情况如图4所示, 大部分节点得分分布在0.25–0.35之间, 只有少部分得分较高较为关键, 且所在位置在图中标星的位置, 即结构复杂流量较多的位置.
最后采用Pearson相关性检验可得节点的各个指标值和评价结果之间的关系, 具体值如表1. 加粗和下划线的含义分别为相关性程度最高和相关性程度最低.
部分关系示意图如图5所示.
结果表明静态指标之间除度和介数关联度较高外, 其他指标之间都相对独立, 动态指标之间关联度不大. 因此在今后航路网络结构优化的过程中, 需要同时考虑多个指标的变化, 而不是考虑从单个指标的角度优化航路网络结构.
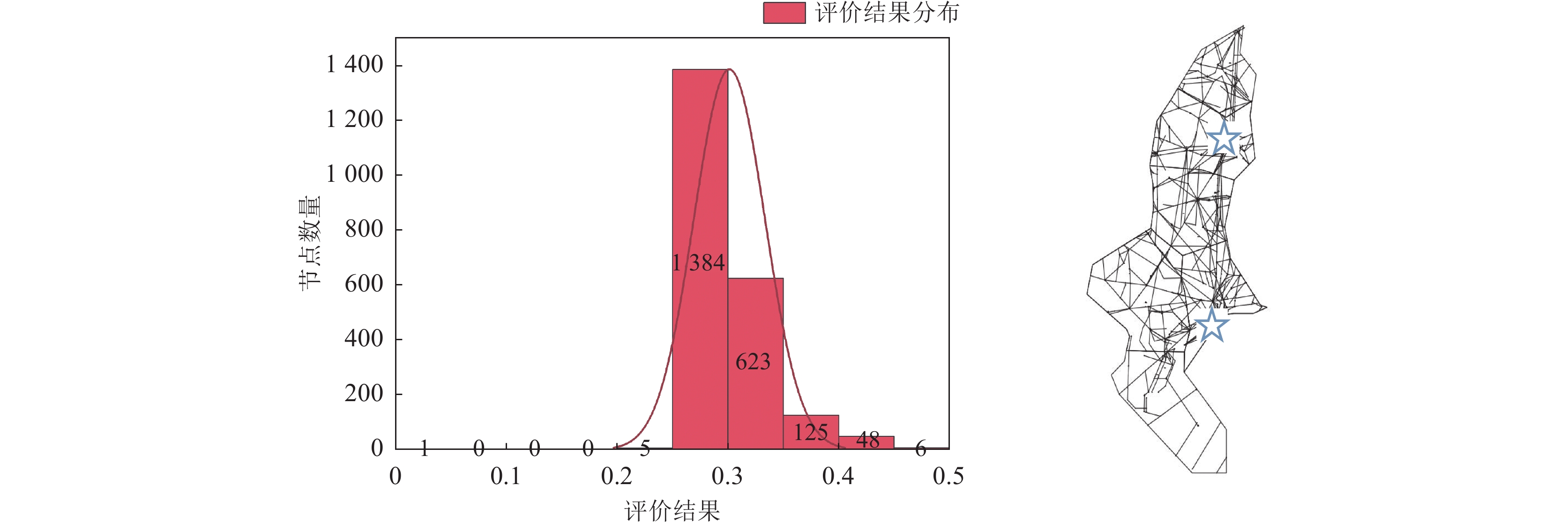
|
图 4 关键节点评价结果分布 |
| 表 1 关键节点识别指标相关性结果 |
|
图 5 关键节点识别部分指标相关性结果 |
5.2 关键连边识别结果
根据前文所选指标, 结合中南地区实际运行情况计算各个航段的指标值, 形成原始决策矩阵, 并对其进行归一化处理, 形成归一化决策矩阵. 并通过熵权法计算各个指标权重, 分布情况如图6所示.
紧接着采用TOPSIS方法计算正负解, 得到连边得分, 对中南地区关键航段进行识别, 结果分布情况如图7所示, 大多数连边得分分布在0.35–0.5之间, 只有部分连边得分较高较为关键, 且所在位置在图中框定区域, 即结构复杂流量较多的位置.
|
图 6 关键连边识别指标权重计算结果 |
最后采用Pearson相关性检验可得节点的各个指标值和评价结果之间的关系, 具体值如表2.
部分关系示意图如图8所示.
结果表明, 各个指标间关联度不高, 都相对独立. 但各个指标与连边得分关联度较高. 因此在今后航路网络结果优化和航线分配的过程中, 需要同时考虑多个指标的变化, 尤其是关注网络拓扑结构, 而不是从单个指标的角度优化航路网络结果和流量分配.
|
图 7 关键连边评价结果分布 |
| 表 2 关键连边识别指标相关性结果 |
|
图 8 关键连边识别部分指标相关性结果 |
6 总结
综合考虑复杂网络拓扑结构和航段流量信息等因素, 从静态和动态两个方面考虑节点和连边重要程度影响因素, 采用熵权法从数据本身特征出发确定各个指标权重, 在此基础上采用TOPSIS评价方法识别航路网络关键连边, 符合航路网络实际运行情况. 同时采用Pearson相关性分析发现各个指标之间及指标与评价结果之间的关联程度, 为实际航路网络规划和调整提供方便. 通过对中南地区航路网络实例分析结果发现, 关键航段和航路点主要分布在航段密集和交通流量密集区域, 这表明了静态指标和动态指标的影响对节点和连边重要程度的影响, 其可以作为参考意见应用在航路网络初步规划和调整过程中, 尽量减少关键航段, 平衡各个航段的流量. 同时在实际运行过程中, 应对关键节点和关键连边予以更多的关注, 降低由于单个节点失效导致网络崩溃的可能性, 在航路网络结构的调整过程中, 注意与关键节点和关键连边关联度高的连边特征的分布有利于网络结构的优化.
| [1] |
Holme P, Kim BJ, Yoon CN, et al. Attack vulnerability of complex networks. Physical Review E, 2002, 65(5): 056109. DOI:10.1103/PhysRevE.65.056109 |
| [2] |
Sun SW, Liu XX, Wang L, et al. New link attack strategies of complex networks based on k-core decomposition. IEEE Transactions on Circuits and Systems II: Express Briefs, 2020, 67(12): 3157-3161. |
| [3] |
李佳威, 吴明功, 温祥西, 等. 基于最小连通支配集的复杂网络关键节点与连边识别方法. 系统工程与电子技术, 2019, 41(11): 2541-2549. |
| [4] |
朱新建, 徐畅, 卢立红, 等. 江苏省货运铁路网络关键节点和连边识别. 山东交通科技, 2022(5): 13-16. |
| [5] |
Liu Y, Tang M, Zhou T, et al. Improving the accuracy of the k-shell method by removing redundant links: From a perspective of spreading dynamics. Scientific Reports, 2015, 5: 13172. DOI:10.1038/srep13172 |
| [6] |
邓贵仕, 武佩剑, 田炜. 全球航运网络鲁棒性和脆弱性研究. 大连理工大学学报, 2008, 48(5): 765-768. |
| [7] |
周漩, 张凤鸣, 李克武, 等. 利用重要度评价矩阵确定复杂网络关键节点. 物理学报, 2012, 61(5): 1-7. |
| [8] |
程光权, 陆永中, 张明星, 等. 复杂网络节点重要度评估及网络脆弱性分析. 国防科技大学学报, 2017, 39(1): 120-127. |
| [9] |
蔡若男. 基于高速铁路光传送网络的节点重要性及保护策略研究 [硕士学位论文]. 北京: 北京交通大学, 2018.
|
| [10] |
贾俊杰. 中欧班列运输网络关键节点识别及鲁棒性优化研究 [硕士学位论文]. 长沙: 中南大学, 2022.
|
| [11] |
田文, 方琴, 周雪芳, 等. 航路网络关键节点识别方法研究. 西南交通大学学报. http://kns.cnki.net/kcms/detail/51.1277.U.20221124.0859.002.html. (2022-11-25)[2023-10-25].
|
| [12] |
徐凤, 朱金福, 陈丹. 东航空铁联运双层加权网络的关键节点识别与抗毁性分析. 铁道运输与经济, 2023, 45(1): 93-100. |
| [13] |
马小琦. 城市道路交通网络关键节点识别方法研究 [硕士学位论文]. 长春: 吉林大学, 2022.
|
| [14] |
宇文翀. 综合交通背景下干线公路网交通需求预测与布局方法研究 [硕士学位论文]. 哈尔滨: 东北林业大学, 2022.
|
 2024, Vol. 33
2024, Vol. 33


