在强化学习领域[1–3], 多智能体协同[4–6]是一个探索如何使多个智能体在环境中共同作用以达到目标的复杂子领域. 在线多智能体强化学习[7,8]是合作多智能体强化学习(MARL)的一种重要算法, 可以有效地处理非平稳性. 当前, 大部分在线MARL算法[9,10]通过实时策略迭代[11]、经验回放[12]以及模型自适应[13]等机制, 让智能体能够与环境交互同时学习策略的即时更新和优化. 其中MADDPG[14]将DDPG[15]算法扩展到了多智能体系统中, 相较于传统多智能体强化学习的分散训练方式, 它采用集中训练分散执行(CTDE)[16–18]的方式, 充分考虑多个智能体之间的潜在合作意向, 实现了协同策略的演进. 然而由于其不能反映每个智能体对团队的贡献度, 学者们提出了COMA[19], 基于反事实差异评估特定智能体的没有采用特定行动会对结果带来什么影响, 来衡量每个智能体的具体贡献. 但是, COMA的信用分配方法是基于全局状态, 与大部分MARL环境的局部观察性相悖. MAPPO[20]不仅维持了信用分配的效能, 还通过更为灵活的状态表征手段优化了智能体基于局部观察下的决策过程. 最近几年注意力模型在深度学习领域取得了显著的成效, MAAC[21]算法将注意力机制引入到多智能体强化学习中, 显著提升了算法在处理多智能体复杂交互中的学习效率和策略适应性.
尽管目前的方法在某种程度上取得了一定的成效, 然而, 大多数MARL算法[22–24]主要集中在宏观层面的协作形成上, 而忽略了在个体层面增强智能体策略对团队策略的演进支持的重要性. 此外, 在多智能体系统(MAS)中, 如何动态学习适应每一次决策过程中与队友合作的程度对MAS最终的性能也有重要的影响[25,26].
为了解决上述问题, 本文提出了一个BiTransformer记忆模型(BTM). 该模型包括双注意力编码器(BTE)和双注意力解码器(BTD)两个部分, 其中BTE由记忆注意力模块(MF)和融合注意力模块(FF)组成. MF依据生活中的经验, 阴天要带伞这种行为是基于过去经验的结果. 因此, 基于这一现象, MF引入了历史决策经验模块, 专注于对历史决策经验的分析、存储, 支持决策经验的持续更新和有效保留, 并为每个智能体配备了定长的记忆空间, 利用先入先出的方式进行更新. 最终实现决策经验辅助下的局部观测的特征提取, 这是本文实现个体决策增强的重要的一步. FF利用注意力分析当前观测为己方团队通信分配机制, 从而为对当前决策过程更具价值的决策个体和环境信息分配更高的关注度. 在BTD中, 本文考虑到智能体如果能够察觉到其他智能体的行为更有利于智能体做出决策, 提出了动态策略调整机制, 首先由合作注意力模块(CF)对已经做出决策的“前辈”智能体的行为策略进行分析, 通过注意力机制计算并分配与不同“前辈”智能体的合作强度, 动态调整智能体的策略进而获取最大的合作收益. 最后在决策注意力模块(PF)中, 通过合作收益与交互状态获取决策序列.
1 背景 1.1 多智能体在线强化学习在线多智能体强化学习[27,28]可以转换成局部可观测的马尔可夫决策过程
优势函数
| $ A(s, a) = Q(s, a) - V(s) $ | (1) |
其中,
| $ \hat A_t^{{\mathrm{GAE}}(\gamma , \lambda )} = \sum\limits_{l = 0}^\infty {{{(\gamma \lambda )}^l}\delta _{t + l}^V} $ | (2) |
其中,
注意力机制[31]包括查询(
| $ {\textit{Attention}}(q, k, \nu ) = {\textit{Softmax}}\left(\frac{{q{k^{\mathrm{T}}}}}{{\sqrt {{d_k}} }}\right)\nu $ | (3) |
其中,
本文提出的BTM旨在强化智能体自身决策能力的同时促进多智能体合作的形成, 整体架构如图1所示. 该模型由BTE和BTD组成, 其中BTE通过引入记忆网络处理历史决策经验
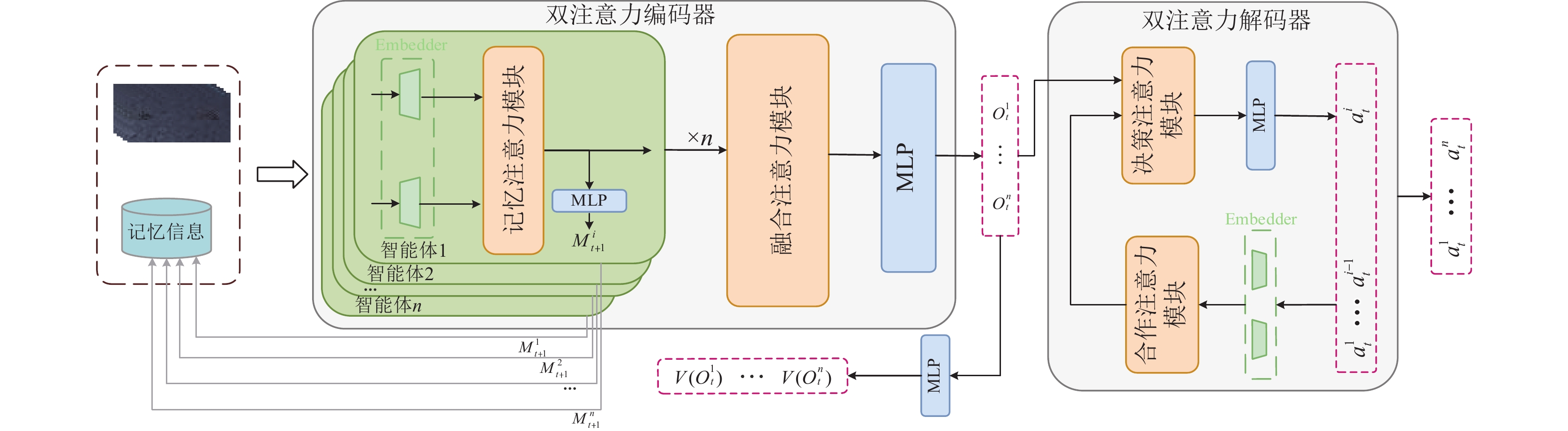
|
图 1 BTM结构示意图 |
2.1 双注意力编码器
BTE负责处理分析输入的观测以及历史决策经验, 以生成更具决策价值的交互状态. BTE增强了智能体处理环境信息的能力, 提高了智能体的个体决策, 为后续解码器提供了有效输入.
记忆注意力模块: 本文设计了记忆注意力模块, 该网络利用注意力机制在历史决策经验
| $ m_t^i = \psi (\kappa (O_t^i, M_t^i)) $ | (4) |
其中,
此外, 该模块为每个智能体开辟了固定的记忆空间, 并采用队列先入先出的方式进行更新, 具体如图2所示. 当记忆空间大小
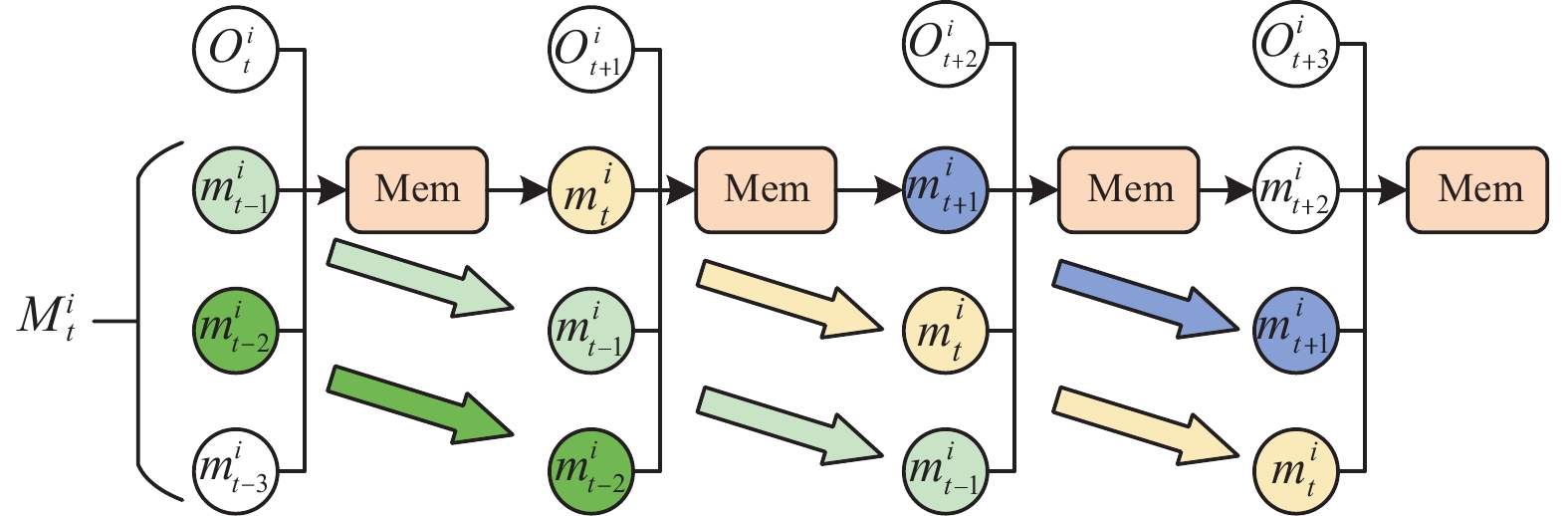
|
图 2 记忆模块框架图 |
融合注意力模块: 本文设计了融合注意力模块, 旨在促进智能体之间的交流并为智能体的决策过程提供更具价值的环境信息, 融合注意力模块综合处理所有智能体的融合历史决策经验的观测, 提高了智能体的交流同时, 为智能体做决策提供了具有重要决策价值的交互状态
最终, 本文通过最小化经验贝尔曼误差来训练BTE, 如式(5)所示:
| $ \begin{split} {L}_{{\mathrm{BTE}}}(\varphi )=&\frac{1}{nT}{\displaystyle \sum _{i=1}^{n}{\displaystyle \sum _{t=0}^{T-1}[R({O}^{t}, {A}^{t})}}+\gamma {V}_{\overline{\varphi }}({\hat{O}}_{t+1}^{i})-{V}_{\varphi }({\hat{O}}_{t}^{i}){]}^{2} \end{split} $ | (5) |
其中,
BTE的方程如式(6)所示:
| $ \hat L_i^t = \chi (L_1^t, L_2^t, \cdots , L_n^t;\varphi ) $ | (6) |
其中,
BTD的核心为利用BTE计算的交互状态
合作注意力模块: 对第
决策注意力模块: 通过决策注意力模块分析与“前辈”智能体的合作收益来处理交互状态, 生成当前智能体的行动决策. 经过
为了训练BTD, 最小化以下基于裁剪的PPO目标, 如式(7)所示:
| $ \begin{split} {L_{{\mathrm{BTD}}}}(\theta ) =& - \frac{1}{{nT}}\sum\limits_{i = 1}^n \sum\limits_{t = 0}^{T - 1} \min \left(r_t^i(\theta ){{\hat A}_t},\right. \\ &\left.{\text{ clip}}(r_t^i(\theta ), 1 - \varepsilon ,1 + \varepsilon ){{\hat A}_t}\right) \end{split} $ | (7) |
其中,
| $ a_t^j = \xi {(\hat O_t^i, a_t^i;\theta )_{i = 1:j - 1}} $ | (8) |
其中,
BTM采用端到端的训练模式, 具体来说, 利用BTE将局部观测和历史决策经验映射到高维空间, 随后BTD将高维特征映射到动作空间完成决策. 在每一轮后, 利用TD算法来计算损失, 然后使用Adam优化器更新模型参数, 训练过程如算法1所示.
算法 1. BTM算法
输入: 轮数
输出: 智能体的动作
初始化: 编码器参数
1) For
2) For
3) 从环境中获得一系列观测值
4) 获取历史决策经验
5) 式(6)计算每个智能体的
6) For
7) 式(8)计算智能体动作
8) End for
9) 执行动作
10)
11) End for
12) 从
13) 式(6)计算
14) 式(5)计算BTE的损失
15) 式(2)计算优势函数
16) BTD利用
17) 式(7)计算
18)
19) End for
20) Return
在本节中, 评估了BTM在星际争霸中的表现. 首先将BTM与典型的MARL模型进行了对比实验. 其次, 对BTM的各个组件进行了消融实验, 以验证BTM的有效性.
3.1 星际争霸多智能体挑战星际争霸多智能体挑战(SMAC)[32]是暴雪星际争霸上进行的多智能体协同强化学习环境. SMAC具有庞大的状态、观测空间和动作空间, 对多智能体协同算法的泛化性和适应性提出了挑战. 图3展示了SMAC中部分场景.

|
图 3 SMAC 场景图 |
3.2 性能研究
图4展示了在SMAC的不同场景下, BTM与基线方法的胜率对比折线图. 实验结果为在不同随机种子的情况下进行10次实验取中位数为评价指标. 值得注意的是, HAPPO和HATRPO仅在难度简单的2s_vs_1sc场景上表现出色. 而在难度较高的5m_vs_6m等场景中, HAPPO和HATRPO方法之所以在复杂场景表现不佳, 源于它们采用的共享参数训练机制, 这导致所有智能体在能力上无法明显区分, 与独立网络的训练方法相比, 它们在信用分配上显得过于简化, 影响了决策精度和适应性. 相较于同样使用注意力机制的TransQMix, BTM在收敛速度和效果上都更加优秀, 证明了历史决策经验的必要性. 在测试场景中, BTM的训练曲线相对于MAPPO等来说增长较慢, 这是因为训练初期历史决策经验不足, 导致其性能提升缓慢. 然而, 随着历史决策经验的逐步融合, BTE的优势逐渐显现, 最终模型性能超越了MAPPO等其他基线模型. BTM在5m_vs_6m场景中取得了次优的表现, 仅低于EMU, 但是在其他场景中, 尤其是在像6h_vs_8z这类困难地图中, BTM的效果远高于EMU, 因为使用了前辈智能体的合作收益的情况下, 增强了模型的泛化性.
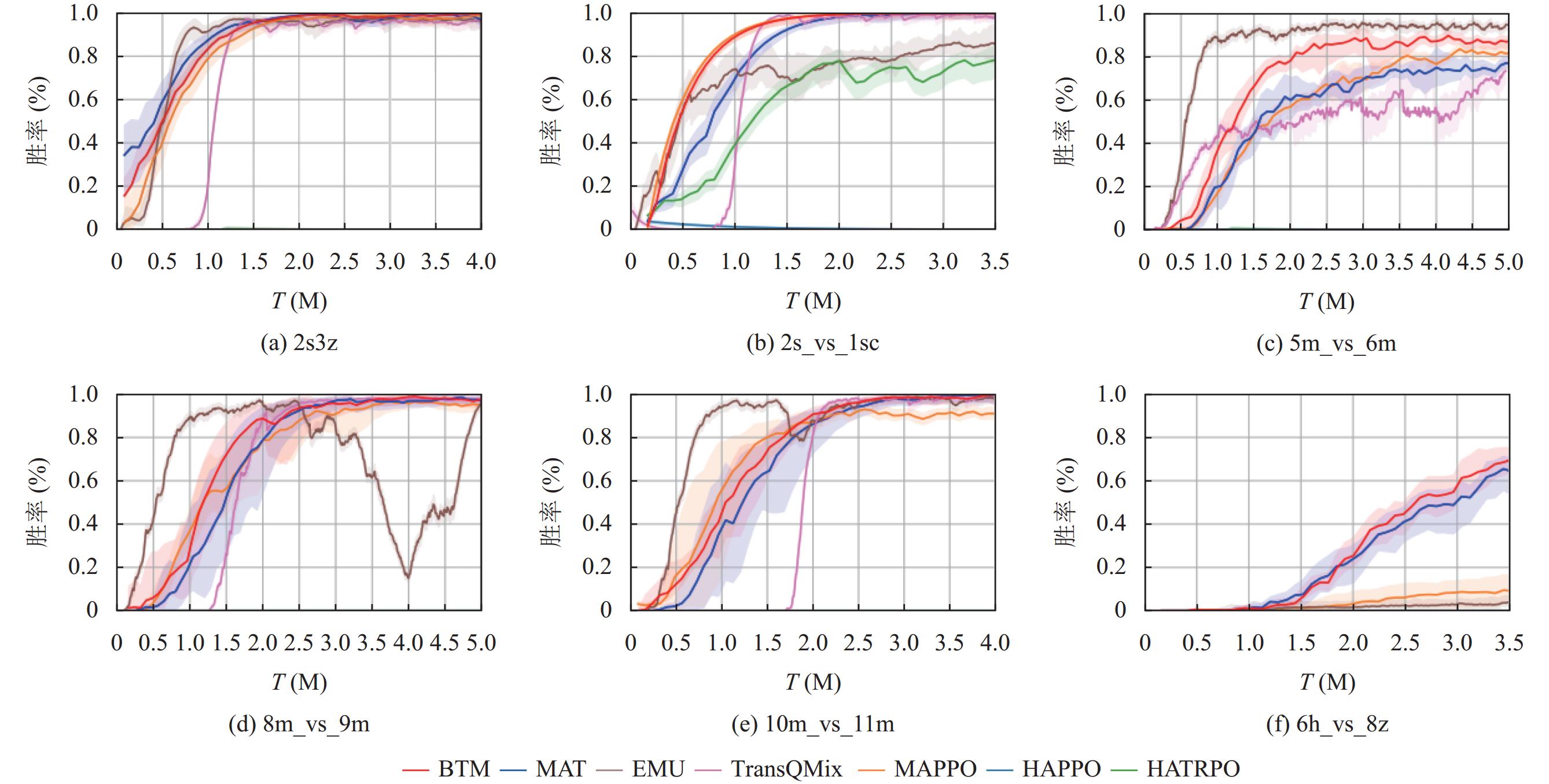
|
图 4 SMAC场景的测试胜率 |
此外, 本文不仅与在线模型进行了比较, 还与离线模型进行比较, 以全面评估BTM的性能, 结果如表1所示. BTM的总体胜率以93%的平均胜率优于其他的10种方法. 除HAPPO和HATRPO外, 其他模型在简单场景下表现良好, 但随着场景难度的增加, 智能体间的协作和各自的独立决策变得更为关键. BTM利用记忆模块管理历史决策经验, 提高智能体在复杂环境中的决策. 同时, 处理“前辈”智能体的动作收益增强了智能体的决策能力, 提升了协作效率. 通过这些模块, 使得BTM在极具挑战性的场景6h_vs_8z中实现了高达67%的胜率, 相较于其他模型的平均胜率高出55%.
3.3 BTM性能分析本节计算了BTM的浮点运算次数(FLOPs)和参数量, 由于不同的场景会产生不同的观测输入, 导致模型的参数量与复杂度有差异性, 因此表2中展示的结果是不同场景的平均值. 最终BTM的FLOPs和参数量分别为1.12×107和1.86×105, 具体如表2所示.
| 表 1 SMAC 场景测试胜率 (%) |
| 表 2 BTM的FLOPs与参数量 |
3.4 消融实验
为了证明BTM模块的有效性, 在5m_vs_6m、8m_vs_9m和6h_vs_8z的场景上做以下两个实验: (1) 将BTM与BT (移除BTM中记忆注意力模块)、BTMbase (移除BTM中解码器模块, 给每一个智能体分配一个全连接层) 和BTbase (在BT的基础上, 移除解码器模块, 给每个智能体分配一个全连接层); (2) 探究记忆块的长度对模型性能的影响. 两个实验的结果均采用不同随机种子并且进行10次训练取平均值, 结果如图5所示. BT的SMAC平均胜率显著下降, 这种性能下降可能是由于模型缺乏足够的历史决策经验, 导致智能体做出了有偏差的决策. 与此同时, 当使用BTMbase时, SMAC的平均胜率也出现了明显下降. 这种效果变差可能是因为智能体并没有考虑到与其他智能体之间的合作, 导致了胜率的下降. BTbase整体模型的效果下降了较大幅度这表明这两个模块对模型性能的贡献是相互叠加的, 去掉它们会导致更大程度的性能下降. 如表3所示, 没有记忆注意力模块和BTD的时候, 模型的平均胜率分别降低10%和7.6%. 这证明了这两个模块对于模型性能的重要性. 当同时去掉这两个模块时, 整体模型的效果下降27.6%. 同时, 也分析了不同的时间步长度对模型的影响. 当时间步长度为1时, 胜率降低了22%, 是因为模型训练过程中所能够利用的决策经验相对较少, 所导致的性能变差. 而当时间步长度为5时, 胜率降低19%, 这因为模型在处理更长的决策经验时需要更多的时间来学习有效的信息, 而且过多的冗余信息会对模型的性能带来负面影响. 总体而言, 通过调整时间步长度, 可以看到在时间步长度为3时获得了最佳效果, 相较于其他两个长度的时间步, 胜率分别提高22%和19%.
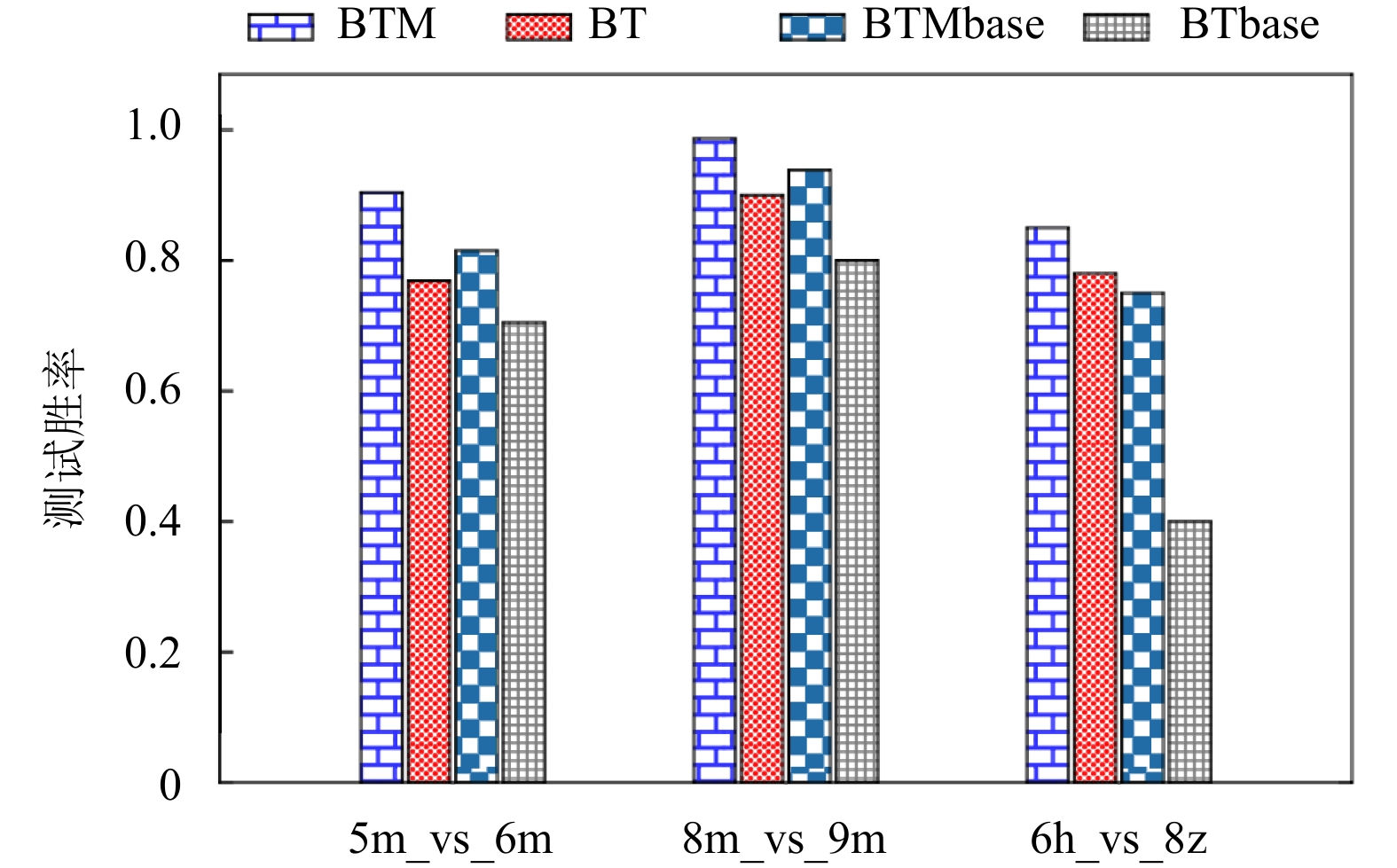
|
图 5 BTM组件消融实验示意图 |
| 表 3 消融实验 (%) |
4 结束语
本文提出了BiTransformer记忆在线强化学习模型, 来解决多智能体协同问题. BTM由编码器和解码器组成, 首先, 利用记忆注意力模块分析的智能体的局部观测和历史决策经验, 提取出智能体观测中有助于决策优化的信息. 然后, 将这些信息传入融合注意力模块中, 在历史决策经验的基础上, 加强智能体间的交流, 得到交互状态. 利用合作注意力模块分析当前智能体与“前辈”智能体动作的合作收益, 从而做出更有助于团队合作的决策. 最后由决策注意力模块综合合作收益与交互状态生成智能体的决策. 在SMAC的不同场景下平均胜率比其他方法高33%. 鉴于这是一种新的方法, 它为进一步研究提供了几个开放的途径. 例如, 可以通过引入更复杂的记忆更新策略来提高模型对复杂环境的建模能力未来的工作将专注于增强智能体之间的协同性, 同时提高模型的解释性和可解释性. 这些努力将有助于推动多智能体系统在复杂任务中取得更优秀的表现.
| [1] |
林谦, 余超, 伍夏威, 等. 面向机器人系统的虚实迁移强化学习综述. 软件学报, 2024, 35(2): 711-738. DOI:10.13328/j.cnki.jos.007006 |
| [2] |
Li SE. Deep reinforcement learning. Reinforcement Learning for Sequential Decision and Optimal Control. Singapore: Springer, 2023. 365–402. [doi: 10.1007/978-981-19-7784-8_10]
|
| [3] |
丁世飞, 杜威, 张健, 等. 多智能体深度强化学习研究进展. 计算机学报, 2024, 47(7): 1547-1567. |
| [4] |
Guo J, Chen YH, Hao YH, et al. Towards comprehensive testing on the robustness of cooperative multi-agent reinforcement learning. Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops. New Orleans: IEEE, 2022. 114–121. [doi: 10.1109/CVPRW56347.2022.00022]
|
| [5] |
Avalos R. Exploration and communication for partially observable collaborative multi-agent reinforcement learning. Proceedings of the 21st International Conference on Autonomous Agents and Multiagent Systems. New Zealand: International Foundation for Autonomous Agents and Multiagent Systems, 2022. 1829–1832.
|
| [6] |
Oroojlooy A, Hajinezhad D. A review of cooperative multi-agent deep reinforcement learning. Applied Intelligence, 2023, 53(11): 13677-13722. DOI:10.1007/s10489-022-04105-y |
| [7] |
Sharma PK, Fernandez R, Zaroukian E, et al. Survey of recent multi-agent reinforcement learning algorithms utilizing centralized training. Proceedings of the 2021 Conference on Artificial Intelligence and Machine Learning for Multi-domain Operations Applications III. SPIE, 2021. 117462K. [doi: 10.1117/12.2585808]
|
| [8] |
Zhang KQ, Yang ZR, Başar T. Multi-agent reinforcement learning: A selective overview of theories and algorithms. In: Vamvoudakis KG, Wan Y, Lewis FL, et al., eds. Handbook of Reinforcement Learning and Control. Cham: Springer, 2021. 321–384. [doi: 10.1007/978-3-030-60990-0_12]
|
| [9] |
李茹杨, 彭慧民, 李仁刚, 等. 强化学习算法与应用综述. 计算机系统应用, 2020, 29(12): 13-25. DOI:10.15888/j.cnki.csa.007701 |
| [10] |
Li C, Wang T, Wu C, et al. Celebrating diversity in shared multi-agent reinforcement learning. Advances in Neural Information Processing Systems, 2021, 34: 3991–4002.
|
| [11] |
周毅, 刘俊. 融合强化学习的多目标路径规划. 计算机系统应用, 2024, 33(3): 158-169. DOI:10.15888/j.cnki.csa.009418 |
| [12] |
Peng CY, Kim M, Zhang Z, et al. VDN: Virtual machine image distribution network for cloud data centers. Proceedings of the 2012 IEEE INFOCOM. Orlando: IEEE, 2012. 181–189. [doi: 10.1109/INFCOM.2012.6195556]
|
| [13] |
Wen MN, Kuba JG, Lin RJ, et al. Multi-agent reinforcement learning is a sequence modeling problem. Proceedings of the 36th International Conference on Neural Information Processing Systems. New Orleans: Curran Associates Inc., 2024. 1201.
|
| [14] |
Jaakkola T, Singh SP, Jordan MI. Reinforcement learning algorithm for partially observable Markov decision problems. Proceedings of the 7th International Conference on Neural Information Processing Systems. Denver: MIT Press, 1994. 345–352.
|
| [15] |
Kwon D, Jeon J, Park S, et al. Multiagent DDPG-based deep learning for smart ocean federated learning IoT networks. IEEE Internet of Things Journal, 2020, 7(10): 9895-9903. DOI:10.1109/JIOT.2020.2988033 |
| [16] |
Shakya AK, Pillai G, Chakrabarty S. Reinforcement learning algorithms: A brief survey. Expert Systems with Applications, 2023, 231: 120495.
|
| [17] |
Gallici M, Martin M, Masmitja I. TransfQMix: Transformers for leveraging the graph structure of multi-agent reinforcement learning problems. Proceedings of the 2023 International Conference on Autonomous Agents and Multiagent Systems. London: International Foundation for Autonomous Agents and Multiagent Systems, 2023. 1679–1687.
|
| [18] |
Yu LL, Li KY, Huo SX, et al. Cooperative offensive decision-making for soccer robots based on bi-channel Q-value evaluation MADDPG. Engineering Applications of Artificial Intelligence, 2023, 121: 105994. DOI:10.1016/j.engappai.2023.105994 |
| [19] |
Foerster J, Farquhar G, Afouras T, et al. Counterfactual multi-agent policy gradients. Proceedings of the 32nd AAAI Conference on Artificial Intelligence. New Orleans: AAAI, 2018. 2974–2982. [doi: 10.1609/aaai.v32i1.11794]
|
| [20] |
Yu C, Velu A, Vinitsky E, et al. The surprising effectiveness of PPO in cooperative multi-agent games. Proceedings of the 36th International Conference on Neural Information Processing Systems. New Orleans: Curran Associates Inc., 2022. 1787.
|
| [21] |
Iqbal S, Sha F. Actor-attention-critic for multi-agent reinforcement learning. Proceedings of the 36th International Conference on Machine Learning. Long Beach: ICML, 2019. 2961–2970.
|
| [22] |
陈妙云, 王雷, 盛捷. 基于值分布的多智能体分布式深度强化学习算法. 计算机系统应用, 2022, 31(1): 145-151. DOI:10.15888/j.cnki.csa.008237 |
| [23] |
Son K, Kim D, Kang WJ, et al. QTRAN: Learning to factorize with transformation for cooperative multi-agent reinforcement learning. Proceedings of the 36th International Conference on Machine Learning. Long Beach: ICML, 2019. 5887–5896.
|
| [24] |
Rashid T, Samvelyan M, De Witt CS, et al. Monotonic value function factorisation for deep multi-agent reinforcement learning. The Journal of Machine Learning Research, 2020, 21(1): 178. |
| [25] |
马佩鑫, 程钰, 侯健, 等. 基于多智能体深度强化学习的协作导航应用. 计算机系统应用, 2023, 32(8): 95-104. DOI:10.15888/j.cnki.csa.009200 |
| [26] |
Geng MH. Scaling up cooperative multi-agent reinforcement learning systems. Proceedings of the 23rd International Conference on Autonomous Agents and Multiagent Systems. Auckland: International Foundation for Autonomous Agents and Multiagent Systems, 2024. 2737–2739.
|
| [27] |
Shen GC, Wang Y. Review on Dec-POMDP model for MARL algorithms. In: Jain JC, Kountchev R, Hu B, et al., eds. Smart Communications, Intelligent Algorithms and Interactive Methods. Singapore: Springer, 2022. 29–35. [doi: 10.1007/978-981-16-5164-9_5]
|
| [28] |
Zhang Z, Ong YS, Wang DQ, et al. A collaborative multiagent reinforcement learning method based on policy gradient potential. IEEE Transactions on Cybernetics, 2021, 51(2): 1015-1027. DOI:10.1109/TCYB.2019.2932203 |
| [29] |
Lauri M, Hsu D, Pajarinen J. Partially observable Markov decision processes in robotics: A survey. IEEE Transactions on Robotics, 2023, 39(1): 21-40. DOI:10.1109/TRO.2022.3200138 |
| [30] |
Raileanu R, Fergus R. Decoupling value and policy for generalization in reinforcement learning. Proceedings of the 38th International Conference on Machine Learning. Berlin: ICML, 2021. 8787–8798.
|
| [31] |
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 6000–6010.
|
| [32] |
Samvelyan M, Rashid T, de Witt CS, et al. The StarCraft multi-agent challenge. Proceedings of the 18th International Conference on Autonomous Agents and Multiagent Systems. Montreal: AAMAS, 2019. 2186–2188.
|
 2024, Vol. 33
2024, Vol. 33


