肺癌是全球发病人数第2位, 死亡人数第1位的癌症. 非小细胞肺癌(non-small cell lung cancer, NSCLC)是肺癌的主要类型之一, 约占肺癌病例的85%以上[1]. 对于非小细胞肺癌患者, 淋巴结转移是评判肿瘤的进展和恶性程度的指标之一, 并且淋巴结转移作为TNM (tumor node metastasis)分期系统中的重要内容, 直接影响肺癌患者的生存预期[2], 所以准确识别淋巴结转移情况对于患者的治疗和预后评估具有重要意义.
目前临床上对于淋巴结转移常用的诊断方法为影像学诊断和病理学检测, 其中病理学检测是淋巴结转移诊断的金标准, 但由于淋巴结活检为有创检查, 对于有些身体状况较差且不耐受的病人, 无法进行穿刺活检, 同时获取某些患者的病理检查较为困难的情况也时有发生. 而无创影像学检查如[18F]-FDG PET/CT, 在提供解剖结构信息的基础上可显示肿瘤细胞的代谢活性, 在无创性淋巴结转移的诊断工作中有一定的优势. 但由于肿瘤的异质性、肿瘤大小深度的限制以及图像成像的质量等因素影响, 经验丰富的医生在同一时期对同一影像的判断也存在分歧, 标签往往存在噪声, 为深度模型的训练带来了挑战.
据此, 本文提出一个对抗噪声标签的深度学习模型, 根据PET/CT图像特征以及放射科医生的诊断, 通过检测纠正医生标签的方法进行数据标签纠正, 并进行模型训练. 本文的主要贡献概括如下.
(1)本文提出了一种对抗噪声标签的图像分类的方法, 可对带有噪声标签的数据进行准确分类.
(2)使用对比学习和样本选择相结合的策略筛选出干净样本和噪声样本, 并采用伪标签提升策略, 将分类网络预测结果作为噪声样本的监督信息, 进一步减少标签噪声对训练的影响.
(3)实验证明, 本文所提出的框架能够有效地应对医学图像噪声标签, 并且优于其他的模型方法和医生的诊断结果.
1 相关研究 1.1 噪声标签学习由于医学图像成像质量、医生水平以及标注过程中的主观性, 放射科医生存在一定程度的误诊和漏诊现象, 不可避免地会产生医学图像上的噪声标签. 尽管有许多应对噪声标签的方法, 如估计噪声转移矩阵[3]、样本选择[4]和标签纠正[5]等, 此外, 一些研究工作通过联合利用平均绝对误差和交叉熵损失[6]、对噪声不敏感的互信息的广义版本[7]或相互增强的鲁棒损失函数组合[8]的优点来研究鲁棒损失函数. 但以上成果主要针对的是自然图像噪声数据集, 针对医学图像噪声标签的应用仍面临挑战. 为了解决这个问题, Xue等人[9]提出了一种使用样本选择模块和样本重加权策略的鲁棒学习框架. Min等人[10]提出了一种带噪声标签的半监督生物医学分割网络. Xing等人[11]提出了一种基于梯度一致性和特征一致性及基于可靠样本的混合增强的两阶段的方法, 均用于处理医学图像中的噪声标签问题.
1.2 对比学习近期研究表明, 基于对比的相似性学习框架在表征学习中表现出良好的性能, 该方法旨在最大化正对的相似性和最小化负对的相似性[12]. 其中正对是指具有相似性的样本对, 通常是来自同一类别或具有相似属性的样本对; 负对是指具有差异性的样本对, 通常是来自不同类别或具有不同属性的样本对. 李俊哲等人[13]采用对比学习最大化两个增强视图的相似度, 并引入了基于类原型的标签去噪模块来避免噪声标签的影响. Li等人[14]提出一种选择性监督对比学习方法, 从构建的样本对中学习相似度分布, 进而识别出干净样本. Xu等人[15]提出了一种新的NAC (noisy-as-clean)策略来训练自监督去噪网络. 该策略将损坏的图像视为“干净目标”, 将损坏图像和第2个类似损坏的图像的组合图像作为输入, 在噪声微弱的情况下, 学习监督网络的最佳参数.
2 NLSS模型 2.1 网络架构本文提出一种基于对比学习的噪声标签样本选择模型, 简称NLSS (noise label sample selection). 模型分为特征提取、样本选择、标签重分配3个部分. 模型的整体构成如图1所示. 首先, 输入图像经过特征提取模块提取特征向量. 其次, 采用样本选择模块对数据集进行划分. 接着, 针对噪声数据集的样本对其进行标签重分配, 并且此部分数据参与训练. 最后, 将交叉熵损失函数和对比损失函数结合起来对网络进行训练.
2.2 特征提取为训练模型使用的图像数据
| $ F = f\left( x \right) $ | (1) |
其中,
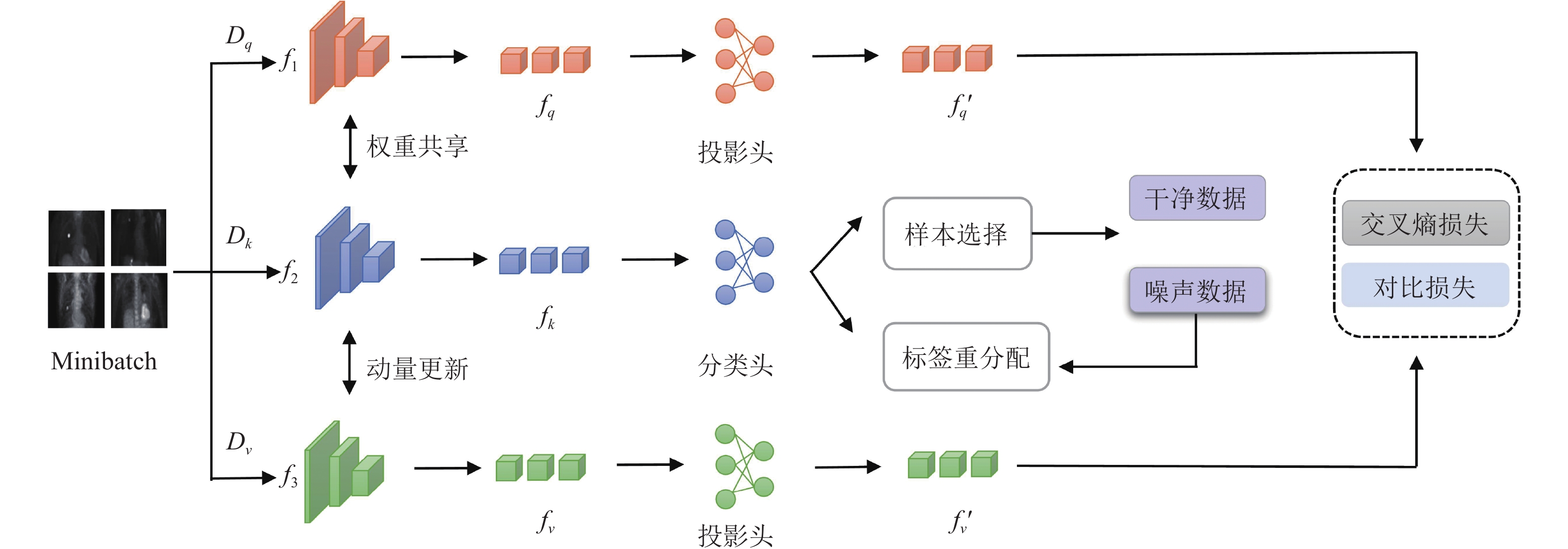
|
图 1 网络整体框架 |
此外,
| $ {\theta _v} \leftarrow m{\theta _v} + \left( {1 - m} \right){\theta _k} $ | (2) |
其中,
模型特征提取部分使用ResNet-18[16]作为骨干网络提取图像的特征
一些研究[17]将交叉熵损失小的样本视为干净样本, Co-teaching[18]和Co-teaching+[19]在每个小批次中选择损失较小的样本视为干净样本, 虽然在一定程度上避免了噪声累积, 但是不同小批量中的噪声比会有波动. 为了缓解不同小批量中噪声比不平衡的问题. 本文采用JS散度 (Jensen-Shannon divergence)[20]来选择干净样本. JS散度是衡量两个概率分布之间的差异, 取值范围在[0, 1]之间, 可作为全局选择度量. 样本选择模块的结构如图2所示.
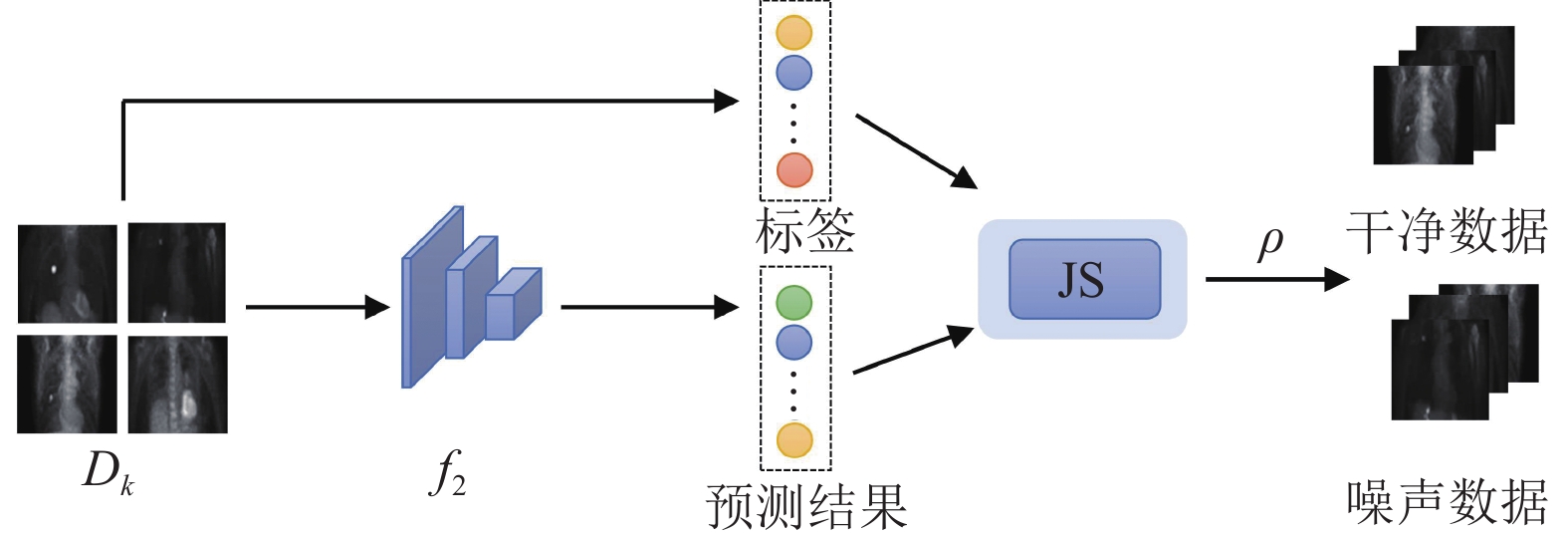
|
图 2 样本选择模块结构 |
给定样本的真实标签分布
| $ {d_i} = JS\left( {{p_i}\parallel {y_i}} \right) $ | (3) |
| $ JS\left( {{p_i}\parallel {y_i}} \right) = \frac{1}{2}KL\left( {{p_i}\parallel \frac{{{p_i} + {y_i}}}{2}} \right) + \frac{1}{2}KL\left( {{y_i}\parallel \frac{{{p_i} + {y_i}}}{2}} \right) $ | (4) |
其中,
其次计算样本
| $ \rho \left( {{x_i}} \right) = 1 - {d_i},\;\; {d_i} \in \left[ {0, 1} \right] $ | (5) |
最后根据阈值, 对样本进行划分.
| $ {D_k} = \left\{ \begin{gathered} {D_{\rm clean}}, \;\;\rho \geqslant {\tau _{\rm clean}} \\ {D_{\rm noisy}}, \;\;\rho < {\tau _{\rm clean}} \\ \end{gathered} \right. $ | (6) |
由于数据集存在噪声, 静态阈值无法适应变化, 对此本文使用可调整的动态阈值进行干净数据集和噪声数据集的划分.
2.4 标签重分配输入网络的样本经过特征提取模块和样本选择模块后, 被划分为干净数据集和噪声数据集, 将噪声数据集中的样本视为无标签样本, 为了不丢弃这些噪声样本并充分挖掘其潜在的信息, 本文采用了伪标签提升策略来进行标签的重分配. 具体而言, 使用分类网络对这些噪声样本进行预测, 得到它们的伪标签. 将这些伪标签作为噪声样本的监督信息, 帮助网络进行训练和优化. 对于干净数据集, 则依旧使用原先的标签作为监督. 通过不断迭代训练, 网络可以利用伪标签提升策略逐渐学习到更准确的特征表示和分类决策. 标签重分配过程如式(7)所示:
| $ \hat y = \left\{ \begin{gathered} {y_i},\;\; {x_i} \in {D_{\rm clean}} \\ {p_i}, \;\;{x_i} \in {D_{\rm noisy}} \\ \end{gathered} \right. $ | (7) |
其中,
本文采用交叉熵损失函数和对比损失函数的组合训练模型.
2.5.1 交叉熵损失函数交叉熵损失函数[23]是机器学习和深度学习中常用的一种损失函数, 通常用于分类问题的模型训练中. 本文中将非小细胞肺癌患者的转移状态视为二分类问题, 构建二元交叉熵损失函数, 实验数据中发生转移个数和未发生转移个数之比约为1:5, 为了减轻数据不平衡的影响, 本文采用加权交叉熵损失函数[24].
| $ {L_{\rm ce}} = - \frac{1}{N}\sum\nolimits_i {{w_p}} \left( {{y_i}\log \left( {\hat y} \right)} \right) + {w_n}\left( {\left( {1 - {y_i}} \right)\log \left( {1 - \hat y} \right)} \right) $ | (8) |
| $ {w_p} = \frac{1}{{pos}} \times total $ | (9) |
| $ {w_n} = \frac{1}{{neg}} \times total $ | (10) |
其中,
对比学习已经成为自监督方法的重要组成部分. 在SimCLR[25]论文中, 研究人员指出数据增强是至关重要的, 而非线性投影头可以进一步提高学习到的表示质量. 受此启发, 本文使用了余弦相似度[26]来计算两个不同增强视图提取的特征之间的对比损失. 具体的计算公式如下:
| $ L_q^{\rm ctr} = - \log \frac{{\exp \left( {sim\left( {{{\textit{z}}_q}, {{\textit{z}}_v}} \right)/\tau } \right)}}{{\displaystyle\sum\nolimits_{m = 1}^{2n} {{l_{q \ne m}} \cdot \exp \left( {sim\left( {{{\textit{z}}_q}, {{\textit{z}}_m}} \right)/\tau } \right)} }} $ | (11) |
| $ {L_{\rm ctr}} = \sum\nolimits_{q = 1}^{2N} {L_q^{\rm ctr}} $ | (12) |
其中, 经过两种不同增强方式增强后的样本数量为2
| $ {L_{\rm total}} = \alpha \times {L_{\rm ce}} + \beta \times {L_{\rm ctr}} $ | (13) |
其中,
本实验基于Ubuntu 20.04 操作系统, 使用PyTorch 1.7.1训练框架[28], 选取ResNet-18作为特征提取器, 输出的特征经过投影头后为128维数据, 优化方法为SGD梯度优化器[29], 动量值为0.99, 学习率为0.001, 网络总共设置的epoch为50.
3.2 数据集本文的实验数据来自芝加哥大学医学院328名NSCLC患者的PET/CT影像数据, 112例患者既有医生的诊断结果, 又有病理学检测的金标准, 216例患者仅有医生的诊断结果. 在此数据集中, 328名患者的医生诊断结果中含有错误的结果, 视为部分含有噪声标签, 而112例患者的金标准诊断结果视为正确标签. 数据集划分策略为: 将112例患者的数据集划分为80%的训练集和20%的测试集, 216名患者数据集全部加入训练集中, 使用五折交叉验证[30]的方法评估网络的性能. 本实验在训练过程中全部使用医生标签进行训练, 而使用112例患者的正确标签进行测试.
本文提出深度网络输入为PET图像正面最大强度投影生成MIP (maximum intensity projection)图像[31]. 如图3所示. MIP是一种图像后处理技术, 常用于医学影像学中, 运用透视法获得二维图像, 是通过计算沿着被扫描物每条射线上所遇到的最大密度像素而产生的. MIP相比于处理完整的3D图像, 图像的特征表示更加紧凑, 具有较低的维度, 使得模型更容易学习和泛化到新的未见过的数据, 更容易捕捉到关键的结构和特征.
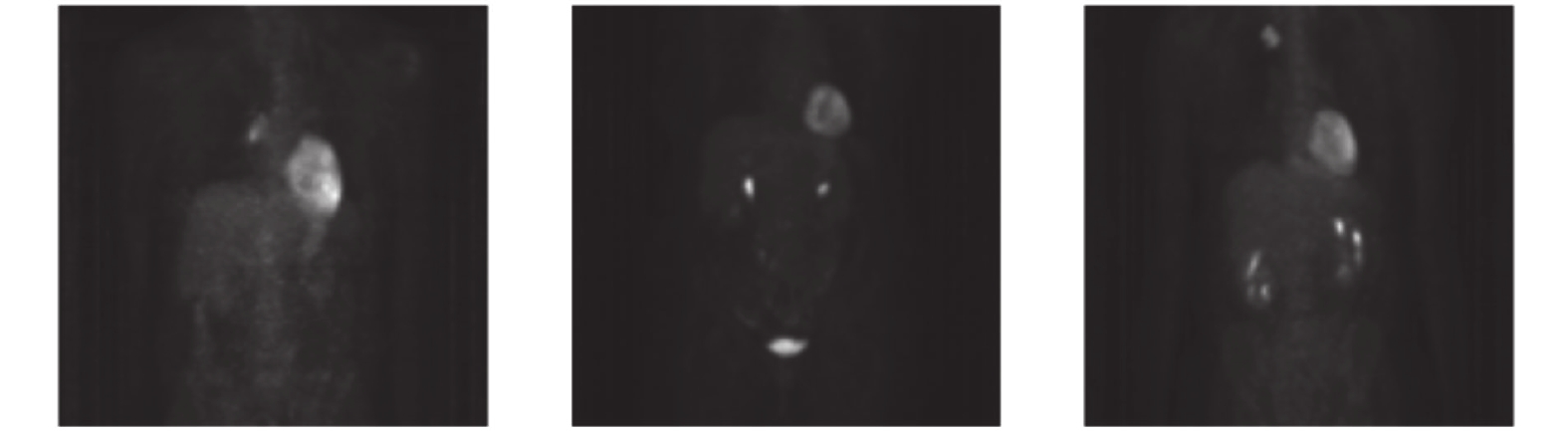
|
图 3 由PET图像投影的正面MIP图像 |
3.3 评价指标
本实验选取准确率(Accuracy), 灵敏度(Sensitivity), 特异性(Specificity), AUC (area under the curve), 作为模型的评价指标.
| $ \mathit{Sensitivity} = \frac{{TP}}{{TP + FN}} $ | (14) |
| $ \mathit{Specificity} = \frac{{TN}}{{TN + FP}} $ | (15) |
| $ Accuracy = \frac{{TP + TN}}{{TP + FP + FN + TN}} $ | (16) |
其中,
为了验证本模型样本选择模块和标签重分配模块的有效性, 进行如下实验.
由于112例患者有病理金标准, 故在训练阶段后输出网络认为干净样本的医生结果的标签与金标准的结果进行对比, 计算方法如式(17)所示, 对比结果的准确率如图4所示.
| $ acc1 = \frac{n}{T} \times 100{\text{%}} $ | (17) |
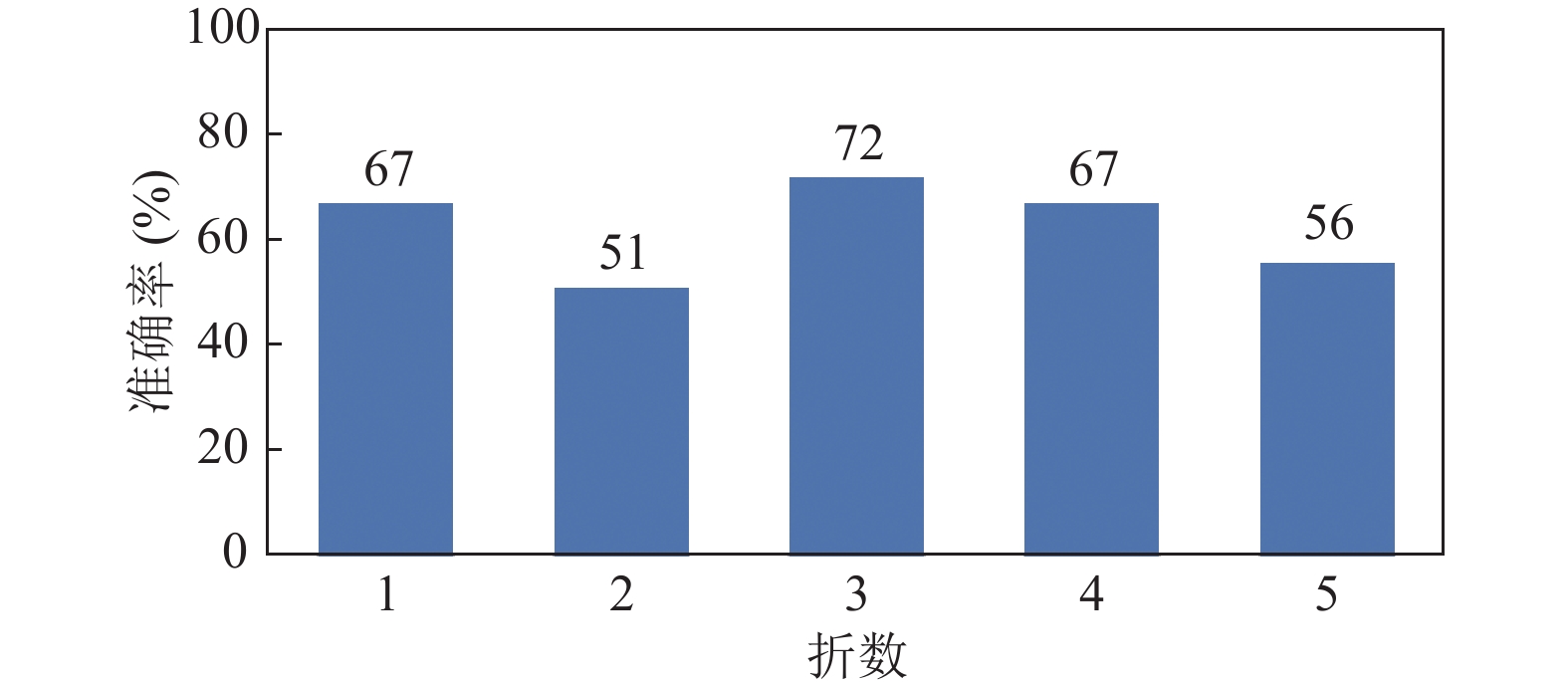
|
图 4 网络挑选结果较于金标准的准确率 |
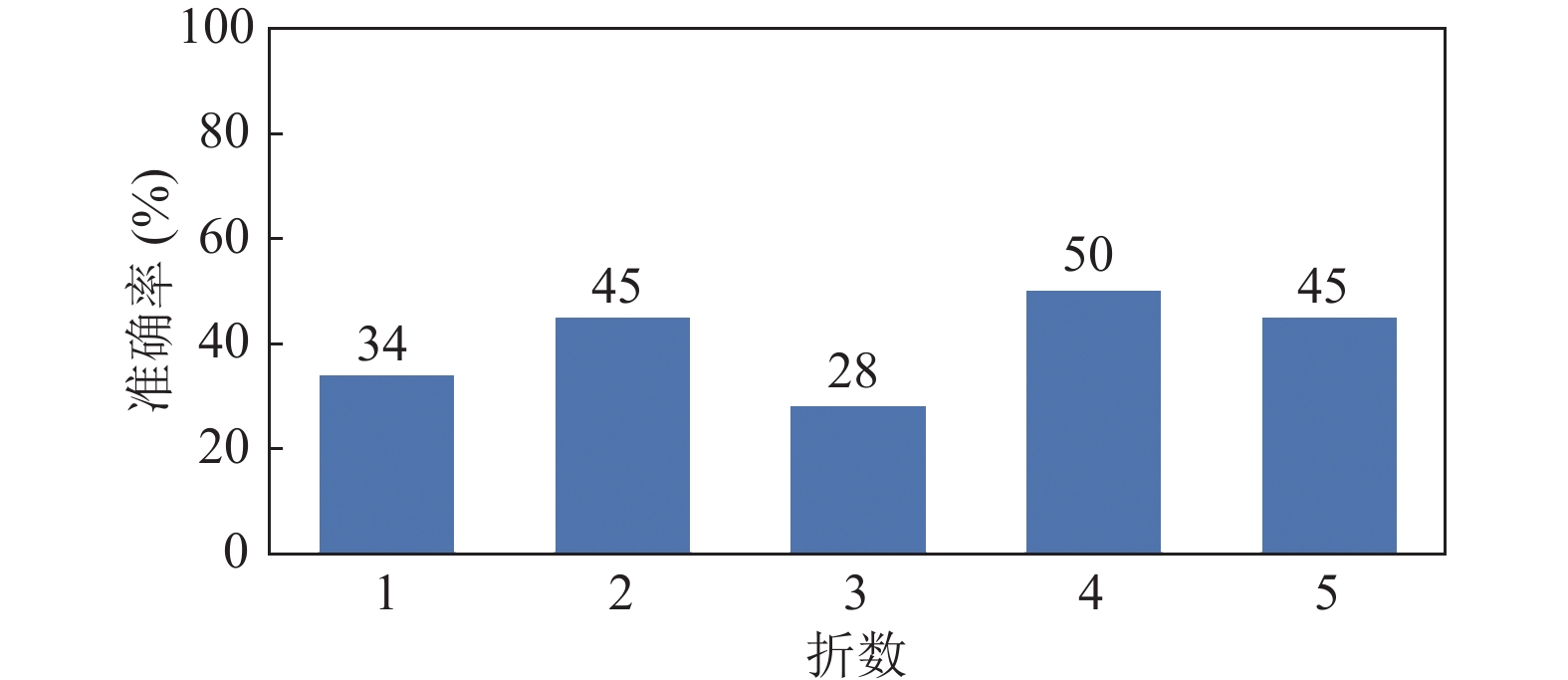
五折实验中最高的准确率为72%, 平均准确率为62%. 同时对网络认为不干净的样本经过标签重分配后输出的结果, 进行标签二值化后与金标准的结果进行再次对比, 计算方法如式(18)所示, 对比结果的准确率如图5所示.
| $ acc2 = \frac{m}{{T - n}} \times 100{\text{%}} $ | (18) |
式(17)和式(18)中,
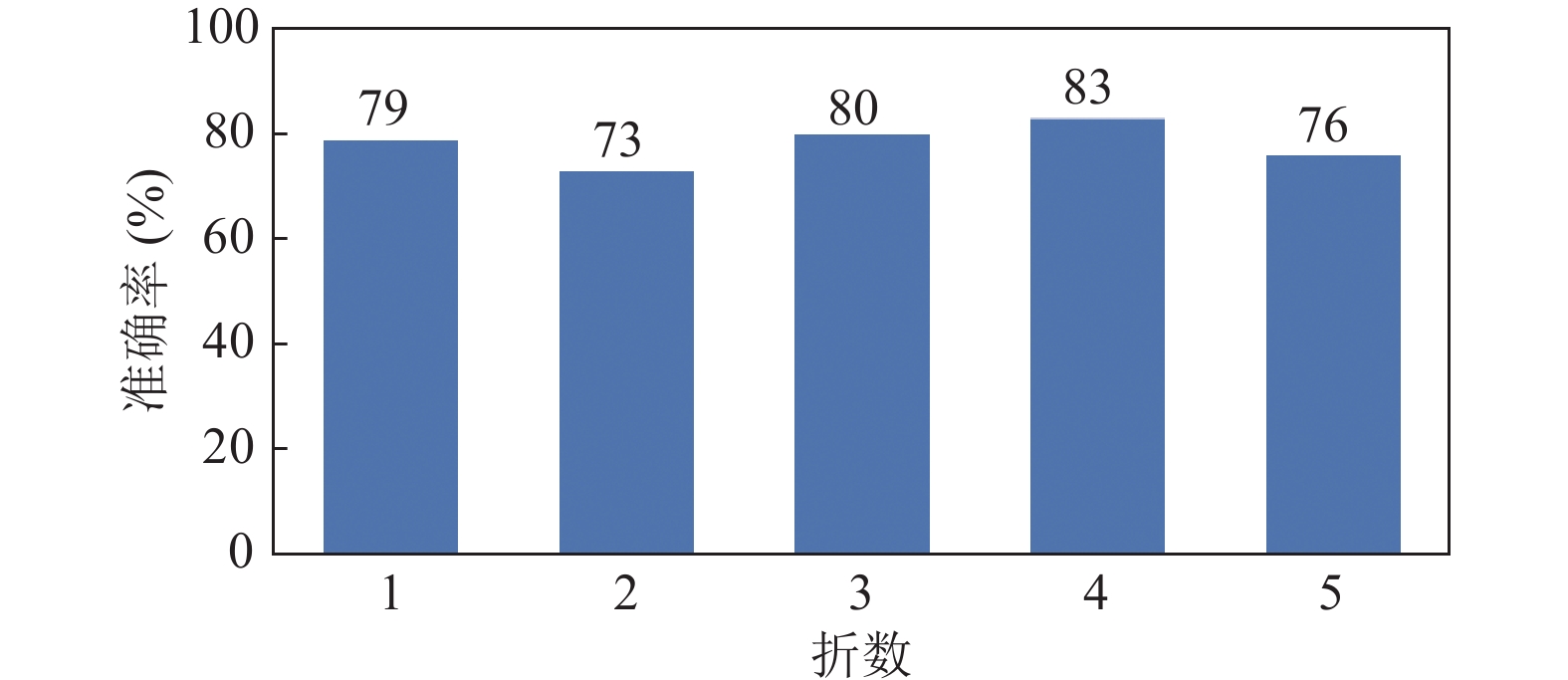
五折实验中最高的准确率为45%, 平均准确率为41%. 综合以上二者, 即判断正确的样本和标签重分配修改正确的样本经过与金标准进行对比, 准确率如图6所示. 五折实验中最高的准确率为83%, 平均准确率为78%.
|
图 5 标签重分配结果较于金标准的准确率 |
|
图 6 去噪模块较于金标准的准确率 |
为了证明本模型的有效性, 还将实验结果与放射科医生诊断结果以及近年来针对噪声标签任务较常用模型进行对比, 其中Co-teaching[18]方法是同时训练两个网络, 在每个批量数据中, 每个网络都将具有小损失的样本视为有用的知识, 并向其另一个网络传授这些样本以更新参数; JoCoR[20]使用两个网络对相同的小批数据进行预测, 并计算每个训练示例的联合损失, 选择损失较小的样本, 同时更新两个网络的参数; Jo-SRC[32]以对比学习的方式训练网络, 使用来自每个样本的两个不同视图的预测用于估计其干净或分布外的“可能性”, 通过引入一致性正则化来提高模型泛化性能; AsyCo[33]采用多视图共识, 使用训练标签和模型预测之间的分歧来选择干净和有噪声的样本. 对比实验结果如表1所示. 由于放射科医生的结果是二元标签而不是概率的形式, 因此本文提出的模型仅与其他实验方法比较AUC.
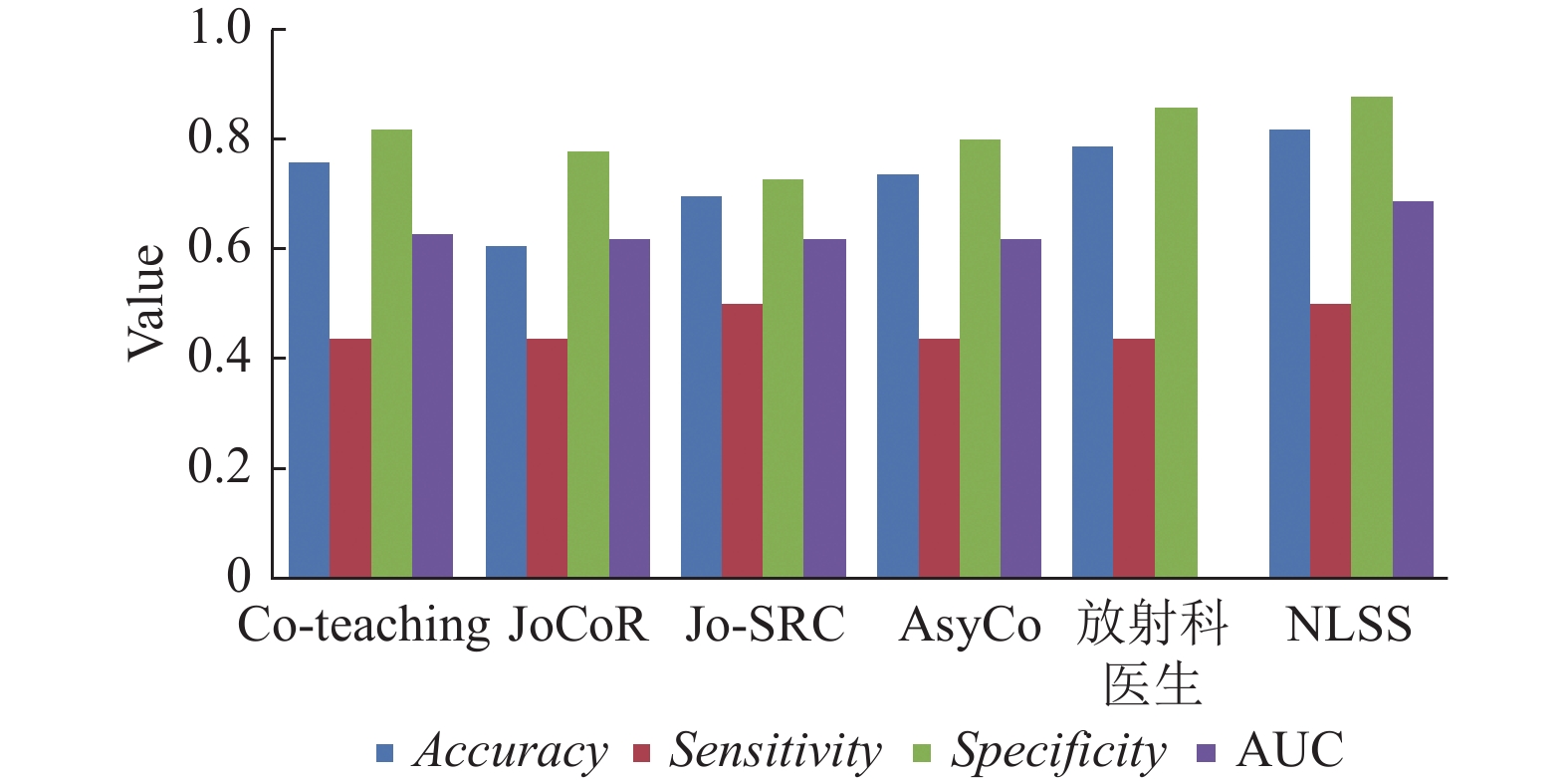
由表1可以看出, 本文提出的方法在各项指标上均优于医生的诊断结果, 其余各项指标较其他方法均有明显的提升, 准确率和特异性的提升较高, 与Co-teaching, JoCoR, Jo-SRC, AsyCo相比, 准确率分别提高了0.06 (7.9%), 0.21 (34.4%), 0.12 (17.1%), 0.08 (10.8%), 特异性分别提高了0.06 (7.3%), 0.1 (12.8%), 0.15 (20.5%), 0.08 (10%). 图7以可视化的形式展示了本实验方法与其他方法在各项评价指标的结果.
| 表 1 与其他方法和放射科医生诊断结果对比实验结果 |
|
图 7 不同模型的评价指标对比结果图 |
3.5 消融实验
本文进行消融实验来验证模块的有效性, 消融实验策略有: 仅使用特征提取模块训练, 仅使用特征提取模块与对比损失训练, 仅使用特征提取模块和标签重分配模块进行训练, 使用本文方法进行训练, 将其实验结果进行对比, 如表2所示.
| 表 2 消融实验 |
上述结果说明了对比损失可利用内在结构的相似性促使模型学习到具有判别性的特征表示, 有效地应对噪声标签, 避免了小样本损失策略造成的噪声累积; 标签重分配模块引入了一种灵活的伪标签提升策略, 对噪声数据进行修正, 在初始分类预测的基础上细化带有伪标签的噪声数据的监督信息, 提高模型的分类性能和泛化能力. 本文使用3种方式的组合, 最终达到在整体上分类效果最佳的成绩.
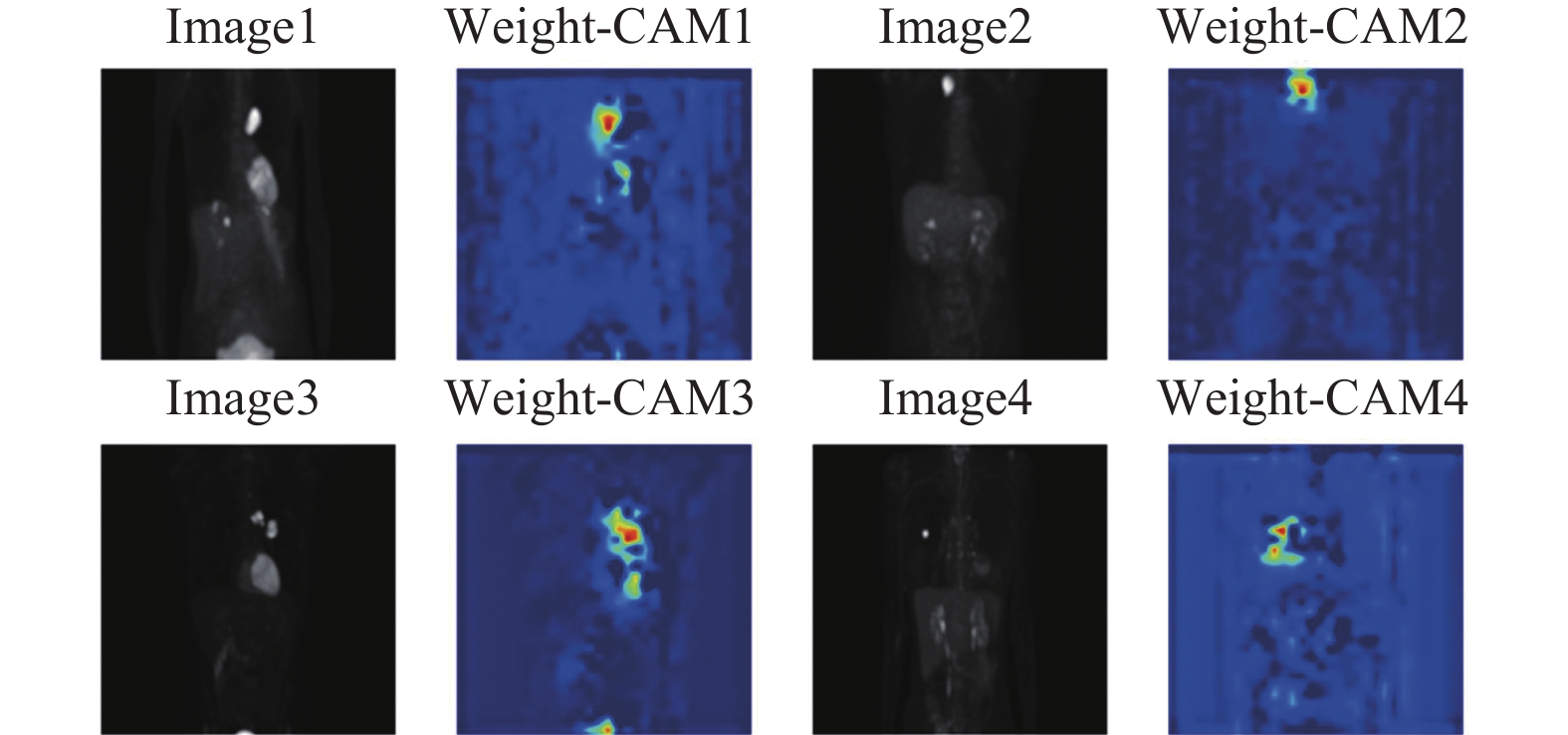
3.6 可视化展示为了增强模型的可解释性, 在数据集中随机选择了4张MIP图片, 并绘制其注意力热图, 结果表明, 网络能够更好地关注到目标区域, 即肺部中的肿瘤部位, 对于高亮的器官部位, 并没有过度关注. 可视化结果如图8所示.
|
图 8 注意力热图 |
4 结论与展望
本研究探索了基于对比学习的标签噪声样本选择模型在非小细胞肺癌患者淋巴结转移诊断中的应用. 通过对比学习的方法, 减少了噪声标签对于模型性能的负面影响, 学习到更具判别性和鲁棒性的特征表示, 以非小细胞患者数据集为例进行了验证, 实验结果表 明模型取得了良好的性能. 本研究还需要进一步验证和扩展, 以确保其在不同数据集和临床场景中的泛化能力和可靠性.
| [1] |
Sung H, Ferlay J, Siegel RL, et al. Global cancer statistics 2020: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA: A Cancer Journal for Clinicians, 2021, 71(3): 209-249. DOI:10.3322/caac.21660 |
| [2] |
陈武飞, 马庄宣, 李铭. 影像组学在非小细胞肺癌诊疗中的应用进展. 中国医学影像学杂志, 2023, 31(7): 781-784. DOI:10.3969/j.issn.1005-5185.2023.07.021 |
| [3] |
Hendrycks D, Mazeika M, Wilson D, et al. Using trusted data to train deep networks on labels corrupted by severe noise. Proceedings of the 32nd International Conference on Neural Information Processing Systems (NIPS 2018). Montreal: Curran Associates Inc., 2018. 10477–10486.
|
| [4] |
Jiang L, Zhou ZY, Leung T, et al. MentorNet: Learning data-driven curriculum for very deep neural networks on corrupted labels. Proceedings of the 35th International Conference on Machine Learning. Stockholm: PMLR, 2018. 2304–2313.
|
| [5] |
Liu JR, Li RR, Sun C. Co-correcting: Noise-tolerant medical image classification via mutual label correction. IEEE Transactions on Medical Imaging, 2021, 40(12): 3580-3592. DOI:10.1109/TMI.2021.3091178 |
| [6] |
Zhang ZL, Sabuncu MR. Generalized cross entropy loss for training deep neural networks with noisy labels. Proceedings of the 32nd International Conference on Neural Information Processing Systems (NIPS 2018). Montreal: Curran Associates Inc., 2018. 8792–8802.
|
| [7] |
Xu YL, Cao P, Kong YQ, et al. LDMI: A novel information-theoretic loss function for training deep nets robust to label noise. Proceedings of the 33rd International Conference on Neural Information Processing Systems (NeurIPS). Vancouver: Curran Associates Inc., 2019. 559.
|
| [8] |
Ma XJ, Huang HX, Wang YS, et al. Normalized loss functions for deep learning with noisy labels. Proceedings of the 37th International Conference on Machine Learning. PMLR, 2020. 6543–6553.
|
| [9] |
Xue C, Dou Q, Shi XY, et al. Robust learning at noisy labeled medical images: Applied to skin lesion classification. Proceedings of the 16th IEEE International Symposium on Biomedical Imaging (ISBI). Venice: IEEE, 2019. 1280–1283. [doi: 10.1109/ISBI.2019.8759203]
|
| [10] |
Min SB, Chen XJ, Zha ZJ, et al. A two-stream mutual attention network for semi-supervised biomedical segmentation with noisy labels. Proceedings of the 33rd AAAI Conference on Artificial Intelligence. Honolulu: AAAI, 2019. 4578–4585.
|
| [11] |
Xing XH, Chen Z, Gao ZF, et al. Gradient and feature conformity-steered medical image classification with noisy labels. Proceedings of the 26th International Conference Medical Image Computing and Computer Assisted Intervention. Vancouver: Springer, 2023. 75–84.
|
| [12] |
Chen T, Kornblith S, Norouzi M, et al. A simple framework for contrastive learning of visual representations. Proceedings of the 37th International Conference on Machine Learning (ICML). PMLR, 2020. 1597–1607.
|
| [13] |
李俊哲, 曹国. 基于对比学习的标签带噪图像分类. 计算机系统应用, 2023, 32(12): 104-111. DOI:10.15888/j.cnki.csa.009339 |
| [14] |
Li SK, Xia XB, Ge SM, et al. Selective-supervised contrastive learning with noisy labels. Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New Orleans: IEEE, 2022. 316–325.
|
| [15] |
Xu J, Huang Y, Cheng MM, et al. Noisy-as-clean: Learning self-supervised denoising from corrupted image. IEEE Transactions on Image Processing, 2020, 29: 9316-9329. DOI:10.1109/TIP.2020.3026622 |
| [16] |
He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas: IEEE, 2016. 770–778. [doi: 10.1109/CVPR.2016.90]
|
| [17] |
Song H, Kim M, Park D, et al. Learning from noisy labels with deep neural networks: A survey. IEEE Transactions on Neural Networks and Learning Systems, 2023, 34(11): 8135-8153. DOI:10.1109/TNNLS.2022.3152527 |
| [18] |
Han B, Yao QM, Yu XR, et al. Co-teaching: Robust training of deep neural networks with extremely noisy labels. Proceedings of the 32nd International Conference on Neural Information Processing Systems (NIPS 2018). Montreal: Curran Associates Inc., 2018. 8536–8546.
|
| [19] |
Yu XR, Han B, Yao JC, et al. How does disagreement help generalization against label corruption? Proceedings of the 36th International Conference on Machine Learning. Long Beach: PMLR, 2019. 7164–7173.
|
| [20] |
Wei HX, Feng L, Chen XY, et al. Combating noisy labels by agreement: A joint training method with co-regularization. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Seattle: IEEE, 2020. 13723–13732.
|
| [21] |
Szegedy C, Vanhoucke V, Ioffe S, et al. Rethinking the inception architecture for computer vision. Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas: IEEE, 2016. 2818–2826.
|
| [22] |
李晓艳, 张子刚, 张逸石, 等. 一种基于KL散度和类分离策略的特征选择算法. 计算机科学, 2012, 39(12): 224-227. DOI:10.3969/j.issn.1002-137X.2012.12.053 |
| [23] |
Le PB, Nguyen ZT. ROC curves, loss functions, and distorted probabilities in binary classification. Mathematics, 2022, 10(9): 1410. DOI:10.3390/math10091410 |
| [24] |
程磊, 吴晓富, 张索非. 数据集类别不平衡性对迁移学习的影响分析. 信号处理, 2020, 36(1): 110-117. |
| [25] |
Zeng H, Cui XH. SimCLRT: A simple framework for contrastive learning of rumor tracking. Engineering Applications of Artificial Intelligence, 2022, 110: 104757. DOI:10.1016/j.engappai.2022.104757 |
| [26] |
Yi L, Liu S, She Q, et al. On learning contrastive representations for learning with noisy labels. Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). New Orleans: IEEE, 2022. 16661–16670.
|
| [27] |
He KM, Fan HQ, Wu YX, et al. Momentum contrast for unsupervised visual representation learning. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Seattle: IEEE, 2020. 9726–9735.
|
| [28] |
Paszke A, Gross S, Massa F, et al. PyTorch: An imperative style, high-performance deep learning library. Proceedings of the 33rd International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2019. 721.
|
| [29] |
常禧龙, 梁琨, 李文涛. 深度学习优化器进展综述. 计算机工程与应用, 2024, 60(7): 1-12. DOI:10.3778/j.issn.1002-8331.2307-0370 |
| [30] |
张剑飞, 王真, 崔文升, 等. 基于交叉验证和神经网络融合的医学数据分类. 齐齐哈尔大学学报(自然科学版), 2019, 35(4): 1-5. |
| [31] |
Aung N, Kechadi T, Chen LM, et al. IP-UNet: Intensity projection UNet architecture for 3D medical volume segmentation. arXiv:2308.12761, 2023.
|
| [32] |
Yao YZ, Sun ZR, Zhang CY, et al. Jo-SRC: A contrastive approach for combating noisy labels. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Nashville: IEEE, 2021. 5188–5197.
|
| [33] |
Liu FB, Chen YH, Wang C, et al. Asymmetric co-teaching with multi-view consensus for noisy label learning. arXiv:2301.01143, 2023.
|
 2024, Vol. 33
2024, Vol. 33


