数字高程模型(digital elevation model, DEM)是一种地理信息系统(GIS)中常用的地形数据模型, DEM在各种地理分析中起着重要作用, 广泛应用于地形分析[1]、水文建模[2]、地形辅助导航[3]和环境模拟[4]等领域. DEM精度越高对于地理分析的结果越准确, 因此如何获得高分辨率DEM已成为研究热点[5–9]. 采用车载激光雷达测量[10]、航空摄影测量[11]和卫星影像测量[12]等方法, 都是直接获取DEM的方法, 但耗时耗力, 对于部分地方并不适合使用大规模的采集方式. 并且随着DEM测量方式的增多, 对同一地区的DEM也越来越多, 呈多分辨率和多时相的特点, 学者们已经开始探索利用多源DEM进行数据融合以提高DEM分辨率[13,14].
然而, 由于部分地区DEM的保密性, 多源DEM的获取存在一定困难. 因此, 目前主流的方法是对低分辨率DEM进行超分辨率重建(super-resolution recon-struction, SRR), 从算法原理上分为基于插值、基于重建和基于学习这3类. 其中基于插值的方法(如最邻近插值、双线性插值和三次样条插值)无法准确推测原始高分辨率图像的细节信息, 导致丢失地形尖锐边缘和细微变化, 并产生不真实的伪影或平滑效果, 缺乏细节和清晰度. 而基于重建的方法(如凸集投影法[15]、迭代反投影法[16]和最大后验估计法[17])受限于假设的模型, 在重建过程中与实际情况不一致, 导致细节损失和无法处理复杂的结构, 重建后可能模糊、失真或产生伪影.
基于学习的图像超分辨率算法与前两种类型有显著区别, 通过学习高分辨率图像与对应低分辨率图像之间的映射关系并计算特征信息来重建高分辨率图像. 并且随着深度学习的发展, 出现了一种新的超分辨率图像重建方法: 将卷积神经网络(convolutional neural network, CNN)应用到超分辨率任务中, 2016年, Chen等人[18]在CNN的基础上, 通过最小化误差的优化方法输出高分辨率的DEM, 该方法重建得到的DEM和传统插值方法相比取得了更好的效果. 2019年, Xu等人[19]利用深度卷积网络结合迁移学习, 成功将自然图像学习的知识迁移到DEM超分辨率重建领域, 实现在少量DEM情况下获得高精度结果. 2020年, Jiao等人[20], 提出了基于深度残差网络的DEM超分辨率重建模型, 该模型通过最小化重建误差来优化模型, 从而提高DEM的分辨率和精度. 2022年, Lin等人[21], 介绍了一个结合内部和外部学习的DEM超分辨率重建模型, 该模型利用DEM数据的内部先验知识和外部图像数据集的学习, 以提升重建后DEM的质量和细节. 2023年, Zhou等人[22], 将地形特征与CNN进行结合, 介绍了一种基于多地形特征的超分辨率深度模型, 从矢量和栅格地形特征的角度出发, 提高了DEM整体精度和保留地形特征的优势.
针对数字高程模型超分辨重建中存在的地理结构细节缺失问题以及传统基于CNN的方法的局限性, 本文提出了深度残差频率自适应DEM超分辨率模型(deep residual frequency-adaptive DEM super-resolution model, DRFA-SR), 首先利用边缘检测算子得到DEM梯度图, 解决将DEM作为二维图像拓展, 所导致高程特征与RGB特征几何线索差异问题, 并加入高低频特征提取模块(high-low frequency feature extraction block, HIFEB)通过频率选择特征提取块(frequency-selective feature extraction block, FreqSelect), 获取DEM高低频特征信息, 为后续DEM重建提供丰富的信息, 然后由空洞空间金字塔池化(atrous spatial pyramid pooling, ASPP)输出最终特征图.
本文的主要工作如下.
(1)提出了一个深度残差频率自适应DEM超分辨重建模型, 通过使用梯度图作为输入数据来获取DEM中高频细节并避免将DEM作为二维图像拓展所引起的误差.
(2)通过引入HIFEB和ASPP模块有效地提取DEM中的高低频信息, 同时降低了模型的复杂性, 提高了超分辨率重建的准确性和效率.
(3)实验表明, 本文提出的DRFA-SR与其他目前先进模型对比, 在不同缩放因子下超分辨率实验上各个指标上均取得了优势.
1 研究方法 1.1 深度残差频率自适应DEM超分辨率模型DRFA-SR由梯度提取模块、浅层特征提取模块、深层特征提取模块、超分辨率重建模块和高度域重建模块组成, 如图1所示.
(1)梯度提取模块
通过Prewitt算子对低分辨率DEM
| DtLR=√(DLR)2x+(DLR)2y | (1) |
其中,
(2)浅层特征提取模块
该模块采用
| F1=Conv(DtLR) | (2) |
其中,
(3)深层特征提取模块
将得到的
| {Fk+1=HIFEB(Fk), k∈1,2,⋯,m−1FE=ASPP(Fk+1) | (3) |
(4)超分辨率重建模块
超分辨率重建模块由两个卷积块、一个ReLU函数和一个亚像素卷积层构成. 在重建高分辨率梯度图时, 将
| DtSR=frec(F1+FE) | (4) |
其中,
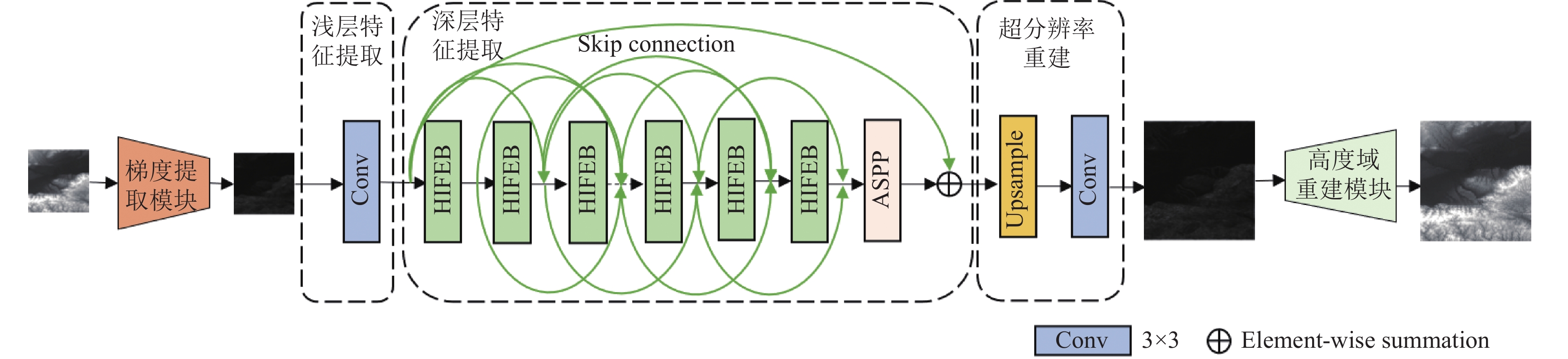
|
图 1 模型结构 |
(5)高度域重建模块
利用重建后高分辨率梯度图
| DSR=minDSR{∑ni=1|DLR−DLR↓|2+μ∑ni=1|DtSR−˜DtSR|2} | (5) |
并采用梯度下降算法(gradient descent), 得出最优
考虑到DEM空间信息极为复杂, 分辨率在水平和垂直方向上的变化影响着地形特征的表达, 使得DEM中微观地表的沟壑、悬崖等在数据呈中现出局部突出的形态, 然而, 在处理复杂地形会导致细节丢失、模糊和失真. 因此, 为了更好地捕获地形数据的细节和结构特征, 提高重建质量, 引入了高低频特征提取残差块, 如图3所示.
在残差神经网络中, 特征图之间的关系可以表示为:
| Y=y+G | (6) |
其中,
| G=Y−y | (7) |
其中,
| Gi=yi+F(yi;θiWi:L;Bi:L), i=1,2,⋯,N | (8) |
DEM包含丰富的高频特征和低频特征, 在残差块内部引入FreqSelect, 通过多尺度特征提取和残差学习, 有效地保留和重建DEM的细节和结构信息, 如图4所示.
在FreqSelect中, 在傅里叶域中通过应用不同的掩码将DEM输入特征图
| y=F−1(Mb⋅F(X)) | (9) |
其中,
| {1,if ϕb⩽k⩽ϕb+10,otherwise | (10) |
其中,

|
图 2 基于高度域重建 |
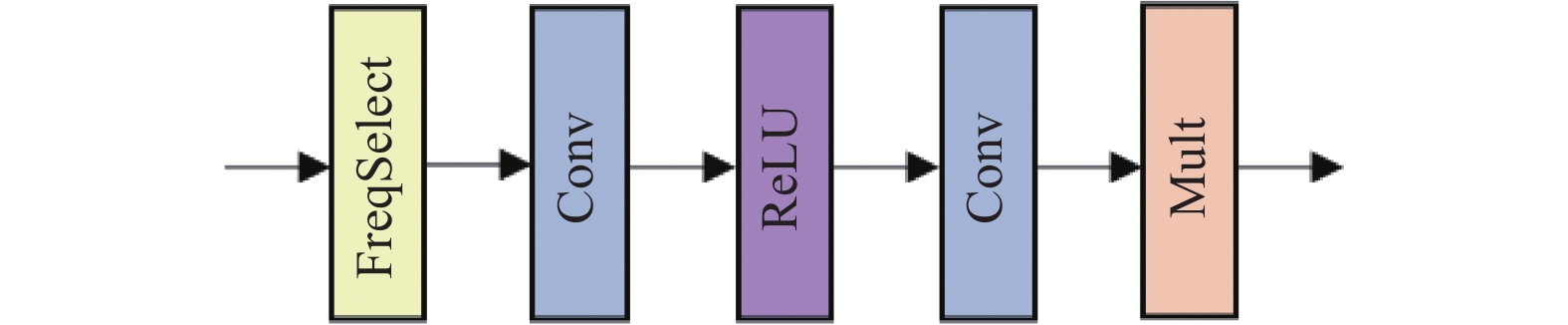
|
图 3 HIFEB结构 |
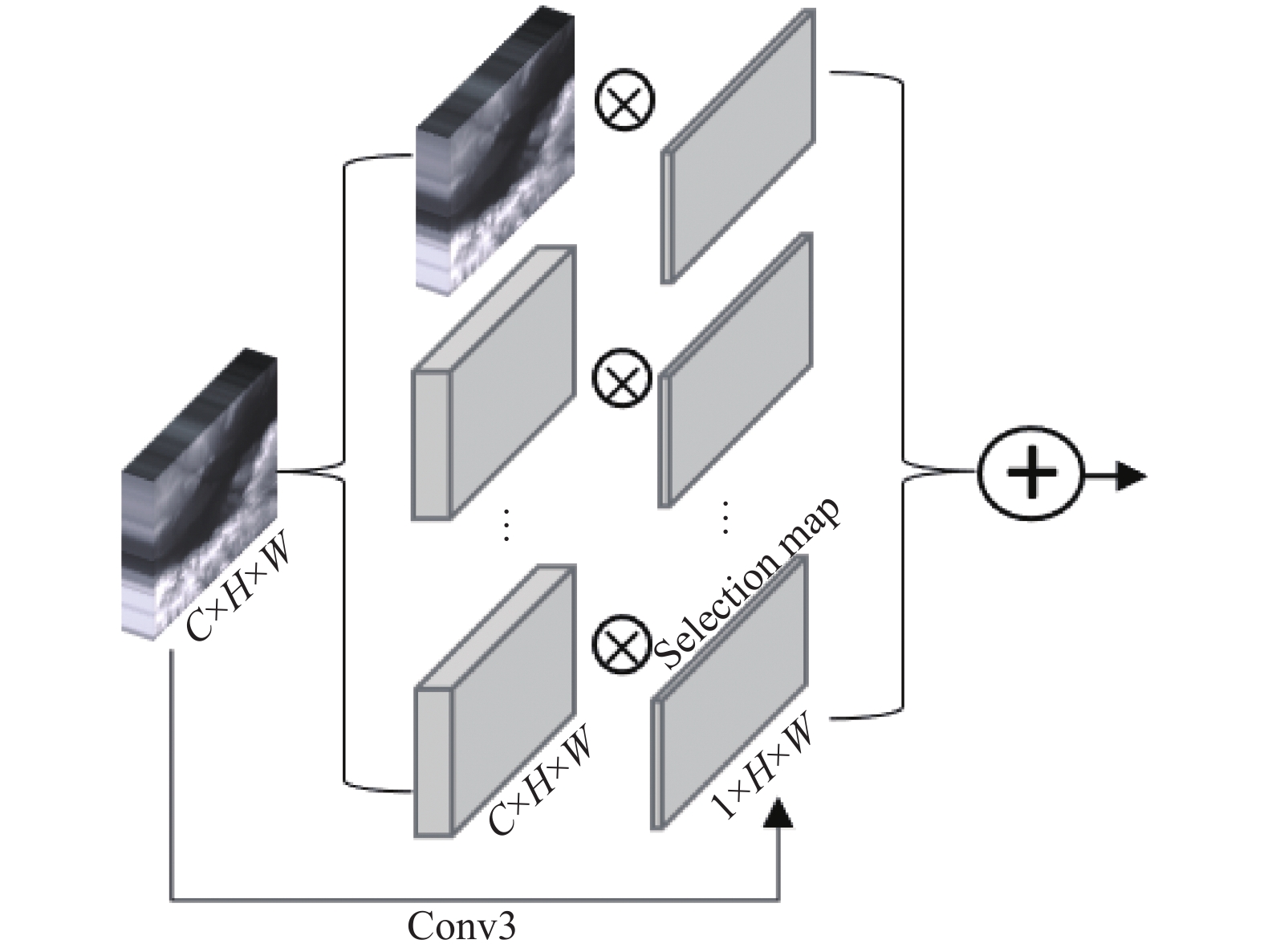
|
图 4 FreqSelect 结构 |
随后, FreqSelect在空间上动态地重新加权不同频率带中的频率成分, 以在重建过程中更好地平衡高低频特征. 其公式为:
| y′=B−1∑b=0Ab(i,j)Xb(i,j) | (11) |
其中,
为解决全局上下文信息整合的问题引入了空洞空间金字塔池化模块, 如图5所示, ASPP通过应用不同膨胀率的卷积操作, 有效地捕捉了不同尺度的地形特征, 同时通过全局平均池化获取了全局上下文信息, 通过将多尺度特征和全局信息进行融合, 提高了特征表示的丰富性和准确性.

|
图 5 ASPP结构 |
设输入特征图为
| Yd=Convd(G) | (12) |
其中,
| Y=Conv([Y1⋅Yd1⋅Yd1⋅Ygap]) | (13) |
其中,
超分辨率重建图像任务中, 一般将
| L1=1nn∑i=1|yi−F(xi)| | (14) |
其中,
本实验所使用平台是国家超级计算西安中心, 基于Python语言和PyTorch 1.8.0深度学习框架下训练DRFA-SR.
2.1 数据集与评价指标本实验使用陕西秦岭DEM作为实验对象, 秦岭山脉地形的起伏变化和高度差使得其具有多样的地形和复杂的地貌特征, 可以充分训练和验证本文模型.
由于DEM数据稀少, 不足以满足神经网络训练, 因此本文使用公开数据集DIV2K用来预训练, 并通过迁移学习, 将训练好的模型进行微调(fine-tune)更好地适应DEM超分辨率重建任务, 提高性能表现. 该DEM精度为30 m, 大小为
实验评价指标采用峰值信噪比和相对误差率(absolute relative error, ARE)来验证模型的有效性. PSNR计算重建图像与原始图像之间的均方误差, 并将其转化为以dB为单位的指标, 数值越高表示重建图像质量越好, 如式(15)所示:
| PSNR=10lgD2×MN∑Mx=1∑Ny=1(I(x,y)−Iw(x,y))2 | (15) |
ARE是预测值和真实值之间的相对差异, 将其绝对值化并除以真实值的指标. 其值表示了预测值与真实值之间的误差相对于真实值的大小. ARE的值越小, 表示预测值和真实值之间的误差越小, 即模型的预测越准确. 相反, 表示预测值和真实值之间的误差越大, 模型的预测准确性越低, 计算公式如下:
| ARE=1M×N∑Mx=1|Iw(x,y)−I(x,y)I(x,y)| | (16) |
式(15)和式(16)中,
训练过程中采用Adam优化器, 设定β1=0.9, β2=0.999, ε=2×0.0001, 每300个epoch学习率衰减一半, 在
为了充分验证DRFA-SR的先进性, 本节将同一地区不同分辨率的DEM进行对比分析, 表1列出了6种模型分别在两种不同精度下进行2倍和3倍超分辨率重建后PSNR和ARE对比结果. 由测试数据集上的评价结果可以看出, 所提DRFA-SR在数据集上均实现了更好的PSNR和ARE结果, 证明其性能优越.
| 表 1 不同模型重建DEM指标 |
具体而言, DRFA-SR与基于Transformer的SwinIR相比, 在缩放因子为2时,
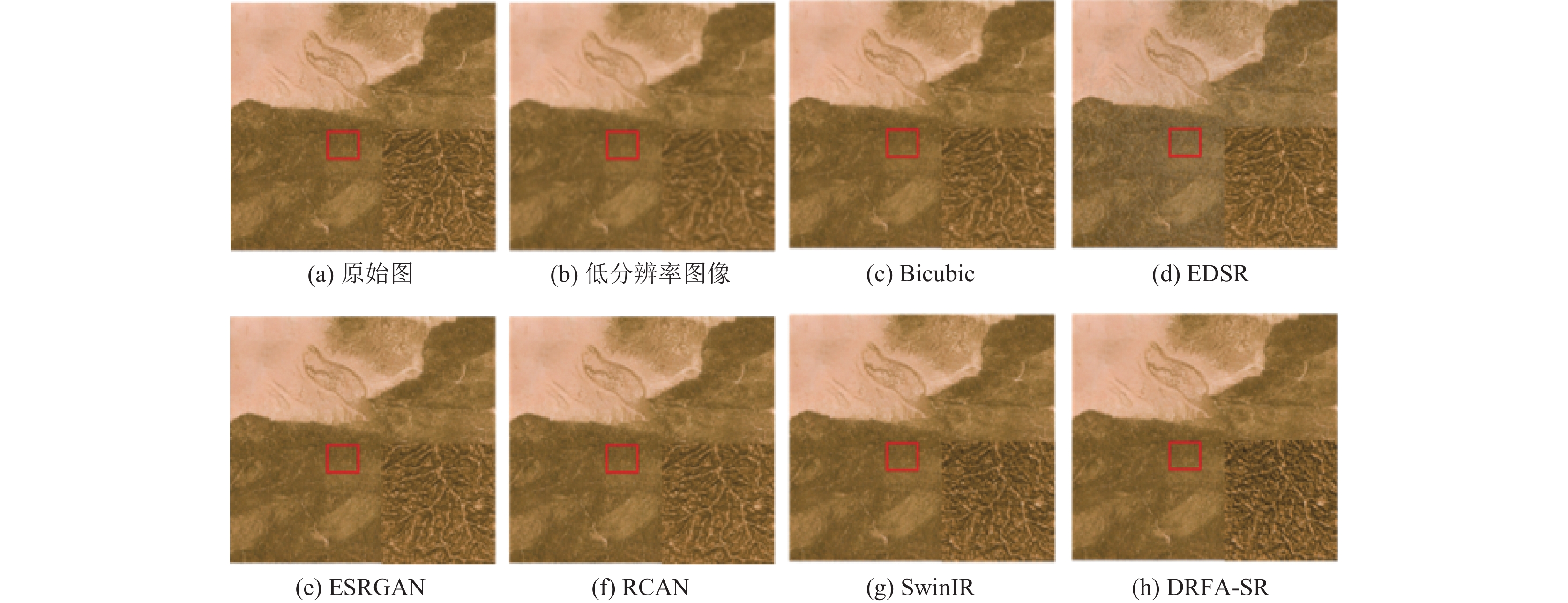
从图6(h)可以得出, DRFA-SR提取结果在平坦区域空间分布上明显好于其他方法, 而在陡峭区域DRFA-SR能够重建出更精确的纹理效果. 在坡向变化复杂的地区, DRFA-SR能够细致恢复出接近原始数据的DEM.
图7是重建后DEM的坡度图, 随着坡度降低, 6种方法提取到的坡度数据精度均得到提升, 且与实际结果逐渐接近, 其中DRFA-SR在6种方法中重建效果最好.
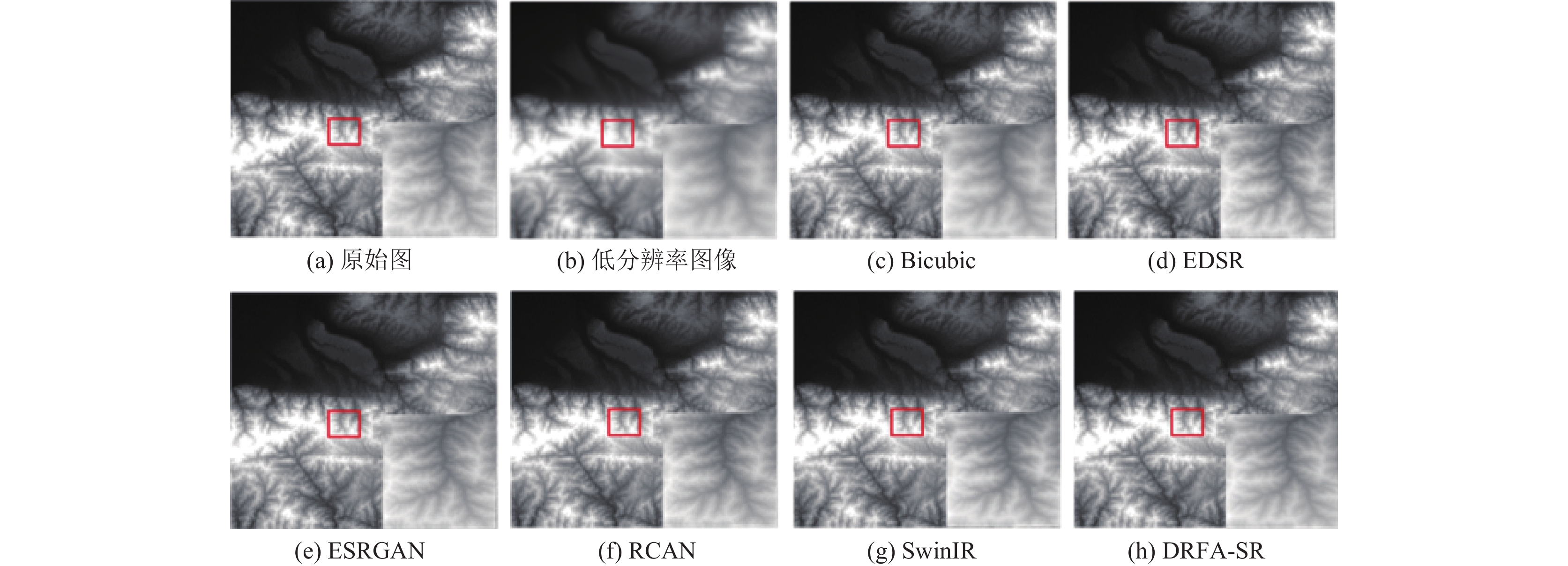
|
图 6 分辨率模型重建结果对比(DEM精度: 30 m; 缩放因子: 3) |
|
图 7 不同超分辨率模型坡度重建结果对比(DEM精度: 30 m; 缩放因子: 3) |
2.4 消融实验
DRFA-SR主要由HIFEB和ASPP组成, 其中HIFEB含有FreqSelect模块, 为了验证FreqSelect模块和ASPP对DEM高低频特征提取以及重建DEM提升的提升效果, 进行了4组对比实验, 结果如表2所示.
通过对比实验表明, 在数字高程模型超分辨率重建中, FreqSelect和ASPP模块的加入均显著提升了模型的重建效果: 基础模型的PSNR为31.67 dB, ARE为0.886, 表现较差. 引入FreqSelect模块后, PSNR提高到32.21 dB, ARE降低至0.843, 表明该模块通过有效提取高低频特征, 增强了模型的特征表示能力. 引入ASPP模块后, PSNR提升至32.41 dB, ARE降低至0.844, 说明ASPP通过多尺度特征提取和扩展感受野, 显著改善了重建质量. 最终, 结合了FreqSelect和ASPP模块的DRFA-SR模型取得了最佳性能, PSNR达到33.93 dB, ARE降至0.824. 这验证了两模块在高低频特征提取和多尺度特征融合方面的协同增效作用, 显著提升了DEM超分辨率重建的整体效果.
| 表 2 HIFEB和ASPP有效性验证结果 |
3 结束语
本文提出一种基于深度残差频率自适应网络模型DRFA-SR, 通过使用高低频特征提取残差模块和空洞空间金字塔池化模块, 更充分地利用特征图中的信息. 并在HIFEB中使用了FreqSelect模块, 根据频率选择出重要的特征信息, 真实地重建出DEM的地理特征.
此外, 在梯度域和高度域双重约束下进行重建, 提升模型的超分辨率重建能力. 实验结果表明, DRFAT-SR通过提取高低频特征和整合多尺度信息取得了显著的模型性能, 与EDSR和SwinIR等最新算法相比, 所提DRFA-SR在各个指标中均取得最优效果.
| [1] |
Xiong LY, Tang G, Yang X, et al. Geomorphology-oriented digital terrain analysis: Progress and perspectives. Journal of Geographical Sciences, 2021, 31(3): 456-476. DOI:10.1007/s11442-021-1853-9 |
| [2] |
Borzi G, Roig A, Tanjal C, et al. Flood hazard assessment in large plain basins with a scarce slope in the Pampean Plain, Argentina. Environmental Monitoring and Assessment, 2021, 193(4): 177. DOI:10.1007/s10661-021-08988-1 |
| [3] |
Wang HX, Cheng YM, Liu N, et al. An illumination-invariant shadow-based scene matching navigation approach in low-altitude flight. Remote Sensing, 2022, 14(16): 3869. DOI:10.3390/rs14163869 |
| [4] |
An R, Lee JA. CAMDLES: CFD-DEM simulation of microbial communities in spaceflight and artificial microgravity. Life, 2022, 12(5): 660. DOI:10.3390/life12050660 |
| [5] |
Li ZX, Zhu XH, Yao SL, et al. A large scale digital elevation model super-resolution Transformer. International Journal of Applied Earth Observation and Geoinformation, 2023, 124: 103496. DOI:10.1016/j.jag.2023.103496 |
| [6] |
Yao S, Cheng YM, Yang F, et al. A continuous digital elevation representation model for DEM super-resolution. ISPRS Journal of Photogrammetry and Remote Sensing, 2024, 208: 1-13. DOI:10.1016/j.isprsjprs.2024.01.001 |
| [7] |
Wang H, Xiong LY, Hu GH, et al. DEM super-resolution framework based on deep learning: Decomposing terrain trends and residuals. International Journal of Digital Earth, 2024, 17(1): 2356121. DOI:10.1080/17538947.2024.2356121 |
| [8] |
Lin R, Mei G, Xu N. Accurate and automatic mapping of complex debris-covered glacier from remote sensing imagery using deep convolutional networks. Geological Journal, 2023 (published online). [doi: 10.1002/gj.4615]
|
| [9] |
Demiray BZ, Sit M, Demir I. D-SRGAN: DEM super-resolution with generative adversarial networks. SN Computer Science, 2021, 2(1): 48. DOI:10.1007/s42979-020-00442-2 |
| [10] |
Vasile I, Tudor E, Sburlan IC, et al. Experimental validation of LiDAR sensors used in vehicular applications by using a mobile platform for distance and speed measurements. Sensors, 2021, 21(23): 8147. DOI:10.3390/s21238147 |
| [11] |
Lenda G, Borowiec N, Marmol U. Study of the precise determination of pipeline geometries using UAV scanning compared to terrestrial scanning, aerial scanning and UAV photogrammetry. Sensors, 2023, 23(19): 8257. DOI:10.3390/s23198257 |
| [12] |
Arroyo-Mora JP, Kalacska M, Roghani A, et al. Assessment of UAS photogrammetry and planet imagery for monitoring water levels around railway tracks. Drones, 2023, 7(9): 553. DOI:10.3390/drones7090553 |
| [13] |
Bagheri H, Schmitt M, Zhu XX. Fusion of multi-sensor-derived heights and OSM-derived building footprints for urban 3D reconstruction. ISPRS International Journal of Geo-information, 2019, 8(4): 193. DOI:10.3390/ijgi8040193 |
| [14] |
Shen HF, Meng XC, Zhang LP. An integrated framework for the spatio-temporal-spectral fusion of remote sensing images. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(12): 7135-7148. DOI:10.1109/TGRS.2016.2596290 |
| [15] |
Kováčová G, Rudloff B. Convex projection and convex multi-objective optimization. Journal of Global Optimization, 2022, 83(2): 301-327. DOI:10.1007/s10898-021-01111-1 |
| [16] |
Zhang X, Liu Q, Li XM, et al. Non-local feature back-projection for image super-resolution. IET Image Processing, 2016, 10(5): 398-408. DOI:10.1049/iet-ipr.2015.0467 |
| [17] |
He Y, Yap KH, Chen L, et al. A soft MAP framework for blind super-resolution image reconstruction. Image and Vision Computing, 2009, 27(4): 364-373. DOI:10.1016/j.imavis.2008.05.010 |
| [18] |
Chen ZX, Wang XW, Xu ZK, et al. Convolutional neural network based DEM super resolution. In: The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Prague: ISPRS, 2016. 247–250.
|
| [19] |
Xu ZK, Chen ZX, Yi WW, et al. Deep gradient prior network for DEM super-resolution: Transfer learning from image to DEM. ISPRS Journal of Photogrammetry and Remote Sensing, 2019, 150: 80-90. DOI:10.1016/j.isprsjprs.2019.02.008 |
| [20] |
Jiao DL, Wang DJ, Lv HY, et al. Super-resolution reconstruction of a digital elevation model based on a deep residual network. Open Geosciences, 2020, 12(1): 1369-1382. DOI:10.1515/geo-2020-0207 |
| [21] |
Lin X, Zhang QQ, Wang HY, et al. A DEM super-resolution reconstruction network combining internal and external learning. Remote Sensing, 2022, 14(9): 2181. DOI:10.3390/rs14092181 |
| [22] |
Zhou AN, Chen YM, Wilson JP, et al. A multi-terrain feature-based deep convolutional neural network for constructing super-resolution DEMs. International Journal of Applied Earth Observation and Geoinformation, 2023, 120: 103338. DOI:10.1016/j.jag.2023.103338 |
| [23] |
Zhao H, Gallo O, Frosio I, et al. Loss functions for image restoration with neural networks. IEEE Transactions on Computational Imaging, 2017, 3(1): 47-57. DOI:10.1109/TCI.2016.2644865 |
| [24] |
Keys R. Cubic convolution interpolation for digital Image processing. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1981, 29(6): 1153-1160. DOI:10.1109/TASSP.1981.1163711 |
| [25] |
Lim B, Son S, Kim H, et al. Enhanced deep residual networks for single image super-resolution. Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW). Honolulu: IEEE, 2017. 136–144.
|
| [26] |
Zhang YL, Li KP, Li K, et al. Image super-resolution using very deep residual channel attention networks. Proceedings of the 15th European Conference on Computer Vision (ECCV). Munich: Springer, 2018. 286–301.
|
| [27] |
Liang J, Cao J, Sun GL, et al. SwinIR: Image restoration using Swin Transformer. Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision Workshops (ICCVW). Montreal: IEEE, 2021. 1833–1844.
|
 2024, Vol. 33
2024, Vol. 33



