近年来, 随着科技的不断发展, 无人机(unmanned aerial vehicle, UAV)由于其高机动和低成本等特点, 在军事、农业、交通以及公共管理等领域展现出了广泛的应用潜力^[1,2]. 应用领域广泛的同时, 其应用场景也在不断扩展, 无人机需要到城市, 农田, 山区等各种存在障碍物和干扰的非净空环境中飞行. 随着无人机任务的多样性和任务环境的复杂性增加, 航迹规划成为确保无人机安全和效率的关键挑战. 为提升无人机的智能性和自主性, 复杂环境中无人机的航迹规划问题成为国内外学者的研究重点. 路径规划算法根据其事先对环境的需求不同, 可以分为全局算法和局部算法. 全局算法主要针对环境已知的静态环境, 常见的算法有Dijkstra^[3]、RRT^[4]、A*^[5,6]等. 局部算法则适用于动态的或部分已知的环境, 局部算法能够实时感知环境的变化来动态调整路径, 常见的算法包括人工势场^[7]、蚁群算法^[8]、遗传算法^[9]等.

传统的局部路径规划算法虽然具备一定的适应能力, 但也存在容易陷入局部最优、灵活性较差和在复杂环境中表现不佳等问题. 相比之下, 深度强化学习在处理不确定性和动态变化方面具有显著优势, 因为它可以通过经验和训练数据学习处理随机和不可预测的情况. 例如, 文献[10,11]通过重新设计奖励函数, 引导无人机更快速地完成任务. 张森等^[12] 提出了一种改进型深度确定性策略梯度算法(deep deterministic policy gradient, DDPG), 通过双经验池分割数据、引入人工势场选择策略以及设计组合奖励因数, 改善了算法的收敛速度和成功率. Grando等^[13]将RNN循环神经网络整合到TD3和SAC算法中, 赋予模型一定的记忆和推理能力, 从而在机动避障时参考前序信息做出更明智的决策.

尽管在无人机路径规划领域取得了诸多进展, 仍存在一些不足之处. 首先, 许多研究未考虑动态障碍物, 或仅考虑了匀速移动的障碍物, 而未考虑实际环境中的随机移动. 其次, 许多研究未考虑无人机电量对任务完成度的约束. 最后, 大部分文献忽略了实际场景中的环境因素对无人机的干扰情况. 为解决这些问题, 本文提出了一种融合先验策略的CMNTD3 (prior-policy conv multi noise twin delayed deep deterministic policy gradient)算法, 该算法兼顾了路径规划的安全性、自主避障能力, 并提升了能效利用.

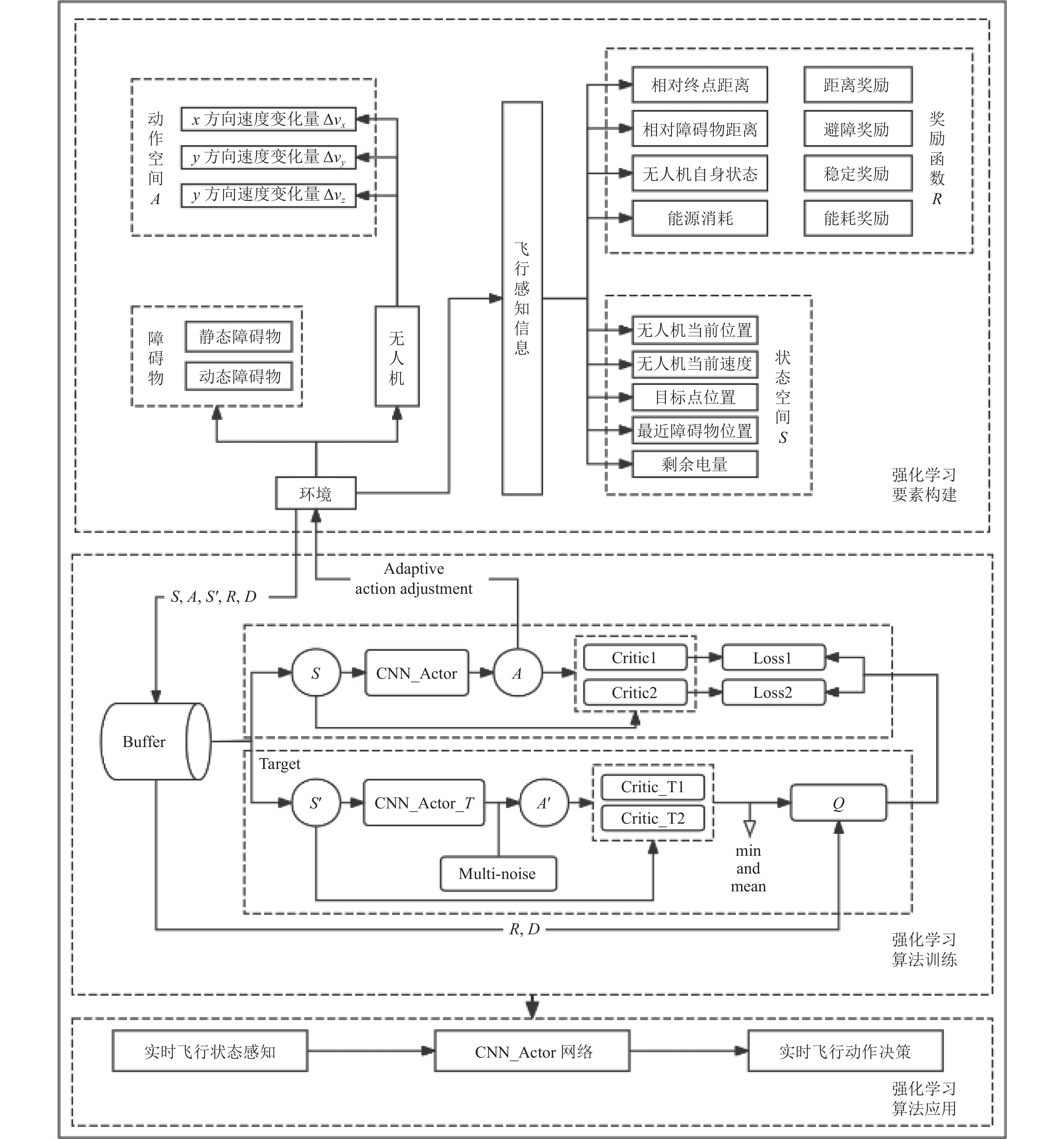
1 无人机航迹规划系统模型

为满足无人机路径规划任务中避障的实时性, 并且保证能够适应一定的环境干扰, 本文提出了基于PP-CMNTD3算法的无人机航迹规划系统模型, 图1为其系统模型.

无人机航迹规划系统模型的构建涉及多个关键步骤, 旨在创建一个能够在负责的动态环境中进行有效路径规划的系统. 整个过程如下.

首先, 构建包含静态和动态障碍物的模拟环境, 该环境旨在模拟无人机在真实世界中可能遇到的复杂情景, 并为航迹规划提供挑战性场景. 其次构建航迹规划问题中的强化学习要素, 基于无人机的动力学模型构建动作空间, 以确保所生成的动作指令在物理上可行; 状态空间则包含与环境和无人机自身相关的关键信息; 此外, 借鉴人工势场的思想, 设计了奖励函数并且提出了一种先验策略, 这些要素共同构成了无人机航迹规划的强化学习框架. 随后根据设计的强化学习要素, 对PP-CMNTD3算法进行训练, 训练中的决策模型由强化学习模型和先验策略相结合. 该模型的输出通过改变无人机的动作和环境状态来不断优化整个系统的性能. 先验策略与强化学习模型结合的策略为前期训练阶段提供高质量的样本, 提高了训练效率. 随着训练的推进, 先验策略的影响逐渐减弱, 最终几乎完全由强化学习模型主导决策. 最后再利用训练过的PP-CMNTD3算法, 输出动作指令以指导无人机的航迹规划, 确保无人机能够在复杂环境中安全抵达目标, 并在能耗和时间之间达到平衡.

2 强化学习要素与先验策略设计 2.1 状态空间

在无人机的飞行操作中, 实时地感知复杂环境及监测自身状态的能力是必不可少的. 这种能力使得无人机能够在评估其剩余电量的基础上, 有效地调整策略避开环境中的障碍地形, 快速而准确地到达设定的关键目标地点.

状态空间的设计通常基于无人机传感器提供的飞行状态信息, 其中无人机的飞行状态包括无人机自身的三维位置, 水平速度, 垂直速度, 航向角信息以及剩余电量, 并且假设无人机在每个时间步内采取匀速飞行的策略; 对于环境信息, 仅使用最近障碍物的绝对位置信息表示对环境的观测.

即无人机在$ {{t}} $时刻的状态空间可以表示为:

$ \begin{split} {s_t} = & ( {x_{{\mathrm{uav}}}}, {y_{{\mathrm{uav}}}}, {{\textit{z}}_{{\mathrm{uav}}}}, {v_{xy}}, {\varphi _{xy}}, {v_{\textit{z}}}, {x_{{\mathrm{dest}}}},\\ &{y_{{\text{dest}}}}, {{\textit{z}}_{{\mathrm{dest}}}}, {x_{{\mathrm{obs}}}}, {y_{{\mathrm{obs}}}}, {{\textit{z}}_{{\mathrm{obs}}}}, {e_{{\mathrm{uav}}}} ) \end{split} $

(1)

其中, $ ({x_{{\mathrm{uav}}}}, {y_{{\mathrm{uav}}}}, {{\textit{z}}_{{\mathrm{uav}}}}) $表示$ {{t}} $时刻无人机的三维位置坐标; $ ({v_{xy}}, {\varphi _{xy}}, {v_{\textit{z}}}) $表示$ {{t}} $时刻无人机的实时速度信息; $ ({x_{{\mathrm{dest}}}}, {y_{{\text{dest}}}}, {{\textit{z}}_{{\mathrm{dest}}}}) $表示无人机飞行目标点的三维位置坐标; $ ({x_{{\mathrm{obs}}}}, {y_{{\mathrm{obs}}}}, {{\textit{z}}_{{\mathrm{obs}}}}) $表示最近障碍物的三维位置坐标, 如果为静态障碍物则为圆柱质心三维位置坐标; $ {e_{{\mathrm{uav}}}} $表示无人机剩余电量.

2.2 动作空间

动作空间的设计可以分为离散型和连续型. 在实际的无人机飞行中, 动作通常是与无人机的状态相关的连续变量, 其取值范围取决于无人机的硬件性能和自身特性. 然而, 在仿真环境中, 为了简化问题, 一些研究使用栅格法将三维空间进行划分, 进而获得离散的动作空间, 或通过组合多个动作构建离散的动作集合. 然而, 离散动作空间可能会限制无人机的机动性, 从而降低其灵活性和性能. 因此, 本文采用连续型动作空间, 并根据以下无人机动力学模型进行研究:

$ \left\{ {\begin{array}{*{20}{l}} {{\varphi' _{xy}} = {\varphi _{xy}} + \Delta {\varphi _{xy}} + {\varepsilon _\varphi }} \\ {{v'_{xy}} = {v_{xy}} + \Delta {v_{xy}} + {\varepsilon _{xy}}} \\ {{v'_{\textit{z}}} = {v_{\textit{z}}} + \Delta {v_{\textit{z}}} + {\varepsilon _{\textit{z}}}} \\ {{x'_{{\text{uav }}}} = {x_{{\text{uav }}}} + {v'_{xy}} \cdot \sin {\varphi' _{xy}} \cdot \Delta t} \\ {{y'_{{\text{uav}}}} = {y_{{\text{uav }}}} + {v'_y} \cdot \cos {\varphi' _{xy}} \cdot \Delta t} \\ {{{\textit{z}}'_{{\text{uav}}}} = {{\textit{z}}_{{\text{uav}}}} + {v'_{\textit{z}}} \cdot \Delta t} \end{array}} \right. $

(2)

其中, $ \Delta t $表示时间间隔, $ ({\varepsilon _{xy}}, {\varepsilon _\varphi }, {\varepsilon _{\textit{z}}}) $表示引入风力干扰模型而产生的干扰. 而基于这个动力学模型, 本文的动作空间设定为:

$ {a_t} = \left( {\Delta {v_{xy}}, \Delta {\varphi _{xy}}, \Delta {v_{\textit{z}}}} \right) $

(3)

其中, $ \Delta {v_{xy}} $表示水平速度变化量, $ \Delta {\varphi _{xy}} $表示航向角变化量, 航向为y轴的夹角, $ \Delta {v_{\textit{z}}} $表示垂直速度变化量. 此外无人机受到自身硬件限制:

$ \left\{ \begin{gathered} \Delta {v_{xy}} \lt \max \Delta {v_{xy}} \\ \Delta {\varphi _{xy}} \lt \max \Delta {\varphi _{xy}} \\ \Delta {v_{\textit{z}}} \lt \max \Delta {v_{\textit{z}}} \\ \end{gathered} \right. $

(4)

2.3 奖励函数设计

在强化学习中, 奖励函数的设计是至关重要的, 因为它直接影响到智能体的行为策略学习和决策过程. 智能体的基本目标是通过与环境的交互, 最大化其获取的累计奖励. 因此, 奖励信号不仅需要准确反映任务的目标, 还应该有效地指导智能体学习到有效的行为策略. 对于复杂任务如无人机的避障导航等, 设计一个既简洁又实用的奖励函数尤其具有挑战性. 这些类型的任务通常涉及多目标考量和多种约束条件, 例如安全性、效率、能耗等. 在这些情况下, 单一的奖励信号(如简单的碰撞检测或目标达成状态)往往是稀疏且不足以覆盖所有重要的行为评价标准, 这种稀疏奖励的问题在于它可能导致学习过程缓慢且不稳定, 智能体在大部分交互中无法获得有效的学习反馈. 本文在综合考虑这些因素后, 借鉴人工势场算法的思想设计了奖励函数, 将稀疏奖励转化为密集奖励, 在飞行过程中给予较小的奖励, 能够更好地引导无人机达成目标, 具体的奖励函数定义为:

$ \begin{split} r = & {r_{{\mathrm{success}}}} + {r_{{\mathrm{collision}}}} + {r_{{\mathrm{bound}}}} + {{{r}}_{{\text{time}}}} + {{{r}}_{{\text{energy}}}} \\ & +{r_{{\mathrm{att}}}} + {r_{{\mathrm{rep}}}} + {r_{{\mathrm{dis}}}} + {r_{{\mathrm{speed}}}} \end{split} $

(5)

2.3.1 路径规划基础奖励

如果无人机成功到达既定目标点, 获得式(6)奖励:

$ {r}_{\text{success}}=\left\{\begin{array}{*{20}{l}} 100,& 如果到达目标点 \\ 0,& 如果没有到达目标点 \end{array}\right. $

(6)

如果无人机与障碍物发生碰撞, 获得式(7)惩罚:

$ {r}_{{\mathrm{collision}}}=\left\{\begin{array}{*{20}{l}} -100\text{, }& 如果发生碰撞\\ 0\text{, }& 如果没有发生碰撞\end{array}\right. $

(7)

如果无人机超出规划空域边界, 获得与碰撞惩罚同等水平的出界惩罚:

$ {r}_{{\mathrm{bound}}}=\left\{\begin{array}{*{20}{l}} -100\text{, }& 如果超出规划空域\\ 0\text{, }& 如果没有超出规划空域\end{array}\right. $

(8)

如果无人机超过规定的规划时间, 获得与碰撞惩罚同等水平的超时惩罚:

$ {r}_{\text{time}}=\left\{\begin{array}{*{20}{l}} -100\text{, }& 如果超出规划时间\\ 0\text{, }& 如果没有超出规划时间\end{array}\right. $

(9)

如果无人机在规划过程中电量耗尽, 获得与碰撞惩罚同等水平的能耗惩罚:

$ {r}_{\text{energy}}=\left\{\begin{array}{*{20}{l}} -100\text{, }& 如果电量耗尽\\ 0\text{, }& 如果电量没有耗尽\end{array}\right. $

(10)

2.3.2 稀疏奖励处理

为了解决强化学习的稀疏奖励问题, 同时进一步提高强化学习的样本利用效率, 引入模拟人工势场算法的引力奖励和斥力奖励. 相比于稀疏奖励, 引力奖励和斥力奖励的引入提供了在整个飞行过程中的连续反馈, 这使得无人机在每一步都能得到明确的指引, 同时连续的奖励信号能够时强化学习算法更快地学习到有效的策略, 因为每个训练样本都包含了有价值的反馈信息, 不再需要等待稀疏的奖励信号, 进一步提高了样本利用效率.

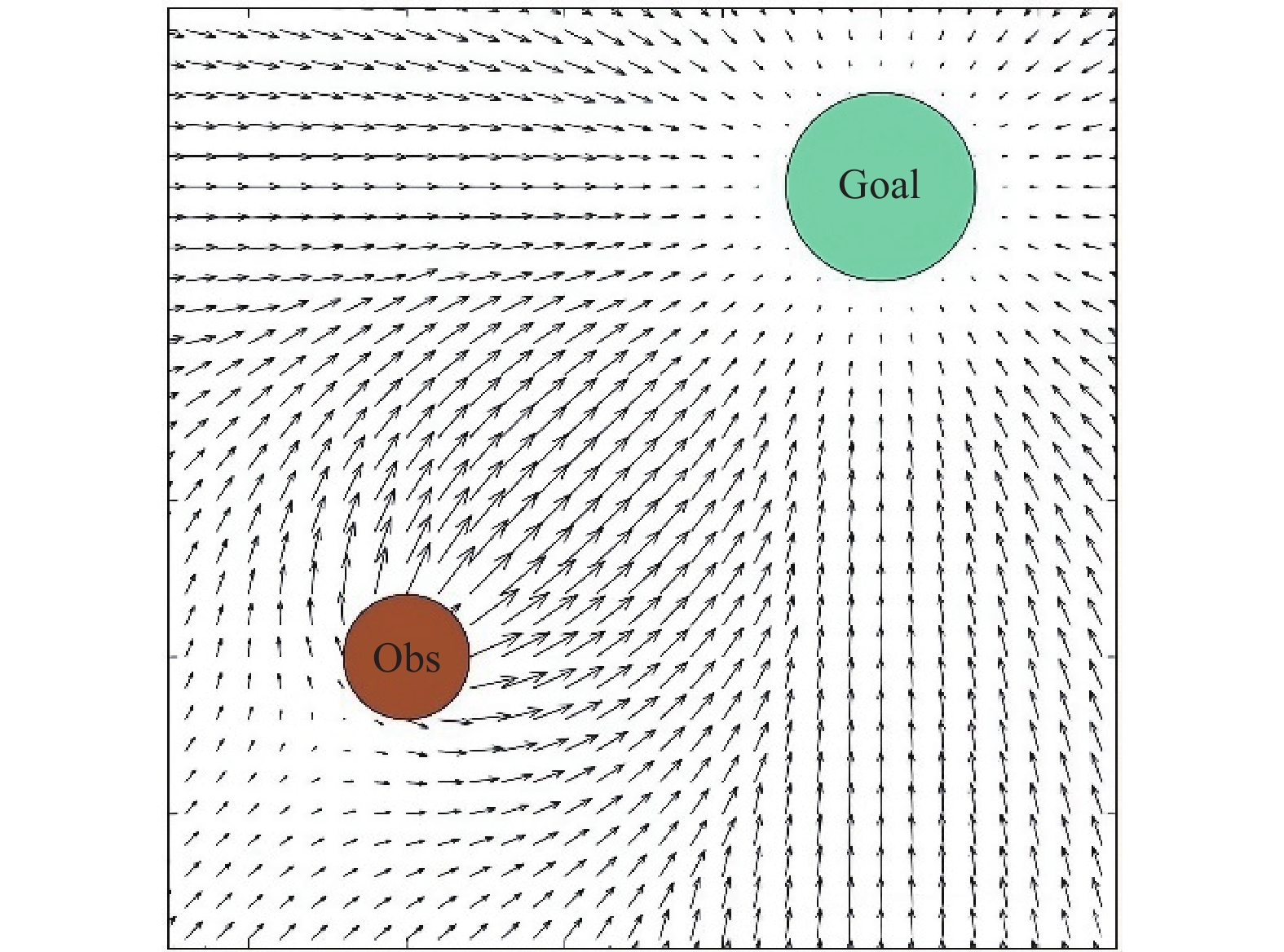
人工势场算法是一种常见的路径规划算法, 通过模拟物理中的电磁场概念来指导物体避开障碍物并向目标移动. 该算法将物体视为处在一个由目标产生的吸引力场和障碍物产生的排斥力场中的质点. 吸引力促使物体向目标移动, 而排斥力使物体远离障碍物. 这些力的叠加决定了物体的运动方向和速度, 如图2.

人工势场由两种力场组成, 分别是由目标点形成的引力场和障碍物形成的斥力场:

$ U(q) = {U_{{\text{att }}}}(q) + {U_{{\text{rep }}}}(q) $

(11)

其中, $ {U_{{\text{att }}}} $是引力场, 引导物体前往目标点; $ {U_{{\text{rep }}}} $是斥力场, 引导物体远离障碍物. 常见的引力场函数如式(12)所示:

$ \begin{split} & {U_{{\text{att }}}}(q) = \\ & \left\{ {\begin{array}{*{20}{l}} {\dfrac{1}{2}\zeta {d^2}\left( {q, {q_{{\text{goal}}}}} \right)},&{d\left( {q, {q_{{\text{goal}}}}} \right) \leqslant d_{{\text{goal}}}^*} \\ {d_{{\text{goal}}}^*\zeta d\left( {q, {q_{{\text{goal}}}}} \right) - \dfrac{1}{2}\zeta {{\left( {d_{{\text{goal}}}^*} \right)}^2}},&{d\left( {q, {q_{{\text{goal}}}}} \right) \gt d_{{\text{goal}}}^*} \end{array}} \right. \end{split} $

(12)

其中, $ d\left( {q, {q_{{\text{goal}}}}} \right) $表示物体与目标点的距离; $ \zeta $是一个正的比例常数, 用于调整引力的强度大小; $ d_{{\text{goal }}}^* $表示物体距离目标位置$ {q_{{\text{goal }}}} $的阈值. 一般来说引力场的函数是一个分段函数, 是为了避免远离目标位置时引力过大的问题. 借鉴这种思想, 本文简化了人工势场的引力函数设计出一种一次函数形式的奖励函数, 公式为:

$ {r_{{\mathrm{att}}}} = - {k_{{\mathrm{att}}}}{d_{{\mathrm{tar}}}} $

(13)

其中, $ {k_{{\mathrm{att}}}} $表示引力相关系数; $ {d_{{\mathrm{tar}}}} $表示无人机实时位置和目标点的距离. 式(13)表明随着无人机接近目标点, 惩罚程度会逐渐趋于0, 这引导无人机能够尽可能地接近目标点.

常见的斥力场函数如下:

$ {U_{{\mathrm{rep}}}}(q) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{1}{2}\eta {{\left( {\dfrac{1}{{D(q)}} - \dfrac{1}{{{Q^*}}}} \right)}^2}, }&{D(q) \leqslant {Q^*}} \\ {0, }&{D(q) \gt {Q^*}} \end{array}} \right. $

(14)

其中, $ \eta $是斥力增益常量; $ D(q) $是距离障碍物的距离; $ {Q^*} $是障碍物的作用范围阈值. 同样的, 本文借鉴斥力场函数的思想并将其简化设计为奖励函数, 对于动态障碍物, 公式为:

$ {r_{{\text{rep}}}} = \left\{ {\begin{array}{*{20}{l}} - {k_{{\text{rep}}}}\left( {\dfrac{1}{{{d_{{\text{obs}}}}}} - \dfrac{1}{{{d_{{\text{range}}}}}}} \right),& {d_{{\mathrm{range}}}} \gt {d_{{\mathrm{obs}}}} \\ 0,& {d_{{\mathrm{range}}}} \leqslant {d_{{\mathrm{obs}}}} \end{array}} \right. $

(15)

其中, $ {k_{{\text{rep}}}} $是斥力的相关系数; $ {d_{{\text{obs}}}} $是无人机实时位置到障碍物的距离; $ {d_{{\text{range}}}} $是无人机受到障碍物斥力的最大作用范围. 式(15)表明, 设置一个阈值, 仅考虑周围的障碍物的斥力, 同时表明惩罚大小与距离的倒数成正比, 即随着距离障碍物的距离越近所受到的惩罚越大, 这会引导无人机在路径规划的途中避开周围的障碍物.

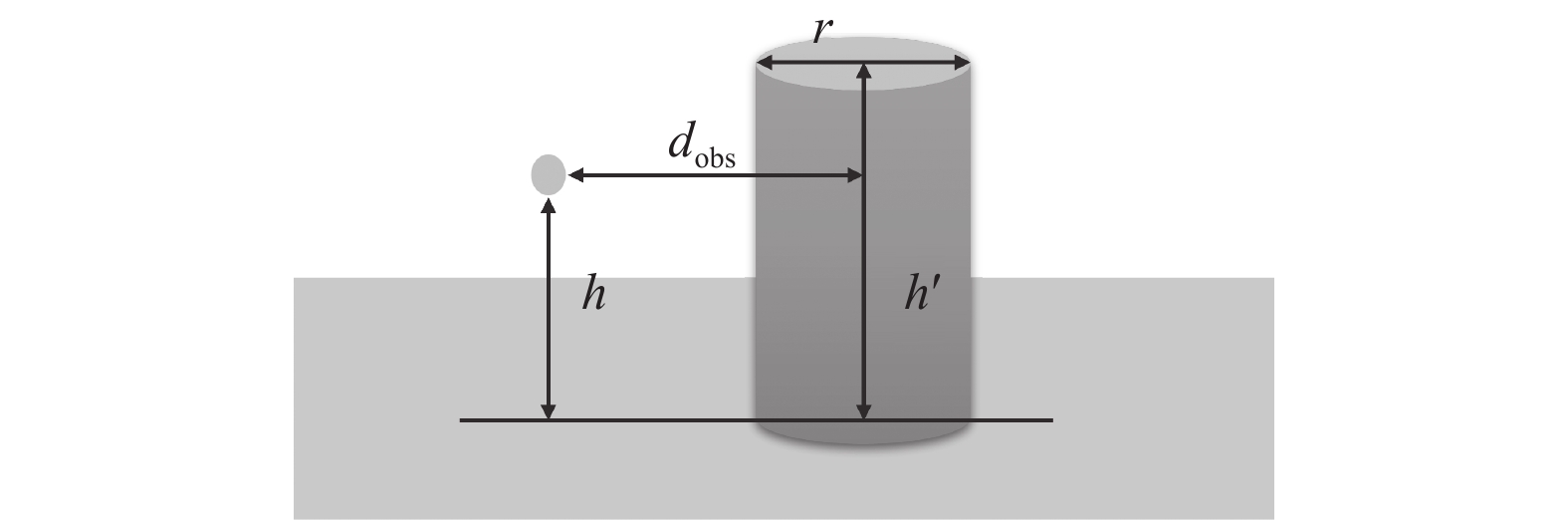
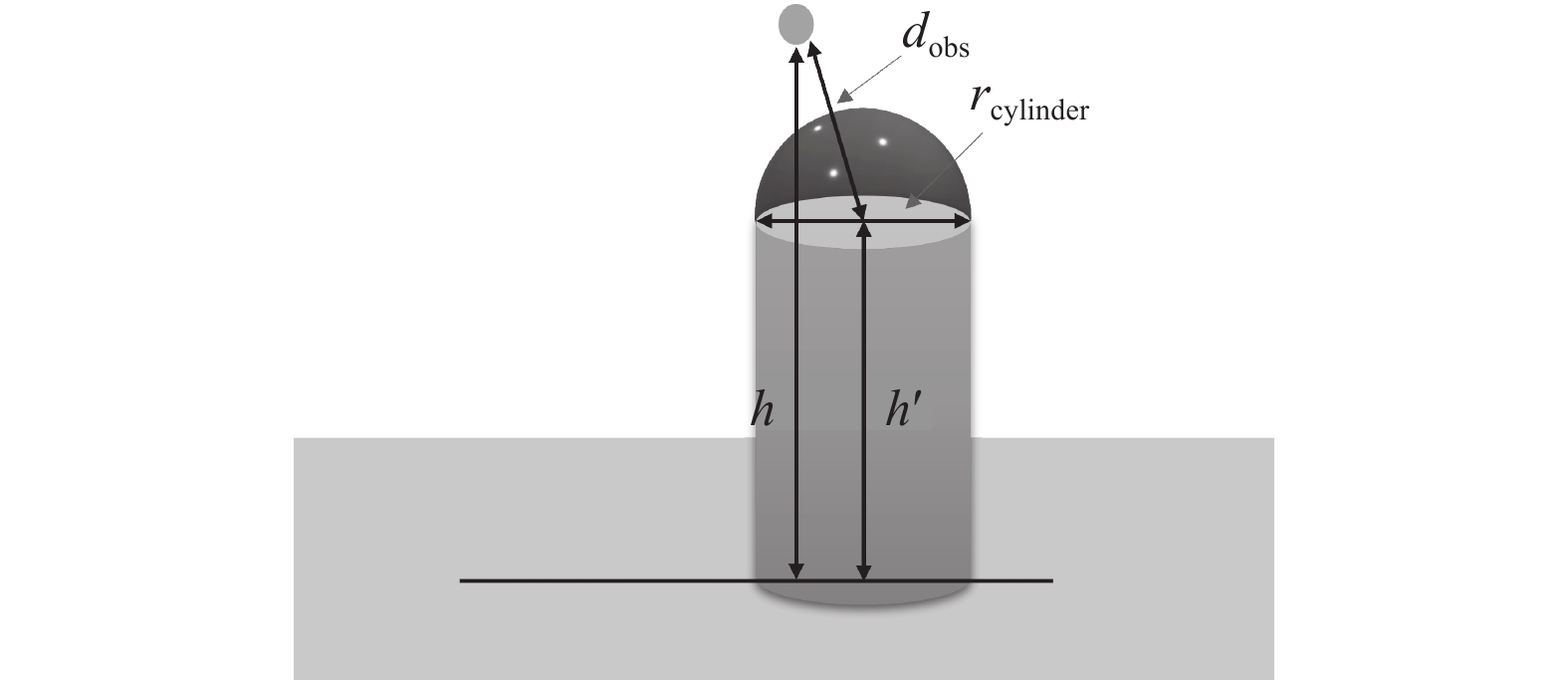
现实中的障碍物的形态是具有多样性的, 很多障碍物由于其本身的形态原因并不能简单的抽象为质点. 在现实中, 障碍物如建筑物、山丘、树木等, 具有显著的垂直维度. 如果将它们简化为质点, 只考虑和质心的距离, 无人机可能会忽略高度差, 从而导致碰撞. 所以在仿真时将静态障碍物抽象为圆柱体而非质点, 可以更准确地反映其三维形态, 从而提高无人机在复杂三维环境中避障和路径规划的精确性与安全性.

对于静态障碍物, 由于其为圆柱体, 所以不能简单地当作质点来看, $ {d_{{\text{obs}}}} $的计算分为两大类, 第1种是无人机飞行高度低于静态障碍物高度, 即$ h \lt h' $. 这种情况无人机显然有与障碍物碰撞的可能性, 与障碍物之间的碰撞距离显然为无人机与圆柱的中心轴线的距离, 如图3所示.

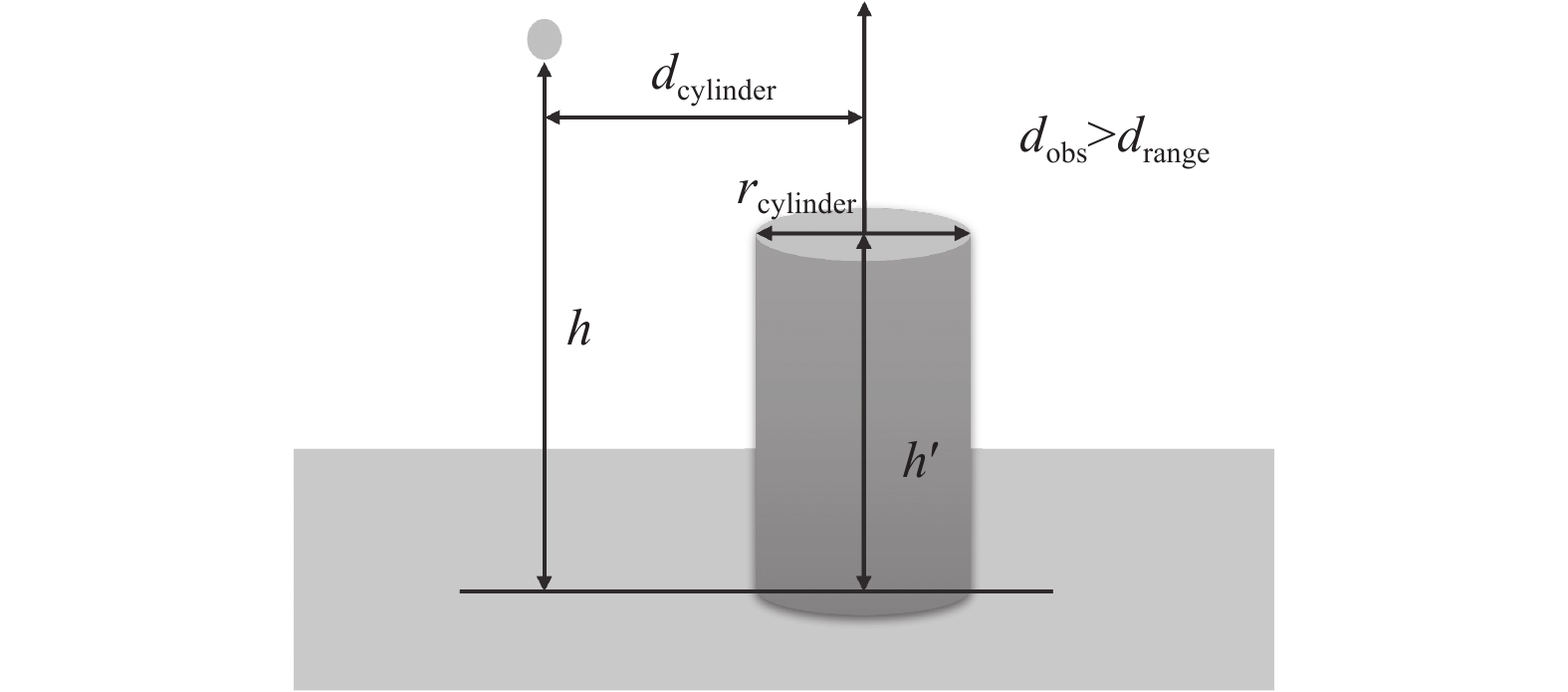
第2种是无人机飞行高度高于静态障碍物高度, 即$ h \gt h' $, 此时也分两种: (1) $ {d_{{\mathrm{cylinder}}}} \gt {r_{{\mathrm{cylinder}}}} $, 这种情况无人机在现有高度飞行或适当降低高度都不会存在与障碍物碰撞的风险, 故这种情况视作$ {d_{{\mathrm{obs}}}} \gt {d_{{\mathrm{range}}}} $, 如图4所示.

(2) $ {d_{{\mathrm{cylinder}}}} \lt {r_{{\mathrm{cylinder}}}} $, 在这种情况下, 无人机虽然高度高于障碍物, 但由于水平距离较近, 仍存在从垂直方向上撞击障碍物的风险. 因此, 无人机需要特别注意避开障碍物的顶部, 在规划路径时不仅要考虑水平距离, 还要确保飞行高度足以避开障碍物的最高点, 以避免发生碰撞. 这种情况的$ {d_{{\text{obs}}}} $计算如图5所示.

引力和斥力函数通过模拟物理中的吸引力和排斥力来指导无人机的飞行路径. 引力函数(式(13))使无人机朝向目标点移动, 确保其有效接近目标, 提高任务完成的效率; 斥力函数(式(15))使无人机远离障碍物, 减少碰撞风险, 确保飞行的安全性. 通过这种引力和斥力的综合作用, 无人机能够在复杂环境中更灵活地避开障碍物并接近目标, 从而在路径规划中获得更好的性能表现.

2.3.3 其他优化目标与约束条件

为了引导无人机更快地到达目标点, 同时综合考虑电量的消耗, 减少飞行和避障的成本, 设计了如下的奖励:

$ \left\{ \begin{gathered} {{c} _{{\text{energy}}}} = {k_{{\mathrm{energy}}}}({{{k}}_{{v}}}{v^2} + {k_a}{a^2}) \\ {r_{{\mathrm{dis}}}} = ({d_{{\mathrm{init}}\_{\mathrm{tar}}}} - {d_{{\mathrm{tar}}}})({{c} _{{\text{energy}}}}/{d_{{\mathrm{init}}\_{\mathrm{tar}}}}) - {{c} _{{\text{energy}}}} \\ \end{gathered} \right. $

(16)

其中, $ v $是无人机的速度; $ a $是无人机的加速度; $ {{{k}}_{{v}}} $是无人机速度能耗系数; $ {k_a} $是无人机加速度能耗系数; $ {k_{{\mathrm{energy}}}} $是总能耗系数; $ {d_{{\mathrm{init}}\_{\mathrm{tar}}}} $是起点和目标的距离; $ {d_{{\mathrm{tar}}}} $是无人机实时位置和目标点的距离; $ {{c} _{{\text{energy}}}} $是无人机的电量消耗. 这个奖励函数的设计综合考虑了能耗和任务效率两大关键因素, 引导无人机提高能源效率, 同时强化了无人机接近目标的重要性, 最后是希望无人机能在平衡能耗和更快接近目标之间取得一个平衡, 希望无人机能够在快速完成目标的同时保持能源的高效利用.

其次, 为了保证无人机的安全飞行, 设定了最大飞行速度, 如果无人机的速度超过了指定速度, 将获得式(17)的超速惩罚, 同时将速度降低至最大速度.

$ {r_{{\text{speed}}}} = \left\{ {\begin{array}{*{20}{l}} - 1,& v \gt {v_{\max }} \\ 0,& v \leqslant {v_{\max }} \end{array}} \right. $

(17)

速度和能耗奖励(式(16))根据无人机的速度和加速度设计, 目的是指导无人机在保证飞行速度的同时, 最小化能量消耗, 提高能源利用效率. 通过综合考虑速度和加速度, 无人机能够以更高效的方式完成任务, 延长飞行时间和续航能力. 而超速惩罚(式(17))则是在无人机速度超过安全阈值时给予一定惩罚, 以确保飞行的安全性. 设定最大飞行速度阈值, 防止无人机以过高速度飞行, 从而降低飞行风险, 确保任务在安全范围内完成.

2.4 先验策略设计

先验策略主要应用于智能体训练的初始阶段, 提供初步的指导以促进智能体对环境的探索, 并增加其在初始阶段达到目标的频率. 这种策略通常能力较弱, 目的是帮助智能体加速度过低效训练初期. 与依赖专家经验的传统方法不同, 先验策略不受专家经验的能力上限的约束. 因此, 它不会限制强化学习算法潜在的学习能力. 通过实施先验策略, 智能体能够在早期训练中有效地接受引导, 并通过逐步减少先验策略的影响, 逐渐增加学习任务的难度, 从而激励智能体不断提升其自主学习的能力. 这种方法有效地结合了引导与自主学习的优势, 旨在实现智能体在复杂环境中的持续自我改进.

本文提出一种简单而有效的先验策略, 希望无人机在前期的探索之中, 能够探索更多有效的路径, 而不是漫无目的的胡乱探索. 二是更多地希望在无人机在前期探索时能够有效避开距离无人机最近的障碍物, 同时向着目标点前进.

先验策略的输入为无人机当前位置$ c\_p $, 目标点位置$ t\_p $, 距离无人机的最近障碍物的位置$ o\_p $, 强化学习模型输出动作$ a $, 动作调整因子$ adj\_f $, 具体步骤如下.

步骤1. 计算目标位置$ t\_p $与当前位置之间$ c\_p $的差异, 形成一个从当前位置指向目标位置的向量, 表示吸引力$ att $, 公式如下:

$ att = t\_p - c\_p $

(18)

步骤2. 计算最近障碍物位置$ o\_p $与当前位置之间$ c\_p $的差异, 形成一个从障碍物指向当前位置的向量, 表示排斥力$ rep $, 公式如下:

$ rep = c\_p - o\_p $

(19)

步骤3. 对吸引力$ att $和排斥力$ rep $的向量按照它们的模(即两点间的距离的倒数)进行权重调整, 距离越短, 影响越大, 公式如下:

$ \left\{ \begin{gathered} att' = 1/\left| {att} \right| \\ rep' = 1/\left| {rep} \right| \\ \end{gathered} \right. $

(20)

步骤4. 合成这两种力的影响, 计算出总的梯度向量$ grad $, 并将其规范化为单位向量, 公式如下:

$ \left\{ \begin{gathered} grad = att'att - rep'rep \\ grad' = grad/\left| {grad} \right| \\ \end{gathered} \right. $

(21)

步骤5. 将原始动作$ a $与梯度向量$ grad' $结合, 通过$ adj\_f $来控制梯度对原始动作$ a $的影响程度, 公式如下:

$ adj\_a = a + adj\_f\times grad' $

(22)

步骤6. 使用$ \tanh $函数处理调整后的动作$ adj\_a $, 确保所有的动作值都在合适的范围内, 公式如下:

$ adj\_a' = \tanh (adj\_a) $

(23)

先验策略对智能体的动作影响随着训练步数的增加而逐渐线性减弱(动作调整因子线性减小), 基本可以分为3个阶段.

训练初期, 智能体的动作主要由先验策略主导. 先验策略通过计算当前状态、目标点位置和障碍物位置, 生成初始动作, 引导智能体快速探索有效路径; 训练前期, 智能体的动作由强化学习算法和先验策略共同影响, 通过动作调整因子调节先验策略和强化学习算法的影响比例; 训练中期, 随着动作调整因子的逐渐减小, 当数值小于界限值ε时, 动作调整因子变为0, 智能体的动作完全由强化学习算法主导.

3 算法设计 3.1 TD3算法

TD3算法^[14]是一种高效的强化学习方法, 主要用于解决连续动作空间中的控制问题. TD3是DDPG算法的改进版本, 它通过几个关键的创新来提高学习的稳定性和性能. TD3的核心创新包括使用双重Q学习、延迟策略更新和目标政策平滑. 首先, 双重Q学习设计了两个独立的价值函数(即两个Critic网络), 并在策略评估时采用这两个价值函数的较小者. 这种机制有助于缓解过估计(overestimation)偏差, 这是在使用单一Critic网络时常见的问题, 公式如下:

$ y = r + \gamma {\min _{i = 1, 2}}{Q_{\theta _i^\prime }}\left( {{s^\prime }, {\mu _{{\phi ^\prime }}}\left( {{s^\prime }} \right)} \right) $

(24)

其中, $ r $是奖励, $ \gamma $是折扣因子, $ {s^\prime } $是下一个状态, $ {\mu _{{\phi ^\prime }}} $是目标策略网络.

其次, TD3中的策略更新(Actor网络更新)是延迟进行的, 即每进行几次价值函数的更新后才执行一次策略更新, 从而减少了评估政策的方差并提高算法的稳定性.

最后, 目标政策平滑是通过向动作添加噪声来实现的, 这有助于平滑策略函数, 并避免在学习过程中对噪声或离群值的过度反应, 公式为:

$ {\mu }_{{\phi }^{\prime }}\left({s}^{\prime }\right)={\mu }_{{\phi }^{\prime }}\left({s}^{\prime }\right)+clip(\epsilon, -c, c) $

(25)

其中, $ \epsilon $是服从某个分布(通常为高斯分布)的噪声, $ clip $函数将噪声限制在$ [ - c, c] $之间.

3.2 面向随机变化场景的CMNTD3算法

现实任务往往具有不完整和嘈杂的状态信息, 在静态障碍物场景中, 无人机的在线避障任务可以有效地模型化为马尔可夫决策过程(MDP), 其中环境状态的全面可观测性允许无人机进行决策时访问所有相关信息. 然而, 在动态障碍物存在的环境中, 情况则更为复杂. 动态障碍物的移动方向和速度等动态特性对无人机的避障策略至关重要, 但这些信息通常无法完全通过传感器直接感知, 导致无人机无法获取环境的全面状态. 在这种情况下, 传统的MDP框架不再适用, 因为它假设环境状态可以完全观测. 相对地, 部分可观测马尔可夫决策过程(POMDP)提供了一种更为适宜的建模方法. 在POMDP模型中, 无人机在每个时间步骤作出决策时, 只能基于有限的、不完全的观测结果. 对于这种情况本文在TD3算法上进行了一些改进, 提出了CMNTD3算法.

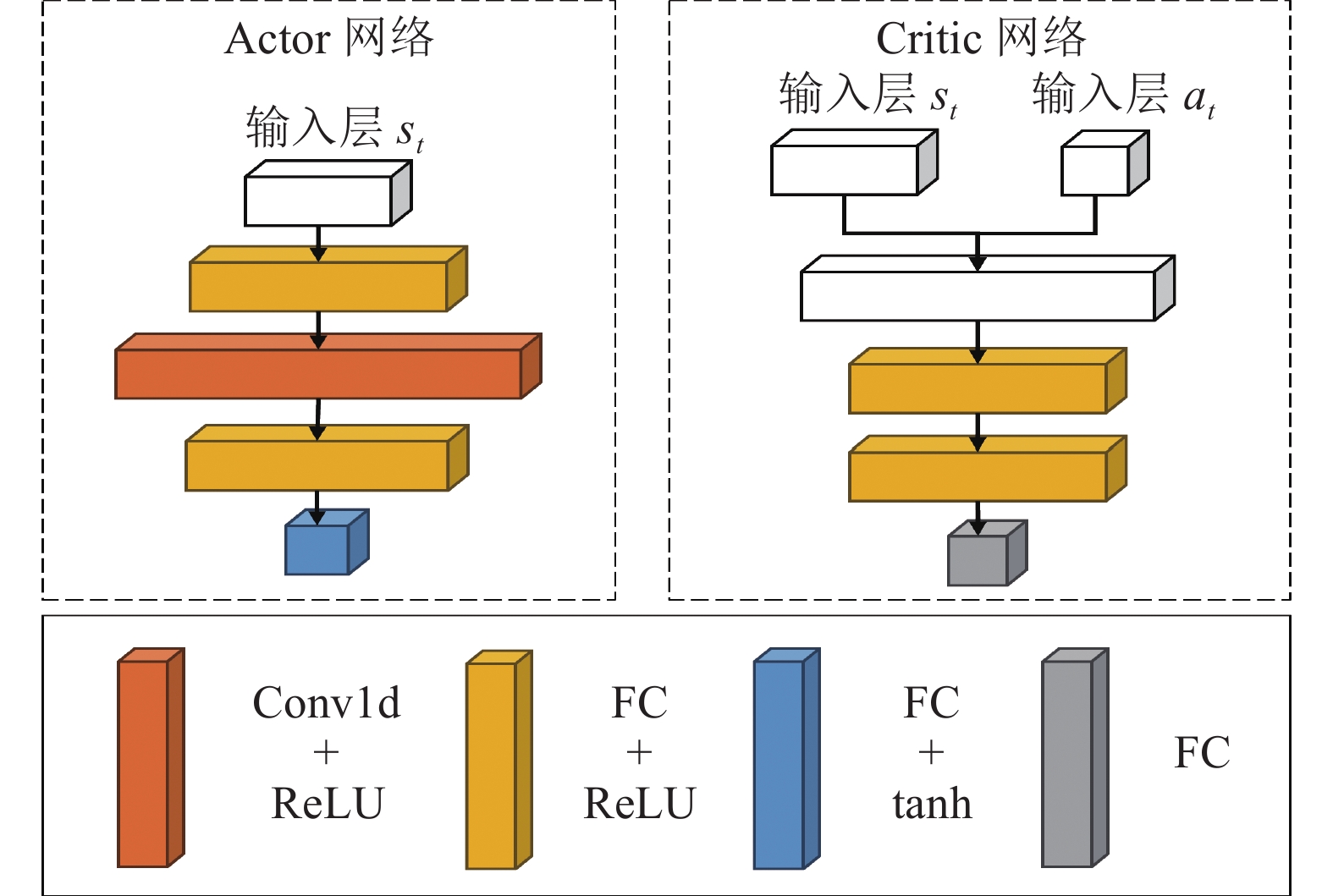
3.2.1 网络结构

CMNTD3网络结构如图6所示.

图6网络结构在原本的TD3之上引入了Conv1d网络, Conv1d的卷积核为$ 1 \times 1 $, 步长也为1. 1×1卷积尽管在空间或时间扩展上没有作用(不捕获更多的上下文信息), 但它可以在不同特征通道间进行有效的信息整合. 1×1卷积层可以将从前一个全连接层学到的各个特征进行重新组合和加权, 实质上这是一个特征变换的过程. 这种操作增加了网络处理数据的非线性能力, 使得网络能够学习到更复杂的函数映射. 这种卷积不会改变数据的空间或时间维度, 仅改变了通道间的特征关系. 这样的设计有助于在不引入额外的空间信息处理的同时, 通过网络深度增强特征的表达能力. 1×1卷积层扮演了一个特征转换器的角色, 它在两个全连接层之间提供了一种高效的方式来重组和加强特征, 同时保持了网络的简洁和计算效率. 这种设计特别适合于那些需要快速且有效特征转换的应用, 如在动态和复杂的环境中进行实时决策. 通过这样的设计, Actor网络能够更好地学习和适应复杂的策略任务, 提高整体的学习性能和稳定性.

同时在TD3的向目标动作添加噪音这一部分内容进行了一些改进, 具体改进如下.

步骤1. 首先生成目标策略动作, 公式如下:

$ {a^\prime } = {\mu _{{\phi ^\prime }}}\left( {{s^\prime }} \right) $

(26)

步骤2. 批量生成噪音, 公式如下:

$ \left\{\begin{array}{l}\epsilon\sim \mathcal{N}\left(0, {\sigma }^{2}\right)且\tilde{\epsilon}=\mathrm{clamp}(\epsilon, -\text{noise\_clip}, \text{noise\_clip})\\ {a}_{\text{noisy}}^{\prime }=\mathrm{clamp}({a}^{\prime }+\tilde{\epsilon}, -\mathrm{max}\_{\mathrm{action}}, {\mathrm{max}}\_{\mathrm{action}})\end{array}\right. $

(27)

其中, $ \epsilon $是符合正态分布的噪声, $ {\text{noise\_clip}} $和$ \max\_{\mathrm{action}} $分别是噪声和动作的裁剪界限.

步骤3. 将状态批量复制并且在动作中添加噪声, 公式如下:

$ \left\{ \begin{gathered} {S^\prime } = {s^\prime } \otimes {{\mathbf{1}}_N} \\ {A^\prime } = \left\{ {a_{{\text{noisy}}1}^\prime , a_{{\text{noisy}}2}^\prime , \cdots , a_{{\text{noisy}}N}^\prime } \right\} \\ \end{gathered} \right. $

(28)

其中, $ {{\mathbf{1}}_N} $表示长度为$ N $的全1向量, 用于扩展状态$ {s^\prime } $至$ N $个样本, $ N $是噪声样本数量.

步骤4. 计算目标Q值并取较小值, 公式如下:

$ \left\{ \begin{gathered} Q_1^\prime , Q_2^\prime = {Q_{\theta _1^\prime }}\left( {{S^\prime }, {A^\prime }} \right), {Q_{\theta _2^\prime }}\left( {{S^\prime }, {A^\prime }} \right) \\ {Q_{{{\min }^\prime }}} = \min \left( {Q_1^\prime , Q_2^\prime } \right) \\ \end{gathered} \right. $

(29)

步骤5. 对较小的目标Q值求平均, 公式如下:

$ \overline {{Q^\prime }} = \frac{1}{N}\sum\limits_{n = 1}^N {Q_{\min , n}^\prime } $

(30)

步骤6. 更新目标Q值, 公式如下:

$ {Q_{{\text{target }}}} = r + \gamma (1 - d)\overline {{Q^\prime }} $

(31)

这样的改进有以下几个作用, 首先是减少方差, 在计算目标Q值时, 使用多个噪声样本的动作来评估状态的值, 并求这些值的均值, 可以有效地减少估计值的方差. 这是因为多样本的平均作用带来了更多信息和更广泛的环境探索, 从而使得Q值估计更为稳定和可靠.

其次是稳定学习过程, 通过减少单次评估的偶然误差影响, 通过批量生成噪音样本后进行均值的操作有助于使学习过程更加平滑. 这种平滑效果可以降低学习过程中由于极端或不常见样本引起的剧烈波动, 从而提高学习算法的整体稳定性.

然后是可以从侧面帮助处理低估问题, 通过批量生成噪音样本后进行均值的操作本身并不直接针对低估问题, 但它可以帮助算法从多个角度观察同一个问题, 从而使得最终的估计更加接近真实值. 通过对多个噪声化动作的评估进行平均, 可以在一定程度上缓解因选择最小值而可能导致的低估问题.

最后是影响过估计问题, 在TD3算法中虽然利用了双重Q学习设计一定程度上缓解了过估问题, 但同样的通过批量生成噪音样本后进行均值的操作可以进一步帮助抑制这种倾向, 因为它考虑了多种可能性而不是仅依赖单一的最优预测.

综上, 批量生成噪音样本之后进行均值操作在减少估计方差、稳定学习过程及缓解低估问题方面发挥着重要作用, 有助于实现更加平衡和稳定的学习动态.

4 仿真实验

整个实验的仿真环境全部基于Python 3.8语言, 深度学习框架采用PyTorch 2.2.1, 计算机配置为Intel i5-10400F CPU, NVIDIA 1080ti GPU, 内存为16 GB.

4.1 仿真环境设计

为了验证PP-CMNTD3算法在随机变化环境中的有效性, 本文设计了三维空间下静态障碍物和动态障碍物同时存在的场景, 采用以下设定, 忽略无人机, 动态障碍物的外形差异, 将其全部等效为质点, 静态障碍物等效为圆柱体, 静态障碍物和动态障碍物的初始位置全部随机生成, 且动态障碍物的移动完全随机. 无人机与静态障碍物以及动态障碍物需要保持安全间隔, 距离低于安全间隔即视为碰撞, 参数见表1.

为了更加符合真实环境和增加环境难度, 引入一个风力扰动模型, 这个模型用于模拟风力对于飞行器, 如无人机, 在三维空间中的动态影响. 风力干扰的模型公式为:

$ \left\{ \begin{gathered} {H_f} = {\left( {\frac{{\textit{z}}}{{200}}} \right)^2} \\ {T_f} = 1.2 \cdot \sin \left( {\frac{t}{{24}} \cdot 2{\text π} } \right) \\ \Delta \vec V = \sigma \cdot N(0, 1, 3) \\ {{\vec V}_w} \leftarrow \left( {{{\vec V}_w} + \Delta \vec V} \right) \cdot {H_f} \cdot {T_f} \\ {{\vec V}_w} \leftarrow \frac{{{{\vec V}_w}}}{{\left\| {{{\vec V}_w}} \right\|}} \cdot {I_{\max }}, \left\| {{{\vec V}_w}} \right\| \gt {I_{\max }} \\ \end{gathered} \right. $

(32)

其中, $ {H_f} $表示高度因子, 这里$ {\textit{z}} $是无人机位置向量中的高度, 假设高度每增加200 m, 风力强度增加的比例按平方增长. $ {T_f} $表示时间因子, 这里$ t $是时间步, 模拟一天中风力的周期变化. $ {{\Delta }}\vec V $表示风力的随机变化量, $ \sigma $表示风力变化的标准差, 用于控制风的随机波动, $ N(0, 1, 3) $表示三维正态分布, 均值为0, 标准差为1. $ {\vec V_w} $表示当前风速向量, $ {I_{\max }} $表示最大风力强度, 定义了风力的最大可能值, 如果$ {\vec V_w} \gt {I_{\max }} $, 则对风速向量进行缩放.

应用流程如下.

步骤1. 首先, 系统在每一个仿真时间步长开始时检查是否存在风力扰动. 此检测基于预定义的概率分布和风力模型的当前状态来判断是否激活风力扰动.

步骤2. 一旦确定风力扰动存在, 根据高度因子和时间因子, 模拟风力随高度变化和日周期变化的自然行为, 并通过加入随机波动来增加模拟的真实性.

步骤3. 更新的风速向量直接加到无人机的控制输入上, 模拟风力对无人机飞行轨迹的即时影响.

步骤4. 扰动持续一段时间后, 系统将风速向量重置为0, 确保在下一次风力扰动激活前无人机操作不受未消除的风力影响.

单局仿真实验的终止有以下5种情况.

情况1. 无人机安全到达终点.

情况2. 无人机与障碍物发生碰撞.

情况3. 无人机超出规划空域边界.

情况4. 无人机电量消耗完毕.

情况5. 无人机规划时间超过最大值.

满足以上任意情况, 单局仿真实验结束.

在实验中, 要求深度强化学习算法在控制无人机进行路径规划任务, 算法需使无人机在面对静态障碍物时能够有效规避并正确规划路径, 同时应对动态障碍物进行实时避障. 鉴于任务执行过程中时间与电量资源有限, 该算法还需在能效和时间效率之间寻求最佳平衡. 此实验的目的在于验证深度强化学习在复杂环境中的实时决策能力及其效率与效能之间的权衡策略.

为确保实验结果的准确性与可比性, 以真实反映算法的性能, 本研究在所有实验中维持主要参数不变. 具体参数详见表2. 此外, 为进一步验证所提算法的有效性, 本文引入了同样基于Actor-Critic架构的软策略梯度算法(soft Actor-Critic, SAC)^[15]与深度确定性策略梯度算法(DDPG)进行仿真对比实验.

4.2 实验结果分析

本节将对CMNTD3、SAC、TD3、DDPG这4种算法进行详细对比, 并选取了规划奖励值、规划成功率、路径规划长度、规划电量消耗这几个指标对算法模型的性能与效果进行评估. 实验结果图的实验数据均做了平滑处理, 训练最大总步数均为2000000.

首先展示初始电量为50 000 mAh的规划效果, 规划结果如图7所示.

在实验结果中, 从图7(a)和图7(b)可以看出, 当初始电量充足时, CMNTD3、SAC和TD3的奖励和成功率都能收敛到较高水平. PP-CMNTD3和SAC的成功率可以达到约90%, 而TD3则可以达到80%以上, DDPG在随机变化较大的环境中表现较差. PP-CMNTD3和TD3比较, PP-CMNTD3的成功率相较于TD3有所提升, 奖励收敛到更高水平, 并且收敛速度也更快.

从图7(c)中可见, PP-CMNTD3在训练稳定性方面表现最佳. 在训练初期, 智能体会经历一段探索过程, 期间碰撞率逐步上升, 但随后碰撞率迅速下降到较低水平. 而TD3和SAC的探索阶段明显更长, 并且TD3在碰撞率下降过程中偶有小幅波动. DDPG则表现为在初期碰撞率下降后, 似乎陷入了长时间的探索状态, 导致碰撞率保持在相对较高的水平, 成功率却显著偏低, 这反映了DDPG在随机变化环境中的适应能力较差.

图7(d)揭示了PP-CMNTD3、SAC和TD3的路径规划长度最终趋于一致, 而DDPG在前期路径长度明显更长, 随后有所下降, 但成功率较低. 这进一步表明DDPG可能处于低效率的探索状态, 印证了其在充满随机变化环境中的劣势.

从图7(f)的结果来看, PP-CMNTD3与SAC的路径规划长度相当, 但PP-CMNTD3的电量消耗更低. 而TD3虽然与PP-CMNTD3的路径规划长度和碰撞率相同, 但成功率更低, 这可能是因为其以较低速度飞行以节省能耗, 然而未能有效权衡能耗与目标接近速度, 导致一些规划任务超过最大步数而失败.

综合来看, PP-CMNTD3可能由于先验策略的使用, 在随机探索阶段提供更高质量的样本, 所以收敛速度更快. 并且多噪音均值的策略使得Critic更准确, 学习效率更高. 此外, 一维卷积的引入增强了Actor网络的表达能力, 使其能够更科学地应对随机变化环境.

基于之前实验结果观察到一个重要信息, 即有效路径规划算法的电量消耗最终收敛在20 000 mAh以上. 因此, 为了验证PP-CMNTD3算法在路径规划中的有效性, 测试其在极限电量条件下的表现, 因此将初始电量设定为20 000 mAh. 这一实验的目的在于评估算法在电量有限情况下的规划能力, 考验算法在电量不足时的情况下如何权衡能耗与到效率之间的平衡.

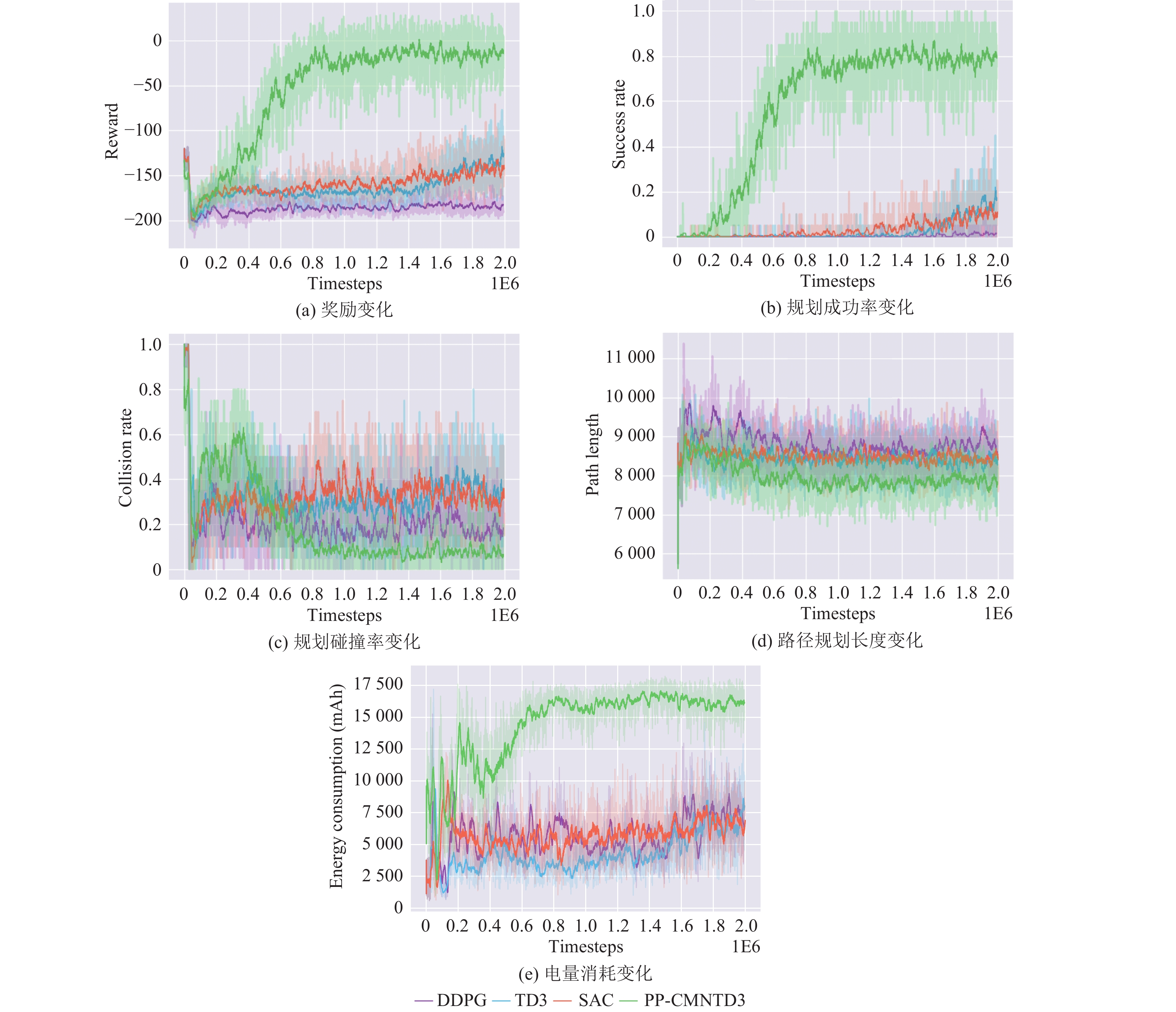
通过这种实验设计, 能够测试算法在极限电量情况下的规划策略, 从而验证其在实际应用场景中的适用性. 图8展示了在初始电量为20 000 mAh时, 各算法的训练结果.

从图8(a)中可以看出, PP-CMNTD3的奖励曲线快速上升, 最后收敛到较高水平, 这与其成功率的趋势相吻合. TD3和SAC的奖励也有所提高, 但明显不及PP-CMNTD3的幅度. DDPG的奖励值始终较低, 说明其在探索过程中未能有效优化策略.

从图8(b)中可以看出, PP-CMNTD3的成功率在整个训练过程中保持领先地位, 并且快速收敛至较高水平, 最终稳定在0.8左右. 相比之下, SAC和TD3的成功率呈现出更长的上升期, 并且在训练结束时成功率显著低于PP-CMNTD3. DDPG的成功率则始终保持在较低水平, 表明其在这种极限电量的环境中难以有效规划路径.

从图8(c)中可以看出, PP-CMNTD3的碰撞率在训练开始阶段稍微上升后, 迅速下降至较低水平, 并保持稳定. TD3和SAC一直在一个较高的水平范围内波动, 甚至高于DDPG. 反映了TD3、SAC和DDPG难以适应这种极限电量的环境.

从图8(d)中可以看出, PP-CMNTD3的路径长度始终保持在相对较短的水平, 与其成功率和电量消耗相符. TD3和SAC的路径长度且一直稳定在同一水平没有波动, 这可能是算法陷入了局部最优. DDPG的路径长度明显较长, 且波动较大, 表明其在路径规划上稳定性和效率都较为低下.

从图8(f)中可以看出, SAC、TD3和DDPG的电量消耗较低, 但它们的规划成功率也相应大幅低于PP-CMNTD3故不具备与PP-CMNTD3算法的可对比性.

总体来看, PP-CMNTD3在初始电量20 000 mAh的条件下仍旧能够表现出较高的成功率、较低的碰撞率和较短的路径长度. 这些结果突出了PP-CMNTD3在极限电量路径规划中的优势, 表明了PP-CMNTD3在极限电量下能够更有效地进行路径规划.

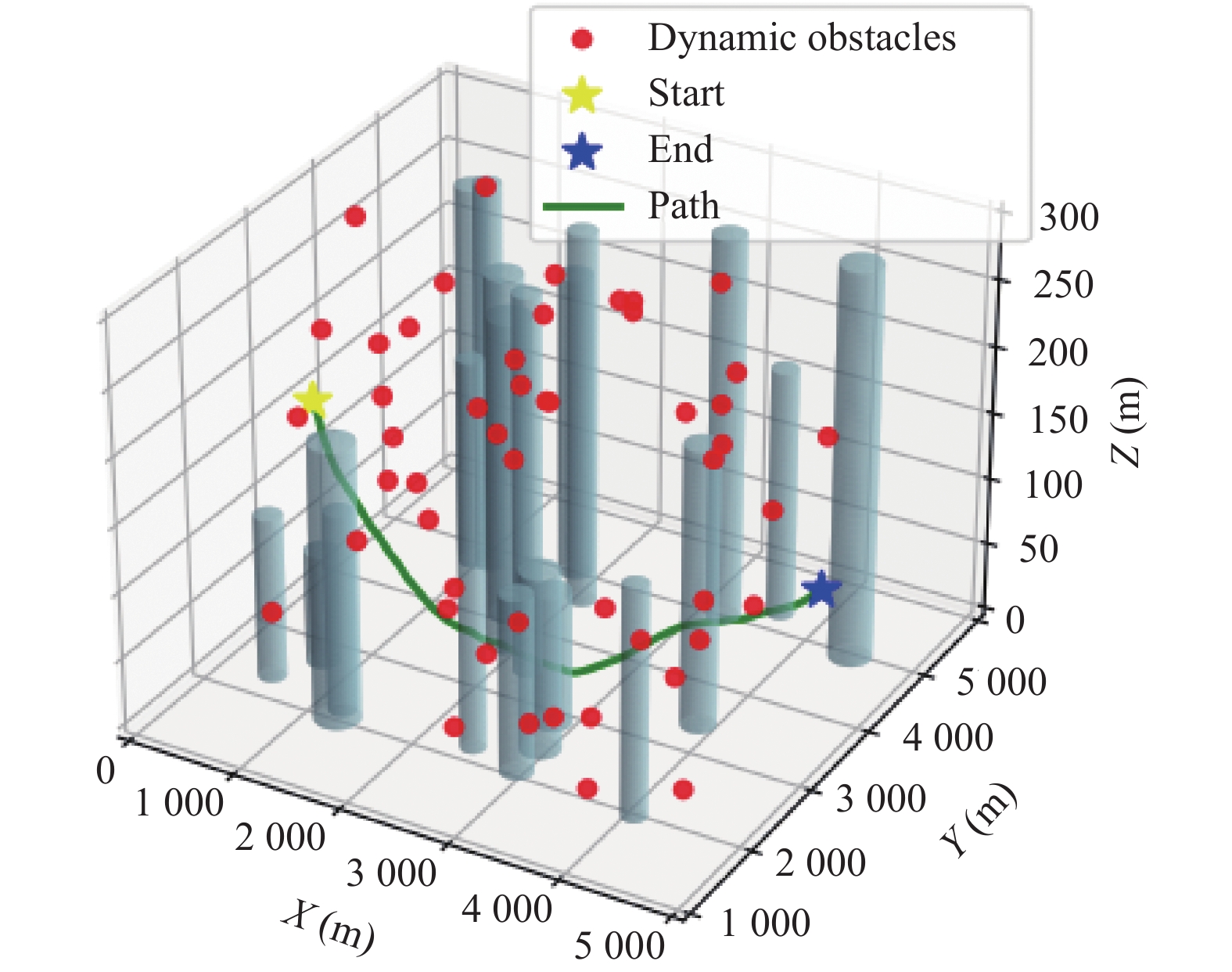
为了测试PP-CMNTD3算法的可行性, 采用固定出发点和目标点对PP-CMNTD3算法进行测试, 可视化结果如图9所示.

在初始电量为50 000 mAh的情况下, PP-CMNTD3算法所获奖励值为35.70; 规划轨迹长度为7 433.84 m; 电量消耗为19 944 mAh. 在初始电量为20 000 mAh的情况下, PP-CMNTD3算法所获奖励值为31.92; 规划轨迹长度为7328.92 m; 电量消耗为18 135 mAh. 从结果可以看出, PP-CMNTD3在不同的初始电量下均到达了终点, 并且获得了较高的奖励值.

为了进一步验证算法的有效性, 对所有训练好的强化学习算法重复分别进行起始电量为50 000 mAh和20 000 mAh的1000次随机起终点的路径规划测试, 选取1000次的平均规划成功率, 平均碰撞率, 规划成功情况下的平均路径规划长度, 以及平均电量消耗对算法进行性能评估, 初始电量为50 000 mAh的测试结果如表3所示. 初始电量为20000 mAh的测试结果如表4所示.

表3和表4的数据表明, PP-CMNTD3算法在路径规划的成功率方面具有显著优势, 碰撞率相对较低, 这表明PP-CMNTD3算法在适应随机环境方面更加出色. 从数据中可以看出, 虽然PP-CMNTD3在初始电量为50 000 mAh的情况下路径规划的平均长度较长, 但其值与其他算法差距不大处于同一水平. 从规划时间步这个数据可以看出PP-CMNTD3算法在初始电量充足时倾向于更快到达目标, 导致较高的电量消耗. 而在初始电量较低的情况下, PP-CMNTD3算法通过降低飞行速度和精细规划来优化路径, 以减少不必要的电量消耗.

在初始电量为20 000 mAh的情况下, PP-CMNTD3的成功率仍然较高, 而其他算法的成功率明显降低. 与PP-CMNTD3相比, 其他算法在这种条件下的有效数据较少, 无法作为有效参考. 这进一步证明了PP-CMNTD3算法的适应性和鲁棒性, 在不同初始电量和环境条件下均能够调整策略, 表现出更好的灵活性和稳定性. PP-CMNTD3在电量充足时注重尽快到达终点, 而在电量较少时则更注重节约电量和精细路径规划, 以确保任务成功.

5 结论

本文旨在研究无人机路径规划问题, 并在包含静态障碍物和动态障碍物以及风力干扰的仿真环境中, 构建了无人机的连续动作空间机动模型. 通过一系列仿真实验, 本文得出以下结论.

1)借鉴人工势场的思想, 本文提出了一种类似人工势场的奖励函数. 这种奖励函数的设计能够帮助强化学习算法克服稀疏奖励的问题使无人机在训练的过程中每一步行动都能够得到有效反馈, 提高了算法的学习效率.

2)为了使强化学习算法在前期探索阶段获得更高质量的样本, 提高训练效率, 并确保最终训练效果不受限制, 本文提出了一种简单而有效的先验策略. 这种策略有助于强化学习算法在前期获得更高的样本质量, 提升前期训练效率, 从而更快收敛.

3)本文提出了基于TD3改进的PP-CMNTD3算法. 在无人机路径规划任务中, PP-CMNTD3表现出更高的成功率、更低的碰撞率以及更强的适应能力. 这种鲁棒性使得PP-CMNTD3算法在电量充足和略有不足的情况下都能取得卓越的效果, 并且展现出优于基础TD3的性能.

综上所述, 本文提出的方法有效提高了无人机在面对随机变化场景时的路径规划能力, 具有一定的工程应用参考价值. 然而, 目前的算法仅解决了单个无人机的路径规划问题, 并未考虑多无人机协同的问题. 此外, 仿真环境的建模中使用了一定的理想化假设. 未来的研究方向可以考虑使用更真实的仿真工具(例如AirSim)进行无人机仿真模拟, 并针对多无人机协同路径规划问题展开进一步的研究.