多旋翼无人机以其轻便、体积小、机动性强、起降方便以及能够实现空中悬停和低空稳定飞行的优点, 已经被广泛应用于航拍摄影、物流、资源勘探等领域[1,2]. 其中, 四旋翼无人机作为一种最常见的多旋翼无人机, 由于其系统的非线性和强耦合特性, 设计一种可靠、稳定而高效的控制算法具有一定的挑战性.
随着无人机应用需求的不断扩展, 保证无人机能够完成预期飞行任务的重要性不言而喻. 为此, 越来越多的研究者正致力于开发鲁棒的无人机控制器. 目前, 已经有多种高效且可靠的控制算法被提出, 包括模型预测控制(MPC)、自适应控制、比例-积分-微分(PID)控制和反步法等. 其中, 模型预测控制尤其适用于处理多变量、多约束的非线性系统控制问题, 将非线性系统引入模型预测控制就得到了非线性模型预测控制(NMPC). 并且相比于其他算法, MPC在控制中能直接考虑输入、输出和状态的约束, 并能通过使用预测模型及优化算法来预测和优化未来一段时间内的控制策略, 从而实现更精确和稳定的控制. 此外, 一些高性能计算包的出现让MPC的计算速度得到了极大的提升, 保证了其实时性. 传统控制算法已然较好地完成了无人机的控制任务, 但是在一些强干扰的场景中, 传统控制算法无法做出及时响应, 这就导致在某些情况下, 传统控制算法可能会极大地偏离任务轨迹导致任务出现差错.
强化学习作为机器学习中的核心领域之一, 已经被广泛应用在各种领域当中. 在无人机控制领域中, 其也被广泛作为无人机控制方法或抗干扰算法的一部分来使用, 文献[3]设计了一种基于风源视觉特征的迁移强化学习四旋翼无人机前馈补偿器来抵抗风扰, 文献[4]设计了一种基于深度强化学习的前馈补偿器来抵抗四旋翼无人机近距离交叉飞行时所产生的剪切气流造成的突然干扰, 文献[5]设计了一种基于强化学习且支持高动态控制的四旋翼无人机控制方法, 该方法对扰动的抵抗效果较传统控制算法更好, 文献[6]设计了一种带干扰探测和补偿的强化学习控制器. 上述文献中直接利用强化学习算法作为控制方案的不确定性较大, 在未知任务下的表现可能会出现较大偏差, 相比之下, 一些传统控制算法虽然抗干扰能力可能不及强化学习算法, 但在未知任务下的稳定性要优于强化学习算法. 另外, 上述文献中提出的强化学习抗干扰补偿器均存在一定的场景限制, 不能广泛地应用在不同的任务场景下.
鉴于此, 本文采用非线性模型预测控制方法作为基础控制器, 以保证每个场景任务下的控制稳定性, 同时引入一个深度强化学习干扰补偿器来抵消不同场景下的干扰, 从而保证在干扰场景下的稳定运行. 同时, 本文将多头注意力机制(MA)以及长短期记忆网络(long short-term memory, LSTM)引入TD3算法的Actor网络当中, 提出了一种基于MALSTM的改进TD3算法作为干扰补偿器, 提高了模型处理空间以及时间信息的能力. 此外, 本文还提出了一种带边界的可控尺度连续型对数奖励函数, 以提高模型的收敛速度和训练稳定性, 并利用带随机干扰的随机空间训练策略来保证模型的泛化性. 实验结果表明, 本文提出的改进模型能够有效地对不同场景下的随机干扰进行抵抗, 并且对传统控制算法的实时性和稳定性影响较小.
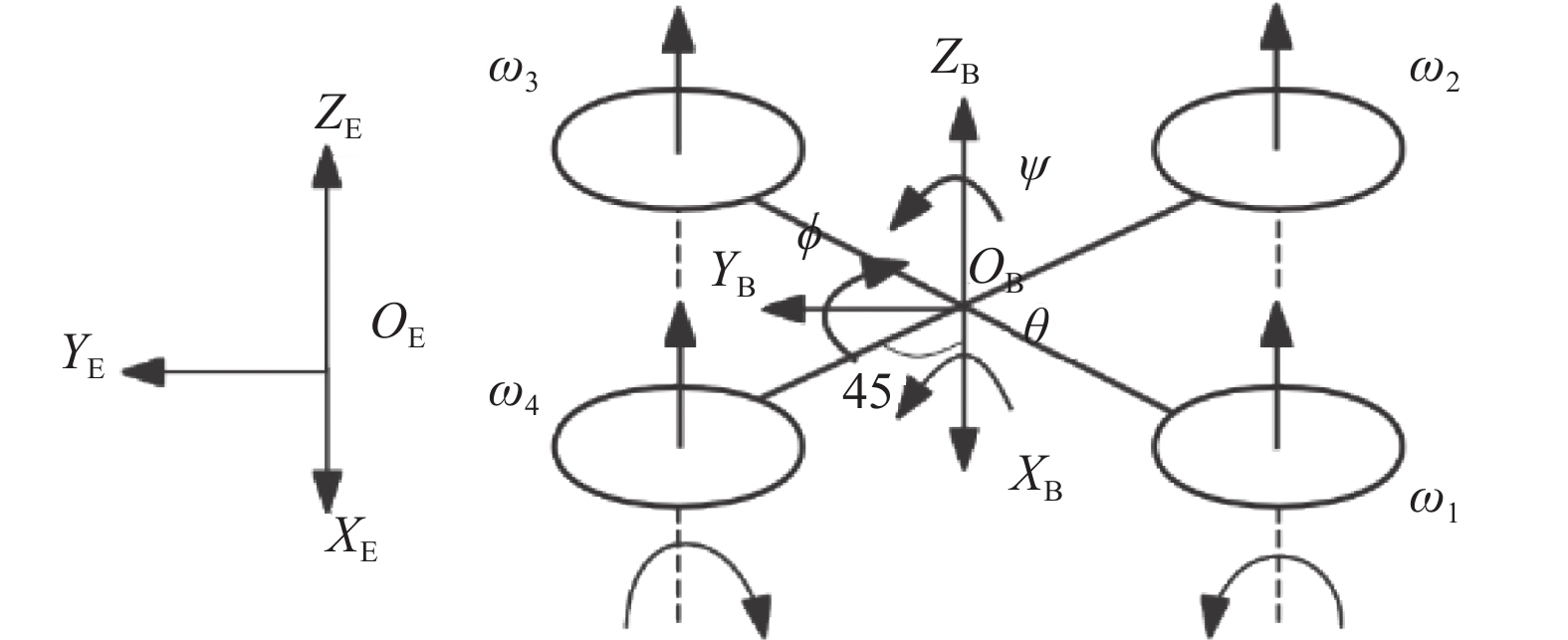
1 四旋翼无人机建模四旋翼无人机是一个欠驱动、非线性、高耦合的系统, 其包含X、Y、Z轴平移运动以及滚转(roll)、俯仰(pitch)和偏航(yaw)这3个旋转运动, 共6个自由度[7], 但只能依靠其自身的4个螺旋桨转动产生的推力来进行位置和姿态控制, 建立四旋翼无人机动力学模型之前, 需要建立描述模型所需的无人机结构和坐标系, 具体结构如图1所示.
|
图 1 四旋翼无人机模型 |
图1中
| q=[q0q1q2q3]T | (1) |
四旋翼无人机4个螺旋桨推力差异会产生扭矩. 当需要改变姿态时, 通过改变不同螺旋桨的转速, 使各旋翼产生不同的推力, 从而产生扭矩, 改变无人机的姿态. 这里绕机体坐标系的扭矩
| τx=lcos(π4)⋅(u2+u3−u1−u4)Fm | (2) |
| τy=lcos(π4)⋅(u3+u4−u1−u2)Fm | (3) |
| τz=c(u2+u4−u1−u3)Fm | (4) |
其中,
利用Newton-Euler法建立四旋翼无人机的动力学方程时, 在表示速度动力学方程时会用到从机体坐标系到惯性坐标系下的正交旋转矩阵
| REB=[1−2q22−2q232q1q2−2q0q32q1q3+2q0q22q1q2+2q0q31−2q21−2q232q2q3−2q0q12q1q3−2q0q22q2q3+2q0q11−2q21−2q22] | (5) |
| Rω=[0−ωx−ωy−ωzωx0ωz−ωyωy−ωz0ωxωzωy−ωx0] | (6) |
其中,
| {˙p=v˙q=12Rωq˙v=REBa−g˙ωx=1Jx(τx+(Jy−Jz)ωyωz)˙ωy=1Jy(τy+(Jz−Jx)ωzωx)˙ωz=1Jz(τz+(Jx−Jy)ωxωy) | (7) |
其中,
| a=[001m∑Fi]T | (8) |
| g=[00g]T | (9) |
NMPC是一种先进的反馈控制策略, 它基于动态优化反馈控制策略. 该策略的整体性能主要取决于系统模型的准确性. NMPC通过优化模型在有限时间域内的行为来计算当前最佳控制输入. 最优系统行为的预测来自开环在线优化, NMPC将其形式化为受约束的有限范围内最优控制问题(OCP) [10].
2.1 离散时间非线性系统在非线性模型预测控制中需要建立离散时间非线性系统模型, 一般的非线性状态空间方程可以表示为:
| {˙X=f(X(t),U(t))Y(t)=X(t) | (10) |
其中,
| X=[xyzq0q1q2q3vxvyvzωxωyωz]T | (11) |
为了方便将上述非线性状态空间方程应用到计算机当中进行计算, 需要将上述非线性状态空间方程转化为离散时间非线性系统模型, 设定采样时间
| {Xk+1=Xk+Δt⋅f(Xk,Uk)Yk=Xk | (12) |
以位置状态空间方程为例, 在采样时间
| {x(t+Δt)=x(t)+Δt⋅vx(t)y(t+Δt)=y(t)+Δt⋅vy(t)z(t+Δt)=z(t)+Δt⋅vz(t)vx(t+Δt)=vx(t)+Δt⋅˙v(t)vy(t+Δt)=vy(t)+Δt⋅˙v(t)vz(t+Δt)=vz(t)+Δt⋅˙v(t) | (13) |
作为基础控制方法, 非线性模型预测控制仅以期望轨迹跟踪为目的而不涉及其他任务, 为此, 简化NMPC的控制约束, 参考MPC标准形式, 以不带终端误差约束的系统状态约束以及控制输入界限约束为基础, 构建第
| {min | (14) |
其中,
为了满足实时性要求, 针对上述最优控制问题, 利用CasADi[11]和ACADOS[12]进行求解, 其主要思路是首先利用多重打靶法将最优控制问题转化为非线性二次规划问题, 再利用实时迭代(real time iteration, RTI)策略下的序列二次规划(sequential quadratic programming, SQP)进行求解[13]. 上述最优控制问题求解后得到控制量序列, 取第1个序列作为四旋翼无人机的控制量.
在ACADOS框架下, 为了高效求解MPC问题中的二次规划问题, 本文选择使用其提供的内点法求解器HPIPM[14]进行求解, HPIPM对于实时性要求较高的场景非常适用, 并且在应用HPIPM时采用全局缩减策略, 使HPIPM处理大规模问题时能够显著减少问题的维度, 从而提高求解速度; Hessian矩阵的近似方法采用Gauss-Newton近似, 其简化了Hessian矩阵的计算, 减少了计算负担的同时也保持了优化问题的求解精度; 此外, 采用四阶龙格库塔方法对系统方程进行数值积分, 来模拟从当前时刻到未来某一时刻系统的状态变化.
3 基于改进TD3的深度强化学习补偿器在非线性模型预测控制中, 当遇到强干扰时NMPC控制器无法及时作出反应, 为了对抗干扰的同时不影响NMPC控制器的实时性, 一种基于改进TD3的端到端控制补偿器被提出. 该补偿器基于当前场景的领航机状态以及被控机状态得到四旋翼无人机的基础控制量补偿
一个标准强化学习问题可以被抽象为一个马尔可夫决策过程(Markov decision process, MDP). 马尔可夫决策过程由元组
| {G_t} = {R_t} + \gamma {R_{t + 1}} + {\gamma ^2}{R_{t + 2}} + \cdots = \sum\limits_{k = 0} {{\gamma ^k}{R_{t + k}}} | (15) |
智能体的策略(policy)通常是一个函数
| \pi \left( {a\mid s} \right) = P\left( {{A_t} = a\mid{S_t} = s} \right) | (16) |
在强化学习中, 定义状态价值函数(state-value function)和动作价值函数(action-value function)来评估当前所处状态
| {V_\pi }\left( s \right) = {\mathbb{E}_\pi }\left[ {{G_t}\mid{S_t} = s} \right] | (17) |
| {Q^\pi }\left( {s, a} \right) = {\mathbb{E}_\pi }\left[ {{G_t}\mid{S_t} = s, {A_t} = a} \right] | (18) |
强化学习的目的是找到期望累计奖励最大时的最优控制策略[15], 为了实现该目的, 在一些强化学习方法, 例如在采用Actor-Critic (AC)架构的算法中, 利用神经网络拟合一个Critic网络作为
深度确定性策略梯度(deep deterministic policy gradient, DDPG) [16]算法是DeepMind于2016年提出的一种深度强化学习算法, 该算法结合了深度神经网络和确定性策略梯度方法, 可以被用于解决高维、连续动作空间下的控制问题, 但该算法学习过程中稳定性不佳且存在高估的问题. 在此基础上Fujimoto等人于2018年提出了双延迟深度确定性策略梯度算法(twin delay DDPG, TD3) [17], 旨在改进DDPG算法中存在的高估等问题.
TD3算法是一种Actor-Critic (AC)架构的强化学习算法, 其中包含了一个目标Actor、两个目标Critic网络以及一个Actor、两个Critic主网络, 引入目标网络是为了减少训练中的不稳定性, 相较于DDPG额外引入了一个Critic网络以解决高估的问题. TD3首先从经验回放池中取出批次样本
| {\tilde a_{i + 1}} = {\pi _{\phi '}}\left( {{s_{i + 1}}} \right) | (19) |
| {\tilde a_{i + 1}} = {\tilde a_{i + 1}} + \varepsilon ,\;\; \varepsilon \sim clip\left( {{N}(0, \sigma ), - c, c} \right) | (20) |
TD3在基于时序差分法(temporal difference, TD)计算目标
| y = {r_i} + \gamma {\mathop{\mathrm{min}} \limits_{j = 1, 2}}{Q_{\theta' _j}}\left( {{s_{i + 1}}, {{\tilde a}_{i + 1}}} \right) | (21) |
| {\theta _j} \leftarrow {\mathop{\arg\min}\limits_{{\theta _j}}}{N^{ - 1}}\sum {{{\left( {y - {Q_{{\theta _j}}}\left( {{s_i}, {a_i}} \right)} \right)}^2}} | (22) |
为了进一步减少
| {\nabla _\phi }J(\phi ) = \frac{1}{N}\sum {{\nabla _a}} {Q_{{\theta _1}}}({s_i}, a)\left| {a = {\pi _\phi }({s_i})} \right.{\nabla _\phi }{\pi _\phi }({s_i}) | (23) |
Critic网络基于一个目标平滑系数
| \left\{ \begin{gathered} \theta' _j \leftarrow \tau {\theta _j} + \left( {1 - \tau } \right)\theta' _j \\ \phi' _j \leftarrow \tau {\phi _j} + \left( {1 - \tau } \right)\phi' _j \\ \end{gathered} \right. | (24) |
该问题下的状态
| S = \left( {{S_l}}\;\;\;\;\;{{S_c}} \right) \in {{{R}}^{24}} | (25) |
另外, 在整个强化学习框架中, 四旋翼无人机的姿态表示被转换为基于欧拉角的表示, 状态
| S = \left\{ {{p_l}, {\Theta _l}, {v_l}, {\Omega _l}, {p_c}, {\Theta _c}, {v_c}, {\Omega _c}} \right\} | (26) |
动作空间为螺旋桨电机激活程度的补偿量, 表示为:
| a = \left[ {\Delta {u_1}, \Delta {u_2}, \Delta {u_3}, \Delta {u_4}} \right] | (27) |
其中,
| {u_i} = {u_i} + \Delta {u_i} | (28) |
奖励设计在强化学习任务中起到至关重要的作用, 奖励设计的好坏直接决定了强化学习的训练结果. 为了提高模型的稳定性和收敛速度, 提出一种带边界的可控尺度连续型对数奖励函数, 该奖励函数可以设置每个物理量的奖励边界, 奖励边界可以将每个物理量的误差映射到统一的尺度上. 每项奖励
| {r_i} = \left\{ \begin{gathered} - {\lambda _i}(\ln {d_i} - \ln {b_i}), \;\;\;\;\;\;{d_i} \gt 0 \\ - {\lambda _i}\left( {\ln 0.01 - \ln {b_i}} \right), \;{d_i} = 0 \\ \end{gathered} \right. | (29) |
其中,
| reward = - \sum\limits_{i = 1}^4 {{\lambda _i}\left( {\ln {d_i} - \ln {b_i}} \right)} | (30) |
为了使模型能够得到更多的探索并增加其泛化能力, 训练时, 每局均采用带随机干扰的随机空间场景进行训练, 如图2所示. 另外, 每局领航机状态均使用前文所述的 NMPC控制器在无干扰情况下进行控制后得到. 训练中, 完全随机干扰以5%的概率在训练过程中的每一时间刻随机出现一个固定时间, 固定时间长度为总时长的1/16, 处于干扰阶段时不会触发下一次干扰, 且每一段干扰大小固定但不同, 随机干扰的生成方法表示为
另外, 每局采用随机参考轨迹策略时, 起始点在一定范围内使用均匀分布抽样得到, 且每一时刻轨迹点按照某种方式随机生成, 每一时间刻的参考轨迹点生成方法表示为:
| \Delta s = \frac{{{l_s}}}{M} | (31) |
| \left\{ \begin{gathered} {x_{i + 1}} = {x_i} + \Delta s \cdot \sin ({\beta _i}) \cdot \cos (\beta' _i),\; i \gt 0 \\ {y_{i + 1}} = {y_i} + \Delta s \cdot \sin ({\beta _i}) \cdot \sin (\beta' _i),\;\; i \gt 0 \\ {{\textit{z}}_{i + 1}} = {{\textit{z}}_i} + \Delta s \cdot \cos ({\beta _i}),\qquad\quad \;\;i \gt 0 \\ {x_0} \sim U({x_{\min }}, {x_{\max }}) \\ {y_0} \sim U({y_{\min }}, {y_{\max }}) \\ {{\textit{z}}_0} \sim U({{\textit{z}}_{\min }}, {{\textit{z}}_{\max }}) \\ \end{gathered} \right. | (32) |
其中,
| \left\{ \begin{gathered} \beta' _i\sim {{U}}( - n, n), \;i \ne 0 \\ {\beta _i}\sim {{U}}( - n, n), \;i \ne 0 \\ \beta' _0\sim {{U}}(0, 2\pi ), \;i = 0 \\ {\beta _0}\sim {{U}}(0, \pi ), \;\;\;i = 0 \\ \end{gathered} \right. | (33) |
|
图 2 训练任务场景示例 |
3.6 MALSTM-TD3补偿器
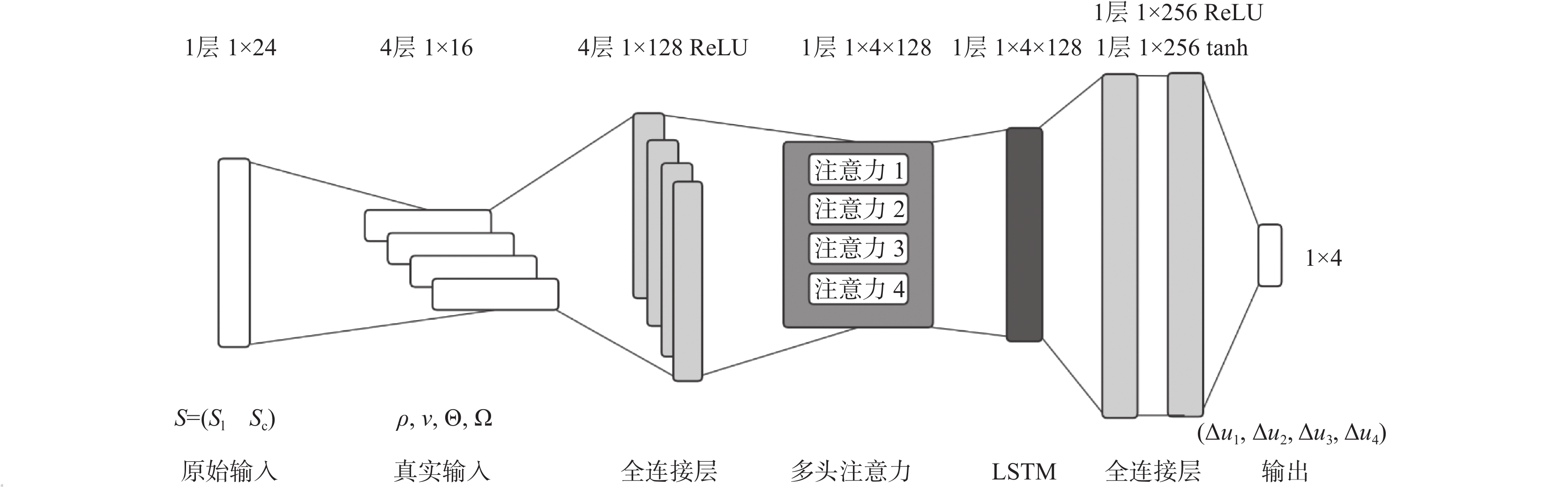
TD3的Actor网络输入中包含领航机和被控机的位置、欧拉角、速度以及角速度, 为了使模型能够更加充分地学习不同物理量之间以及领航机与被控机之间的关系, 引入多头注意力机制(multi-head attention, MA)进行处理. 多头注意力机制能够处理多个序列, 从而发掘不同序列之间的相互关系. 此外, 它还能关注每个序列中不同位置的信息, 进而揭示序列内部的结构性关联. 多头注意力机制通过将注意力分解为多个“头”, 使得每个头可以独立学习序列的不同特征表达, 这种分解方式允许模型在处理信息时获得更为丰富的上下文信息, 从而改善对信息的整体理解. 另外, 在无人机控制过程中, 存在显著的时间关联性, 为了有效捕获这种时间依赖性, 引入长短期记忆网络(long short-term memory, LSTM), LSTM是一种专门用于处理和记忆时间序列数据中的长期依赖关系的循环神经网络.
对于每一时间刻下的状态
|
图 3 MALSTM-Actor网络架构 |
3.7 整体架构
NMPC-MALSTM-TD3控制器的整体架构如图4所示, 图中白色虚线框中的架构为引入MALSTM后的TD3算法单步训练过程, 详细原理见第3.2节所示, 其中策略函数与目标策略函数均被替换为MALSTM-Actor网络架构, 领航机
本文利用不同的强化学习方法在相同场景下进行了训练, 包括TD3、DDPG、SAC、PPO, 以及本文提出的MALSTM-TD3, 对比了它们的效果和差异, 并在不同场景下测试了基于TD3、DDPG、SAC、MALSTM-TD3的模型稳定性以及抗干扰效果, 同时测试了引入MALSTM-TD3给系统带来的实时性影响. 本文所采用的仿真平台基于Windows WSL2创建的Ubuntu 22.04.4LTS系统下的3.8版本Python环境, CUDA版本为12.4, PyTorch版本为12.1, ACADOS计算平台版本为0.3.0, CasADi版本3.6.4; 硬件运行环境采用AMD平台R7-5800H处理器, 32 GB内存, NVIDIA RTX3070 Laptop GPU. 仿真实验中NMPC的采样时间为0.05 s, 仿真时间为10 s, 预测时域长度为10, 系统状态误差权重矩阵
| \begin{split} {Q_t} = &{\text{diag}}\left( {\left[ {\begin{array}{*{20}{c}} {10}&{10}&{10}&{0.1}&{0.1}&{0.1}&{0.1} \end{array}} \right.} \right. \\ & \left. {\left. {\begin{array}{*{20}{c}} {0.05}&{0.05}&{0.05}&{0.05}&{0.05}&{0.05} \end{array}} \right]} \right) \end{split} | (34) |
| {Q_r} = {\text{diag}}\left( {\left[\begin{array}{*{20}{c}} {0.1}&{0.1}&{0.1}&{0.1} \end{array}\right]} \right) | (35) |
另外, 仿真所使用的强化学习模型参数基本相同, 除MALSTM-TD3以外的模型架构均相同且处于训练任务下的较优水平, 经过实验测试采用4层或以上的全连接层效果较差, 对于该问题采用3层256维全连接层网络架构为较优架构. 仿真实验中四旋翼无人机参数、MALSTM-TD3算法训练参数以及训练场景相关参数分别如表1、表2、表3所示.

|
图 4 整体架构图 |
| 表 1 四旋翼无人机参数 |
| 表 2 MALSTM-TD3算法训练参数 |
| 表 3 训练场景参数 |
4.2 仿真实验结果与分析
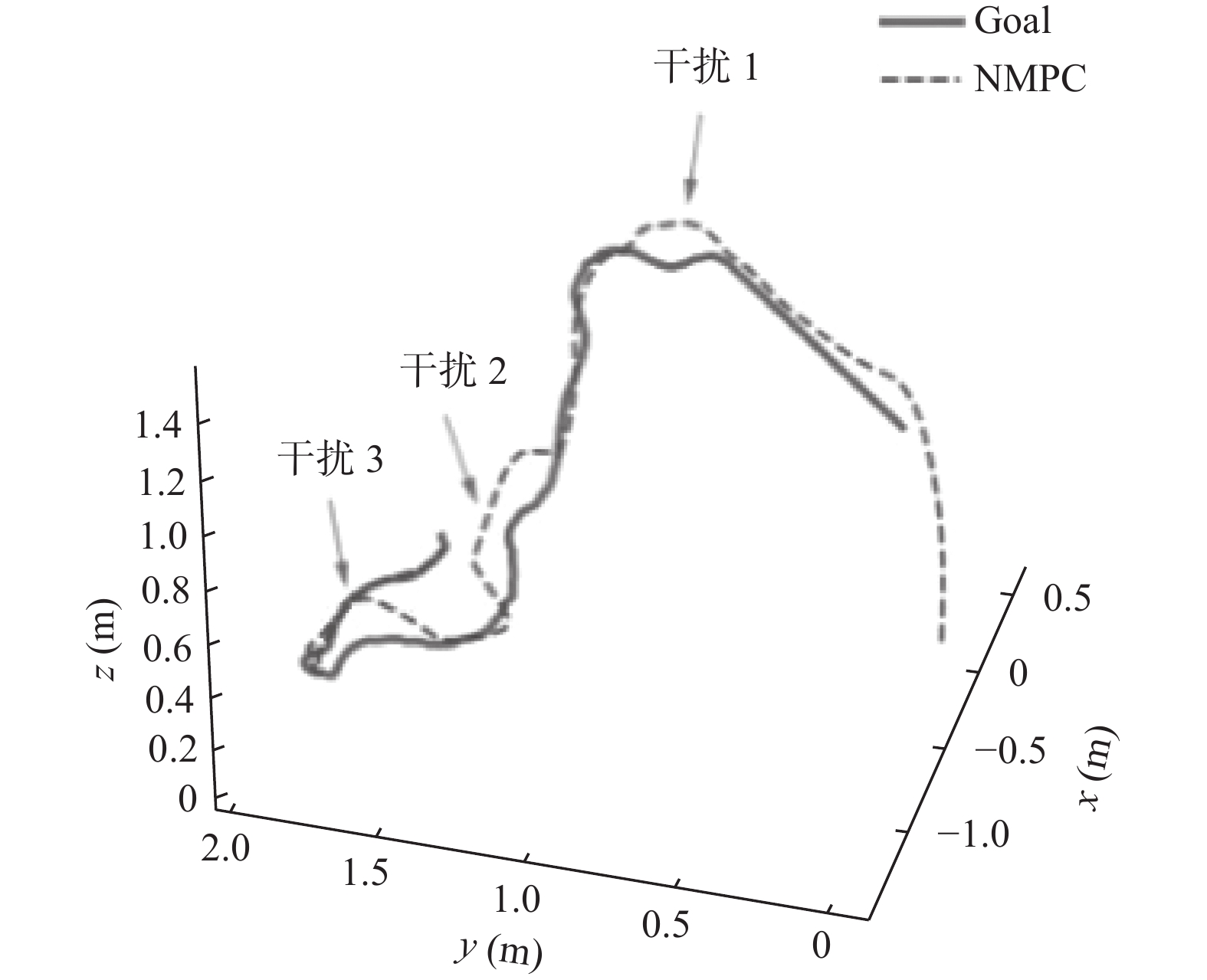
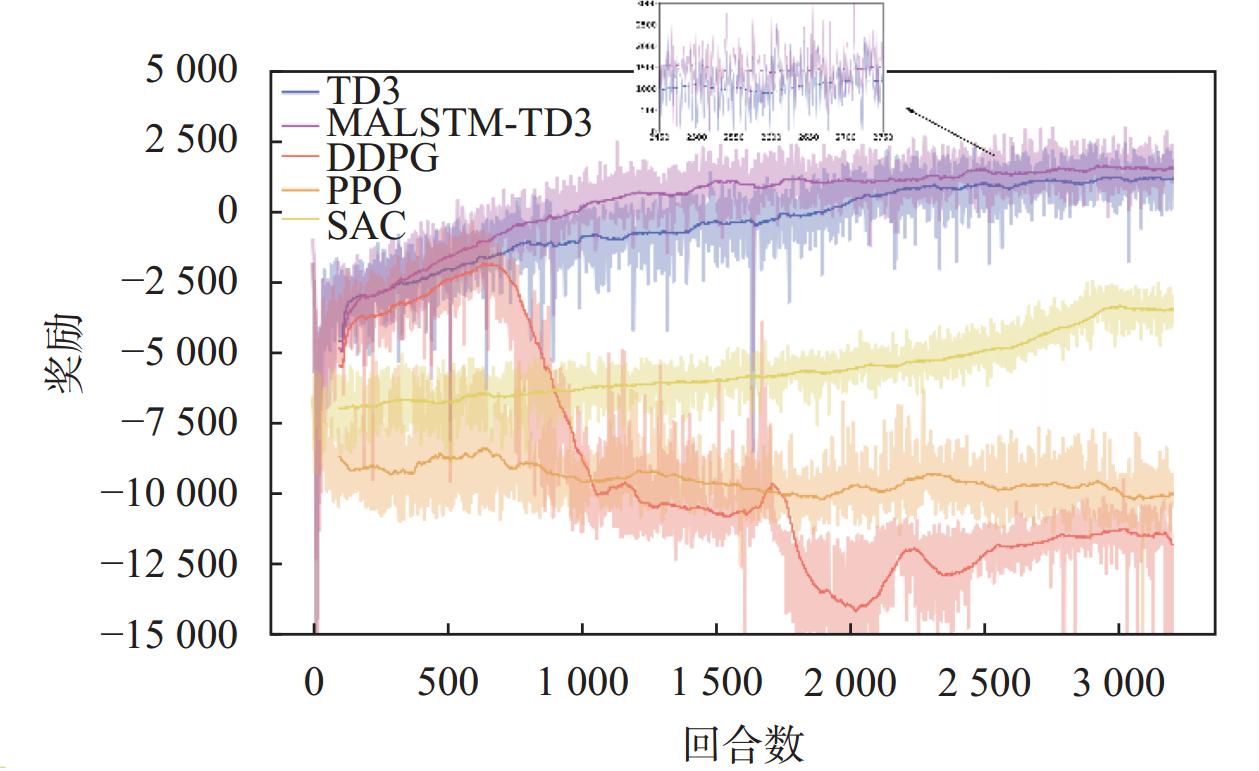
本文以不同强化学习方法作为补偿器进行训练, 并对比了它们的奖励趋势初步分析不同模型的优劣, 训练过程中单局奖励为该回合每一采样时间下的奖励总和, 训练得到的奖励如图5所示, 图中阴影部分代表真实奖励变化趋势, 实线代表真实奖励进行移动平均后的平均奖励变化趋势. 相比于TD3和MALSTM-TD3, DDPG、SAC和PPO算法在该场景下的表现较差, DDPG在600局左右奖励出现了大幅下降, SAC整体训练稳定在
由于PPO算法的效果不佳, 故仅利用上述训练得到的DDPG、TD3、SAC以及MALSTM-TD3模型作为补偿器分别在一个六边形场景下进行测试, 且DDPG采用训练600局时的参数. 在仿真中, 于第7 s左右加入一个
|
图 5 每局奖励变化 |
|
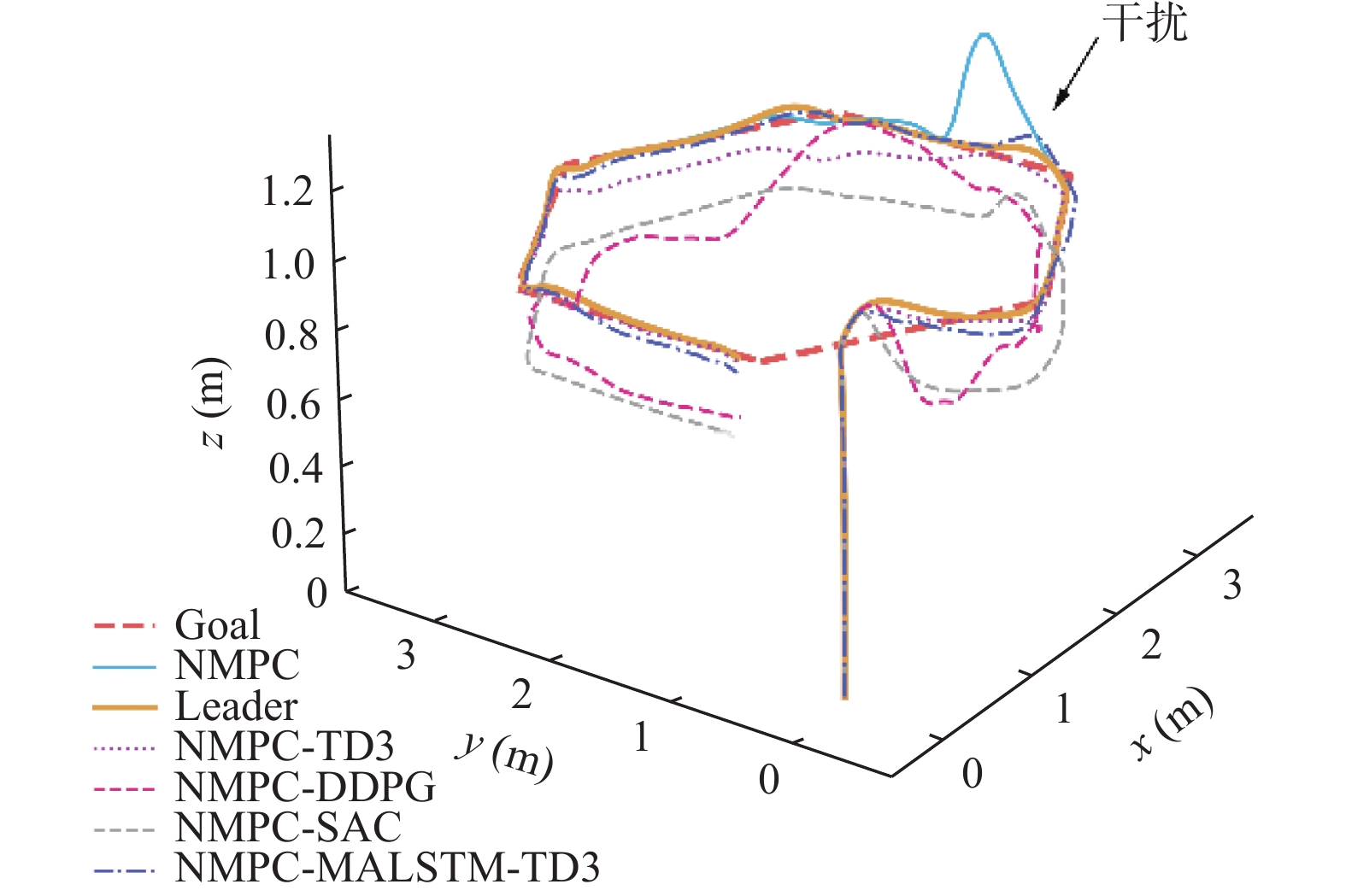
图 6 六边形轨迹任务表现 |
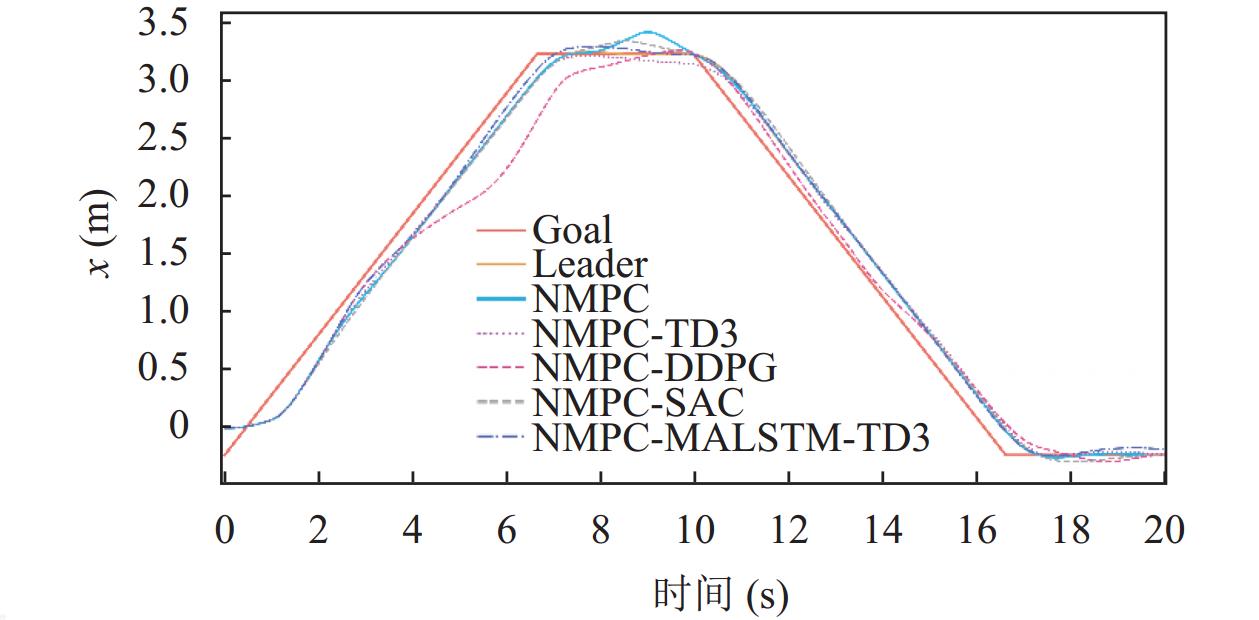
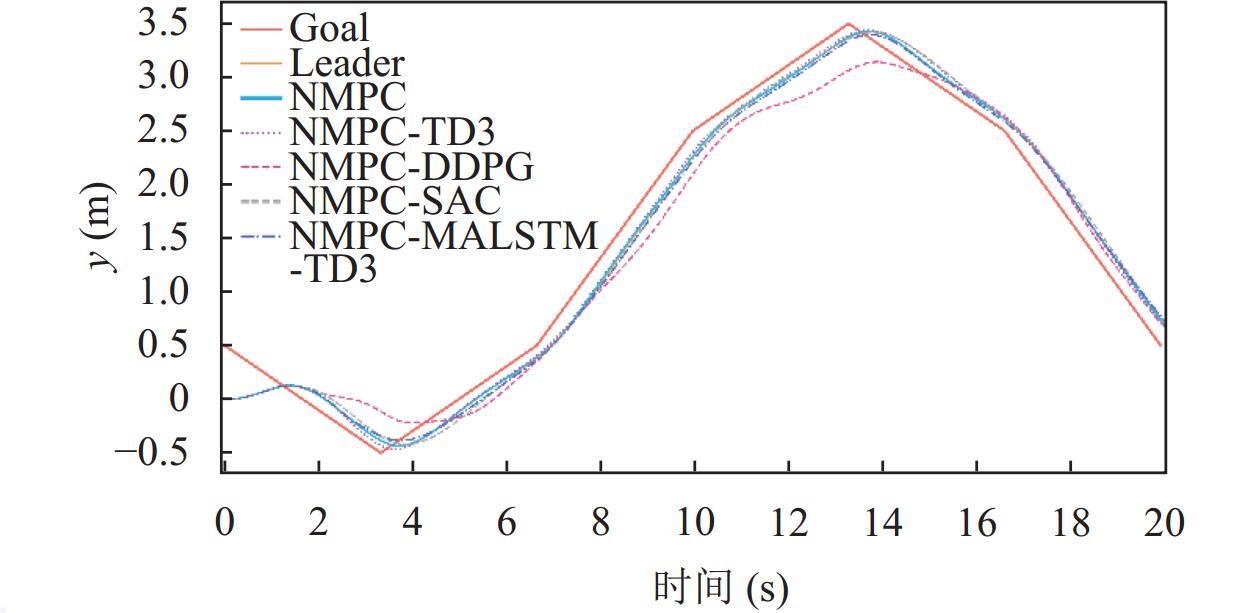
基于图6分析, 单NMPC控制器下的无人机状态在干扰处均处产生了较大的偏差. 在基于不同补偿器的控制算法下的位置控制表现中, 不同算法下的四旋翼无人机的
|
图 7 |
|
图 8 |

|
图 9 |
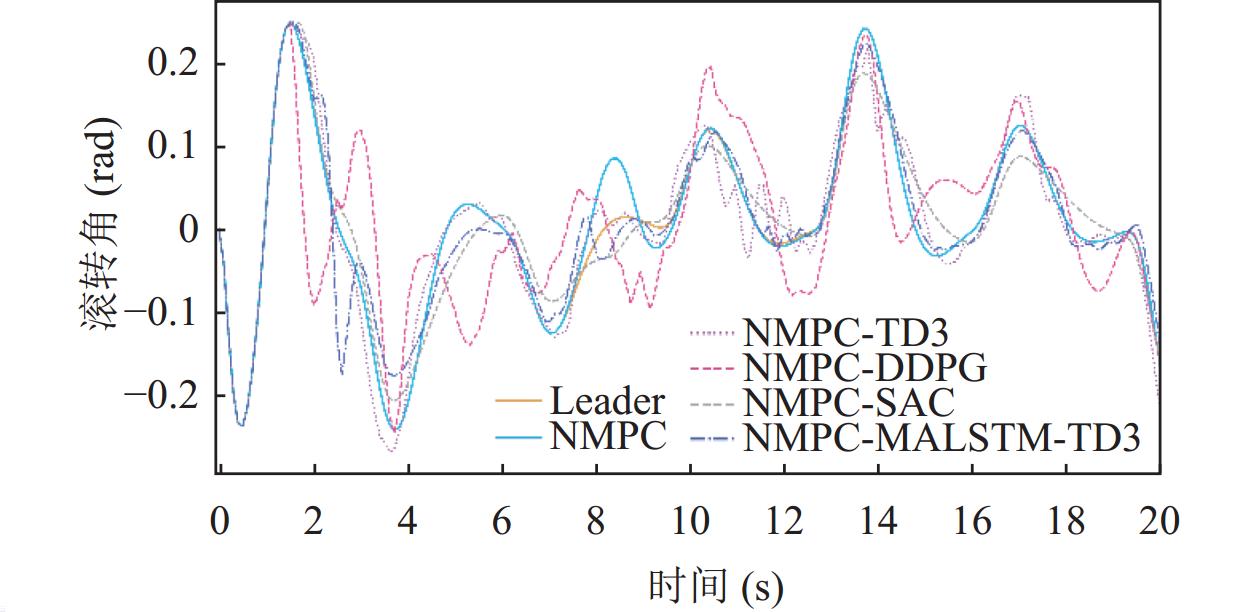
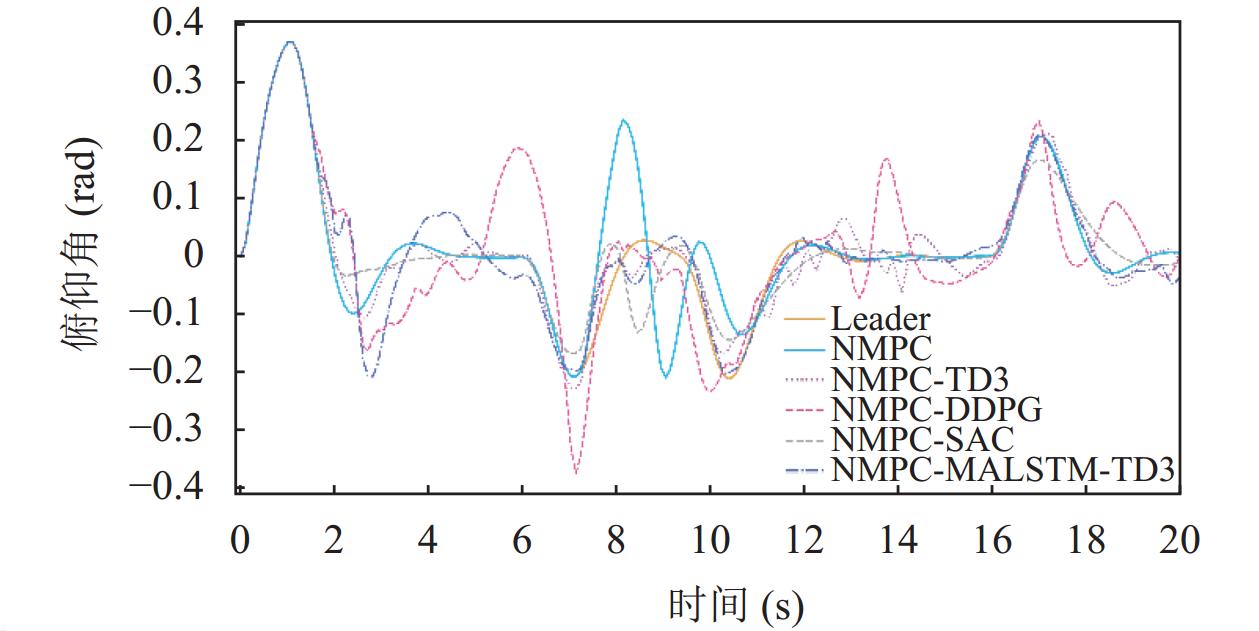
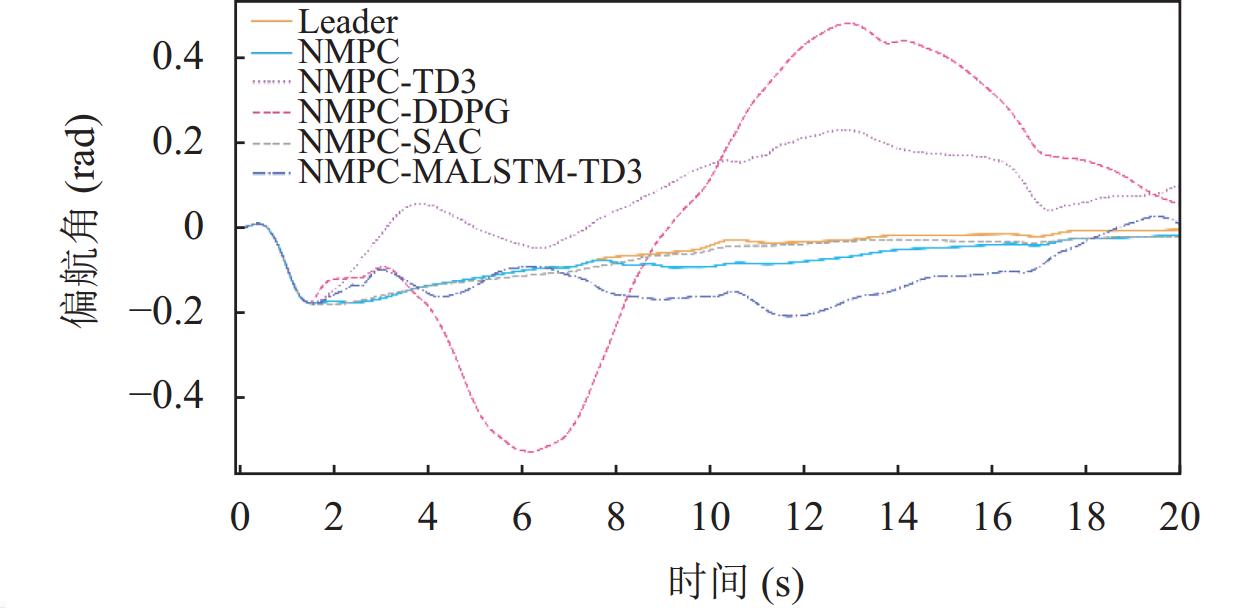
在基于不同补偿器的控制算法下的姿态控制表现中, 无人机的滚转角姿态表现如图10所示, DDPG在整体表现中出现了较大的偏移, SAC在滚转角控制上的表现整体都较为稳定, TD3在10–13 s间出现了明显的波动, MALSTM-TD3在3 s左右出现了一个明显的抖动但整体状态更加稳定, TD3与MALSTM-TD3在干扰处均有较好的抵抗效果; 无人机的俯仰角姿态表现如图11所示, 在俯仰角的控制表现上不同模型的效果与在滚转角姿态控制的表现较为类似; 无人机的偏航角控制表现如图12所示, 相比之下MALSTM-TD3虽也出现了偏差但较DDPG与TD3更好, 在此场景下SAC的表现最佳, 全程都能够稳定贴合领航机状态飞行.
|
图 10 滚转角姿态变化曲线 |
|
图 11 俯仰角姿态变化曲线 |
|
图 12 偏航角姿态变化曲线 |
另外, 基于不同算法的补偿器在该场景下与领航机的平均状态误差表现如表4所示, 可以看出在主要的位置跟踪任务中除了DDPG以外其他算法的
| 表 4 不同算法在六边形轨迹任务下的平均状态误差 |
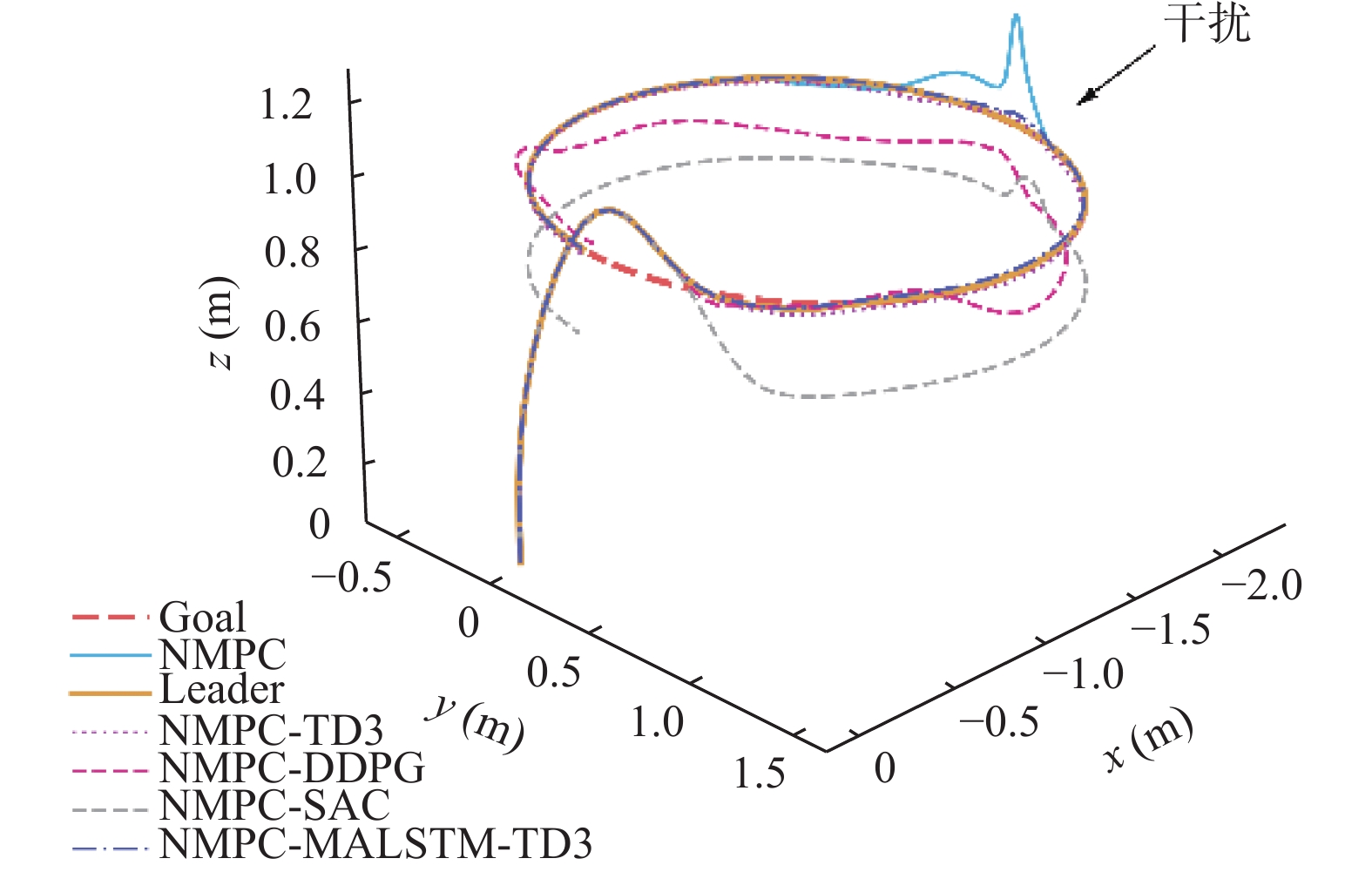
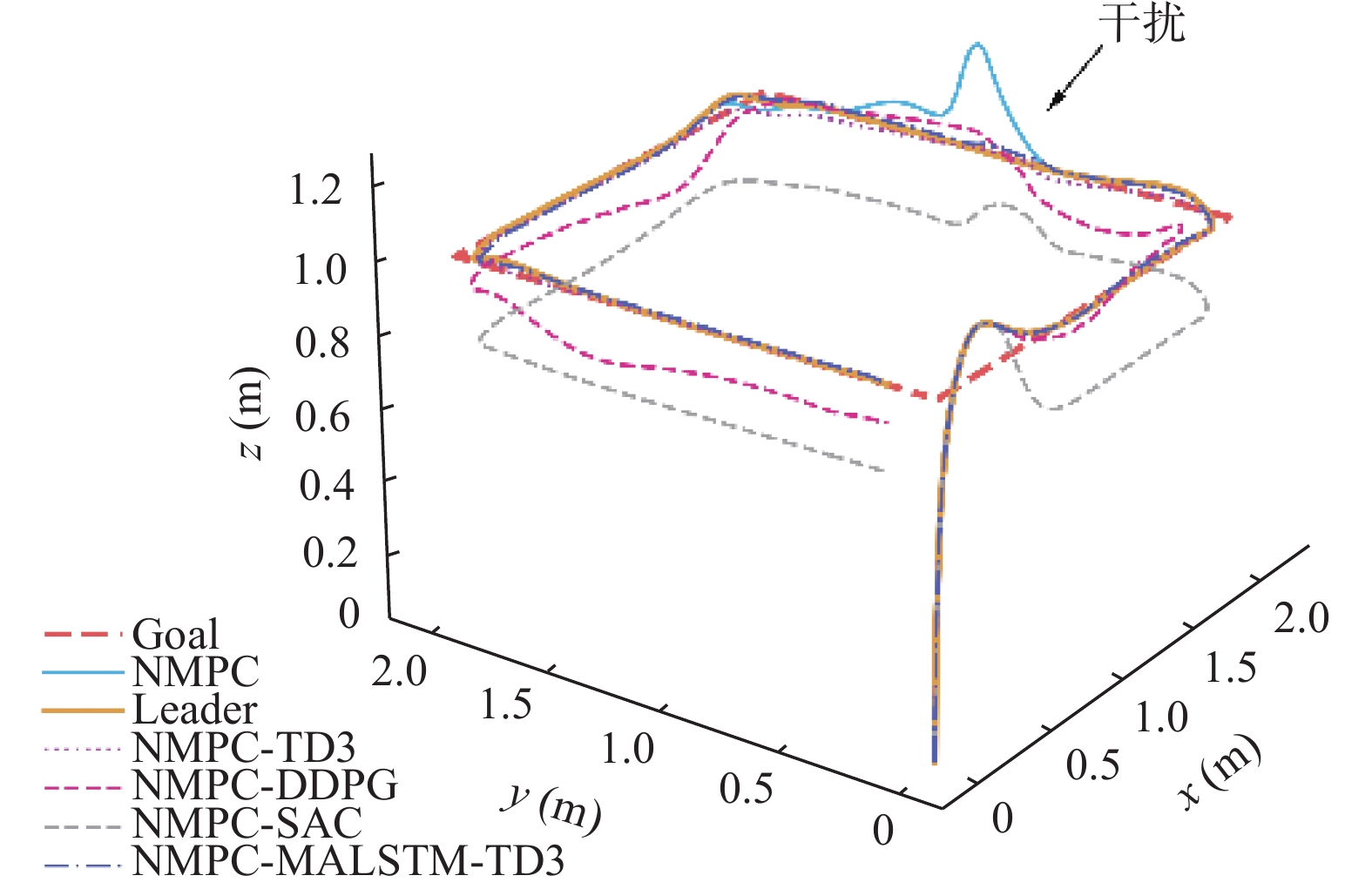
为了确保模型能够被应用在不同的场景中, 将不同模型分别在圆形以及方形轨迹场景下进行测试, 并在其中某段施加一个相同的
|
图 13 圆形轨迹任务表现 |
另外, 在基于R7-5800H的单核实验平台下进行实时性测试, 将任务全部放于CPU中进行处理, 分别利用NMPC-MALSTM-TD3与NMPC在六边形轨迹任务下分别进行10局控制任务并记录每局的程序运行时间后进行平均得到平均运行时间, 其中NMPC控制器的平均运行时间为2.11 s, NMPC-MALSTM-TD3控制器的平均运行时间为2.29 s. 根据实验结果, 相比于仿真时长10 s, 该方法能在2 s左右就完成控制决策, 且引入MALSTM-TD3补偿器以后的时间复杂度增加不超过10%, 在本文的实验平台中具有较好的实时性. 然而主流的PC级计算平台并不适用于四旋翼无人机控制这样的移动计算任务, 需要将其与移动计算平台进行对比, 表5为本文的计算平台与近年来主流移动计算平台的单核计算能力的相对分数.
|
图 14 方形轨迹任务表现 |
| 表 5 不同计算平台单核相对测试分数 |
理论上, 只要程序运行时间不超过仿真时间, 就可以认为计算平台性能足以应对实际场景, 然而计算平台不仅承担控制计算, 可能还承担其他计算任务, 故这里以运行时间5 s作为计算性能允许的最小值, 那么以上面实验结果为例, 相对测试分数值至少为0.458才满足要求. 而根据表5, 近几年主流移动计算平台的计算性能要远远高于该标准, 理论上本文提出的控制方法可以被应用于实际四旋翼无人机控制领域当中. 事实上, 移动计算平台的计算性能已经能够达到一些主流PC级计算平台的水平, 且算力出现了较大的冗余, 采用一些旧的移动计算平台不仅能够完成相关控制任务, 成本也能够得到控制.
5 结论与展望本文针对NMPC控制器在抗干扰方面的不足进行了改进, 提出了一种基于深度强化学习的混合抗干扰控制器, 用于解决NMPC控制器在遇到干扰时产生的剧烈波动, 在此基础上对TD3算法进行了改进, 引入了MALSTM-Actor网络, 将多头注意力机制与LSTM进行融合以后加入Actor网络, 提升了模型对于空间和时间信息的表达能力, 并提出了一种带边界的可控尺度连续型对数奖励函数让模型训练稳定性得到一定提升, 同时采用了一种带随机干扰的随机场景训练策略来提升模型的泛化性. 仿真实验结果表明, 基于MALSTM-TD3的补偿器在综合表现上最佳, 特别是在
| [1] |
Chen LL, Liu ZB, Gao HG, et al. Robust adaptive recursive sliding mode attitude control for a quadrotor with unknown disturbances. ISA Transactions, 2022, 122: 114-125. DOI:10.1016/j.isatra.2021.04.046 |
| [2] |
Zou X, Liu ZB, Zhao W, et al. Optimal hovering control of a tail-sitter via model-free fast terminal slide mode controller and cuckoo search algorithm. Proceedings of the 2021 International Conference on Unmanned Aircraft Systems (ICUAS). Athens: IEEE, 2021. 978–984.
|
| [3] |
Song FL, Li Z, Yu XH. A feedforward quadrotor disturbance rejection method for visually identified gust sources based on transfer reinforcement learning. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(5): 6612-6623. |
| [4] |
Song FL, Li Z, Yang SC, et al. Anti-disturbance compensation for quadrotor close crossing flight based on deep reinforcement learning. IEEE Transactions on Industrial Electronics, 2023, 70(3): 3013-3023. DOI:10.1109/TIE.2022.3172764 |
| [5] |
Li MJ, Cai ZH, Zhao J, et al. Disturbance rejection and high dynamic quadrotor control based on reinforcement learning and supervised learning. Neural Computing and Applications, 2022, 34(13): 11141-11161. DOI:10.1007/s00521-022-07033-7 |
| [6] |
Pi CH, Ye WY, Cheng S. Robust quadrotor control through reinforcement learning with disturbance compensation. Applied Sciences, 2021, 11(7): 3257. DOI:10.3390/app11073257 |
| [7] |
范文茹, 刘权威, 田栢苓. 基于干扰补偿的四旋翼无人机轨迹跟踪控制. 现代防御技术, 2024, 52(2): 87-93. |
| [8] |
Islam M, Okasha M, Sulaeman E. A model predictive control (MPC) approach on unit quaternion orientation based quadrotor for trajectory tracking. International Journal of Control, Automation and Systems, 2019, 17(11): 2819-2832. DOI:10.1007/s12555-018-0860-9 |
| [9] |
Zhang TH, Kahn G, Levine S, et al. Learning deep control policies for autonomous aerial vehicles with MPC-guided policy search. Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA). Stockholm: IEEE, 2016. 528–535.
|
| [10] |
刘昊. 基于非线性模型预测控制的无人船路径跟踪方法研究 [硕士学位论文]. 哈尔滨: 哈尔滨工业大学, 2022.
|
| [11] |
Andersson JAE, Gillis J, Horn G, et al. CasADi: A software framework for nonlinear optimization and optimal control. Mathematical Programming Computation, 2019, 11(1): 1-36. DOI:10.1007/s12532-018-0139-4 |
| [12] |
Verschueren R, Frison G, Kouzoupis D, et al. ACADOS—A modular open-source framework for fast embedded optimal control. Mathematical Programming Computation, 2022, 14(1): 147-183. DOI:10.1007/s12532-021-00208-8 |
| [13] |
柳子然, 戴梓健, 岳程斐, 等. 基于高斯混合过程的空间机器人任务空间预测控制方法. 系统工程与电子技术, 2023, 45(11): 3597-3605. |
| [14] |
Frison G, Diehl M. HPIPM: A high-performance quadratic programming framework for model predictive control. IFAC-PapersOnLine, 2020, 53(2): 6563-6569. DOI:10.1016/j.ifacol.2020.12.073 |
| [15] |
梁吉, 王立松, 黄昱洲, 等. 基于深度强化学习的四旋翼无人机自主控制方法. 计算机科学, 2023, 50(11A): 220900257. DOI:10.11896/jsjkx.220900257 |
| [16] |
Lillicrap TP, Hunt J J, Pritzel A, et al. Continuous control with deep reinforcement learning. arXiv:1509.02971, 2015.
|
| [17] |
Fujimoto S, Hoof H, Meger D. Addressing function approximation error in Actor-Critic methods. Proceedings of the 35th International Conference on Machine Learning. Stockholm: PMLR, 2018. 1587–1596.
|
 2024, Vol. 33
2024, Vol. 33



