雾霾天气的频繁出现已经成为中国乃至全球的严重环境问题, 而PM_2.5作为构成雾霾天气的主要因素, 其浓度的增加不仅会对人体健康产生影响^[1], 还会引起气候的变化^[2]. 在中国, PM_2.5污染问题尤为严重, 已经成为主要的污染物之一. 据统计, 在全国339个地级及以上城市中, 有高达86个城市的PM_2.5浓度超标, 这意味着近1/4的城市居民正生活在PM_2.5浓度超标的环境中^[3]. 因此, 探索有效的PM_2.5浓度预测模型, 对于人类健康和环境保护至关重要.

目前, 为了应对PM_2.5的污染问题, 许多研究人员都在寻求更好的预测方法对PM_2.5浓度进行预测研究, 以便制定有效的规划和应对措施. 可以通过基于物理化学反应的原理模型与基于深度学习模型进行PM_2.5浓度的预测. 基于物理化学变化原理的方式强调了对大气中物理和化学过程的深入理解, 包括污染物的生成和转化等, 从而对PM_2.5浓度进行建模. Wang等^[4]使用WRF-Chem模型模拟了汾渭平原PM_2.5的复杂空气污染情况. 秦思达等^[5]使用WRF-CMAQ模型对辽宁中部城市群的PM_2.5化学组分进行了模拟分析. 随着人工智能的快速发展, 深度学习已成为先进人工智能的前沿领域, 可通过深度学习预测PM_2.5浓度. 基于深度学习的预测方法是通过构建复杂的神经网络模型来捕捉PM_2.5浓度与其相关影响因素之间的关系. Hu等^[6]提出一种基于小波变换和长短期记忆的PM_2.5浓度组合预测模型, 小波变换用于在多个尺度上分解和细化相关因素的时间序列. 并利用长短期记忆网络对不同尺度的时间序列进行训练, 通过重构生成最终的预测结果. Zhang等^[7]提出了一种基于时间差分的图变压器网络, 能够从时间序列PM_2.5数据中学习长期时间依赖关系和复杂关系, 用于空气质量PM_2.5预测. Li等^[8]通过将卷积神经网络与长短期记忆神经网络相结合, 建立了一种混合模型CNN-LSTM, 用于预测PM_2.5浓度. Liu等^[9]提出了一种基于长短期记忆网络的注意力机制, 使用长短期记忆网络对邻近区域的空气质量进行了初步预估, 随后采用基于XGBoost的集成方法, 将初步预估结果与天气预报进行有效结合, 从而实现了对PM_2.5浓度的精准预测.

可以发现, 虽然上述模型能较好地预测PM_2.5浓度, 但无法直接给出明确的函数表达式, 难以揭示PM_2.5浓度与各影响因素之间的函数关系. 相比之下, 基因表达式编程不仅具备与神经网络一样强大的泛函学习能力, 还能够针对具体问题构建出相应的数学模型. 因此, 将GEP应用于PM_2.5浓度预测中是很有价值的. 但GEP与其他进化算法一样, 在解决具体问题时, 常会出现收敛速度慢、早熟收敛等情况^[10]. 为解决此问题, 充分利用GEP算法的优势, 对传统GEP算法进行改进, 提出一种基于病毒进化的基因表达式编程算法(VE-GEP)对PM_2.5浓度进行预测建模, 并分析该算法用于PM_2.5浓度预测的有效性与先进性.

1 方法 1.1 GEP简介

基因表达式编程(GEP)模拟一般生物的遗传和进化, 它结合了遗传算法(GA)和遗传编程(GP)的优点, 实现了基因型(定长字符串)与表现型(表达式树)之间的分离与转化, 能够使用简单的编码方式来解决复杂问题, 比传统的进化算法效率高出2–4个数量级. GEP不需要先验知识为指导, 不局限于问题的具体领域, 非常适用于解决分类问题^[11]和符号回归问题^[12]. 目前该算法也已成功应用到了建筑物的能源性能预测^[13]、土壤渗透系数预测^[14]、混凝土抗压强度预测^[15]和城市用水量预测^[16]等多个领域.

在GEP中, 种群是最高实体, 它是多个个体(染色体)的集合. 个体的表示是算法的关键部分, GEP个体包含一个或多个等长基因. 每个基因由头部与尾部组成, 采用线性符号串编码, 符号串即为基因的基因型. 为保证产生的基因是合法的, 头尾的长度需满足一定的关系, 具体如式(1)所示:

$ \begin{array}{*{20}{c}} {t = h\times\left( {n - 1} \right) + 1} \end{array} $

(1)

其中, t为基因尾部的长度, h为基因头部的长度, n为所有函数中的最大目数.

头部和尾部是基因的重要组成部分, 头部的基因元素是通过函数符集合F与终结符集合T中的元素构成, 而尾部的基因元素仅由终结符集合T中的元素构成. 其中函数符集合F的元素组成十分广泛, 包含问题领域相关的所有函数符号; 终结符集合T的元素组成通常为算法的自变量个数.

1.2 基于病毒进化的基因表达式编程算法

病毒是一类特殊的生物, 其进化速度非常快, 能够快速适应不同的环境变化. 多样性是病毒生存和进化的首要条件^[17], 与一般生物相比, 病毒可以通过不同的方式快速地变异和重组, 增加病毒遗传的多样性. 病毒重组可以发生在同一种病毒的不同株之间, 也可以发生在不同种类的病毒之间. 对于活性病毒与灭活病毒可以通过交叉复活的方式, 从而产生具有新遗传特性的病毒. 病毒的突变可以自发产生, 也可以由物理、化学诱变剂诱导产生, 使得病毒更好地适应环境变化和宿主免疫反应. 病毒依赖于宿主来进行生命活动, 利用宿主细胞内的物质和能量来维持其生命周期. 相较于生物体之间的水平基因转移, 病毒与其宿主之间的基因流动是病毒繁殖的关键特征. 病毒的进化过程就是一个不断从宿主获取基因的过程^[18]. 这些优势有助于病毒在各种环境条件下快速适应和进化, 从而更好地生存和繁殖.

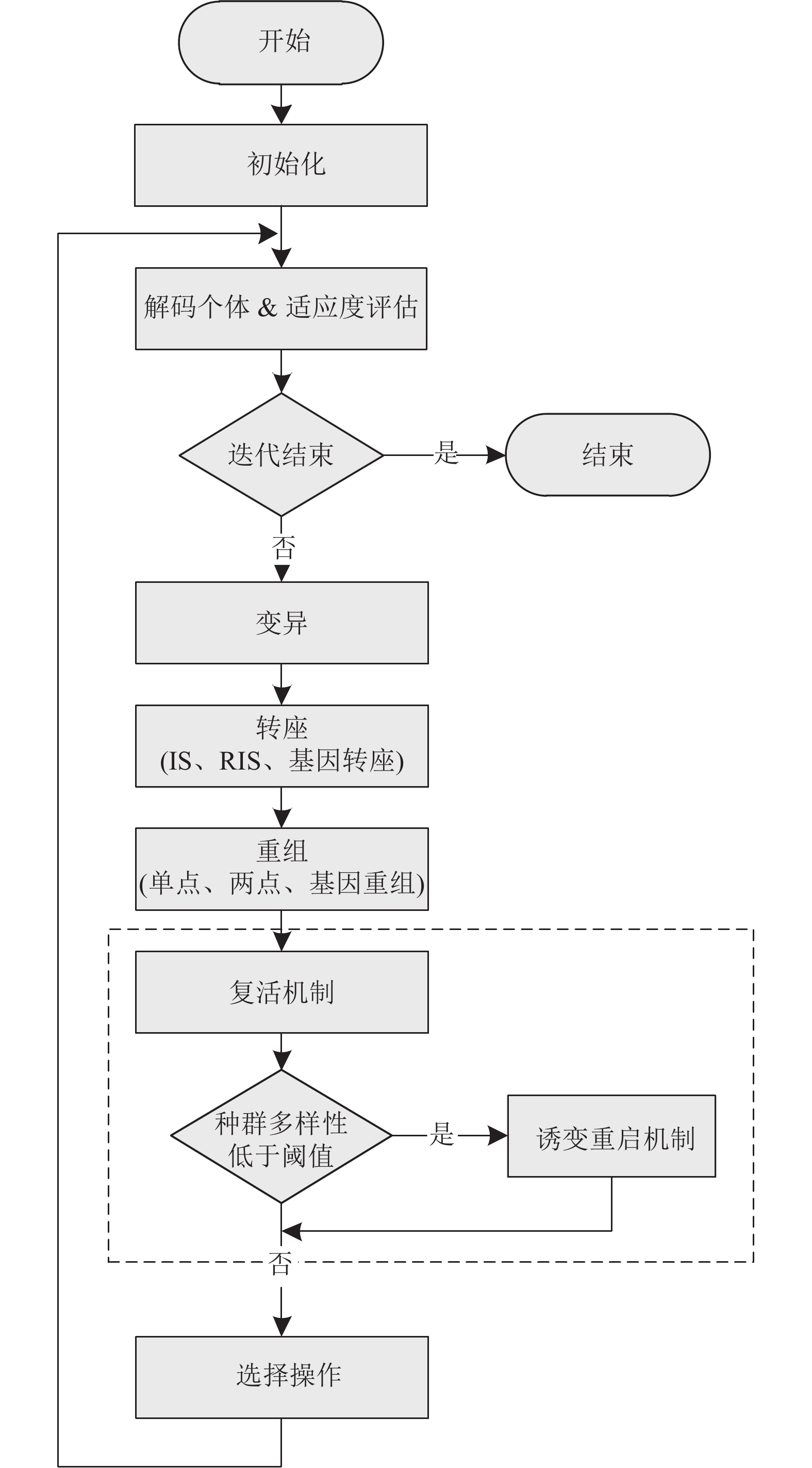
受此启发, 本文提出了一种基于病毒进化的基因表达式编程算法(VE-GEP), 在GEP基础上引入了复活机制与诱变重启机制, 复活机制通过将种群中的不可行解复活成可行解, 来改善种群中个体的质量. 诱变重启机制通过增强种群的多样性, 避免算法过早收敛到局部最优解. 其算法具体内容如图1所示.

1.2.1 基本定义

VE-GEP算法中涉及的相关概念定义如下.

定义1. 病毒种群, 是指由病毒个体组成的种群, 对应所求问题的解集. 病毒种群又可以分为存活病毒种群与灭活病毒种群.

定义2. 病毒个体, 在编码方式上采用与传统基因表达式编程中个体相同的策略.

定义3. 重启病毒个体, 是指病毒个体将其基因信息传递给宿主细胞, 并从宿主细胞中获取新的基因信息, 从而产生的新个体. 其编码方式遵循了与病毒个体相同的规则, 并且两者在编码长度上保持一致.

定义4. 灭活病毒个体, 是指在病毒个体中携带了灭活基因的个体. 例如, 在病毒种群中, 若第i个病毒个体的第j位上的函数符为“/”, 则需要对第j位的两个操作数进行计算. 在这个过程中, 若第2个操作数为0, 这时计算后得到的值就是一个非法结果, 那么第j位上的基因就是一个灭活基因, 该个体就是一个灭活病毒个体.

定义5. 存活病毒个体, 是指在病毒个体中未携带灭活基因的个体.

1.2.2 复活机制

在个体进化积累的过程中, 可能会受到基因遗传操作的破坏, 从而产生一些灭活病毒个体. 灭活病毒个体不仅增加了计算的成本, 还可能导致算法需要更多的迭代次数才能找到最优解. 为了避免或减少这些灭活病毒个体, 本文通过借鉴病毒进化中交叉复活的思想, 设计复活机制操作, 利用存活病毒个体对灭活病毒个体中的灭活基因或灭活基因片段进行等位替换.

在进行复活机制操作时, 设置相同的灭活病毒个体数量与存活病毒个体数量, 这里采用的存活病毒个体是从存活病毒种群中随机选择的优质个体. 具体分为以下两种情况, 依据灭活病毒个体基因位上的灭活基因与存活病毒个体中的等位基因元素是否相同分别进行等位基因元素的替换或等位基因元素片段的替换. 如果相同, 则进行等位基因元素片段的替换; 如果不同, 则进行等位基因元素替换. 计算式如(2)所示:

$ \begin{array}{*{20}{c}} {inVIRUS = \left\{ {\begin{array}{*{20}{l}} surVIRUS\left( {{x_m}} \right),& {x_m} \ne {x_n} \\ surVIRUS\left( {{a_m}:{a_n}} \right),& {x_m} = {x_n}, {a_n} > {a_m} \end{array}} \right.} \end{array} $

(2)

其中, inVIRUS为灭活病毒个体, surVIRUS为存活病毒个体, x_m为灭活病毒个体中存在的第m个灭活基因元素, x_n为存活病毒个体中与x_m的等位基因元素. a_m、a_n均为替换的基因位点, ${a_m} \in \left( {S_x^{m - 1}, S_x^m} \right), {a_n} \in \left( {S_x^m, S_x^{m + 1}} \right)$, $S_x^m$为第m个灭活基因的基因位, a_m:a_n为a_m–a_n一段基因元素片段.

1.2.3 种群信息熵

随着进化迭代的发生, 可能会出现种群趋同, 不利于种群进化. 为此, 本文采用信息熵^[19]作为种群多样性的衡量标准. 信息熵是一种定量计量标尺, 用于表示状态的多样性和丰富程度. 具体计算如下所示.

(1)统计第i个函数符或终结符在种群的同一基因位置j上出现的次数C_ij.

(2)求第i个函数符或终结符在种群的同一基因位置j上出现的概率P_ij, 计算式如式(3)所示:

$ {P}_{ij} = \frac{{C}_{ij}}{M} $

(3)

其中, M为种群的规模.

(3)计算种群的信息熵, 计算式如式(4)所示:

$ \begin{array}{c}H = \dfrac{1}{L} {\displaystyle \sum }_{j=1}^{L}{\displaystyle \sum }_{i=1}^{N}-{P}_{ij}\mathrm{log}{P}_{ij}\end{array} $

(4)

其中, L为每个个体的总长度, N为函数符和终结符的总数.

依据设定的信息熵阈值判断是否需要对当前病毒种群采用诱变重启机制. 种群的最大进化代数为Max, 分别设置多样性判断阶段1–Max/3、Max/3–2×Max/3和2×Max/3–Max, 及对应的种群多样性阈值h, 理想种群信息熵H_i, 当代种群信息熵H_c. 若H_c<h×H_i, 则对病毒种群中的病毒个体采取诱变重启机制.

1.2.4 诱变重启机制

在GEP中, 随着迭代次数的不断增加, 种群中的个体逐渐收敛于适应度较高的区域, 表现出较高的相似性, 致使种群的多样性降低. 在个体变异时还存在一定的盲目性, 可能会产生出与问题无关或者甚至有害的基因. 当种群中的个体接近某个局部最优解时, 变异可能无法帮助算法跳出局部区域, 而是在附近进行搜索, 这也是导致算法在后期陷入停滞的原因. 为了解决上述问题, 在VE-GEP算法中采用诱变重启机制, 该机制包含诱变操作和重启操作. 诱变操作是通过记录自然进化过程中的优质变异基因对个体进行变异, 探索可能存在最优值的搜索空间, 有助于提高算法的收敛性. 重启操作是将诱变操作后适应度值低的病毒个体淘汰, 同时引入等量的重启病毒个体, 保持种群个体数量的一致性, 并提高种群的多样性.

(1)诱变操作

在进行诱变操作时, 对病毒个体中的每个基因位设置一个相对应的诱变基因库, 用来保存自然进化过程中的优质变异基因. 诱变基因库随着进化的发生始终保持动态更新, 若在自然进化中经过自然变异后的个体适应度值增加, 则称这类变异基因为优质变异基因, 这类基因将直接存入诱变基因库中; 反之, 若个体适应度值降低, 则称为劣质变异基因, 如果这类基因存在于诱变基因库中, 则需要从诱变基因库中删除. 计算如式(5)所示:

$ \begin{array}{*{20}{c}} {G = \left\{ {\begin{array}{*{20}{l}} {add\left( j \right),\; {f_m} > {f_p}} \\ {pop\left( j \right),\; {f_m} < {f_p}, j \in G} \end{array}} \right.} \end{array} $

(5)

其中, G为诱变基因库, j为变异基因, add(j)表示将基因j存入诱变基因库G中, pop(j)表示将基因j从诱变基因库G中删除, f_m为变异后的个体适应度值, f_p为变异前的个体适应度值.

诱变操作是针对最大规模的诱变基因库所对应基因位上的基因进行变异, 变异基因从诱变基因库中进行选取. 在诱变基因库中, 诱变基因选取概率通过式(6)进行计算.

$ \begin{array}{*{20}{c}} {P\left( i \right) = \dfrac{{\displaystyle\mathop \sum \nolimits_0^{len\left( G \right)} G\left( i \right)}}{{len\left( G \right)}},\; i \in G} \end{array} $

(6)

其中, P(i)为选取基因i的概率, i为诱变基因库中的基因, len(G)为诱变基因库规模.

将选取到的诱变基因通过式(7)进行诱变操作.

$ \begin{array}{*{20}{c}} {p_n^s\left( i \right) = G\left( k \right),\; k \in G} \end{array} $

(7)

其中, $p_n^s$为第s代种群中的第n个个体, i为个体n的基因, k为诱变基因库中的基因. 若个体为最优个体时, 诱变操作后个体适应度值增加, 则进行诱变操作; 否则, 不进行诱变操作.

(2)重启操作

为了提高种群的多样性, 采取重启操作, 将重启病毒个体引入当前病毒种群中, 帮助病毒种群进化. 在进化过程中将适应度低的病毒个体进行淘汰, 用重启病毒个体对其进行替换. 根据信息熵的计算原理, 如果种群内的个体在同一基因位上都表现出不同的等位基因元素时, 那么该种群的信息熵将会达到最大, 此时的种群多样性表现最佳. 结合这个思想, 重启病毒个体采用随机生成的方式, 且生成的重启病毒个体与当前被淘汰的病毒个体等位基因元素不同. 计算如式(8)所示:

$ \begin{array}{*{20}{c}} {VIRUS\left( i \right) = newVIRUS\left( j \right),\; i \ne j} \end{array} $

(8)

其中, VIRUS为病毒个体, newVIRUS为重启病毒个体, i为VIRUS中的基因元素, j为重启病毒个体中与基因元素i不相同的等位基因元素.

2 实验结果与分析 2.1 数据集

本实验采用西安市2018年3月1日–2022年2月28日每日的空气质量数据(PM₁₀, NO₂, CO, SO₂, O₃)与气象数据(露点, 降水, 气压, 温度, 风速)为实验的样本数据, 分别来源于中国空气质量在线监测分析平台与美国国家气候数据中心, 并将70%的数据组成训练集, 30%的数据组成测试集.

2.2 评价指标

本实验分别以拟合度R²、均方根误差RMSE以及平均绝对误差MAE对模型的预测性能进行评价. 通过拟合优度R²近似表征模型学习到的有用信息的量, 计算如式(9)所示. 式中SSE与SST分别为残差平方和与总离差平方和, 具体计算如式(10)与式(11)所示. RMSE是实际观测值与预测值偏差的平方与观测次数n比值的平方根, 计算式如式(12)所示. MAE表示实际观测值和预测值之间绝对误差的平均值, 计算式如式(13)所示.

$ \begin{array}{*{20}{c}} {{R^2} = 1 - \dfrac{\textit{SSE}}{\textit{SST}}} \end{array} $

(9)

$ {{\textit{SSE}} = \mathop \sum \limits_{j = 1}^n {{\left( {{y_j} - {{{{\hat y}}}_j}} \right)}^2}} $

(10)

$ {{\textit{SST}} = \mathop \sum \limits_{j = 1}^n {{\left( {{y_j} - \bar y} \right)}^2}} $

(11)

$ {{\textit{RMSE}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{j = 1}^n {{\left( {{y_j} - {{{{\hat y}}}_j}} \right)}^2}} } $

(12)

$ {MAE = \frac{1}{n}\mathop \sum \limits_{j = 1}^n \left| {{y_j} - {{{{\hat y}}}_j}} \right|} $

(13)

其中, y_j表示实际观测值, ${{{\hat y}}_j}$表示预测值, ${{\bar y}}$为变量y的平均值.

2.3 实验环境及参数设置

实验环境: Windows 10 64 位, i5-7300HQ, 16 GB内存. 基因重组为0.1, 其余的具体实验运行参数设置如表1所示, 其中函数符集合中S代表平方运算, R代表开方运算, exp代表e^x, ~代表10^x.

2.4 PM_2.5浓度变化特征分析

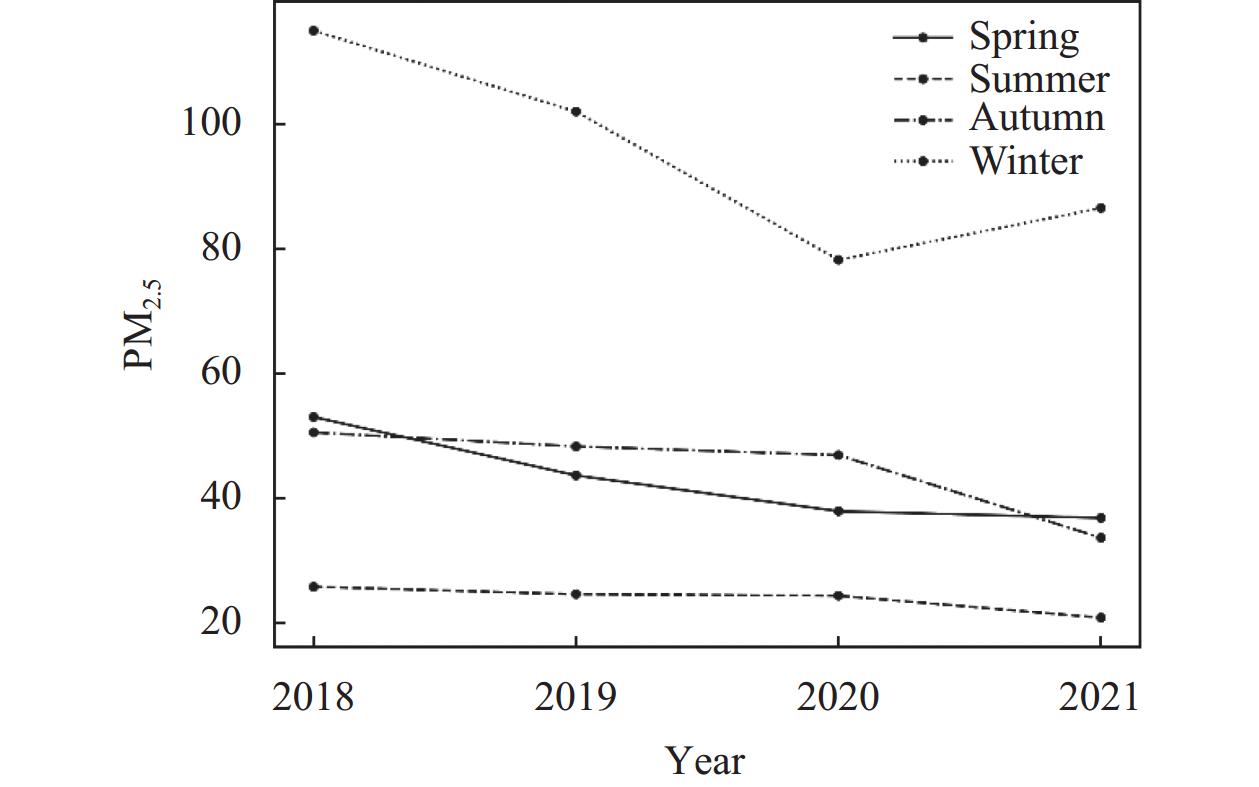
PM_2.5浓度具有明显的季节变化趋势, PM_2.5的浓度常会受到气象因子和大气污染物的影响, 而这些因素往往随季节的变化而变化^[20–22]. 为了更直观了解PM_2.5浓度变化特征, 对2018–2021年四季的PM_2.5浓度进行均值计算, 并做出相对应的四季PM_2.5浓度均值变化图, 如图2所示.

从图2可以看出, 冬季的PM_2.5浓度明显高于其他季节, 而春季和秋季的PM_2.5浓度相对较低, 夏季则呈现出最低的PM_2.5浓度. 不同季度的PM_2.5浓度呈现出明显的差异性, 因此本文按四季划分对PM_2.5浓度进行预测建模.

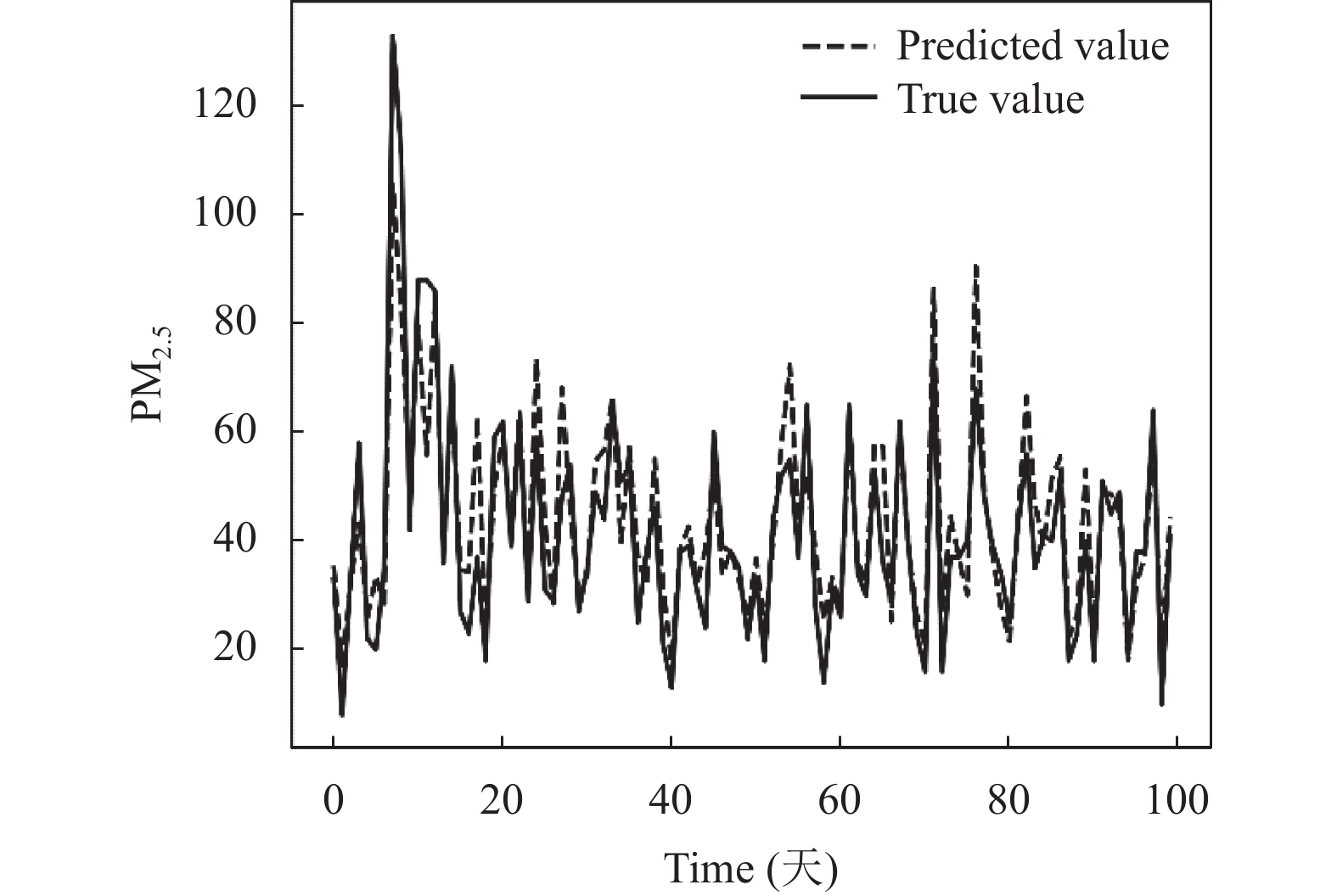
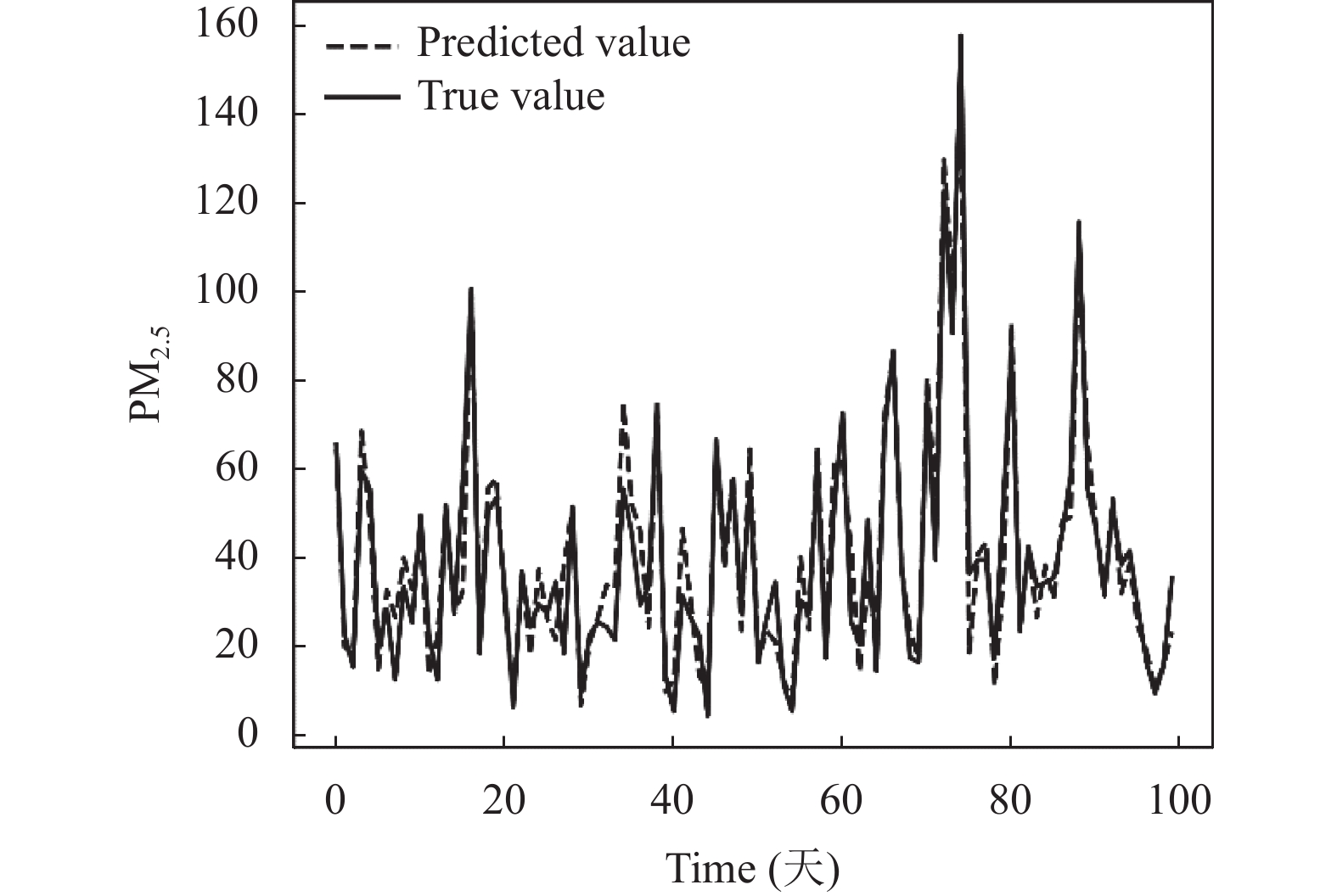
2.5 VE-GEP实验结果与分析

为了详细描述VE-GEP在PM_2.5浓度预测建模中的应用, 本实验将春季、夏季、秋季和冬季分别采用VE-GEP算法进行建模, 最终得到四季的PM_2.5浓度预测值与实际值的对比曲线分别如图3–图6所示, 图中虚线代表的是预测值, 实线代表的是实际值.

通过观察图3–图6, 可以发现采用VE-GEP算法对PM_2.5浓度进行预测, 得到的预测值与实际值基本一致, 该算法能较好地预测PM_2.5浓度. 基于该算法得到的四季的预测模型分别如式(14)–式(17)所示. 其中x₀–x₉分别代表PM₁₀、NO₂、CO、SO₂、O₃、露点、降水、气压、温度和风速.

$ {y = \sqrt {{{{x}}_4}} + {{{x}}_3} + {{{{\mathrm{e}}}}^{{{{x}}_2}}} + \frac{{\left| {{{{x}}_3} + 2{{{x}}_8} - {{{x}}_0}} \right|}}{{\ln \left| {{{{x}}_4} + {{{x}}_9}} \right|}} + {{10}^{{{{x}}_2}}} + {{{x}}_2}} $

(14)

$ \begin{split} y = & \sqrt {{{{x}}_0}} \times{{{x}}_2} + \sqrt {{{{x}}_0}} \times\log {{{x}}_0} + \frac{{{{{x}}_0}{{\times}}{{{x}}_2}}}{{{{{x}}_3}}} \\ & + {{{x}}_2} + \cos {10^{{{{x}}_6}}} \end{split} $

(15)

$ \begin{split} y = & \frac{{{{{x}}_0}}}{{\log {{{x}}_0}}} + \cos {{{x}}_8} + {{{x}}_0}\times\log {{{x}}_2} \\ & + \cos \left( {\log {{10}^{{{{x}}_6}}}} \right) + \frac{{{{{x}}_0}}}{{{{{x}}_1}}} + {\left( {\cos {{{x}}_6}} \right)^2} \end{split} $

(16)

$ \begin{split} y = & {{{x}}_0} + {{{x}}_2} + {{{x}}_6} + 2{{{x}}_5} - \frac{{x_0^2}}{{{{{x}}_7}{{\times}}\left| {\log x_1^2} \right|}} \\ & - 2{{{x}}_8} + \sin {{{x}}_2} - \frac{{{{{x}}_0}^2}}{{{{{x}}_7}{{\times}}\left| {{{{x}}_2}} \right|}} \end{split} $

(17)

通过式(14)–式(17)可以看到, PM_2.5的浓度与各影响因素之间的函数关系. 在不同季节中污染物对PM_2.5浓度产生的影响也各不相同, 在各个季节中PM₁₀对PM_2.5浓度都产生了较大的影响. NO₂、SO₂和CO对PM_2.5浓度的影响则因季节而异, 其中秋季和冬季影响更强的因素是CO和NO₂, 而春季和夏季影响更强的因素是CO和SO₂. 此外, 温度、风速和气压等因素对PM_2.5浓度的形成也具有季节性的不同影响. 因此, 采用VE-GEP算法对PM_2.5浓度进行预测建模, 还能够捕捉与当季的PM_2.5浓度密切相关成函数关系的影响因子, 综合考虑各种污染物的排放特征和季节变化特点, 采取针对性的措施来降低PM_2.5浓度.

2.6 实验结果比较与分析

为了进一步验证VE-GEP算法的先进性, 将VE-GEP算法与GEP、DSCE-GEP^[23]和CNN-LSTM^[8]进行对比实验, 通过实验得到拟合度、均方根误差和平均绝对误差如表2所示.

通过表2可以看出, 这些算法的预测值与真实值都比较接近. VE-GEP算法相较于其他算法在春季、夏季和秋季中的预测模型均有不同程度的提高, 冬季预测模型稍差于CNN-LSTM, 但它无法得到PM_2.5浓度与各影响因素之间的具体函数关系. 整体来说, VE-GEP算法性能更好, 能有效应用在PM_2.5浓度预测中, 为PM_2.5浓度预测提供新的解决方案和思路.

3 算法性能分析

从前面的研究可以看出, VE-GEP算法具有明显的优势. 为了进一步探究算法复活机制和诱变重启机制的改进效果, 借助F函数^[24]对VE-GEP算法性能进行分析.

F函数由Ferreira^[24]首次应用于GEP中, 具有维度高, 自变量个数少的特点, 通常被用于算法的性能分析及比较, 具体如式(18)所示:

$ \begin{array}{*{20}{c}} {F = 5a_n^4 + 4a_n^3 + 3a_n^2 + 2{a_n} + 1} \end{array} $

(18)

连续实验200次, 实验参数设置如表3所示, 实验结果如表4所示.

从表4可以看出, 加入复活机制后, 算法的成功率提高了1.5%, 充分说明了该机制能够通过改善种群中解的质量来提高算法的全局寻优能力; 而加入诱变重启机制后, 算法的成功率提高了8%, 充分说明了该机制通过增强种群的多样性, 提高了算法的全局寻优能力. 同时加入这两种机制后, 算法的成功率最高. 充分说明了算法能够在改善解质量的同时提高对优质解的开采能力, 进一步提高了算法的全局寻优能力.

4 结论

受病毒进化的启发, 本文提出了一种新的基因表达式编程算法(VE-GEP). 该算法在GEP的基础上引入复活机制与诱变重启机制, 不仅可以改善解的质量, 还可以提高算法对优质解的开采能力, 增强算法的寻优能力. 并将该算法应用到PM_2.5浓度预测中, 依据PM_2.5浓度的季节变化特点, 分别建立了不同季节的PM_2.5浓度预测模型. 同时, 将VE-GEP算法与其他预测模型进行对比实验. 结果表明该算法不仅预测精度更高, 还能够得到PM_2.5浓度与各影响因素之间的函数关系, 对于PM_2.5浓度预测研究具有重要的现实意义.

虽然该算法在PM_2.5浓度预测中具有较好的实用性与较高的预测精度, 但由于引入了一些新的遗传算子, 需要更多的计算资源作为代价. 在下一步工作中, 将致力于解决这些约束, 并进一步改善算法性能.