2. 广东省特种设备检测研究院 佛山检测院, 佛山 528041
2. Foshan Branch, Guangdong Institute of Special Equipment Inspection and Research, Foshan 528041, China
自19世纪电梯面世以来, 电梯已成为商业建筑、住宅区、医疗场所的重要组成部分. 为了确保电梯的安全性, 一系列措施被实施, 旨在建立可靠的电梯系统, 保障乘客和工作人员的安全.
随着科技的发展, 预测性维护逐渐成为设备维护的重要策略. 在这种背景下, 电梯行业也尝试结合先进检测技术和数据分析以实现电梯按需维护. 然而, 这些尝试多为建立在传感器数据上的、基于状态的预测性维护研究[1–3]. 由于监测设备安装成本高且安装位置暂未规范, 这些方法推广受限[4]. 相较之下, 电梯的维修记录易获取, 但未被充分利用. 因此, 如果可以对这些历史维护数据采取基于统计和机器学习的方法, 从对不同来源的电梯大数据进行融合、关联、分析, 挖掘其潜在的故障风险, 将会对推进目前的电梯维护保养工作提供新的思路.
众多方法和模型被应用到预测性维护领域来进行研究工作, 其中包括使用机器学习对故障的发生时间与概率进行预测, 但这些直接回归方法在基于统计的预测维护领域中效果有限, 因为该领域使用数据往往是稀疏采样的. 对此, 生存分析领域中的Cox比例风险模型被广泛用于分析时间与故障的关系[5,6], 但该传统模型有风险比例恒定和因子线性组合等限制[7]. 而随着神经网络的发展, 深度生存回归模型在生存分析基础上引入了神经网络结构, 结合了生存回归的建模优势和深度学习的非线性表达能力, 能处理大规模数据, 捕捉非线性模式[8].
本研究利用电梯维修记录, 采用深度生存分析预测电梯大型故障风险(如停梯或困人事件). 研究包括4部分: (1)构建动态静态生存状态向量, 关联电梯属性与故障; (2)讨论生存分析中的左删失问题及数据分割策略; (3)使用不同深度生存模型预测生存曲线, 分析数据分割和补充方式对模型精度的影响; (4) 使用SHAP分析不同模型和策略下的故障风险归因. 本文创新点在于: (1)将累计故障量纳入风险协变量, 捕获影响故障风险的因素, 而在以往工作中仅选取电梯静态属性作为协变量; (2)讨论了数据左删失和数据颗粒度划分, 以往工作中未涉及; (3)使用深度生存模型而非传统的统计模型来建模故障风险. 此外, 本研究方法对基于历史数据的预测性维护具有一定泛用性.
1 相关工作 1.1 基于统计的预测性维护对电梯的运行风险预测, 隶属于预测性维护领域工作. 预测性维护的核心是通过数据和分析预测设备或系统可能出现故障的情况, 在众多领域都有广泛应用. 根据建模使用的数据不同, 预测性维护可以分为两种类型: (1)基于状态的预测性维护和(2)基于统计的预测性维护[9].
基于状态的预测性维护依赖更强调实时性检测, 这种方法所使用的数据为传感器等实时监测数据. 而基于统计的预测性维护多使用日志数据、维护数据和故障数据, 这种类型的数据具有粗时间颗粒、稀疏发生的特点. 在这种情况下, 使用统计学模型进行故障预测是一个常见处理方案. Yang等人[10]使用多种参数和非参数模型估算了移动工作设备种机器部件的生存曲线和危险率, 确定了各种机器部件随时间变化的故障概率, 发现不同类型的数据删失问题掩盖了不同类型的问题的存在, 这为最终的统计估算和结果解释带来了严重问题.
生存分析作为一种良好处理删失问题的方法, 近年来也常被使用到预测性维护领域工作中. Xiao等人[11]使用随机生存模型(random survival forest, RSF)与Cox比例风险模型(Cox proportional hazard model)对管道故障数据进行建模, 有效结合了管道故障和数据删失的非线性特征, 其预测结果优于其他机器学习方法, 并提高了天然气管道故障的预测准确性. Chen等人[12]对包含了汽车维修时间、车库位置、地区、故障发生时累积行程等的汽车维修记录与汽车属性进行研究, 以预测. 文献[12]使用了统计学模型Cox模型对发生了删失的数据进行初步的预测, 对删失数据进行了补偿, 然后使用一个3层的LSTM网络进行故障预测. Snider等人[13]对北美的输水管道进行了研究, 使用梯度提升决策树和Weibull比例危险生存分析模型, 对45年的水管破裂数据进行分析, 以预测输水系统中铸铁管道的下一次断裂时间. 文章认为, 在短期的管道破损预测准确性上, 机器学习模型有效, 但生存回归模型在处理右删失数据有更领先表现, 在数字资产管理上更有潜力. 王莲等人[14]则对电梯维修、属性数据使用了Cox模型+阈值划分的方式得到故障预测结果, 并通过最小化所提出的单位时间内平均维修保养成本来获得电梯最优保养周期.
1.2 生存分析与深度生存分析模型生存回归方法是一类用于生存分析的统计模型, 用于研究时间和兴趣事件发生的关系, 目标事件发生的风险、概率. 常见的生存回归模型包括Cox比例风险模型、Weibull回归模型、Aalen加性模型等模型. 生存回归方法在医学研究、可靠性分析、用户流失等领域得到了广泛应用.
生存回归方法对删失情况的良好处理是其独特之处之一. 删失情况指的是在研究期间未能确切观察到兴趣事件发生. 删失事件可大致分成3种类型: (1) 右删失: 右删失是指个体在研究结束时, 仍未发生兴趣事件的情况. (2) 左删失: 左删失是指个体在研究开始前就已经发生了事件, 但由于研究未开始, 因此无法得知事件发生的具体时间. (3) 区间删失: 区间删失是指无法精确观察到事件发生的时间, 仅知道该事件发生在一个特定时间区间内的情况.
在实际情况下, 人们对右删失情况的关注更多, 这也因为在实际应用中, 右删失情况更常见也更易被发现. 通过使用偏序风险集合来估计参数, 大部分生存回归模型能够对数据集中的右删失情况进行有效估计.
在以往使用生存分析模型对历史数据进行故障概率建模时, 往往使用的是传统的统计学模型, 如Cox模型与Weibull模型. 然而, 随着数据收集、处理手段的成熟, 使用单纯的Cox比例风险模型来对日渐复杂的数据集进行生存分析是不足够的. Cox比例风险模型在有着半参数的灵活特性的同时对数据有着严苛的时间要求, 它要求协变量的效应不随时间变化, 即危险比是恒定的, 这在现实的长时间随访或极端事件发生的情况下几乎不可能达到. 因此, 一系列深度生存模型被提出, 主要动机在于消除统计方法为模型带来的固有限制, 以及保持深度范式在生存分析方面的竞争力.
DeepSurv方法[15]使用网络结构来近似实际对数风险函数. DeepSurv使用由全连接层、dropout层组成的多层感知机结构对对数风险函数进行拟合. 网络将目标函数设为平均负对数偏似然, 并加上
Cox-CC和 Cox-Time[16]方法可视为对DeepSurv方法的一种扩展. 通过将生存时间t视为自变量的之一, 这两种方法允许经典CoxPH方法的相对风险函数依赖于时间协变量, 以此来打破经典CoxPH方法中的时间比例风险约束. DeepHit网络[17]则使用了一种非常不同的生存分析方法, 使用深度神经网络来直接学习事件发生时间的分布. 通过单个共享子网和一系列特定原因自网络的组合, DeepHit通过直接学习协变量与事件、生存时间的关系, 使随机过程的参数和形式都完全取决于协变量而不对此做任何硬性假定. 除了使用网络结构来进行生存分析研究以外, 使用基础学习器构建集合来进行学习也是一个研究方向. Ishwarn等人提出的随机生存森林[18]沿用集成学习的思想, 通过整合多个生存树的预测来提高模型的准确性和鲁棒性. 然而, 上述新兴的深度生存分析模型多用于医学领域, 在预测性维护领域中尚未得到应用.
1.3 SHAP分析SHAP (Shapley additive explanation)是一种用于解释机器学习模型预测结果的方法. 基于合作博弈论中的Shapley值, 该方法提供了一个统一的框架来解释任何模型的输出, 其使用SHAP值衡量每个特征对预测结果的贡献, 并确保贡献是公平分配的.
SHAP值通过计算某个特征加入所有可能子集时, 对模型输出的边际贡献的平均值, 来评估该特征对预测结果的影响, 作为该特征的SHAP值输出. SHAP值具有公平性、一致性、模型无关性的优势.
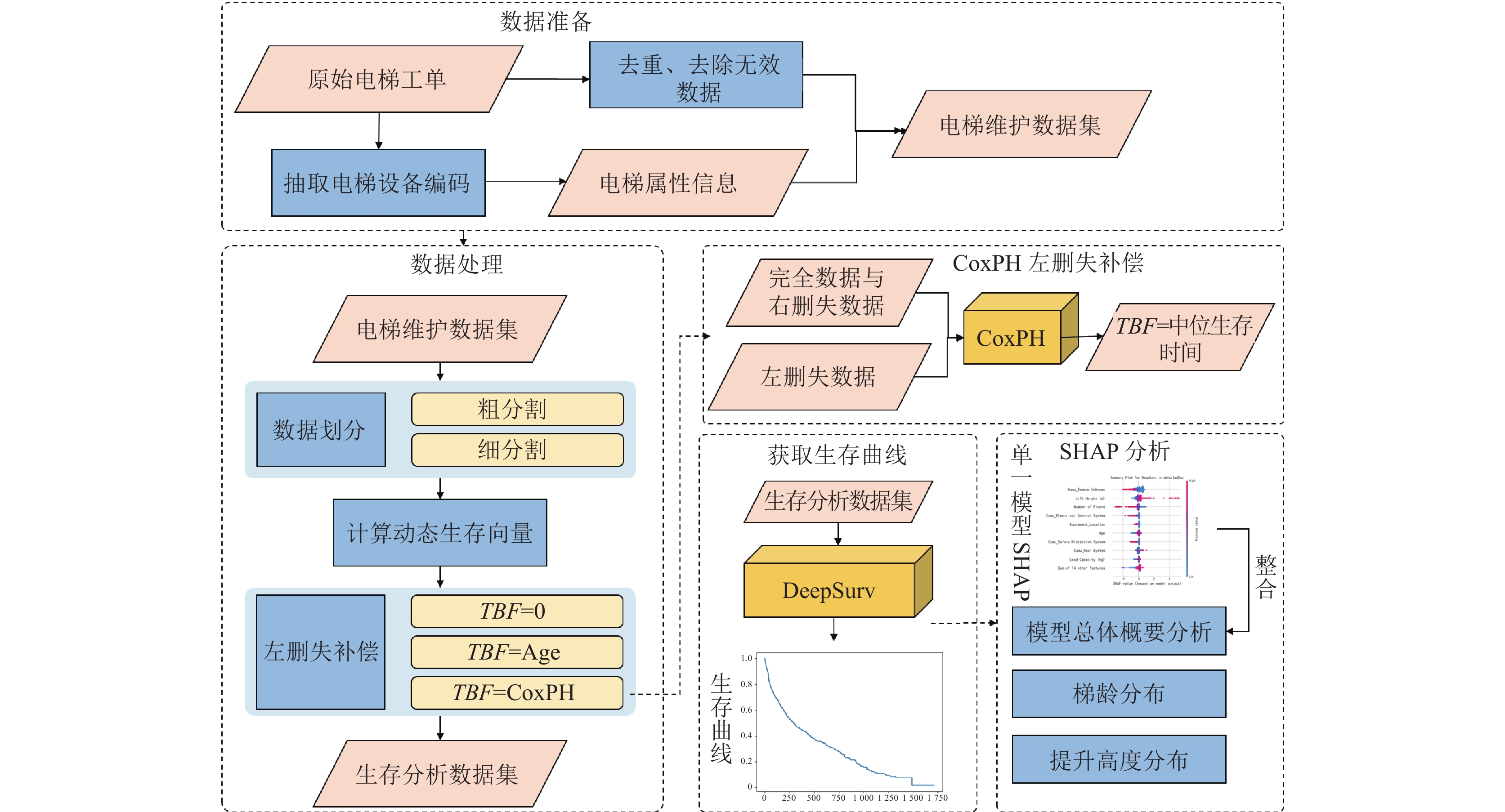
2 方法与设计 2.1 任务流程本文总体流程设计如图1所示. 数据准备阶段涉及电梯工单与电梯静态属性信息的组合与简单清洗, 在该阶段得到简单的电梯维护数据集, 对该阶段本文不再赘述; 数据处理阶段主要包括数据划分、动态生存向量构建、左删失补偿这3部分内容, 该部分将得到完整的生存分析数据集; 获取生存曲线阶段则是使用经过处理得到的生存分析数据集, 对DeepSurv及其他对比模型进行训练; 最后, 使用经训练的深度生存模型进行SHAP分析.
2.2 数据切割项目以造成停梯、困人事件的故障事件作为目标事件. 这类事件在低频、不规则时间周期的工单数据中属于稀发事件, 因为大部分维修工单所涉及的故障为小型故障. 数据切割、划分操作涉及后续TBF (time between failures)与动态协变量的计算. 根据目标事件还是故障发生来对数据集进行划分, 将会影响生存回归分析数据集的大小、删失率.
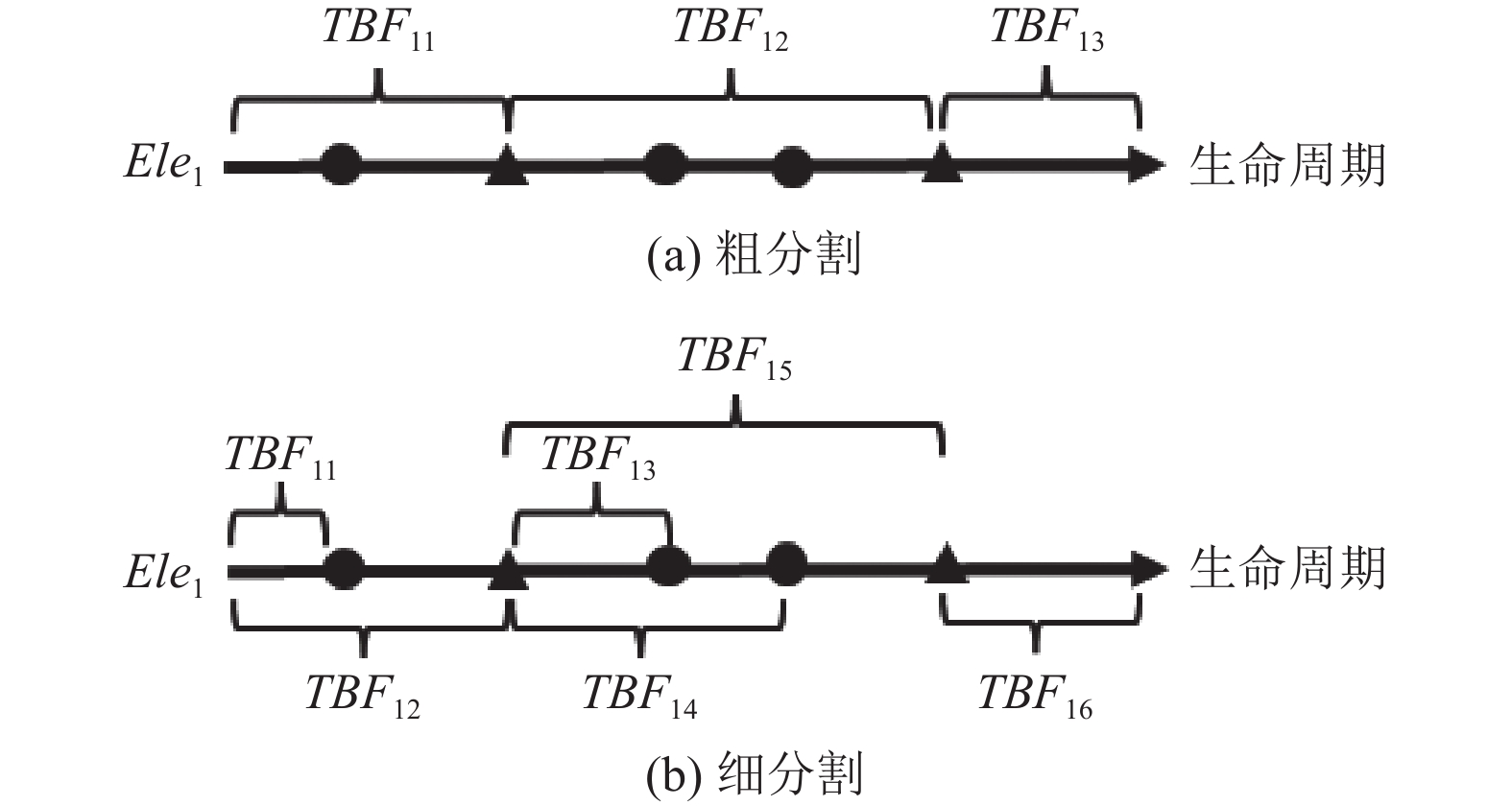
论文对两种数据划分方式进行了讨论, 如图2所示. 第1种是按照目标事件的发生进行划分, 在本文后续部分称为粗分割; 另一种分割方式是按故障发生进行划分, 在本文后续部分称为细分割.
2.3 构建动态生存向量生存回归分析模型需要形如
在实际运维中, 电梯的停梯、困人事件往往与一定时间段内电梯的小型故障发生量有关. 对此, 本文在使用电梯属性作为静态协变量的基础上, 提出了一种基于电梯工单数据的动态生存向量构建方法: 使用N表示电梯编号, M表示对应电梯发生重大故障的编号,
|
图 1 总体任务流程图 |
|
图 2 两种数据划分方式 |
将数据集划分为各片段, 每个片段对应为每个
经过上述操作, 可将原始数据集转化为一个具有生存分析格式的数据集
|
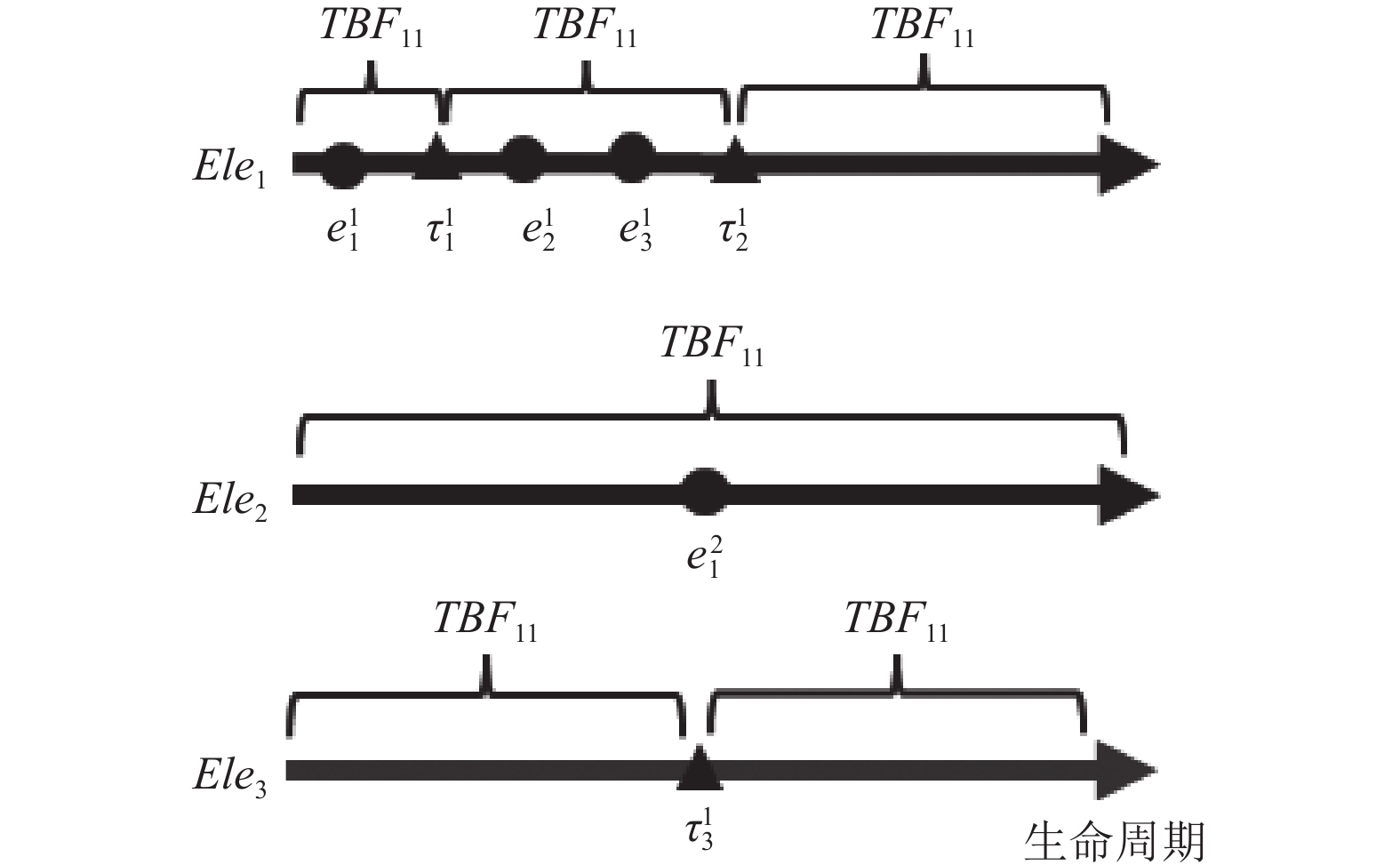
图 3 数据分割示意图 |
对数据集按上述方法进行切割以标记事件发生. 如图3所示, 三角形对应停梯、困人事件的发生, 圆形对应普通故障的发生. 对于电梯1,
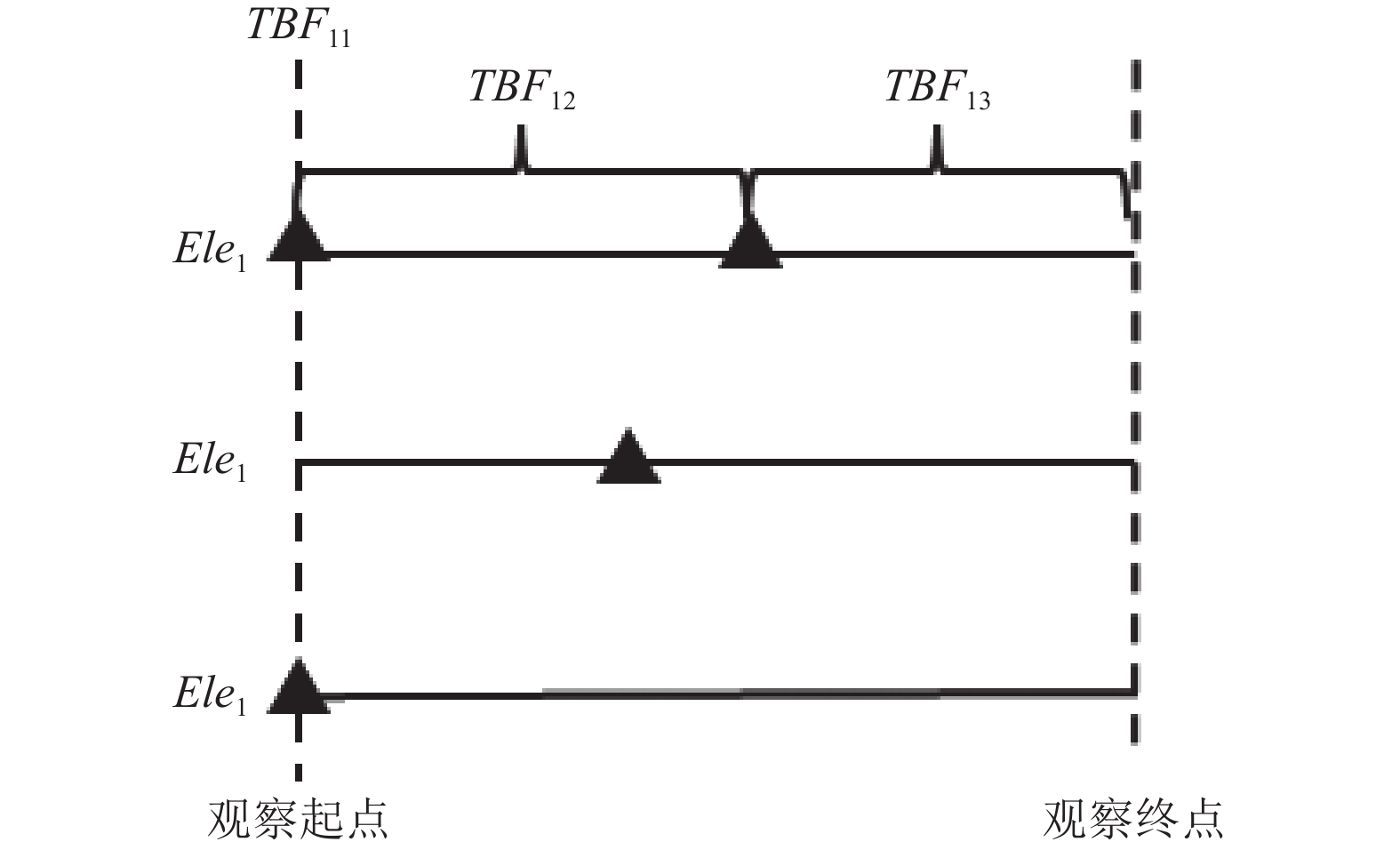
电梯维修工单数据本身无法体现电梯进入观察期的时间. 当电梯在数据集中的首条记录为目标事件时,
|
图 4 数据左删失情况示意图 |
生存回归分析模型擅长处理右删失问题, 但对左删失事件处理乏力. 项目分别使用3种方法对左删失数据进行补偿以解决左删失问题: ① 以0填充左删失TBF: 这种做法将数据集作为真正观察时间, 不做任何改动. ② 以梯龄填充左删失TBF: 这种做法假定左删失问题出现前, 电梯始终没有发生过目标事件. ③ 模型填充: 使用数据集中具有确切截尾的数据拟合Cox比例风险模型, 再用Cox模型对左删失数据进行预测.
对左删失数据使用模型填充的具体做法如下: 选取数据集中非左删失的数据, 包括完整数据与右删失数据, 对Cox模型进行拟合后, 使用该模型对左删失数据进行预测, 取其中位生存时间, 即每个数据生存概率为0.5时对应的生存时间, 作为预测TBF, 即生存分析数据格式中的
此处, Cox预测的结果中可能存在
在生存回归分析领域工作中, 常用一致性指数(concordance index)与布莱尔分数(Brier score)对模型性能与准确性进行评价.
一致性指数是用于评估生存回归模型性能一个最常用指标之一[19]. 它衡量模型对样本对子中目标事件发生的顺序的预测准确性. 具体而言, 一致性指数通过比较模型对样本对子的排序与实际上数据集中的样本对子排序之间的一致性, 来衡量模型的预测能力. 其计算方式是, 生存回归分析模型为数据集中每个研究个体赋予一个风险评分或所预测的生存时间, 而后将数据集中所有研究个体随机地两两组成对子, 如果组内满足风险高的个体先发生目标事件这一条件, 则认为该组为一致的组, 否则则为不一致的组. 数学上可表示为:
| C-index=P{ˆS(Ti|xi)<ˆS(Tj|xj)|Ti<Tj,Di=1} |
与AUC类似, C-index=0.5时, 认为模型在做完全随机预测, 即模型没有预测作用; C-index=1则认为模型预测结果与实际结果完全一致; C-index=0时, 认为模型预测结果与实际结果完全相反.
在传统的二分类问题中, 布莱尔分数(Brier score)主要用于评估概率预测模型的性能, 度量了模型对观测到的事件发生的概率的精确度. 在生存分析中, 布莱尔分数加入了对时间因素的考虑.
在生存分析中, 布莱尔分数用于评估在给定时间生存模型预测生存函数的准确性, 使用观察到的生存状态与预测生存概率之间的平均距离平方来表示准确性, 其内在判断逻辑在于, 在某特定时刻, 若观察到个体的事件发生状态为0, 即未发生事件, 则模型应认为个体此时的生存概率无限大, 反之模型应该认为个体的生存概率无限小. 数学表达可为:
| Brierscore=1NN∑i=1[ˆS(t|xi)2⋅1{Ti⩽t,Di=1}ˆG(Ti)+(1−ˆS(t|xi))2⋅1{Ti>t}ˆG(Ti)] |
其中,
理想状态下, 布莱尔分数应为0. 然而在实际的生存分析中, 考虑到右删失样本对布莱尔分数的贡献未知, 认为在
上述单时间点布莱尔分数进行扩展, 即可得到整体布莱尔分数(integrated Brier score), 描述生命周期内的布莱尔分数, 数学表达为:
| integratedBrierscore=1t2−t1∫t2t1BS(s)ds |
本文的数据主体为电梯维修工单数据. 这些工单数据用以记录和管理电梯维修服务, 来源于现实世界中的电梯维保企业, 其内容包括电梯故障发现日期、故障描述、电梯基本信息、维修人员等信息. 显然, 工单数据集直接来源于电梯故障, 具有不规则发生、稀疏发生的特点, 且本身并不携带与电梯状态相关的信息.
本文的数据由3家电梯维保企业提供, 在对这些数据进行拼接和融合之前, 已对数据进行必要的质量检查与清洗, 以确保不同数据源的数据一致性和可靠性, 并以统一标准, 对所有电梯故障, 根据电梯领域专家意见, 将故障一对一分类到14分类中的唯一一类.
原始数据集涉及故障记录共
| 表 1 两种分割模式下TBF的统计性指标 |
4.2 实验设置
本研究使用DeepSurv深度生存分析模型对电梯大型故障发生风险进行建模. 在本研究中, 我们还将DeepSurv与其他4种深度生存分析模型, 包括CoxCC、Logistic、DeepHit、随机生存森林(random survival forest, RSF)的性能进行了比较.
DeepSurv、CoxCC、Logistic、DeepHit都是以多层感知机(multilayer perceptron, MLP)的网络结构实现的, 随机生存森林是树型结构, 使用贝叶斯优化的超参数搜索策略对其进行最优参数的寻找. 以最大化一致性指数为超参数优化方向. 数据集以8:2的比例被划分成训练集、测试集, 划分已考虑两个集合中TBF与目标事件的均衡分配. 在训练集中使用5折交叉验证进行超参数寻找, 以交叉验证中C-index的平均值作为该组超参数的最终分数, 并以最终有最大一致性指数的组合作为最佳超参数组合.
本研究中预测模型与相关分析使用PyTorch、Pycox、Scikit-survival、SHAP开源库进行, 实验在48 GB显存的NVIDIA RTX A6000计算资源上进行. 生存分析实验目的是探究在电梯场景下, 2种数据分割策略、3种数据补偿方式对模型性能与概率准确性造成的影响.
针对SHAP分析, SHAP通过解释模型的输出, 以模型对特定样本的预测结果作为基准进行评估. 然而, 上述使用到的深度生存模型输出内容并不都是特定协变量下的电梯风险. DeepSurv与CoxCC预测的是Cox比例风险模型中的相对风险函数, 本质上输出为相对风险值; DeepHit与Logistic模型则直接预测个体在不同时间点的生存概率, 为一个矩阵; RSF预测得到的是累积风险函数值. 对此, 对DeepHit与Logistic模型的产出做以下变换, 以进行模型间归因对比: 根据生存分析领域中生存函数与风险函数的转换, 对每个时间窗口内的生存概率进行求反加1, 得到该窗口内的风险概率, 最后对观察期内所有风险概率进行平均操作. 这样, 将Logistic模型与DeepHit模型的输出转为观察期内的平均风险值, 再作SHAP分析.
不同模型的输出对应的SHAP值存在数量级的差异, 因此, 先对模型的各特征SHAP值进行了标准化处理, 消除量纲的影响并统一到相同尺度范围内. 同时, 对于独热编码过的种类数据类型, 在进行SHAP分析前, 须经过相应的特征组合.
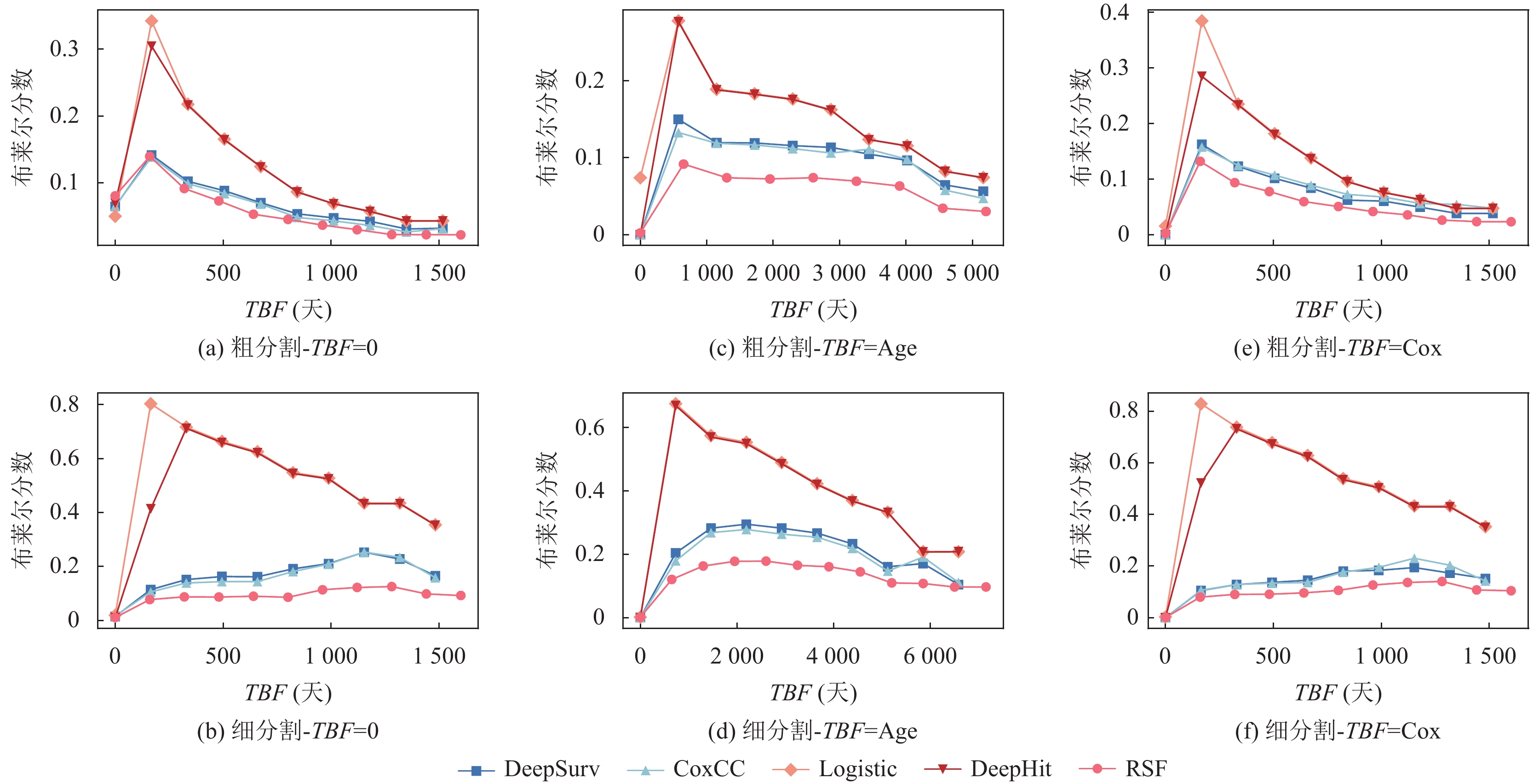
4.3 实验及分析 4.3.1 生存分析实验结果与分析表2、表3展示了DeepSurv的一致性指数与总体布莱尔分数的情况, 包括用于对比的基准模型CoxCC、Logistic、DeepHit、RSF、CoxPH. 图4展示了模型在观察期内不同时间点的布莱尔分数.
| 表 2 各模型在测试集上的一致性指数 |
| 表 3 各模型在测试集上的整体布莱尔分数 |
总体而言, 各模型在一致性指数指标上较高, 反映深度生存模型对个体生存时间的排序能力较强, 具有较强的时间预测能力. 在TBF=0的方式下, 深度生存模型表现都较传统的Cox比例风险模型更好. 在TBF=Age的补充方式下, 大部分深度生存模型的表现也较Cox比例风险模型更优. 这表明, 在处理电梯大型风险预测的问题上, 深度生存模型的预测能力要较传统的Cox比例风险模型更强, 这是由于深度生存模型打破了Cox模型的线性限制, 更能学习现实世界的复杂情况.
而从整体布莱尔分数角度看, 大部分模型的整体布莱尔分数小于0.25, 证明大部分模型的概率预测是可信的, 但在整体布莱尔分数指标下, 粗分割-TBF=0的CoxCC、CoxPH, 细分割下的Logistic、DeepHit表现不佳, 整体分数都超过0.25. 这表明, 这两种基于离散区间的对风险函数进行直接预测的方法并不适用于电梯场景.
从左删失补充方式角度来看, TBF=0的补充方式与TBF=Cox的补充方式在对个体生存时间排序能力上表现相当, TBF=0的补充方式在排序能力上更优. 与之相对应的是TBF=Age的方式表现较差. 同时, 图5(c)、图5(d)显示TBF=Age补充下, 各模型在布莱尔分数上表现都较高, 基本都超过0.25, 体现模型对于生存时间事件的概率预测与实际观察的概率之间存在较大的偏差. 这是由于TBF=Age填充方法会在时间维度上稀释事件发生, 使目标事件在时间维度上过于稀疏, 模型对事件的捕捉能力相较变弱导致的.
从数据分割角度来看, 细分割方式的一致性指数表现要较粗分割方式更好. 然而, 在按时间的布莱尔分数表达上, 细分割方式的布莱尔分数普遍较高. 这是由于细分割方式会导致数据集中右删失比例显著变高, 意味着模型在学习生存时间分布和相关因素时缺乏充分的信息, 从而影响模型的准确性.
综上所述, 对数据进行粗分割, 使用TBF=0, TBF=Cox的左删失填充方式, 得到的DeepSurv、CoxCC、RSF模型总体表现较好, 在具有强时间排序能力的同时具有较准确的概率预测能力. 细分割方式导致数据右删失比例过高, 会使模型布莱尔分数过高, 影响模型的概率预测能力; 同模型下TBF=0和TBF=Cox的预测能力相当, 但TBF=Age的左删失填充方式会严重损害模型概率预测能力.
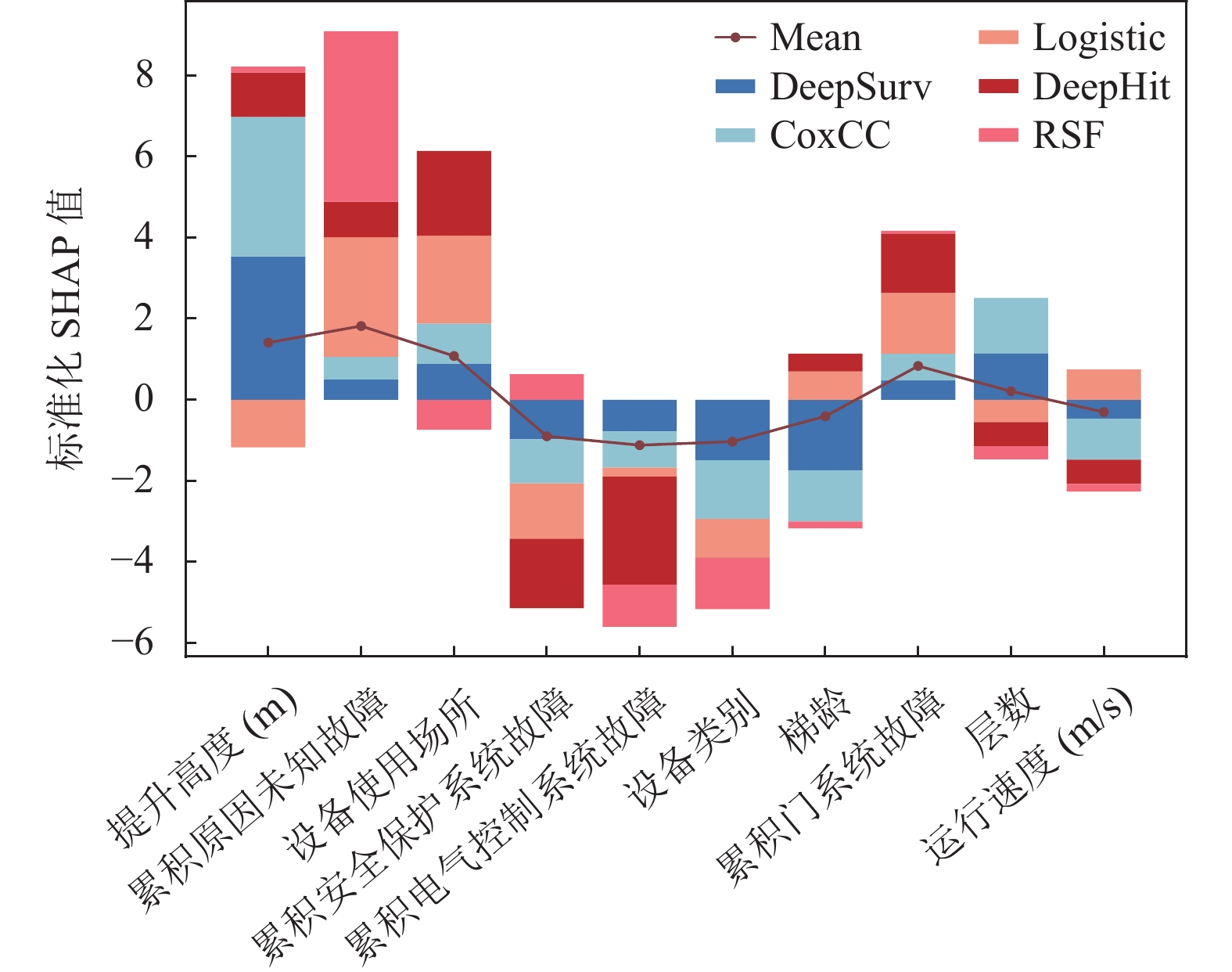
4.3.2 SHAP实验结果与分析图6为粗分割下左删失补充方式为TBF=Cox的模型特征概要总结图. 图6展示了在对数据进行粗分割的情况下, 使用左删失补充方式TBF=Cox时, 所有模型在平均 SHAP 值情况下的特征排序情况. 可以看到, 在该左删失补充情况下, 生存分析模型认为电梯提升高度、累积未知原因故障、电梯设备所在场所对电梯大型故障的发生具有最重要的影响. 其中, 各模型的平均SHAP值显示, 对于电梯提升高度、累积未知原因故障对电梯大型故障的发生都有正向贡献, 换言之, 高层电梯、电梯在一段时间内的累积未知原因故障次数越高, 两种因素都会使得电梯大型故障的风险增高. 这与文献[20]的观点一致, 且符合直觉认知: 累积未知原因故障次数的增多, 意味电梯运行存在未解决的安全隐患, 这些问题可能涉及电梯各个系统.
|
图 5 各模型在观察期内的布莱尔分数 |
|
图 6 粗分割下左删失补充方式为TBF=Cox的模型SHAP概要总结图 |
在10大影响因素中, 电梯设备所在场所、电梯类型为种类数据, 其SHAP值排行较前说明该种类数据对电梯大型故障发生具有一定正向影响. 与之相反的是累积安全保护系统故障、累积电力控制系统故障, 所有模型在平均SHAP值下认为这两项对模型的风险预测具有负向贡献, 即该两项故障量越高, 电梯大型故障风险反而越低. 这可能是由于电梯安全保护系统、电梯电力控制系统的故障涉及电梯更深入的部件, 如电梯安全装置、各传感器、电机等部件. 这些系统的故障维修往往需要更全面细致的检查, 并且在维修后会多次反复进行检查, 以确保电梯后续运行的安全性和可靠性. 这种全面性的维护工作有助于发现和修复潜在的故障隐患, 从而降低了电梯大型故障的风险.
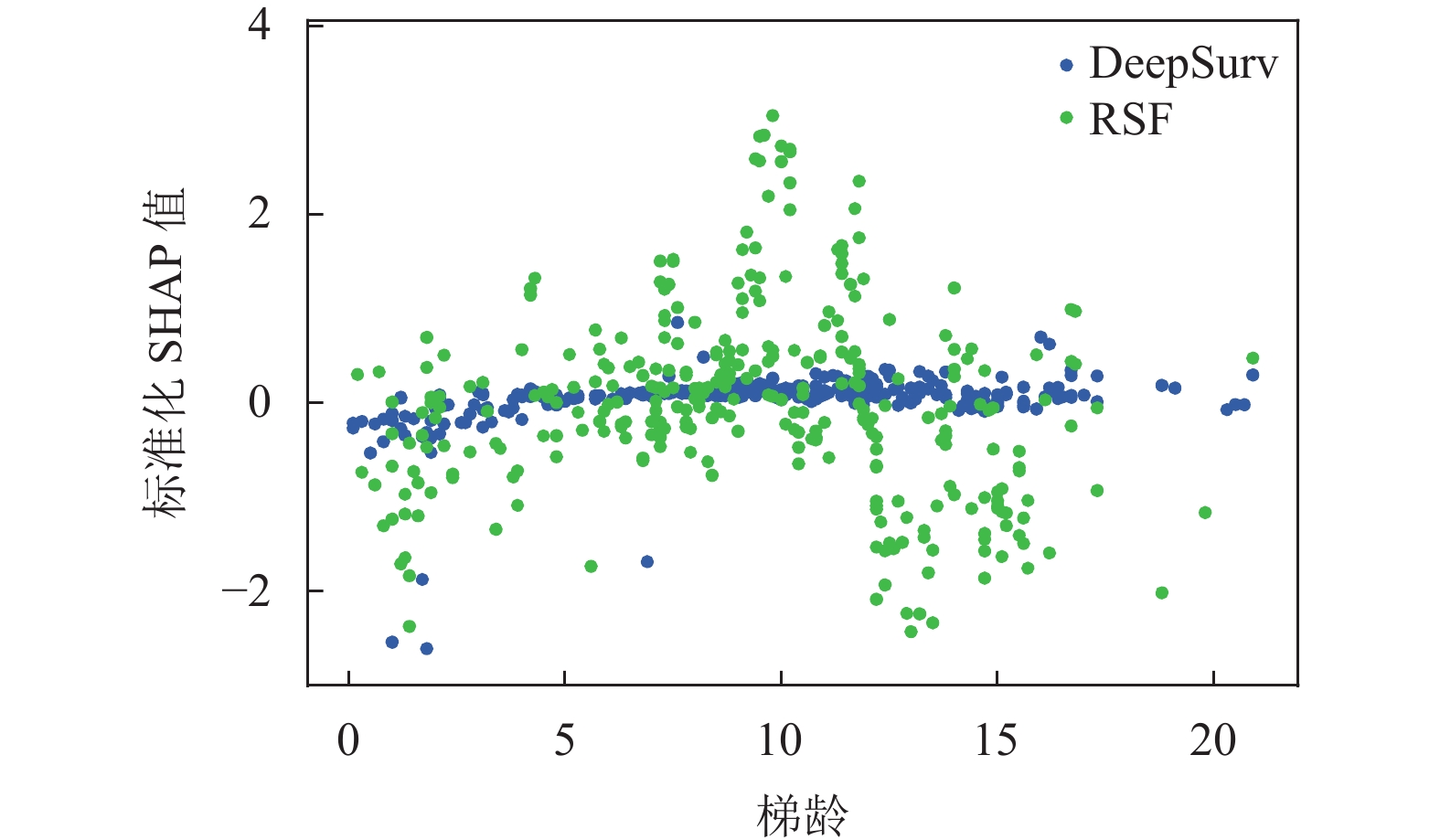
图7展示了在粗分割-Cox补充下, DeepSurv模型与随机生存森林(RSF)模型对梯龄的标准化SHAP值分布. 总体而言, 两个模型都认为随着电梯使用年份增加, 梯龄逐渐成为电梯大型故障风险的正向因素. 但从图中各点分布来看, DeepSurv在梯龄为0–2年的阶段, 梯龄SHAP值主要分布在0以上; 而在5–10年阶段, 梯龄SHAP值主要分布在0以下. 这表示在梯龄为0–2年阶段中, 梯龄是电梯大型故障的正向贡献因素之一, 换言之在该区间内的电梯可能有更大的大型故障风险; 而梯龄在5–10年阶段中, 梯龄更多作为电梯大型故障的负向贡献因素. 这在一定程度上符合文献[21]中提出的电梯故障呈现“浴盆曲线”规律, 即在电梯使用初期, 由于部件磨合和用户使用问题, 故障率较高; 经过磨合阶段后, 电梯运行逐渐平稳阶段, 故障率下降; 到达磨损阶段, 即经过常年使用后, 电梯的故障率再次上升. 但RSF模型认为, 电梯在梯龄为10年的阶段更易发生故障, 且电梯故障受梯龄影响呈现倒U型形态, 表明其认为梯龄在5–12年间的电梯, 使用时长是造成大型故障的正向影响因素之一.
|
图 7 DeepSurv与RSF对梯龄的标准化SHAP分布 |
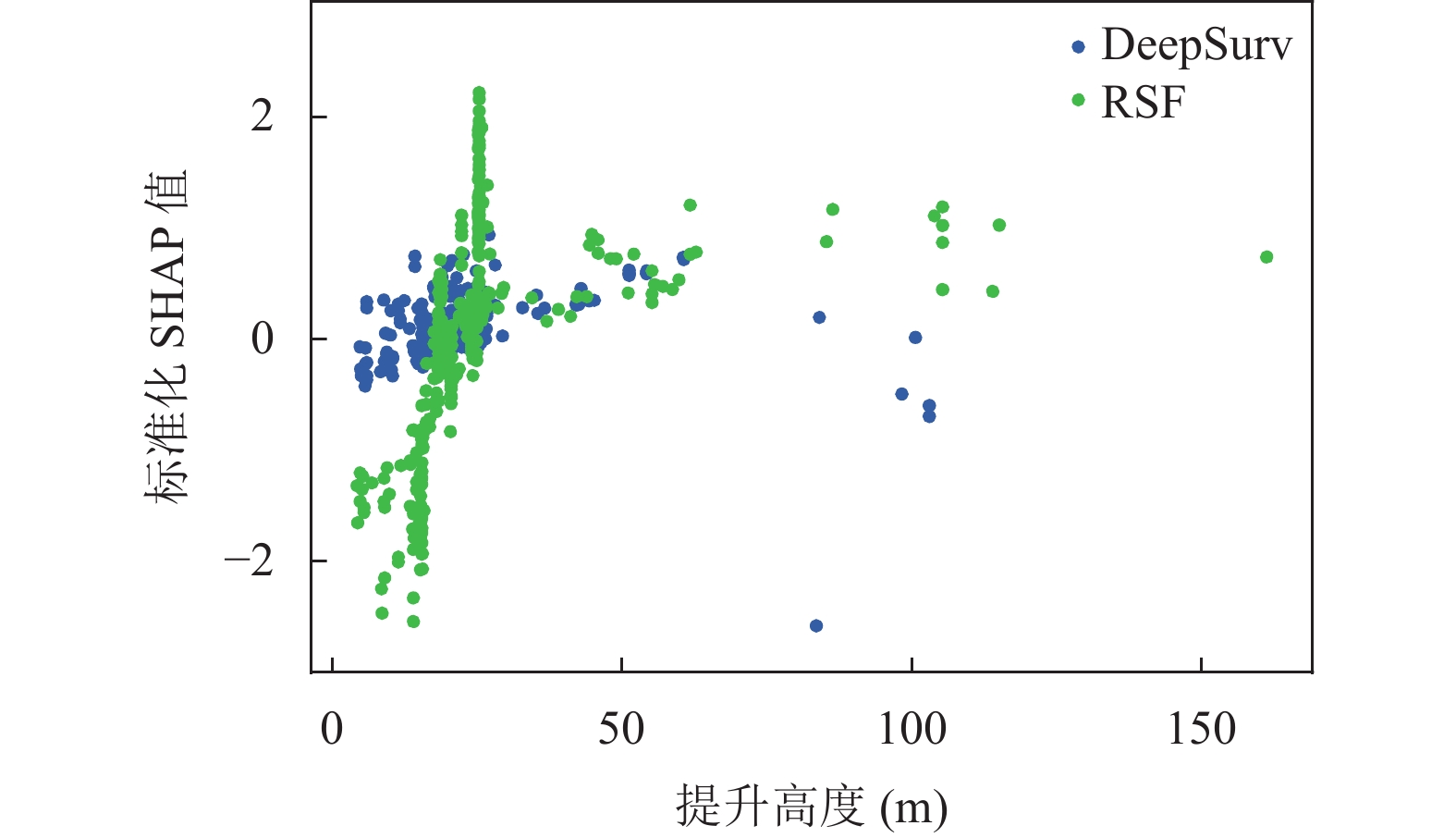
图8展示了两个模型在粗分割-Cox补充下电梯提升高度对电梯大型故障的发生的影响. 总体而言, 随着电梯提升高度增加, 各模型的SHAP值也呈线性增加趋势. RSF模型认为, 在分析不同提升高度范围内的电梯时, 提升高度对电梯大型事故发生风险的贡献表现出非线性关系. 具体而言, 对于提升高度在20 m以内的电梯, 这些模型认为提升高度对电梯大型事故发生的风险是一个负向贡献因素, 即较低的提升高度与较低的事故风险相关联. 然而, 对于提升高度超过20 m的电梯, RSF模型认为提升高度对电梯大型事故发生风险的贡献转变为正向, 即高度的提升会增加电梯大型故障发生的风险. 但DeepSurv观点相反, 认为提升高度对于低层电梯而言是一个负向因素, 但对于高层电梯而言是一个正向因素.
|
图 8 DeepSurv与RSF在提升高度特征上SHAP分布 |
5 结语
随着电梯按需维保工作的推进, 深入了解电梯在不同时间点的运行状况, 成为一种重要的实践, 有助于保障电梯运行的健康与稳定. 为此, 本文使用在医学领域活跃的深度生存分析方法, 对现实世界中的电梯进行健康状况的研究和评估, 并使用SHAP分析为相关管理决策提供科学依据. 本文提出了一种基于现实电梯工单数据的静态动态生存状态向量构建方法, 将电梯工单中的动态信息纳入到生存分析中, 并对两种不同的数据分割方式进行了一定讨论; 提出了一种数据左删失的补充方式, 对工单数据中存在的数据左删失问题进行了填充与讨论; 最后, 文章使用SHAP分析方法, 对各模型在最优分割补偿下的电梯大型故障成因进行了分析. 生存分析实验研究结果显示, 细分割的数据切割策略会使模型布莱尔分数偏高, 梯龄填充的左删失补充方法会因稀释事件而使模型概率预测能力大幅下降; 采取粗分割的Cox填充是数据处理的较优选择; 从模型角度来看, DeepSurv在预测能力和预测稳定性、准确性上较其他深度生存分析模型更优. 而从SHAP归因分析角度来看, 电梯提升高度、梯龄等因素对电梯运行风险造成的影响不是固定的, 而是随着特定条件的变化发生转折. 深入理解这些影响因素, 对于制定有效的电梯维护管理策略至关重要. 文章所提出的方法与策略, 在面对其他系统的基于统计的预测性维护问题有一定的泛用性.
| [1] |
Niu DP, Guo L, Bi XL, et al. Preventive maintenance period decision for elevator parts based on multi-objective optimization method. Journal of Building Engineering, 2021, 44: 102984. DOI:10.1016/j.jobe.2021.102984 |
| [2] |
Mishra KM, Huhtala KJ. Fault detection of elevator systems using multilayer perceptron neural network. Proceedings of the 24th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA). Zaragoza: IEEE, 2019. 904–909.
|
| [3] |
Yao W, Jagota V, Kumar R, et al. Study and application of an elevator failure monitoring system based on the Internet of Things technology. Scientific Programming, 2022, 2022: 2517077. |
| [4] |
Theissler A, Pérez-Velázquez J, Kettelgerdes M, et al. Predictive maintenance enabled by machine learning: Use cases and challenges in the automotive industry. Reliability Engineering & System Safety, 2021, 215: 107864. |
| [5] |
Moncada-Torres A, van Maaren MC, Hendriks MP, et al. Explainable machine learning can outperform Cox regression predictions and provide insights in breast cancer survival. Scientific Reports, 2021, 11(1): 6968. DOI:10.1038/s41598-021-86327-7 |
| [6] |
Cheng B, Potter M. Bayesian weapon system reliability modeling with Cox-Weibull neural network. Proceedings of the 2023 Annual Reliability and Maintainability Symposium (RAMS). Orlando: IEEE, 2023. 1–6.
|
| [7] |
Yu H, Yang W, Wu S, et al. Deep-learning-based survival prediction of patients with cutaneous malignant melanoma. Frontiers in Medicine, 2023, 10: 1165865. DOI:10.3389/fmed.2023.1165865 |
| [8] |
Wiegrebe S, Kopper P, Sonabend R, et al. Deep learning for survival analysis: A review. Artificial Intelligence Review, 2024, 57(3): 65. DOI:10.1007/s10462-023-10681-3 |
| [9] |
Civerchia F, Bocchino S, Salvadori C, et al. Industrial Internet of Things monitoring solution for advanced predictive maintenance applications. Journal of Industrial Information Integration, 2017, 7: 4-12. DOI:10.1016/j.jii.2017.02.003 |
| [10] |
Yang Z, Kanniainen J, Krogerus T, et al. Prognostic modeling of predictive maintenance with survival analysis for mobile work equipment. Scientific Reports, 2022, 12(1): 8529. DOI:10.1038/s41598-022-12572-z |
| [11] |
Xiao R, Zayed T, Meguid MA, et al. Improving failure modeling for gas transmission pipelines: A survival analysis and machine learning integrated approach. Reliability Engineering & System Safety, 2024, 241: 109672. |
| [12] |
Chen C, Liu Y, Sun XF, et al. Automobile maintenance prediction using deep learning with GIS data. Procedia CIRP, 2019, 81: 447-452. DOI:10.1016/j.procir.2019.03.077 |
| [13] |
Snider B, McBean EA. Improving urban water security through pipe-break prediction models: Machine learning or survival analysis. Journal of Environmental Engineering, 2020, 146(3): 04019129. DOI:10.1061/(ASCE)EE.1943-7870.0001657 |
| [14] |
王莲, 蒋炜. 基于Cox比例风险模型的电梯保养决策研究. 上海管理科学, 2017, 39(1): 94-96. DOI:10.3969/j.issn.1005-9679.2017.01.019 |
| [15] |
Katzman JL, Shaham U, Cloninger A, et al. DeepSurv: Personalized treatment recommender system using a Cox proportional hazards deep neural network. BMC Medical Research Methodology, 2018, 18(1): 24. DOI:10.1186/s12874-018-0482-1 |
| [16] |
Kvamme H, Borgan Ø, Scheel I. Time-to-event prediction with neural networks and Cox regression. Journal of Machine Learning Research, 2019, 20(129): 1-30. |
| [17] |
Lee C, Zame W, Yoon J, et al. DeepHit: A deep learning approach to survival analysis with competing risks. Proceedings of the 32nd AAAI Conference on Artificial Intelligence. New Orleans: AAAI, 2018. 2314–2321.
|
| [18] |
Ishwaran H, Kogalur UB, Blackstone EH, et al. Random survival forests. The Annals of Applied Statistics, 2008, 2(3): 841-860. |
| [19] |
Turkson AJ, Ayiah-Mensah F, Nimoh V. Handling censoring and censored data in survival analysis: A standalone systematic literature review. International Journal of Mathematics and Mathematical Sciences, 2021, 2021: 9307475. |
| [20] |
McGough SF, Incerti D, Lyalina S, et al. Penalized regression for left-truncated and right-censored survival data. Statistics in Medicine, 2021, 40(25): 5487-5500. DOI:10.1002/sim.9136 |
| [21] |
Zhang XQ, Zubair MU. Extending the useful life of elevators through appropriate maintenance strategies. Journal of Building Engineering, 2022, 51: 104347. DOI:10.1016/j.jobe.2022.104347 |
 2024, Vol. 33
2024, Vol. 33



